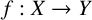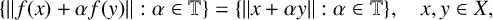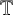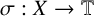1. Introduction
Let X and Y be normed spaces over
![]() $\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
, where
$\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
, where
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\mathbb {C}$
are the fields of real and complex numbers, respectively. Denote
$\mathbb {C}$
are the fields of real and complex numbers, respectively. Denote
![]() $\mathbb {T}=\{\alpha \in \mathbb {F}:|\alpha |=1\}$
. A function
$\mathbb {T}=\{\alpha \in \mathbb {F}:|\alpha |=1\}$
. A function
![]() $\sigma :X\rightarrow \mathbb {T}$
whose values are of modulus one is called a phase function on X. A mapping
$\sigma :X\rightarrow \mathbb {T}$
whose values are of modulus one is called a phase function on X. A mapping
![]() ${f: X \rightarrow Y}$
is said to be phase equivalent to another mapping
${f: X \rightarrow Y}$
is said to be phase equivalent to another mapping
![]() $g: X \rightarrow Y$
if there exists a phase function
$g: X \rightarrow Y$
if there exists a phase function
![]() $\sigma :X\rightarrow \mathbb {T}$
such that
$\sigma :X\rightarrow \mathbb {T}$
such that
![]() $f=\sigma \cdot g$
, that is,
$f=\sigma \cdot g$
, that is,
![]() $f(x)=\sigma (x)g(x)$
for
$f(x)=\sigma (x)g(x)$
for
![]() $x\in X$
.
$x\in X$
.
The celebrated Wigner’s unitary–anti-unitary theorem is particularly important in the mathematical foundations of quantum mechanics. It states that for inner product spaces
![]() $(X,\langle \cdot ,\cdot \rangle )$
and
$(X,\langle \cdot ,\cdot \rangle )$
and
![]() $(Y,\langle \cdot ,\cdot \rangle )$
over
$(Y,\langle \cdot ,\cdot \rangle )$
over
![]() $\mathbb {F}$
, a mapping
$\mathbb {F}$
, a mapping
![]() $f: X \rightarrow Y$
satisfies
$f: X \rightarrow Y$
satisfies
if and only if f is phase equivalent to a linear or anti-linear isometry in the case
![]() $\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
$\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
![]() $\mathbb {F}=\mathbb {R}$
. There are several proofs of this result, see [Reference Almeida and Sharma1, Reference Bargmann2, Reference Gehér4, Reference Győry6, Reference Maksa and Páles13, Reference Rätz18, Reference Turnšek22] to list just some of them. For further generalisations of this fundamental result, we mention the papers [Reference Chevalier3, Reference Gehér5, Reference Molnár15, Reference Qian, Wang, Wu and Yuan17]. Wigner’s theorem is very important and therefore worthy of study from various points of view.
$\mathbb {F}=\mathbb {R}$
. There are several proofs of this result, see [Reference Almeida and Sharma1, Reference Bargmann2, Reference Gehér4, Reference Győry6, Reference Maksa and Páles13, Reference Rätz18, Reference Turnšek22] to list just some of them. For further generalisations of this fundamental result, we mention the papers [Reference Chevalier3, Reference Gehér5, Reference Molnár15, Reference Qian, Wang, Wu and Yuan17]. Wigner’s theorem is very important and therefore worthy of study from various points of view.
A mapping
![]() $f: X \rightarrow Y$
between normed spaces over
$f: X \rightarrow Y$
between normed spaces over
![]() $\mathbb {F}$
is called a phase-isometry if it satisfies the functional equation
$\mathbb {F}$
is called a phase-isometry if it satisfies the functional equation
It is worth noting that if X and Y are inner product spaces, then
![]() $f: X \rightarrow Y$
satisfies (1.1) if and only if f satisfies (1.2). Indeed, with the substitution
$f: X \rightarrow Y$
satisfies (1.1) if and only if f satisfies (1.2). Indeed, with the substitution
![]() $y=x$
, we deduce from either (1.1) or (1.2) that f is norm-preserving. Squaring the norms on both sides of (1.2), it follows that (1.2) holds if and only if
$y=x$
, we deduce from either (1.1) or (1.2) that f is norm-preserving. Squaring the norms on both sides of (1.2), it follows that (1.2) holds if and only if
which happens if and only if (1.1) holds. Due to Wigner’s theorem, a mapping between inner product spaces is a phase-isometry if and only if it is phase equivalent to a linear or anti-linear isometry in the case
![]() $\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
$\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
![]() $\mathbb {F}=\mathbb {R}$
.
$\mathbb {F}=\mathbb {R}$
.
When X and Y are normed spaces, one can easily see that if
![]() $f:X \rightarrow Y$
is phase equivalent to a linear or anti-linear isometry, then f is a phase-isometry. For instance, if
$f:X \rightarrow Y$
is phase equivalent to a linear or anti-linear isometry, then f is a phase-isometry. For instance, if
![]() $f=\sigma \cdot U$
, where U is a linear isometry and
$f=\sigma \cdot U$
, where U is a linear isometry and
![]() $\sigma :X\rightarrow \mathbb {T}$
is a phase function, then for
$\sigma :X\rightarrow \mathbb {T}$
is a phase function, then for
![]() $x,y\in X$
and
$x,y\in X$
and
![]() $\alpha \in \mathbb {T}$
,
$\alpha \in \mathbb {T}$
,
 $$ \begin{align*} \|f(x)+\alpha f(y)\|&=\|\sigma(x)U(x)+\alpha\sigma(y)U(y)\|=\|U(\sigma(x)x+\alpha\sigma(y)y)\|\\ &=\|\sigma(x)x+\alpha\sigma(y)y\|=\|x+\alpha\overline{\sigma(x)}\sigma(y)y\| \end{align*} $$
$$ \begin{align*} \|f(x)+\alpha f(y)\|&=\|\sigma(x)U(x)+\alpha\sigma(y)U(y)\|=\|U(\sigma(x)x+\alpha\sigma(y)y)\|\\ &=\|\sigma(x)x+\alpha\sigma(y)y\|=\|x+\alpha\overline{\sigma(x)}\sigma(y)y\| \end{align*} $$
and then
Similar reasoning applies when U is an anti-linear isometry. Therefore, a natural problem posed by Maksa and Páles [Reference Maksa and Páles13] (the case
![]() $\mathbb {F}=\mathbb {R}$
), and Wang and Bugajewski [Reference Wang and Bugajewski23] (the case
$\mathbb {F}=\mathbb {R}$
), and Wang and Bugajewski [Reference Wang and Bugajewski23] (the case
![]() $\mathbb {F}=\mathbb {C}$
), can be restated as the following problem.
$\mathbb {F}=\mathbb {C}$
), can be restated as the following problem.
Problem 1.1. Under what conditions is every phase-isometry between two normed spaces over
![]() $\mathbb {F}$
phase equivalent to a linear or anti-linear isometry in the case
$\mathbb {F}$
phase equivalent to a linear or anti-linear isometry in the case
![]() $\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
$\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
![]() $\mathbb {F}=\mathbb {R}$
?
$\mathbb {F}=\mathbb {R}$
?
A normed space X over
![]() $\mathbb {F}$
is said to have the Wigner property if for any normed space Y over
$\mathbb {F}$
is said to have the Wigner property if for any normed space Y over
![]() $\mathbb {F}$
, every surjective phase-isometry
$\mathbb {F}$
, every surjective phase-isometry
![]() $f: X \rightarrow Y$
is phase equivalent to a linear or anti-linear isometry in the case
$f: X \rightarrow Y$
is phase equivalent to a linear or anti-linear isometry in the case
![]() $\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
$\mathbb {F}=\mathbb {C}$
and to a linear isometry in the case
![]() $\mathbb {F}=\mathbb {R}$
.
$\mathbb {F}=\mathbb {R}$
.
There have been several recent papers considering Problem 1.1 or the Wigner property in the case
![]() $\mathbb {F}=\mathbb {R}$
. For relevant results, please refer to [Reference Huang and Tan7–Reference Ilišević, Omladič and Turnšek9, Reference Ilišević and Turnšek11–Reference Maksa and Páles13, Reference Tan and Huang19–Reference Tan and Zhang21, Reference Wang and Bugajewski23]. In particular, Tan and Huang [Reference Tan and Huang19] proved that smooth real normed spaces have the Wigner property. Further, Ilišević et al. [Reference Ilišević, Omladič and Turnšek9] proved that any real normed spaces have the Wigner property. However, to the best of our knowledge, apart from the case where X and Y are inner product spaces, there has been no progress in addressing Problem 1.1 in the case
$\mathbb {F}=\mathbb {R}$
. For relevant results, please refer to [Reference Huang and Tan7–Reference Ilišević, Omladič and Turnšek9, Reference Ilišević and Turnšek11–Reference Maksa and Páles13, Reference Tan and Huang19–Reference Tan and Zhang21, Reference Wang and Bugajewski23]. In particular, Tan and Huang [Reference Tan and Huang19] proved that smooth real normed spaces have the Wigner property. Further, Ilišević et al. [Reference Ilišević, Omladič and Turnšek9] proved that any real normed spaces have the Wigner property. However, to the best of our knowledge, apart from the case where X and Y are inner product spaces, there has been no progress in addressing Problem 1.1 in the case
![]() $\mathbb {F}=\mathbb {C}$
. The aim of this paper is to give a partial solution for the case
$\mathbb {F}=\mathbb {C}$
. The aim of this paper is to give a partial solution for the case
![]() $\mathbb {F}=\mathbb {C}$
. Specifically, we show that every smooth complex normed space has the Wigner property. As a by-product, we give a Figiel-type result for phase-isometries. Although our paper is interesting in its own right, we hope that it will serve as a stepping stone to show that all complex normed spaces have the Wigner property.
$\mathbb {F}=\mathbb {C}$
. Specifically, we show that every smooth complex normed space has the Wigner property. As a by-product, we give a Figiel-type result for phase-isometries. Although our paper is interesting in its own right, we hope that it will serve as a stepping stone to show that all complex normed spaces have the Wigner property.
2. Results
In the remainder of this paper, unless otherwise specified, all the normed spaces are over
![]() $\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
. Although the real case has been solved, for the sake of brevity and universality, we will present our lemmas, theorems and proofs in the united form
$\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
. Although the real case has been solved, for the sake of brevity and universality, we will present our lemmas, theorems and proofs in the united form
![]() $\mathbb {F}$
rather than the single form
$\mathbb {F}$
rather than the single form
![]() $\mathbb {C}$
. For a normed space X, we use the notation
$\mathbb {C}$
. For a normed space X, we use the notation
![]() $S_X, B_X$
and
$S_X, B_X$
and
![]() $X^*$
to represent the unit sphere, closed unit ball and dual space of X, respectively. The set of positive integers is denoted by
$X^*$
to represent the unit sphere, closed unit ball and dual space of X, respectively. The set of positive integers is denoted by
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
We start this section with a simple and frequently-used property of phase-isometries between two normed spaces.
Lemma 2.1. Let X and Y be normed spaces and
![]() $f: X \rightarrow Y$
a phase-isometry. Then f is a norm-preserving map. Moreover, if f is surjective, then
$f: X \rightarrow Y$
a phase-isometry. Then f is a norm-preserving map. Moreover, if f is surjective, then
Proof. With the substitution
![]() $y=x$
, it follows from (1.2) that
$y=x$
, it follows from (1.2) that
which shows that f is norm-preserving.
Now suppose that f is surjective. Let us take a nonzero
![]() $x\in X$
and
$x\in X$
and
![]() $\alpha \in \mathbb {T}$
. The surjectivity guarantees that there exists some
$\alpha \in \mathbb {T}$
. The surjectivity guarantees that there exists some
![]() $y\in X$
such that
$y\in X$
such that
![]() $f(y)=\alpha f(x)$
. Then
$f(y)=\alpha f(x)$
. Then
which implies that
Moreover, we conclude from (1.2) that
which shows that
This competes the proof.
From [Reference Tan and Huang19, Lemma 2], it follows that every surjective phase-isometry between two real normed spaces is injective. The following example shows that a surjective phase-isometry between two complex normed spaces may not be injective.
Example 2.2. Let X be a complex normed space and
![]() $x_0\in X\backslash \{0\}$
. Define
$x_0\in X\backslash \{0\}$
. Define
![]() ${f:X\rightarrow X}$
by
${f:X\rightarrow X}$
by
![]() $f(\alpha x_0)=\alpha ^2x_0$
for all
$f(\alpha x_0)=\alpha ^2x_0$
for all
![]() $\alpha \in \mathbb {T}$
and
$\alpha \in \mathbb {T}$
and
![]() $f(x)=x$
otherwise. Then f is a surjective phase-isometry, but it is not injective since
$f(x)=x$
otherwise. Then f is a surjective phase-isometry, but it is not injective since
![]() $f(-x_0)=x_0=f(x_0)$
.
$f(-x_0)=x_0=f(x_0)$
.
In Example 2.2, f is phase equivalent to the identity mapping, letting the phase function
![]() $\sigma $
be
$\sigma $
be
![]() $\sigma (\alpha x_0)=\alpha $
for all
$\sigma (\alpha x_0)=\alpha $
for all
![]() $\alpha \in \mathbb {T}$
and
$\alpha \in \mathbb {T}$
and
![]() $\sigma (x)=1$
otherwise.
$\sigma (x)=1$
otherwise.
Recall that a support functional
![]() $\phi $
at
$\phi $
at
![]() $x\in X\backslash \{0\}$
is a norm-one linear functional in
$x\in X\backslash \{0\}$
is a norm-one linear functional in
![]() $X^*$
such that
$X^*$
such that
![]() $\phi (x)=\|x\|$
. Denote by
$\phi (x)=\|x\|$
. Denote by
![]() $D(x)$
the set of all support functionals at
$D(x)$
the set of all support functionals at
![]() $x\neq 0$
, that is,
$x\neq 0$
, that is,
The Hahn–Banach theorem implies that
![]() $D(x)\neq \emptyset $
for every
$D(x)\neq \emptyset $
for every
![]() $x\in X\backslash \{0\}$
. A normed space X is said to be smooth at
$x\in X\backslash \{0\}$
. A normed space X is said to be smooth at
![]() $x\neq 0$
if there exists a unique supporting functional at x, that is,
$x\neq 0$
if there exists a unique supporting functional at x, that is,
![]() $D(x)$
consists of only one element. If X is smooth at every
$D(x)$
consists of only one element. If X is smooth at every
![]() $x\neq 0$
, then X is said to be smooth. It follows from [Reference Megginson14, Proposition 5.4.20] that each subspace of a smooth normed space is smooth.
$x\neq 0$
, then X is said to be smooth. It follows from [Reference Megginson14, Proposition 5.4.20] that each subspace of a smooth normed space is smooth.
Recall also the concept of Gateaux differentiability. Let X be a normed space,
![]() ${x, y\in X}$
. Define
${x, y\in X}$
. Define
and
It is known [Reference Megginson14, Reference Phelps16] that both
![]() $G_+(x,y)$
and
$G_+(x,y)$
and
![]() $G_-(x,y)$
exist for each
$G_-(x,y)$
exist for each
![]() $x,y\in X$
and
$x,y\in X$
and
We say that the norm of X is Gateaux differentiable at
![]() $x\neq 0$
whenever
$x\neq 0$
whenever
![]() $G_+(x,y)=G_-(x,y)$
for all
$G_+(x,y)=G_-(x,y)$
for all
![]() $y\in X$
, in which case the common value of
$y\in X$
, in which case the common value of
![]() $G_+(x,y)$
and
$G_+(x,y)$
and
![]() $G_-(x,y)$
is denoted by
$G_-(x,y)$
is denoted by
![]() $G(x,y)$
. It is easy to see that a normed space X is smooth at x if and only if the norm is Gateaux differentiable at x.
$G(x,y)$
. It is easy to see that a normed space X is smooth at x if and only if the norm is Gateaux differentiable at x.
A point
![]() $\phi \in S_{X^*}$
is said to be a
$\phi \in S_{X^*}$
is said to be a
![]() $w^*$
-exposed point of
$w^*$
-exposed point of
![]() $B_{X^*}$
provided that
$B_{X^*}$
provided that
![]() $\phi $
is the only supporting functional for some smooth point
$\phi $
is the only supporting functional for some smooth point
![]() $u\in S_X$
. Recently, Tan and Huang [Reference Tan and Huang19] showed that for every phase-isometry f of a real normed space X into another real normed space Y and every
$u\in S_X$
. Recently, Tan and Huang [Reference Tan and Huang19] showed that for every phase-isometry f of a real normed space X into another real normed space Y and every
![]() $w^*$
-exposed point
$w^*$
-exposed point
![]() $\phi $
of
$\phi $
of
![]() $B_{X^*}$
, there exists
$B_{X^*}$
, there exists
![]() $\varphi \in S_{Y^*}$
such that
$\varphi \in S_{Y^*}$
such that
![]() $\phi (x)=\pm \varphi (f(x))$
for all
$\phi (x)=\pm \varphi (f(x))$
for all
![]() $x\in X$
. This result can be viewed as an extension of Figiel’s theorem, which plays an important role in the study of isometric embedding. We will present a similar result for a phase-isometry between two normed spaces over
$x\in X$
. This result can be viewed as an extension of Figiel’s theorem, which plays an important role in the study of isometric embedding. We will present a similar result for a phase-isometry between two normed spaces over
![]() ${\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}}$
.
${\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}}$
.
Lemma 2.3. Let X and Y be normed spaces and
![]() $f:X\rightarrow Y$
a phase-isometry. Then for every
$f:X\rightarrow Y$
a phase-isometry. Then for every
![]() $w^*$
-exposed point
$w^*$
-exposed point
![]() $\phi $
of
$\phi $
of
![]() $B_{X^*}$
, there exists
$B_{X^*}$
, there exists
![]() $\varphi \in S_{Y^*}$
such that
$\varphi \in S_{Y^*}$
such that
Proof. Let
![]() $u\in S_X$
be a smooth point such that
$u\in S_X$
be a smooth point such that
![]() $\phi (u)=1$
. For every
$\phi (u)=1$
. For every
![]() $n\in \mathbb {N}$
, the Hahn–Banach theorem guarantees the existence of
$n\in \mathbb {N}$
, the Hahn–Banach theorem guarantees the existence of
![]() $\varphi _n\in S_{Y^*}$
such that
$\varphi _n\in S_{Y^*}$
such that
For
![]() $t\in [0,n]$
, there exists some
$t\in [0,n]$
, there exists some
![]() $\alpha _{t,n}\in \mathbb {T}$
such that
$\alpha _{t,n}\in \mathbb {T}$
such that
Consequently, we deduce that
 $$ \begin{align*} 2n&=|\varphi_n (f(nu)-\alpha_{t,n}f(tu))+\varphi_n(f(nu)+\alpha_{t,n}f(tu))|\\ &\leq|\varphi_n (f(nu)-\alpha_{t,n}f(tu))|+|\varphi_n(f(nu)+\alpha_{t,n}f(tu))|\\ &\leq\|f(nu)-\alpha_{t,n}f(tu)\|+\|f(nu)+\alpha_{t,n}f(tu)\|\\&\leq (n-t)+(n+t)=2n, \end{align*} $$
$$ \begin{align*} 2n&=|\varphi_n (f(nu)-\alpha_{t,n}f(tu))+\varphi_n(f(nu)+\alpha_{t,n}f(tu))|\\ &\leq|\varphi_n (f(nu)-\alpha_{t,n}f(tu))|+|\varphi_n(f(nu)+\alpha_{t,n}f(tu))|\\ &\leq\|f(nu)-\alpha_{t,n}f(tu)\|+\|f(nu)+\alpha_{t,n}f(tu)\|\\&\leq (n-t)+(n+t)=2n, \end{align*} $$
which implies that
![]() $\varphi _n(\alpha _{t,n}f(tu))=t$
. This means that for each
$\varphi _n(\alpha _{t,n}f(tu))=t$
. This means that for each
![]() $t\in (0, n]$
, there exists a unique
$t\in (0, n]$
, there exists a unique
![]() $\alpha _{t,n}\in \mathbb {T}$
such that
$\alpha _{t,n}\in \mathbb {T}$
such that
![]() $\varphi _n(f(tu))=\overline {\alpha _{t,n}}t$
. By Alaoglu’s theorem, the sequence
$\varphi _n(f(tu))=\overline {\alpha _{t,n}}t$
. By Alaoglu’s theorem, the sequence
![]() $\{\varphi _n\}$
has a cluster point
$\{\varphi _n\}$
has a cluster point
![]() $\varphi \in S_{Y^*}$
in the
$\varphi \in S_{Y^*}$
in the
![]() $w^*$
topology. It follows that for each
$w^*$
topology. It follows that for each
![]() $t>0$
, there exists
$t>0$
, there exists
![]() $\alpha _t\in \mathbb {T}$
depending only on t such that
$\alpha _t\in \mathbb {T}$
depending only on t such that
![]() $\varphi (f(tu))=\alpha _t t$
.
$\varphi (f(tu))=\alpha _t t$
.
For each
![]() $x\in X$
, there exist
$x\in X$
, there exist
![]() $\alpha _x, \beta _x\in \mathbb {T}$
such that
$\alpha _x, \beta _x\in \mathbb {T}$
such that
![]() $\alpha _x\phi (x)=|\phi (x)|$
and
$\alpha _x\phi (x)=|\phi (x)|$
and
![]() $\beta _x\varphi (f(x))=|\varphi (f(x))|$
. For each
$\beta _x\varphi (f(x))=|\varphi (f(x))|$
. For each
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $\alpha _{x,n}, \beta _{x,n}\in \mathbb {T}$
such that
$\alpha _{x,n}, \beta _{x,n}\in \mathbb {T}$
such that
 $$ \begin{align*} \|nu-\alpha_xx\|=\|f(nu)-\alpha_{x,n}\alpha_nf(x)\| & \geq |\varphi(f(nu))-\alpha_{x,n}\alpha_n\varphi(f(x))|\\ &=|\alpha_n n-\alpha_{x,n}\alpha_n\varphi(f(x))|=|n-\alpha_{x,n}\varphi(f(x))| \end{align*} $$
$$ \begin{align*} \|nu-\alpha_xx\|=\|f(nu)-\alpha_{x,n}\alpha_nf(x)\| & \geq |\varphi(f(nu))-\alpha_{x,n}\alpha_n\varphi(f(x))|\\ &=|\alpha_n n-\alpha_{x,n}\alpha_n\varphi(f(x))|=|n-\alpha_{x,n}\varphi(f(x))| \end{align*} $$
and
 $$ \begin{align*} |n+\beta_x\varphi(f(x))|=|\alpha_n n+\alpha_n\beta_x\varphi(f(x))| & =|\varphi(f(nu))+\alpha_n\beta_x \varphi(f(x))|\\ &\leq \|f(nu)+\alpha_n\beta_xf(x)\|=\| nu+\beta_{x,n}x\|. \end{align*} $$
$$ \begin{align*} |n+\beta_x\varphi(f(x))|=|\alpha_n n+\alpha_n\beta_x\varphi(f(x))| & =|\varphi(f(nu))+\alpha_n\beta_x \varphi(f(x))|\\ &\leq \|f(nu)+\alpha_n\beta_xf(x)\|=\| nu+\beta_{x,n}x\|. \end{align*} $$
Given that
![]() $\mathbb {T}$
is compact, there must be a strictly increasing sequence
$\mathbb {T}$
is compact, there must be a strictly increasing sequence
![]() $\{n_j:j\in \mathbb {N}\}$
in
$\{n_j:j\in \mathbb {N}\}$
in
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\alpha ^{\prime }_x,\beta ^{\prime }_x\in \mathbb {T}$
such that
$\alpha ^{\prime }_x,\beta ^{\prime }_x\in \mathbb {T}$
such that
![]() $\lim _{j\to \infty }\alpha _{x,n_j}=\alpha ^{\prime }_x$
and
$\lim _{j\to \infty }\alpha _{x,n_j}=\alpha ^{\prime }_x$
and
![]() $\lim _{j\to \infty }\beta _{x,n_j}=\beta ^{\prime }_x$
. Since
$\lim _{j\to \infty }\beta _{x,n_j}=\beta ^{\prime }_x$
. Since
![]() $\phi $
is the only supporting functional at u,
$\phi $
is the only supporting functional at u,
 $$ \begin{align*} |\phi(x)|&=\mbox{Re}\,\phi(\alpha_xx)=\lim_{j\to\infty}(\|n_ju\|-\|n_ju-\alpha_xx\|)\\ &\leq\lim_{j\to\infty}(n_j-| n_j-\alpha_{x,n_j}\varphi(f(x))|)=\lim_{j\to\infty}(n_j-| n_j-\alpha^{\prime}_x\varphi(f(x))|)\\ &=\mbox{Re}\,(\alpha^{\prime}_x\varphi(f(x)))\leq|\varphi(f(x))| \end{align*} $$
$$ \begin{align*} |\phi(x)|&=\mbox{Re}\,\phi(\alpha_xx)=\lim_{j\to\infty}(\|n_ju\|-\|n_ju-\alpha_xx\|)\\ &\leq\lim_{j\to\infty}(n_j-| n_j-\alpha_{x,n_j}\varphi(f(x))|)=\lim_{j\to\infty}(n_j-| n_j-\alpha^{\prime}_x\varphi(f(x))|)\\ &=\mbox{Re}\,(\alpha^{\prime}_x\varphi(f(x)))\leq|\varphi(f(x))| \end{align*} $$
and
 $$ \begin{align*} |\varphi(f(x))|&=\mbox{Re}\,(\beta_x\varphi(f(x)))=\lim_{j\to\infty}(|n_j+\beta_x\varphi(f(x))|-n_j)\\ &\leq\lim_{j\to\infty} (\| n_ju+\beta_{x,n_j}x\|-\|n_ju\|)=\lim_{j\to\infty} (\|n_ju+\beta^{\prime}_xx\|-\|n_ju\|)\\ &=\mbox{Re}\,\phi(\beta^{\prime}_xx)\leq|\phi(x)|. \end{align*} $$
$$ \begin{align*} |\varphi(f(x))|&=\mbox{Re}\,(\beta_x\varphi(f(x)))=\lim_{j\to\infty}(|n_j+\beta_x\varphi(f(x))|-n_j)\\ &\leq\lim_{j\to\infty} (\| n_ju+\beta_{x,n_j}x\|-\|n_ju\|)=\lim_{j\to\infty} (\|n_ju+\beta^{\prime}_xx\|-\|n_ju\|)\\ &=\mbox{Re}\,\phi(\beta^{\prime}_xx)\leq|\phi(x)|. \end{align*} $$
This completes the proof.
Let V be a vector space. For
![]() $M\subset V$
,
$M\subset V$
,
![]() $[M]$
denotes the subspace generated by M. If
$[M]$
denotes the subspace generated by M. If
![]() $x,y\in V$
, then we write
$x,y\in V$
, then we write
![]() $[x]:=[\{x\}]$
and
$[x]:=[\{x\}]$
and
![]() $[x,y]:=[\{x,y\}]$
for simplicity.
$[x,y]:=[\{x,y\}]$
for simplicity.
Lemma 2.4. Let X and Y be normed spaces with X being smooth. Suppose that
![]() ${f: X \rightarrow Y}$
is a surjective phase-isometry. Then for every
${f: X \rightarrow Y}$
is a surjective phase-isometry. Then for every
![]() $x\in X$
,
$x\in X$
,
Proof. We first prove that
![]() $[f(x)]\subset f([x])$
for each
$[f(x)]\subset f([x])$
for each
![]() $x\in X$
. Assume, for a contradiction, that
$x\in X$
. Assume, for a contradiction, that
![]() $tf(x)\notin f([x])$
for some nonzero
$tf(x)\notin f([x])$
for some nonzero
![]() $x\in X$
and
$x\in X$
and
![]() $t\in \mathbb {F}$
. Since f is surjective, there exists
$t\in \mathbb {F}$
. Since f is surjective, there exists
![]() $y\in X$
such that
$y\in X$
such that
![]() $f(y)=tf(x)$
. The function
$f(y)=tf(x)$
. The function
![]() $s\mapsto \|y-sx\|$
is continuous and its value tends to infinity when
$s\mapsto \|y-sx\|$
is continuous and its value tends to infinity when
![]() $|s|$
tends to infinity. Hence, there is at least one point
$|s|$
tends to infinity. Hence, there is at least one point
![]() $s_0\in \mathbb {F}$
such that
$s_0\in \mathbb {F}$
such that
Set
![]() $E:=[x,y]$
. By the Hahn–Banach theorem, there exists
$E:=[x,y]$
. By the Hahn–Banach theorem, there exists
![]() $\phi \in S_{E^*}$
which satisfies
$\phi \in S_{E^*}$
which satisfies
![]() $\phi (y)=d$
and
$\phi (y)=d$
and
![]() $\phi (x)=0$
. Note that E being a two-dimensional subspace of X is reflexive. This guarantees the existence of some
$\phi (x)=0$
. Note that E being a two-dimensional subspace of X is reflexive. This guarantees the existence of some
![]() $z\in S_E$
such that
$z\in S_E$
such that
![]() $\phi (z)=1$
. Since X is smooth, so is its subspace E. Therefore,
$\phi (z)=1$
. Since X is smooth, so is its subspace E. Therefore,
![]() $\phi $
is the only supporting functional at
$\phi $
is the only supporting functional at
![]() $z\in S_E$
. We apply Lemma 2.3 to
$z\in S_E$
. We apply Lemma 2.3 to
![]() $f|_E: E\rightarrow Y$
to obtain
$f|_E: E\rightarrow Y$
to obtain
![]() $\varphi \in S_{Y^*}$
such that
$\varphi \in S_{Y^*}$
such that
![]() $|\phi |=|\varphi \circ f|$
on E. Then
$|\phi |=|\varphi \circ f|$
on E. Then
which is a contradiction. This proves
![]() $[f(x)]\subset f([x])$
.
$[f(x)]\subset f([x])$
.
Conversely, fix a nonzero
![]() $x\in X$
. For each
$x\in X$
. For each
![]() $r\in (0,+\infty )$
, by the above inclusion and the norm preserving property of f, there exists some
$r\in (0,+\infty )$
, by the above inclusion and the norm preserving property of f, there exists some
![]() $\alpha _r\in \mathbb {T}$
such that
$\alpha _r\in \mathbb {T}$
such that
![]() $r^{-1}f(rx)=f(\alpha _r x)$
. For each
$r^{-1}f(rx)=f(\alpha _r x)$
. For each
![]() $\alpha \in \mathbb {T}$
, by Lemma 2.1, there exist
$\alpha \in \mathbb {T}$
, by Lemma 2.1, there exist
![]() $\beta _{r,\alpha },\alpha ^{\prime }_r\in \mathbb {T}$
such that
$\beta _{r,\alpha },\alpha ^{\prime }_r\in \mathbb {T}$
such that
which implies that
![]() $f([x])\subset [f(x)]$
. The proof is complete.
$f([x])\subset [f(x)]$
. The proof is complete.
Note that the conclusion of Lemma 2.4 is equivalent to
Lemma 2.5. Let X and Y be normed spaces with X being smooth. Suppose that
![]() ${f: X \rightarrow Y}$
is a surjective phase-isometry. Then for every
${f: X \rightarrow Y}$
is a surjective phase-isometry. Then for every
![]() $x,y\in X$
,
$x,y\in X$
,
Proof. We only prove the first equality, the second being similar. Let
![]() $x, y\in X$
be nonzero and
$x, y\in X$
be nonzero and
![]() $\alpha \in \mathbb {T}$
. For each
$\alpha \in \mathbb {T}$
. For each
![]() $n\in \mathbb {N}$
, Lemma 2.4 and (1.2) imply that there exist
$n\in \mathbb {N}$
, Lemma 2.4 and (1.2) imply that there exist
![]() $\alpha _n,\beta _n,\gamma _n\in \mathbb {T}$
such that
$\alpha _n,\beta _n,\gamma _n\in \mathbb {T}$
such that
![]() $f(nx)=\alpha _nnf(x)$
and
$f(nx)=\alpha _nnf(x)$
and
By the compactness of
![]() $\mathbb {T}$
, there is a strictly increasing sequence
$\mathbb {T}$
, there is a strictly increasing sequence
![]() $\{n_j:j\in \mathbb {N}\}$
in
$\{n_j:j\in \mathbb {N}\}$
in
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\beta ,\gamma \in \mathbb {T}$
such that
$\beta ,\gamma \in \mathbb {T}$
such that
![]() $\lim _{j\to \infty }\beta _{n_j}=\beta $
and
$\lim _{j\to \infty }\beta _{n_j}=\beta $
and
![]() $\lim _{j\to \infty }\gamma _{n_j}=\gamma $
. Then
$\lim _{j\to \infty }\gamma _{n_j}=\gamma $
. Then
 $$ \begin{align*} G_+(f(x),\alpha f(y)) & =\lim_{j\to\infty}(\|n_jf(x)+\alpha f(y)\|-\|n_jf(x)\|)\\ & = \lim_{j\to\infty}(\|f(n_jx)+\alpha_{n_j}\alpha f(y)\|-\|n_jf(x)\|) \\ &= \lim_{j\to\infty}(\|n_jx+\beta_{n_j}y\|-\|n_jx\|) = \lim_{j\to\infty}(\|n_jx+\beta y\|-\|n_jx\|)=G(x,\beta y) \end{align*} $$
$$ \begin{align*} G_+(f(x),\alpha f(y)) & =\lim_{j\to\infty}(\|n_jf(x)+\alpha f(y)\|-\|n_jf(x)\|)\\ & = \lim_{j\to\infty}(\|f(n_jx)+\alpha_{n_j}\alpha f(y)\|-\|n_jf(x)\|) \\ &= \lim_{j\to\infty}(\|n_jx+\beta_{n_j}y\|-\|n_jx\|) = \lim_{j\to\infty}(\|n_jx+\beta y\|-\|n_jx\|)=G(x,\beta y) \end{align*} $$
and
 $$ \begin{align*} G(x,\alpha y)&=\lim_{j\to\infty}(\|n_jx+\alpha y\|-\|n_jx\|)\\ &=\lim_{j\to\infty}(\|f(n_jx)+\alpha_{n_j}\gamma_{n_j}f(y)\|-\|f(n_jx)\|)\\ &=\lim_{j\to\infty}(\|n_jf(x)+\gamma_{n_j}f(y)\|-\|n_jf(x)\|)\\ &=\lim_{j\to\infty}(\|n_jf(x)+\gamma f(y)\|-\|n_jf(x)\|)=G_+(f(x),\gamma f(y)). \end{align*} $$
$$ \begin{align*} G(x,\alpha y)&=\lim_{j\to\infty}(\|n_jx+\alpha y\|-\|n_jx\|)\\ &=\lim_{j\to\infty}(\|f(n_jx)+\alpha_{n_j}\gamma_{n_j}f(y)\|-\|f(n_jx)\|)\\ &=\lim_{j\to\infty}(\|n_jf(x)+\gamma_{n_j}f(y)\|-\|n_jf(x)\|)\\ &=\lim_{j\to\infty}(\|n_jf(x)+\gamma f(y)\|-\|n_jf(x)\|)=G_+(f(x),\gamma f(y)). \end{align*} $$
The proof is complete.
Lemma 2.6. Let X and Y be normed spaces with X being smooth. Suppose that
![]() ${f: X \rightarrow Y}$
is a surjective phase-isometry. Then Y is smooth.
${f: X \rightarrow Y}$
is a surjective phase-isometry. Then Y is smooth.
Proof. Let
![]() $x\in X$
be a nonzero element with the unique supporting functional
$x\in X$
be a nonzero element with the unique supporting functional
![]() ${\phi _x\in D(x)}$
. It suffices to prove that
${\phi _x\in D(x)}$
. It suffices to prove that
![]() $D(f(x))$
is a singleton set. Let
$D(f(x))$
is a singleton set. Let
![]() $\varphi ,\psi \in D(f(x))$
and
$\varphi ,\psi \in D(f(x))$
and
![]() $f(y)\in \ker \varphi $
. For each
$f(y)\in \ker \varphi $
. For each
![]() $\alpha \in \mathbb T$
, Lemma 2.5 implies that there exists
$\alpha \in \mathbb T$
, Lemma 2.5 implies that there exists
![]() $\beta ,\gamma \in \mathbb T$
such that
$\beta ,\gamma \in \mathbb T$
such that
and
Using the arbitrariness of
![]() $\alpha \in \mathbb T$
twice gives
$\alpha \in \mathbb T$
twice gives
![]() $\phi _{x}(y)=0$
by the first inequality and therefore
$\phi _{x}(y)=0$
by the first inequality and therefore
![]() $\psi (f(y))=0$
by the second inequality. This shows that
$\psi (f(y))=0$
by the second inequality. This shows that
![]() $\ker \varphi \subset \ker \psi $
. Thus,
$\ker \varphi \subset \ker \psi $
. Thus,
![]() $\psi =\lambda \varphi $
for some
$\psi =\lambda \varphi $
for some
![]() $\lambda \in \mathbb F$
. Considering that
$\lambda \in \mathbb F$
. Considering that
![]() $\psi ,\varphi \in D(f(x))$
, we find that
$\psi ,\varphi \in D(f(x))$
, we find that
![]() $\lambda =1$
. This implies that
$\lambda =1$
. This implies that
![]() $\psi =\varphi $
, which completes the proof.
$\psi =\varphi $
, which completes the proof.
Recently, Ilišević and Turnšek [Reference Ilišević and Turnšek10, Theorem 2.2 and Remark 2.1] generalised Wigner’s theorem to smooth normed spaces via semi-inner products. This can be translated into the following theorem in the language of supporting functionals.
Theorem 2.7. Let X and Y be smooth normed spaces over
![]() $\mathbb {F}$
and
$\mathbb {F}$
and
![]() $f:X\rightarrow Y$
a surjective mapping satisfying, for all nonzero
$f:X\rightarrow Y$
a surjective mapping satisfying, for all nonzero
![]() $x, y\in X$
,
$x, y\in X$
,
Then f is phase equivalent to a linear or anti-linear surjective isometry in the case
![]() $\mathbb {F}=\mathbb {C}$
and to a linear surjective isometry in the case
$\mathbb {F}=\mathbb {C}$
and to a linear surjective isometry in the case
![]() $\mathbb {F}=\mathbb {R}$
.
$\mathbb {F}=\mathbb {R}$
.
Combining the above results gives our main theorem.
Theorem 2.8. Every smooth normed space has the Wigner property.
Proof. Let X and Y be normed spaces with X being smooth. Suppose that
![]() $f: X \rightarrow Y$
is a surjective phase-isometry. By Lemma 2.6, Y is smooth. Then Lemma 2.5 implies that for all nonzero
$f: X \rightarrow Y$
is a surjective phase-isometry. By Lemma 2.6, Y is smooth. Then Lemma 2.5 implies that for all nonzero
![]() $x, y\in X$
,
$x, y\in X$
,
Taking the maximum on both sides, for all nonzero
![]() $x, y\in X$
,
$x, y\in X$
,
By Theorem 2.7, f is phase equivalent to a linear or anti-linear surjective isometry in the case
![]() $\mathbb {F}=\mathbb {C}$
and to a linear surjective isometry in the case
$\mathbb {F}=\mathbb {C}$
and to a linear surjective isometry in the case
![]() $\mathbb {F}=\mathbb {R}$
. This completes the proof.
$\mathbb {F}=\mathbb {R}$
. This completes the proof.
It is well known that
![]() $L^p(\mu )$
is a smooth normed space, where
$L^p(\mu )$
is a smooth normed space, where
![]() $\mu $
is a measure and
$\mu $
is a measure and
![]() $1<p<\infty $
. The following corollary is immediate.
$1<p<\infty $
. The following corollary is immediate.
Corollary 2.9.
![]() $L^{p}(\mu )$
has the Wigner property, where
$L^{p}(\mu )$
has the Wigner property, where
![]() $\mu $
is a measure and
$\mu $
is a measure and
![]() ${1<p<\infty }$
.
${1<p<\infty }$
.