Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vesel, Aleksander
and
Žerovnik, Janez
2000.
On the linearK-arboricity of cubic graphs.
International Journal of Computer Mathematics,
Vol. 75,
Issue. 4,
p.
431.
Plummer, Michael D.
2007.
Graph factors and factorization: 1985–2003: A survey.
Discrete Mathematics,
Vol. 307,
Issue. 7-8,
p.
791.




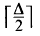 Linear Forests
Linear Forests linear forests. We show that almost every graph can be covered with this number of linear forests.
linear forests. We show that almost every graph can be covered with this number of linear forests.