Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-31T21:47:53.260Z Has data issue: false hasContentIssue false
  • English
  • Français

Intersecting families without unique shadow

Part of: Extremal combinatorics

Published online by Cambridge University Press:  02 October 2023

Peter Frankl  and
Jian Wang
Peter Frankl
Affiliation:
Rényi Institute, Budapest, Hungary
Jian Wang*
Affiliation:
Department of Mathematics, Taiyuan University of Technology, Taiyuan, P. R. China
*
Corresponding author: Jian Wang; Email: wangjian01@tyut.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 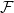$\mathcal{F}$ be an intersecting family. A 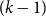$(k-1)$-set 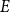$E$ is called a unique shadow if it is contained in exactly one member of 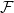$\mathcal{F}$. Let 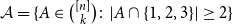${\mathcal{A}}=\{A\in \binom{[n]}{k}\colon |A\cap \{1,2,3\}|\geq 2\}$. In the present paper, we show that for 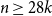$n\geq 28k$, 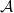$\mathcal{A}$ is the unique family attaining the maximum size among all intersecting families without unique shadow. Several other results of a similar flavour are established as well.

Keywords

Finite setsintersectionshadow

MSC classification

Primary: 05D05: Extremal set theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 1 , January 2024 , pp. 91 - 109
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bollobás, B. (1965) On generalized graph. Acta Math. Acad. Sci. Hungar. 16(3-4) 447–452.CrossRefGoogle Scholar
Chvátal, V. and Hanson, D. (1976) Degrees and matchings. J. Combin. Theory Ser. B 20 128–138.CrossRefGoogle Scholar
Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. Oxford Ser. 12(1) 313–320.CrossRefGoogle Scholar
Erdős, P. and Rado, R. (1960) Intersection theorems for systems of sets. J. Lond. Math. Soc. 35(1) 85–90.Google Scholar
Frankl, P. (1978) The Erdős-Ko-Rado theorem is true for $n = ckt$ . Coll. Math. Soc. J. Bolyai 18 365–375.Google Scholar
Frankl, P. (1978) On intersecting families of finite sets. J. Combin. Theory Ser. A 24(2) 146–161.CrossRefGoogle Scholar
Frankl, P. (1987) The shifting technique in extremal set theory. Surv. Combin. 123 81–110.Google Scholar
Frankl, P. (1991) Shadows and shifting. Graph Combin. 7(1) 23–29.CrossRefGoogle Scholar
Frankl, P. (2013) Improved bounds for Erdős’ matching conjecture. J. Combin. Theory Ser. A 120(5) 1068–1072.CrossRefGoogle Scholar
Frankl, P., Kupavskii, A. and Kiselev, S. (2022) On the maximum number of distinct intersections in an intersecting family. Discrete Math. 345(4) 112757.CrossRefGoogle Scholar
Frankl, P. and Wang, J. (2022) On the sum of sizes of overlapping families. Discrete Math. 345(11) 113027.CrossRefGoogle Scholar
Frankl, P. and Wang, J. (2023) Intersections and distinct intersections in cross-intersecting families. Eur. J. Combin. 110 103665.Google Scholar
Gerbner, D. and Patkós, B. (2018) Extremal Finite Set Theory. CRC Press, 1st edition.Google Scholar
Hilton, A. J. W. and Milner, E. C. (1967) Some intersection theorems for systems of finite sets. Q. J. Math. 18(1) 369–384.Google Scholar
Katona, G. O. H. (1964) Intersection theorems for systems of finite sets. Acta Math. Acad. Sci. Hungar 15(3-4) 329–337.Google Scholar
Katona, G. O. H. (1974) Solution of a problem of Ehrenfeucht and Mycielski. J. Combin. Theory Ser. A 17(2) 265–266.Google Scholar
Kostochka, A., Mubayi, D. and Verstraëte, J. (2017) Turán problems and shadows II: trees. J. Combin. Theory Ser. B 122 457–478.CrossRefGoogle Scholar
Kostochka, A., Mubayi, D. and Verstraëte, J. (2015) Turán problems and shadows I: paths and cycles. J. Combin. Theory Ser. A 129 57–79.Google Scholar
Kostochka, A., Mubayi, D. and Verstraëte, J. (2015) Turán problems and shadows III: expansions of graphs. SIAM J. Discrete Math. 29(2) 868–876.CrossRefGoogle Scholar
Liu, E. L. L. and Wang, J. (2020) The Maximum number of cliques in hypergraphs without large matchings. Electron. J. Combin. 27(4) P4.14.CrossRefGoogle Scholar
Wilson, R. M. (1984) The exact bound in the Erdős-Ko-Rado theorem. Combinatorica 4(2-3) 247–257.CrossRefGoogle Scholar