No CrossRef data available.
Article contents
On Ramsey numbers of hedgehogs
Published online by Cambridge University Press: 18 October 2019
Abstract
The hedgehog Ht is a 3-uniform hypergraph on vertices 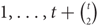 $1, \ldots ,t + \left({\matrix{t \cr 2}}\right)$ such that, for any pair (i, j) with 1 ≤ i < j ≤ t, there exists a unique vertex k > t such that {i, j, k} is an edge. Conlon, Fox and Rödl proved that the two-colour Ramsey number of the hedgehog grows polynomially in the number of its vertices, while the four-colour Ramsey number grows exponentially in the square root of the number of vertices. They asked whether the two-colour Ramsey number of the hedgehog Ht is nearly linear in the number of its vertices. We answer this question affirmatively, proving that r(Ht) = O(t2 ln t).
$1, \ldots ,t + \left({\matrix{t \cr 2}}\right)$ such that, for any pair (i, j) with 1 ≤ i < j ≤ t, there exists a unique vertex k > t such that {i, j, k} is an edge. Conlon, Fox and Rödl proved that the two-colour Ramsey number of the hedgehog grows polynomially in the number of its vertices, while the four-colour Ramsey number grows exponentially in the square root of the number of vertices. They asked whether the two-colour Ramsey number of the hedgehog Ht is nearly linear in the number of its vertices. We answer this question affirmatively, proving that r(Ht) = O(t2 ln t).
Information
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
Research supported by a Packard Fellowship, and by NSF Career Award DMS-1352121.
Research supported by the National Science Foundation Graduate Research Fellowship Program under grant DGE-1656518.

