Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-31T08:40:13.324Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of 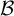${\mathcal B}$-free and other Toeplitz shifts

Part of: Topological dynamics

Published online by Cambridge University Press:  13 June 2023

AURELIA DYMEK Open the ORCID record for AURELIA DYMEK [Opens in a new window] ,
STANISŁAW KASJAN Open the ORCID record for STANISŁAW KASJAN [Opens in a new window]  and
GERHARD KELLER Open the ORCID record for GERHARD KELLER [Opens in a new window]
AURELIA DYMEK*
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Toruń, Poland (e-mail: skasjan@mat.umk.pl)
STANISŁAW KASJAN
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Toruń, Poland (e-mail: skasjan@mat.umk.pl)
GERHARD KELLER
Affiliation:
Department of Mathematics, Friedrich-Alexander University, Erlangen, Germany (e-mail: keller@math.fau.de)
*
e-mail: aurbart@mat.umk.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

We present sufficient conditions for the triviality of the automorphism group of regular Toeplitz subshifts and give a broad class of examples from the class of 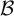${\mathcal B}$-free subshifts satisfying them, extending the work of Dymek [Automorphisms of Toeplitz 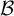${\mathcal B}$-free systems. Bull. Pol. Acad. Sci. Math. 65(2) (2017), 139–152]. Additionally, we provide an example of a 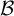${\mathcal B}$-free Toeplitz subshift whose automorphism group has elements of arbitrarily large finite order, answering Question 11 of S. Ferenczi et al [Sarnak’s conjecture: what’s new. Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics (Lecture Notes in Mathematics, 2213). Eds. S. Ferenczi, J. Kułaga-Przymus and M. Lemańczyk. Springer, Cham, 2018, pp. 163–235].

Keywords

ℬ-free dynamicsToeplitz dynamical systemsets of multiplesautomorphisms grouptrivial centralizer

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 37B10: Symbolic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 4 , April 2024 , pp. 1058 - 1101
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baake, M., Jäger, T. and Lenz, D.. Toeplitz flows and model sets. Bull. Lond. Math. Soc. 48(4) (2016), 691–698.Google Scholar
Bułatek, W. and Kwiatkowski, J.. The topological centralizers of Toeplitz flows and their ${Z}_2$ -extensions. Publ. Mat. 34(1) (1990), 45–65.Google Scholar
Bułatek, W. and Kwiatkowski, J.. Strictly ergodic Toeplitz flows with positive entropies and trivial centralizers. Studia Math. 103(2) (1992), 133–142.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of linear growth: beyond transitivity. Forum Math. Sigma 3 (2015), e5, 27 pp.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of subquadratic growth. Proc. Amer. Math. Soc. 144(2) (2016), 613–621.Google Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys. 36(1) (2016), 64–95.Google Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. On automorphism groups of Toeplitz subshifts. Discrete Anal. 11 (2017), 19 pp.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385). Eds. Kolyada, S., Manin, Y. and Ward, T.. American Mathematical Society, Providence, RI, 2005, pp. 7–37.Google Scholar
Downarowicz, T., Kwiatkowski, J. and Lacroix, Y.. A criterion for Toeplitz flows to be topologically isomorphic and applications. Colloq. Math. 68(2) (1995), 219–228.Google Scholar
Dymek, A.. Automorphisms of Toeplitz $\mathbf{\mathcal{B}}$ -free systems. Bull. Pol. Acad. Sci. Math. 65(2) (2017), 139–152.Google Scholar
Dymek, A., Kasjan, S. and Kułaga-Przymus, J.. Minimality of $\mathbf{\mathcal{B}}$ -free systems in number fields. Discrete Contin. Dyn. Syst. doi: 10.3934/dcds.2023056. Published online May 2023.Google Scholar
Dymek, A., Kasjan, S., Kułaga-Przymus, J. and Lemańczyk, M.. $\mathbf{\mathcal{B}}$ -free sets and dynamics. Trans. Amer. Math. Soc. 370(8) (2018), 5425–5489.Google Scholar
Ferenczi, S., Kułaga Przymus, J. and Lemańczyk, M.. Sarnak’s conjecture: what’s new. Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics (Lecture Notes in Mathematics, 2213). Eds. Ferenczi, S., Kułaga-Przymus, J. and Lemańczyk, M.. Springer, Cham, 2018, pp. 163–235.Google Scholar
Garcia, M. and Hedlund, G. A.. The structure of minimal sets. Bull. Amer. Math. Soc. 54(10) (1948), 954–964.Google Scholar
Hall, R. R.. Sets of Multiples (Cambridge Tracts in Mathematics, 118). Cambridge University Press, Cambridge, 1996.Google Scholar
Hedlund, G. A.. Endomorphisms and automorphisms of the shift dynamical system. Math. Syst. Theory 3 (1969), 320–375.Google Scholar
Jacobs, K. and Keane, M.. $0-1$ -sequences of Toeplitz type. Z. Wahrsch. Verw. Gebiete 13 (1969), 123–131.Google Scholar
Kasjan, S., Keller, G. and Lemańczyk, M.. Dynamics of $\mathbf{\mathcal{B}}$ -free sets: a view through the window. Int. Math. Res. Not. IMRN 2019(9) (2019), 2690–2734.Google Scholar
Keller, G.. Maximal equicontinuous generic factors and weak model sets. Discrete Contin. Dyn. Syst. 40(12) (2020), 6855–6875.Google Scholar
Keller, G., Lemańczyk, M., Richard, C. and Sell, D.. On the Garden of Eden theorem for $\mathbf{\mathcal{B}}$ -free subshifts. Israel J. Math. 251 (2022), 567–594.Google Scholar
Keller, G. and Richard, C.. Periods and factors of weak model sets. Israel J. Math. 229(1) (2019), 85–132.Google Scholar
Mentzen, M. K.. Automorphisms of subshifts defined by $\mathbf{\mathcal{B}}$ -free sets of integers. Colloq. Math. 147(1) (2017), 87–94.Google Scholar
Salo, V.. Toeplitz subshift whose automorphism group is not finitely generated. Colloq. Math. 146(1) (2017), 53–76.Google Scholar
Salo, V. and Törmä, I.. Block maps between primitive uniform and Pisot substitutions. Ergod. Th. & Dynam. Sys. 35(7) (2015), 2292–2310.Google Scholar
Williams, S.. Toeplitz minimal flows which are not uniquely ergodic. Z. Wahrsch. Verw. Gebiete 67(1) (1984), 95–107.Google Scholar