Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-17T20:50:54.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of induced systems

Published online by Cambridge University Press:  12 May 2016

ETHAN AKIN ,
JOSEPH AUSLANDER  and
ANIMA NAGAR
ETHAN AKIN
Affiliation:
Mathematics Department, The City College, 137 Street and Convent Avenue, New York, NY 10031, USA email ethanakin@earthlink.net
JOSEPH AUSLANDER
Affiliation:
Mathematics Department, University of Maryland, College Park, MD 20742, USA email jna@math.umd.edu
ANIMA NAGAR
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, Hauz Khas, New Delhi 110016, India email anima@maths.iitd.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the dynamical properties of actions on the space of compact subsets of the phase space. More precisely, if 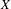$X$ is a metric space, let 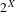$2^{X}$ denote the space of non-empty compact subsets of 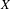$X$ provided with the Hausdorff topology. If 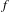$f$ is a continuous self-map on 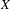$X$, there is a naturally induced continuous self-map 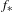$f_{\ast }$ on 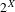$2^{X}$. Our main theme is the interrelation between the dynamics of 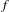$f$ and $f_{\ast }$. For such a study, it is useful to consider the space 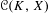${\mathcal{C}}(K,X)$ of continuous maps from a Cantor set 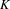$K$ to 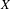$X$ provided with the topology of uniform convergence, and 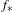$f_{\ast }$ induced on 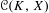${\mathcal{C}}(K,X)$ by composition of maps. We mainly study the properties of transitive points of the induced system 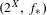$(2^{X},f_{\ast })$ both topologically and dynamically, and give some examples. We also look into some more properties of the system 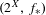$(2^{X},f_{\ast })$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2034 - 2059
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E.. Recurrence in Topological Dynamics: Furstenberg Families and Ellis Actions (University Series in Mathematics) . Plenum Press, New York, 1997.Google Scholar
Akin, E.. Lectures on Cantor and Mycielski sets for dynamical systems. Contemp. Math. 356 (2004), 21–79.Google Scholar
Akin, E. and Glasner, E.. Residual properties and almost equicontinuity. J. Anal. Math. 84 (2001), 243–286.CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and Their Extensions. North Holland, Amsterdam, 1988.Google Scholar
Auslander, J.. Ellis groups of quasi-factors of minimal flow. Colloq. Math. 84/85 (2000), 319–326.CrossRefGoogle Scholar
Banks, J.. Chaos for induced hyperspace maps. Chaos Solitons Fractals 25 (2005), 681–685.Google Scholar
Bauer, W. and Sigmund, K.. Topological dynamics of transformations induced on the space of probability measures. Monatsh. Math. 79 (1975), 81–92.CrossRefGoogle Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets and a problem in diophantine approximation. Syst. Theory 1 (1967), 1–49.Google Scholar
Glasner, E.. Quasifactors of minimal systems. Topol. Methods Nonlinear Anal. 16 (2000), 351–370.Google Scholar
Glasner, S. and Maon, D.. Rigidity in topological dynamics. Ergod. Th. & Dynam. Sys. 9(2) (1989), 309–320.Google Scholar
Glasner, E. and Weiss, B.. Quasi-factors of zero-entropy systems. J. Amer. Math. Soc. 8(3) (1995), 665–686.Google Scholar
Hernandez, P., King, J. and Mendez-Lango, H.. Compact sets with dense orbit in 2 X . Topology Proc. 40 (2012), 319–330.Google Scholar
Illanes, A. and Nadler, S. B. Jr.. Hyperspaces: Fundamentals and Recent Advances (Monographs and Textbooks in Pure and Applied Mathematics, 216) . Marcel Dekker, New York, 1999.Google Scholar
Iwanik, A.. Independent sets of transitive points. Dynamical Systems and Ergodic Theory (Banach Center Publications, 23) . Ed. Krzyżewski, K.. PWN, Warsaw, 1989, pp. 277–282.Google Scholar
Katznelson, Y.. An Introduction to Harmonic Analysis. Wiley, New York, 1968.Google Scholar
Li, J., Oprocha, P., Ye, X. and Zhang, R.. When all closed subsets are recurrent? Ergod. Th. & Dynam. Sys., to appear. Preprint, 2015, arXiv:1504.08191.Google Scholar
Li, J., Yan, K. and Ye, X.. Recurrence properties and disjointness on the induced spaces. Discrete Contin. Dyn. Syst. A 35 (2015), 1059–1073.Google Scholar
Micheal, E.. Topologies on spaces of subsets. Trans. Amer. Math. Soc. 71 (1951), 152–182.CrossRefGoogle Scholar
Petersen, K. E.. Disjointness and weak mixing of minimal sets. Proc. Amer. Math. Soc. 24 (1970), 278–280.Google Scholar
Schori, R. M. and West, J. E.. The hyperspace of the closed unit interval is a Hilbert cube. Trans. Amer. Math. Soc. 213 (1975), 217–235.CrossRefGoogle Scholar
Segal, J.. Hyperspaces of the inverse limit space. Proc. Amer. Math. Soc. 10 (1959), 706–709.Google Scholar
Sharma, P. and Nagar, A.. Inducing sensitivity on hyperspaces. Topology Appl. 157(13) (2010), 2052–2058.CrossRefGoogle Scholar
Sharma, P. and Nagar, A.. Topological dynamics on hyperspaces. Appl. Gen. Topol. 11(1) (2010), 1–19.Google Scholar