Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-01T23:16:04.482Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of non-hyperbolic ergodic measures as the limit of periodic measures

Published online by Cambridge University Press:  12 February 2018

CHRISTIAN BONATTI  and
JINHUA ZHANG
CHRISTIAN BONATTI
Affiliation:
Institut de Mathématiques de Bourgogne, UMR 5584 du CNRS, Université de Bourgogne, 21004 Dijon, France email bonatti@u-bourgogne.fr, jinhua.zhang@u-bourgogne.fr
JINHUA ZHANG
Affiliation:
Institut de Mathématiques de Bourgogne, UMR 5584 du CNRS, Université de Bourgogne, 21004 Dijon, France email bonatti@u-bourgogne.fr, jinhua.zhang@u-bourgogne.fr School of Mathematical Sciences, Peking University, Beijing 100871, China email zjh200889@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Gorodetski et al. [Nonremovability of zero Lyapunov exponents. Funktsional. Anal. i Prilozhen.39(1) (2005), 27–38 (in Russian); Engl. Transl. Funct. Anal. Appl.39(1) (2005), 21–30] and Bochi et al. [Robust criterion for the existence of nonhyperbolic ergodic measures. Comm. Math. Phys.344(3) (2016), 751–795] propose two very different ways for building non-hyperbolic measures, Gorodetski et al. (2005) building such a measure as the limit of periodic measures and Bochi et al. (2016) as the $\unicode[STIX]{x1D714}$-limit set of a single orbit, with a uniformly vanishing Lyapunov exponent. The technique in Gorodetski et al. (2005) has been used in a generic setting in Bonatti et al. [Non-hyperbolic ergodic measures with large support. Nonlinearity23(3) (2010), 687–705] and Díaz and Gorodetski [Non-hyperbolic ergodic measures for non-hyperbolic homoclinic classes. Ergod. Th. & Dynam. Sys.29(5) (2009), 1479–1513], as the periodic orbits were built by small perturbations. It is not known if the measures obtained by the technique in Bochi et al. (2016) are accumulated by periodic measures. In this paper we use a shadowing lemma from Gan [A generalized shadowing lemma. Discrete Contin. Dyn. Syst.8(3) (2002), 527–632]:

  • ∙ for getting the periodic orbits in Gorodetski et al. (2005) without perturbing the dynamics;

  • ∙ for recovering the compact set in Bochi et al. (2016) with a uniformly vanishing Lyapunov exponent by considering the limit of periodic orbits.

As a consequence, we prove that there exists an open and dense subset 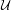${\mathcal{U}}$ of the set of robustly transitive non-hyperbolic diffeomorphisms far from homoclinic tangencies, such that for any 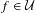$f\in {\mathcal{U}}$, there exists a non-hyperbolic ergodic measure with full support and approximated by hyperbolic periodic measures. We also prove that there exists an open and dense subset 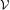${\mathcal{V}}$ of the set of diffeomorphisms exhibiting a robust cycle, such that for any 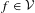$f\in {\mathcal{V}}$, there exists a non-hyperbolic ergodic measure approximated by hyperbolic periodic measures.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 2932 - 2967
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, Ch. and Crovisier, S.. Nonumiform hyperbolicity for C 1 generic diffeomorphisms. Israel J. Math. 183 (2011), 1–60.10.1007/s11856-011-0041-5Google Scholar
Abdenur, F., Bonatti, Ch., Crovisier, S., Díaz, L. J. and Wen, L.. Periodic points and homoclinic class. Ergod. Th. & Dynam. Sys. 27(1) (2007), 1–22.Google Scholar
Arbieto, A., Catalan, T. and Santiago, B.. Mixing-like properties for some generic and robust dynamics. Nonlinearity 28(11) (2015), 4103–4115.10.1088/0951-7715/28/11/4103Google Scholar
Abraham, R. and Smale, S.. Nongenericity of đ›ș-stablity. Global Analysis (Proceedings of Symposia in Pure Mathematics, 14) . American Mathematical Society, Providence, RI, 1970, pp. 5–8.10.1090/pspum/014/0271986Google Scholar
Bochi, J., Bonatti, Ch. and Díaz, L. J.. Robust criterion for the existence of nonhyperbolic ergodic measures. Comm. Math. Phys. 344(3) (2016), 751–795.10.1007/s00220-016-2644-5Google Scholar
Bochi, J., Bonatti, Ch. and DĂ­az, L. J.. A criterion for zero averages and full support of ergodic measures. Preprint, 2016, arXiv:1609.07764. Moscow Math. J. to appear.Google Scholar
Bonatti, Ch. and Crovisier, S.. RĂ©currence et gĂ©nĂ©ricitĂ©. Invent. Math. 158(1) (2004), 33–104.10.1007/s00222-004-0368-1Google Scholar
Bonatti, Ch. and Díaz, L. J.. Persistent nonhyperbolic transitive diffeomorphism. Ann. of Math. (2) 143 (1996), 357–396.Google Scholar
Bonatti, Ch. and Díaz, L. J.. Robust heterodimensional cycles and C 1 generic dynamics. J. Inst. Math. Jussieu 7(3) (2008), 469–525.10.1017/S1474748008000030Google Scholar
Bonatti, Ch. and Díaz, L. J.. Abundance of C 1 -robust homoclinic tangencies. Trans. Amer. Math. Soc. 364(10) (2012), 5111–5148.Google Scholar
Bonatti, Ch., Díaz, L. J. and Gorodetski, A.. Non-hyperbolic ergodic measures with large support. Nonlinearity 23(3) (2010), 687–705.Google Scholar
Bonatti, Ch., DĂ­az, L. J., Pujals, E. and Rocha, J.. Robustly transitive sets and heterodimensional cycles. Geom. Meth. Dyn. I. AstĂ©risque 286 (2003), xix, 187–222.Google Scholar
Bonatti, Ch., DĂ­az, L. J. and Viana, M.. Dynamics beyond Uniform Hyperbolicity. A global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102 (Mathematical Physics, III)) . Springer, Berlin, 2005.Google Scholar
Cheng, C., Crovisier, S., Gan, S., Wang, X. and Yang, D.. Hyperbolicity versus non-hyperbolic ergodic measures inside homoclinic classes. Preprint, 2015, arXiv:1507.08253. Ergod. Th. & Dynam. Sys., doi:10.1017/etds.2017.106, to appear.Google Scholar
Cao, Y., Luzatto, S. and Rios, I.. Some non-hyperbolic systems with strictly non-zero Lyapunov exponents for all invariant measures: horseshoes with internal tangencies. Discrete Contin. Dyn. Syst. 15(1) (2006), 61–71.Google Scholar
Crovisier, S., Sambarino, M. and Yang, D.. Partial hyperbolicity and homoclinic tangencies. J. Eur. Math. Soc. 1 (2015), 1–49.Google Scholar
Díaz, L. J. and Gorodetski, A.. Non-hyperbolic ergodic measures for non-hyperbolic homoclinic classes. Ergod. Th. & Dynam. Sys. 29(5) (2009), 1479–1513.Google Scholar
Gan, S.. A generalized shadowing lemma. Discrete Contin. Dyn. Syst. 8(3) (2002), 527–632.10.3934/dcds.2002.8.627Google Scholar
Gorodetski, A., Ilyashenko, Yu. S., Kleptsyn, V. A. and Nalsky, M. B.. Nonremovability of zero Lyapunov exponents. Funktsional. Anal. i Prilozhen. 39(1) (2005), 27–38 (in Russian); Engl. Transl. Funct. Anal. Appl. 39(1) (2005), 21–30.10.1007/s10688-005-0014-8Google Scholar
Gourmelon, N.. Adapted metrics for dominated splittings. Ergod. Th. & Dynam. Sys. 27(6) (2007), 1839–1849.10.1017/S0143385707000272Google Scholar
Hayashi, S.. Connecting invariant manifolds and the solution of C 1 -stability and đ›ș-stability conjectures for flows. Ann. Math. 145 (1997), 81–137.10.2307/2951824Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, Berlin, 1977.10.1007/BFb0092042Google Scholar
Kleptsyn, V. A. and Nalsky, M. B.. Stability of the existence of nonhyperbolic measures for C 1 diffeomorphisms. Funktsional. Anal. i Prilozhen. 41(4) (2007), 30–45 (in Russian); Engl. Transl. Funct. Anal. Appl. 41(4) (2007), 271–283.10.1007/s10688-007-0025-8Google Scholar
Liao, S. T.. An existence theorem for periodic orbits. Acta Sci. Natur. Univ. Pekinensis 1 (1979), 1–20.Google Scholar
Liao, S. T.. Certain uniformity properties of differential systems and a generalization of an existence theorem for periodic orbits. Acta Sci. Natur. Univ. Pekinensis 2 (1985), 1–19.Google Scholar
Mane, R.. Contributions to the stability conjecture. Topology 17 (1978), 383–396.10.1016/0040-9383(78)90005-8Google Scholar
Oseledets, V. I.. A multiplicative ergodic theorem: Lyapunov characteristic numbers for dynamical systems. Trans. Moscow. Math. Soc. 19 (1968), 197–231.Google Scholar
Pliss, V.. On a conjecture due to Smale. Differ. Uravn. 8 (1972), 262–268.Google Scholar
Shub, M.. Topological Transitive Diffeomorphisms on 𝕋4 (Lecture Notes in Mathematics, 206) . Springer, Berlin, 1971, p. 39.Google Scholar
Walter, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Wang, X.. Hyperbolicity versus weak periodic orbits inside homoclinic classes. Preprint, 2015, arXiv:1504.03153. Ergod. Th. & Dynam. Sys., doi:10.1017/etds.2016.122, to appear.Google Scholar
Wen, L. and Xia, Z.. C 1 connecting lemmas. Trans. Amer. Math. Soc. 352(11) (2000), 5213–5230.10.1090/S0002-9947-00-02553-8Google Scholar