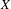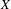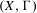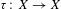Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barbieri, Sebastián
García-Ramos, Felipe
and
Li, Hanfeng
2022.
Markovian properties of continuous group actions: Algebraic actions, entropy and the homoclinic group.
Advances in Mathematics,
Vol. 397,
Issue. ,
p.
108196.
Ceccherini-Silberstein, Tullio
and
Coornaert, Michel
2023.
Cellular Automata and Groups.
p.
89.
Ceccherini-Silberstein, Tullio
Coornaert, Michel
and
Li, Hanfeng
2024.
Expansive actions with specification of sofic groups, strong topological Markov property, and surjunctivity.
Journal of Functional Analysis,
Vol. 286,
Issue. 9,
p.
110376.