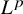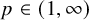1 Introduction
1.1 A brief history
In 1933, Khintchin [Reference Khintchin40] had the great insight to see how to generalize the classical equidistribution result of Bohl [Reference Bohl12], Sierpiński [Reference Sierpiński56] and Weyl [Reference Weyl66] from 1910 to a pointwise ergodic theorem, observing that as a consequence of Birkhoff’s famous ergodic theorem [Reference Birkhoff11], the following equidistribution result holds: namely, for any irrational
![]() $\theta \in {\mathbb R}$
, for any Lebesgue measurable set
$\theta \in {\mathbb R}$
, for any Lebesgue measurable set
![]() $E\subseteq [0,1)$
and for almost every
$E\subseteq [0,1)$
and for almost every
![]() $x\in {\mathbb R}$
,
$x\in {\mathbb R}$
,
where
![]() $\{x\}$
denotes the fractional part of
$\{x\}$
denotes the fractional part of
![]() $x\in \mathbb {R}$
, and
$x\in \mathbb {R}$
, and
![]() $[N]:=(0, N]\cap {\mathbb {Z}}$
for any real number
$[N]:=(0, N]\cap {\mathbb {Z}}$
for any real number
![]() $N\ge 1$
. In 1916, Weyl [Reference Weyl67] extended the classical equidistribution theorem to general polynomial sequences
$N\ge 1$
. In 1916, Weyl [Reference Weyl67] extended the classical equidistribution theorem to general polynomial sequences
![]() $(\{P(n)\})_{n\in \mathbb {N}}$
having at least one irrational coefficient, and so it was natural to ask whether a pointwise ergodic extension of Weyl’s equidistribution theorem holds. This question was posed by Bellow [Reference Bellow5] and Furstenberg [Reference Furstenberg24] in the early 1980s; precisely, they asked if for any polynomial
$(\{P(n)\})_{n\in \mathbb {N}}$
having at least one irrational coefficient, and so it was natural to ask whether a pointwise ergodic extension of Weyl’s equidistribution theorem holds. This question was posed by Bellow [Reference Bellow5] and Furstenberg [Reference Furstenberg24] in the early 1980s; precisely, they asked if for any polynomial
![]() $P \in {\mathbb Z}[\mathrm {m}]$
with integer coefficients and
$P \in {\mathbb Z}[\mathrm {m}]$
with integer coefficients and
![]() $P(0)=0$
and for any invertible measure-preserving transformation
$P(0)=0$
and for any invertible measure-preserving transformation
![]() $T: X \to X$
on a probability space
$T: X \to X$
on a probability space
![]() $(X,\mathcal B(X), \mu )$
, does the limit
$(X,\mathcal B(X), \mu )$
, does the limit
exist for almost every
![]() $x\in X$
and for every
$x\in X$
and for every
![]() $f \in L^\infty (X)$
? Here and throughout the paper we use the notation
$f \in L^\infty (X)$
? Here and throughout the paper we use the notation
![]() $\mathbb {E}_{y\in Y}f(y):=\frac {1}{\#Y}\sum _{y\in Y}f(y)$
for any finite set
$\mathbb {E}_{y\in Y}f(y):=\frac {1}{\#Y}\sum _{y\in Y}f(y)$
for any finite set
![]() $Y\neq \emptyset $
and any function
$Y\neq \emptyset $
and any function
![]() $f:Y\to \mathbb {C}$
. In the mid 1980s, the first author [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] established that this is indeed the case whenever
$f:Y\to \mathbb {C}$
. In the mid 1980s, the first author [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] established that this is indeed the case whenever
![]() $f \in L^p(X)$
and
$f \in L^p(X)$
and
![]() $p\in (1,\infty )$
, leaving open the question of what happens on
$p\in (1,\infty )$
, leaving open the question of what happens on
![]() $L^1(X)$
. Interestingly, it was shown much later by Buczolich and Mauldin [Reference Buczolich and Mauldin18] that the above pointwise convergence result fails for general
$L^1(X)$
. Interestingly, it was shown much later by Buczolich and Mauldin [Reference Buczolich and Mauldin18] that the above pointwise convergence result fails for general
![]() $L^1$
functions when
$L^1$
functions when
![]() $P(m) = m^2$
; see also [Reference LaVictoire42] for further refinements. In any case, the papers [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] represent a far-reaching common generalization of Birkhoff’s pointwise ergodic theorem and Weyl’s equidistribution theorem.
$P(m) = m^2$
; see also [Reference LaVictoire42] for further refinements. In any case, the papers [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] represent a far-reaching common generalization of Birkhoff’s pointwise ergodic theorem and Weyl’s equidistribution theorem.
Both Birkhoff’s and Weyl’s results have natural multi-parameter extensions. In 1951, Dunford [Reference Dunford23] and Zygmund [Reference Zygmund72] independently extended Birkhoff’s theorem to multiple measure-preserving transformations
![]() $T_1, \ldots , T_k : X \to X$
. They showed that the limit
$T_1, \ldots , T_k : X \to X$
. They showed that the limit
exists for almost every
![]() $x \in X$
and for any
$x \in X$
and for any
![]() $f\in L^p(X)$
with
$f\in L^p(X)$
with
![]() $p\in (1, \infty )$
, where
$p\in (1, \infty )$
, where
![]() $\prod _{j=1}^k[M_j]:=[M_1]\times \ldots \times [M_k]$
. The limit is taken in the unrestricted sense; that is, when
$\prod _{j=1}^k[M_j]:=[M_1]\times \ldots \times [M_k]$
. The limit is taken in the unrestricted sense; that is, when
![]() $\min \{M_1,\ldots ,M_k\} \to \infty $
. Here, when
$\min \{M_1,\ldots ,M_k\} \to \infty $
. Here, when
![]() $k\ge 2$
, the pointwise convergence result is manifestly false for general
$k\ge 2$
, the pointwise convergence result is manifestly false for general
![]() $f\in L^1(X)$
.
$f\in L^1(X)$
.
In 1979, Arkhipov, Chubarikov and Karatsuba [Reference Arkhipov, Chubarikov and Karatsuba2] extended Weyl’s equidistribution result to polynomials (even multiple polynomials) of several variables. In its simplest form, their result asserts that for any k-variate polynomial
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
, any irrational
$P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
, any irrational
![]() $\theta \in \mathbb {R}$
and any interval
$\theta \in \mathbb {R}$
and any interval
![]() $[a, b)\subseteq [0, 1)$
, one has
$[a, b)\subseteq [0, 1)$
, one has
 $$ \begin{align} \lim_{\min\{M_1,\ldots,M_k\} \to \infty} \frac{\# \{(m_1, \ldots, m_k)\in\prod_{j=1}^k[M_j]: \{\theta P(m_1,\ldots, m_k)\} \in [a, b) \}}{M_1 \cdots M_k} = b-a. \end{align} $$
$$ \begin{align} \lim_{\min\{M_1,\ldots,M_k\} \to \infty} \frac{\# \{(m_1, \ldots, m_k)\in\prod_{j=1}^k[M_j]: \{\theta P(m_1,\ldots, m_k)\} \in [a, b) \}}{M_1 \cdots M_k} = b-a. \end{align} $$
In the late 1980s, after [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] and in light of these results, it was natural to seek a common generalization of the results of Dunford and Zygmund on the one hand (which generalize Birkhoff’s original theorem) and Arkhipov, Chubarikov and Karatsuba on the other hand (which generalize Weyl’s theorem), which can be subsumed under the following conjecture, a multi-parameter variant of the Bellow–Furstenberg problem:
Conjecture 1.3. Let
![]() $k\in {\mathbb {Z}}_+$
with
$k\in {\mathbb {Z}}_+$
with
![]() $k\ge 2$
be given and let
$k\ge 2$
be given and let
![]() $(X, \mathcal B(X), \mu )$
be a probability measure space with an invertible measure-preserving transformation
$(X, \mathcal B(X), \mu )$
be a probability measure space with an invertible measure-preserving transformation
![]() $T:X\to X$
. Assume that
$T:X\to X$
. Assume that
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
with
$P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
with
![]() $P(0)=0$
. Then for any
$P(0)=0$
. Then for any
![]() $f\in L^{\infty }(X)$
, the limit
$f\in L^{\infty }(X)$
, the limit
Our main theorem resolves this conjecture.
Theorem 1.5. Conjecture 1.3 is true for all
![]() $k\in {\mathbb {Z}}_+$
.
$k\in {\mathbb {Z}}_+$
.
The case
![]() $k=1$
corresponds to the classical one-parameter question of Bellow [Reference Bellow5] and Furstenberg [Reference Furstenberg24] and was resolved in [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15]. In this paper, we will establish the cases
$k=1$
corresponds to the classical one-parameter question of Bellow [Reference Bellow5] and Furstenberg [Reference Furstenberg24] and was resolved in [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15]. In this paper, we will establish the cases
![]() $k\ge 2$
. In fact, we will prove stronger quantitative results including corresponding multi-parameter maximal and oscillation estimates (see Theorem 1.11 below), which will imply Conjecture 1.3. This paper also represents a first systematic treatment of multi-parameter oscillation semi-norms which allows an efficient handling of multi-parameter pointwise convergence problems for ergodic averaging operators with polynomial orbits. Before we formulate our main quantitative results, we briefly describe the interesting history of Conjecture 1.3.
$k\ge 2$
. In fact, we will prove stronger quantitative results including corresponding multi-parameter maximal and oscillation estimates (see Theorem 1.11 below), which will imply Conjecture 1.3. This paper also represents a first systematic treatment of multi-parameter oscillation semi-norms which allows an efficient handling of multi-parameter pointwise convergence problems for ergodic averaging operators with polynomial orbits. Before we formulate our main quantitative results, we briefly describe the interesting history of Conjecture 1.3.
The theorems of Dunford [Reference Dunford23] and Zygmund [Reference Zygmund72] have simple proofs, which can be deduced by iterative applications of the classical Birkhoff ergodic theorem. For this purpose, it suffices to note that the Dunford–Zygmund averages from (1.1) can be written as a composition of k classical Birkhoff averages as follows
The order in this composition is important since the transformations
![]() $T_1,\ldots , T_k$
do not need to commute. The first author, in view of [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15], extended the observation from (1.6) to polynomial orbits and showed that for every
$T_1,\ldots , T_k$
do not need to commute. The first author, in view of [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15], extended the observation from (1.6) to polynomial orbits and showed that for every
![]() $f\in L^p(X)$
with
$f\in L^p(X)$
with
![]() $p\in (1, \infty )$
, the limit
$p\in (1, \infty )$
, the limit
exists for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in X$
, whenever
$x\in X$
, whenever
![]() $P_1,\ldots , P_k\in {\mathbb {Z}}[\mathrm {m}]$
with
$P_1,\ldots , P_k\in {\mathbb {Z}}[\mathrm {m}]$
with
![]() $P_1(0)=\ldots =P_k(0)=0$
and
$P_1(0)=\ldots =P_k(0)=0$
and
![]() $T_1,\ldots , T_d:X\to X$
is a family of commuting and invertible measure-preserving transformations. The result from (1.7) was never published; nonetheless, it can be thought of as a polynomial extension of the theorem of Dunford [Reference Dunford23] and Zygmund [Reference Zygmund72] (the arguments in Section 3.4 can be used to derive a quantitative version of (1.7)). Interestingly, as observed by Benjamin Weiss (privately communicated to the first author), any ergodic theorem for these averages fails in general for
$T_1,\ldots , T_d:X\to X$
is a family of commuting and invertible measure-preserving transformations. The result from (1.7) was never published; nonetheless, it can be thought of as a polynomial extension of the theorem of Dunford [Reference Dunford23] and Zygmund [Reference Zygmund72] (the arguments in Section 3.4 can be used to derive a quantitative version of (1.7)). Interestingly, as observed by Benjamin Weiss (privately communicated to the first author), any ergodic theorem for these averages fails in general for
![]() $k\ge 2$
when the
$k\ge 2$
when the
![]() $T_1,\ldots , T_k$
are general non-commuting transformations. It may even fail in the one-parameter situation for the averages of the form
$T_1,\ldots , T_k$
are general non-commuting transformations. It may even fail in the one-parameter situation for the averages of the form
![]() $\mathbb {E}_{m\in [M]} f(T_1^{P_1(m)} \cdots T_k^{P_k(m)} x)$
; see also [Reference Bergelson and Leibman10] for interesting counterexamples.
$\mathbb {E}_{m\in [M]} f(T_1^{P_1(m)} \cdots T_k^{P_k(m)} x)$
; see also [Reference Bergelson and Leibman10] for interesting counterexamples.
This was a turning point, illustrating that the multi-parameter theory for averages with orbits along polynomials with separated variables as in (1.7) is well-understood and can be readily deduced from the one-parameter theory [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] by simple iteration as in (1.6). However, the equidistribution result (1.2) of Arkhipov, Chubarikov and Karatsuba [Reference Arkhipov, Chubarikov and Karatsuba2], based on the so-called multi-parameter circle method (deep and intricate tools in analytic number theory which go beyond the classical circle method) showed that the situation may be dramatically different when orbits are defined along genuinely k-variate polynomials
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
and led to Conjecture 1.3. Even for
$P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
and led to Conjecture 1.3. Even for
![]() $k=2$
with
$k=2$
with
![]() $P(m_1, m_2)=m_1^2m_2^3$
in (1.4), the problem becomes very challenging. Surprisingly it seems that there is no simple way (like changing variables or interpreting the average from (1.4) as a composition of simpler one-parameter averages as in (1.6)) that would help us to reduce the matter to the setup where pointwise convergence is known.
$P(m_1, m_2)=m_1^2m_2^3$
in (1.4), the problem becomes very challenging. Surprisingly it seems that there is no simple way (like changing variables or interpreting the average from (1.4) as a composition of simpler one-parameter averages as in (1.6)) that would help us to reduce the matter to the setup where pointwise convergence is known.
The multi-parameter case
![]() $k\ge 2$
in Conjecture 1.3 lies in sharp contrast to the one-parameter situation
$k\ge 2$
in Conjecture 1.3 lies in sharp contrast to the one-parameter situation
![]() $k=1$
, causing serious difficulties that were not apparent in [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15]. The most notable differences are multi-parameter estimates of corresponding exponential sums and a delicate control of error terms that arise in implementing the circle method. These difficulties arise from the lack of nestedness when the parameters
$k=1$
, causing serious difficulties that were not apparent in [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15]. The most notable differences are multi-parameter estimates of corresponding exponential sums and a delicate control of error terms that arise in implementing the circle method. These difficulties arise from the lack of nestedness when the parameters
![]() $M_1,\ldots ,M_k$
are independent; see Figure 1 and Figure 2 below. We now turn to a more detailed discussion and precise formulation of the results in this paper.
$M_1,\ldots ,M_k$
are independent; see Figure 1 and Figure 2 below. We now turn to a more detailed discussion and precise formulation of the results in this paper.

Figure 1 Family of nested rectangles (cubes)
![]() $Q_{M,M}\subset Q_{N,N}$
with
$Q_{M,M}\subset Q_{N,N}$
with
![]() $M<N$
, for
$M<N$
, for
![]() $k=2$
.
$k=2$
.

Figure 2 Family of un-nested rectangles
![]() $Q_{M_1, M_2}\not \subseteq Q_{N_1, N_2}$
with
$Q_{M_1, M_2}\not \subseteq Q_{N_1, N_2}$
with
![]() $M_1<N_1$
and
$M_1<N_1$
and
![]() $M_2>N_2$
, for
$M_2>N_2$
, for
![]() $k=2$
.
$k=2$
.
1.2 Statement of the main results
Throughout this paper, the triple
![]() $(X, \mathcal B(X), \mu )$
denotes a
$(X, \mathcal B(X), \mu )$
denotes a
![]() $\sigma $
-finite measure space, and
$\sigma $
-finite measure space, and
![]() ${\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
denotes the space of all formal k-variate polynomials
${\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
denotes the space of all formal k-variate polynomials
![]() $P(\mathrm {m}_1, \ldots , \mathrm {m}_k)$
with
$P(\mathrm {m}_1, \ldots , \mathrm {m}_k)$
with
![]() $k\in {\mathbb {Z}}_+$
indeterminates
$k\in {\mathbb {Z}}_+$
indeterminates
![]() $\mathrm {m}_1, \ldots , \mathrm {m}_k$
and integer coefficients. Each polynomial
$\mathrm {m}_1, \ldots , \mathrm {m}_k$
and integer coefficients. Each polynomial
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
will always be identified with a map
$P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
will always be identified with a map
![]() ${\mathbb {Z}}^k\ni (m_1,\ldots , m_k)\mapsto P(m_1,\ldots , m_k)\in {\mathbb {Z}}$
.
${\mathbb {Z}}^k\ni (m_1,\ldots , m_k)\mapsto P(m_1,\ldots , m_k)\in {\mathbb {Z}}$
.
Let
![]() $d, k \in {\mathbb {Z}}_+$
, and given a family
$d, k \in {\mathbb {Z}}_+$
, and given a family
![]() ${\mathcal T} = \{T_1,\ldots , T_d\}$
of invertible commuting measure-preserving transformations on X, a measurable function f on X, polynomials
${\mathcal T} = \{T_1,\ldots , T_d\}$
of invertible commuting measure-preserving transformations on X, a measurable function f on X, polynomials
![]() ${\mathcal P} = \{P_1,\ldots , P_d\} \subset {\mathbb {Z}}[\mathrm m_1, \ldots , \mathrm {m}_k]$
and a vector of real numbers
${\mathcal P} = \{P_1,\ldots , P_d\} \subset {\mathbb {Z}}[\mathrm m_1, \ldots , \mathrm {m}_k]$
and a vector of real numbers
![]() $M = (M_1,\ldots , M_k)$
whose entries are greater than
$M = (M_1,\ldots , M_k)$
whose entries are greater than
![]() $1$
, we define the multi-parameter polynomial ergodic average by
$1$
, we define the multi-parameter polynomial ergodic average by
where
![]() $Q_{M}:=[M_1]\times \ldots \times [M_k]$
is a rectangle in
$Q_{M}:=[M_1]\times \ldots \times [M_k]$
is a rectangle in
![]() ${\mathbb {Z}}^k$
. We will often abbreviate
${\mathbb {Z}}^k$
. We will often abbreviate
![]() $A_{M; X, {\mathcal T}}^{{\mathcal P}}$
to
$A_{M; X, {\mathcal T}}^{{\mathcal P}}$
to
![]() $A_{M; X}^{{\mathcal P}}$
when the tranformations are understood. In some instances, we will write out the averages
$A_{M; X}^{{\mathcal P}}$
when the tranformations are understood. In some instances, we will write out the averages
depending on how explicit we want to be.
Example 1.9. From the point of view of pointwise convergence problems, due to the Calderón transference principle [Reference Calderón19], the most important dynamical system is the integer shift system. Consider the d-dimensional lattice
![]() $({\mathbb {Z}}^d, \mathcal B({\mathbb {Z}}^d), \mu _{{\mathbb {Z}}^d})$
equipped with a family of shifts
$({\mathbb {Z}}^d, \mathcal B({\mathbb {Z}}^d), \mu _{{\mathbb {Z}}^d})$
equipped with a family of shifts
![]() $S_1,\ldots , S_d:{\mathbb {Z}}^d\to {\mathbb {Z}}^d$
, where
$S_1,\ldots , S_d:{\mathbb {Z}}^d\to {\mathbb {Z}}^d$
, where
![]() $\mathcal B({\mathbb {Z}}^d)$
denotes the
$\mathcal B({\mathbb {Z}}^d)$
denotes the
![]() $\sigma $
-algebra of all subsets of
$\sigma $
-algebra of all subsets of
![]() ${\mathbb {Z}}^d$
,
${\mathbb {Z}}^d$
,
![]() $\mu _{{\mathbb {Z}}^d}$
denotes counting measure on
$\mu _{{\mathbb {Z}}^d}$
denotes counting measure on
![]() ${\mathbb {Z}}^d$
, and
${\mathbb {Z}}^d$
, and
![]() $S_j(x)=x-e_j$
for every
$S_j(x)=x-e_j$
for every
![]() $x\in {\mathbb {Z}}^d$
(here,
$x\in {\mathbb {Z}}^d$
(here,
![]() $e_j$
is j-th basis vector from the standard basis in
$e_j$
is j-th basis vector from the standard basis in
![]() ${\mathbb {Z}}^d$
for each
${\mathbb {Z}}^d$
for each
![]() $j\in [d]$
). The average
$j\in [d]$
). The average
![]() $A_{M; X, {\mathcal T}}^{{\mathcal P}}$
with
$A_{M; X, {\mathcal T}}^{{\mathcal P}}$
with
![]() ${\mathcal T} = (T_1,\ldots , T_d)=(S_1,\ldots , S_d)$
can be rewritten for any
${\mathcal T} = (T_1,\ldots , T_d)=(S_1,\ldots , S_d)$
can be rewritten for any
![]() $x=(x_1,\ldots , x_d)\in {\mathbb {Z}}^d$
and any finitely supported function
$x=(x_1,\ldots , x_d)\in {\mathbb {Z}}^d$
and any finitely supported function
![]() $f:{\mathbb {Z}}^d\to \mathbb {C}$
as
$f:{\mathbb {Z}}^d\to \mathbb {C}$
as
The main result of this paper, which implies Conjecture 1.3, is the following ergodic theorem.
Theorem 1.11. Let
![]() $(X, \mathcal B(X), \mu )$
be a
$(X, \mathcal B(X), \mu )$
be a
![]() $\sigma $
-finite measure space with an invertible measure-preserving transformation
$\sigma $
-finite measure space with an invertible measure-preserving transformation
![]() $T:X\to X$
. Let
$T:X\to X$
. Let
![]() $k\in {\mathbb {Z}}_+$
with
$k\in {\mathbb {Z}}_+$
with
![]() $k\ge 2$
be given, and
$k\ge 2$
be given, and
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
be a polynomial such that
$P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
be a polynomial such that
![]() $P(0)=0$
. Let
$P(0)=0$
. Let
![]() $f\in L^p(X)$
for some
$f\in L^p(X)$
for some
![]() $1\le p\le \infty $
, and let
$1\le p\le \infty $
, and let
![]() $A_{M_1,\ldots , M_k; X, T}^P f$
be the average defined in (1.8) with
$A_{M_1,\ldots , M_k; X, T}^P f$
be the average defined in (1.8) with
![]() $d=1$
and arbitrary
$d=1$
and arbitrary
![]() $k\in {\mathbb {Z}}_+$
.
$k\in {\mathbb {Z}}_+$
.
-
(i) (Mean ergodic theorem) If
 $1<p<\infty $
, then the averages
$1<p<\infty $
, then the averages
 $A_{M_1,\ldots , M_k; X, T}^{P}f$
converge in
$A_{M_1,\ldots , M_k; X, T}^{P}f$
converge in
 $L^p(X)$
norm.
$L^p(X)$
norm. -
(ii) (Pointwise ergodic theorem) If
 $1<p<\infty $
, then the averages
$1<p<\infty $
, then the averages
 $A_{M_1,\ldots , M_k; X, T}^{P}f$
converge pointwise almost everywhere.
$A_{M_1,\ldots , M_k; X, T}^{P}f$
converge pointwise almost everywhere. -
(iii) (Maximal ergodic theorem) If
 $1<p\le \infty $
, then one has (1.12)
$1<p\le \infty $
, then one has (1.12) $$ \begin{align} \big\|\sup_{M_1,\ldots, M_k\in{\mathbb{Z}}_+}|A_{M_1,\ldots, M_k; X, T}^{P}f|\big\|_{L^p(X)}\lesssim_{p, P}\|f\|_{L^p(X)}. \end{align} $$
$$ \begin{align} \big\|\sup_{M_1,\ldots, M_k\in{\mathbb{Z}}_+}|A_{M_1,\ldots, M_k; X, T}^{P}f|\big\|_{L^p(X)}\lesssim_{p, P}\|f\|_{L^p(X)}. \end{align} $$
-
(iv) (Oscillation ergodic theorem) If
 $1<p<\infty $
and
$1<p<\infty $
and
 $\tau>1$
, then one has (1.13)where
$\tau>1$
, then one has (1.13)where $$ \begin{align} \qquad \qquad\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^k) }\big\|O_{I, J}(A_{M_1,\ldots, M_k; X, T}^{P}f: M_1, \ldots, M_k\in\mathbb{D}_{\tau})\|_{L^p(X)}\lesssim_{p, \tau, P}\|f\|_{L^p(X)}, \end{align} $$
$$ \begin{align} \qquad \qquad\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^k) }\big\|O_{I, J}(A_{M_1,\ldots, M_k; X, T}^{P}f: M_1, \ldots, M_k\in\mathbb{D}_{\tau})\|_{L^p(X)}\lesssim_{p, \tau, P}\|f\|_{L^p(X)}, \end{align} $$
 $\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
; see Section 2 for a definition of the oscillation semi-norm
$\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
; see Section 2 for a definition of the oscillation semi-norm
 $O_{I, J}$
. The implicit constant in (1.12) and (1.13) may depend on
$O_{I, J}$
. The implicit constant in (1.12) and (1.13) may depend on
 $p, \tau , P$
.
$p, \tau , P$
.
For ease of exposition, we only prove Theorem 1.11 in the two-parameter setting
![]() $k=2$
, though there are some places in the paper where some arguments are formulated and proved in the multi-parameter setting to convince the reader that our arguments are adaptable to the general multi-parameter setup. However, the patient reader will readily see that all two-parameter arguments are adaptable (at the expense of introducing cumbersome notation, which would make the exposition unreadable) to the general multi-parameter setting for arbitrary
$k=2$
, though there are some places in the paper where some arguments are formulated and proved in the multi-parameter setting to convince the reader that our arguments are adaptable to the general multi-parameter setup. However, the patient reader will readily see that all two-parameter arguments are adaptable (at the expense of introducing cumbersome notation, which would make the exposition unreadable) to the general multi-parameter setting for arbitrary
![]() $k\ge 2$
, by multiple iterations of the arguments presented in the paper.
$k\ge 2$
, by multiple iterations of the arguments presented in the paper.
We now give some remarks about Theorem 1.11.
-
1. Theorem 1.11 establishes Conjecture 1.3 for the averages
 $A_{M; X, T}^{P}f$
. This is the first nontrivial result in the literature establishing pointwise almost everywhere convergence for polynomial ergodic averages in the multi-parameter setting. See [Reference Mirek, Szarek and Wright53] for other pointwise convergence results in the multi-parameter setting.
$A_{M; X, T}^{P}f$
. This is the first nontrivial result in the literature establishing pointwise almost everywhere convergence for polynomial ergodic averages in the multi-parameter setting. See [Reference Mirek, Szarek and Wright53] for other pointwise convergence results in the multi-parameter setting. -
2. The proof of Theorem 1.11 is relatively simple if
 $P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
is degenerate; see inequality (3.5) in Section 3. We will say that
$P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
is degenerate; see inequality (3.5) in Section 3. We will say that
 $P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
is degenerate if it can be written as (1.14)where
$P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_k]$
is degenerate if it can be written as (1.14)where $$ \begin{align} P(\mathrm{m}_1,\ldots, \mathrm{m}_k)=P_1(\mathrm{m}_1)+\ldots+ P_k(\mathrm{m}_k), \end{align} $$
$$ \begin{align} P(\mathrm{m}_1,\ldots, \mathrm{m}_k)=P_1(\mathrm{m}_1)+\ldots+ P_k(\mathrm{m}_k), \end{align} $$
 $P_1\in {\mathbb {Z}}[\mathrm {m}_1],\ldots , P_k\in {\mathbb {Z}}[\mathrm {m}_k]$
with
$P_1\in {\mathbb {Z}}[\mathrm {m}_1],\ldots , P_k\in {\mathbb {Z}}[\mathrm {m}_k]$
with
 $P_1(0)=\ldots = P_k(0)=0$
. Otherwise, we say that
$P_1(0)=\ldots = P_k(0)=0$
. Otherwise, we say that
 $P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
is non-degenerate. The method of proof of Theorem 1.11 in the degenerate case can be also used to derive quantitative oscillation bounds for the polynomial Dunford and Zygmund theorem establishing (1.7).
$P\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
is non-degenerate. The method of proof of Theorem 1.11 in the degenerate case can be also used to derive quantitative oscillation bounds for the polynomial Dunford and Zygmund theorem establishing (1.7).
-
3. At the expense of great complexity, one can also prove that inequality (1.13) holds with
 ${\mathbb {Z}}_+$
in place of
${\mathbb {Z}}_+$
in place of
 $\mathbb {D}_{\tau }$
. However, we do not address this question here, since (1.13) is sufficient for our purposes and will allow us to establish Theorem 1.11(ii).
$\mathbb {D}_{\tau }$
. However, we do not address this question here, since (1.13) is sufficient for our purposes and will allow us to establish Theorem 1.11(ii). -
4. If
 $(X, \mathcal B(X), \mu )$
is a probability space and the measure preserving transformation T in Theorem 1.11 is totally ergodic, then Theorem 1.11(ii) implies (1.15)
$(X, \mathcal B(X), \mu )$
is a probability space and the measure preserving transformation T in Theorem 1.11 is totally ergodic, then Theorem 1.11(ii) implies (1.15) $$ \begin{align} \lim_{\min\{M_1,\ldots, M_k\}\to\infty}A_{M_1,\ldots, M_k; X, T}^{P}f(x)=\int_Xf(y)d\mu(y) \end{align} $$
$$ \begin{align} \lim_{\min\{M_1,\ldots, M_k\}\to\infty}A_{M_1,\ldots, M_k; X, T}^{P}f(x)=\int_Xf(y)d\mu(y) \end{align} $$
 $\mu $
-almost everywhere on X. We recall that a measure preserving transformation T is called ergodic on X if
$\mu $
-almost everywhere on X. We recall that a measure preserving transformation T is called ergodic on X if
 $T^{-1}[B]=B$
implies
$T^{-1}[B]=B$
implies
 $\mu (B)=0$
or
$\mu (B)=0$
or
 $\mu (B)=1$
, and totally ergodic if
$\mu (B)=1$
, and totally ergodic if
 $T^n$
is ergodic for every
$T^n$
is ergodic for every
 $n\in {\mathbb {Z}}_+$
.
$n\in {\mathbb {Z}}_+$
.
-
5. This paper is the first systematic treatment of multi-parameter oscillation semi-norms; see (2.9), Proposition 2.16 and Proposition 2.18. Moreover, it seems that the oscillation semi-norm is the only available tool that allows us to handle efficiently multi-parameter pointwise convergence problems with arithmetic features. This contrasts sharply with the one-parameter setting, where we have a variety of tools including oscillations, variations or jumps to handle pointwise convergence problems; see [Reference Jones, Seeger and Wright38, Reference Mirek, Stein and Trojan49] and the references therein. Multi-parameter oscillations (2.9) were considered for the first time in [Reference Jones, Rosenblatt and Wierdl37] in the context of the Dunford–Zygmund averages (1.1) for commuting measure-preserving transformations.
We close this subsection by emphasizing that the methods developed in this paper allow us to handle averages (1.8) with multiple polynomials. At the expense of some additional work, one can prove the following ergodic theorem.
Theorem 1.16. Let
![]() $(X, \mathcal B(X), \mu )$
be a
$(X, \mathcal B(X), \mu )$
be a
![]() $\sigma $
-finite measure space equipped with a family of commuting invertible and measure-preserving transformations
$\sigma $
-finite measure space equipped with a family of commuting invertible and measure-preserving transformations
![]() $T_1,T_2, T_{3}:X\to X$
. Let
$T_1,T_2, T_{3}:X\to X$
. Let
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial such that
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial such that
![]() $P(0, 0)=\partial _1P(0, 0)=\partial _2P(0, 0)=0$
, which additionally has partial degrees (as a polynomial of the variable
$P(0, 0)=\partial _1P(0, 0)=\partial _2P(0, 0)=0$
, which additionally has partial degrees (as a polynomial of the variable
![]() $\mathrm {m}_1$
and a polynomial of the variable
$\mathrm {m}_1$
and a polynomial of the variable
![]() $\mathrm {m}_2$
) at least two. Let
$\mathrm {m}_2$
) at least two. Let
![]() $f\in L^p(X)$
for some
$f\in L^p(X)$
for some
![]() $1\le p\le \infty $
, and let
$1\le p\le \infty $
, and let
![]() $ A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm { m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
be the average defined in (1.8) with
$ A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm { m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
be the average defined in (1.8) with
![]() $d=3$
,
$d=3$
,
![]() $k=2$
, and
$k=2$
, and
![]() $P_1(\mathrm {m}_1, \mathrm {m}_2)=\mathrm {m}_1$
,
$P_1(\mathrm {m}_1, \mathrm {m}_2)=\mathrm {m}_1$
,
![]() $P_2(\mathrm {m}_1, \mathrm {m}_2)=\mathrm {m}_2$
and
$P_2(\mathrm {m}_1, \mathrm {m}_2)=\mathrm {m}_2$
and
![]() $P_3(\mathrm {m}_1, \mathrm {m}_2)=P(\mathrm {m}_1, \mathrm {m}_2)$
.
$P_3(\mathrm {m}_1, \mathrm {m}_2)=P(\mathrm {m}_1, \mathrm {m}_2)$
.
-
(i) (Mean ergodic theorem) If
 $1<p<\infty $
, then the averages
$1<p<\infty $
, then the averages
 $A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm {m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
converge in
$A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm {m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
converge in
 $L^p(X)$
norm.
$L^p(X)$
norm. -
(ii) (Pointwise ergodic theorem) If
 $1<p<\infty $
, then the averages
$1<p<\infty $
, then the averages
 $A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm {m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
converge pointwise almost everywhere.
$A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm {m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
converge pointwise almost everywhere. -
(iii) (Maximal ergodic theorem) If
 $1<p\le \infty $
, then one has (1.17)
$1<p\le \infty $
, then one has (1.17) $$ \begin{align} \big\|\sup_{M_1, M_2\in{\mathbb{Z}}_+}|A_{M_1, M_2; X}^{\mathrm{m}_1,\mathrm{m}_2 , P(\mathrm{m}_1, \mathrm{m}_2)}f|\big\|_{L^p(X)}\lesssim_{p, P}\|f\|_{L^p(X)}. \end{align} $$
$$ \begin{align} \big\|\sup_{M_1, M_2\in{\mathbb{Z}}_+}|A_{M_1, M_2; X}^{\mathrm{m}_1,\mathrm{m}_2 , P(\mathrm{m}_1, \mathrm{m}_2)}f|\big\|_{L^p(X)}\lesssim_{p, P}\|f\|_{L^p(X)}. \end{align} $$
-
(iv) (Oscillation ergodic theorem) If
 $1<p<\infty $
and
$1<p<\infty $
and
 $\tau>1$
, then one has (1.18)where
$\tau>1$
, then one has (1.18)where $$ \begin{align} \qquad \qquad\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^2) }\big\|O_{I, J}(A_{M_1, M_2; X}^{\mathrm{m}_1,\mathrm{m}_2 , P(\mathrm{m}_1, \mathrm{m}_2)}f: M_1, M_2\in\mathbb{D}_{\tau})\|_{L^p(X)}\lesssim_{p, \tau, P}\|f\|_{L^p(X)}, \end{align} $$
$$ \begin{align} \qquad \qquad\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^2) }\big\|O_{I, J}(A_{M_1, M_2; X}^{\mathrm{m}_1,\mathrm{m}_2 , P(\mathrm{m}_1, \mathrm{m}_2)}f: M_1, M_2\in\mathbb{D}_{\tau})\|_{L^p(X)}\lesssim_{p, \tau, P}\|f\|_{L^p(X)}, \end{align} $$
 $\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
. The implicit constant in (1.17) and (1.18) may depend on
$\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
. The implicit constant in (1.17) and (1.18) may depend on
 $p, \tau , P$
.
$p, \tau , P$
.
For simplicity of notation, we have only formulated Theorem 1.16 in the two-parameter setting, but it can be extended to a multi-parameter setting as well. Namely, let
![]() $d\ge 2$
and let
$d\ge 2$
and let
![]() $(X, \mathcal B(X), \mu )$
be a
$(X, \mathcal B(X), \mu )$
be a
![]() $\sigma $
-finite measure space equipped with a family of commuting invertible and measure-preserving transformations
$\sigma $
-finite measure space equipped with a family of commuting invertible and measure-preserving transformations
![]() $T_1,\ldots , T_{d}:X\to X$
. Suppose that
$T_1,\ldots , T_{d}:X\to X$
. Suppose that
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_{d-1}]$
is a polynomial such that
$P\in {\mathbb {Z}}[\mathrm {m}_1,\ldots , \mathrm {m}_{d-1}]$
is a polynomial such that
which has partial degrees (as a polynomial of the variable
![]() $\mathrm {m}_i$
for any
$\mathrm {m}_i$
for any
![]() $i\in [d-1]$
) at least two. Then the conclusions of Theorem 1.16 remain true for the averages
$i\in [d-1]$
) at least two. Then the conclusions of Theorem 1.16 remain true for the averages
All remarks from items 1–4 after Theorem 1.11 remain true for ergodic averages from (1.19). Finally, we emphasize that Theorem 1.11 and Theorem 1.16 make a contribution to the famous Furstenberg–Bergelson–Leibman conjecture, which we now discuss.
1.3 Contributions to the Furstenberg–Bergelson–Leibman conjecture
Furstenberg’s ergodic proof [Reference Furstenberg27] of Szemerédi’s theorem [Reference Szemerédi59] (on the existence arbitrarily long arithmetic progressions in subsets of integers with positive density) was a departure point for modern ergodic Ramsey theory. We refer to the survey articles [Reference Bergelson, Pollicott and Schmidt7], [Reference Bergelson, Hasselblatt and Katok8] and [Reference Frantzikinakis25], where details (including comprehensive historical background) and an extensive literature are given about this fascinating subject. Ergodic Ramsey theory is a very rich body of research, consisting of many natural generalizations of Szemerédi’s theorem, including the celebrated polynomial Szemerédi theorem of Bergelson and Leibman [Reference Bergelson and Leibman9] that motivates the following far-reaching conjecture:
Conjecture 1.20 (Furstenberg–Bergelson–Leibman conjecture [Reference Bergelson and Leibman10, Section 5.5, p. 468])
For given parameters
![]() $d, k, n\in \mathbb {N}$
, let
$d, k, n\in \mathbb {N}$
, let
![]() $T_1,\ldots , T_d:X\to X$
be a family of invertible measure-preserving transformations of a probability measure space
$T_1,\ldots , T_d:X\to X$
be a family of invertible measure-preserving transformations of a probability measure space
![]() $(X, \mathcal B(X), \mu )$
that generates a nilpotent group of step
$(X, \mathcal B(X), \mu )$
that generates a nilpotent group of step
![]() $l\in {\mathbb {Z}}_{+}$
, and assume that
$l\in {\mathbb {Z}}_{+}$
, and assume that
![]() $P_{1, 1},\ldots ,P_{i, j},\ldots , P_{d, n}\in {\mathbb {Z}}[\mathrm m_1,\ldots , \mathrm m_k]$
. Then for any
$P_{1, 1},\ldots ,P_{i, j},\ldots , P_{d, n}\in {\mathbb {Z}}[\mathrm m_1,\ldots , \mathrm m_k]$
. Then for any
![]() $f_1, \ldots , f_n\in L^{\infty }(X)$
, the nonconventional multiple polynomial averages
$f_1, \ldots , f_n\in L^{\infty }(X)$
, the nonconventional multiple polynomial averages
 $$ \begin{align} A_{M; X, T_1,\ldots, T_d}^{P_{1, 1}, \ldots, P_{d, n}}(f_1,\ldots, f_n)(x) =\mathbb{E}_{m\in\prod_{j=1}^k[M_j]}\prod_{j=1}^nf_j(T_1^{P_{1, j}(m)}\cdots T_d^{P_{d, j}(m)} x) \end{align} $$
$$ \begin{align} A_{M; X, T_1,\ldots, T_d}^{P_{1, 1}, \ldots, P_{d, n}}(f_1,\ldots, f_n)(x) =\mathbb{E}_{m\in\prod_{j=1}^k[M_j]}\prod_{j=1}^nf_j(T_1^{P_{1, j}(m)}\cdots T_d^{P_{d, j}(m)} x) \end{align} $$
converge for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in X$
as
$x\in X$
as
![]() $\min \{M_1,\ldots , M_k\}\to \infty $
.
$\min \{M_1,\ldots , M_k\}\to \infty $
.
Variants of this conjecture were promoted in person by Furstenberg (we refer to Austin’s article [Reference Austin3, pp. 6662]) before it was published by Bergelson and Leibman [Reference Bergelson and Leibman10, Section 5.5, pp. 468] for
![]() $k=1$
. The nilpotent and multi-parameter setting is the appropriate setting for Conjecture 1.20 as convergence may fail if the transformations
$k=1$
. The nilpotent and multi-parameter setting is the appropriate setting for Conjecture 1.20 as convergence may fail if the transformations
![]() $T_1,\ldots , T_d$
generate a solvable group, as shown by Bergelson and Leibman [Reference Bergelson and Leibman10]. The
$T_1,\ldots , T_d$
generate a solvable group, as shown by Bergelson and Leibman [Reference Bergelson and Leibman10]. The
![]() $L^2(X)$
norm convergence of (1.21) has been studied since Furstenberg’s ergodic proof [Reference Furstenberg27] of Szemerédi’s theorem [Reference Szemerédi59] and is fairly well-understood (even in the setting of nilpotent groups) due to the groundbreaking work of Walsh [Reference Wooley70] with
$L^2(X)$
norm convergence of (1.21) has been studied since Furstenberg’s ergodic proof [Reference Furstenberg27] of Szemerédi’s theorem [Reference Szemerédi59] and is fairly well-understood (even in the setting of nilpotent groups) due to the groundbreaking work of Walsh [Reference Wooley70] with
![]() $M_1=\ldots =M_k$
. Prior to Walsh’s paper, extensive efforts had been made towards understanding
$M_1=\ldots =M_k$
. Prior to Walsh’s paper, extensive efforts had been made towards understanding
![]() $L^2(X)$
norm convergence, including breakthrough works of Host–Kra [Reference Host and Kra31], Ziegler [Reference Ziegler71], Bergelson [Reference Bergelson6] and Leibman [Reference Leibman43]. For more details and references, we also refer to [Reference Austin4, Reference Chu, Frantzikinakis and Host21, Reference Frantzikinakis and Kra26, Reference Host and Kra32, Reference Tao61] and the survey articles [Reference Bergelson, Pollicott and Schmidt7, Reference Bergelson, Hasselblatt and Katok8, Reference Frantzikinakis25].
$L^2(X)$
norm convergence, including breakthrough works of Host–Kra [Reference Host and Kra31], Ziegler [Reference Ziegler71], Bergelson [Reference Bergelson6] and Leibman [Reference Leibman43]. For more details and references, we also refer to [Reference Austin4, Reference Chu, Frantzikinakis and Host21, Reference Frantzikinakis and Kra26, Reference Host and Kra32, Reference Tao61] and the survey articles [Reference Bergelson, Pollicott and Schmidt7, Reference Bergelson, Hasselblatt and Katok8, Reference Frantzikinakis25].
The situation is dramatically different for the pointwise convergence problem (1.21), but recently, significant progress has been made towards establishing the Furstenberg–Bergelson–Leibman conjecture. Now let us make a few remarks about this conjecture, its history and the current state of the art.
-
1. The case
 $d=k=n=1$
of Conjecture 1.20 with
$d=k=n=1$
of Conjecture 1.20 with
 $P_{1, 1}(m)=m$
follows from Birkhoff’s ergodic theorem [Reference Birkhoff11]. In fact, the almost everywhere limit (as well as the norm limit; see also [Reference von Neumann64]) of (1.21) exists also for all functions
$P_{1, 1}(m)=m$
follows from Birkhoff’s ergodic theorem [Reference Birkhoff11]. In fact, the almost everywhere limit (as well as the norm limit; see also [Reference von Neumann64]) of (1.21) exists also for all functions
 $f\in L^p(X)$
, with
$f\in L^p(X)$
, with
 $1\le p<\infty $
, defined on any
$1\le p<\infty $
, defined on any
 $\sigma $
-finite measure space
$\sigma $
-finite measure space
 $(X, \mathcal B(X), \mu )$
.
$(X, \mathcal B(X), \mu )$
. -
2. The case
 $d=k=n=1$
of Conjecture 1.20 with arbitrary polynomials
$d=k=n=1$
of Conjecture 1.20 with arbitrary polynomials
 $P_{1, 1}\in {\mathbb {Z}}[\mathrm {m}]$
(as we have seen above) was the famous open problem of Bellow [Reference Bellow5] and Furstenberg [Reference Furstenberg24], which was solved by the first author [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] in the mid 1980s. In fact, in [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15], it was shown that the almost everywhere limit (as well as the norm limit; see also [Reference Furstenberg29]) of (1.21) exists also for all functions
$P_{1, 1}\in {\mathbb {Z}}[\mathrm {m}]$
(as we have seen above) was the famous open problem of Bellow [Reference Bellow5] and Furstenberg [Reference Furstenberg24], which was solved by the first author [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15] in the mid 1980s. In fact, in [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15], it was shown that the almost everywhere limit (as well as the norm limit; see also [Reference Furstenberg29]) of (1.21) exists also for all functions
 $f\in L^p(X)$
, with
$f\in L^p(X)$
, with
 $1< p<\infty $
, defined on any
$1< p<\infty $
, defined on any
 $\sigma $
-finite measure space
$\sigma $
-finite measure space
 $(X, \mathcal B(X), \mu )$
. In contrast to the Birkhoff theorem, if
$(X, \mathcal B(X), \mu )$
. In contrast to the Birkhoff theorem, if
 $P_{1,1}\in {\mathbb {Z}}[\mathrm {n}]$
is a polynomial of degree at least two, the pointwise convergence at the endpoint for
$P_{1,1}\in {\mathbb {Z}}[\mathrm {n}]$
is a polynomial of degree at least two, the pointwise convergence at the endpoint for
 $p=1$
may fail as was shown by Buczolich and Mauldin [Reference Buczolich and Mauldin18] for
$p=1$
may fail as was shown by Buczolich and Mauldin [Reference Buczolich and Mauldin18] for
 $P_{1,1}(m)=m^2$
and by LaVictoire [Reference LaVictoire42] for
$P_{1,1}(m)=m^2$
and by LaVictoire [Reference LaVictoire42] for
 $P_{1,1}(m)=m^k$
for any
$P_{1,1}(m)=m^k$
for any
 $k\ge 2$
.
$k\ge 2$
. -
3. In the commutative case (step
 $\ell = 1$
) where
$\ell = 1$
) where
 $d,k\in {\mathbb {Z}}_+$
and
$d,k\in {\mathbb {Z}}_+$
and
 $n=1$
of Conjecture 1.20 with arbitrary polynomials
$n=1$
of Conjecture 1.20 with arbitrary polynomials
 $P_{1,1},\ldots , P_{d,1}\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
in the diagonal setting
$P_{1,1},\ldots , P_{d,1}\in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
in the diagonal setting
 $M_1=\ldots =M_k$
– that is, the multi-dimensional one-parameter setting – was solved by the second author with Trojan in [Reference Mirek and Trojan54]. As before, it was shown that the almost everywhere limit (as well as the norm limit) of (1.21) exists also for all functions
$M_1=\ldots =M_k$
– that is, the multi-dimensional one-parameter setting – was solved by the second author with Trojan in [Reference Mirek and Trojan54]. As before, it was shown that the almost everywhere limit (as well as the norm limit) of (1.21) exists also for all functions
 $f\in L^p(X)$
, with
$f\in L^p(X)$
, with
 $1< p<\infty $
, defined on any
$1< p<\infty $
, defined on any
 $\sigma $
-finite measure space
$\sigma $
-finite measure space
 $(X, \mathcal B(X), \mu )$
.
$(X, \mathcal B(X), \mu )$
. -
4. The question to what extent one can relax the commutation relations between
 $T_1,\ldots , T_d$
in (1.21), even in the one-parameter case
$T_1,\ldots , T_d$
in (1.21), even in the one-parameter case
 $M_1=\ldots =M_k$
, is very intriguing. Some particular examples of averages (1.21) with
$M_1=\ldots =M_k$
, is very intriguing. Some particular examples of averages (1.21) with
 $d,k\in {\mathbb {Z}}_+$
and
$d,k\in {\mathbb {Z}}_+$
and
 $n=1$
and polynomial mappings with degree at most two in the step two nilpotent setting were studied in [Reference Ionescu, Magyar, Stein and Wainger33, Reference Magyar, Stein and Wainger45]. Recently, the second author with Ionescu, Magyar and Szarek [Reference Ionescu, Magyar, Mirek and Szarek36] established Conjecture 1.20 with
$n=1$
and polynomial mappings with degree at most two in the step two nilpotent setting were studied in [Reference Ionescu, Magyar, Stein and Wainger33, Reference Magyar, Stein and Wainger45]. Recently, the second author with Ionescu, Magyar and Szarek [Reference Ionescu, Magyar, Mirek and Szarek36] established Conjecture 1.20 with
 $d\in {\mathbb {Z}}_+$
and
$d\in {\mathbb {Z}}_+$
and
 $k=n=1$
and arbitrary polynomials
$k=n=1$
and arbitrary polynomials
 $P_{1,1},\ldots , P_{d,1}\in {\mathbb {Z}}[\mathrm {m}]$
in the nilpotent setting (i.e., when
$P_{1,1},\ldots , P_{d,1}\in {\mathbb {Z}}[\mathrm {m}]$
in the nilpotent setting (i.e., when
 $T_1,\ldots , T_{d}:X\to X$
is a family of invertible measure-preserving transformations of a
$T_1,\ldots , T_{d}:X\to X$
is a family of invertible measure-preserving transformations of a
 $\sigma $
-finite measure space
$\sigma $
-finite measure space
 $(X, \mathcal B(X), \mu )$
that generates a nilpotent group of step two).
$(X, \mathcal B(X), \mu )$
that generates a nilpotent group of step two). -
5. In contrast to the commutative linear theory, the multilinear theory is wide open. Only a few results are known in the bilinear
 $n=2$
and commutative
$n=2$
and commutative
 $d=k=1$
setting. The first author [Reference Bourgain16] established pointwise convergence when
$d=k=1$
setting. The first author [Reference Bourgain16] established pointwise convergence when
 $P_{1,1}(m)=am$
and
$P_{1,1}(m)=am$
and
 $P_{1,2}(m)=bm$
, with
$P_{1,2}(m)=bm$
, with
 $a, b\in {\mathbb {Z}}$
. Recently, the third author with Krause and Tao [Reference Krause, Mirek and Tao41] proved pointwise convergence for the polynomial Furstenberg–Weiss averages [Reference Furstenberg28, Reference Furstenberg and Weiss30] corresponding to
$a, b\in {\mathbb {Z}}$
. Recently, the third author with Krause and Tao [Reference Krause, Mirek and Tao41] proved pointwise convergence for the polynomial Furstenberg–Weiss averages [Reference Furstenberg28, Reference Furstenberg and Weiss30] corresponding to
 $P_{1,1}(m)=m$
and
$P_{1,1}(m)=m$
and
 $P_{1, 2}(m)=P(m)$
with
$P_{1, 2}(m)=P(m)$
with
 $P\in {\mathbb {Z}}[\mathrm {m}]$
and
$P\in {\mathbb {Z}}[\mathrm {m}]$
and
 $\mathrm {deg }\,P\ge 2$
.
$\mathrm {deg }\,P\ge 2$
. -
6. A genuinely multi-parameter case
 $d=k\ge 2$
with
$d=k\ge 2$
with
 $n=1$
of Conjecture 1.20 for averages (1.21) with linear orbits (i.e.
$n=1$
of Conjecture 1.20 for averages (1.21) with linear orbits (i.e.
 $P_{j,1}(m_1, \ldots , m_d)=m_j$
for
$P_{j,1}(m_1, \ldots , m_d)=m_j$
for
 $j\in [d]$
) was established independently by Dunford [Reference Dunford23] and Zygmund [Reference Zygmund72] in the early 1950s. Moreover, it follows from [Reference Dunford23, Reference Zygmund72] that the almost everywhere convergence (as well as the norm convergence) of (1.21) holds for all functions
$j\in [d]$
) was established independently by Dunford [Reference Dunford23] and Zygmund [Reference Zygmund72] in the early 1950s. Moreover, it follows from [Reference Dunford23, Reference Zygmund72] that the almost everywhere convergence (as well as the norm convergence) of (1.21) holds for all functions
 $f\in L^p(X)$
, with
$f\in L^p(X)$
, with
 $1< p<\infty $
, defined on any
$1< p<\infty $
, defined on any
 $\sigma $
-finite measure space
$\sigma $
-finite measure space
 $(X, \mathcal B(X), \mu )$
equipped with a family of measure-preserving transformations
$(X, \mathcal B(X), \mu )$
equipped with a family of measure-preserving transformations
 $T_1,\ldots , T_d:X\to X$
, which does not need to be commutative. One also knows that pointwise convergence fails if
$T_1,\ldots , T_d:X\to X$
, which does not need to be commutative. One also knows that pointwise convergence fails if
 $p=1$
. A polynomial variant of the Dunford and Zygmund theorem was discussed above; see (1.7).
$p=1$
. A polynomial variant of the Dunford and Zygmund theorem was discussed above; see (1.7).
We close this discussion by emphasizing that Theorem 1.11 and Theorem 1.16 also contribute to the Furstenberg–Bergelson–Leibman conjecture and, together with all the results listed above, support the evidence that Conjecture 1.20 may be true in full generality though a complete solution seems very difficult.
1.4 Overview of the paper
The paper is organized as follows. In Section 2, we fix necessary notation and terminology. We also introduce the definition of multi-parameter oscillations (2.9) and collect their useful properties; see Proposition 2.16 and Proposition 2.18. In Section 3, we give a detailed proof of Theorem 1.11 by reducing the matter to oscillation estimates for truncated variants of averages
![]() $A_{M_1, M_2; X}^{ P}f$
; see definition (3.6) and Theorem 3.16, which in turn is reduced to the integer shift system, and Theorem 3.19. A result that may be of independent interest is Proposition 3.7, which shows that oscillations for
$A_{M_1, M_2; X}^{ P}f$
; see definition (3.6) and Theorem 3.16, which in turn is reduced to the integer shift system, and Theorem 3.19. A result that may be of independent interest is Proposition 3.7, which shows that oscillations for
![]() $A_{M_1, M_2; X}^{P}f$
and their truncated variants are, in fact, comparable. In Section 3, see inequality (3.5), and we also illustrate how to prove Theorem 1.11 in the degenerate case in the sense of definition (1.14) stated after Theorem 1.11. These arguments can be also used to prove oscillation bounds for the polynomial Dunford and Zygmund theorem, which in turn imply (1.7).
$A_{M_1, M_2; X}^{P}f$
and their truncated variants are, in fact, comparable. In Section 3, see inequality (3.5), and we also illustrate how to prove Theorem 1.11 in the degenerate case in the sense of definition (1.14) stated after Theorem 1.11. These arguments can be also used to prove oscillation bounds for the polynomial Dunford and Zygmund theorem, which in turn imply (1.7).
We start with a brief overview of the proof of Theorem 3.19, which implies Theorem 1.5 when
![]() $k=2$
and takes up the bulk of this paper. The proof requires substantial new ideas to overcome a series of new difficulties arising in the multi-parameter setting. These complications do not arise in the one-parameter setup [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15]. The most notable obstacle is the lack of nestedness in the definition of averaging operators (1.8) when the parameters
$k=2$
and takes up the bulk of this paper. The proof requires substantial new ideas to overcome a series of new difficulties arising in the multi-parameter setting. These complications do not arise in the one-parameter setup [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15]. The most notable obstacle is the lack of nestedness in the definition of averaging operators (1.8) when the parameters
![]() $M_1,\ldots , M_k$
are allowed to run independently. The lack of nestedness complicates every argument in the circle method, which is the main tool in these kinds of problems. In order to understand how the lack of nestedness may affect the underlying arguments, it will be convenient to illustrate this phenomenon by comparing Figure 1 and Figure 2 below. The first picture (Figure 1) represents the family of nested cubes, which is increasing when the time parameter increases. The diagonal relation between parameters
$M_1,\ldots , M_k$
are allowed to run independently. The lack of nestedness complicates every argument in the circle method, which is the main tool in these kinds of problems. In order to understand how the lack of nestedness may affect the underlying arguments, it will be convenient to illustrate this phenomenon by comparing Figure 1 and Figure 2 below. The first picture (Figure 1) represents the family of nested cubes, which is increasing when the time parameter increases. The diagonal relation between parameters
![]() $M_1=\ldots =M_k$
is critical.
$M_1=\ldots =M_k$
is critical.
The second picture (Figure 2) represents the family which is genuinely multi-parameter and there is no nestedness as the parameters
![]() $M_1,\ldots , M_k$
vary independently.
$M_1,\ldots , M_k$
vary independently.
Our remedy to overcome the lack of nestedness will be to develop the so-called multi-parameter circle method, which will be based on an iterative implementation of the classical circle method. Although this idea sounds very simple, it is fairly challenging to formalize it in the context of Conjecture 1.3. We remark that the multi-parameter circle method has been developed for many years in the context of various problems arising in number theory (see [Reference Arkhipov, Chubarikov and Karatsuba1] for more details and references, including a comprehensive historical background) though it is not applicable directly in the ergodic context. We now highlight the key ingredients that we develop in this paper and that will lead us to develop the multi-parameter circle method in the context of Theorem 3.19:
-
(i) ‘Backwards’ Newton diagram is the key tool allowing us to overcome the problem with the lack of nestedness. In particular, it permits us to understand geometric properties of the underlying polynomials in Theorem 3.19 by extracting dominating monomials. The latter are critical in making a distinction between minor and major arcs in the multi-parameter circle method. As far as we know, this is the first time when the concept of Newton diagrams is exploited in problems concerning pointwise ergodic theory. We refer to Section 4 for details.
-
(ii) We derive new estimates for multi-parameter exponential sums arising in the analysis of Fourier multipliers corresponding to averages (1.10). In Section 5, we build a theory of double exponential sums, which is dictated by the geometry of the corresponding ‘backwards’ Newton diagrams. Although the theory of multi-parameter exponential sums is rich (see for example, [Reference Arkhipov, Chubarikov and Karatsuba1]), our results seem to be new and the idea of exploiting ‘backwards’ Newton diagrams and iterative applications of the Vinogradov mean value theorem [Reference Bourgain, Demeter and Guth17] in estimates of exponential sums is quite efficient.
-
(iii) A multi-parameter Ionescu–Wainger multiplier theory is developed in Section 6. The Ionescu–Wainger multiplier theorem [Reference Ionescu and Wainger34] was originally proved for linear operators; see also [Reference Mirek46, Reference Mirek, Stein and Zorin-Kranich52, Reference Pierce55, Reference Tao62]. In this paper, we prove a semi-norm variant of the Ionescu–Wainger theory in the one-parameter setting, which is consequently upgraded to the multi-parameter setup. ‘Backwards’ Newton diagrams play an essential role in our considerations here as well.
-
(iv) Finally, we arrive at the stage where the multi-parameter circle method is feasible by a delicate iterative application of the classical circle method. In this part of the argument, the lack of nestedness is particularly unpleasant, causing serious difficulties in controlling error terms that arise in estimating contributions of the corresponding Fourier multipliers on minor and major arcs, which are genuinely multi-parameter. In Section 7, we illustrate how one can use all the tools developed in the previous sections to give a rigorous proof of Theorem 3.19.
We now take a closer look at the tools highlighted above. In Section 4, we introduce the concept of ‘backwards’ Newton diagram, which is the key to circumvent the difficulties caused by the lack of nestedness. The ‘backwards’ Newton diagram splits the parameter space into a finite number of sectors, where certain relations between parameters are given. In each of these sectors there is a dominating monomial which, in turn, gives rise to an implementation of the circle method to each of the sectors separately. The distinctions between minor and major arcs are then dictated by the degree of the associated dominating monomial. At this stage, we eliminate minor arcs by invoking estimates of double exponential sums from Proposition 5.37. This proposition is essential in our argument; its proof is given in Section 5. The key ingredients are Proposition 5.22, which may be thought of as a two parameter counterpart of the classical Weyl’s inequality, and the properties of the ‘backwards’ Newton diagram. Although the theory of multi-parameter exponential sums has been developed over the years (see [Reference Arkhipov, Chubarikov and Karatsuba1] for a comprehensive treatment of the subject), we require more delicate estimates than those available in the existing literature. In this paper, we give an ad-hoc proof of Proposition 5.22, which follows from an iterative application of Vinogradov’s mean value theorem, and may be interesting in its own right. In Section 5, we also develop estimates for complete exponential sums. In Section 6, we develop the Ionescu–Wainger multiplier theory for various semi-norms in one-parameter as well as in multi-parameter settings. Our result in the one-parameter setting, Theorem 6.14, is formulated for oscillations and maximal functions, but the proofs also work for
![]() $\rho $
-variations or jumps. In fact, Theorem 6.14 is the starting point for establishing the corresponding multi-parameter Ionescu–Wainger theory for oscillations. The latter theorem will be directly applicable in the analysis of multipliers associated with the averages
$\rho $
-variations or jumps. In fact, Theorem 6.14 is the starting point for establishing the corresponding multi-parameter Ionescu–Wainger theory for oscillations. The latter theorem will be directly applicable in the analysis of multipliers associated with the averages
![]() $A_{M_1, M_2; X}^{P}f$
. The results of Section 6 are critical in our multi-parameter circle method that is presented in Section 7, as it allows us to efficiently control the error terms that arise on major arcs as well as the contribution coming from the main part. In contrast to the one-parameter theory [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15], the challenge here is to control, for instance, maximal functions corresponding to error terms. For this purpose, all error terms have to be provided with asymptotic precision, which usually requires careful arguments. The details of the multi-parameter circle method are presented in Section 7 in the context of the proof of Theorem 3.19.
$A_{M_1, M_2; X}^{P}f$
. The results of Section 6 are critical in our multi-parameter circle method that is presented in Section 7, as it allows us to efficiently control the error terms that arise on major arcs as well as the contribution coming from the main part. In contrast to the one-parameter theory [Reference Bourgain13, Reference Bourgain14, Reference Bourgain15], the challenge here is to control, for instance, maximal functions corresponding to error terms. For this purpose, all error terms have to be provided with asymptotic precision, which usually requires careful arguments. The details of the multi-parameter circle method are presented in Section 7 in the context of the proof of Theorem 3.19.
1.5 More about Conjecture 1.20
Conjecture 1.20 is one of the major open problems in pointwise ergodic theory, which seems to be very difficult due to its multilinear nature. Here, in light of the Arkhipov, Chubarikov and Karatsuba [Reference Arkhipov, Chubarikov and Karatsuba2] equidistribution theory which works also for multiple polynomials, it seems reasonable to propose a slightly more modest problem (implied by Conjecture 1.20) though still very interesting and challenging that can be subsumed under the following conjecture:
Conjecture 1.22. Let
![]() $d, k\in {\mathbb {Z}}_+$
be given and let
$d, k\in {\mathbb {Z}}_+$
be given and let
![]() $(X, \mathcal B(X), \mu )$
be a probability measure space endowed with a family of invertible commuting measure-preserving transformations
$(X, \mathcal B(X), \mu )$
be a probability measure space endowed with a family of invertible commuting measure-preserving transformations
![]() $T_1,\ldots , T_d:X\to X$
. Assume that
$T_1,\ldots , T_d:X\to X$
. Assume that
![]() $P_1,\ldots , P_d \in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
. Then for any
$P_1,\ldots , P_d \in {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
. Then for any
![]() $f\in L^{\infty }(X)$
, the multi-parameter linear polynomial averages
$f\in L^{\infty }(X)$
, the multi-parameter linear polynomial averages
converge for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in X$
, as
$x\in X$
, as
![]() $\min \{M_1,\ldots , M_k\}\to \infty $
.
$\min \{M_1,\ldots , M_k\}\to \infty $
.
Even though we prove Conjecture 1.3 here, it is not clear whether Conjecture 1.22 is true for all polynomials. If it is not true for all polynomials, it would be interesting, in view of Theorem 1.16, to characterize the class of those polynomials for which Conjecture 1.22 holds. Although the averages from Theorem 1.11 and Theorem 1.16 share a lot of difficulties that arise in the general case, there are some cases that are not covered by the methods of this paper. An interesting difficulty arises for the so-called partially complete exponential sums when we are seeking estimates of the form
 $$ \begin{align} \frac{1}{M_1q}\sum_{m_1=1}^{M_1}\Big|\sum_{m_2=1}^q\boldsymbol{e}(a_2m_2/q+a_3P(m_1, m_2)/q)\Big|\lesssim q^{-\delta}, \end{align} $$
$$ \begin{align} \frac{1}{M_1q}\sum_{m_1=1}^{M_1}\Big|\sum_{m_2=1}^q\boldsymbol{e}(a_2m_2/q+a_3P(m_1, m_2)/q)\Big|\lesssim q^{-\delta}, \end{align} $$
for all
![]() $M_1, q\in {\mathbb {Z}}_+$
and some
$M_1, q\in {\mathbb {Z}}_+$
and some
![]() $\delta \in (0,1)$
, whenever
$\delta \in (0,1)$
, whenever
![]() $(a_2, a_3, q)=1$
. These kinds of estimates arise from applications of the circle method with respect to the second variable
$(a_2, a_3, q)=1$
. These kinds of estimates arise from applications of the circle method with respect to the second variable
![]() $m_2$
for the averages
$m_2$
for the averages
![]() $A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm {m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
when we are at the stage of applying the circle method with respect to the first variable
$A_{M_1, M_2; X}^{\mathrm {m}_1,\mathrm {m}_2 , P(\mathrm {m}_1, \mathrm {m}_2)}f$
when we are at the stage of applying the circle method with respect to the first variable
![]() $m_1$
. Here, the assumption that P has partial degrees (as a polynomial of the variable
$m_1$
. Here, the assumption that P has partial degrees (as a polynomial of the variable
![]() $m_1$
and a polynomial of the variable
$m_1$
and a polynomial of the variable
![]() $m_2$
) at least two is essential. Otherwise, if
$m_2$
) at least two is essential. Otherwise, if
![]() $M_1<q$
, the decay
$M_1<q$
, the decay
![]() $q^{-\delta }$
in (1.23) is not possible. In order to see this, it suffices to take
$q^{-\delta }$
in (1.23) is not possible. In order to see this, it suffices to take
![]() $P(m_1, m_2)=m_1^2m_2$
. A proof of Theorem 1.16 for polynomials of this type, as well as Conjecture 1.22, will require a deeper understanding and substantially new methods. We believe that the proof of Theorem 1.11 is an important contribution towards understanding Conjecture 1.22 that may shed new light on the general case and either lead to its full resolution or to a counterexample. The second and fourth authors plan to pursue this problem in the future.
$P(m_1, m_2)=m_1^2m_2$
. A proof of Theorem 1.16 for polynomials of this type, as well as Conjecture 1.22, will require a deeper understanding and substantially new methods. We believe that the proof of Theorem 1.11 is an important contribution towards understanding Conjecture 1.22 that may shed new light on the general case and either lead to its full resolution or to a counterexample. The second and fourth authors plan to pursue this problem in the future.
1.6 In Memoriam
It was a great privilege and an unforgettable experience for the second and fourth authors to know and work with Elias M. Stein (January 13, 1931–December 23, 2018) and Jean Bourgain (February 28, 1954–December 22, 2018). Eli and Jean had an immeasurable effect on our lives and careers. It was a very sad time for us when we learned that Eli and Jean passed away within an interval of one day in December 2018. We miss our friends and collaborators dearly.
We now briefly describe how the collaboration on this project arose. In 2011, the second and fourth authors started to work on some aspects of a multi-parameter circle method in the context of various discrete multi-parameter operators. These efforts resulted in a draft on estimates for certain two-parameter exponential sums. This draft was sent to the first author sometime in the first part of 2016. In October 2016, when the second author was a member of the Institute for Advanced Study, it was realized (during a discussion between the first two authors) that the estimates from this draft are closely related to a multi-parameter Vinogradov’s mean value theorem. This was interesting to the first author who at that time was involved in developing the theory of decoupling. We also realized that some ideas of a multi-parameter circle method from the draft of the second and fourth authors may be upgraded and used in attacking a multi-parameter variant of the Bellow and Furstenberg problem formulated in Conjecture 1.3. That was the first time when the second, third and fourth authors learned about this conjecture and unpublished observations of the first author from the late 1980s that resulted in establishing pointwise convergence in (1.7). This was the starting point of our collaboration. At that time another question arose, which is also related to this paper. It is interesting whether a sharp multi-parameter variant of Vinogradov’s mean value theorem can be proved using the recent developments in the decoupling theory from [Reference Bourgain, Demeter and Guth17]. A multi-parameter Vinogradov’s mean value theorem was investigated in [Reference Arkhipov, Chubarikov and Karatsuba1], but the bounds are not optimal. So the question is about adapting the methods from [Reference Bourgain, Demeter and Guth17] to the multi-parameter setting in order to obtain sharp bounds, and their applications in the exponential sum estimates.
A substantial part of this project was completed at the end of November/beginning of December 2016, when the fourth author visited Princeton University and the Institute for Advanced Study. At that time, we discussed (more or less) all tools that were needed to establish Theorem 1.11 for the monomial
![]() $P(m_1, m_2)=m_1^2m_2^3$
. Then we were convinced that we could establish Conjecture 1.22 in full generality, but various difficulties arose when we started to work out the details, and we ultimately only managed to prove Theorem 1.11 and Theorem 1.16. The second and fourth authors decided to illustrate the arguments in the two-parameter setting and the reason is twofold. On the one hand, we wanted to avoid introducing heavy multi-parameter notation capturing all combinatorial nuances arising in this project. On the other hand, what is more important is that we wanted to illustrate the spirit of our discussions that took place in 2016. For instance, the arguments presented in Section 5 can be derived by using Weyl differencing argument, which may be even simpler and can be easily adapted to the multi-parameter setting, though our presentation is very close to the arguments that we developed in 2016, and also motivates the question about the role of decoupling theory in the multi-parameter Vinogradov’s mean value theorem that we have stated above.
$P(m_1, m_2)=m_1^2m_2^3$
. Then we were convinced that we could establish Conjecture 1.22 in full generality, but various difficulties arose when we started to work out the details, and we ultimately only managed to prove Theorem 1.11 and Theorem 1.16. The second and fourth authors decided to illustrate the arguments in the two-parameter setting and the reason is twofold. On the one hand, we wanted to avoid introducing heavy multi-parameter notation capturing all combinatorial nuances arising in this project. On the other hand, what is more important is that we wanted to illustrate the spirit of our discussions that took place in 2016. For instance, the arguments presented in Section 5 can be derived by using Weyl differencing argument, which may be even simpler and can be easily adapted to the multi-parameter setting, though our presentation is very close to the arguments that we developed in 2016, and also motivates the question about the role of decoupling theory in the multi-parameter Vinogradov’s mean value theorem that we have stated above.
2 Notation and useful tools
We now set up notation that will be used throughout the paper. We also collect useful tools and basic properties of oscillation semi-norms that will be used in the paper.
2.1 Basic notation
The set of positive integers and nonnegative integers will be denoted, respectively, by
![]() ${\mathbb {Z}}_+:=\{1, 2, \ldots \}$
and
${\mathbb {Z}}_+:=\{1, 2, \ldots \}$
and
![]() $\mathbb {N}:=\{0,1,2,\ldots \}$
. For
$\mathbb {N}:=\{0,1,2,\ldots \}$
. For
![]() $d\in {\mathbb {Z}}_+$
, the sets
$d\in {\mathbb {Z}}_+$
, the sets
![]() ${\mathbb {Z}}^d$
,
${\mathbb {Z}}^d$
,
![]() $\mathbb {R}^d$
,
$\mathbb {R}^d$
,
![]() $\mathbb {C}^d$
and
$\mathbb {C}^d$
and
![]() $\mathbb {T}^d:=\mathbb {R}^d/{\mathbb {Z}}^d$
have standard meaning. For any
$\mathbb {T}^d:=\mathbb {R}^d/{\mathbb {Z}}^d$
have standard meaning. For any
![]() $x\in \mathbb {R}$
, we will use the floor and fractional part functions
$x\in \mathbb {R}$
, we will use the floor and fractional part functions
For
![]() $x, y\in \mathbb {R}$
, we shall also write
$x, y\in \mathbb {R}$
, we shall also write
![]() $x \vee y := \max \{x,y\}$
and
$x \vee y := \max \{x,y\}$
and
![]() $x \wedge y := \min \{x,y\}$
. We denote
$x \wedge y := \min \{x,y\}$
. We denote
![]() $\mathbb {R}_+:=(0, \infty )$
, and for every
$\mathbb {R}_+:=(0, \infty )$
, and for every
![]() $N\in \mathbb {R}_+$
, we set
$N\in \mathbb {R}_+$
, we set
and we will also write
 $$ \begin{align*} \mathbb{N}_{\le N}:= [0, N]\cap\mathbb{N},\ \: \quad &\text{ and } \quad \mathbb{N}_{< N}:= [0, N)\cap\mathbb{N},\\ \mathbb{N}_{\ge N}:= [N, \infty)\cap\mathbb{N}, \quad &\text{ and } \quad \mathbb{N}_{> N}:= (N, \infty)\cap\mathbb{N}. \end{align*} $$
$$ \begin{align*} \mathbb{N}_{\le N}:= [0, N]\cap\mathbb{N},\ \: \quad &\text{ and } \quad \mathbb{N}_{< N}:= [0, N)\cap\mathbb{N},\\ \mathbb{N}_{\ge N}:= [N, \infty)\cap\mathbb{N}, \quad &\text{ and } \quad \mathbb{N}_{> N}:= (N, \infty)\cap\mathbb{N}. \end{align*} $$
For any
![]() $\tau>1$
, we will consider the set
$\tau>1$
, we will consider the set
For
![]() $a = (a_1,\ldots , a_n) \in {\mathbb {Z}}^n$
and
$a = (a_1,\ldots , a_n) \in {\mathbb {Z}}^n$
and
![]() $q\ge 1$
an integer, we denote by
$q\ge 1$
an integer, we denote by
![]() $(a,q)$
the greatest common divisor of a and q; that is, the largest integer
$(a,q)$
the greatest common divisor of a and q; that is, the largest integer
![]() $d\ge 1$
that divides q and all the components
$d\ge 1$
that divides q and all the components
![]() $a_1, \ldots , a_n$
. Clearly, any vector in
$a_1, \ldots , a_n$
. Clearly, any vector in
![]() $\mathbb {Q}^n$
has a unique representation as
$\mathbb {Q}^n$
has a unique representation as
![]() $a/q$
with
$a/q$
with
![]() $q\in {\mathbb {Z}}_{+}$
,
$q\in {\mathbb {Z}}_{+}$
,
![]() $a \in {\mathbb {Z}}^n$
and
$a \in {\mathbb {Z}}^n$
and
![]() $(a,q)=1$
.
$(a,q)=1$
.
We use
![]() to denote the indicator function of a set A. If S is a statement, we write
to denote the indicator function of a set A. If S is a statement, we write
![]() to denote its indicator, equal to
to denote its indicator, equal to
![]() $1$
if S is true and
$1$
if S is true and
![]() $0$
if S is false. For instance,
$0$
if S is false. For instance,
![]() .
.
Throughout the paper,
![]() $C>0$
is an absolute constant which may change from occurrence to occurrence. For two nonnegative quantities
$C>0$
is an absolute constant which may change from occurrence to occurrence. For two nonnegative quantities
![]() $A, B$
, we write
$A, B$
, we write
![]() $A \lesssim B$
if there is an absolute constant
$A \lesssim B$
if there is an absolute constant
![]() $C>0$
such that
$C>0$
such that
![]() $A\le CB$
. We will write
$A\le CB$
. We will write
![]() $A \simeq B$
when
$A \simeq B$
when
![]() $A \lesssim B\lesssim A$
. We will write
$A \lesssim B\lesssim A$
. We will write
![]() $\lesssim _{\delta }$
or
$\lesssim _{\delta }$
or
![]() $\simeq _{\delta }$
to emphasize that the implicit constant depends on
$\simeq _{\delta }$
to emphasize that the implicit constant depends on
![]() $\delta $
. For a function
$\delta $
. For a function
![]() $f:X\to \mathbb {C}$
and positive-valued function
$f:X\to \mathbb {C}$
and positive-valued function
![]() $g:X\to (0, \infty )$
, we write
$g:X\to (0, \infty )$
, we write
![]() $f = O(g)$
if there exists a constant
$f = O(g)$
if there exists a constant
![]() $C>0$
such that
$C>0$
such that
![]() $|f(x)| \le C g(x)$
for all
$|f(x)| \le C g(x)$
for all
![]() $x\in X$
. We will also write
$x\in X$
. We will also write
![]() $f = O_{\delta }(g)$
if the implicit constant depends on
$f = O_{\delta }(g)$
if the implicit constant depends on
![]() $\delta $
.
$\delta $
.
2.2 Summation by parts
For any real numbers
![]() $u<v$
and any sequences
$u<v$
and any sequences
![]() $(a_n:n\in {\mathbb {Z}})\subseteq \mathbb {C}$
and
$(a_n:n\in {\mathbb {Z}})\subseteq \mathbb {C}$
and
![]() $(b_n:n\in {\mathbb {Z}})\subseteq \mathbb {C}$
, we will use the following version of the summation by parts formula
$(b_n:n\in {\mathbb {Z}})\subseteq \mathbb {C}$
, we will use the following version of the summation by parts formula
where
![]() $S_w:=\sum _{k\in (u, w]\cap {\mathbb {Z}}}a_k$
for any
$S_w:=\sum _{k\in (u, w]\cap {\mathbb {Z}}}a_k$
for any
![]() $w>u$
.
$w>u$
.
2.3 Euclidean spaces
For
![]() $d\in {\mathbb {Z}}_+$
, the set
$d\in {\mathbb {Z}}_+$
, the set
denotes the standard basis in
![]() $\mathbb {R}^d$
. The standard inner product and the corresponding Euclidean norm on
$\mathbb {R}^d$
. The standard inner product and the corresponding Euclidean norm on
![]() $\mathbb {R}^d$
are denoted by
$\mathbb {R}^d$
are denoted by

for every
![]() $x=(x_1,\ldots , x_d)$
and
$x=(x_1,\ldots , x_d)$
and
![]() $\xi =(\xi _1, \ldots , \xi _d)\in \mathbb {R}^d$
.
$\xi =(\xi _1, \ldots , \xi _d)\in \mathbb {R}^d$
.
Throughout the paper, the d-dimensional torus
![]() $\mathbb {T}^d$
, which unless otherwise stated will be identified with
$\mathbb {T}^d$
, which unless otherwise stated will be identified with
![]() $[-1/2, 1/2)^d$
, is a priori endowed with the periodic norm
$[-1/2, 1/2)^d$
, is a priori endowed with the periodic norm
 $$ \begin{align*} \left\lVert {\xi} \right\rVert :=\Big(\sum_{k=1}^d \left\lVert {\xi_k} \right\rVert ^2\Big)^{1/2} \qquad \text{for}\qquad \xi=(\xi_1,\ldots,\xi_d)\in\mathbb{T}^d, \end{align*} $$
$$ \begin{align*} \left\lVert {\xi} \right\rVert :=\Big(\sum_{k=1}^d \left\lVert {\xi_k} \right\rVert ^2\Big)^{1/2} \qquad \text{for}\qquad \xi=(\xi_1,\ldots,\xi_d)\in\mathbb{T}^d, \end{align*} $$
where
![]() $ \left \lVert {\xi _k} \right \rVert =\operatorname {\mathrm {disr}}(\xi _k, {\mathbb {Z}})$
for all
$ \left \lVert {\xi _k} \right \rVert =\operatorname {\mathrm {disr}}(\xi _k, {\mathbb {Z}})$
for all
![]() $\xi _k\in \mathbb {T}$
and
$\xi _k\in \mathbb {T}$
and
![]() $k\in [d]$
. However, identifying
$k\in [d]$
. However, identifying
![]() $\mathbb {T}^d$
with
$\mathbb {T}^d$
with
![]() $[-1/2, 1/2)^d$
, we see that the norm
$[-1/2, 1/2)^d$
, we see that the norm
![]() $ \left \lVert {\:\cdot \:} \right \rVert $
coincides with the Euclidean norm
$ \left \lVert {\:\cdot \:} \right \rVert $
coincides with the Euclidean norm
![]() $ \left \lvert {\:\cdot \:} \right \rvert $
restricted to
$ \left \lvert {\:\cdot \:} \right \rvert $
restricted to
![]() $[-1/2, 1/2)^d$
.
$[-1/2, 1/2)^d$
.
2.4 Smooth functions
The partial derivative of a differentiable function
![]() $f:\mathbb {R}^d\to \mathbb {C}$
with respect to the j-th variable
$f:\mathbb {R}^d\to \mathbb {C}$
with respect to the j-th variable
![]() $x_j$
will be denoted by
$x_j$
will be denoted by
![]() $\partial _{x_j}f=\partial _j f$
, while for any multi-index
$\partial _{x_j}f=\partial _j f$
, while for any multi-index
![]() $\alpha \in \mathbb {N}^d$
, let
$\alpha \in \mathbb {N}^d$
, let
![]() $\partial ^{\alpha }f$
denote the derivative operator
$\partial ^{\alpha }f$
denote the derivative operator
![]() $\partial ^{\alpha _1}_{x_1}\cdots \partial ^{\alpha _d}_{x_d}f=\partial ^{\alpha _1}_1\cdots \partial ^{\alpha _d}_df$
of total order
$\partial ^{\alpha _1}_{x_1}\cdots \partial ^{\alpha _d}_{x_d}f=\partial ^{\alpha _1}_1\cdots \partial ^{\alpha _d}_df$
of total order
![]() $|\alpha |:=\alpha _1+\ldots +\alpha _d$
.
$|\alpha |:=\alpha _1+\ldots +\alpha _d$
.
Let
![]() $\eta :\mathbb {R}\to [0, 1]$
be a smooth and even cutoff function such that
$\eta :\mathbb {R}\to [0, 1]$
be a smooth and even cutoff function such that
For any
![]() $n, \xi \in \mathbb {R}$
, we define
$n, \xi \in \mathbb {R}$
, we define
For any
![]() $\xi =(\xi _1,\ldots , \xi _d)\in \mathbb {R}^d$
and
$\xi =(\xi _1,\ldots , \xi _d)\in \mathbb {R}^d$
and
![]() $i\in [d]$
, we also define
$i\in [d]$
, we also define
More generally, for any
![]() $A=\{i_1,\ldots , i_m\}\subseteq [d]$
for some
$A=\{i_1,\ldots , i_m\}\subseteq [d]$
for some
![]() $m\in [d]$
, and numbers
$m\in [d]$
, and numbers
![]() $n_{i_1},\ldots , n_{i_m}\in \mathbb {R}$
corresponding to the set A, we will write
$n_{i_1},\ldots , n_{i_m}\in \mathbb {R}$
corresponding to the set A, we will write
 $$ \begin{align} \eta_{\le n_{i_1},\ldots, \le n_{i_m}}^{A}(\xi):=\prod_{j=1}^m\eta_{\le n_{i_j}}(\xi_{i_j})=\prod_{j=1}^m\eta_{\le n_{i_j}}^{(i_j)}(\xi). \end{align} $$
$$ \begin{align} \eta_{\le n_{i_1},\ldots, \le n_{i_m}}^{A}(\xi):=\prod_{j=1}^m\eta_{\le n_{i_j}}(\xi_{i_j})=\prod_{j=1}^m\eta_{\le n_{i_j}}^{(i_j)}(\xi). \end{align} $$
If the elements of the set A are ordered increasingly
![]() $1\le i_1<\ldots < i_m\le d$
, we will also write
$1\le i_1<\ldots < i_m\le d$
, we will also write
 $$ \begin{align*} \eta_{\le n_{i_1},\ldots, \le n_{i_m}}^{(i_1,\ldots, i_m)}(\xi):=\eta_{\le n_{i_1},\ldots, \le n_{i_m}}^{A}(\xi)=\prod_{j=1}^m\eta_{\le n_{i_j}}(\xi_{i_j})=\prod_{j=1}^m\eta_{\le n_{i_j}}^{(i_j)}(\xi). \end{align*} $$
$$ \begin{align*} \eta_{\le n_{i_1},\ldots, \le n_{i_m}}^{(i_1,\ldots, i_m)}(\xi):=\eta_{\le n_{i_1},\ldots, \le n_{i_m}}^{A}(\xi)=\prod_{j=1}^m\eta_{\le n_{i_j}}(\xi_{i_j})=\prod_{j=1}^m\eta_{\le n_{i_j}}^{(i_j)}(\xi). \end{align*} $$
If
![]() $n_{i_1}=\ldots = n_{i_m}=n\in \mathbb {R}$
, we will abbreviate
$n_{i_1}=\ldots = n_{i_m}=n\in \mathbb {R}$
, we will abbreviate
![]() $\eta _{\le n_{i_1},\ldots , \le n_{i_m}}^{A}$
to
$\eta _{\le n_{i_1},\ldots , \le n_{i_m}}^{A}$
to
![]() $\eta _{\le n}^{A}$
and
$\eta _{\le n}^{A}$
and
![]() $\eta _{\le n_{i_1},\ldots , \le n_{i_m}}^{(i_1,\ldots , i_m)}$
to
$\eta _{\le n_{i_1},\ldots , \le n_{i_m}}^{(i_1,\ldots , i_m)}$
to
![]() $\eta _{\le n}^{(i_1,\ldots , i_m)}$
.
$\eta _{\le n}^{(i_1,\ldots , i_m)}$
.
2.5 Function spaces
All vector spaces in this paper will be defined over the complex numbers
![]() $\mathbb {C}$
. The triple
$\mathbb {C}$
. The triple
![]() $(X, \mathcal B(X), \mu )$
is a measure space X with
$(X, \mathcal B(X), \mu )$
is a measure space X with
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal B(X)$
and
$\mathcal B(X)$
and
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\mu $
. The space of all
$\mu $
. The space of all
![]() $\mu $
-measurable complex-valued functions defined on X will be denoted by
$\mu $
-measurable complex-valued functions defined on X will be denoted by
![]() $L^0(X)$
. The space of all functions in
$L^0(X)$
. The space of all functions in
![]() $L^0(X)$
whose modulus is integrable with p-th power is denoted by
$L^0(X)$
whose modulus is integrable with p-th power is denoted by
![]() $L^p(X)$
for
$L^p(X)$
for
![]() $p\in (0, \infty )$
, whereas
$p\in (0, \infty )$
, whereas
![]() $L^{\infty }(X)$
denotes the space of all essentially bounded functions in
$L^{\infty }(X)$
denotes the space of all essentially bounded functions in
![]() $L^0(X)$
. These notions can be extended to functions taking values in a finite dimensional normed vector space
$L^0(X)$
. These notions can be extended to functions taking values in a finite dimensional normed vector space
![]() $(B, \|\cdot \|_B)$
; for instance,
$(B, \|\cdot \|_B)$
; for instance,
where
![]() $L^0(X;B)$
denotes the space of measurable functions from X to B (up to almost everywhere equivalence). Of course, if B is separable, these notions can be extended to infinite-dimensional B. In this paper, we will always be able to work in finite-dimensional settings by appealing to standard approximation arguments. In our case, we will usually have
$L^0(X;B)$
denotes the space of measurable functions from X to B (up to almost everywhere equivalence). Of course, if B is separable, these notions can be extended to infinite-dimensional B. In this paper, we will always be able to work in finite-dimensional settings by appealing to standard approximation arguments. In our case, we will usually have
![]() $X=\mathbb {R}^d$
or
$X=\mathbb {R}^d$
or
![]() $X=\mathbb {T}^d$
equipped with Lebesgue measure, and
$X=\mathbb {T}^d$
equipped with Lebesgue measure, and
![]() $X={\mathbb {Z}}^d$
endowed with counting measure. If X is endowed with counting measure, we will abbreviate
$X={\mathbb {Z}}^d$
endowed with counting measure. If X is endowed with counting measure, we will abbreviate
![]() $L^p(X)$
to
$L^p(X)$
to
![]() $\ell ^p(X)$
and
$\ell ^p(X)$
and
![]() $L^p(X; B)$
to
$L^p(X; B)$
to
![]() $\ell ^p(X; B)$
.
$\ell ^p(X; B)$
.
If
![]() $T : B_1 \to B_2$
is a continuous linear map between two normed vector spaces
$T : B_1 \to B_2$
is a continuous linear map between two normed vector spaces
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, we use
$B_2$
, we use
![]() $\|T\|_{B_1 \to B_2}$
to denote its operator norm.
$\|T\|_{B_1 \to B_2}$
to denote its operator norm.
The following extension of the Marcinkiewicz–Zygmund inequality to the Hilbert space setting will be very useful in Section 6.
Lemma 2.3. Let
![]() $(X, \mathcal B(X), \mu )$
be a
$(X, \mathcal B(X), \mu )$
be a
![]() $\sigma $
-finite measure space endowed with a family
$\sigma $
-finite measure space endowed with a family
![]() $T=(T_m: m\in \mathbb {N})$
of bounded linear operators
$T=(T_m: m\in \mathbb {N})$
of bounded linear operators
![]() $T_m:L^p(X)\to L^p(X)$
for some
$T_m:L^p(X)\to L^p(X)$
for some
![]() $p\in (0, \infty )$
. Suppose that
$p\in (0, \infty )$
. Suppose that

Then there is a constant
![]() $C_p>0$
such that for every sequence
$C_p>0$
such that for every sequence
![]() $(f_j: j\in \mathbb {N})\in L^p(X;\ell ^2(\mathbb {N}))$
, we have
$(f_j: j\in \mathbb {N})\in L^p(X;\ell ^2(\mathbb {N}))$
, we have

The index set
![]() $\mathbb {N}$
in the inner sum of (2.4) can be replaced by any other countable set and the result remains valid.
$\mathbb {N}$
in the inner sum of (2.4) can be replaced by any other countable set and the result remains valid.
The proof of Lemma 2.3 can be found in [Reference Mirek, Stein and Trojan48].
2.6 Fourier transform
We shall write
![]() $\boldsymbol {e}(z)=e^{2\pi \boldsymbol {i} z}$
for every
$\boldsymbol {e}(z)=e^{2\pi \boldsymbol {i} z}$
for every
![]() $z\in \mathbb {C}$
, where
$z\in \mathbb {C}$
, where
![]() $\boldsymbol {i}^2=-1$
. Let
$\boldsymbol {i}^2=-1$
. Let
![]() $\mathcal {F}_{\mathbb {R}^d}$
denote the Fourier transform on
$\mathcal {F}_{\mathbb {R}^d}$
denote the Fourier transform on
![]() $\mathbb {R}^d$
defined for any
$\mathbb {R}^d$
defined for any
![]() $f \in L^1(\mathbb {R}^d)$
and for any
$f \in L^1(\mathbb {R}^d)$
and for any
![]() $\xi \in \mathbb {R}^d$
as
$\xi \in \mathbb {R}^d$
as
If
![]() $f \in \ell ^1({\mathbb {Z}}^d)$
, we define the discrete Fourier transform (Fourier series)
$f \in \ell ^1({\mathbb {Z}}^d)$
, we define the discrete Fourier transform (Fourier series)
![]() $\mathcal {F}_{{\mathbb {Z}}^d}$
, for any
$\mathcal {F}_{{\mathbb {Z}}^d}$
, for any
![]() $\xi \in \mathbb {T}^d$
, by setting
$\xi \in \mathbb {T}^d$
, by setting
Sometimes we shall abbreviate
![]() $\mathcal {F}_{{\mathbb {Z}}^d}f$
to
$\mathcal {F}_{{\mathbb {Z}}^d}f$
to
![]() $\hat {f}$
.
$\hat {f}$
.
Let
![]() $\mathbb {G}=\mathbb {R}^d$
or
$\mathbb {G}=\mathbb {R}^d$
or
![]() $\mathbb {G}={\mathbb {Z}}^d$
. The corresponding dual groups are
$\mathbb {G}={\mathbb {Z}}^d$
. The corresponding dual groups are
![]() $\mathbb {G}^*=(\mathbb {R}^d)^*=\mathbb {R}^d$
or
$\mathbb {G}^*=(\mathbb {R}^d)^*=\mathbb {R}^d$
or
![]() $\mathbb {G}^*=({\mathbb {Z}}^d)^*=\mathbb {T}^d$
, respectively. For any bounded function
$\mathbb {G}^*=({\mathbb {Z}}^d)^*=\mathbb {T}^d$
, respectively. For any bounded function
![]() $\mathfrak m: \mathbb {G}^*\to \mathbb {C}$
and a test function
$\mathfrak m: \mathbb {G}^*\to \mathbb {C}$
and a test function
![]() $f:\mathbb {G}\to \mathbb {C}$
, we define the Fourier multiplier operator by
$f:\mathbb {G}\to \mathbb {C}$
, we define the Fourier multiplier operator by
One may think that
![]() $f:\mathbb {G}\to \mathbb {C}$
is a compactly supported function on
$f:\mathbb {G}\to \mathbb {C}$
is a compactly supported function on
![]() $\mathbb {G}$
(and smooth if
$\mathbb {G}$
(and smooth if
![]() $\mathbb {G}=\mathbb {R}^d$
) or any other function for which (2.5) makes sense.
$\mathbb {G}=\mathbb {R}^d$
) or any other function for which (2.5) makes sense.
Let
![]() $\mathbb {R}_{\le d}[\mathrm {x}_1,\ldots , \mathrm {x}_n]$
be the vector space of all polynomials on
$\mathbb {R}_{\le d}[\mathrm {x}_1,\ldots , \mathrm {x}_n]$
be the vector space of all polynomials on
![]() $\mathbb {R}^n$
of degree at most
$\mathbb {R}^n$
of degree at most
![]() $d\in {\mathbb {Z}}_+$
, which is equipped with the norm
$d\in {\mathbb {Z}}_+$
, which is equipped with the norm
![]() $\|P\|:=\sum _{0\le |\beta |\le d}|c_{\beta }|$
whenever
$\|P\|:=\sum _{0\le |\beta |\le d}|c_{\beta }|$
whenever
 $$ \begin{align*} P(x)=\sum_{0\le|\beta|\le d}c_{\beta}x_1^{\beta_1}\cdots x_n^{\beta_n} \quad \text{ for } \quad x=(x_1,\ldots, x_n)\in\mathbb{R}^n. \end{align*} $$
$$ \begin{align*} P(x)=\sum_{0\le|\beta|\le d}c_{\beta}x_1^{\beta_1}\cdots x_n^{\beta_n} \quad \text{ for } \quad x=(x_1,\ldots, x_n)\in\mathbb{R}^n. \end{align*} $$
We now formulate a multidimensional variant of the van der Corput lemma for polynomials that will be useful in our further applications.
Proposition 2.6. For each
![]() $d, n\in {\mathbb {Z}}_+$
, there exists a constant
$d, n\in {\mathbb {Z}}_+$
, there exists a constant
![]() $C_{d, n}>0$
such that for any
$C_{d, n}>0$
such that for any
![]() $P\in \mathbb {R}_{\le d}[\mathrm {x}_1,\ldots , \mathrm {x}_n]$
with
$P\in \mathbb {R}_{\le d}[\mathrm {x}_1,\ldots , \mathrm {x}_n]$
with
![]() $P(0) = 0$
, one has
$P(0) = 0$
, one has
 $$ \begin{align*} \bigg|\int_{[0, 1]^n}\boldsymbol{e}(P(x))dx\bigg|\le C_{d, n}\|P\|^{-1/d}. \end{align*} $$
$$ \begin{align*} \bigg|\int_{[0, 1]^n}\boldsymbol{e}(P(x))dx\bigg|\le C_{d, n}\|P\|^{-1/d}. \end{align*} $$
The proof of Proposition 2.6 can be found in [Reference Carbery, Christ and Wright20, Corollary 7.3., p. 1008]; see also [Reference Arkhipov, Chubarikov and Karatsuba1, Section 1].
2.7 Comparing sums to integrals
A well-known but useful lemma comparing sums to integrals is the following. The proof can be found in [Reference Zygmund73, Chapter V]; see also [Reference Vinogradov63].
Lemma 2.7. Suppose
![]() $f:[a,b] \to \mathbb {R}$
is
$f:[a,b] \to \mathbb {R}$
is
![]() $C^1$
such that
$C^1$
such that
![]() $f'$
is monotonic and
$f'$
is monotonic and
![]() $|f'(s)| \le 1/2$
on
$|f'(s)| \le 1/2$
on
![]() $[a,b]$
. Then there is an absolute constant A such that
$[a,b]$
. Then there is an absolute constant A such that
 $$ \begin{align*} \Big| \sum_{a<n\le b}\boldsymbol{e}(f(n)) \ - \ \int_a^b \boldsymbol{e}(f(s)) ds \Big| \ \le \ A. \end{align*} $$
$$ \begin{align*} \Big| \sum_{a<n\le b}\boldsymbol{e}(f(n)) \ - \ \int_a^b \boldsymbol{e}(f(s)) ds \Big| \ \le \ A. \end{align*} $$
2.8 Coordinatewise order
 $\preceq $
$\preceq $
For any
![]() $x=(x_1,\ldots , x_k)\in \mathbb {R}^k$
and
$x=(x_1,\ldots , x_k)\in \mathbb {R}^k$
and
![]() $y=(y_1,\ldots , y_k)\in \mathbb {R}^k$
, we say
$y=(y_1,\ldots , y_k)\in \mathbb {R}^k$
, we say
![]() $x\preceq y$
if and only if
$x\preceq y$
if and only if
![]() $x_i\le y_i$
for each
$x_i\le y_i$
for each
![]() $i\in [k]$
. We also write
$i\in [k]$
. We also write
![]() $x\prec y$
if and only if
$x\prec y$
if and only if
![]() $x\preceq y$
and
$x\preceq y$
and
![]() $x\neq y$
, and
$x\neq y$
, and
![]() $x\prec _{\mathrm {s}} y$
if and only if
$x\prec _{\mathrm {s}} y$
if and only if
![]() $x_i< y_i$
for each
$x_i< y_i$
for each
![]() $i\in [k]$
. Let
$i\in [k]$
. Let
![]() $\mathbb {I}\subseteq \mathbb {R}^k$
be an index set such that
$\mathbb {I}\subseteq \mathbb {R}^k$
be an index set such that
![]() $\# \mathbb {I}\ge 2$
and for every
$\# \mathbb {I}\ge 2$
and for every
![]() $J\in {\mathbb {Z}}_+\cup \{\infty \}$
, define the set
$J\in {\mathbb {Z}}_+\cup \{\infty \}$
, define the set
where
![]() $\mathbb {N}_{\le \infty }:=\mathbb {N}$
. In other words,
$\mathbb {N}_{\le \infty }:=\mathbb {N}$
. In other words,
![]() $\mathfrak S_J(\mathbb {I})$
is a family of all strictly increasing sequences (with respect to the coordinatewise order) of length
$\mathfrak S_J(\mathbb {I})$
is a family of all strictly increasing sequences (with respect to the coordinatewise order) of length
![]() $J+1$
taking their values in the set
$J+1$
taking their values in the set
![]() $\mathbb {I}$
.
$\mathbb {I}$
.
2.9 Oscillation semi-norms
Let
![]() $\mathbb {I}\subseteq \mathbb {R}^k$
be an index set such that
$\mathbb {I}\subseteq \mathbb {R}^k$
be an index set such that
![]() $\#{\mathbb {I}}\ge 2$
. Let
$\#{\mathbb {I}}\ge 2$
. Let
![]() $(\mathfrak a_{t}(x): t\in \mathbb {I})\subseteq \mathbb {C}$
be a k-parameter family of measurable functions defined on X. For any
$(\mathfrak a_{t}(x): t\in \mathbb {I})\subseteq \mathbb {C}$
be a k-parameter family of measurable functions defined on X. For any
![]() $\mathbb {J}\subseteq \mathbb {I}$
and a sequence
$\mathbb {J}\subseteq \mathbb {I}$
and a sequence
![]() $I=(I_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I})$
, the multi-parameter oscillation semi-norm is defined by
$I=(I_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I})$
, the multi-parameter oscillation semi-norm is defined by
 $$ \begin{align} O_{I, J}(\mathfrak a_{t}(x): t \in \mathbb{J}):= \Big(\sum_{j=0}^{J-1}\sup_{t\in \mathbb{B}[I,j]\cap\mathbb{J}} \left\lvert {\mathfrak a_{t}(x) - \mathfrak a_{I_j}(x)} \right\rvert ^2\Big)^{1/2}, \end{align} $$
$$ \begin{align} O_{I, J}(\mathfrak a_{t}(x): t \in \mathbb{J}):= \Big(\sum_{j=0}^{J-1}\sup_{t\in \mathbb{B}[I,j]\cap\mathbb{J}} \left\lvert {\mathfrak a_{t}(x) - \mathfrak a_{I_j}(x)} \right\rvert ^2\Big)^{1/2}, \end{align} $$
where
![]() $\mathbb {B}[I,i]:=[I_{i1}, I_{(i+1)1})\times \ldots \times [I_{ik}, I_{(i+1)k})$
is a box determined by the element
$\mathbb {B}[I,i]:=[I_{i1}, I_{(i+1)1})\times \ldots \times [I_{ik}, I_{(i+1)k})$
is a box determined by the element
![]() $I_i=(I_{i1}, \ldots , I_{ik})$
of the sequence
$I_i=(I_{i1}, \ldots , I_{ik})$
of the sequence
![]() $I\in \mathfrak S_J(\mathbb {I})$
. In order to avoid problems with measurability, we always assume that
$I\in \mathfrak S_J(\mathbb {I})$
. In order to avoid problems with measurability, we always assume that
![]() $\mathbb {I}\ni t\mapsto \mathfrak a_{t}(x)\in \mathbb {C}$
is continuous for
$\mathbb {I}\ni t\mapsto \mathfrak a_{t}(x)\in \mathbb {C}$
is continuous for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in X$
, or
$x\in X$
, or
![]() $\mathbb {J}$
is countable. We also use the convention that the supremum taken over the empty set is zero.
$\mathbb {J}$
is countable. We also use the convention that the supremum taken over the empty set is zero.
Remark 2.10. Some remarks concerning the definition of oscillation semi-norms are in order.
-
1. Clearly,
 $O_{I, J}(\mathfrak a_{t}: t \in \mathbb {J})$
defines a semi-norm.
$O_{I, J}(\mathfrak a_{t}: t \in \mathbb {J})$
defines a semi-norm. -
2. Let
 $\mathbb {I}\subseteq \mathbb {R}^k$
be an index set such that
$\mathbb {I}\subseteq \mathbb {R}^k$
be an index set such that
 $\#{\mathbb {I}}\ge 2$
, and let
$\#{\mathbb {I}}\ge 2$
, and let
 $\mathbb {J}_1, \mathbb {J}_2\subseteq \mathbb {I}$
be disjoint. Then for any family
$\mathbb {J}_1, \mathbb {J}_2\subseteq \mathbb {I}$
be disjoint. Then for any family
 $(\mathfrak a_t:t\in \mathbb {I})\subseteq \mathbb {C}$
, any
$(\mathfrak a_t:t\in \mathbb {I})\subseteq \mathbb {C}$
, any
 $J\in {\mathbb {Z}}_+$
and any
$J\in {\mathbb {Z}}_+$
and any
 $I\in \mathfrak S_J(\mathbb {I})$
, one has (2.11)
$I\in \mathfrak S_J(\mathbb {I})$
, one has (2.11) $$ \begin{align} O_{I, J}(\mathfrak a_{t}: t\in\mathbb{J}_1\cup\mathbb{J}_2)\le O_{I, J}(\mathfrak a_{t}: t\in\mathbb{J}_1)+O_{I, J}(\mathfrak a_{t}: t\in\mathbb{J}_2). \end{align} $$
$$ \begin{align} O_{I, J}(\mathfrak a_{t}: t\in\mathbb{J}_1\cup\mathbb{J}_2)\le O_{I, J}(\mathfrak a_{t}: t\in\mathbb{J}_1)+O_{I, J}(\mathfrak a_{t}: t\in\mathbb{J}_2). \end{align} $$
-
3. Let
 $\mathbb {I}\subseteq \mathbb {R}^k$
be a countable index set such that
$\mathbb {I}\subseteq \mathbb {R}^k$
be a countable index set such that
 $\#{\mathbb {I}}\ge 2$
and
$\#{\mathbb {I}}\ge 2$
and
 $\mathbb {J}\subseteq \mathbb {I}$
. Then for any family
$\mathbb {J}\subseteq \mathbb {I}$
. Then for any family
 $(\mathfrak a_t:t\in \mathbb {I})\subseteq \mathbb {C}$
, any
$(\mathfrak a_t:t\in \mathbb {I})\subseteq \mathbb {C}$
, any
 $J\in {\mathbb {Z}}_+$
, any
$J\in {\mathbb {Z}}_+$
, any
 $I\in \mathfrak S_J(\mathbb {I})$
, one has
$I\in \mathfrak S_J(\mathbb {I})$
, one has  $$ \begin{align*} O_{I, J}(\mathfrak a_{t}: t \in \mathbb{J})\lesssim \Big(\sum_{t\in\mathbb{I}}|\mathfrak a_{t}|^2\Big)^{1/2}. \end{align*} $$
$$ \begin{align*} O_{I, J}(\mathfrak a_{t}: t \in \mathbb{J})\lesssim \Big(\sum_{t\in\mathbb{I}}|\mathfrak a_{t}|^2\Big)^{1/2}. \end{align*} $$
-
4. Let
 $\mathbb {I}\subseteq \mathbb {R}^k$
be a countable index set such that
$\mathbb {I}\subseteq \mathbb {R}^k$
be a countable index set such that
 $\#{\mathbb {I}}\ge 2$
. For
$\#{\mathbb {I}}\ge 2$
. For
 $l\in [k]$
, let
$l\in [k]$
, let
 $\mathrm {p}_l:\mathbb {R}^k \to \mathbb {R}$
be the lth coordinate projection. Note that for any family
$\mathrm {p}_l:\mathbb {R}^k \to \mathbb {R}$
be the lth coordinate projection. Note that for any family
 $(\mathfrak a_t:t\in \mathbb {I})\subseteq \mathbb {C}$
, any
$(\mathfrak a_t:t\in \mathbb {I})\subseteq \mathbb {C}$
, any
 $J\in {\mathbb {Z}}_+$
, any
$J\in {\mathbb {Z}}_+$
, any
 $I\in \mathfrak S_J(\mathbb {I})$
and any
$I\in \mathfrak S_J(\mathbb {I})$
and any
 $l\in [k]$
, one has (2.12)where
$l\in [k]$
, one has (2.12)where
 $\mathrm {p}_l(\mathbb {I}) \subset \mathbb {R}$
is the image of
$\mathrm {p}_l(\mathbb {I}) \subset \mathbb {R}$
is the image of
 $\mathbb {I}$
under
$\mathbb {I}$
under
 $\mathrm {p}_l$
. Inequality (2.12) will be repeatedly used in Section 7. It is important to note that the parameter
$\mathrm {p}_l$
. Inequality (2.12) will be repeatedly used in Section 7. It is important to note that the parameter
 $t\in \mathbb {I}$
in the definition of oscillations and the sequence
$t\in \mathbb {I}$
in the definition of oscillations and the sequence
 $I\in \mathfrak S_J(\mathbb {I})$
both take values in
$I\in \mathfrak S_J(\mathbb {I})$
both take values in
 $\mathbb {I}$
.
$\mathbb {I}$
.
-
5. We also recall the definition of
 $\rho $
-variations. For any
$\rho $
-variations. For any
 $\mathbb I\subseteq \mathbb {R}$
, any family
$\mathbb I\subseteq \mathbb {R}$
, any family
 $(\mathfrak a_t: t\in \mathbb I)\subseteq \mathbb {C}$
and any exponent
$(\mathfrak a_t: t\in \mathbb I)\subseteq \mathbb {C}$
and any exponent
 $1 \leq \rho < \infty $
, the
$1 \leq \rho < \infty $
, the
 $\rho $
-variation semi-norm is defined to be where the supremum is taken over all finite increasing sequences in
$\rho $
-variation semi-norm is defined to be where the supremum is taken over all finite increasing sequences in $$ \begin{align*} V^{\rho}( \mathfrak a_t: t\in\mathbb I):= \sup_{J\in{\mathbb{Z}}_+} \sup_{\substack{t_{0}<\dotsb<t_{J}\\ t_{j}\in\mathbb I}} \Big(\sum_{j=0}^{J-1} |\mathfrak a_{t_{j+1}}-\mathfrak a_{t_{j}}|^{\rho} \Big)^{1/\rho}, \end{align*} $$
$$ \begin{align*} V^{\rho}( \mathfrak a_t: t\in\mathbb I):= \sup_{J\in{\mathbb{Z}}_+} \sup_{\substack{t_{0}<\dotsb<t_{J}\\ t_{j}\in\mathbb I}} \Big(\sum_{j=0}^{J-1} |\mathfrak a_{t_{j+1}}-\mathfrak a_{t_{j}}|^{\rho} \Big)^{1/\rho}, \end{align*} $$
 $\mathbb I$
.
$\mathbb I$
.
It is clear that for any
 $\mathbb {I}\subseteq \mathbb {R}$
such that
$\mathbb {I}\subseteq \mathbb {R}$
such that
 $\#{\mathbb {I}}\ge 2$
, any
$\#{\mathbb {I}}\ge 2$
, any
 $J\in {\mathbb {Z}}_+\cup \{\infty \}$
and any sequence
$J\in {\mathbb {Z}}_+\cup \{\infty \}$
and any sequence
 $I=(I_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I})$
, one has (2.13)whenever
$I=(I_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I})$
, one has (2.13)whenever $$ \begin{align} O_{I, J}(\mathfrak a_{t}: t \in \mathbb{I})\le V^{\rho}( \mathfrak a_t: t\in\mathbb I), \end{align} $$
$$ \begin{align} O_{I, J}(\mathfrak a_{t}: t \in \mathbb{I})\le V^{\rho}( \mathfrak a_t: t\in\mathbb I), \end{align} $$
 $1\le \rho \le 2$
.
$1\le \rho \le 2$
.
-
6. Inequality (2.13) allows us to deduce the Rademacher–Menshov inequality for oscillations, which asserts that for any
 $j_0, m\in \mathbb {N}$
so that
$j_0, m\in \mathbb {N}$
so that
 $j_0< 2^m$
and any sequence of complex numbers
$j_0< 2^m$
and any sequence of complex numbers
 $(\mathfrak a_k: k\in \mathbb {N})$
, any
$(\mathfrak a_k: k\in \mathbb {N})$
, any
 $J\in [2^m]$
and any
$J\in [2^m]$
and any
 $I\in \mathfrak S_J([j_0, 2^m))$
, we have (2.14)where
$I\in \mathfrak S_J([j_0, 2^m))$
, we have (2.14)where $$ \begin{align} \begin{split} O_{I, J}(\mathfrak a_{j}: j_0\leq j< 2^m)&\le V^{2}( \mathfrak a_j: j_0\leq j< 2^m)\\ &\leq \sqrt{2}\sum_{i=0}^m\Big(\sum_{j=0}^{2^{m-i}-1}\big|\sum_{\substack{k\in U_{j}^i\\ U_{j}^i\subseteq [j_0, 2^m)}} \mathfrak a_{k+1}-\mathfrak a_{k}\big|^2\Big)^{1/2}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} O_{I, J}(\mathfrak a_{j}: j_0\leq j< 2^m)&\le V^{2}( \mathfrak a_j: j_0\leq j< 2^m)\\ &\leq \sqrt{2}\sum_{i=0}^m\Big(\sum_{j=0}^{2^{m-i}-1}\big|\sum_{\substack{k\in U_{j}^i\\ U_{j}^i\subseteq [j_0, 2^m)}} \mathfrak a_{k+1}-\mathfrak a_{k}\big|^2\Big)^{1/2}, \end{split} \end{align} $$
 $U_j^i:=[j2^i, (j+1)2^i)$
for any
$U_j^i:=[j2^i, (j+1)2^i)$
for any
 $i, j\in {\mathbb {Z}}$
. The latter inequality in (2.14) immediately follows from [Reference Mirek, Stein and Zorin-Kranich51, Lemma 2.5., p. 534]. Inequality (2.14) will be used in Section 6.
$i, j\in {\mathbb {Z}}$
. The latter inequality in (2.14) immediately follows from [Reference Mirek, Stein and Zorin-Kranich51, Lemma 2.5., p. 534]. Inequality (2.14) will be used in Section 6.
-
7. For any
 $p\in [1, \infty ]$
and for any family
$p\in [1, \infty ]$
and for any family
 $(\mathfrak a_t:t\in \mathbb {N}^k)\subseteq \mathbb {C}$
of k-parameter measurable functions on X, one has (2.15)
$(\mathfrak a_t:t\in \mathbb {N}^k)\subseteq \mathbb {C}$
of k-parameter measurable functions on X, one has (2.15)
This easily follows from the definition of the set
 $\mathfrak S_J(\mathbb {N}^k)$
; see (2.8).
$\mathfrak S_J(\mathbb {N}^k)$
; see (2.8). -
8. For any
 $\mathbb {I}\subseteq \mathbb {R}$
with
$\mathbb {I}\subseteq \mathbb {R}$
with
 $\#{\mathbb {I}}\ge 2$
and any sequence
$\#{\mathbb {I}}\ge 2$
and any sequence
 $I=(I_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I})$
of length
$I=(I_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I})$
of length
 $J\in {\mathbb {Z}}_+\cup \{\infty \}$
, we define the diagonal sequence
$J\in {\mathbb {Z}}_+\cup \{\infty \}$
, we define the diagonal sequence
 $\bar {I}=(\bar {I}_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I}^k)$
by setting
$\bar {I}=(\bar {I}_i : i\in \mathbb {N}_{\le J}) \in \mathfrak S_J(\mathbb {I}^k)$
by setting
 $\bar {I}_i=(I_i,\ldots ,I_i)\in \mathbb {I}^k$
for each
$\bar {I}_i=(I_i,\ldots ,I_i)\in \mathbb {I}^k$
for each
 $i\in \mathbb {N}_{\le J}$
. Then for any
$i\in \mathbb {N}_{\le J}$
. Then for any
 $\mathbb {J}\subseteq \mathbb {I}^k$
, one has
$\mathbb {J}\subseteq \mathbb {I}^k$
, one has 
It is not difficult to show that oscillation semi-norms always dominate maximal functions.
Proposition 2.16. Assume that
![]() $k\in {\mathbb {Z}}_+$
and let
$k\in {\mathbb {Z}}_+$
and let
![]() $(\mathfrak a_{t}: t\in \mathbb {R}^k)\subseteq \mathbb {C}$
be a k-parameter family of measurable functions on X. Let
$(\mathfrak a_{t}: t\in \mathbb {R}^k)\subseteq \mathbb {C}$
be a k-parameter family of measurable functions on X. Let
![]() $\mathbb {I}\subseteq \mathbb {R}$
and
$\mathbb {I}\subseteq \mathbb {R}$
and
![]() $\#{\mathbb {I}}\ge 2$
. Then for every
$\#{\mathbb {I}}\ge 2$
. Then for every
![]() $p\in [1, \infty ]$
, we have
$p\in [1, \infty ]$
, we have
where
![]() $\bar {I}\in \mathfrak S_J(\mathbb {I}^k)$
is the diagonal sequence corresponding to a sequence
$\bar {I}\in \mathfrak S_J(\mathbb {I}^k)$
is the diagonal sequence corresponding to a sequence
![]() $I\in \mathfrak S_J(\mathbb {I})$
as in Remark 2.10.
$I\in \mathfrak S_J(\mathbb {I})$
as in Remark 2.10.
A remarkable feature of the oscillation semi-norms is that they imply pointwise convergence, which is formulated precisely in the following proposition.
Proposition 2.18. Let
![]() $(X, \mathcal {B}(X), \mu )$
be a
$(X, \mathcal {B}(X), \mu )$
be a
![]() $\sigma $
-finite measure space. For
$\sigma $
-finite measure space. For
![]() $k\in {\mathbb {Z}}_+$
, let
$k\in {\mathbb {Z}}_+$
, let
![]() $(\mathfrak a_{t}: t\in \mathbb {N}^k)\subseteq \mathbb {C}$
be a k-parameter family of measurable functions on X. Suppose that there is
$(\mathfrak a_{t}: t\in \mathbb {N}^k)\subseteq \mathbb {C}$
be a k-parameter family of measurable functions on X. Suppose that there is
![]() $p\in [1, \infty )$
and a constant
$p\in [1, \infty )$
and a constant
![]() $C_p>0$
such that
$C_p>0$
such that
where
![]() $\bar {I}\in \mathfrak S_J(\mathbb {N}^k)$
is the diagonal sequence corresponding to a sequence
$\bar {I}\in \mathfrak S_J(\mathbb {N}^k)$
is the diagonal sequence corresponding to a sequence
![]() $I\in \mathfrak S_J(\mathbb {N})$
as in Remark 2.10. Then the limit
$I\in \mathfrak S_J(\mathbb {N})$
as in Remark 2.10. Then the limit
exists
![]() $\mu $
-almost everywhere on X.
$\mu $
-almost everywhere on X.
For detailed proofs of Proposition 2.16 and Proposition 2.18, we refer to [Reference Mirek, Szarek and Wright53].
3 Basic reductions and ergodic theorems: Proof of Theorem 1.11
This section is intended to establish Theorem 1.11 for general measure-preserving systems by reducing the matter to the integer shift system. We first briefly explain that the oscillation inequality (1.13) from item (iv) of Theorem 1.11 implies conclusions from items (i)–(iii) of this theorem.
3.1 Proof of Theorem 1.11(iii)
Assuming Theorem 1.11(iv) with
![]() $\tau =2$
and invoking Proposition 2.16 (this permits us to dominate maximal functions by oscillations), we see that for every
$\tau =2$
and invoking Proposition 2.16 (this permits us to dominate maximal functions by oscillations), we see that for every
![]() $p\in (1, \infty )$
, there is a constant
$p\in (1, \infty )$
, there is a constant
![]() $C_p>0$
such that for any
$C_p>0$
such that for any
![]() $f\in L^p(X)$
, one has
$f\in L^p(X)$
, one has
But for any
![]() $f\ge 0$
, we have also a simple pointwise bound
$f\ge 0$
, we have also a simple pointwise bound
3.2 Proof of Theorem 1.11(ii)
We fix
![]() $p\in (1, \infty )$
and
$p\in (1, \infty )$
and
![]() $f\in L^p(X)$
. We can also assume that
$f\in L^p(X)$
. We can also assume that
![]() $f\ge 0$
. Using (1.13) with
$f\ge 0$
. Using (1.13) with
![]() $\tau =2^{1/s}$
for every
$\tau =2^{1/s}$
for every
![]() $s\in {\mathbb {Z}}_+$
and invoking Proposition 2.18, we conclude that there is
$s\in {\mathbb {Z}}_+$
and invoking Proposition 2.18, we conclude that there is
![]() $f_{s}^*\in L^p(X)$
such that
$f_{s}^*\in L^p(X)$
such that
![]() $\mu $
-almost everywhere on X for every
$\mu $
-almost everywhere on X for every
![]() $s\in {\mathbb {Z}}_+$
. It is not difficult to see that
$s\in {\mathbb {Z}}_+$
. It is not difficult to see that
![]() $f^*_{1}=f^*_{s}$
for all
$f^*_{1}=f^*_{s}$
for all
![]() $s\in {\mathbb {Z}}_+$
, since
$s\in {\mathbb {Z}}_+$
, since
![]() $\mathbb D_2\subseteq \mathbb D_{2^{1/s}}$
. Now for each
$\mathbb D_2\subseteq \mathbb D_{2^{1/s}}$
. Now for each
![]() $s\in {\mathbb {Z}}_+$
and each
$s\in {\mathbb {Z}}_+$
and each
![]() $M_1, M_2\in {\mathbb {Z}}_+$
, let
$M_1, M_2\in {\mathbb {Z}}_+$
, let
![]() $n_{M_i}^i \in \mathbb {N}$
be such that
$n_{M_i}^i \in \mathbb {N}$
be such that
![]() $2^{n_{M_i}^i/s}\le M_i<2^{(n_{M_i}^i+1)/s}$
for
$2^{n_{M_i}^i/s}\le M_i<2^{(n_{M_i}^i+1)/s}$
for
![]() $i\in [2]$
. Then we may conclude
$i\in [2]$
. Then we may conclude
Letting
![]() $s\to \infty $
, we obtain
$s\to \infty $
, we obtain
![]() $\mu $
-almost everywhere on X. This completes the proof of Theorem 1.11(ii).
$\mu $
-almost everywhere on X. This completes the proof of Theorem 1.11(ii).
3.3 Proof of Theorem 1.11(i)
Finally, pointwise convergence from Theorem 1.11(ii) combined with the maximal inequality (1.12) and dominated convergence theorem gives norm convergence for any
![]() $f\in L^p(X)$
with
$f\in L^p(X)$
with
![]() $1<p<\infty $
. This completes the proof of Theorem 1.11.
$1<p<\infty $
. This completes the proof of Theorem 1.11.
3.4 Proof of Theorem 1.11 in the degenerate case
It is perhaps worth remarking that the proof of Theorem 1.11 is fairly easy when
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
is degenerate in the sense that it can be written as
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
is degenerate in the sense that it can be written as
![]() $P(\mathrm {m}_1, \mathrm {m}_2)=P_1(\mathrm {m}_1)+P_2(\mathrm {m}_2)$
, where
$P(\mathrm {m}_1, \mathrm {m}_2)=P_1(\mathrm {m}_1)+P_2(\mathrm {m}_2)$
, where
![]() $P_1\in {\mathbb {Z}}[\mathrm {m}_1]$
and
$P_1\in {\mathbb {Z}}[\mathrm {m}_1]$
and
![]() $P_2\in {\mathbb {Z}}[\mathrm {m}_2]$
such that
$P_2\in {\mathbb {Z}}[\mathrm {m}_2]$
such that
![]() $P_1(0)=P_2(0)=0$
(see (1.14)). It suffices to prove (1.13). The crucial observation is the following identity:
$P_1(0)=P_2(0)=0$
(see (1.14)). It suffices to prove (1.13). The crucial observation is the following identity:
Recall from [Reference Mirek, Stein and Trojan48] that for every
![]() $p\in (1, \infty )$
, there is
$p\in (1, \infty )$
, there is
![]() $C_p>0$
such that for every
$C_p>0$
such that for every
![]() $f=(f_{\iota }:\iota \in \mathbb {N})\in L^p(X; \ell ^2(\mathbb {N}))$
and
$f=(f_{\iota }:\iota \in \mathbb {N})\in L^p(X; \ell ^2(\mathbb {N}))$
and
![]() $i\in [2]$
, one has
$i\in [2]$
, one has
 $$ \begin{align} \Big\|\Big(\sum_{\iota\in\mathbb{N}}\sup_{M_i\in{\mathbb{Z}}_+}\big|A_{M_i; X}^{P_i(\mathrm{m}_i)}f_{\iota}\big|^2\Big)^{1/2}\Big\|_{L^p(X)}\le C_p\|f\|_{L^p(X; \ell^2)}. \end{align} $$
$$ \begin{align} \Big\|\Big(\sum_{\iota\in\mathbb{N}}\sup_{M_i\in{\mathbb{Z}}_+}\big|A_{M_i; X}^{P_i(\mathrm{m}_i)}f_{\iota}\big|^2\Big)^{1/2}\Big\|_{L^p(X)}\le C_p\|f\|_{L^p(X; \ell^2)}. \end{align} $$
Moreover, from [Reference Mirek, Slomian and Szarek47], it was proved that for every
![]() $p\in (1, \infty )$
, there is
$p\in (1, \infty )$
, there is
![]() $C_p>0$
such that for every
$C_p>0$
such that for every
![]() $f\in L^p(X)$
and
$f\in L^p(X)$
and
![]() $i\in [2]$
, one has
$i\in [2]$
, one has
By (3.2), for every
![]() $J\in {\mathbb {Z}}_+$
,
$J\in {\mathbb {Z}}_+$
,
![]() $I\in \mathfrak S_J({\mathbb {Z}}_+^2)$
and
$I\in \mathfrak S_J({\mathbb {Z}}_+^2)$
and
![]() $j\in \mathbb {N}_{<J}$
, one can write
$j\in \mathbb {N}_{<J}$
, one can write
 $$ \begin{align*} \sup_{(M_1, M_2)\in\mathbb{B}[I,j]}\big|A_{M_1, M_2; X}^{P(\mathrm{m}_1, \mathrm{m}_2)}f-A_{I_{j1}, I_{j2}; X}^{P(\mathrm{m}_1, \mathrm{m}_2)}f\big| &\le \sup_{M_1\in{\mathbb{Z}}_+}\big|A_{M_1; X}^{P_1(\mathrm{m}_1)}\big(\sup_{I_{j2}\le M_2<I_{(j+1)2}}|A_{M_2; X}^{P_2(\mathrm{m}_2)}f-A_{I_{j2}; X}^{P_2(\mathrm{m}_2)}f|\big)\\ &\quad + \sup_{M_2\in{\mathbb{Z}}_+}\big|A_{M_2; X}^{P_2(\mathrm{m}_2)}\big(\sup_{I_{j1}\le M_1<I_{(j+1)1}}|A_{M_1; X}^{P_1(\mathrm{m}_1)}f-A_{I_{j1}; X}^{P_1(\mathrm{m}_1)}f|\big)\big|. \end{align*} $$
$$ \begin{align*} \sup_{(M_1, M_2)\in\mathbb{B}[I,j]}\big|A_{M_1, M_2; X}^{P(\mathrm{m}_1, \mathrm{m}_2)}f-A_{I_{j1}, I_{j2}; X}^{P(\mathrm{m}_1, \mathrm{m}_2)}f\big| &\le \sup_{M_1\in{\mathbb{Z}}_+}\big|A_{M_1; X}^{P_1(\mathrm{m}_1)}\big(\sup_{I_{j2}\le M_2<I_{(j+1)2}}|A_{M_2; X}^{P_2(\mathrm{m}_2)}f-A_{I_{j2}; X}^{P_2(\mathrm{m}_2)}f|\big)\\ &\quad + \sup_{M_2\in{\mathbb{Z}}_+}\big|A_{M_2; X}^{P_2(\mathrm{m}_2)}\big(\sup_{I_{j1}\le M_1<I_{(j+1)1}}|A_{M_1; X}^{P_1(\mathrm{m}_1)}f-A_{I_{j1}; X}^{P_1(\mathrm{m}_1)}f|\big)\big|. \end{align*} $$
Using this inequality with the vector-valued maximal inequality (3.3) and one-parameter oscillation inequality (3.4), one obtains
 $$ \begin{align} &\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J({\mathbb{Z}}_+^2) }\big\|O_{I, J}(A_{M_1, M_2; X}^{P(\mathrm{m}_1, \mathrm{m}_2)}f: M_1, M_2\in{\mathbb{Z}}_+)\|_{L^p(X)}\nonumber\\ &\quad \lesssim \sum_{i\in[2]} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J({\mathbb{Z}}_+) }\big\|O_{I, J}(A_{M_i; X}^{P_i(\mathrm{m}_i)}f: M_i\in{\mathbb{Z}}_+)\|_{L^p(X)}\lesssim_p\|f\|_{L^p(X)}. \end{align} $$
$$ \begin{align} &\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J({\mathbb{Z}}_+^2) }\big\|O_{I, J}(A_{M_1, M_2; X}^{P(\mathrm{m}_1, \mathrm{m}_2)}f: M_1, M_2\in{\mathbb{Z}}_+)\|_{L^p(X)}\nonumber\\ &\quad \lesssim \sum_{i\in[2]} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J({\mathbb{Z}}_+) }\big\|O_{I, J}(A_{M_i; X}^{P_i(\mathrm{m}_i)}f: M_i\in{\mathbb{Z}}_+)\|_{L^p(X)}\lesssim_p\|f\|_{L^p(X)}. \end{align} $$
This completes the proof of Theorem 1.11 in the degenerate case. From now on we will additionally assume that
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
is non-degenerate.
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
is non-degenerate.
3.5 Reductions to truncated averages
We have seen that the proof of Theorem 1.11 has been reduced to proving the oscillation inequality (1.13). We begin with certain general reductions that will simplify our further arguments. Let us fix our measure-preserving transformations
![]() $T_1, \ldots , T_d$
, our polynomials
$T_1, \ldots , T_d$
, our polynomials
![]() ${\mathcal P} = \{P_1,\ldots , P_d\}\subset {\mathbb Z}[\mathrm {m}_1,\ldots ,\mathrm {m}_k]$
and define a truncated version of the average (1.8) by
${\mathcal P} = \{P_1,\ldots , P_d\}\subset {\mathbb Z}[\mathrm {m}_1,\ldots ,\mathrm {m}_k]$
and define a truncated version of the average (1.8) by
where
is a rectangle in
![]() ${\mathbb {Z}}^k$
.
${\mathbb {Z}}^k$
.
We will abbreviate
![]() $\tilde {A}_{M_1,\ldots , M_k; X}^{{\mathcal P}}$
to
$\tilde {A}_{M_1,\ldots , M_k; X}^{{\mathcal P}}$
to
![]() $\tilde {A}_{M; X}^{{\mathcal P}}$
and
$\tilde {A}_{M; X}^{{\mathcal P}}$
and
![]() $R_{M_1,\ldots , M_k}$
to
$R_{M_1,\ldots , M_k}$
to
![]() $R_M$
whenever
$R_M$
whenever
![]() $M=(M_1,\ldots , M_k)\in {\mathbb {Z}}_+^k$
. We now show that the
$M=(M_1,\ldots , M_k)\in {\mathbb {Z}}_+^k$
. We now show that the
![]() $L^p(X)$
norms of the oscillation semi-norms associated with the averages from (1.8) and (3.6) have comparable norms in the following sense.
$L^p(X)$
norms of the oscillation semi-norms associated with the averages from (1.8) and (3.6) have comparable norms in the following sense.
Proposition 3.7. Let
![]() $d, k\in {\mathbb {Z}}_+$
be given. Let
$d, k\in {\mathbb {Z}}_+$
be given. Let
![]() $(X, \mathcal B(X), \mu )$
be a
$(X, \mathcal B(X), \mu )$
be a
![]() $\sigma $
-finite measure space equipped with a family of commuting invertible and measure-preserving transformations
$\sigma $
-finite measure space equipped with a family of commuting invertible and measure-preserving transformations
![]() $T_1,\ldots , T_d:X\to X$
. Let
$T_1,\ldots , T_d:X\to X$
. Let
![]() ${\mathcal P} = \{P_1,\ldots , P_d\}\subset {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
,
${\mathcal P} = \{P_1,\ldots , P_d\}\subset {\mathbb {Z}}[\mathrm {m}_1, \ldots , \mathrm {m}_k]$
,
![]() $M=(M_1,\ldots ,M_k)$
and let
$M=(M_1,\ldots ,M_k)$
and let
![]() $A_{M; X}^{{\mathcal P}}$
and
$A_{M; X}^{{\mathcal P}}$
and
![]() $\tilde {A}_{M; X}^{{\mathcal P}}$
be the corresponding averaging operators defined respectively in (1.8) and (3.6). For every
$\tilde {A}_{M; X}^{{\mathcal P}}$
be the corresponding averaging operators defined respectively in (1.8) and (3.6). For every
![]() $\tau>1$
and every
$\tau>1$
and every
![]() $1\le p\le \infty $
, there is a finite constant
$1\le p\le \infty $
, there is a finite constant
![]() $C:=C_{d, k, p, \tau }>0$
such that for any
$C:=C_{d, k, p, \tau }>0$
such that for any
![]() $f\in L^p(X)$
, one has
$f\in L^p(X)$
, one has
An oscillation variant of (3.8) also holds

Proof. The proof will proceed in two steps. We begin with some general observations which will permit us to simplify further arguments leading to the proofs of (3.8) and (3.9).
Step 1. Suppose that
![]() $(\mathfrak a_{m}: m\in {\mathbb {Z}}_+^k)$
is a k-parameter sequence of measurable functions on X. Then for
$(\mathfrak a_{m}: m\in {\mathbb {Z}}_+^k)$
is a k-parameter sequence of measurable functions on X. Then for
![]() $M=(M_1,\ldots , M_k)=(\tau ^{n_1},\ldots , \tau ^{n_k})\in \mathbb {D}_{\tau }^k$
, one can write
$M=(M_1,\ldots , M_k)=(\tau ^{n_1},\ldots , \tau ^{n_k})\in \mathbb {D}_{\tau }^k$
, one can write
 $$ \begin{align*} \sum_{m\in Q_{M_1,\ldots, M_k}}\mathfrak a_{m}=\sum_{(l_1,\ldots, l_k)\in\mathbb{N}_{\le n_1}\times\cdots\times\mathbb{N}_{\le n_k}}\sum_{m\in R_{\tau^{l_1},\ldots, \tau^{l_k}}}\mathfrak a_{m}, \end{align*} $$
$$ \begin{align*} \sum_{m\in Q_{M_1,\ldots, M_k}}\mathfrak a_{m}=\sum_{(l_1,\ldots, l_k)\in\mathbb{N}_{\le n_1}\times\cdots\times\mathbb{N}_{\le n_k}}\sum_{m\in R_{\tau^{l_1},\ldots, \tau^{l_k}}}\mathfrak a_{m}, \end{align*} $$
and
 $$ \begin{align*} \sum_{(l_1,\ldots, l_k)\in\mathbb{N}_{\le n_1}\times\cdots\times\mathbb{N}_{\le n_k}}\frac{|R_{\tau^{l_1},\ldots, \tau^{l_k}}|}{|Q_{\tau^{n_1},\ldots, \tau^{n_k}}|}\lesssim_{k,\tau}1. \end{align*} $$
$$ \begin{align*} \sum_{(l_1,\ldots, l_k)\in\mathbb{N}_{\le n_1}\times\cdots\times\mathbb{N}_{\le n_k}}\frac{|R_{\tau^{l_1},\ldots, \tau^{l_k}}|}{|Q_{\tau^{n_1},\ldots, \tau^{n_k}}|}\lesssim_{k,\tau}1. \end{align*} $$
Combining these two estimates, one sees that
Applying (3.10) with
![]() $\mathfrak a_{m}(x)=f(T_1^{P_1(m)}\cdots T_d^{P_d(m)}x)$
, we obtain (3.8).
$\mathfrak a_{m}(x)=f(T_1^{P_1(m)}\cdots T_d^{P_d(m)}x)$
, we obtain (3.8).
Step 2. As before, let
![]() $(\mathfrak a_{m}: m\in {\mathbb {Z}}_+^k)$
be a k-parameter sequence of measurable functions on X. For
$(\mathfrak a_{m}: m\in {\mathbb {Z}}_+^k)$
be a k-parameter sequence of measurable functions on X. For
![]() $l\in \mathbb {N}_{\le k}$
and
$l\in \mathbb {N}_{\le k}$
and
![]() $M=(M_1,\ldots , M_k)=(\tau ^{n_1},\ldots , \tau ^{n_k})\in \mathbb {D}_{\tau }^k$
, define the sets
$M=(M_1,\ldots , M_k)=(\tau ^{n_1},\ldots , \tau ^{n_k})\in \mathbb {D}_{\tau }^k$
, define the sets

Note that
![]() $B_M^0=Q_M$
and
$B_M^0=Q_M$
and
![]() $B_M^k=R_M$
, and
$B_M^k=R_M$
, and
![]() $B_M^{l-1}=B_M^{l}\cup D_M^{l}$
. Moreover, for
$B_M^{l-1}=B_M^{l}\cup D_M^{l}$
. Moreover, for
![]() $l\in [k]$
, one sees
$l\in [k]$
, one sees

where
 $$ \begin{align*} u_{M_l}:=\frac{|B_M^{l}|}{|B_M^{l-1}|}=\frac{\lfloor M_l\rfloor-\lfloor \tau^{-1}M_l\rfloor}{\lfloor M_l\rfloor} \quad\text{ and } \quad v_{M_l}:=\frac{|D_M^{l}|}{|B_M^{l-1}|}= \frac{\lfloor \tau^{-1}M_l\rfloor}{\lfloor M_l\rfloor}. \end{align*} $$
$$ \begin{align*} u_{M_l}:=\frac{|B_M^{l}|}{|B_M^{l-1}|}=\frac{\lfloor M_l\rfloor-\lfloor \tau^{-1}M_l\rfloor}{\lfloor M_l\rfloor} \quad\text{ and } \quad v_{M_l}:=\frac{|D_M^{l}|}{|B_M^{l-1}|}= \frac{\lfloor \tau^{-1}M_l\rfloor}{\lfloor M_l\rfloor}. \end{align*} $$
Considering
![]() $\tilde {u}_{M_l}:=u_{M_l}-1+\tau ^{-1}$
and
$\tilde {u}_{M_l}:=u_{M_l}-1+\tau ^{-1}$
and
![]() $\tilde {v}_{M_l}:=v_{M_l}-\tau ^{-1}$
, we see that
$\tilde {v}_{M_l}:=v_{M_l}-\tau ^{-1}$
, we see that
Thus, using (2.12), one sees that

By (2.15), there is
![]() $C_{p, \tau }>0$
such that
$C_{p, \tau }>0$
such that

Finally, combining (3.11), (3.12) and (3.13), one obtains the following bootstrap inequality:

which immediately yields

Iterating (3.14) k times and using (3.10) to control the maximal function, we conclude that

Finally, using (3.15) with
![]() $\mathfrak a_{m}(x)=f(T_1^{P_1(m)}\cdots T_d^{P_d(m)}x)$
and invoking Proposition 2.16 (to control the maximal function from (3.15) by oscillation semi-norms), we obtain (3.9) as desired.
$\mathfrak a_{m}(x)=f(T_1^{P_1(m)}\cdots T_d^{P_d(m)}x)$
and invoking Proposition 2.16 (to control the maximal function from (3.15) by oscillation semi-norms), we obtain (3.9) as desired.
Now using Proposition 3.7, we can reduce the oscillation inequality (1.13) from Theorem 1.11 to establish the following result for non-degenerate polynomials in the sense of (1.14).
Theorem 3.16. Let
![]() $(X, \mathcal B(X), \mu )$
be a
$(X, \mathcal B(X), \mu )$
be a
![]() $\sigma $
-finite measure space equipped with an invertible measure-preserving transformation
$\sigma $
-finite measure space equipped with an invertible measure-preserving transformation
![]() $T:X\to X$
. Let
$T:X\to X$
. Let
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a non-degenerate polynomial such that
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a non-degenerate polynomial such that
![]() $P(0, 0)=0$
. Let
$P(0, 0)=0$
. Let
![]() $\tilde {A}_{M; X}^{P}f$
with
$\tilde {A}_{M; X}^{P}f$
with
![]() $M=(M_1,M_2)$
be the average defined in (3.6) with
$M=(M_1,M_2)$
be the average defined in (3.6) with
![]() $d=1$
,
$d=1$
,
![]() $k=2$
and
$k=2$
and
![]() $P_1 =P$
. If
$P_1 =P$
. If
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $\tau>1$
, and
$\tau>1$
, and
![]() $\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
, then one has
$\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
, then one has
The implicit constant in (3.17) can be taken to depend only on
![]() $p, \tau , P$
.
$p, \tau , P$
.
3.6 Reduction to the integer shift system
As mentioned in Example 1.9, the integer shift system is the most important for pointwise convergence problems. For
![]() $T=S_1$
, for any
$T=S_1$
, for any
![]() $x\in {\mathbb {Z}}$
and for any finitely supported function
$x\in {\mathbb {Z}}$
and for any finitely supported function
![]() $f:{\mathbb {Z}}\to \mathbb {C}$
, we may write
$f:{\mathbb {Z}}\to \mathbb {C}$
, we may write
We shall also abbreviate
![]() $\tilde {A}_{M_1, M_2; {\mathbb {Z}}, S_1}^{P}$
to
$\tilde {A}_{M_1, M_2; {\mathbb {Z}}, S_1}^{P}$
to
![]() $\tilde {A}_{M_1, M_2; {\mathbb {Z}}}^{P}$
. In fact, we will be able to deduce Theorem 3.16 from its integer counterpart.
$\tilde {A}_{M_1, M_2; {\mathbb {Z}}}^{P}$
. In fact, we will be able to deduce Theorem 3.16 from its integer counterpart.
Theorem 3.19. Let
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a non-degenerate polynomial (see (1.14)) such that
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a non-degenerate polynomial (see (1.14)) such that
![]() $P(0, 0)=0$
. Let
$P(0, 0)=0$
. Let
![]() $\tilde {A}_{M_1, M_2; {\mathbb {Z}}}^{P}f$
be the average defined in (3.18). If
$\tilde {A}_{M_1, M_2; {\mathbb {Z}}}^{P}f$
be the average defined in (3.18). If
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $\tau>1$
, and
$\tau>1$
, and
![]() $\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
, then one has
$\mathbb {D}_{\tau }:=\{\tau ^n:n\in \mathbb {N}\}$
, then one has
The implicit constant in (3.20) can be taken to depend only on
![]() $p, \tau , P$
.
$p, \tau , P$
.
We immediately see that Theorem 3.19 is a special case of Theorem 3.16. However, it is also a standard matter, in view of the Calderón transference principle [Reference Calderón19], that this implication can be reversed. So in order to prove (3.17), it suffices to establish (3.20). This reduction is important since we can use Fourier methods in the integer setting which are not readily available in abstract measure spaces.
From now on, we will focus our attention on establishing Theorem 3.19.
4 ‘Backwards’ Newton diagram: Proof of Theorem 3.19
The ‘backwards’ Newton diagram
![]() $N_P$
of a nontrivial polynomial
$N_P$
of a nontrivial polynomial
![]() $P\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
,
$P\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
,
is defined as the closed convex hull of the set
 $$ \begin{align*} \bigcup_{(\gamma_1, \gamma_2)\in S_P}\{(x+\gamma_1, y+\gamma_2)\in\mathbb{R}^2: x\le 0, y\le 0\}, \end{align*} $$
$$ \begin{align*} \bigcup_{(\gamma_1, \gamma_2)\in S_P}\{(x+\gamma_1, y+\gamma_2)\in\mathbb{R}^2: x\le 0, y\le 0\}, \end{align*} $$
where
![]() $S_P:=\{(\gamma _1, \gamma _2)\in \mathbb {N}\times \mathbb {N}: c_{\gamma _1, \gamma _2}\neq 0\}$
denotes the set of non-vanishing coefficients of P.
$S_P:=\{(\gamma _1, \gamma _2)\in \mathbb {N}\times \mathbb {N}: c_{\gamma _1, \gamma _2}\neq 0\}$
denotes the set of non-vanishing coefficients of P.
Let
![]() $V_P\subseteq S_P$
be the set of vertices (corner points) of
$V_P\subseteq S_P$
be the set of vertices (corner points) of
![]() $N_P$
. Suppose that
$N_P$
. Suppose that
![]() $V_P:=\{v_1, \ldots , v_r\}$
, where
$V_P:=\{v_1, \ldots , v_r\}$
, where
![]() $v_j=(v_{j,1}, v_{j,2})$
satisfies
$v_j=(v_{j,1}, v_{j,2})$
satisfies
![]() $v_{j, 1}<v_{j+1, 1}$
, and
$v_{j, 1}<v_{j+1, 1}$
, and
![]() $v_{j+1, 2}<v_{j, 2}$
for each
$v_{j+1, 2}<v_{j, 2}$
for each
![]() $j\in [r]$
.
$j\in [r]$
.
Let
![]() $\omega _0=(0, 1)$
and
$\omega _0=(0, 1)$
and
![]() $\omega _r=(1, 0)$
and for
$\omega _r=(1, 0)$
and for
![]() $j\in [r-1]$
, let
$j\in [r-1]$
, let
![]() $\omega _j=(\omega _{j, 1}, \omega _{j,2})$
denote a normal vector to the edge
$\omega _j=(\omega _{j, 1}, \omega _{j,2})$
denote a normal vector to the edge
![]() $\overline {v_jv_{j+1}}:=v_{j+1}-v_j$
such that
$\overline {v_jv_{j+1}}:=v_{j+1}-v_j$
such that
![]() $\omega _{j, 1}, \omega _{j, 2}$
are positive integers (the choice is not unique but it is not an issue here). Observe that the slopes of the lines along
$\omega _{j, 1}, \omega _{j, 2}$
are positive integers (the choice is not unique but it is not an issue here). Observe that the slopes of the lines along
![]() $\omega _j$
’s are decreasing as j increases since
$\omega _j$
’s are decreasing as j increases since
![]() $N_P$
is convex. The convexity of
$N_P$
is convex. The convexity of
![]() $N_P$
also yields that
$N_P$
also yields that
for all
and
![]() $j\in [r]$
. Now for
$j\in [r]$
. Now for
![]() $j\in [r]$
, let us define
$j\in [r]$
, let us define

which is the intersection of various half planes. If
![]() $\mathrm {V}_P=\{v_1\}$
, then we simply define
$\mathrm {V}_P=\{v_1\}$
, then we simply define
![]() $W(1)={\mathbb {Z}}_+\times {\mathbb {Z}}_+$
.
$W(1)={\mathbb {Z}}_+\times {\mathbb {Z}}_+$
.
Remark 4.3. Obviously, if
![]() $1\le i<j\le r$
, then
$1\le i<j\le r$
, then
![]() $W(i)\cap W(j)=\emptyset $
. Indeed, if
$W(i)\cap W(j)=\emptyset $
. Indeed, if
![]() $(a, b)\in W(i)\cap W(j)$
, then
$(a, b)\in W(i)\cap W(j)$
, then
![]() $(a, b)\cdot (v-v_i)<0$
for all
$(a, b)\cdot (v-v_i)<0$
for all
![]() and
and
![]() $(a, b)\cdot (v-v_j)<0$
for all
$(a, b)\cdot (v-v_j)<0$
for all
![]() . In particular,
. In particular,
![]() $(a, b)\cdot (v_j-v_i)<0$
and
$(a, b)\cdot (v_j-v_i)<0$
and
![]() $(a, b)\cdot (v_i-v_j)<0$
, which is impossible.
$(a, b)\cdot (v_i-v_j)<0$
, which is impossible.
Lemma 4.4. For
![]() $j\in [r]$
, we have
$j\in [r]$
, we have
Proof. The convexity of
![]() $N_P$
implies that the normals
$N_P$
implies that the normals
![]() $\omega _{j-1}, \omega _{j}$
are linearly independent; therefore, for every
$\omega _{j-1}, \omega _{j}$
are linearly independent; therefore, for every
![]() $(a, b)\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
, there are
$(a, b)\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
, there are
![]() $\alpha , \beta $
such that
$\alpha , \beta $
such that
![]() $(a, b)=\alpha \omega _{j-1}+\beta \omega _{j}$
. We only need to show that
$(a, b)=\alpha \omega _{j-1}+\beta \omega _{j}$
. We only need to show that
![]() $(a, b)\in W(j)$
if and only if
$(a, b)\in W(j)$
if and only if
![]() $\alpha , \beta>0$
. First, suppose that
$\alpha , \beta>0$
. First, suppose that
![]() $(a, b)\in W(j)$
. Then
$(a, b)\in W(j)$
. Then
![]() $(a, b)\cdot (v-v_j)<0$
for all
$(a, b)\cdot (v-v_j)<0$
for all
![]() . In particular,
. In particular,
![]() $(a, b)\cdot (v_{j+1}-v_j)=(\alpha \omega _{j-1}+\beta \omega _{j})\cdot (v_{j+1}-v_j)<0$
. But this implies that
$(a, b)\cdot (v_{j+1}-v_j)=(\alpha \omega _{j-1}+\beta \omega _{j})\cdot (v_{j+1}-v_j)<0$
. But this implies that
![]() $\alpha \omega _{j-1}\cdot (v_{j+1}-v_j)<0$
, since
$\alpha \omega _{j-1}\cdot (v_{j+1}-v_j)<0$
, since
![]() $\omega _j\cdot (v_{j+1}-v_j)=0$
. This immediately gives that
$\omega _j\cdot (v_{j+1}-v_j)=0$
. This immediately gives that
![]() $\alpha>0$
, provided that
$\alpha>0$
, provided that
![]() $j\in [r-1]$
, since
$j\in [r-1]$
, since
![]() $\omega _{j-1}\cdot (v_{j+1}-v_j)\le 0$
by (4.2). When
$\omega _{j-1}\cdot (v_{j+1}-v_j)\le 0$
by (4.2). When
![]() $j=r$
, then
$j=r$
, then
![]() $\alpha>0$
since
$\alpha>0$
since
![]() $\omega _{r}=(1, 0)$
and
$\omega _{r}=(1, 0)$
and
![]() $0<b=(a, b)\cdot (0, 1)=(\alpha \omega _{r-1}+\beta \omega _{r})\cdot (0, 1)=\alpha \omega _{r-1}\cdot (0, 1)=\alpha \omega _{r-1, 2}$
. Similarly, taking
$0<b=(a, b)\cdot (0, 1)=(\alpha \omega _{r-1}+\beta \omega _{r})\cdot (0, 1)=\alpha \omega _{r-1}\cdot (0, 1)=\alpha \omega _{r-1, 2}$
. Similarly, taking
![]() $v=v_{j-1}$
for
$v=v_{j-1}$
for
![]() $1<j\le r$
, we obtain
$1<j\le r$
, we obtain
![]() $\beta>0$
. When
$\beta>0$
. When
![]() $j=1$
, then
$j=1$
, then
![]() $\beta>0$
because
$\beta>0$
because
![]() $\omega _{0}=(0, 1)$
and
$\omega _{0}=(0, 1)$
and
![]() $0<a=(a, b)\cdot (1, 0)=(\alpha \omega _{0}+\beta \omega _{1})\cdot (1, 0)=\beta \omega _{1}\cdot (1, 0)=\beta \omega _{1,1}$
. Conversely, if
$0<a=(a, b)\cdot (1, 0)=(\alpha \omega _{0}+\beta \omega _{1})\cdot (1, 0)=\beta \omega _{1}\cdot (1, 0)=\beta \omega _{1,1}$
. Conversely, if
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $\beta>0$
, then for any
$\beta>0$
, then for any
![]() , we have
, we have
![]() $(a, b)\cdot (v-v_j)=\alpha \omega _{j-1}\cdot (v-v_j)+\beta \omega _{j}\cdot (v-v_j)<0$
, since
$(a, b)\cdot (v-v_j)=\alpha \omega _{j-1}\cdot (v-v_j)+\beta \omega _{j}\cdot (v-v_j)<0$
, since
![]() $\omega _{j-1}\cdot (v-v_j)\le 0$
and
$\omega _{j-1}\cdot (v-v_j)\le 0$
and
![]() $\omega _{j}\cdot (v-v_j)\le 0$
, with at least one inequality strict.
$\omega _{j}\cdot (v-v_j)\le 0$
, with at least one inequality strict.
Lemma 4.4 means that
![]() $W(j)$
consists of those lattice points of
$W(j)$
consists of those lattice points of
![]() ${\mathbb {Z}}_+\times {\mathbb {Z}}_+$
which are within the cone centered at the origin with the boundaries determined by the lines along the normals
${\mathbb {Z}}_+\times {\mathbb {Z}}_+$
which are within the cone centered at the origin with the boundaries determined by the lines along the normals
![]() $\omega _{j-1}$
and
$\omega _{j-1}$
and
![]() $\omega _{j}$
, respectively. Now for
$\omega _{j}$
, respectively. Now for
![]() $j\in [r]$
, we set
$j\in [r]$
, we set
Remark 4.5. Some comments are in order.
-
1. Having defined the sets
 $S(j)$
for
$S(j)$
for
 $j\in [r]$
, it is not difficult to see that (4.6)
$j\in [r]$
, it is not difficult to see that (4.6) $$ \begin{align} \bigcup_{j=1}^rS(j)=\mathbb{N}\times\mathbb{N}. \end{align} $$
$$ \begin{align} \bigcup_{j=1}^rS(j)=\mathbb{N}\times\mathbb{N}. \end{align} $$
-
2. We note that for
 $(a, b)\in S(j)$
, we have
$(a, b)\in S(j)$
, we have
 $(a, b)\cdot (v-v_j)\le 0$
for all
$(a, b)\cdot (v-v_j)\le 0$
for all
 $v\in S_P$
by (4.2). However, the strict inequality may not be achieved even for
$v\in S_P$
by (4.2). However, the strict inequality may not be achieved even for
 $v\not =v_j$
.
$v\not =v_j$
. -
3. If
 $r\ge 2$
, then by construction of the sets
$r\ge 2$
, then by construction of the sets
 $S(j)$
, one sees that if
$S(j)$
, one sees that if
 $(a, b)\in S(j)$
, then (4.7)for any
$(a, b)\in S(j)$
, then (4.7)for any $$ \begin{align} \frac{\omega_{j,2}}{\omega_{j,1}}a\le b\le \frac{\omega_{j-1,2}}{\omega_{j-1,1}}a \end{align} $$
$$ \begin{align} \frac{\omega_{j,2}}{\omega_{j,1}}a\le b\le \frac{\omega_{j-1,2}}{\omega_{j-1,1}}a \end{align} $$
 $1< j< r$
; and if
$1< j< r$
; and if
 $j=1$
or
$j=1$
or
 $j=r$
one has, respectively, (4.8)
$j=r$
one has, respectively, (4.8) $$ \begin{align} \frac{\omega_{1,2}}{\omega_{1,1}}a\le b<\infty, \qquad \text{ and } \qquad 0\le b\le \frac{\omega_{r-1,2}}{\omega_{r-1,1}}a. \end{align} $$
$$ \begin{align} \frac{\omega_{1,2}}{\omega_{1,1}}a\le b<\infty, \qquad \text{ and } \qquad 0\le b\le \frac{\omega_{r-1,2}}{\omega_{r-1,1}}a. \end{align} $$
-
4. If
 $r=1$
and
$r=1$
and
 $(a, b)\in S(1)$
, then
$(a, b)\in S(1)$
, then
 $0\le a, b<\infty $
.
$0\le a, b<\infty $
.
Now for any given
![]() $(a, b)\in S(j)$
, we try to determine
$(a, b)\in S(j)$
, we try to determine
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
explicitly. Let
$\beta $
explicitly. Let
![]() $A_j:=[\omega _{j-1}|\omega _j]$
be the matrix whose column vectors are the normals
$A_j:=[\omega _{j-1}|\omega _j]$
be the matrix whose column vectors are the normals
![]() $\omega _{j-1}, \omega _j$
. Then
$\omega _{j-1}, \omega _j$
. Then
 $$ \begin{align*} \left( \begin{array}{c} a \\ b \\ \end{array} \right)= \left( \begin{array}{cc} \omega_{j-1, 1} & \omega_{j,1} \\ \omega_{j-1, 2} & \omega_{j, 2} \\ \end{array} \right) \left( \begin{array}{c} \alpha \\ \beta \\ \end{array} \right). \end{align*} $$
$$ \begin{align*} \left( \begin{array}{c} a \\ b \\ \end{array} \right)= \left( \begin{array}{cc} \omega_{j-1, 1} & \omega_{j,1} \\ \omega_{j-1, 2} & \omega_{j, 2} \\ \end{array} \right) \left( \begin{array}{c} \alpha \\ \beta \\ \end{array} \right). \end{align*} $$
The convexity of
![]() $N_P$
(and the orientation we chose) ensures that
$N_P$
(and the orientation we chose) ensures that
![]() $\det A_j<0$
. Taking
$\det A_j<0$
. Taking
![]() $d_j:=-\det A_j>0$
, one has
$d_j:=-\det A_j>0$
, one has
 $$ \begin{align*} \left( \begin{array}{c} \alpha \\ \beta \\ \end{array} \right)=\frac{1}{\det A_j} \left( \begin{array}{cc} \omega_{j,2} & -\omega_{j,1} \\ -\omega_{j-1, 2} & \omega_{j-1, 1} \\ \end{array} \right) \left( \begin{array}{c} a \\ b \\ \end{array} \right)=\frac{1}{d_j} \left( \begin{array}{c} -a\omega_{j,2} \ +\ b\omega_{j,1} \\ a\omega_{j-1, 2} - b\omega_{j-1, 1} \\ \end{array} \right). \end{align*} $$
$$ \begin{align*} \left( \begin{array}{c} \alpha \\ \beta \\ \end{array} \right)=\frac{1}{\det A_j} \left( \begin{array}{cc} \omega_{j,2} & -\omega_{j,1} \\ -\omega_{j-1, 2} & \omega_{j-1, 1} \\ \end{array} \right) \left( \begin{array}{c} a \\ b \\ \end{array} \right)=\frac{1}{d_j} \left( \begin{array}{c} -a\omega_{j,2} \ +\ b\omega_{j,1} \\ a\omega_{j-1, 2} - b\omega_{j-1, 1} \\ \end{array} \right). \end{align*} $$
We have chosen the components of
![]() $\omega _{j-1}$
and
$\omega _{j-1}$
and
![]() $\omega _{j}$
to be non-negative integers; therefore, for
$\omega _{j}$
to be non-negative integers; therefore, for
![]() $j\in [r-1]$
(keeping in mind that
$j\in [r-1]$
(keeping in mind that
![]() $\alpha ,\beta \ge 0$
and
$\alpha ,\beta \ge 0$
and
![]() $d_j>0$
), we may rewrite
$d_j>0$
), we may rewrite
We allow
![]() $t_1$
to be zero when
$t_1$
to be zero when
![]() $j=r$
.
$j=r$
.
We now split
![]() $S(j)$
into
$S(j)$
into
![]() $S_1(j)$
and
$S_1(j)$
and
![]() $S_2(j)$
, where
$S_2(j)$
, where
 $$ \begin{align*} S_1(j):=\{(a, b)\in S(j): (a, b)=\frac{(n+N)}{d_j}\omega_{j-1}+\frac{N}{d_j}\omega_{j},\ n\in\mathbb{N}, \ N\in\mathbb{N}\},\\ S_2(j):=\{(a, b)\in S(j): (a, b)=\frac{N}{d_j}\omega_{j-1}+\frac{(n+N)}{d_j}\omega_{j},\ n\in\mathbb{N}, \ N\in\mathbb{N}\}. \end{align*} $$
$$ \begin{align*} S_1(j):=\{(a, b)\in S(j): (a, b)=\frac{(n+N)}{d_j}\omega_{j-1}+\frac{N}{d_j}\omega_{j},\ n\in\mathbb{N}, \ N\in\mathbb{N}\},\\ S_2(j):=\{(a, b)\in S(j): (a, b)=\frac{N}{d_j}\omega_{j-1}+\frac{(n+N)}{d_j}\omega_{j},\ n\in\mathbb{N}, \ N\in\mathbb{N}\}. \end{align*} $$
We can further decompose
where
 $$ \begin{align} \begin{split} S_1^N(j):=&\{(a, b)\in S(j): (a, b)=\frac{(n+N)}{d_j}\omega_{j-1}+\frac{N}{d_j}\omega_{j},\ n\in\mathbb{N}\},\\ S_2^N(j):=&\{(a, b)\in S(j): (a, b)=\frac{N}{d_j}\omega_{j-1}+\frac{(n+N)}{d_j}\omega_{j},\ n\in\mathbb{N}\}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} S_1^N(j):=&\{(a, b)\in S(j): (a, b)=\frac{(n+N)}{d_j}\omega_{j-1}+\frac{N}{d_j}\omega_{j},\ n\in\mathbb{N}\},\\ S_2^N(j):=&\{(a, b)\in S(j): (a, b)=\frac{N}{d_j}\omega_{j-1}+\frac{(n+N)}{d_j}\omega_{j},\ n\in\mathbb{N}\}. \end{split} \end{align} $$
Lemma 4.10. For each
![]() $j\in [r]$
, there exists
$j\in [r]$
, there exists
![]() $\sigma _j>0$
such that for every
$\sigma _j>0$
such that for every
![]() , one has
, one has
for all
![]() $(a, b)\in S_1^N(j)$
. The same conclusion is true for
$(a, b)\in S_1^N(j)$
. The same conclusion is true for
![]() $S_2^N(j)$
.
$S_2^N(j)$
.
Proof. For every
![]() $(a, b)\in S_1^N(j)$
, we can write
$(a, b)\in S_1^N(j)$
, we can write
 $$ \begin{align*} (a, b)=\frac{(n+N)}{d_j}\omega_{j-1}+\frac{N}{d_j}\omega_{j} =\frac{n}{d_j}\omega_{j-1}+\frac{N}{d_j}(\omega_{j}+\omega_{j-1}) \end{align*} $$
$$ \begin{align*} (a, b)=\frac{(n+N)}{d_j}\omega_{j-1}+\frac{N}{d_j}\omega_{j} =\frac{n}{d_j}\omega_{j-1}+\frac{N}{d_j}(\omega_{j}+\omega_{j-1}) \end{align*} $$
for some
![]() $n\in \mathbb {N}$
. By (4.2), we have
$n\in \mathbb {N}$
. By (4.2), we have
for all
, since
![]() $\omega _{j-1}$
and
$\omega _{j-1}$
and
![]() $\omega _{j}$
are linearly independent. Taking
$\omega _{j}$
are linearly independent. Taking
one sees, by (4.2) again, that
 $$ \begin{align*} (a, b)\cdot (v-v_j) =\frac{n}{d_j}\omega_{j-1}\cdot (v-v_j)+\frac{N}{d_j}(\omega_{j}+\omega_{j-1})\cdot (v-v_j)\le -\sigma_j N \end{align*} $$
$$ \begin{align*} (a, b)\cdot (v-v_j) =\frac{n}{d_j}\omega_{j-1}\cdot (v-v_j)+\frac{N}{d_j}(\omega_{j}+\omega_{j-1})\cdot (v-v_j)\le -\sigma_j N \end{align*} $$
for all
![]() $(a, b)\in S_1^N(j)$
. This immediately yields (4.11) and the proof is finished.
$(a, b)\in S_1^N(j)$
. This immediately yields (4.11) and the proof is finished.
For any
![]() $\tau>1$
using the decomposition (4.6), we may write
$\tau>1$
using the decomposition (4.6), we may write
 $$ \begin{align} \mathbb{D}_{\tau}\times\mathbb{D}_{\tau}=\bigcup_{j=1}^r\mathbb{S}_{\tau}(j), \end{align} $$
$$ \begin{align} \mathbb{D}_{\tau}\times\mathbb{D}_{\tau}=\bigcup_{j=1}^r\mathbb{S}_{\tau}(j), \end{align} $$
where
Using (4.9), we can further write
where for any
![]() $j\in [r]$
, one has
$j\in [r]$
, one has
 $$ \begin{align} \begin{split} \mathbb{S}_{\tau, 1}^N(j):=&\{(\tau^{n_1}, \tau^{n_2})\in \mathbb{D}_{\tau}\times\mathbb{D}_{\tau}: (n_1, n_2)\in S_1^N(j) \},\\ \mathbb{S}_{\tau, 2}^N(j):=&\{(\tau^{n_1}, \tau^{n_2})\in \mathbb{D}_{\tau}\times\mathbb{D}_{\tau}: (n_1, n_2)\in S_2^N(j) \}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathbb{S}_{\tau, 1}^N(j):=&\{(\tau^{n_1}, \tau^{n_2})\in \mathbb{D}_{\tau}\times\mathbb{D}_{\tau}: (n_1, n_2)\in S_1^N(j) \},\\ \mathbb{S}_{\tau, 2}^N(j):=&\{(\tau^{n_1}, \tau^{n_2})\in \mathbb{D}_{\tau}\times\mathbb{D}_{\tau}: (n_1, n_2)\in S_2^N(j) \}. \end{split} \end{align} $$
In view of decomposition (4.12), our aim will be to restrict the estimates for oscillations to sectors from (4.13).
Theorem 4.16. Let
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a non-degenerate polynomial (see (1.14)) such that
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a non-degenerate polynomial (see (1.14)) such that
![]() $P(0, 0)=0$
. Let
$P(0, 0)=0$
. Let
![]() $r\in {\mathbb {Z}}_+$
be the number of corners in the corresponding Newton diagram
$r\in {\mathbb {Z}}_+$
be the number of corners in the corresponding Newton diagram
![]() $N_P$
. Let
$N_P$
. Let
![]() $f\in \ell ^p({\mathbb {Z}})$
for some
$f\in \ell ^p({\mathbb {Z}})$
for some
![]() $1\le p\le \infty $
, and let
$1\le p\le \infty $
, and let
![]() $\tilde {A}_{M_1, M_2; {\mathbb {Z}}}^{P}f$
be the average defined in (3.18). If
$\tilde {A}_{M_1, M_2; {\mathbb {Z}}}^{P}f$
be the average defined in (3.18). If
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $\tau>1$
and
$\tau>1$
and
![]() $j\in [r]$
, and
$j\in [r]$
, and
![]() $\mathbb {S}_{\tau }(j)$
is a sector from (4.13), then one has
$\mathbb {S}_{\tau }(j)$
is a sector from (4.13), then one has
The implicit constant in (4.17) may only depend on
![]() $p, \tau , P$
.
$p, \tau , P$
.
The proof of Theorem 4.16 is postponed to Section 7. However, assuming momentarily Theorem 4.16, we can derive Theorem 3.19.
Proof of Theorem 3.19
Assume that (4.17) holds for all
![]() $j\in [r]$
. By (4.12) and (2.11), one has
$j\in [r]$
. By (4.12) and (2.11), one has
 $$ \begin{align*} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^2) }\big\|O_{I, J}(\tilde{A}_{M; {\mathbb{Z}}}^{P}f: M\in\mathbb{D}_{\tau}^2)\|_{\ell^p({\mathbb{Z}})} \lesssim \sum_{j\in[r]}\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^2) }\big\|O_{I, J}(\tilde{A}_{M; {\mathbb{Z}}}^{P}f: M\in\mathbb{S}_{\tau}(j))\|_{\ell^p({\mathbb{Z}})}. \end{align*} $$
$$ \begin{align*} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^2) }\big\|O_{I, J}(\tilde{A}_{M; {\mathbb{Z}}}^{P}f: M\in\mathbb{D}_{\tau}^2)\|_{\ell^p({\mathbb{Z}})} \lesssim \sum_{j\in[r]}\sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{D}_{\tau}^2) }\big\|O_{I, J}(\tilde{A}_{M; {\mathbb{Z}}}^{P}f: M\in\mathbb{S}_{\tau}(j))\|_{\ell^p({\mathbb{Z}})}. \end{align*} $$
Step 1. If suffices to show that for every
![]() $j\in [r]$
, every
$j\in [r]$
, every
![]() $J\in {\mathbb {Z}}_+$
and every
$J\in {\mathbb {Z}}_+$
and every
![]() $I\in \mathfrak S_J(\mathbb {D}_{\tau }^2)$
, one has
$I\in \mathfrak S_J(\mathbb {D}_{\tau }^2)$
, one has
 $$ \begin{align} &\Big\|\Big(\sum_{i\in\mathbb{N}_{<J}}\sup_{M\in\mathbb{B}[I,i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{I_{i}; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\nonumber\\ &\quad\lesssim \sum_{j\in[r]} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{S}_{\tau}(j))}\big\|O_{I, J}(\tilde{A}_{M; {\mathbb{Z}}}^{P}f: M\in\mathbb{S}_{\tau}(j))\big\|_{\ell^p({\mathbb{Z}})}. \end{align} $$
$$ \begin{align} &\Big\|\Big(\sum_{i\in\mathbb{N}_{<J}}\sup_{M\in\mathbb{B}[I,i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{I_{i}; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\nonumber\\ &\quad\lesssim \sum_{j\in[r]} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\mathbb{S}_{\tau}(j))}\big\|O_{I, J}(\tilde{A}_{M; {\mathbb{Z}}}^{P}f: M\in\mathbb{S}_{\tau}(j))\big\|_{\ell^p({\mathbb{Z}})}. \end{align} $$
We can assume that
![]() $J>Cr$
for a large
$J>Cr$
for a large
![]() $C>0$
; otherwise, the estimate in (4.18) easily follows from maximal function estimates. Let us fix a sequence
$C>0$
; otherwise, the estimate in (4.18) easily follows from maximal function estimates. Let us fix a sequence
![]() $I = (I_0, \ldots , I_J) \in \mathfrak S_J(\mathbb {D}_{\tau }^2)$
and a sector
$I = (I_0, \ldots , I_J) \in \mathfrak S_J(\mathbb {D}_{\tau }^2)$
and a sector
![]() $\mathbb {S}_{\tau }(j)$
. Let
$\mathbb {S}_{\tau }(j)$
. Let
![]() $\omega _*:=\max \{\omega _{i1}, \omega _{i2}: i\in [r]\}$
and we split the set
$\omega _*:=\max \{\omega _{i1}, \omega _{i2}: i\in [r]\}$
and we split the set
![]() $\mathbb {N}_{<J}$
into
$\mathbb {N}_{<J}$
into
![]() $O(r)$
sparse sets
$O(r)$
sparse sets
![]() $\mathbb {J}_1,\ldots , \mathbb {J}_{O(r)}\subset \mathbb {N}_{<J}$
, where each
$\mathbb {J}_1,\ldots , \mathbb {J}_{O(r)}\subset \mathbb {N}_{<J}$
, where each
![]() $\mathbb {J}\in \{\mathbb {J}_1,\ldots , \mathbb {J}_{O(r)}\}$
satisfies the separation condition:
$\mathbb {J}\in \{\mathbb {J}_1,\ldots , \mathbb {J}_{O(r)}\}$
satisfies the separation condition:
for every
![]() $i_1, i_2\in \mathbb {J}$
such that
$i_1, i_2\in \mathbb {J}$
such that
![]() $i_1< i_2$
. Our task now is to establish (4.18) with the summation over
$i_1< i_2$
. Our task now is to establish (4.18) with the summation over
![]() $\mathbb {J}$
satisfying (4.19) in place of
$\mathbb {J}$
satisfying (4.19) in place of
![]() $\mathbb {N}_{<J}$
in the sum on the left-hand side of (4.18).
$\mathbb {N}_{<J}$
in the sum on the left-hand side of (4.18).
Step 2. To every element
![]() $I_i = (I_{i1}, I_{i2})$
with
$I_i = (I_{i1}, I_{i2})$
with
![]() $i\in \mathbb {N}_{<J}$
in the sequence I (which say lies in the sector
$i\in \mathbb {N}_{<J}$
in the sequence I (which say lies in the sector
![]() $\mathbb {S}_{\tau }(j_i)$
), we associate at most one point
$\mathbb {S}_{\tau }(j_i)$
), we associate at most one point
![]() $P_i(j) \in \mathbb {S}_{\tau }(j)$
in the following way. If
$P_i(j) \in \mathbb {S}_{\tau }(j)$
in the following way. If
![]() $j_i<j$
and the box
$j_i<j$
and the box
![]() $\mathbb {B}[I,i]$
intersects the sector
$\mathbb {B}[I,i]$
intersects the sector
![]() $\mathbb {S}_{\tau }(j)$
, then the box intersects the sector along the bottom edge. We set
$\mathbb {S}_{\tau }(j)$
, then the box intersects the sector along the bottom edge. We set
![]() $P_i(j) = (I_i^j, I_{i2})$
, where
$P_i(j) = (I_i^j, I_{i2})$
, where
![]() $I_i^j$
is the least element in
$I_i^j$
is the least element in
![]() $\mathbb {D}_{\tau }$
such that
$\mathbb {D}_{\tau }$
such that
![]() $(I_i^j, I_{i2}) \in \mathbb {S}_{\tau }(j)$
. If
$(I_i^j, I_{i2}) \in \mathbb {S}_{\tau }(j)$
. If
![]() $j<j_i$
and the box
$j<j_i$
and the box
![]() $\mathbb {B}[I,i]$
intersects the sector
$\mathbb {B}[I,i]$
intersects the sector
![]() $\mathbb {S}_{\tau }(j)$
, then it intersects the sector along the left edge. We set
$\mathbb {S}_{\tau }(j)$
, then it intersects the sector along the left edge. We set
![]() $P_i(j) = (I_{i1}, {\tilde {I}}_i^j)$
, where
$P_i(j) = (I_{i1}, {\tilde {I}}_i^j)$
, where
![]() ${\tilde {I}}_i^j$
is the least element in
${\tilde {I}}_i^j$
is the least element in
![]() $\mathbb {D}_{\tau }$
such that
$\mathbb {D}_{\tau }$
such that
![]() $(I_{i1}, {\tilde {I}}_i^j) \in \mathbb {S}_{\tau }(j)$
. Finally if
$(I_{i1}, {\tilde {I}}_i^j) \in \mathbb {S}_{\tau }(j)$
. Finally if
![]() $j_i=j$
, we set
$j_i=j$
, we set
![]() $P_i(j) = I_i$
. The sequence
$P_i(j) = I_i$
. The sequence
![]() $P(j) = (P_i(j): i\in \mathbb {N}_{\le J'})$
forms a strictly increasing sequence lying in
$P(j) = (P_i(j): i\in \mathbb {N}_{\le J'})$
forms a strictly increasing sequence lying in
![]() $\mathfrak S_{J'}(\mathbb {S}_{\tau }(j))$
for some
$\mathfrak S_{J'}(\mathbb {S}_{\tau }(j))$
for some
![]() $J'\le J$
and each
$J'\le J$
and each
![]() $P_i(j)=(P_{i1}(j), P_{i2}(j))$
is the least element among all the elements
$P_i(j)=(P_{i1}(j), P_{i2}(j))$
is the least element among all the elements
![]() $(M_1,M_2) \in \mathbb {B}[I,i] \cap \mathbb {S}_{\tau }(j)$
.
$(M_1,M_2) \in \mathbb {B}[I,i] \cap \mathbb {S}_{\tau }(j)$
.
Step 3. We now produce a sequence of length at most
![]() $r+2$
, which will allow us to move from
$r+2$
, which will allow us to move from
![]() $I_i$
to
$I_i$
to
![]() $P_i(j)$
when
$P_i(j)$
when
![]() $I_i\neq P_i(j)$
. More precisely, we claim that there exists a sequence
$I_i\neq P_i(j)$
. More precisely, we claim that there exists a sequence
![]() $u^i:=(u^i_m : m\in \mathbb {N}_{<m_{I_i}})\subset \mathbb {D}_{\tau }^2$
for some
$u^i:=(u^i_m : m\in \mathbb {N}_{<m_{I_i}})\subset \mathbb {D}_{\tau }^2$
for some
![]() $m_{I_i}\in [r+1]$
, with the property that
$m_{I_i}\in [r+1]$
, with the property that
where
![]() $(u_0^i, u_{m_{I_i}}^i)=(I_i, P_i(j))$
or
$(u_0^i, u_{m_{I_i}}^i)=(I_i, P_i(j))$
or
![]() $(u_0^i, u_{m_{I_i}}^i)=(P_i(j), I_i)$
. Moreover, two consecutive elements
$(u_0^i, u_{m_{I_i}}^i)=(P_i(j), I_i)$
. Moreover, two consecutive elements
![]() $u_m^i, u_{m+1}^i$
of this sequence belong to a unique sector
$u_m^i, u_{m+1}^i$
of this sequence belong to a unique sector
![]() $\mathbb {S}_{\tau }(j_{u_m^i})$
except the elements
$\mathbb {S}_{\tau }(j_{u_m^i})$
except the elements
![]() $u_{m_{I_i}-2}^i, u_{m_{I_i}-1}^i$
and
$u_{m_{I_i}-2}^i, u_{m_{I_i}-1}^i$
and
![]() $u_{m_{I_i}-1}^i, u_{m_{I_i}}^i$
, which may belong to the same sector. Suppose now that
$u_{m_{I_i}-1}^i, u_{m_{I_i}}^i$
, which may belong to the same sector. Suppose now that
![]() $\mathbb {B}[I,i] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
and
$\mathbb {B}[I,i] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
and
![]() $I_i\in \mathbb {S}_{\tau }(j_i)$
and
$I_i\in \mathbb {S}_{\tau }(j_i)$
and
![]() $j_i< j$
. Let
$j_i< j$
. Let
![]() $u_{0}^i:=I_i$
be the starting point. Suppose that the elements
$u_{0}^i:=I_i$
be the starting point. Suppose that the elements
![]() $u_{0}^i\succ u_{1}^i\succ \ldots \succ u_{m}^i$
have been chosen for some
$u_{0}^i\succ u_{1}^i\succ \ldots \succ u_{m}^i$
have been chosen for some
![]() $m\in \mathbb {N}_{< r}$
so that
$m\in \mathbb {N}_{< r}$
so that
![]() $u_{s}^i$
lies on the bottom boundary ray of
$u_{s}^i$
lies on the bottom boundary ray of
![]() $\mathbb {S}_{\tau }(j_{i}+s-1)$
and
$\mathbb {S}_{\tau }(j_{i}+s-1)$
and
![]() $u_{s}^i\prec u_{s-1}^i$
for each
$u_{s}^i\prec u_{s-1}^i$
for each
![]() $s\in [m]$
. Then we take
$s\in [m]$
. Then we take
![]() $u_m^i$
and move southwesterly to
$u_m^i$
and move southwesterly to
![]() $u_{m+1}^i$
, the nearest point on the bottom boundary ray of
$u_{m+1}^i$
, the nearest point on the bottom boundary ray of
![]() $\mathbb {S}_{\tau }(j_i+m)$
such that
$\mathbb {S}_{\tau }(j_i+m)$
such that
![]() $u_{m+1}^i\prec u_{m}^i$
. Continuing this way after
$u_{m+1}^i\prec u_{m}^i$
. Continuing this way after
![]() $m_{I_i}-1=j-j_i+1\le r$
steps, we arrive at
$m_{I_i}-1=j-j_i+1\le r$
steps, we arrive at
![]() $u_{m_{I_i}-1}^i\in \mathbb {S}_{\tau }(j)$
which will allow us to reach the last point of this sequence
$u_{m_{I_i}-1}^i\in \mathbb {S}_{\tau }(j)$
which will allow us to reach the last point of this sequence
![]() $u_{m_{I_i}}^i:=P_i(j)$
as claimed in (4.20). Assume now that
$u_{m_{I_i}}^i:=P_i(j)$
as claimed in (4.20). Assume now that
![]() $\mathbb {B}[I,i] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
and
$\mathbb {B}[I,i] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
and
![]() $I_i\in \mathbb {S}_{\tau }(j_i)$
and
$I_i\in \mathbb {S}_{\tau }(j_i)$
and
![]() $j_i> j$
. We start from the point
$j_i> j$
. We start from the point
![]() $u_0^i:=P_i(j)$
and proceed exactly the same as in the previous case until we reach the point
$u_0^i:=P_i(j)$
and proceed exactly the same as in the previous case until we reach the point
![]() $u_{m_{I_i}}^i:=I_i$
.
$u_{m_{I_i}}^i:=I_i$
.
Step 4. To complete the proof, we use the sequence from (4.20) for each
![]() $i\in \mathbb {J}$
and observe that
$i\in \mathbb {J}$
and observe that
 $$ \begin{align*} &\Big\|\Big(\sum_{i\in\mathbb{J}}\sup_{M\in\mathbb{B}[I,i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{I_{i}; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\\ &\quad \le \Big\|\Big(\sum_{i\in\mathbb{J}}\sup_{M\in\mathbb{B}[P(j), i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{I_{i}; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\\ &\quad\lesssim_r \Big\|\Big(\sum_{i\in\mathbb{J}}\sup_{M\in\mathbb{B}[P(j), i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{P_{i}(j); {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\\ &\qquad+\Big\|\Big(\sum_{i\in\mathbb{J}}\sum_{m\in \mathbb{N}_{<m_{I_i}}}|\tilde{A}_{u_{m+1}^i; {\mathbb{Z}}}^{P}f-\tilde{A}_{u_m^i; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}. \end{align*} $$
$$ \begin{align*} &\Big\|\Big(\sum_{i\in\mathbb{J}}\sup_{M\in\mathbb{B}[I,i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{I_{i}; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\\ &\quad \le \Big\|\Big(\sum_{i\in\mathbb{J}}\sup_{M\in\mathbb{B}[P(j), i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{I_{i}; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\\ &\quad\lesssim_r \Big\|\Big(\sum_{i\in\mathbb{J}}\sup_{M\in\mathbb{B}[P(j), i]\cap\mathbb{S}_{\tau}(j)}|\tilde{A}_{M; {\mathbb{Z}}}^{P}f-\tilde{A}_{P_{i}(j); {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}\\ &\qquad+\Big\|\Big(\sum_{i\in\mathbb{J}}\sum_{m\in \mathbb{N}_{<m_{I_i}}}|\tilde{A}_{u_{m+1}^i; {\mathbb{Z}}}^{P}f-\tilde{A}_{u_m^i; {\mathbb{Z}}}^{P}f|^2\Big)^{1/2}\Big\|_{\ell^p({\mathbb{Z}})}. \end{align*} $$
Clearly, the first norm is dominated by the right-hand side of (4.18). The same is true for the second norm. It follows from the fact that for two consecutive integers
![]() $i_1< i_2$
such that
$i_1< i_2$
such that
![]() $\mathbb {B}[I,{i_1}] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
and
$\mathbb {B}[I,{i_1}] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
and
![]() $\mathbb {B}[I,{i_2}] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
, if we have
$\mathbb {B}[I,{i_2}] \cap \mathbb {S}_{\tau }(j)\neq \emptyset $
, if we have
![]() $u_{j_1}^{i_1}$
and
$u_{j_1}^{i_1}$
and
![]() $u_{j_2}^{i_2}$
belonging to the same sector, they must satisfy
$u_{j_2}^{i_2}$
belonging to the same sector, they must satisfy
![]() $u_{j_1}^{i_1}\prec u_{j_2}^{i_2}$
by the separation condition (4.19). This completes the proof of the theorem.
$u_{j_1}^{i_1}\prec u_{j_2}^{i_2}$
by the separation condition (4.19). This completes the proof of the theorem.
5 Exponential sum estimates
This section is intended to establish certain double exponential sum estimates which will be used later. We begin by recalling the classical Weyl inequality with a logarithmic loss.
Proposition 5.1. Let
![]() $d\in {\mathbb {Z}}_+$
,
$d\in {\mathbb {Z}}_+$
,
![]() $d\ge 2$
and let
$d\ge 2$
and let
![]() $P\in \mathbb {R}[\mathrm {m}]$
be such that
$P\in \mathbb {R}[\mathrm {m}]$
be such that
![]() $P(m):=c_dm^d+\ldots +c_1m$
. Then there exists a constant
$P(m):=c_dm^d+\ldots +c_1m$
. Then there exists a constant
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $M\in {\mathbb {Z}}_+$
, the following is true. Suppose that for some
$M\in {\mathbb {Z}}_+$
, the following is true. Suppose that for some
![]() $2\le j\le d$
, there are
$2\le j\le d$
, there are
![]() $a, q\in {\mathbb {Z}}$
such that
$a, q\in {\mathbb {Z}}$
such that
![]() $1\le q\le M^j$
and
$1\le q\le M^j$
and
![]() $(a, q)=1$
and
$(a, q)=1$
and
Then for
![]() $\sigma (d):=2d^2-2d+1$
, one has
$\sigma (d):=2d^2-2d+1$
, one has
 $$ \begin{align} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|\le CM\log(2M)\bigg(\frac{1}{q}+\frac{1}{M}+\frac q{M^j}\bigg)^{\frac{1}{\sigma(d)}}. \end{align} $$
$$ \begin{align} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|\le CM\log(2M)\bigg(\frac{1}{q}+\frac{1}{M}+\frac q{M^j}\bigg)^{\frac{1}{\sigma(d)}}. \end{align} $$
For the proof, we refer to [Reference Wooley70, Theorem 1.5]. The range of summation in (5.2) can be shifted to any segment of length M without affecting the bound. We will also recall a simple lemma from [Reference Mirek, Stein and Zorin-Kranich52, Lemma A.15, p. 53] (see also [Reference Stein and Wainger58, Lemma 1, p. 1298]), which follows from the Dirichlet principle.
Lemma 5.3. Let
![]() $\theta \in \mathbb {R}$
and
$\theta \in \mathbb {R}$
and
. Suppose that
for some integers
![]() $0\le a<q \leq M$
with
$0\le a<q \leq M$
with
![]() $(a,q)=1$
for some
$(a,q)=1$
for some
![]() $M\ge 1$
. Then there is a reduced fraction
$M\ge 1$
. Then there is a reduced fraction
![]() $a'/q'$
so that
$a'/q'$
so that
![]() $(a', q') = 1$
and
$(a', q') = 1$
and
with
![]() $q/(2|Q|) \leq q' \leq 2 M$
.
$q/(2|Q|) \leq q' \leq 2 M$
.
We now extend Weyl’s inequality in Proposition 5.1 to include the
![]() $j=1$
case.
$j=1$
case.
Proposition 5.4. Let
![]() $d\in {\mathbb {Z}}_+$
and let
$d\in {\mathbb {Z}}_+$
and let
![]() $P\in \mathbb {R}[\mathrm {m}]$
be such that
$P\in \mathbb {R}[\mathrm {m}]$
be such that
![]() $P(m):=c_dm^d+\ldots +c_1m$
. Then there exists a constant
$P(m):=c_dm^d+\ldots +c_1m$
. Then there exists a constant
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $M\in {\mathbb {Z}}_+$
, the following is true. Suppose that for some
$M\in {\mathbb {Z}}_+$
, the following is true. Suppose that for some
![]() $1\le j\le d$
, there are
$1\le j\le d$
, there are
![]() $a, q\in {\mathbb {Z}}$
such that
$a, q\in {\mathbb {Z}}$
such that
![]() $1\le q\le M^j$
and
$1\le q\le M^j$
and
![]() $(a, q)=1$
and
$(a, q)=1$
and
Then for certain
![]() $\tau (d)\in {\mathbb {Z}}_+$
, one has
$\tau (d)\in {\mathbb {Z}}_+$
, one has
 $$ \begin{align} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|\le CM\log(2M)\bigg(\frac{1}{q}+\frac{1}{M}+\frac q{M^j}\bigg)^{\frac{1}{\tau(d)}}. \end{align} $$
$$ \begin{align} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|\le CM\log(2M)\bigg(\frac{1}{q}+\frac{1}{M}+\frac q{M^j}\bigg)^{\frac{1}{\tau(d)}}. \end{align} $$
Proof. We first assume that
![]() $d=1$
. Then
$d=1$
. Then
![]() $P(m)=c_1m$
and
$P(m)=c_1m$
and
![]() $j=1$
. We can also assume that
$j=1$
. We can also assume that
![]() $q\ge 2$
; otherwise, (5.6) is obvious. Now it is easy to see that
$q\ge 2$
; otherwise, (5.6) is obvious. Now it is easy to see that
 $$ \begin{align*} \Big|\sum_{m=1}^M \boldsymbol{e}(c_1m)\Big|\le \frac{1}{\|c_1\|}\lesssim q. \end{align*} $$
$$ \begin{align*} \Big|\sum_{m=1}^M \boldsymbol{e}(c_1m)\Big|\le \frac{1}{\|c_1\|}\lesssim q. \end{align*} $$
Thus, (5.6) holds with
![]() $\tau (1)=1$
. Now we assume that
$\tau (1)=1$
. Now we assume that
![]() $d\ge 2$
. If (5.5) holds for some
$d\ge 2$
. If (5.5) holds for some
![]() $2\le j\le d$
, then (5.6) follows from Proposition 5.1 with
$2\le j\le d$
, then (5.6) follows from Proposition 5.1 with
![]() $\tau (d)=\sigma (d)$
, where
$\tau (d)=\sigma (d)$
, where
![]() $\sigma (d)$
is the exponent as in (5.2). Hence, we can assume that
$\sigma (d)$
is the exponent as in (5.2). Hence, we can assume that
![]() $j=1$
. Define
$j=1$
. Define
![]() $\kappa :=\min \{q, M/q\}$
, and let
$\kappa :=\min \{q, M/q\}$
, and let
![]() $\chi \in (0, (4d)^{-1})$
. We may assume that
$\chi \in (0, (4d)^{-1})$
. We may assume that
![]() $\kappa>100$
; otherwise, (5.6) obviously follows. For every
$\kappa>100$
; otherwise, (5.6) obviously follows. For every
![]() $2\le j'\le d$
, by Dirichlet’s principle, there is a reduced fraction
$2\le j'\le d$
, by Dirichlet’s principle, there is a reduced fraction
![]() $a_{j'}/q_{j'}$
such that
$a_{j'}/q_{j'}$
such that
 $$ \begin{align} \Big|c_{j'}-\frac{a_{j'}}{ q_{j'}}\Big|\le\frac{\kappa^{\chi}}{q_{j'} M^{j'}} \end{align} $$
$$ \begin{align} \Big|c_{j'}-\frac{a_{j'}}{ q_{j'}}\Big|\le\frac{\kappa^{\chi}}{q_{j'} M^{j'}} \end{align} $$
with
![]() $(a_{j'}, q_{j'})$
and
$(a_{j'}, q_{j'})$
and
![]() $1\le q_j'\le M^{j'}\kappa ^{-\chi }$
. We may assume that
$1\le q_j'\le M^{j'}\kappa ^{-\chi }$
. We may assume that
![]() $1\le q_{j'}\le \kappa ^{\chi }$
for all
$1\le q_{j'}\le \kappa ^{\chi }$
for all
![]() $2\le j'\le d$
, since otherwise the claim follows from (5.2) with
$2\le j'\le d$
, since otherwise the claim follows from (5.2) with
![]() $\tau (d)=\lceil \sigma (d)\chi ^{-1}\rceil $
. Let
$\tau (d)=\lceil \sigma (d)\chi ^{-1}\rceil $
. Let
![]() $Q:=\operatorname {\mathrm {lcm}}\{q_{j'}: 2\le j'\le d\}\le \kappa ^{d\chi }$
and note that
$Q:=\operatorname {\mathrm {lcm}}\{q_{j'}: 2\le j'\le d\}\le \kappa ^{d\chi }$
and note that
![]() $Q \le M$
follows from the definition of
$Q \le M$
follows from the definition of
![]() $\kappa $
. We have
$\kappa $
. We have
 $$ \begin{align*} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|&\le \sum_{r=1}^Q\Big|\sum_{-\frac{r}{Q}< \ell\le \frac{M-r}{Q}} \boldsymbol{e}(P(Q\ell+r))\Big|\\ &=\sum_{r=1}^Q\Big|\sum_{U< \ell\le V} A_{\ell} B_{\ell}\Big|, \end{align*} $$
$$ \begin{align*} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|&\le \sum_{r=1}^Q\Big|\sum_{-\frac{r}{Q}< \ell\le \frac{M-r}{Q}} \boldsymbol{e}(P(Q\ell+r))\Big|\\ &=\sum_{r=1}^Q\Big|\sum_{U< \ell\le V} A_{\ell} B_{\ell}\Big|, \end{align*} $$
where
![]() $U:=-\frac {r}{Q}$
,
$U:=-\frac {r}{Q}$
,
![]() $V:=\frac {M-r}{Q}$
and
$V:=\frac {M-r}{Q}$
and
![]() $A_{\ell }:=\boldsymbol {e}(c_1Q\ell )$
and
$A_{\ell }:=\boldsymbol {e}(c_1Q\ell )$
and
 $$ \begin{align*}B_{\ell}:=\boldsymbol{e}\left(\sum_{j'=2}^d c_{j'} (Q\ell+r)^{j'} \right) = \boldsymbol{e}\left(\sum_{j'=2}^d \alpha_{j'} (Q\ell + r)^{j'} + \sum_{j'=2}^d \frac{a_{j'}}{q_{j'}} r^{j'}\right), \end{align*} $$
$$ \begin{align*}B_{\ell}:=\boldsymbol{e}\left(\sum_{j'=2}^d c_{j'} (Q\ell+r)^{j'} \right) = \boldsymbol{e}\left(\sum_{j'=2}^d \alpha_{j'} (Q\ell + r)^{j'} + \sum_{j'=2}^d \frac{a_{j'}}{q_{j'}} r^{j'}\right), \end{align*} $$
where
![]() $\alpha _{j'} := c_{j'} - a_{j'}/q_{j'}$
satisfies the estimate (5.7). Using the summation by parts formula (2.1), we obtain
$\alpha _{j'} := c_{j'} - a_{j'}/q_{j'}$
satisfies the estimate (5.7). Using the summation by parts formula (2.1), we obtain
with
![]() $S_{\ell }:=\sum _{k\in (U, \ell ]\cap {\mathbb {Z}}}A_k$
.
$S_{\ell }:=\sum _{k\in (U, \ell ]\cap {\mathbb {Z}}}A_k$
.
From above, since
![]() $Q \le M$
, we see that
$Q \le M$
, we see that
By Lemma 5.3 (with
![]() $M=q$
), there is a reduced fraction
$M=q$
), there is a reduced fraction
![]() $a'/q'$
such that
$a'/q'$
such that
![]() $(a', q')=1$
and
$(a', q')=1$
and
Hence,
![]() $q'\ge \kappa ^{1-d\chi }/2\ge 2$
and so
$q'\ge \kappa ^{1-d\chi }/2\ge 2$
and so
Consequently, we conclude that
 $$ \begin{align*} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|\lesssim M\kappa^{-1/2}. \end{align*} $$
$$ \begin{align*} \Big|\sum_{m=1}^M \boldsymbol{e}(P(m))\Big|\lesssim M\kappa^{-1/2}. \end{align*} $$
This implies (5.6) with
![]() $\tau (d)=2$
, and the proof of Proposition 5.4 is complete.
$\tau (d)=2$
, and the proof of Proposition 5.4 is complete.
We shall also use the Vinogradov mean value theorem. A detailed exposition of Vinogradov’s method can be found in [Reference Iwaniec and Kowalski35, Section 8.5, p. 216]; see also [Reference Wooley70]. We shall follow [Reference Iwaniec and Kowalski35]. For each integer
![]() $s\ge 1$
and
$s\ge 1$
and
![]() $k, N\ge 2$
and for
$k, N\ge 2$
and for
![]() $\lambda _1,\ldots , \lambda _k\in {\mathbb {Z}}$
let
$\lambda _1,\ldots , \lambda _k\in {\mathbb {Z}}$
let
![]() $J_{s, k}(N; \lambda _1, \ldots , \lambda _k)$
denote the number of solutions to the system of k inhomogeneous equations in
$J_{s, k}(N; \lambda _1, \ldots , \lambda _k)$
denote the number of solutions to the system of k inhomogeneous equations in
![]() $2s$
variables given by
$2s$
variables given by
 $$ \begin{align} \left\{ \begin{array}{c} x_1+\ldots+x_s-y_1-\ldots-y_s=\lambda_1\\ x_1^2+\ldots+x_s^2-y_1^2-\ldots-y_s^2=\lambda_2\\ \vdots \\ x_1^k+\ldots+x_s^k-y_1^k-\ldots-y_s^k=\lambda_k, \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{c} x_1+\ldots+x_s-y_1-\ldots-y_s=\lambda_1\\ x_1^2+\ldots+x_s^2-y_1^2-\ldots-y_s^2=\lambda_2\\ \vdots \\ x_1^k+\ldots+x_s^k-y_1^k-\ldots-y_s^k=\lambda_k, \end{array} \right. \end{align} $$
where
![]() $x_j, y_j\in [N]$
for every
$x_j, y_j\in [N]$
for every
![]() $j\in [s]$
. The number
$j\in [s]$
. The number
![]() $J_{s, k}(N; \lambda _1, \ldots , \lambda _k)$
can be expressed in terms of a certain exponential sum. Let
$J_{s, k}(N; \lambda _1, \ldots , \lambda _k)$
can be expressed in terms of a certain exponential sum. Let
![]() $R_k(x):=(x, x^2, \ldots , x^k)\in \mathbb {R}^k$
denote the moment curve for
$R_k(x):=(x, x^2, \ldots , x^k)\in \mathbb {R}^k$
denote the moment curve for
![]() $x\in \mathbb {R}$
. For
$x\in \mathbb {R}$
. For
![]() $\xi =(\xi _1,\ldots , \xi _k)\in \mathbb {R}^k$
, define the exponential sum
$\xi =(\xi _1,\ldots , \xi _k)\in \mathbb {R}^k$
, define the exponential sum
 $$ \begin{align*} S_k(\xi; N):=\sum_{n=1}^N\boldsymbol{e}(\xi\cdot R_k(n))=\sum_{n=1}^N\boldsymbol{e}(\xi_1n+\ldots+\xi_kn^k). \end{align*} $$
$$ \begin{align*} S_k(\xi; N):=\sum_{n=1}^N\boldsymbol{e}(\xi\cdot R_k(n))=\sum_{n=1}^N\boldsymbol{e}(\xi_1n+\ldots+\xi_kn^k). \end{align*} $$
One easily obtains
 $$ \begin{align} |S_k(\xi; N)|^{2s}=\sum_{|\lambda_1|\le sN}\ldots\sum_{|\lambda_k|\le sN^k}J_{s, k}(N; \lambda_1, \ldots, \lambda_k)\boldsymbol{e}(\xi\cdot\lambda), \end{align} $$
$$ \begin{align} |S_k(\xi; N)|^{2s}=\sum_{|\lambda_1|\le sN}\ldots\sum_{|\lambda_k|\le sN^k}J_{s, k}(N; \lambda_1, \ldots, \lambda_k)\boldsymbol{e}(\xi\cdot\lambda), \end{align} $$
which by the Fourier inversion formula gives
Moreover, from (5.10), one has
where the number
![]() $J_{s, k}(N)$
represents the number of solutions to the system of k homogeneous equations in
$J_{s, k}(N)$
represents the number of solutions to the system of k homogeneous equations in
![]() $2s$
variables as in (5.8) with
$2s$
variables as in (5.8) with
![]() $\lambda _1=\ldots =\lambda _k=0$
.
$\lambda _1=\ldots =\lambda _k=0$
.
Vinogradov’s mean value theorem can be formulated as follows:
Theorem 5.12. For all integers
![]() $s\ge 1$
and
$s\ge 1$
and
![]() $k\ge 2$
and any
$k\ge 2$
and any
![]() $\varepsilon>0$
, there is a constant
$\varepsilon>0$
, there is a constant
![]() $C_{\varepsilon }>0$
such that for every integer
$C_{\varepsilon }>0$
such that for every integer
![]() $N\ge 2$
, one has
$N\ge 2$
, one has
Moreover, if additionally
![]() $s>\frac {1}{2}k(k+1)$
, then there is a constant
$s>\frac {1}{2}k(k+1)$
, then there is a constant
![]() $C>0$
such that
$C>0$
such that
Apart from the
![]() $N^{\varepsilon }$
loss in (5.13), this bound is known to be sharp. Inequality (5.13) is fairly simple for
$N^{\varepsilon }$
loss in (5.13), this bound is known to be sharp. Inequality (5.13) is fairly simple for
![]() $k=2$
and follows from elementary estimates for the divisor function. The conclusion of Theorem 5.12 for
$k=2$
and follows from elementary estimates for the divisor function. The conclusion of Theorem 5.12 for
![]() $k\ge 3$
, known as Vinogradov’s mean value theorem, was a central problem in analytic number theory and had been open until recently. The cubic case
$k\ge 3$
, known as Vinogradov’s mean value theorem, was a central problem in analytic number theory and had been open until recently. The cubic case
![]() $k=3$
was solved by Wooley [Reference Wooley69] using the efficient congruencing method. The case for any
$k=3$
was solved by Wooley [Reference Wooley69] using the efficient congruencing method. The case for any
![]() $k\ge 3$
was solved by the first author with Demeter and Guth [Reference Bourgain, Demeter and Guth17] using the decoupling method. Not long afterwards, Wooley [Reference Wooley68] also showed that the efficient congruencing method can be used to solve the Vinogradov mean value conjecture for all
$k\ge 3$
was solved by the first author with Demeter and Guth [Reference Bourgain, Demeter and Guth17] using the decoupling method. Not long afterwards, Wooley [Reference Wooley68] also showed that the efficient congruencing method can be used to solve the Vinogradov mean value conjecture for all
![]() $k\ge 3$
. In fact, later we will only use (5.14), which easily follows from (5.13); the details can be found in [Reference Bourgain, Demeter and Guth17, Section 5].
$k\ge 3$
. In fact, later we will only use (5.14), which easily follows from (5.13); the details can be found in [Reference Bourgain, Demeter and Guth17, Section 5].
5.1 Double Weyl’s inequality
Let
![]() $K_1, K_2\in \mathbb {N}$
,
$K_1, K_2\in \mathbb {N}$
,
![]() $M_1, M_2\in {\mathbb {Z}}_+$
satisfy
$M_1, M_2\in {\mathbb {Z}}_+$
satisfy
![]() $K_1< M_1$
and
$K_1< M_1$
and
![]() $K_2< M_2$
. Let
$K_2< M_2$
. Let
![]() $Q\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be given and define double exponential sums by
$Q\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be given and define double exponential sums by
 $$ \begin{align} S_{K_1, M_1, K_2, M_2}(Q):=&\sum_{m_1=K_1+1}^{M_1}\sum_{m_2=K_2+1}^{M_2}\boldsymbol{e}(Q(m_1, m_2)), \end{align} $$
$$ \begin{align} S_{K_1, M_1, K_2, M_2}(Q):=&\sum_{m_1=K_1+1}^{M_1}\sum_{m_2=K_2+1}^{M_2}\boldsymbol{e}(Q(m_1, m_2)), \end{align} $$
 $$ \begin{align} S_{K_1, M_1, K_2, M_2}^1(Q):=&\sum_{m_1=K_1+1}^{M_1}\Big|\sum_{m_2=K_2+1}^{M_2}\boldsymbol{e}(Q(m_1, m_2))\Big|, \end{align} $$
$$ \begin{align} S_{K_1, M_1, K_2, M_2}^1(Q):=&\sum_{m_1=K_1+1}^{M_1}\Big|\sum_{m_2=K_2+1}^{M_2}\boldsymbol{e}(Q(m_1, m_2))\Big|, \end{align} $$
 $$ \begin{align} S_{K_1, M_1, K_2, M_2}^2(Q):=&\sum_{m_2=K_2+1}^{M_2}\Big|\sum_{m_1=K_1+1}^{M_1}\boldsymbol{e}(Q(m_1, m_2))\Big|. \end{align} $$
$$ \begin{align} S_{K_1, M_1, K_2, M_2}^2(Q):=&\sum_{m_2=K_2+1}^{M_2}\Big|\sum_{m_1=K_1+1}^{M_1}\boldsymbol{e}(Q(m_1, m_2))\Big|. \end{align} $$
If
![]() $K_1=K_2=0$
, we will abbreviate (5.15), (5.16) and (5.17), respectively, to
$K_1=K_2=0$
, we will abbreviate (5.15), (5.16) and (5.17), respectively, to
By the triangle inequality, we have
We now provide estimates for (5.15), (5.16) and (5.17) in the spirit of Proposition 5.1 above. We first recall a technical lemma from [Reference Karatsuba and Nathanson39, Chapter IV, Lemma 5, p. 82].
Lemma 5.20. Let
![]() $\alpha \in \mathbb {R}$
and suppose that there are
$\alpha \in \mathbb {R}$
and suppose that there are
![]() $a\in {\mathbb {Z}}, q\in {\mathbb {Z}}_+$
such that
$a\in {\mathbb {Z}}, q\in {\mathbb {Z}}_+$
such that
![]() $(a, q)=1$
and
$(a, q)=1$
and
Then for every
![]() $\beta \in \mathbb {R}$
,
$\beta \in \mathbb {R}$
,
![]() $U>0$
and
$U>0$
and
![]() $P\ge 1$
, one has
$P\ge 1$
, one has
 $$ \begin{align} \sum_{n=1}^P\min\bigg\{U, \frac{1}{\|\alpha n+\beta\|}\bigg\}\le 6\bigg(1+\frac{P}{q}\bigg)(U+q\log q). \end{align} $$
$$ \begin{align} \sum_{n=1}^P\min\bigg\{U, \frac{1}{\|\alpha n+\beta\|}\bigg\}\le 6\bigg(1+\frac{P}{q}\bigg)(U+q\log q). \end{align} $$
Estimate (5.21) will be useful in the proof of the following counterpart of Weyl’s inequality for double sums.
Proposition 5.22. Let
![]() $d_1, d_2\in {\mathbb {Z}}_+$
and
$d_1, d_2\in {\mathbb {Z}}_+$
and
![]() $Q\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be such that
$Q\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be such that
 $$ \begin{align*} Q(m_1, m_2):=\sum_{\gamma_1=0}^{d_1}\sum_{\gamma_2=0}^{d_2} c_{\gamma_1, \gamma_2}m_1^{\gamma_1}m_2^{\gamma_2}, \quad \text{ and } \quad c_{0, 0}=0. \end{align*} $$
$$ \begin{align*} Q(m_1, m_2):=\sum_{\gamma_1=0}^{d_1}\sum_{\gamma_2=0}^{d_2} c_{\gamma_1, \gamma_2}m_1^{\gamma_1}m_2^{\gamma_2}, \quad \text{ and } \quad c_{0, 0}=0. \end{align*} $$
Then there exists a constant
![]() $C>0$
such that for every
$C>0$
such that for every
![]() $K_1, K_2\in \mathbb {N}$
,
$K_1, K_2\in \mathbb {N}$
,
![]() $M_1, M_2\in {\mathbb {Z}}_+$
satisfying
$M_1, M_2\in {\mathbb {Z}}_+$
satisfying
![]() $K_1\le M_1$
and
$K_1\le M_1$
and
![]() $K_2\le M_2$
, the following holds. Suppose that for some
$K_2\le M_2$
, the following holds. Suppose that for some
![]() $1 \le \rho _1\le d_1$
and
$1 \le \rho _1\le d_1$
and
![]() $1\le \rho _2\le d_2$
, there are
$1\le \rho _2\le d_2$
, there are
![]() $a_{\rho _1, \rho _2}\in {\mathbb {Z}}, q_{\rho _1, \rho _2}\in {\mathbb {Z}}_+$
such that
$a_{\rho _1, \rho _2}\in {\mathbb {Z}}, q_{\rho _1, \rho _2}\in {\mathbb {Z}}_+$
such that
![]() $(a_{\rho _1, \rho _2}, q_{\rho _1, \rho _2})=1$
and
$(a_{\rho _1, \rho _2}, q_{\rho _1, \rho _2})=1$
and
 $$ \begin{align} \Big|c_{\rho_1, \rho_2}-\frac{a_{\rho_1, \rho_2}}{q_{\rho_1, \rho_2}}\Big|\le\frac{1}{q_{\rho_1, \rho_2}^2}. \end{align} $$
$$ \begin{align} \Big|c_{\rho_1, \rho_2}-\frac{a_{\rho_1, \rho_2}}{q_{\rho_1, \rho_2}}\Big|\le\frac{1}{q_{\rho_1, \rho_2}^2}. \end{align} $$
Set
![]() $k_i:=d_i(d_i+1)$
for
$k_i:=d_i(d_i+1)$
for
![]() $i\in [2]$
,
$i\in [2]$
,
![]() $M_{-} := \min (M_1^{\rho _1}, M_2^{\rho _2})$
and
$M_{-} := \min (M_1^{\rho _1}, M_2^{\rho _2})$
and
![]() $M_{+} := \max (M_1^{\rho _1}, M_2^{\rho _2})$
. Then for
$M_{+} := \max (M_1^{\rho _1}, M_2^{\rho _2})$
. Then for
![]() $i\in [2]$
,
$i\in [2]$
,
 $$ \begin{align} S_{K_1, M_1, K_2, M_2}^i(Q) &\le CM_1M_2\bigg( \frac{1}{M_{-}}+\frac{q_{\rho_1, \rho_2}\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q_{\rho_1, \rho_2}}+\frac{\log q_{\rho_1, \rho_2}}{M_{+}}\bigg)^{\frac{1}{4k_1k_2}}. \end{align} $$
$$ \begin{align} S_{K_1, M_1, K_2, M_2}^i(Q) &\le CM_1M_2\bigg( \frac{1}{M_{-}}+\frac{q_{\rho_1, \rho_2}\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q_{\rho_1, \rho_2}}+\frac{\log q_{\rho_1, \rho_2}}{M_{+}}\bigg)^{\frac{1}{4k_1k_2}}. \end{align} $$
In view of (5.19), estimates (5.24) clearly hold for
![]() $|S_{K_1, M_1, K_2, M_2}(Q)|$
.
$|S_{K_1, M_1, K_2, M_2}(Q)|$
.
Remark 5.25. The bracketed expression in (5.24) is equal to
![]() $\min (A,B)$
where
$\min (A,B)$
where
 $$ \begin{align*}A \ = \ \frac{1}{M_2^{\rho_2}}+\frac{q_{\rho_1, \rho_2}\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q_{\rho_1, \rho_2}}+\frac{\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}} \end{align*} $$
$$ \begin{align*}A \ = \ \frac{1}{M_2^{\rho_2}}+\frac{q_{\rho_1, \rho_2}\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q_{\rho_1, \rho_2}}+\frac{\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}} \end{align*} $$
and
 $$ \begin{align*}B \ = \ \frac{1}{M_1^{\rho_1}}+\frac{q_{\rho_1, \rho_2}\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q_{\rho_1, \rho_2}}+\frac{\log q_{\rho_1, \rho_2}}{M_2^{\rho_2}}. \end{align*} $$
$$ \begin{align*}B \ = \ \frac{1}{M_1^{\rho_1}}+\frac{q_{\rho_1, \rho_2}\log q_{\rho_1, \rho_2}}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q_{\rho_1, \rho_2}}+\frac{\log q_{\rho_1, \rho_2}}{M_2^{\rho_2}}. \end{align*} $$
Multi-parameter exponential sums were extensively investigated over the years. The best source about this subject is [Reference Arkhipov, Chubarikov and Karatsuba1]. However, here we need bounds as in (5.24), which will allow us to gain logarithmic factors on minor arcs (see Proposition 5.37) in contrast to polynomial factors, which were obtained in [Reference Arkhipov, Chubarikov and Karatsuba1]. We prove Proposition 5.22 by giving an argument based on an iterative application of the Vinogradov mean value theorem.
Proof of Proposition 5.22
We only prove (5.24) for
![]() $i=1$
. The proof of (5.24) for
$i=1$
. The proof of (5.24) for
![]() $i=2$
can be obtained similarly by symmetry. To prove inequality (5.24) when
$i=2$
can be obtained similarly by symmetry. To prove inequality (5.24) when
![]() $i=1$
, we shall follow [Reference Iwaniec and Kowalski35, Section 8.5., p. 216] and proceed in five steps.
$i=1$
, we shall follow [Reference Iwaniec and Kowalski35, Section 8.5., p. 216] and proceed in five steps.
Step 1. For
![]() $i\in [2]$
, let us define the
$i\in [2]$
, let us define the
![]() $d_i$
-dimensional box
$d_i$
-dimensional box
 $$\begin{align*}\mathcal B_{d_i}(M_{i}):=\Big(\prod_{j=1}^{d_i}[-k_iM_i^{j}, k_iM_i^{j}]\Big)\cap{\mathbb{Z}}^{d_i}. \end{align*}$$
$$\begin{align*}\mathcal B_{d_i}(M_{i}):=\Big(\prod_{j=1}^{d_i}[-k_iM_i^{j}, k_iM_i^{j}]\Big)\cap{\mathbb{Z}}^{d_i}. \end{align*}$$
Observe that
 $$ \begin{align*} Q(m_1, m_2)= \sum_{\gamma_2=0}^{d_2}c_{\gamma_2}(m_1)m_2^{\gamma_2}=c(m_1)\cdot R_{d_2}(m_2)+c_0(m_1), \end{align*} $$
$$ \begin{align*} Q(m_1, m_2)= \sum_{\gamma_2=0}^{d_2}c_{\gamma_2}(m_1)m_2^{\gamma_2}=c(m_1)\cdot R_{d_2}(m_2)+c_0(m_1), \end{align*} $$
where for
![]() $\gamma _2\in [d_2]\cup \{0\}$
, one has
$\gamma _2\in [d_2]\cup \{0\}$
, one has
 $$ \begin{align*} c(m_1):=(c_1(m_1),\ldots, c_{d_2}(m_1)) \qquad\text{ and } \qquad c_{\gamma_2}(m_1):=\sum_{\gamma_1=0}^{d_1} c_{\gamma_1, \gamma_2}m_1^{\gamma_1}. \end{align*} $$
$$ \begin{align*} c(m_1):=(c_1(m_1),\ldots, c_{d_2}(m_1)) \qquad\text{ and } \qquad c_{\gamma_2}(m_1):=\sum_{\gamma_1=0}^{d_1} c_{\gamma_1, \gamma_2}m_1^{\gamma_1}. \end{align*} $$
Recall that
![]() $R_{d_2}(m_2) = (m_2, m_2^2, \ldots , m_2^{d_2})$
. By (5.16), we note that
$R_{d_2}(m_2) = (m_2, m_2^2, \ldots , m_2^{d_2})$
. By (5.16), we note that
For any
![]() $k_2\in {\mathbb {Z}}_+$
, by Hölder’s inequality and by (5.9), we obtain
$k_2\in {\mathbb {Z}}_+$
, by Hölder’s inequality and by (5.9), we obtain
 $$ \begin{align} \begin{split} S_{K_1, M_1, K_2, M_2}^1(Q)^{2k_2}&\lesssim M_1^{2k_2-1}\max_{N_2\in[M_2]} \sum_{m_1=1}^{M_1}|S_{d_2}(c(m_1); N_2)|^{2k_2}\\ &=M_1^{2k_2-1}\max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) \sum_{m_1=1}^{M_1} \boldsymbol{e}(c(m_1)\cdot u). \end{split} \end{align} $$
$$ \begin{align} \begin{split} S_{K_1, M_1, K_2, M_2}^1(Q)^{2k_2}&\lesssim M_1^{2k_2-1}\max_{N_2\in[M_2]} \sum_{m_1=1}^{M_1}|S_{d_2}(c(m_1); N_2)|^{2k_2}\\ &=M_1^{2k_2-1}\max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) \sum_{m_1=1}^{M_1} \boldsymbol{e}(c(m_1)\cdot u). \end{split} \end{align} $$
Step 2. We see that
 $$\begin{align*}c(m_1)\cdot u=\sum_{\gamma_1=0}^{d_1} \sum_{\gamma_2=1}^{d_2}c_{\gamma_1, \gamma_2}u_{\gamma_2}m_1^{\gamma_1} =\beta^1(u)\cdot R_{d_1}(m_1)+\beta_0^1(u), \end{align*}$$
$$\begin{align*}c(m_1)\cdot u=\sum_{\gamma_1=0}^{d_1} \sum_{\gamma_2=1}^{d_2}c_{\gamma_1, \gamma_2}u_{\gamma_2}m_1^{\gamma_1} =\beta^1(u)\cdot R_{d_1}(m_1)+\beta_0^1(u), \end{align*}$$
where for
![]() $u=(u_1,\ldots , u_{d_2})\in {\mathbb {Z}}^{d_2}$
and
$u=(u_1,\ldots , u_{d_2})\in {\mathbb {Z}}^{d_2}$
and
![]() $\gamma _1\in [d_1]\cup \{0\}$
we set
$\gamma _1\in [d_1]\cup \{0\}$
we set
 $$\begin{align*}\beta^1(u):=(\beta_1^1(u),\ldots, \beta_{d_1}^1(u))\qquad\text{ and } \qquad\beta_{\gamma_1}^1(u):=\sum_{\gamma_2=1}^{d_2}c_{\gamma_1, \gamma_2}u_{\gamma_2}. \end{align*}$$
$$\begin{align*}\beta^1(u):=(\beta_1^1(u),\ldots, \beta_{d_1}^1(u))\qquad\text{ and } \qquad\beta_{\gamma_1}^1(u):=\sum_{\gamma_2=1}^{d_2}c_{\gamma_1, \gamma_2}u_{\gamma_2}. \end{align*}$$
Similarly, for
![]() $v=(v_1,\ldots , v_{d_1})\in {\mathbb {Z}}^{d_1}$
and
$v=(v_1,\ldots , v_{d_1})\in {\mathbb {Z}}^{d_1}$
and
![]() $\gamma _2\in [d_2]\cup \{0\}$
, we also set
$\gamma _2\in [d_2]\cup \{0\}$
, we also set
 $$\begin{align*}\beta^2(v):=(\beta_1^2(v),\ldots, \beta_{d_2}^2(v))\qquad\text{ and } \qquad\beta_{\gamma_2}^2(v):=\sum_{\gamma_1=1}^{d_1}c_{\gamma_1, \gamma_2}v_{\gamma_1}. \end{align*}$$
$$\begin{align*}\beta^2(v):=(\beta_1^2(v),\ldots, \beta_{d_2}^2(v))\qquad\text{ and } \qquad\beta_{\gamma_2}^2(v):=\sum_{\gamma_1=1}^{d_1}c_{\gamma_1, \gamma_2}v_{\gamma_1}. \end{align*}$$
This implies, raising both sides of (5.26) to power
![]() $2k_1$
for any
$2k_1$
for any
![]() $k_1\in {\mathbb {Z}}_+$
, that
$k_1\in {\mathbb {Z}}_+$
, that
 $$ \begin{align} \begin{split} S_{K_1, M_1, K_2, M_2}^1(Q)^{4k_1k_2} &\lesssim M_1^{4k_1k_2-2k_1}\max_{N_2\in[M_2]}\Big(\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|\Big)^{2k_1}\\ &\lesssim M_1^{4k_1k_2-2k_1}M_2^{4k_1k_2-2k_2}\max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} S_{K_1, M_1, K_2, M_2}^1(Q)^{4k_1k_2} &\lesssim M_1^{4k_1k_2-2k_1}\max_{N_2\in[M_2]}\Big(\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|\Big)^{2k_1}\\ &\lesssim M_1^{4k_1k_2-2k_1}M_2^{4k_1k_2-2k_2}\max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}. \end{split} \end{align} $$
In (5.27), we used Hölder’s inequality and
 $$\begin{align*}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u)=N_2^{2k_2}. \end{align*}$$
$$\begin{align*}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u)=N_2^{2k_2}. \end{align*}$$
Step 3. For
![]() $v=(v_1, \ldots , v_{d_1})\in {\mathbb {Z}}^{d_1}$
, we have
$v=(v_1, \ldots , v_{d_1})\in {\mathbb {Z}}^{d_1}$
, we have
 $$ \begin{align} \beta^1(u)\cdot v=\sum_{\gamma_2=1}^{d_2}\sum_{\gamma_1=1}^{d_1}c_{\gamma_1, \gamma_2}v_{\gamma_1}u_{\gamma_2}=\beta^2(v)\cdot u. \end{align} $$
$$ \begin{align} \beta^1(u)\cdot v=\sum_{\gamma_2=1}^{d_2}\sum_{\gamma_1=1}^{d_1}c_{\gamma_1, \gamma_2}v_{\gamma_1}u_{\gamma_2}=\beta^2(v)\cdot u. \end{align} $$
Applying (5.9) and (5.11) to the last sum in (5.27), we obtain
 $$ \begin{align} \nonumber \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}& J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}\\ \nonumber &\le J_{k_2,d_2}(M_2) \sum_{u\in \mathcal B_{d_2}(M_2)} |S_{d_1}(\beta^1(u);M_1)|^{2k_1}\\ \nonumber &= J_{k_2,d_2}(M_2) \sum_{u\in \mathcal B_{d_2}(M_2)}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_1, d_1}(M_1; v)\boldsymbol{e}(\beta^1(u)\cdot v)\\ &\le J_{k_1, d_1}(M_1) J_{k_2,d_2}(M_2) \sum_{v\in \mathcal B_{d_1}(M_1)} \big|\sum_{u\in \mathcal B_{d_2}(M_2)} \boldsymbol{e}(\beta^2(v)\cdot u)\big|, \end{align} $$
$$ \begin{align} \nonumber \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}& J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}\\ \nonumber &\le J_{k_2,d_2}(M_2) \sum_{u\in \mathcal B_{d_2}(M_2)} |S_{d_1}(\beta^1(u);M_1)|^{2k_1}\\ \nonumber &= J_{k_2,d_2}(M_2) \sum_{u\in \mathcal B_{d_2}(M_2)}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_1, d_1}(M_1; v)\boldsymbol{e}(\beta^1(u)\cdot v)\\ &\le J_{k_1, d_1}(M_1) J_{k_2,d_2}(M_2) \sum_{v\in \mathcal B_{d_1}(M_1)} \big|\sum_{u\in \mathcal B_{d_2}(M_2)} \boldsymbol{e}(\beta^2(v)\cdot u)\big|, \end{align} $$
where we used (5.28) in the last inequality. In a slightly more involved process, we now obtain a different estimate for the last sum in (5.27). We apply (5.9) twice to obtain
 $$ \begin{align*} \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}& J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}\\ &= \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_2, d_2}(N_2; u) J_{k_1, d_1}(M_1; v)\boldsymbol{e}(\beta^1(u)\cdot v)\\ &= \max_{N_2\in[M_2]}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_1, d_1}(M_1; v) \sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u)\boldsymbol{e}(\beta^2(v)\cdot u)\\ &= \max_{N_2\in[M_2]}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_1, d_1}(M_1; v) |S_{d_2}(\beta^2(v);N_2)|^{2k_2}, \end{align*} $$
$$ \begin{align*} \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}& J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}\\ &= \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_2, d_2}(N_2; u) J_{k_1, d_1}(M_1; v)\boldsymbol{e}(\beta^1(u)\cdot v)\\ &= \max_{N_2\in[M_2]}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_1, d_1}(M_1; v) \sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u)\boldsymbol{e}(\beta^2(v)\cdot u)\\ &= \max_{N_2\in[M_2]}\sum_{v\in \mathcal B_{d_1}(M_1)} J_{k_1, d_1}(M_1; v) |S_{d_2}(\beta^2(v);N_2)|^{2k_2}, \end{align*} $$
where we used (5.28) in the penultimate equality. Hence, by (5.9), (5.11) and (5.28),
 $$ \begin{align} \nonumber \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}& J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}\\ \nonumber &\le J_{k_1,d_1}(M_1) \max_{N_2\in[M_2]}\sum_{v\in \mathcal B_{d_1}(M_1)} |S_{d_2}(\beta^2(v);N_2)|^{2k_2}\\ \nonumber &= J_{k_1, d_1}(M_1) \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) \sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v)\\ & \le J_{k_1, d_1}(M_1)J_{k_2, d_2}(M_2)\sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big|. \end{align} $$
$$ \begin{align} \nonumber \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)}& J_{k_2, d_2}(N_2; u) |S_{d_1}(\beta^1(u); M_1)|^{2k_1}\\ \nonumber &\le J_{k_1,d_1}(M_1) \max_{N_2\in[M_2]}\sum_{v\in \mathcal B_{d_1}(M_1)} |S_{d_2}(\beta^2(v);N_2)|^{2k_2}\\ \nonumber &= J_{k_1, d_1}(M_1) \max_{N_2\in[M_2]}\sum_{u\in \mathcal B_{d_2}(N_2)} J_{k_2, d_2}(N_2; u) \sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v)\\ & \le J_{k_1, d_1}(M_1)J_{k_2, d_2}(M_2)\sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big|. \end{align} $$
Step 4. In this step, we prove (for
![]() $q = q_{\rho _1,\rho _2}$
)
$q = q_{\rho _1,\rho _2}$
)
 $$ \begin{align} \sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big| \lesssim \prod_{j=1}^2 M_j^{\frac{d_j(d_j+1)}{2}} \bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg) \end{align} $$
$$ \begin{align} \sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big| \lesssim \prod_{j=1}^2 M_j^{\frac{d_j(d_j+1)}{2}} \bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg) \end{align} $$
and
 $$ \begin{align} \sum_{v\in \mathcal B_{d_1}(M_1)} \big|\sum_{u\in \mathcal B_{d_2}(M_2)} \boldsymbol{e}(\beta^2(v)\cdot u) \big| \lesssim \prod_{j=1}^2 M_j^{\frac{d_j(d_j+1)}{2}} \bigg( \frac{1}{M_1^{\rho_1}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_2^{\rho_2}}\bigg). \end{align} $$
$$ \begin{align} \sum_{v\in \mathcal B_{d_1}(M_1)} \big|\sum_{u\in \mathcal B_{d_2}(M_2)} \boldsymbol{e}(\beta^2(v)\cdot u) \big| \lesssim \prod_{j=1}^2 M_j^{\frac{d_j(d_j+1)}{2}} \bigg( \frac{1}{M_1^{\rho_1}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_2^{\rho_2}}\bigg). \end{align} $$
We only establish (5.31). The symmetric bound (5.32) is similar. The exponential sum
 $$ \begin{align*}\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) = \prod_{\gamma_1=1}^{d_1} \sum_{|v_{\gamma_1}| \le k_1 M_1^{\gamma_1}} \boldsymbol{e}(\beta^1_{\gamma_1}(u) v_{\gamma_1}) \end{align*} $$
$$ \begin{align*}\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) = \prod_{\gamma_1=1}^{d_1} \sum_{|v_{\gamma_1}| \le k_1 M_1^{\gamma_1}} \boldsymbol{e}(\beta^1_{\gamma_1}(u) v_{\gamma_1}) \end{align*} $$
is a product of geometric series which we can easily evaluate to conclude
 $$ \begin{align*} \nonumber \sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big| &\lesssim \sum_{u\in \mathcal B_{d_2}(M_2)} \prod_{\gamma_1=1}^{d_1} \min\bigg\{2d_1M_1^{\gamma_1}, \frac{1}{\|\beta_{\gamma_1}^1(u)\|}\bigg\}\\ &\le (2d_1M_1)^{\frac{d_1(d_1+1)}{2}-\rho_1} \sum_{u\in \mathcal B_{d_2}(M_2)} \min\bigg\{2d_1M_1^{\rho_1}, \frac{1}{\|\beta_{\rho_1}^1(u)\|}\bigg\}. \end{align*} $$
$$ \begin{align*} \nonumber \sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big| &\lesssim \sum_{u\in \mathcal B_{d_2}(M_2)} \prod_{\gamma_1=1}^{d_1} \min\bigg\{2d_1M_1^{\gamma_1}, \frac{1}{\|\beta_{\gamma_1}^1(u)\|}\bigg\}\\ &\le (2d_1M_1)^{\frac{d_1(d_1+1)}{2}-\rho_1} \sum_{u\in \mathcal B_{d_2}(M_2)} \min\bigg\{2d_1M_1^{\rho_1}, \frac{1}{\|\beta_{\rho_1}^1(u)\|}\bigg\}. \end{align*} $$
Since (5.23) holds and
 $$\begin{align*}\beta_{\rho_1}^1(u)=c_{\rho_1,\rho_2}u_{\rho_2}+\beta(u), \qquad\text{ where } \qquad \beta(u):=\sum_{\substack{\gamma_2=1\\\gamma_2\neq\rho_2}}^{d_2}c_{\rho_1, \gamma_2}u_{\gamma_2}, \end{align*}$$
$$\begin{align*}\beta_{\rho_1}^1(u)=c_{\rho_1,\rho_2}u_{\rho_2}+\beta(u), \qquad\text{ where } \qquad \beta(u):=\sum_{\substack{\gamma_2=1\\\gamma_2\neq\rho_2}}^{d_2}c_{\rho_1, \gamma_2}u_{\gamma_2}, \end{align*}$$
we can apply (5.21) with
![]() $P=k_{2}M_2^{\rho _2}$
,
$P=k_{2}M_2^{\rho _2}$
,
![]() $U=2d_1M_1^{\rho _1}$
and
$U=2d_1M_1^{\rho _1}$
and
![]() $q=q_{\rho _1, \rho _2}$
and obtain
$q=q_{\rho _1, \rho _2}$
and obtain
 $$ \begin{align*} \sum_{|u_{\rho_2}|\le k_{2}M_2^{\rho_2}} \min\bigg\{2d_1M_1^{\rho_1}, \frac{1}{\|\beta_{\rho_1}^1(u)\|}\bigg\} &\lesssim M_1^{\rho_1}+q\log q+\frac{M_1^{\rho_1}M_2^{\rho_2}}{q}+M_2^{\rho_2}\log q\\ &\lesssim M_1^{\rho_1}M_2^{\rho_2}\bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg). \end{align*} $$
$$ \begin{align*} \sum_{|u_{\rho_2}|\le k_{2}M_2^{\rho_2}} \min\bigg\{2d_1M_1^{\rho_1}, \frac{1}{\|\beta_{\rho_1}^1(u)\|}\bigg\} &\lesssim M_1^{\rho_1}+q\log q+\frac{M_1^{\rho_1}M_2^{\rho_2}}{q}+M_2^{\rho_2}\log q\\ &\lesssim M_1^{\rho_1}M_2^{\rho_2}\bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg). \end{align*} $$
Hence
 $$ \begin{align*}\sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big| \lesssim \bigg(\prod_{j=1}^2 M_j^{\frac{d_j(d_j+1)}{2}} \bigg) \bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg), \end{align*} $$
$$ \begin{align*}\sum_{u\in \mathcal B_{d_2}(M_2)} \big|\sum_{v\in \mathcal B_{d_1}(M_1)} \boldsymbol{e}(\beta^1(u)\cdot v) \big| \lesssim \bigg(\prod_{j=1}^2 M_j^{\frac{d_j(d_j+1)}{2}} \bigg) \bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg), \end{align*} $$
establishing (5.31).
Step 5. We use the bound (5.31) in (5.30) to conclude
 $$ \begin{align*} S_{K_1, M_1, K_2, M_2}^1(Q)^{4k_1k_2} &\lesssim M_1^{4k_1k_2-2k_1}M_2^{4k_1k_2-2k_2}J_{k_1, d_1}(M_1)J_{k_2, d_2}(M_2)\\ &\quad \times M_1^{\frac{d_1(d_1+1)}{2}}M_2^{\frac{d_2(d_2+1)}{2}} \bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg). \end{align*} $$
$$ \begin{align*} S_{K_1, M_1, K_2, M_2}^1(Q)^{4k_1k_2} &\lesssim M_1^{4k_1k_2-2k_1}M_2^{4k_1k_2-2k_2}J_{k_1, d_1}(M_1)J_{k_2, d_2}(M_2)\\ &\quad \times M_1^{\frac{d_1(d_1+1)}{2}}M_2^{\frac{d_2(d_2+1)}{2}} \bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg). \end{align*} $$
From Vinogradov’s mean value theorem (or more precisely from (5.14) with
![]() $s=k_i:=d_i(d_i+1)$
and
$s=k_i:=d_i(d_i+1)$
and
![]() $k=d_i$
for
$k=d_i$
for
![]() $i\in [2]$
), we conclude from (5.14),
$i\in [2]$
), we conclude from (5.14),
![]() $J_{k_i, d_i}(M_i) \le C M_i^{3 k_i/2}, i=1,2$
and so
$J_{k_i, d_i}(M_i) \le C M_i^{3 k_i/2}, i=1,2$
and so
 $$ \begin{align*} S_{K_1, M_1, M_2, M_2}^1(Q)^{4k_1k_2} \lesssim M_1^{4k_1k_2}M_2^{4k_1k_2}\bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg). \end{align*} $$
$$ \begin{align*} S_{K_1, M_1, M_2, M_2}^1(Q)^{4k_1k_2} \lesssim M_1^{4k_1k_2}M_2^{4k_1k_2}\bigg( \frac{1}{M_2^{\rho_2}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_1^{\rho_1}}\bigg). \end{align*} $$
In a similar way, using (5.32) in (5.29), we also have
 $$ \begin{align*} S_{K_1, M_1, M_2, M_2}^1(Q)^{4k_1k_2} \lesssim M_1^{4k_1k_2}M_2^{4k_1k_2}\bigg( \frac{1}{M_1^{\rho_1}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_2^{\rho_2}}\bigg). \end{align*} $$
$$ \begin{align*} S_{K_1, M_1, M_2, M_2}^1(Q)^{4k_1k_2} \lesssim M_1^{4k_1k_2}M_2^{4k_1k_2}\bigg( \frac{1}{M_1^{\rho_1}}+\frac{q\log q}{M_1^{\rho_1}M_2^{\rho_2}}+\frac{1}{q}+\frac{\log q}{M_2^{\rho_2}}\bigg). \end{align*} $$
Therefore,
![]() $S_{K_1, M_1, M_2, M_2}^1(Q)^{4k_1k_2}$
is bounded from above by the minimum of these two bounds. By Remark 5.25, this completes the proof of Proposition 5.22.
$S_{K_1, M_1, M_2, M_2}^1(Q)^{4k_1k_2}$
is bounded from above by the minimum of these two bounds. By Remark 5.25, this completes the proof of Proposition 5.22.
5.2 Double Weyl’s inequality in the Newton diagram sectors
Throughout this subsection, we assume that
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
and
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
and
![]() $P(0, 0)=0$
. Moreover, we assume that P is non-degenerate in the sense of (1.14); see the remark below Theorem 1.11. Then for every
$P(0, 0)=0$
. Moreover, we assume that P is non-degenerate in the sense of (1.14); see the remark below Theorem 1.11. Then for every
![]() $\xi \in \mathbb {R}$
, we define a corresponding polynomial
$\xi \in \mathbb {R}$
, we define a corresponding polynomial
![]() $P_{\xi }\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
by setting
$P_{\xi }\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
by setting
It is clear to see that the backwards Newton diagrams of P and
![]() $P_{\xi }$
are the same
$P_{\xi }$
are the same
![]() $N_P=N_{P_{\xi }}$
. Let
$N_P=N_{P_{\xi }}$
. Let
![]() $r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
$r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
![]() $N_{P}$
. In view of (4.7) and (4.8) from Remark 4.5 for
$N_{P}$
. In view of (4.7) and (4.8) from Remark 4.5 for
![]() $r\ge 2$
, we have
$r\ge 2$
, we have
 $$ \begin{align} \begin{split} &\log M_1\lesssim \log M_2 \quad \text{ if } \quad (M_1, M_2)\in\mathbb{S}_{\tau}(1),\\ &\log M_1\simeq \log M_2 \quad \text{ if } \quad (M_1, M_2)\in\mathbb{S}_{\tau}(j) \text{ for } 1<j<r,\\ &\log M_2\lesssim \log M_1 \quad \text{ if } \quad (M_1, M_2)\in\mathbb{S}_{\tau}(r). \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\log M_1\lesssim \log M_2 \quad \text{ if } \quad (M_1, M_2)\in\mathbb{S}_{\tau}(1),\\ &\log M_1\simeq \log M_2 \quad \text{ if } \quad (M_1, M_2)\in\mathbb{S}_{\tau}(j) \text{ for } 1<j<r,\\ &\log M_2\lesssim \log M_1 \quad \text{ if } \quad (M_1, M_2)\in\mathbb{S}_{\tau}(r). \end{split} \end{align} $$
Consequently, we may define a quantity
![]() $M_{r, j}^*$
as follows. If
$M_{r, j}^*$
as follows. If
![]() $r=1$
, we simply set
$r=1$
, we simply set
If
![]() $r\ge 2$
, we set
$r\ge 2$
, we set
 $$ \begin{align} M_{r, j}^*:= \begin{cases} M_2 & \text{ if } (M_1, M_2)\in\mathbb{S}_{\tau}(1) \text{ for } j=1,\\ M_1\vee M_2 & \text{ if } (M_1, M_2)\in\mathbb{S}_{\tau}(j) \text{ for } 1<j<r,\\ M_1 & \text{ if } (M_1, M_2)\in\mathbb{S}_{\tau}(r)\text{ for } j=r. \end{cases} \end{align} $$
$$ \begin{align} M_{r, j}^*:= \begin{cases} M_2 & \text{ if } (M_1, M_2)\in\mathbb{S}_{\tau}(1) \text{ for } j=1,\\ M_1\vee M_2 & \text{ if } (M_1, M_2)\in\mathbb{S}_{\tau}(j) \text{ for } 1<j<r,\\ M_1 & \text{ if } (M_1, M_2)\in\mathbb{S}_{\tau}(r)\text{ for } j=r. \end{cases} \end{align} $$
The quantity
![]() $\log M_{r,j}^*$
will always allow us to extract the larger parameter (larger up to a multiplicative constant as in (5.34)) from
$\log M_{r,j}^*$
will always allow us to extract the larger parameter (larger up to a multiplicative constant as in (5.34)) from
![]() $\log M_1$
and
$\log M_1$
and
![]() $\log M_2$
. We estimate
$\log M_2$
. We estimate
![]() $|S_{K_1, M_1, K_2, M_2}(P_{\xi })|$
in terms of
$|S_{K_1, M_1, K_2, M_2}(P_{\xi })|$
in terms of
![]() $\log M_{r, j}^*$
, whenever
$\log M_{r, j}^*$
, whenever
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
for
$(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
for
![]() $j\in [r]$
, and
$j\in [r]$
, and
![]() $(K_1, K_2)\in \mathbb {N}^2$
satisfying
$(K_1, K_2)\in \mathbb {N}^2$
satisfying
![]() $M_1\lesssim K_1\le M_1$
and
$M_1\lesssim K_1\le M_1$
and
![]() $M_2\lesssim K_2\le M_2$
.
$M_2\lesssim K_2\le M_2$
.
Proposition 5.37. Let
![]() $P_{\xi }\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be the polynomial in (5.33) corresponding to a polynomial
$P_{\xi }\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be the polynomial in (5.33) corresponding to a polynomial
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
with the properties above. Let
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
with the properties above. Let
![]() $r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
$r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
![]() $N_{P}$
. Let
$N_{P}$
. Let
![]() $\tau>1$
,
$\tau>1$
,
![]() $\alpha>1$
,
$\alpha>1$
,
![]() $j\in [r]$
be given. Let
$j\in [r]$
be given. Let
![]() $v_j=(v_{j, 1}, v_{j, 2})$
be the vertex of the backwards Newton diagram
$v_j=(v_{j, 1}, v_{j, 2})$
be the vertex of the backwards Newton diagram
![]() $N_{P}$
. Then there exists a constant
$N_{P}$
. Then there exists a constant
![]() $\beta _0:=\beta _0(\alpha )>\alpha $
such that for every
$\beta _0:=\beta _0(\alpha )>\alpha $
such that for every
![]() $\beta \in (\beta _0,\infty )\cap {\mathbb {Z}}_+$
, we find a constant
$\beta \in (\beta _0,\infty )\cap {\mathbb {Z}}_+$
, we find a constant
![]() $0<C=C(\alpha , \beta _0, \beta , j, \tau , P)<\infty $
such that for every
$0<C=C(\alpha , \beta _0, \beta , j, \tau , P)<\infty $
such that for every
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
and
$(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
and
![]() $(K_1, K_2)\in \mathbb {N}^2$
satisfying
$(K_1, K_2)\in \mathbb {N}^2$
satisfying
![]() $M_1\lesssim K_1\le M_1$
and
$M_1\lesssim K_1\le M_1$
and
![]() $M_2\lesssim K_2\le M_2$
the following holds. Suppose that there are
$M_2\lesssim K_2\le M_2$
the following holds. Suppose that there are
![]() $a\in {\mathbb {Z}}, q\in {\mathbb {Z}}_+$
such that
$a\in {\mathbb {Z}}, q\in {\mathbb {Z}}_+$
such that
![]() $(a, q)=1$
and
$(a, q)=1$
and
and
 $$ \begin{align} \Big|\xi-\frac{a}{q}\Big|\le\frac{(\log M_{r, j}^*)^{\beta}}{qM_1^{v_{j, 1}}M_2^{v_{j, 2}}}, \end{align} $$
$$ \begin{align} \Big|\xi-\frac{a}{q}\Big|\le\frac{(\log M_{r, j}^*)^{\beta}}{qM_1^{v_{j, 1}}M_2^{v_{j, 2}}}, \end{align} $$
where
![]() $M_{r, j}^*$
is defined in (5.36). Then one has
$M_{r, j}^*$
is defined in (5.36). Then one has
Proof. We note that the following three scenarios may occur when
![]() $r>1$
:
$r>1$
:
-
1. If
 $j=1$
, we have
$j=1$
, we have
 $v_{1, 1}=0$
or
$v_{1, 1}=0$
or
 $v_1\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
. In this case, we also have
$v_1\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
. In this case, we also have
 $\log M_1\lesssim \log M_2$
.
$\log M_1\lesssim \log M_2$
. -
2. If
 $j=r$
, we have
$j=r$
, we have
 $v_{r, 2}=0$
or
$v_{r, 2}=0$
or
 $v_r\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
. In this case, we also have
$v_r\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
. In this case, we also have
 $\log M_1\gtrsim \log M_2$
.
$\log M_1\gtrsim \log M_2$
. -
3. If
 $1<j<r$
, we have
$1<j<r$
, we have
 $v_j\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
. In this case, we also have
$v_j\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
. In this case, we also have
 $\log M_1\simeq \log M_2$
.
$\log M_1\simeq \log M_2$
.
Note that if
![]() $r=1$
, then
$r=1$
, then
![]() $\mathbb {S}_{\tau }(1)=\mathbb {D}_{\tau }\times \mathbb {D}_{\tau }$
and
$\mathbb {S}_{\tau }(1)=\mathbb {D}_{\tau }\times \mathbb {D}_{\tau }$
and
![]() $v_1\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
, since P is non-degenerate in the sense of (1.14). Throughout the proof, in the case of
$v_1\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
, since P is non-degenerate in the sense of (1.14). Throughout the proof, in the case of
![]() $r=1$
, we will additionally assume that
$r=1$
, we will additionally assume that
![]() $\log M_1\le \log M_2$
. Taking into account (5.35) and (5.36), we can also assume that
$\log M_1\le \log M_2$
. Taking into account (5.35) and (5.36), we can also assume that
![]() $\log M_1\vee \log M_2$
is sufficiently large (i.e.,
$\log M_1\vee \log M_2$
is sufficiently large (i.e.,
![]() $\log M_1\vee \log M_2>C_{0}$
, where
$\log M_1\vee \log M_2>C_{0}$
, where
![]() $C_{0}=C_0(\alpha , \beta _0, j, \tau , P)>0$
is a large absolute constant). Otherwise, inequality (5.40) follows. The proof will be divided into three steps.
$C_{0}=C_0(\alpha , \beta _0, j, \tau , P)>0$
is a large absolute constant). Otherwise, inequality (5.40) follows. The proof will be divided into three steps.
Step 1. We first establish (5.40) when
![]() $j=1$
and
$j=1$
and
![]() $v_{1, 1}=0$
or
$v_{1, 1}=0$
or
![]() $j=r$
and
$j=r$
and
![]() $v_{r, 2}=0$
. Suppose that
$v_{r, 2}=0$
. Suppose that
![]() $j=1$
and
$j=1$
and
![]() $v_{1, 1}=0$
holds. The case when
$v_{1, 1}=0$
holds. The case when
![]() $j=r$
and
$j=r$
and
![]() $v_{r, 2}=0$
can be proved in a similar way, so we omit the details. As we have seen above,
$v_{r, 2}=0$
can be proved in a similar way, so we omit the details. As we have seen above,
![]() $\log M_1\lesssim \log M_2$
. By (5.38) and (5.39), we obtain
$\log M_1\lesssim \log M_2$
. By (5.38) and (5.39), we obtain
Applying Lemma 5.3 with
![]() $Q= c_{0, v_{1, 2}}$
and
$Q= c_{0, v_{1, 2}}$
and
![]() $M=q$
, we may find a fraction
$M=q$
, we may find a fraction
![]() $a'/q'$
such that
$a'/q'$
such that
![]() $(a', q')=1$
and
$(a', q')=1$
and
![]() $q/(2c_{0, v_{1, 2}})\le q'\le 2q$
and
$q/(2c_{0, v_{1, 2}})\le q'\le 2q$
and
Thus, by Proposition 5.4, noting that
![]() $v_{1,2}\ge 1$
, we obtain
$v_{1,2}\ge 1$
, we obtain
 $$ \begin{align*} |S_{K_1, M_1, K_2, M_2}(P_{\xi})|&\le S_{K_1, M_1, K_2, M_2}^1(P_{\xi})\\ &\lesssim M_1M_2\log(M_2)\bigg(\frac 1{q'}+\frac{1}{M_2}+\frac{q'}{M_2^{v_{1, 2}}}\bigg)^{\frac{1}{\tau(\deg P)}}\\ &\lesssim M_1M_2 (\log M_{r, j}^*)^{-\frac{\beta}{\tau(\deg P)}+1}, \end{align*} $$
$$ \begin{align*} |S_{K_1, M_1, K_2, M_2}(P_{\xi})|&\le S_{K_1, M_1, K_2, M_2}^1(P_{\xi})\\ &\lesssim M_1M_2\log(M_2)\bigg(\frac 1{q'}+\frac{1}{M_2}+\frac{q'}{M_2^{v_{1, 2}}}\bigg)^{\frac{1}{\tau(\deg P)}}\\ &\lesssim M_1M_2 (\log M_{r, j}^*)^{-\frac{\beta}{\tau(\deg P)}+1}, \end{align*} $$
since
![]() $\log M_{r, j}^*\simeq \log M_2$
. It suffices to take
$\log M_{r, j}^*\simeq \log M_2$
. It suffices to take
![]() $\beta>\tau (\deg P)(\alpha +1)$
and the claim in (5.40) follows.
$\beta>\tau (\deg P)(\alpha +1)$
and the claim in (5.40) follows.
Step 2. We now establish (5.40) when
![]() $1\le j\le r$
and
$1\le j\le r$
and
![]() $v_j\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
(note that when
$v_j\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
(note that when
![]() $1<j<r$
, we automatically have
$1<j<r$
, we automatically have
![]() $v_j\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
). If
$v_j\in {\mathbb {Z}}_+\times {\mathbb {Z}}_+$
). If
![]() $r=1$
, then we assume that
$r=1$
, then we assume that
![]() $\log M_1\le \log M_2$
. If
$\log M_1\le \log M_2$
. If
![]() $r\ge 2$
, we will assume that
$r\ge 2$
, we will assume that
![]() $1\le j<r$
, which gives that
$1\le j<r$
, which gives that
![]() $\log M_1\lesssim \log M_2$
. The case when
$\log M_1\lesssim \log M_2$
. The case when
![]() $j=r$
can be proved in much the same way (with the difference that
$j=r$
can be proved in much the same way (with the difference that
![]() $\log M_1\gtrsim \log M_2$
), we omit the details. In this step, we additionally assume that
$\log M_1\gtrsim \log M_2$
), we omit the details. In this step, we additionally assume that
![]() $M_1\le (\log M_{r, j}^*)^{\chi }$
for some
$M_1\le (\log M_{r, j}^*)^{\chi }$
for some
![]() $0<\chi <\beta /(8\deg P)$
with
$0<\chi <\beta /(8\deg P)$
with
![]() $\beta $
to be specified later.
$\beta $
to be specified later.
Notice that (5.38) and (5.39) imply
By (5.38) and
![]() $M_1\le (\log M_{r, j}^*)^{\chi }$
, we conclude
$M_1\le (\log M_{r, j}^*)^{\chi }$
, we conclude
since
![]() $\chi < \beta /(8\deg P)$
. We note that the polynomial P can be written as
$\chi < \beta /(8\deg P)$
. We note that the polynomial P can be written as
 $$ \begin{align*} P(m_1, m_2)=P_{v_{j, 1}}(m_1)m_2^{v_{j, 2}}+\sum_{\substack{(\gamma_1, \gamma_2)\in S_P\\ \gamma_2\neq v_{j, 2}}}c_{\gamma_1, \gamma_2}m_1^{\gamma_1}m_2^{\gamma_2}, \end{align*} $$
$$ \begin{align*} P(m_1, m_2)=P_{v_{j, 1}}(m_1)m_2^{v_{j, 2}}+\sum_{\substack{(\gamma_1, \gamma_2)\in S_P\\ \gamma_2\neq v_{j, 2}}}c_{\gamma_1, \gamma_2}m_1^{\gamma_1}m_2^{\gamma_2}, \end{align*} $$
where
![]() $P_{v_{j, 1}}\in {\mathbb {Z}}[\mathrm {m}_1]$
and
$P_{v_{j, 1}}\in {\mathbb {Z}}[\mathrm {m}_1]$
and
![]() $\deg P_{v_{j, 1}}=v_{j, 1}$
.
$\deg P_{v_{j, 1}}=v_{j, 1}$
.
Observe that for every
![]() $1\le m_1\le M_1\le (\log M_{r, j}^*)^{\chi }$
, one has
$1\le m_1\le M_1\le (\log M_{r, j}^*)^{\chi }$
, one has
Applying Lemma 5.3 with
![]() $M=M_2^{v_{j, 2}}(\log M_{r, j}^*)^{-3\beta /4}$
and
$M=M_2^{v_{j, 2}}(\log M_{r, j}^*)^{-3\beta /4}$
and
![]() $Q=P_{v_{j, 1}}(m_1)$
for each
$Q=P_{v_{j, 1}}(m_1)$
for each
![]() $K_1< m_1\le M_1$
(noting that
$K_1< m_1\le M_1$
(noting that
![]() $P_{v_{j,1}}(m_1) \not = 0$
for large
$P_{v_{j,1}}(m_1) \not = 0$
for large
![]() $m_1$
), we find a fraction
$m_1$
), we find a fraction
![]() $a'/q'$
so that
$a'/q'$
so that
![]() $(a', q')=1$
and
$(a', q')=1$
and
![]() $(\log M_{r, j}^*)^{3\beta /4}\lesssim q'\le 2M_2^{v_{j, 2}}(\log M_{r, j}^*)^{-3\beta /4}$
and
$(\log M_{r, j}^*)^{3\beta /4}\lesssim q'\le 2M_2^{v_{j, 2}}(\log M_{r, j}^*)^{-3\beta /4}$
and
 $$ \begin{align*} \Big|P_{v_{j, 1}}(m_1)\xi-\frac{a'}{q'}\Big|\le\frac{(\log M_{r, j}^*)^{3\beta/4}}{2q'M_2^{v_{j, 2}}}\le \frac{1}{(q')^2}. \end{align*} $$
$$ \begin{align*} \Big|P_{v_{j, 1}}(m_1)\xi-\frac{a'}{q'}\Big|\le\frac{(\log M_{r, j}^*)^{3\beta/4}}{2q'M_2^{v_{j, 2}}}\le \frac{1}{(q')^2}. \end{align*} $$
We apply Proposition 5.4 for each
![]() $1\le m_1\le M_1$
, noting that
$1\le m_1\le M_1$
, noting that
![]() $v_{j,2}\ge 1$
, to bound
$v_{j,2}\ge 1$
, to bound
 $$ \begin{align*} \Big|\sum_{m_2=K_2+1}^{M_2}\boldsymbol{e}(P_{\xi}(m_1, m_2))\Big| \lesssim M_2\log(M_2)\bigg(\frac 1{q'}+\frac{1}{M_2}+\frac{q'}{M_2^{v_{j, 2}}}\bigg)^{\frac{1}{\tau(\deg P)}}\lesssim M_2 (\log M_{r, j}^*)^{-\frac{3\beta}{4\tau(\deg P)}+1}, \end{align*} $$
$$ \begin{align*} \Big|\sum_{m_2=K_2+1}^{M_2}\boldsymbol{e}(P_{\xi}(m_1, m_2))\Big| \lesssim M_2\log(M_2)\bigg(\frac 1{q'}+\frac{1}{M_2}+\frac{q'}{M_2^{v_{j, 2}}}\bigg)^{\frac{1}{\tau(\deg P)}}\lesssim M_2 (\log M_{r, j}^*)^{-\frac{3\beta}{4\tau(\deg P)}+1}, \end{align*} $$
since
![]() $\log M_{r, j}^*\simeq \log M_2$
for
$\log M_{r, j}^*\simeq \log M_2$
for
![]() $j\in [r-1]$
. It suffices to take
$j\in [r-1]$
. It suffices to take
![]() $\beta>\frac {4}{3}\tau (\deg P)(\alpha +1)$
and (5.40) follows.
$\beta>\frac {4}{3}\tau (\deg P)(\alpha +1)$
and (5.40) follows.
Step 3. As in the previous step,
![]() $1\le j<r$
(or
$1\le j<r$
(or
![]() $r=1$
and
$r=1$
and
![]() $\log M_1\le \log M_2$
) and we now assume that
$\log M_1\le \log M_2$
) and we now assume that
![]() $(\log M_{r, j}^*)^{\chi }\le M_1\lesssim M_2$
for some
$(\log M_{r, j}^*)^{\chi }\le M_1\lesssim M_2$
for some
![]() $0<\chi <\beta /(8\deg P)$
, which will be further adjusted. The case when
$0<\chi <\beta /(8\deg P)$
, which will be further adjusted. The case when
![]() $j=r$
can be established in a similar fashion keping in mind that
$j=r$
can be established in a similar fashion keping in mind that
![]() $\log M_1\gtrsim \log M_2$
. In fact, we take
$\log M_1\gtrsim \log M_2$
. In fact, we take
![]() $\chi :=\beta /(16\deg P)+1$
, which forces
$\chi :=\beta /(16\deg P)+1$
, which forces
![]() $\beta>16\deg P$
.
$\beta>16\deg P$
.
Applying Lemma 5.3 with
![]() $Q=c_{v_{j, 1}, v_{j,2}}$
and
$Q=c_{v_{j, 1}, v_{j,2}}$
and
![]() $M=q$
, we find a fraction
$M=q$
, we find a fraction
![]() $a'/q'$
so that
$a'/q'$
so that
![]() $(a', q')=1$
and
$(a', q')=1$
and
![]() $(\log M_{r, j}^*)^{\beta }\lesssim _P q (2Q)^{-1} \le q'\le 2q$
and
$(\log M_{r, j}^*)^{\beta }\lesssim _P q (2Q)^{-1} \le q'\le 2q$
and
From Proposition 5.22, we obtain (with
![]() $M_{-} = \min (M_1^{v_{j,1}}, M_2^{v_{j,2}})$
and
$M_{-} = \min (M_1^{v_{j,1}}, M_2^{v_{j,2}})$
and
![]() $M_{+} = \max (M_1^{v_{j,1}}, M_2^{v_{j,2}})$
)
$M_{+} = \max (M_1^{v_{j,1}}, M_2^{v_{j,2}})$
)
 $$ \begin{align*} |S_{K_1, M_1, K_2, M_2}(P_{\xi})|&\lesssim M_1M_2 \bigg( \frac{1}{M_{-}}+\frac{q'\log q'}{M_1^{v_{j, 1}}M_2^{v_{j, 2}}}+\frac{1}{q'}+\frac{\log q'}{M_{+}}\bigg)^{\frac{1}{4(1+\deg P)^5}}\\ &\lesssim M_1M_2(\log M_{r, j}^*)^{-\frac{\beta}{64(1+\deg P)^5}}. \end{align*} $$
$$ \begin{align*} |S_{K_1, M_1, K_2, M_2}(P_{\xi})|&\lesssim M_1M_2 \bigg( \frac{1}{M_{-}}+\frac{q'\log q'}{M_1^{v_{j, 1}}M_2^{v_{j, 2}}}+\frac{1}{q'}+\frac{\log q'}{M_{+}}\bigg)^{\frac{1}{4(1+\deg P)^5}}\\ &\lesssim M_1M_2(\log M_{r, j}^*)^{-\frac{\beta}{64(1+\deg P)^5}}. \end{align*} $$
Taking
![]() $\beta>64(1+\deg P)^5(\alpha +1)$
, we obtain (5.40). This completes the proof of Proposition 5.37.
$\beta>64(1+\deg P)^5(\alpha +1)$
, we obtain (5.40). This completes the proof of Proposition 5.37.
5.3 Estimates for double complete exponential sums
In this subsection, we provide estimates for double complete exponential sums in the spirit of Gauss. We begin with a well-known bound which is also a simple consequence of Proposition 5.22.
Lemma 5.41 [Reference Arkhipov, Chubarikov and Karatsuba1]
Let
![]() $P\in \mathbb {Q}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial as in (4.1) and let
$P\in \mathbb {Q}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial as in (4.1) and let
![]() $a_{\gamma _1, \gamma _2}\in {\mathbb {Z}}$
and
$a_{\gamma _1, \gamma _2}\in {\mathbb {Z}}$
and
![]() $q\in {\mathbb {Z}}_+$
satisfy
$q\in {\mathbb {Z}}_+$
satisfy
![]() $c_{\gamma _1, \gamma _2}=a_{\gamma _1, \gamma _2}/q$
for each
$c_{\gamma _1, \gamma _2}=a_{\gamma _1, \gamma _2}/q$
for each
![]() $(\gamma _1, \gamma _2)\in S_P$
such that
$(\gamma _1, \gamma _2)\in S_P$
such that
Consider the exponential sum
![]() $S_{q,q}$
from (5.18). Then there are
$S_{q,q}$
from (5.18). Then there are
![]() $C>0$
and
$C>0$
and
![]() $\delta \in (0, 1)$
such that
$\delta \in (0, 1)$
such that
holds. The constant C can be taken to depend only on the degree of P.
We now derive simple consequences of Lemma 5.41 for exponential sums that arise in the proof of our main result. Let
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be such that
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be such that
 $$ \begin{align} P(m_1, m_2):=\sum_{(\gamma_1, \gamma_2)\in S_P}c_{\gamma_1, \gamma_2}^Pm_1^{\gamma_1}m_2^{\gamma_2}, \end{align} $$
$$ \begin{align} P(m_1, m_2):=\sum_{(\gamma_1, \gamma_2)\in S_P}c_{\gamma_1, \gamma_2}^Pm_1^{\gamma_1}m_2^{\gamma_2}, \end{align} $$
where
![]() $c_{(0,0)}^P=0$
. We additionally assume that P is non-degenerate (see the remark below Theorem 1.11). That is, we have
$c_{(0,0)}^P=0$
. We additionally assume that P is non-degenerate (see the remark below Theorem 1.11). That is, we have
![]() $S_{P}\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
. Using the definition of
$S_{P}\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
. Using the definition of
![]() $P_{\xi }$
from (5.33), we define the complete exponential sum by
$P_{\xi }$
from (5.33), we define the complete exponential sum by
 $$ \begin{align} G(a/q):=\frac{1}{q^2}\sum_{r_1=1}^q\sum_{r_2=1}^q\boldsymbol{e}(P_{a/q}(r_1, r_2)),\qquad a/q\in\mathbb{Q}, \end{align} $$
$$ \begin{align} G(a/q):=\frac{1}{q^2}\sum_{r_1=1}^q\sum_{r_2=1}^q\boldsymbol{e}(P_{a/q}(r_1, r_2)),\qquad a/q\in\mathbb{Q}, \end{align} $$
and we also have partial complete exponential sums defined by
 $$ \begin{align} \begin{split} G_{m_1}^1(a/q):=\frac{1}{q}\sum_{r_2=1}^q\boldsymbol{e}(P_{a/q}(m_1, r_2)), \qquad a/q\in\mathbb{Q},\; m_1\in{\mathbb{Z}},\\ G_{m_2}^2(a/q):=\frac{1}{q}\sum_{r_1=1}^q\boldsymbol{e}(P_{a/q}(r_1, m_2)), \qquad a/q\in\mathbb{Q},\; m_2\in{\mathbb{Z}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} G_{m_1}^1(a/q):=\frac{1}{q}\sum_{r_2=1}^q\boldsymbol{e}(P_{a/q}(m_1, r_2)), \qquad a/q\in\mathbb{Q},\; m_1\in{\mathbb{Z}},\\ G_{m_2}^2(a/q):=\frac{1}{q}\sum_{r_1=1}^q\boldsymbol{e}(P_{a/q}(r_1, m_2)), \qquad a/q\in\mathbb{Q},\; m_2\in{\mathbb{Z}}. \end{split} \end{align} $$
Proposition 5.46. Let
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial as in (5.43) which is non-degenerate (that is,
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial as in (5.43) which is non-degenerate (that is,
![]() $S_{P}\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
). Then there is
$S_{P}\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
). Then there is
![]() $C_P>0$
and
$C_P>0$
and
![]() $\delta \in (0, 1)$
such that the following inequalities hold. If
$\delta \in (0, 1)$
such that the following inequalities hold. If
![]() $a/q\in \mathbb {Q}$
and
$a/q\in \mathbb {Q}$
and
![]() $(a, q)=1$
, then
$(a, q)=1$
, then
Moreover, for every sufficiently large
![]() $K_1, M_1\in {\mathbb {Z}}_+$
depending on P, one has
$K_1, M_1\in {\mathbb {Z}}_+$
depending on P, one has
 $$ \begin{align} \frac{1}{M_1}\sum_{m_1=K_1 + 1}^{M_1}|G_{m_1}^1(a/q)|\le C_P \, q^{-\delta}, \end{align} $$
$$ \begin{align} \frac{1}{M_1}\sum_{m_1=K_1 + 1}^{M_1}|G_{m_1}^1(a/q)|\le C_P \, q^{-\delta}, \end{align} $$
and similarly, for every sufficiently large
![]() $K_2, M_2\in {\mathbb {Z}}_+$
depending on P, one has
$K_2, M_2\in {\mathbb {Z}}_+$
depending on P, one has
 $$ \begin{align} \frac{1}{M_2}\sum_{m_2=K_2 + 1}^{M_2}|G_{m_2}^2(a/q)|\le C_P \, q^{-\delta}. \end{align} $$
$$ \begin{align} \frac{1}{M_2}\sum_{m_2=K_2 + 1}^{M_2}|G_{m_2}^2(a/q)|\le C_P \, q^{-\delta}. \end{align} $$
Proof. We prove Proposition 5.46 in two steps.
Step 1. In this step, we establish (5.47). Fix
![]() $a/q\in \mathbb {Q}$
such that
$a/q\in \mathbb {Q}$
such that
![]() $(a, q)=1$
. For any
$(a, q)=1$
. For any
![]() $(\gamma _1, \gamma _2)\in S_P$
, we let
$(\gamma _1, \gamma _2)\in S_P$
, we let
![]() $a_{\gamma _1, \gamma _2}:=ac_{\gamma _1, \gamma _2}^P/(c_{\gamma _1, \gamma _2}^P, q)$
and
$a_{\gamma _1, \gamma _2}:=ac_{\gamma _1, \gamma _2}^P/(c_{\gamma _1, \gamma _2}^P, q)$
and
![]() $q_{\gamma _1, \gamma _2}:=q/(c_{\gamma _1, \gamma _2}^P, q)$
. Now with this notation, we see that
$q_{\gamma _1, \gamma _2}:=q/(c_{\gamma _1, \gamma _2}^P, q)$
. Now with this notation, we see that
 $$ \begin{align*} P_{a/q}(r_1, r_2)=Q(r_1, r_2):=\sum_{\gamma_1=0}^{d_1}\sum_{\gamma_2=0}^{d_2}\frac{a_{\gamma_1, \gamma_2}}{q_{\gamma_1, \gamma_2}}r_1^{\gamma_1}r_2^{\gamma_2}, \end{align*} $$
$$ \begin{align*} P_{a/q}(r_1, r_2)=Q(r_1, r_2):=\sum_{\gamma_1=0}^{d_1}\sum_{\gamma_2=0}^{d_2}\frac{a_{\gamma_1, \gamma_2}}{q_{\gamma_1, \gamma_2}}r_1^{\gamma_1}r_2^{\gamma_2}, \end{align*} $$
for some integers
![]() $d_1, d_2\ge 1$
. Furthermore,
$d_1, d_2\ge 1$
. Furthermore,
![]() $G(a/q) = q^{-2} S_{q,q}(Q)$
; see (5.44). We take
$G(a/q) = q^{-2} S_{q,q}(Q)$
; see (5.44). We take
![]() $(\rho _1, \rho _2)\in S_{P}\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
and use (5.42), which yields
$(\rho _1, \rho _2)\in S_{P}\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
and use (5.42), which yields
This completes the proof of (5.47).
Step 2. We only prove (5.48); the proof of (5.49) is exactly the same. We fix
![]() $a/q\in \mathbb {Q}$
such that
$a/q\in \mathbb {Q}$
such that
![]() $(a, q)=1$
, and we also fix
$(a, q)=1$
, and we also fix
![]() $(\rho _1, \rho _2)\in S_{P}\cap ({\mathbb {Z}}_+\times {\mathbb {Z}}_+)\neq \emptyset $
. Using Lemma 5.3, we find a reduced fraction
$(\rho _1, \rho _2)\in S_{P}\cap ({\mathbb {Z}}_+\times {\mathbb {Z}}_+)\neq \emptyset $
. Using Lemma 5.3, we find a reduced fraction
![]() $a_{\rho _1, \rho _2}/q_{\rho _1, \rho _2}$
so that
$a_{\rho _1, \rho _2}/q_{\rho _1, \rho _2}$
so that
![]() $(a_{\rho _1, \rho _2},q_{\rho _1, \rho _2})=1$
and
$(a_{\rho _1, \rho _2},q_{\rho _1, \rho _2})=1$
and
 $$ \begin{align*} \Big|\frac{a c_{\rho_1, \rho_2}^P}{q}-\frac{a_{\rho_1, \rho_2}}{q_{\rho_1, \rho_2}}\Big|\le\frac{1}{2q_{\rho_1, \rho_2}q} \end{align*} $$
$$ \begin{align*} \Big|\frac{a c_{\rho_1, \rho_2}^P}{q}-\frac{a_{\rho_1, \rho_2}}{q_{\rho_1, \rho_2}}\Big|\le\frac{1}{2q_{\rho_1, \rho_2}q} \end{align*} $$
with
![]() $q/(2c_{\rho _1, \rho _2})\le q_{\rho _1, \rho _2}\le 2q$
. We fix
$q/(2c_{\rho _1, \rho _2})\le q_{\rho _1, \rho _2}\le 2q$
. We fix
![]() $\chi>0$
and assume first that
$\chi>0$
and assume first that
![]() $M_1\ge q^{\chi }$
. Appealing to inequality (5.24) with
$M_1\ge q^{\chi }$
. Appealing to inequality (5.24) with
![]() $M_2=q$
, we obtain for some
$M_2=q$
, we obtain for some
![]() $\delta \in (0, 1)$
that
$\delta \in (0, 1)$
that
 $$ \begin{align*} \frac{1}{M_1}\sum_{m_1=K_1+1}^{M_1}|G_{m_1}^1(a/q)|\lesssim_P q^{-\delta}. \end{align*} $$
$$ \begin{align*} \frac{1}{M_1}\sum_{m_1=K_1+1}^{M_1}|G_{m_1}^1(a/q)|\lesssim_P q^{-\delta}. \end{align*} $$
We now establish a similar bound assuming that
![]() $M_1< q^{\chi }$
for a sufficiently small
$M_1< q^{\chi }$
for a sufficiently small
![]() $\chi>0$
, which will be specified momentarily. Our polynomial P from (5.43) can be rewritten as
$\chi>0$
, which will be specified momentarily. Our polynomial P from (5.43) can be rewritten as
 $$ \begin{align*} P(m_1, m_2)=\sum_{\gamma_2=1}^{d_2}P_{\gamma_2}(m_1)m_2^{\gamma_2}+P_{0}(m_1), \end{align*} $$
$$ \begin{align*} P(m_1, m_2)=\sum_{\gamma_2=1}^{d_2}P_{\gamma_2}(m_1)m_2^{\gamma_2}+P_{0}(m_1), \end{align*} $$
for some
![]() $d_2\ge 1$
where
$d_2\ge 1$
where
![]() $P_{\gamma _2}\in {\mathbb {Z}}[\mathrm {m}_1]$
and
$P_{\gamma _2}\in {\mathbb {Z}}[\mathrm {m}_1]$
and
![]() $\deg P_{\gamma _2}\le \deg P$
. Take
$\deg P_{\gamma _2}\le \deg P$
. Take
![]() $0<\chi <\frac {1}{10\deg P}$
and observe that for every
$0<\chi <\frac {1}{10\deg P}$
and observe that for every
![]() $1\le \gamma _2\le d_2$
and for every
$1\le \gamma _2\le d_2$
and for every
![]() $1\le m_1\le M_1\le q^{\chi }$
, one has
$1\le m_1\le M_1\le q^{\chi }$
, one has
whenever q is sufficiently large in terms of the coefficients of P.
Assume first that
![]() $d_2\ge 2$
, and we may take
$d_2\ge 2$
, and we may take
![]() $\rho _2=d_2$
. Applying Lemma 5.3 with
$\rho _2=d_2$
. Applying Lemma 5.3 with
![]() $Q=P_{\rho _2}(m_1)$
for each
$Q=P_{\rho _2}(m_1)$
for each
![]() $K_1< m_1\le M_1$
(noting that
$K_1< m_1\le M_1$
(noting that
![]() $P_{\rho _2}(m_1) \not = 0$
for sufficiently large
$P_{\rho _2}(m_1) \not = 0$
for sufficiently large
![]() $m_1\ge K_1$
), we find a fraction
$m_1\ge K_1$
), we find a fraction
![]() $a'/q'$
so that
$a'/q'$
so that
![]() $(a', q')=1$
and
$(a', q')=1$
and
![]() $\frac {1}{2}q^{3/4}\le q'\le 2q$
and
$\frac {1}{2}q^{3/4}\le q'\le 2q$
and
Then we apply Proposition 5.4 for each
![]() $K_1 < m_1\le M_1$
, which gives
$K_1 < m_1\le M_1$
, which gives
 $$ \begin{align*} |G_{m_1}^1(a/q)| \lesssim \log(2q)\bigg(\frac 1{q'}+\frac 1 q+\frac{q'}{q^{d_2}}\bigg)^{\frac{1}{\tau(d_2)}}\lesssim (\log q)q^{-\frac{3}{4\tau(d_2)}}\lesssim q^{-\delta}, \end{align*} $$
$$ \begin{align*} |G_{m_1}^1(a/q)| \lesssim \log(2q)\bigg(\frac 1{q'}+\frac 1 q+\frac{q'}{q^{d_2}}\bigg)^{\frac{1}{\tau(d_2)}}\lesssim (\log q)q^{-\frac{3}{4\tau(d_2)}}\lesssim q^{-\delta}, \end{align*} $$
for some
![]() $\delta \in (0, 1)$
and (5.48) follows, since
$\delta \in (0, 1)$
and (5.48) follows, since
![]() $d_2\ge 2$
.
$d_2\ge 2$
.
Assume now that
![]() $d_2=1$
. Then
$d_2=1$
. Then
 $$ \begin{align*} \frac{1}{M_1}\sum_{m_1=K_1 + 1}^{M_1}|G_{m_1}^1(a/q)|= \frac{1}{M_1}\#\{K_1 < m_1\le M_1: P_{1}(m_1)\equiv 0 \bmod q \}=0, \end{align*} $$
$$ \begin{align*} \frac{1}{M_1}\sum_{m_1=K_1 + 1}^{M_1}|G_{m_1}^1(a/q)|= \frac{1}{M_1}\#\{K_1 < m_1\le M_1: P_{1}(m_1)\equiv 0 \bmod q \}=0, \end{align*} $$
in view of (5.50), which ensures that
![]() $\{m_1\in [M_1]: P_{1}(m_1)\equiv 0 \bmod q \}=\emptyset $
.
$\{m_1\in [M_1]: P_{1}(m_1)\equiv 0 \bmod q \}=\emptyset $
.
6 Multi-parameter Ionescu–Wainger theory
One of the most important ingredients in our argument is the Ionescu–Wainger multiplier theorem [Reference Ionescu and Wainger34] (see also [Reference Mirek46]), and its vector-valued variant from [Reference Mirek, Stein and Zorin-Kranich52] (see also [Reference Tao62]). We begin with recalling the results from [Reference Ionescu and Wainger34] and [Reference Mirek, Stein and Zorin-Kranich52] and fixing necessary notation and terminology.
6.1 Ionescu–Wainger multiplier theorem
Let
![]() $\mathbb {P}$
be the set of all prime numbers, and let
$\mathbb {P}$
be the set of all prime numbers, and let
![]() $\rho \in (0, 1)$
be a sufficiently small absolute constant. We then define the natural number
$\rho \in (0, 1)$
be a sufficiently small absolute constant. We then define the natural number
and for any integer
![]() $l\in \mathbb {N}$
, set
$l\in \mathbb {N}$
, set
We also define the set
where
 $$ \begin{align*} W_{\leq l}:=\bigcup_{k\in[D]}\bigcup_{(\gamma_1,\dots,\gamma_k)\in[D]^k}\big\{p_1^{\gamma_1} \cdots p_k^{\gamma_k}\colon p_1,\ldots, p_k\in(N_0^{(l)}, 2^l]\cap\mathbb{P} \text{ are distinct}\big\}. \end{align*} $$
$$ \begin{align*} W_{\leq l}:=\bigcup_{k\in[D]}\bigcup_{(\gamma_1,\dots,\gamma_k)\in[D]^k}\big\{p_1^{\gamma_1} \cdots p_k^{\gamma_k}\colon p_1,\ldots, p_k\in(N_0^{(l)}, 2^l]\cap\mathbb{P} \text{ are distinct}\big\}. \end{align*} $$
In other words,
![]() $W_{\leq l}$
is the set of all products of prime factors from
$W_{\leq l}$
is the set of all products of prime factors from
![]() $(N_0^{(l)}, 2^l]\cap \mathbb {P}$
of length at most D, at powers between
$(N_0^{(l)}, 2^l]\cap \mathbb {P}$
of length at most D, at powers between
![]() $1$
and D.
$1$
and D.
Remark 6.1. For every
![]() $\rho \in (0, 1)$
, there exists a large absolute constant
$\rho \in (0, 1)$
, there exists a large absolute constant
![]() $C_{\rho }\ge 1$
such that the following elementary facts about the sets
$C_{\rho }\ge 1$
such that the following elementary facts about the sets
![]() $P_{\leq l}$
hold:
$P_{\leq l}$
hold:
-
(i) If
 $l_1\le l_2$
, then
$l_1\le l_2$
, then
 $P_{\leq l_1}\subseteq P_{\leq l_2}$
.
$P_{\leq l_1}\subseteq P_{\leq l_2}$
. -
(ii) One has
 $[2^l] \subseteq P_{\leq l} \subseteq [2^{C_\rho 2^{\rho l}}]$
.
$[2^l] \subseteq P_{\leq l} \subseteq [2^{C_\rho 2^{\rho l}}]$
. -
(iii) If
 $q \in P_{\leq l}$
, then all factors of q also lie in
$q \in P_{\leq l}$
, then all factors of q also lie in
 $P_{\leq l}$
.
$P_{\leq l}$
. -
(iv) One has
 $Q_{\le l}:=\operatorname {\mathrm {lcm}} (P_{\leq l})\lesssim 2^{C_\rho 2^l}$
.
$Q_{\le l}:=\operatorname {\mathrm {lcm}} (P_{\leq l})\lesssim 2^{C_\rho 2^l}$
.
By property (i), it makes sense to define
![]() $P_l := P_{\leq l} \backslash P_{\leq l-1}$
, with the convention that
$P_l := P_{\leq l} \backslash P_{\leq l-1}$
, with the convention that
![]() $P_{\leq l}$
is empty for negative l. From property (ii), for all
$P_{\leq l}$
is empty for negative l. From property (ii), for all
![]() $q \in P_l$
, we have
$q \in P_l$
, we have
Let
![]() $d\in {\mathbb {Z}}_+$
and define
$d\in {\mathbb {Z}}_+$
and define
![]() $1$
-periodic sets
$1$
-periodic sets
where
![]() $(a, q)=(a_1,\ldots , a_d, q)=1$
for any
$(a, q)=(a_1,\ldots , a_d, q)=1$
for any
![]() $a=(a_1,\ldots , a_d)\in {\mathbb {Z}}^d$
. Then by (6.2), we see
$a=(a_1,\ldots , a_d)\in {\mathbb {Z}}^d$
. Then by (6.2), we see
Let
![]() $k\in {\mathbb {Z}}_+$
be fixed. For any finite family of fractions
$k\in {\mathbb {Z}}_+$
be fixed. For any finite family of fractions
![]() $\Sigma \subseteq (\mathbb {T}\cap \mathbb {Q})^k$
and a measurable function
$\Sigma \subseteq (\mathbb {T}\cap \mathbb {Q})^k$
and a measurable function
![]() $\mathfrak m: \mathbb {R}^k \to B$
taking its values in a separable Banach space B which is supported on the unit cube
$\mathfrak m: \mathbb {R}^k \to B$
taking its values in a separable Banach space B which is supported on the unit cube
![]() $[-1/2, 1/2)^k$
, define a
$[-1/2, 1/2)^k$
, define a
![]() $1$
-periodic extension of
$1$
-periodic extension of
![]() $\mathfrak m$
by
$\mathfrak m$
by
We will also need to introduce the notion of
![]() $\Gamma $
-lifted extensions of
$\Gamma $
-lifted extensions of
![]() $\mathfrak m$
. For
$\mathfrak m$
. For
![]() $d\in {\mathbb {Z}}_+$
consider
$d\in {\mathbb {Z}}_+$
consider
![]() $\Gamma :=\{i_1,\ldots , i_k\}\subseteq [d]$
of size
$\Gamma :=\{i_1,\ldots , i_k\}\subseteq [d]$
of size
![]() $k\in [d]$
. We define a
$k\in [d]$
. We define a
![]() $\Gamma $
-lifted
$\Gamma $
-lifted
![]() $1$
-periodic extension of
$1$
-periodic extension of
![]() $\mathfrak m$
by
$\mathfrak m$
by
We now recall the following vector-valued Ionescu–Wainger multiplier theorem from [Reference Mirek, Stein and Zorin-Kranich52, Reference Tao62].
Theorem 6.5. Let
![]() $d\in {\mathbb {Z}}_+$
be given. For every
$d\in {\mathbb {Z}}_+$
be given. For every
![]() $\rho \in (0, 1)$
and for every
$\rho \in (0, 1)$
and for every
![]() $p \in (1,\infty )$
, there exists an absolute constant
$p \in (1,\infty )$
, there exists an absolute constant
![]() $C_{p, \rho , d}>0$
, that depends only on p,
$C_{p, \rho , d}>0$
, that depends only on p,
![]() $\rho $
and d, such that, for every
$\rho $
and d, such that, for every
![]() $l\in \mathbb {N}$
, the following holds. Let
$l\in \mathbb {N}$
, the following holds. Let
![]() $0<\varepsilon _l \le 2^{-10 C_\rho 2^{2\rho l}}$
, and let
$0<\varepsilon _l \le 2^{-10 C_\rho 2^{2\rho l}}$
, and let
![]() $\mathfrak m: \mathbb {R}^d \to L(H_0,H_1)$
be a measurable function supported on
$\mathfrak m: \mathbb {R}^d \to L(H_0,H_1)$
be a measurable function supported on
![]() $\varepsilon _{l}[-1/2, 1/2)^d$
, with values in the space
$\varepsilon _{l}[-1/2, 1/2)^d$
, with values in the space
![]() $L(H_{0},H_{1})$
of bounded linear operators between separable Hilbert spaces
$L(H_{0},H_{1})$
of bounded linear operators between separable Hilbert spaces
![]() $H_{0}$
and
$H_{0}$
and
![]() $H_{1}$
. Let
$H_{1}$
. Let
Then the
![]() $1$
-periodic multiplier
$1$
-periodic multiplier
 $$ \begin{align} \Theta_{\Sigma_{\le l}^d}[\mathfrak m](\xi)=\sum_{a/q \in\Sigma_{\le l}^d} \mathfrak m(\xi - a/q) \quad \text{ for } \quad \xi\in\mathbb{T}^d, \end{align} $$
$$ \begin{align} \Theta_{\Sigma_{\le l}^d}[\mathfrak m](\xi)=\sum_{a/q \in\Sigma_{\le l}^d} \mathfrak m(\xi - a/q) \quad \text{ for } \quad \xi\in\mathbb{T}^d, \end{align} $$
where
![]() $\Sigma _{\le l}^d$
is the set of all reduced fractions in (6.3), satisfies
$\Sigma _{\le l}^d$
is the set of all reduced fractions in (6.3), satisfies
for every
![]() $f\in \ell ^p({\mathbb {Z}}^d;H_0)$
.
$f\in \ell ^p({\mathbb {Z}}^d;H_0)$
.
The advantage of applying Theorem 6.5 is that one can directly transfer square function estimates from the continuous to the discrete setting, which will be useful in Section 7. The hypothesis (6.6), unlike the support hypothesis, is scale-invariant, in the sense that the constant
![]() $\mathbf A_{p}$
does not change when
$\mathbf A_{p}$
does not change when
![]() $\mathfrak m$
is replaced by
$\mathfrak m$
is replaced by
![]() $\mathfrak m(A\cdot )$
for any invertible linear transformation
$\mathfrak m(A\cdot )$
for any invertible linear transformation
![]() $A:\mathbb {R}^d\to \mathbb {R}^d$
.
$A:\mathbb {R}^d\to \mathbb {R}^d$
.
Theorem 6.5 was originally established by Ionescu and Wainger [Reference Ionescu and Wainger34] in the scalar-valued setting with an extra factor
![]() $(l+1)^D$
in the right-hand side of (6.8). Their proof is based on an intricate inductive argument that exploits super-orthogonality phenomena. A slightly different proof with factor
$(l+1)^D$
in the right-hand side of (6.8). Their proof is based on an intricate inductive argument that exploits super-orthogonality phenomena. A slightly different proof with factor
![]() $(l+1)$
in (6.8) was given in [Reference Mirek46]. The latter proof, instead of induction as in [Reference Ionescu and Wainger34], used certain recursive arguments, which clarified the role of the underlying square functions and orthogonalities (see also [Reference Mirek, Stein and Zorin-Kranich52, Section 2]). The theorem in the context of super-orthogonality phenomena is discussed in a survey by Pierce [Reference Pierce55] in a much broader context. Finally, we refer to the recent paper of Tao [Reference Tao62], where Theorem 6.5 as stated above, with a uniform constant
$(l+1)$
in (6.8) was given in [Reference Mirek46]. The latter proof, instead of induction as in [Reference Ionescu and Wainger34], used certain recursive arguments, which clarified the role of the underlying square functions and orthogonalities (see also [Reference Mirek, Stein and Zorin-Kranich52, Section 2]). The theorem in the context of super-orthogonality phenomena is discussed in a survey by Pierce [Reference Pierce55] in a much broader context. Finally, we refer to the recent paper of Tao [Reference Tao62], where Theorem 6.5 as stated above, with a uniform constant
![]() $\mathbf A_{p}$
, is established.
$\mathbf A_{p}$
, is established.
For future reference, we also recall the sampling principle of Magyar–Stein–Wainger from [Reference Magyar, Stein and Wainger44], which was an important ingredient in the proof of Theorem 6.5.
Proposition 6.9. Let
![]() $d\in {\mathbb {Z}}_+$
be given. There exists an absolute constant
$d\in {\mathbb {Z}}_+$
be given. There exists an absolute constant
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() $p \in [1,\infty ]$
and
$p \in [1,\infty ]$
and
![]() $q\in {\mathbb {Z}}_+$
, and let
$q\in {\mathbb {Z}}_+$
, and let
![]() $B_1, B_2$
be finite-dimensional Banach spaces. Let
$B_1, B_2$
be finite-dimensional Banach spaces. Let
![]() $\mathfrak m : \mathbb {R}^d \to L(B_1, B_2)$
be a bounded operator-valued function supported on
$\mathfrak m : \mathbb {R}^d \to L(B_1, B_2)$
be a bounded operator-valued function supported on
![]() $[-1/2,1/2)^d/q$
and let
$[-1/2,1/2)^d/q$
and let
![]() $\mathfrak m^{q}_{\mathrm {per}}$
be the periodic multiplier
$\mathfrak m^{q}_{\mathrm {per}}$
be the periodic multiplier
Then
The proof can be found in [Reference Magyar, Stein and Wainger44, Corollary 2.1, pp. 196]. We also refer to [Reference Mirek, Stein and Zorin-Kranich50] for a generalization of Proposition 6.9 to real interpolation spaces. We emphasize that
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are general (finite dimensional) Banach spaces in Proposition 6.9, in contrast to the Hilbert space-valued multipliers appearing in Theorem 6.5, and so Proposition 6.9 includes maximal function formulations and can also accommodate oscillation semi-norms.
$B_2$
are general (finite dimensional) Banach spaces in Proposition 6.9, in contrast to the Hilbert space-valued multipliers appearing in Theorem 6.5, and so Proposition 6.9 includes maximal function formulations and can also accommodate oscillation semi-norms.
6.2 One-parameter semi-norm variant of Theorem 6.5
Let
![]() $\Lambda :=\{\lambda _1,\ldots ,\lambda _k\}\subset {\mathbb {Z}}_+$
be a set of size
$\Lambda :=\{\lambda _1,\ldots ,\lambda _k\}\subset {\mathbb {Z}}_+$
be a set of size
![]() $k\in {\mathbb {Z}}_+$
of natural exponents, and consider the associated one-parameter family of dilations which for every
$k\in {\mathbb {Z}}_+$
of natural exponents, and consider the associated one-parameter family of dilations which for every
![]() $x\in \mathbb {R}^k$
, is defined by
$x\in \mathbb {R}^k$
, is defined by
Let
![]() $\Upsilon :=(\Upsilon _n:\mathbb {R}^k\to \mathbb {C}: n\in \mathbb {N})$
be a sequence of measurable functions which define a positive sequence of operators in the sense that for every
$\Upsilon :=(\Upsilon _n:\mathbb {R}^k\to \mathbb {C}: n\in \mathbb {N})$
be a sequence of measurable functions which define a positive sequence of operators in the sense that for every
![]() $n\in \mathbb {N}$
, one has
$n\in \mathbb {N}$
, one has
Furthermore, suppose there exist
![]() $C_{\Upsilon }>0$
,
$C_{\Upsilon }>0$
,
![]() $0<\delta _{\Upsilon }<1$
and
$0<\delta _{\Upsilon }<1$
and
![]() $1<\tau \le 2$
such that for every
$1<\tau \le 2$
such that for every
![]() $\xi \in \mathbb {R}^k$
and
$\xi \in \mathbb {R}^k$
and
![]() $n\in \mathbb {N}$
, one has
$n\in \mathbb {N}$
, one has
The condition (6.10) implies that the operator
![]() $T_{\mathbb {R}^k}[\Upsilon _n] f = f *\mu _n$
is convolution with positive measure
$T_{\mathbb {R}^k}[\Upsilon _n] f = f *\mu _n$
is convolution with positive measure
![]() $\mu _n$
and condition (6.12) implies
$\mu _n$
and condition (6.12) implies
![]() $\Upsilon _n(0) = 1$
and so each
$\Upsilon _n(0) = 1$
and so each
![]() $\mu _n$
is a probability measure. Hence, for every
$\mu _n$
is a probability measure. Hence, for every
![]() $p\in [1, \infty )$
,
$p\in [1, \infty )$
,
In this generality,
![]() $L^p(\mathbb {R}^k)$
estimates with
$L^p(\mathbb {R}^k)$
estimates with
![]() $1<p\le \infty $
for the maximal function
$1<p\le \infty $
for the maximal function
![]() $\sup _{n\in \mathbb {N}}|T_{\mathbb {R}^k}[\Upsilon _n] f(x)|$
were obtained in [Reference Duoandikoetxea and Rubio de Francia22] and corresponding r-variational and jump inequalites were established in [Reference Jones, Seeger and Wright38] (see also [Reference Mirek, Stein and Zorin-Kranich51]). Here we extend these results further.
$\sup _{n\in \mathbb {N}}|T_{\mathbb {R}^k}[\Upsilon _n] f(x)|$
were obtained in [Reference Duoandikoetxea and Rubio de Francia22] and corresponding r-variational and jump inequalites were established in [Reference Jones, Seeger and Wright38] (see also [Reference Mirek, Stein and Zorin-Kranich51]). Here we extend these results further.
For
![]() $d\in {\mathbb {Z}}_+$
, consider
$d\in {\mathbb {Z}}_+$
, consider
![]() $\Gamma :=\{i_1,\ldots , i_k\}\subseteq [d]$
of size
$\Gamma :=\{i_1,\ldots , i_k\}\subseteq [d]$
of size
![]() $k\in [d]$
and define a
$k\in [d]$
and define a
![]() $\Gamma $
-lifted sequence of measurable functions
$\Gamma $
-lifted sequence of measurable functions
![]() $\Upsilon ^{\Gamma }:=(\Upsilon _n^{\Gamma }:\mathbb {R}^d\to \mathbb {C}: n\in \mathbb {N})$
by setting
$\Upsilon ^{\Gamma }:=(\Upsilon _n^{\Gamma }:\mathbb {R}^d\to \mathbb {C}: n\in \mathbb {N})$
by setting
Our first main result is the following one-parameter semi-norm variant of Theorem 6.5.
Theorem 6.14. Let
![]() $d\in {\mathbb {Z}}_+$
and
$d\in {\mathbb {Z}}_+$
and
![]() $\Gamma \subseteq [d]$
of size
$\Gamma \subseteq [d]$
of size
![]() $k\in [d]$
be given. Let
$k\in [d]$
be given. Let
![]() $\Upsilon =(\Upsilon _n:\mathbb {R}^k\to \mathbb {C}: n\in \mathbb {N})$
be a sequence of measurable functions satisfying conditions (6.10), (6.11) and (6.12), and let
$\Upsilon =(\Upsilon _n:\mathbb {R}^k\to \mathbb {C}: n\in \mathbb {N})$
be a sequence of measurable functions satisfying conditions (6.10), (6.11) and (6.12), and let
![]() $\Upsilon ^{\Gamma }:=(\Upsilon _n^{\Gamma }:\mathbb {R}^d\to \mathbb {C}: n\in \mathbb {N})$
be the corresponding
$\Upsilon ^{\Gamma }:=(\Upsilon _n^{\Gamma }:\mathbb {R}^d\to \mathbb {C}: n\in \mathbb {N})$
be the corresponding
![]() $\Gamma $
-lifted sequence. For every
$\Gamma $
-lifted sequence. For every
![]() $\rho \in (0, 1)$
and for every
$\rho \in (0, 1)$
and for every
![]() $p \in (1,\infty )$
, there exists an absolute constant
$p \in (1,\infty )$
, there exists an absolute constant
![]() $0<C=C(d, p, \rho , \tau , \Gamma , A_p^{\Upsilon }, C_{\Upsilon })<\infty $
such that for every integer
$0<C=C(d, p, \rho , \tau , \Gamma , A_p^{\Upsilon }, C_{\Upsilon })<\infty $
such that for every integer
![]() $l\in \mathbb {N}$
and
$l\in \mathbb {N}$
and
![]() $m\le -10C_{\rho }2^{2\rho l}$
, the following holds. If
$m\le -10C_{\rho }2^{2\rho l}$
, the following holds. If
then for every
![]() $f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))$
, one has
$f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))$
, one has

with
![]() $\Theta _{\Sigma ^d_{\le l}}$
defined in (6.7). In particular, (6.16) implies the maximal estimate
$\Theta _{\Sigma ^d_{\le l}}$
defined in (6.7). In particular, (6.16) implies the maximal estimate

Some remarks about Theorem 6.14 are in order.
-
1. Theorem 6.14 is a semi-norm variant of the Ionescu–Wainger [Reference Ionescu and Wainger34] theorem for oscillations. The proof below works also for r-variations or jumps in place of oscillations as well as for norms corresponding to real interpolation spaces. We refer to [Reference Mirek, Stein and Zorin-Kranich50] for definitions.
-
2. In practice, Theorem 6.14 will be applied with
 $\Gamma =[d]$
. However, the concept of
$\Gamma =[d]$
. However, the concept of
 $\Gamma $
-lifted sequences is introduced here for further references.
$\Gamma $
-lifted sequences is introduced here for further references. -
3. A careful inspection of the proof below allows us to show that the conclusion of Theorem 6.14 also holds in
 $\mathbb {R}^d$
. For every
$\mathbb {R}^d$
. For every
 $d\in {\mathbb {Z}}_+$
, every sequence
$d\in {\mathbb {Z}}_+$
, every sequence
 $\Upsilon =(\Upsilon _n:\mathbb {R}^d\to \mathbb {C}: n\in {\mathbb {Z}})$
of measurable functions satisfying conditions (6.10), (6.11), (6.12) and (6.13), and for every
$\Upsilon =(\Upsilon _n:\mathbb {R}^d\to \mathbb {C}: n\in {\mathbb {Z}})$
of measurable functions satisfying conditions (6.10), (6.11), (6.12) and (6.13), and for every
 $p\in (1, \infty )$
, there exists a constant
$p\in (1, \infty )$
, there exists a constant
 $C>0$
such that for every
$C>0$
such that for every
 $f=(f_{\iota }:\iota \in \mathbb {N})\in L^p(\mathbb {R}^d; \ell ^2(\mathbb {N}))$
, one has (6.17)
$f=(f_{\iota }:\iota \in \mathbb {N})\in L^p(\mathbb {R}^d; \ell ^2(\mathbb {N}))$
, one has (6.17)
An important feature of our approach is that we do not need to invoke the corresponding inequality for martingales in the proof. This stands in a sharp contrast to variants of inequality (6.17) involving r-variations, where all arguments to the best of our knowledge use the corresponding r-variational inequalities for martingales.
Proof of Theorem 6.14
Fix
![]() $p\in (1, \infty )$
and a sequence
$p\in (1, \infty )$
and a sequence
![]() $f=(f_\iota :\iota \in \mathbb {N})\in \ell ^2({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))\cap \ell ^p({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))$
. For each
$f=(f_\iota :\iota \in \mathbb {N})\in \ell ^2({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))\cap \ell ^p({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))$
. For each
![]() $l\in \mathbb {N}$
, define an integer
$l\in \mathbb {N}$
, define an integer
where
![]() $C_\rho $
is the constant from Remark 6.1; see property (iv). By (2.17), it only suffices to establish (6.16), which will follow from the oscillation inequalities, respectively, for small scales
$C_\rho $
is the constant from Remark 6.1; see property (iv). By (2.17), it only suffices to establish (6.16), which will follow from the oscillation inequalities, respectively, for small scales

and large scales

Step 1. We now prove inequality (6.19). We fix
![]() $J\in {\mathbb {Z}}_+$
and a sequence
$J\in {\mathbb {Z}}_+$
and a sequence
![]() $I\in \mathfrak S_J(\mathbb {N}_{<2^{\kappa _l}})$
. Then, by the Rademacher–Menshov inequality (2.14), we see that
$I\in \mathfrak S_J(\mathbb {N}_{<2^{\kappa _l}})$
. Then, by the Rademacher–Menshov inequality (2.14), we see that

where
![]() $U_u^v=[u2^v, (u+1)2^v)\cap {\mathbb {Z}}$
. Hence, it suffices to prove
$U_u^v=[u2^v, (u+1)2^v)\cap {\mathbb {Z}}$
. Hence, it suffices to prove

uniformly in v. By Theorem 6.5 and by our choice of
![]() $\kappa _l$
in (6.18), since
$\kappa _l$
in (6.18), since
![]() $m\le -10C_{\rho }2^{2\rho l}$
, (6.21) will follow if for every sequence
$m\le -10C_{\rho }2^{2\rho l}$
, (6.21) will follow if for every sequence
![]() $(f_\iota :\iota \in \mathbb {N})\in L^2(\mathbb {R}^d; \ell ^2(\mathbb {N}))\cap L^p(\mathbb {R}^d; \ell ^2(\mathbb {N}))$
,
$(f_\iota :\iota \in \mathbb {N})\in L^2(\mathbb {R}^d; \ell ^2(\mathbb {N}))\cap L^p(\mathbb {R}^d; \ell ^2(\mathbb {N}))$
,

holds uniformly in v.
To prove inequality (6.22), in view of Lemma 2.3, it suffices to show that for every
![]() $p\in (1, \infty )$
and for every
$p\in (1, \infty )$
and for every
![]() $f\in L^p(\mathbb {R}^d)$
, one has
$f\in L^p(\mathbb {R}^d)$
, one has

unformly in
![]() $v \in [0,\kappa _l]$
and l. The proof of (6.23), using conditions (6.10), (6.11), (6.12) and (6.13), follows from standard Littlewood–Paley theory as developed in [Reference Duoandikoetxea and Rubio de Francia22]. We refer, for instance, to [Reference Mirek, Stein and Zorin-Kranich51] for details in this context.
$v \in [0,\kappa _l]$
and l. The proof of (6.23), using conditions (6.10), (6.11), (6.12) and (6.13), follows from standard Littlewood–Paley theory as developed in [Reference Duoandikoetxea and Rubio de Francia22]. We refer, for instance, to [Reference Mirek, Stein and Zorin-Kranich51] for details in this context.
Step 2. We now prove inequality (6.20). By the support condition (6.15), we may write (see property (iv) from Remark 6.1)
where
![]() $\eta _{\le -2^{2C_\rho l}}^{\Gamma }:=\prod _{i\in \Gamma }\eta _{\le -2^{2C_\rho l}}^{(i)}$
, (see definition (2.2)). The proof of (6.20) will be complete if we show (6.20) with
$\eta _{\le -2^{2C_\rho l}}^{\Gamma }:=\prod _{i\in \Gamma }\eta _{\le -2^{2C_\rho l}}^{(i)}$
, (see definition (2.2)). The proof of (6.20) will be complete if we show (6.20) with
![]() $T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }(1-\eta _{\le -2^{2C_\rho l}}^{\Gamma })\eta _{\le m}^{\Gamma ^c}]\big ]$
, and
$T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }(1-\eta _{\le -2^{2C_\rho l}}^{\Gamma })\eta _{\le m}^{\Gamma ^c}]\big ]$
, and
![]() $T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le -2^{2C_\rho l}}^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
in place of
$T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le -2^{2C_\rho l}}^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
in place of
![]() $T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
. To establish (6.20) with
$T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
. To establish (6.20) with
![]() $T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }(1-\eta _{\le -2^{2C_\rho l}}^{\Gamma })\eta _{\le m}^{\Gamma ^c}]\big ]$
, it suffices to prove that for every
$T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }(1-\eta _{\le -2^{2C_\rho l}}^{\Gamma })\eta _{\le m}^{\Gamma ^c}]\big ]$
, it suffices to prove that for every
![]() $p\in (1, \infty )$
, there exists
$p\in (1, \infty )$
, there exists
![]() $\delta _p\in (0, 1)$
such that for every
$\delta _p\in (0, 1)$
such that for every
![]() $n\ge 2^{\kappa _l}$
and every
$n\ge 2^{\kappa _l}$
and every
![]() $f=(f_\iota :\iota \in \mathbb {N})\in \ell ^2({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))\cap \ell ^p({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))$
, one has
$f=(f_\iota :\iota \in \mathbb {N})\in \ell ^2({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))\cap \ell ^p({\mathbb {Z}}^d; \ell ^2(\mathbb {N}))$
, one has

Inequality (6.24), in view of Lemma 2.3 and Theorem 6.5, can be reduced to showing that for every
![]() $p\in (1, \infty )$
, there exists
$p\in (1, \infty )$
, there exists
![]() $\delta _p\in (0, 1)$
such that
$\delta _p\in (0, 1)$
such that
holds for every
![]() $n\ge 2^{\kappa _l}$
. By interpolation, it suffices to prove (6.25) for
$n\ge 2^{\kappa _l}$
. By interpolation, it suffices to prove (6.25) for
![]() $p=2$
and by Plancherel’s theorem, this reduces to showing that
$p=2$
and by Plancherel’s theorem, this reduces to showing that
holds uniformly in
![]() $\xi $
for all
$\xi $
for all
![]() $n\ge 2^{\kappa _l}$
. This follows from the definition of
$n\ge 2^{\kappa _l}$
. This follows from the definition of
![]() $\kappa _l$
and (6.11).
$\kappa _l$
and (6.11).
Step 3. We now establish (6.20) with
![]() $T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le -2^{2C_\rho l}}^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
in place of
$T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le -2^{2C_\rho l}}^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
in place of
![]() $T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
. Taking
$T_{{\mathbb {Z}}^d}\big [\Theta _{\Sigma _{\le l}^d}[\Upsilon _n^{\Gamma }\eta _{\le m}^{\Gamma ^c}]\big ]$
. Taking
![]() $Q_{\le l}$
from property (iv), note that
$Q_{\le l}$
from property (iv), note that
Using this factorization, it suffices to show that

and

By Lemma 2.3 and Theorem 6.5, the bound (6.26) follows from
which clearly holds for all
![]() $p\in [1, \infty ]$
. To prove (6.27), we can use the sampling principle formulated in Proposition 6.9 to reduce matters to proving
$p\in [1, \infty ]$
. To prove (6.27), we can use the sampling principle formulated in Proposition 6.9 to reduce matters to proving

To do this, we carefully choose the finite dimensional Banach spaces
![]() $B_1$
and
$B_1$
and
![]() $B_2$
in Proposition 6.9 to accommodate the oscillation semi-norm
$B_2$
in Proposition 6.9 to accommodate the oscillation semi-norm
![]() $O_{I,J}$
. See the remark after Proposition 6.9.
$O_{I,J}$
. See the remark after Proposition 6.9.
Step 4. Let
![]() $\eta $
be a smooth function with
$\eta $
be a smooth function with
![]() and set
and set
![]() $\chi _{n}(\xi ):= \eta (\tau ^{-n} \circ \xi )$
Using conditions (6.10), (6.11), (6.12) and (6.13), we see that Theorem B in [Reference Duoandikoetxea and Rubio de Francia22] implies
$\chi _{n}(\xi ):= \eta (\tau ^{-n} \circ \xi )$
Using conditions (6.10), (6.11), (6.12) and (6.13), we see that Theorem B in [Reference Duoandikoetxea and Rubio de Francia22] implies

for
![]() $1<p<\infty $
since
$1<p<\infty $
since
![]() $|\Upsilon _n(\xi ) - \chi _{-n}(\xi )| \lesssim \min (|\tau ^n\circ \xi |, |\tau ^n \circ \xi |^{-1})^{\delta _{\Upsilon }}$
and both maximal functions
$|\Upsilon _n(\xi ) - \chi _{-n}(\xi )| \lesssim \min (|\tau ^n\circ \xi |, |\tau ^n \circ \xi |^{-1})^{\delta _{\Upsilon }}$
and both maximal functions
![]() $\sup _{n\in \mathbb {N}} |T_{\mathbb {R}^k}[\Upsilon _n]f|$
and
$\sup _{n\in \mathbb {N}} |T_{\mathbb {R}^k}[\Upsilon _n]f|$
and
![]() $\sup _{n\in \mathbb {N}} |T_{\mathbb {R}^k}[\chi _{-n}]f|$
are both bounded on all
$\sup _{n\in \mathbb {N}} |T_{\mathbb {R}^k}[\chi _{-n}]f|$
are both bounded on all
![]() $L^q(\mathbb {R}^k)$
for all
$L^q(\mathbb {R}^k)$
for all
![]() $1<q<\infty $
.
$1<q<\infty $
.
Using Lemma 2.3, we see that inequality (6.29) reduces (6.28) to proving

To prove (6.30), we note that for every
![]() $m < n$
, we have
$m < n$
, we have
We fix
![]() $J\in {\mathbb {Z}}_+$
and a sequence
$J\in {\mathbb {Z}}_+$
and a sequence
![]() $I\in \mathfrak S_J(\mathbb {N})$
. Then
$I\in \mathfrak S_J(\mathbb {N})$
. Then
 $$ \begin{align*} O_{I, J}\big(T_{\mathbb{R}^k}[\chi_{n}] f_{\iota}:n\in\mathbb{N}\big)&\lesssim\Big(\sum_{j=0}^{J-1}\sup_{I_j\le n<I_{j+1}}\big|T_{\mathbb{R}^k}[\chi_{n}-\chi_{ I_{j}}]f_{\iota}\big|^2\Big)^{1/2}\\ &= \Big(\sum_{j=0}^{J-1}\sup_{I_j< n< I_{j+1}}\big|T_{\mathbb{R}^k}[\chi_{n}]T_{\mathbb{R}^k}[\chi_{I_{j+1}}-\chi_{I_{j}}]f_{\iota}\big|^2\Big)^{1/2}\\ &\le\Big(\sum_{j\in\mathbb{N}}\sup_{n\in{\mathbb{Z}}}\big(\varphi_n*\big|T_{\mathbb{R}^k}[\chi_{I_{j+1}}-\chi_{I_{j}}]f_{\iota}\big|\big)^2\Big)^{1/2}, \end{align*} $$
$$ \begin{align*} O_{I, J}\big(T_{\mathbb{R}^k}[\chi_{n}] f_{\iota}:n\in\mathbb{N}\big)&\lesssim\Big(\sum_{j=0}^{J-1}\sup_{I_j\le n<I_{j+1}}\big|T_{\mathbb{R}^k}[\chi_{n}-\chi_{ I_{j}}]f_{\iota}\big|^2\Big)^{1/2}\\ &= \Big(\sum_{j=0}^{J-1}\sup_{I_j< n< I_{j+1}}\big|T_{\mathbb{R}^k}[\chi_{n}]T_{\mathbb{R}^k}[\chi_{I_{j+1}}-\chi_{I_{j}}]f_{\iota}\big|^2\Big)^{1/2}\\ &\le\Big(\sum_{j\in\mathbb{N}}\sup_{n\in{\mathbb{Z}}}\big(\varphi_n*\big|T_{\mathbb{R}^k}[\chi_{I_{j+1}}-\chi_{I_{j}}]f_{\iota}\big|\big)^2\Big)^{1/2}, \end{align*} $$
where
![]() $\varphi _n(x):=|T_{\mathbb {R}^k}[\chi _{n}](x)|$
. Using this estimate and the Fefferman-Stein vector-valued maximal function estimate (see [Reference Stein57]), we conclude that
$\varphi _n(x):=|T_{\mathbb {R}^k}[\chi _{n}](x)|$
. Using this estimate and the Fefferman-Stein vector-valued maximal function estimate (see [Reference Stein57]), we conclude that

As above, using Theorem B in [Reference Duoandikoetxea and Rubio de Francia22], we see that for every
![]() $p\in (1, \infty )$
,
$p\in (1, \infty )$
,

Then invoking (6.32) and Lemma 2.3, we obtain

Combining (6.31) with (6.33), we obtain the desired claim in (6.30), and this completes the proof of Theorem 6.14.
6.3 Multi-parameter semi-norm variant of Theorem 6.5
We will generalize Theorem 6.14 to the multi-parameter setting for a class of multipliers arising in our question. We formulate our main result in the two-parameter setting, but all arguments are adaptable to multi-parameter settings.
Let
![]() $P\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial with
$P\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial with
![]() $\deg P\ge 2$
such that
$\deg P\ge 2$
such that
 $$ \begin{align} P(m_1, m_2):=\sum_{(\gamma_1, \gamma_2)\in S_P}c_{\gamma_1, \gamma_2}m_1^{\gamma_1}m_2^{\gamma_2}, \end{align} $$
$$ \begin{align} P(m_1, m_2):=\sum_{(\gamma_1, \gamma_2)\in S_P}c_{\gamma_1, \gamma_2}m_1^{\gamma_1}m_2^{\gamma_2}, \end{align} $$
where
![]() $c_{(0,0)}=0$
. In addition, we assume that P is non-degenerate in the sense that
$c_{(0,0)}=0$
. In addition, we assume that P is non-degenerate in the sense that
![]() $S_P\cap ({\mathbb {Z}}_+\times {\mathbb {Z}}_+)\neq \emptyset $
; see the remark below Theorem 1.11. Let
$S_P\cap ({\mathbb {Z}}_+\times {\mathbb {Z}}_+)\neq \emptyset $
; see the remark below Theorem 1.11. Let
![]() $r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
$r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
![]() $N_{P}$
corresponding to the polynomial P from (6.34). For any vertex
$N_{P}$
corresponding to the polynomial P from (6.34). For any vertex
![]() $v_j=(v_{j, 1}, v_{j, 2})$
of
$v_j=(v_{j, 1}, v_{j, 2})$
of
![]() $N_P$
, we denote the associated monomial by
$N_P$
, we denote the associated monomial by
From Section 4 (see Remark 4.5), we know that
![]() $P^j$
is the main monomial in the sector
$P^j$
is the main monomial in the sector
![]() $S(j)$
for
$S(j)$
for
![]() $j\in [r]$
.
$j\in [r]$
.
We fix the lacunarity factor
![]() $\tau>1$
. Throughout this subsection, we allow all the implied constants to depend on
$\tau>1$
. Throughout this subsection, we allow all the implied constants to depend on
![]() $\tau $
. For real numbers
$\tau $
. For real numbers
![]() $M_1, M_2\ge 1$
and
$M_1, M_2\ge 1$
and
![]() $\xi \in \mathbb {R}$
, we consider the multiplier
$\xi \in \mathbb {R}$
, we consider the multiplier
 $$ \begin{align} \mathfrak m_{M_1, M_2}^P(\xi):=\frac{1}{(1-\tau^{-1})^2}\int_{\tau^{-1}}^1\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(M_1y_1, M_2y_2))dy_1dy_2, \end{align} $$
$$ \begin{align} \mathfrak m_{M_1, M_2}^P(\xi):=\frac{1}{(1-\tau^{-1})^2}\int_{\tau^{-1}}^1\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(M_1y_1, M_2y_2))dy_1dy_2, \end{align} $$
where recall
![]() $P_{\xi }\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
is defined as
$P_{\xi }\in \mathbb {R}[\mathrm {m}_1, \mathrm {m}_2]$
is defined as
![]() $P_{\xi }(m_1,m_2) = \xi P(m_1,m_2)$
.
$P_{\xi }(m_1,m_2) = \xi P(m_1,m_2)$
.
As an application of Theorem 6.14, we obtain the following two-parameter oscillation inequality.
Theorem 6.37. Let
![]() $\tau>1$
be given and let
$\tau>1$
be given and let
![]() $(\mathfrak m_{M_1, M_2}^{P}: (M_1, M_2)\in \mathbb {D}_{\tau }\times \mathbb {D}_{\tau })$
be the two-parameter sequence of multipliers from (6.36) corresponding to the polynomial P from (6.34). Let
$(\mathfrak m_{M_1, M_2}^{P}: (M_1, M_2)\in \mathbb {D}_{\tau }\times \mathbb {D}_{\tau })$
be the two-parameter sequence of multipliers from (6.36) corresponding to the polynomial P from (6.34). Let
![]() $r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
$r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
![]() $N_{P}$
. For every
$N_{P}$
. For every
![]() $\rho \in (0, 1)$
and
$\rho \in (0, 1)$
and
![]() $p \in (1,\infty )$
and any
$p \in (1,\infty )$
and any
![]() $j\in [r]$
, there exists an absolute constant
$j\in [r]$
, there exists an absolute constant
![]() $0<C=C(p, \rho , \tau , j, P)<\infty $
such that for every integers
$0<C=C(p, \rho , \tau , j, P)<\infty $
such that for every integers
![]() $l\in \mathbb {N}$
and
$l\in \mathbb {N}$
and
![]() $m\le -10C_{\rho }2^{2\rho l}$
and for every
$m\le -10C_{\rho }2^{2\rho l}$
and for every
![]() $f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}; \ell ^2(\mathbb {N}))$
, one has
$f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}; \ell ^2(\mathbb {N}))$
, one has

with
![]() $\Theta _{\Sigma _{\le l}}$
defined in (6.7). In particular, (6.38) also implies the maximal estimate
$\Theta _{\Sigma _{\le l}}$
defined in (6.7). In particular, (6.38) also implies the maximal estimate

Some remarks about Theorem 6.37 are in order.
-
1. Theorem 6.37 is the simplest instance of a multi-parameter oscillation variant of the Ionescu–Wainger theorem [Reference Ionescu and Wainger34]. More general variants of Theorem 6.37 can be also proved. For instance, an analogue of Theorem 6.37 for the following multipliers
can be established using the methods of the paper. However, this goes beyond the scope of this paper and will be discussed in the future. $$\begin{align*}\ \ \ \ \ \ \mathfrak m_{M_1, M_2}^P(\xi_1, \xi_2, \xi_3)=\int_{0}^1\int_{0}^1\boldsymbol{e}(\xi_1(M_1y_1)+\xi_2(M_2y_2)+\xi_3 P(M_1y_1, M_2y_2))dy_1dy_2 \end{align*}$$
$$\begin{align*}\ \ \ \ \ \ \mathfrak m_{M_1, M_2}^P(\xi_1, \xi_2, \xi_3)=\int_{0}^1\int_{0}^1\boldsymbol{e}(\xi_1(M_1y_1)+\xi_2(M_2y_2)+\xi_3 P(M_1y_1, M_2y_2))dy_1dy_2 \end{align*}$$
-
2. In contrast to the one-parameter theory, it is not clear whether multi-parameter r-variational or jump counterparts of Theorem 6.37 are available. As far as we know, it is not even clear if there are useful multi-parameter definitions of r-variational or jump semi-norms. From this point of view, the multi-parameter oscillation semi-norm is an invaluable tool allowing us to handle pointwise convergence problems in the multi-parameter setting.
-
3. A careful inspection of the proof allows us to establish an analogue of Theorem 6.37 in the continuous setting. Namely, for every
 $p\in (1, \infty )$
, there is a constant
$p\in (1, \infty )$
, there is a constant
 $C>0$
such that for every
$C>0$
such that for every
 $f=(f_{\iota }:\iota \in \mathbb {N})\in L^p(\mathbb {R}; \ell ^2(\mathbb {N}))$
, one has
$f=(f_{\iota }:\iota \in \mathbb {N})\in L^p(\mathbb {R}; \ell ^2(\mathbb {N}))$
, one has 
Proof of Theorem 6.37
We will only prove Theorem 6.37 for
![]() $j=r=1$
or for
$j=r=1$
or for
![]() $1\le j<r$
with
$1\le j<r$
with
![]() $r\ge 2$
. The same argument can be used to prove the case for
$r\ge 2$
. The same argument can be used to prove the case for
![]() $j=r$
. In view of (2.17), it suffices to prove (6.38). We divide the proof into two steps to make the argument clearer.
$j=r$
. In view of (2.17), it suffices to prove (6.38). We divide the proof into two steps to make the argument clearer.
Step 1. We prove that for every
![]() $p\in (1, \infty )$
and every
$p\in (1, \infty )$
and every
![]() $f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}; \ell ^2(\mathbb {N}))$
, one has
$f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}; \ell ^2(\mathbb {N}))$
, one has

Using (4.14) and (4.15), it suffices to prove that for every
![]() $p\in (1, \infty )$
, there is
$p\in (1, \infty )$
, there is
![]() $\sigma _{j, p}\in (0, 1)$
such that for every
$\sigma _{j, p}\in (0, 1)$
such that for every
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
![]() $i\in [2]$
and every
$i\in [2]$
and every
![]() $f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}; \ell ^2(\mathbb {N}))$
, one has
$f=(f_{\iota }:\iota \in \mathbb {N})\in \ell ^p({\mathbb {Z}}; \ell ^2(\mathbb {N}))$
, one has

We only prove (6.39) for
![]() $i=1$
, as the proof for
$i=1$
, as the proof for
![]() $i=2$
is the same. By the construction of the sets
$i=2$
is the same. By the construction of the sets
![]() $\mathbb {S}_{\tau , 1}^N(j)$
(see definition (4.15)), the problem becomes a one-parameter problem. Indeed, if
$\mathbb {S}_{\tau , 1}^N(j)$
(see definition (4.15)), the problem becomes a one-parameter problem. Indeed, if
![]() $(M_1, M_2)\in \mathbb {S}_{\tau , 1}^N(j)$
, then
$(M_1, M_2)\in \mathbb {S}_{\tau , 1}^N(j)$
, then
![]() $(M_1, M_2)=(\tau ^{n_1}, \tau ^{n_2})$
and
$(M_1, M_2)=(\tau ^{n_1}, \tau ^{n_2})$
and
 $$ \begin{align*} (n_1, n_2)=\frac{n}{d_j}\omega_{j-1}+\frac{N}{d_j}(\omega_{j}+\omega_{j-1}) \quad \text{ for some } \quad n \in{\mathbb{Z}}_+. \end{align*} $$
$$ \begin{align*} (n_1, n_2)=\frac{n}{d_j}\omega_{j-1}+\frac{N}{d_j}(\omega_{j}+\omega_{j-1}) \quad \text{ for some } \quad n \in{\mathbb{Z}}_+. \end{align*} $$
Defining
![]() $(n_1^k, n_2^k):=\frac {k}{d_j}\omega _{j-1}+\frac {N}{d_j}(\omega _{j}+\omega _{j-1})$
for any
$(n_1^k, n_2^k):=\frac {k}{d_j}\omega _{j-1}+\frac {N}{d_j}(\omega _{j}+\omega _{j-1})$
for any
![]() $k\in {\mathbb {Z}}_+$
, inequality (6.39) can be written as
$k\in {\mathbb {Z}}_+$
, inequality (6.39) can be written as

By Lemma 2.3 and Theorem 6.5, it suffices to prove that for every
![]() $p\in (1, \infty )$
, there is
$p\in (1, \infty )$
, there is
![]() $\sigma _{j, p}\in (0, 1)$
such that for every
$\sigma _{j, p}\in (0, 1)$
such that for every
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $f\in L^p(\mathbb {R})$
, one has
$f\in L^p(\mathbb {R})$
, one has

By (6.34), (6.35) and Lemma 4.10, we obtain

whenever
![]() $|y_1|, |y_2|\le 1$
, with
$|y_1|, |y_2|\le 1$
, with
![]() $\sigma _j>0$
defined in (4.11). Consequently, we have
$\sigma _j>0$
defined in (4.11). Consequently, we have
Moreover, by van der Corput’s lemma (Proposition 2.6), we can find a
![]() $\delta _0\in (0, 1)$
such that
$\delta _0\in (0, 1)$
such that
for sufficiently large
![]() $N\in \mathbb {N}$
. A convex combination of (6.41) and (6.42) gives
$N\in \mathbb {N}$
. A convex combination of (6.41) and (6.42) gives
for some
![]() $\delta _0', \sigma _j'\in (0, 1)$
.
$\delta _0', \sigma _j'\in (0, 1)$
.
Using (6.43) and Plancherel’s theorem, we obtain (6.40) for
![]() $p=2$
. Standard Littlewood–Paley theory arguments (see, for example, Theorem D in [Reference Duoandikoetxea and Rubio de Francia22]) allows us then to obtain (6.40) for all
$p=2$
. Standard Littlewood–Paley theory arguments (see, for example, Theorem D in [Reference Duoandikoetxea and Rubio de Francia22]) allows us then to obtain (6.40) for all
![]() $p\in (1, \infty )$
.
$p\in (1, \infty )$
.
Step 2. The argument from the first step allows us to reduce matters to proving

We define a new one-parameter multiplier
 $$ \begin{align*} \mathfrak g_{M}^{P^j}(\xi):=\frac{1}{(1-\tau^{-1})^2}\int_{\tau^{-1}}^1\int_{\tau^{-1}}^1 \boldsymbol{e}(c_{(v_{j, 1}, v_{j, 2})} M\xi y_1^{v_{j, 1}}y_2^{v_{j, 2}})dy_1dy_2. \end{align*} $$
$$ \begin{align*} \mathfrak g_{M}^{P^j}(\xi):=\frac{1}{(1-\tau^{-1})^2}\int_{\tau^{-1}}^1\int_{\tau^{-1}}^1 \boldsymbol{e}(c_{(v_{j, 1}, v_{j, 2})} M\xi y_1^{v_{j, 1}}y_2^{v_{j, 2}})dy_1dy_2. \end{align*} $$
Observe that by Theorem 6.14, we obtain

This completes the proof of the theorem.
7 Two-parameter circle method: Proof of Theorem 4.16
Throughout this section,
![]() $\tau>1$
is fixed, and we allow all the implied constants to depend on
$\tau>1$
is fixed, and we allow all the implied constants to depend on
![]() $\tau $
. Let
$\tau $
. Let
![]() $P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial obeying
$P\in {\mathbb {Z}}[\mathrm {m}_1, \mathrm {m}_2]$
be a polynomial obeying
![]() $P(0, 0)=0$
, which is non-degenerate in the sense that
$P(0, 0)=0$
, which is non-degenerate in the sense that
![]() $S_P\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
; see (1.14). For every real number
$S_P\cap ({\mathbb {Z}}_{+}\times {\mathbb {Z}}_{+})\neq \emptyset $
; see (1.14). For every real number
![]() $N\ge 1$
, define
$N\ge 1$
, define
For every real number
![]() $M_1, M_2\ge 1$
and
$M_1, M_2\ge 1$
and
![]() $\xi \in \mathbb {R}$
, we consider the multiplier
$\xi \in \mathbb {R}$
, we consider the multiplier
with
![]() $P_{\xi }(m_1,m_2) = \xi P(m_1,m_2)$
. The corresponding partial multipliers are defined by
$P_{\xi }(m_1,m_2) = \xi P(m_1,m_2)$
. The corresponding partial multipliers are defined by
 $$ \begin{align} \begin{split} m_{m_1, M_2}^1(\xi):=&\sum_{m_2\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_2}(m_2), \qquad m_1\in{\mathbb{Z}},\\ m_{M_1, m_2}^2(\xi):=&\sum_{m_1\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_1}(m_1), \qquad m_2\in{\mathbb{Z}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} m_{m_1, M_2}^1(\xi):=&\sum_{m_2\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_2}(m_2), \qquad m_1\in{\mathbb{Z}},\\ m_{M_1, m_2}^2(\xi):=&\sum_{m_1\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_1}(m_1), \qquad m_2\in{\mathbb{Z}}. \end{split} \end{align} $$
We fix further notation and terminology. For functions
![]() $G:\mathbb {Q}\cap \mathbb {T}\to \mathbb {C}$
,
$G:\mathbb {Q}\cap \mathbb {T}\to \mathbb {C}$
,
![]() $\mathfrak m:\mathbb {T}\to \mathbb {C}$
, a finite set
$\mathfrak m:\mathbb {T}\to \mathbb {C}$
, a finite set
![]() $\Sigma \subset \mathbb {Q}\cap \mathbb {T}$
, any
$\Sigma \subset \mathbb {Q}\cap \mathbb {T}$
, any
![]() $n\in {\mathbb {Z}}$
and any
$n\in {\mathbb {Z}}$
and any
![]() $\xi \in \mathbb {T}$
, we define the following
$\xi \in \mathbb {T}$
, we define the following
![]() $1$
-periodic multiplier:
$1$
-periodic multiplier:
In a similar way, for any
![]() $l\in \mathbb {N}$
,
$l\in \mathbb {N}$
,
![]() $n\in {\mathbb {Z}}$
, any
$n\in {\mathbb {Z}}$
, any
![]() $\xi \in \mathbb {T}$
, we define the following projection multipliers (recall the definition of
$\xi \in \mathbb {T}$
, we define the following projection multipliers (recall the definition of
![]() $\Sigma _{\le l}:=\Sigma _{\le l}^1$
from (6.3))
$\Sigma _{\le l}:=\Sigma _{\le l}^1$
from (6.3))
 $$ \begin{align*} \Delta_{\le l, \le n}(\xi):=\sum_{a/q\in\Sigma_{\le l}}\eta_{\le n}(\xi-a/q), \qquad \text{ and } \qquad \Delta_{\le l, \le n}^{c}(\xi):=1-\Delta_{\le l, \le n}(\xi). \end{align*} $$
$$ \begin{align*} \Delta_{\le l, \le n}(\xi):=\sum_{a/q\in\Sigma_{\le l}}\eta_{\le n}(\xi-a/q), \qquad \text{ and } \qquad \Delta_{\le l, \le n}^{c}(\xi):=1-\Delta_{\le l, \le n}(\xi). \end{align*} $$
All these multipliers will be applied with different choices of parameters. For
![]() $\beta>0$
,
$\beta>0$
,
![]() $M_1, M_2, M>0$
,
$M_1, M_2, M>0$
,
![]() $N\ge 0$
, and
$N\ge 0$
, and
![]() $v=(v_1, v_2)\in {\mathbb {Z}}^2$
, we define
$v=(v_1, v_2)\in {\mathbb {Z}}^2$
, we define
Using (7.3), we also set
Definitions (7.3) and (7.4) will be applied with
![]() $v\in {\mathbb {Z}}^2$
being a vertex of the backwards Newton diagram
$v\in {\mathbb {Z}}^2$
being a vertex of the backwards Newton diagram
![]() $N_{P}$
. In this section, we shall abbreviate
$N_{P}$
. In this section, we shall abbreviate
![]() $\mathfrak m_{M_1, M_2}^P$
to
$\mathfrak m_{M_1, M_2}^P$
to
 $$ \begin{align*} \mathfrak m_{M_1, M_2}(\xi):=\frac{1}{(1-\tau^{-1})^2}\int_{\tau^{-1}}^1\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(M_1y_1, M_2y_2))dy_1dy_2, \qquad \xi\in\mathbb{R}. \end{align*} $$
$$ \begin{align*} \mathfrak m_{M_1, M_2}(\xi):=\frac{1}{(1-\tau^{-1})^2}\int_{\tau^{-1}}^1\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(M_1y_1, M_2y_2))dy_1dy_2, \qquad \xi\in\mathbb{R}. \end{align*} $$
We also define the following two partial multipliers:
 $$ \begin{align} \begin{split} \mathfrak m_{m_1, M_2}^1(\xi):=\frac{1}{1-\tau^{-1}}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(m_1, M_2y_2))dy_2, \qquad \xi\in\mathbb{R}, \; m_1\in{\mathbb{Z}},\\ \mathfrak m_{M_1, m_2}^2(\xi):=\frac{1}{1-\tau^{-1}}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(M_1y_1, m_2))dy_1, \qquad \xi\in\mathbb{R}, \; m_2\in{\mathbb{Z}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathfrak m_{m_1, M_2}^1(\xi):=\frac{1}{1-\tau^{-1}}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(m_1, M_2y_2))dy_2, \qquad \xi\in\mathbb{R}, \; m_1\in{\mathbb{Z}},\\ \mathfrak m_{M_1, m_2}^2(\xi):=\frac{1}{1-\tau^{-1}}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\xi}(M_1y_1, m_2))dy_1, \qquad \xi\in\mathbb{R}, \; m_2\in{\mathbb{Z}}. \end{split} \end{align} $$
Our main result of this section is Theorem 7.6, which is a restatement of Theorem 4.16.
Theorem 7.6. Let
![]() $r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
$r\in {\mathbb {Z}}_+$
be the number of vertices in the backwards Newton diagram
![]() $N_{P}$
. Then for every
$N_{P}$
. Then for every
![]() $p\in (1, \infty )$
and
$p\in (1, \infty )$
and
![]() $j\in [r]$
and for every
$j\in [r]$
and for every
![]() $f\in \ell ^p({\mathbb {Z}})$
, one has
$f\in \ell ^p({\mathbb {Z}})$
, one has
The proof of Theorem 7.6 is divided into several steps. We apply iteratively the classical circle method, taking into account the geometry of the backwards Newton diagram
![]() $N_P$
.
$N_P$
.
7.1 Preliminaries
The number of vertices
![]() $r\in {\mathbb {Z}}_+$
in the backwards Newton diagram
$r\in {\mathbb {Z}}_+$
in the backwards Newton diagram
![]() $N_{P}$
is fixed. Let
$N_{P}$
is fixed. Let
![]() $v_j=(v_{j, 1}, v_{j, 2})$
denote the vertex of
$v_j=(v_{j, 1}, v_{j, 2})$
denote the vertex of
![]() $N_{P}$
corresponding to
$N_{P}$
corresponding to
![]() $j\in [r]$
.
$j\in [r]$
.
It suffices to establish inequality (7.7) for
![]() $j=r=1$
assuming additionally that
$j=r=1$
assuming additionally that
![]() $\log M_1\le \log M_2$
when
$\log M_1\le \log M_2$
when
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(1)$
, or for any
$(M_1, M_2)\in \mathbb {S}_{\tau }(1)$
, or for any
![]() $r\ge 2$
and any
$r\ge 2$
and any
![]() $1\le j<r$
. Both cases ensure that
$1\le j<r$
. Both cases ensure that
which means that
![]() $M_1\le M_2^{K_j}$
for some
$M_1\le M_2^{K_j}$
for some
![]() $K_j>0$
; see Remark 4.5. The case when
$K_j>0$
; see Remark 4.5. The case when
![]() $j=r$
with
$j=r$
with
![]() $r\ge 2$
can be proved in much the same way, with the difference that
$r\ge 2$
can be proved in much the same way, with the difference that
![]() $\log M_1\gtrsim \log M_2$
whenever
$\log M_1\gtrsim \log M_2$
whenever
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(r)$
. We only outline the most important changes, omitting the details, which can be easily adjusted using the arguments below.
$(M_1, M_2)\in \mathbb {S}_{\tau }(r)$
. We only outline the most important changes, omitting the details, which can be easily adjusted using the arguments below.
From now on,
![]() $p\in (1, \infty )$
is fixed and we let
$p\in (1, \infty )$
is fixed and we let
![]() $p_0\in (1, 2)$
be such that
$p_0\in (1, 2)$
be such that
![]() $p\in (p_0, p_0')$
. The proof will involve several parameters that have to be suitably adjusted to
$p\in (p_0, p_0')$
. The proof will involve several parameters that have to be suitably adjusted to
![]() $p\in (p_0,p_0')$
.
$p\in (p_0,p_0')$
.
We begin by setting
 $$ \begin{align*} \theta_p:=\bigg(\frac{1}{p_0}-\frac{1}{\min\{p, p'\}}\bigg)\bigg(\frac{1}{p_0}-\frac{1}{2}\bigg)^{-1}\in(0, 1). \end{align*} $$
$$ \begin{align*} \theta_p:=\bigg(\frac{1}{p_0}-\frac{1}{\min\{p, p'\}}\bigg)\bigg(\frac{1}{p_0}-\frac{1}{2}\bigg)^{-1}\in(0, 1). \end{align*} $$
We will take
where
![]() $\beta \in {\mathbb {Z}}_+$
plays the role of the parameter
$\beta \in {\mathbb {Z}}_+$
plays the role of the parameter
![]() $\beta \in {\mathbb {Z}}_+$
from Proposition 5.37, and
$\beta \in {\mathbb {Z}}_+$
from Proposition 5.37, and
![]() $\delta \in (0, 1)$
is the parameter that arises in the complete sum estimates; see Proposition 5.46.
$\delta \in (0, 1)$
is the parameter that arises in the complete sum estimates; see Proposition 5.46.
Finally, we need the parameter
![]() $\rho>0$
, introduced in the Ionescu–Wainger multiplier theorem (see Theorem 6.5 as well as Theorem 6.14 and Theorem 6.37), to satisfy
$\rho>0$
, introduced in the Ionescu–Wainger multiplier theorem (see Theorem 6.5 as well as Theorem 6.14 and Theorem 6.37), to satisfy
7.2 Minor arc estimates
We first establish the minor arcs estimates.
Claim 7.11. For every
![]() $1\le j<r$
and for every
$1\le j<r$
and for every
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
, one has
$(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
, one has
with
![]() $\alpha $
as in (7.9). The same estimate holds when
$\alpha $
as in (7.9). The same estimate holds when
![]() $j=r=1$
, as long as
$j=r=1$
, as long as
![]() $\log M_1\le \log M_2$
.
$\log M_1\le \log M_2$
.
The case
![]() $j=r\ge 2$
requires a minor modification. Keeping in mind that
$j=r\ge 2$
requires a minor modification. Keeping in mind that
![]() $\log M_2\lesssim \log M_1$
, it suffices to establish an analogue of (7.12). Namely, one has
$\log M_2\lesssim \log M_1$
, it suffices to establish an analogue of (7.12). Namely, one has
Proof of Claim 7.11
Since
![]() $\log M_1\lesssim \log M_2$
, one has
$\log M_1\lesssim \log M_2$
, one has
![]() $\log M_{r, j}^*\simeq \log M_2$
, where
$\log M_{r, j}^*\simeq \log M_2$
, where
![]() $M_{r, j}^*$
was defined in (5.36). We can also assume that
$M_{r, j}^*$
was defined in (5.36). We can also assume that
![]() $M_2$
is a large number. To prove (7.12), by Plancherel’s theorem, it suffices to show for every
$M_2$
is a large number. To prove (7.12), by Plancherel’s theorem, it suffices to show for every
![]() $\xi \in \mathbb {T}$
that
$\xi \in \mathbb {T}$
that
For this purpose, we use Dirichlet’s principle to find a rational fraction
![]() $a_0/q_0$
such that
$a_0/q_0$
such that
![]() $(a_0, q_0)=1$
and
$(a_0, q_0)=1$
and
![]() $1\le q_0 \le C M_1^{v_{j, 1}}M_2^{v_{j, 2}}\log (M_{r, j}^*)^{-\beta }=C 2^{n_{M_1, M_2}^{v_j, \beta }(M_{r, j}^*)}$
and
$1\le q_0 \le C M_1^{v_{j, 1}}M_2^{v_{j, 2}}\log (M_{r, j}^*)^{-\beta }=C 2^{n_{M_1, M_2}^{v_j, \beta }(M_{r, j}^*)}$
and
 $$ \begin{align*} \Big|\xi-\frac{a_0}{q_0}\Big|\le\frac{\log(M_{r, j}^*)^{\beta}}{q_0CM_1^{v_{j, 1}}M_2^{v_{j, 2}}}\le \frac{1}{q_0^2} \end{align*} $$
$$ \begin{align*} \Big|\xi-\frac{a_0}{q_0}\Big|\le\frac{\log(M_{r, j}^*)^{\beta}}{q_0CM_1^{v_{j, 1}}M_2^{v_{j, 2}}}\le \frac{1}{q_0^2} \end{align*} $$
for a large constant
![]() $C>1$
to be specified later. If
$C>1$
to be specified later. If
![]() $q_0< \log (M_2)^{\beta }$
, then
$q_0< \log (M_2)^{\beta }$
, then
![]() $a_0/q_0\in \Sigma _{\le l^{\beta }(M_2)}$
and consequently the left-hand side of (7.13) vanishes (if
$a_0/q_0\in \Sigma _{\le l^{\beta }(M_2)}$
and consequently the left-hand side of (7.13) vanishes (if
![]() $C>1$
is large enough) and there is nothing to prove. Thus, we can assume that
$C>1$
is large enough) and there is nothing to prove. Thus, we can assume that
![]() $ \log (M_{r, j}^*)^{\beta }\lesssim q_0\lesssim M_1^{v_{j, 1}}M_2^{v_{j, 2}}\log (M_{r, j}^*)^{-\beta }$
. We now can apply Proposition 5.37 and obtain (7.13) as claimed.
$ \log (M_{r, j}^*)^{\beta }\lesssim q_0\lesssim M_1^{v_{j, 1}}M_2^{v_{j, 2}}\log (M_{r, j}^*)^{-\beta }$
. We now can apply Proposition 5.37 and obtain (7.13) as claimed.
7.3 Major arcs estimates
Recalling (7.2), we begin with a simple approximation formula.
Lemma 7.14. Suppose that
![]() $1\le j<r$
and
$1\le j<r$
and
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
. Then for every
$(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
. Then for every
![]() $0\le l, l'\le l^{\beta }(M_2)$
and
$0\le l, l'\le l^{\beta }(M_2)$
and
![]() $(M_1', M_2')\in \mathbb {S}_{\tau }(j)$
and
$(M_1', M_2')\in \mathbb {S}_{\tau }(j)$
and
![]() $m_1\simeq M_1'$
such that
$m_1\simeq M_1'$
such that
![]() $1\le M_1'\le M_1$
and
$1\le M_1'\le M_1$
and
![]() $2^{C_{\rho }2^{\rho l}}\le M_2'\le M_2$
, one has
$2^{C_{\rho }2^{\rho l}}\le M_2'\le M_2$
, one has
where
![]() $n_{M_1, M_2}^{v}(N)$
,
$n_{M_1, M_2}^{v}(N)$
,
![]() $G_{m_1}^1$
,
$G_{m_1}^1$
,
![]() $m_{m_1, M_2}^1$
and
$m_{m_1, M_2}^1$
and
![]() $\mathfrak m_{m_1, M_2}^1$
were defined respectively in (7.4), (5.45), (7.1) and (7.5). In particular, (7.15) immediately yields
$\mathfrak m_{m_1, M_2}^1$
were defined respectively in (7.4), (5.45), (7.1) and (7.5). In particular, (7.15) immediately yields
 $$ \begin{align} \begin{split} m_{M_1', M_2'}(\xi)\Delta_{\le l, \le -n_{M_1, M_2}^{v_j}(l')}(\xi) =&\sum_{m_1\in{\mathbb{Z}}}\Phi_{\le -n_{M_1, M_2}^{v_j}(l')}^{\Sigma_{\le l}}[G_{m_1}^1, \mathfrak m_{m_1, M_2'}^1](\xi)\chi_{M_1'}(m_1)\\ &+O(2^{C_{\rho}2^{\rho l}}(M_{2}')^{-1}). \end{split} \end{align} $$
$$ \begin{align} \begin{split} m_{M_1', M_2'}(\xi)\Delta_{\le l, \le -n_{M_1, M_2}^{v_j}(l')}(\xi) =&\sum_{m_1\in{\mathbb{Z}}}\Phi_{\le -n_{M_1, M_2}^{v_j}(l')}^{\Sigma_{\le l}}[G_{m_1}^1, \mathfrak m_{m_1, M_2'}^1](\xi)\chi_{M_1'}(m_1)\\ &+O(2^{C_{\rho}2^{\rho l}}(M_{2}')^{-1}). \end{split} \end{align} $$
The same claims hold when
![]() $j=r=1$
, as long as
$j=r=1$
, as long as
![]() $\log M_1\le \log M_2$
.
$\log M_1\le \log M_2$
.
A similar conclusion holds when
![]() $j=r\ge 2$
. Taking into account that
$j=r\ge 2$
. Taking into account that
![]() $\log M_2\lesssim \log M_1$
whenever
$\log M_2\lesssim \log M_1$
whenever
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(r)$
and assuming that
$(M_1, M_2)\in \mathbb {S}_{\tau }(r)$
and assuming that
![]() $0\le l, l'\le l^{\beta }(M_1)$
, one has for every
$0\le l, l'\le l^{\beta }(M_1)$
, one has for every
![]() $(M_1', M_2')\in \mathbb {S}_{\tau }(j)$
and
$(M_1', M_2')\in \mathbb {S}_{\tau }(j)$
and
![]() $m_2\simeq M_2'$
satisfying
$m_2\simeq M_2'$
satisfying
![]() $2^{C_{\rho }2^{\rho l}}\le M_1'\le M_1$
and
$2^{C_{\rho }2^{\rho l}}\le M_1'\le M_1$
and
![]() $1\le M_2'\le M_2$
that
$1\le M_2'\le M_2$
that
In particular, (7.17) yields
Proof of Lemma 7.14
For every
![]() $a/q\in \Sigma _{\le l}$
, we note
$a/q\in \Sigma _{\le l}$
, we note
whenever
![]() $m_1\in {\mathbb {Z}}$
,
$m_1\in {\mathbb {Z}}$
,
![]() $m_2 = qm + r_2$
and
$m_2 = qm + r_2$
and
![]() $r_2\in {\mathbb {Z}}_q$
. Then, by (7.18), since
$r_2\in {\mathbb {Z}}_q$
. Then, by (7.18), since
![]() $q\le 2^{C_{\rho }2^{\rho l}}\le M_2'$
, we have
$q\le 2^{C_{\rho }2^{\rho l}}\le M_2'$
, we have
 $$ \begin{align} &\sum_{m_2\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_2'}(m_2)= \sum_{r_2=1}^q\boldsymbol{e}(P_{a/q}(m_1, r_2))\sum_{m\in {\mathbb{Z}}}\boldsymbol{e}(P_{\xi-a/q}(m_1, qm+r_2))\chi_{M_2'}(qm + r_2). \end{align} $$
$$ \begin{align} &\sum_{m_2\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_2'}(m_2)= \sum_{r_2=1}^q\boldsymbol{e}(P_{a/q}(m_1, r_2))\sum_{m\in {\mathbb{Z}}}\boldsymbol{e}(P_{\xi-a/q}(m_1, qm+r_2))\chi_{M_2'}(qm + r_2). \end{align} $$
The summation in m ranges over
![]() $m_{*}\le m \le m_{**}$
, where
$m_{*}\le m \le m_{**}$
, where
![]() $m_{*}/m_{**}$
is minimal/maximal with respect to
$m_{*}/m_{**}$
is minimal/maximal with respect to
![]() $\tau ^{-1}M_2' \le qm + r_2 \le M_2'$
. We will use Lemma 2.7 to compare
$\tau ^{-1}M_2' \le qm + r_2 \le M_2'$
. We will use Lemma 2.7 to compare
 $$ \begin{align*}\mathrm{the \ sum} \ \ \sum_{m_{*} <m \le m_{**}} \boldsymbol{e}(f(m)) \ \ \ \mathrm{to \ the \ integral} \ \ \int_{m_{*}}^{m_{**}} \boldsymbol{e}(f(s)) ds, \end{align*} $$
$$ \begin{align*}\mathrm{the \ sum} \ \ \sum_{m_{*} <m \le m_{**}} \boldsymbol{e}(f(m)) \ \ \ \mathrm{to \ the \ integral} \ \ \int_{m_{*}}^{m_{**}} \boldsymbol{e}(f(s)) ds, \end{align*} $$
where
![]() $f(m) = P_{\xi -a/q}(m_1, qm+r_2))$
. Suppose that
$f(m) = P_{\xi -a/q}(m_1, qm+r_2))$
. Suppose that
![]() $a/q\in \Sigma _{\le l}$
approximates
$a/q\in \Sigma _{\le l}$
approximates
![]() $\xi $
in the following sense:
$\xi $
in the following sense:
 $$ \begin{align} \Big|\xi-\frac{a}{q}\Big|\le \frac{(\log_{\tau} M_2)^{\beta}}{M_1^{v_{j, 1}}M_2^{v_{j, 2}}}. \end{align} $$
$$ \begin{align} \Big|\xi-\frac{a}{q}\Big|\le \frac{(\log_{\tau} M_2)^{\beta}}{M_1^{v_{j, 1}}M_2^{v_{j, 2}}}. \end{align} $$
From the definition of
![]() $\Sigma _{\le l}$
, we see that
$\Sigma _{\le l}$
, we see that
![]() $q \le 2^{C_{\rho }2^{\rho l}}$
. Therefore, by (7.20), the derivative
$q \le 2^{C_{\rho }2^{\rho l}}$
. Therefore, by (7.20), the derivative
![]() $f'$
satisfies
$f'$
satisfies
since
![]() $v_{j,2}\ge 1$
,
$v_{j,2}\ge 1$
,
![]() $\log _2 q \lesssim 2^{\rho l^{\beta }(M_2)} \le (\log _{\tau }M_2)^{\rho \beta }$
and
$\log _2 q \lesssim 2^{\rho l^{\beta }(M_2)} \le (\log _{\tau }M_2)^{\rho \beta }$
and
![]() $\rho \beta \le 1/10$
by (7.10). By Lemma 2.7, we have
$\rho \beta \le 1/10$
by (7.10). By Lemma 2.7, we have
 $$ \begin{align*}\Big| q \sum_{m_{*}\le m\le m_{**}}\boldsymbol{e}(P_{\xi-a/q}(m_1, qm+r_2)) - \int_{\tau^{-1}M_2'}^{M_2'} \boldsymbol{e}(P_{\xi-a/q}(m_1, t)) dt\Big| \lesssim q, \end{align*} $$
$$ \begin{align*}\Big| q \sum_{m_{*}\le m\le m_{**}}\boldsymbol{e}(P_{\xi-a/q}(m_1, qm+r_2)) - \int_{\tau^{-1}M_2'}^{M_2'} \boldsymbol{e}(P_{\xi-a/q}(m_1, t)) dt\Big| \lesssim q, \end{align*} $$
and hence by (7.19), we obtain
 $$ \begin{align*}\Big|\sum_{m_2\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_2'}(m_2) - G_{m_1}^1(a/q) \mathfrak m_{m_1, M_2'}^1(\xi-a/q)\Big|\lesssim q (M_2')^{-1}, \end{align*} $$
$$ \begin{align*}\Big|\sum_{m_2\in{\mathbb{Z}}}\boldsymbol{e}(P_{\xi}(m_1, m_2))\chi_{M_2'}(m_2) - G_{m_1}^1(a/q) \mathfrak m_{m_1, M_2'}^1(\xi-a/q)\Big|\lesssim q (M_2')^{-1}, \end{align*} $$
which by
![]() $q \le 2^{C_{\rho }2^{\rho l}}$
proves (7.15) as desired.
$q \le 2^{C_{\rho }2^{\rho l}}$
proves (7.15) as desired.
For
![]() $i\in [2]$
and
$i\in [2]$
and
![]() $j\in [r]$
let
$j\in [r]$
let
![]() $M_1^c = M_2, M_2^c = M_1$
,
$M_1^c = M_2, M_2^c = M_1$
,
and for
![]() $M_1, M_2\in \mathbb {D}_{\tau }$
we also let
$M_1, M_2\in \mathbb {D}_{\tau }$
we also let
 $$ \begin{align*} \mathbb{S}_{\tau}^1(j; M_2):=&\{M_1\in\mathbb{D}_{\tau}: (M_1, M_2)\in \mathbb{S}_{\tau}(j)\},\\ \mathbb{S}_{\tau}^2(j; M_1):=&\{M_2\in\mathbb{D}_{\tau}: (M_1, M_2)\in \mathbb{S}_{\tau}(j)\}. \end{align*} $$
$$ \begin{align*} \mathbb{S}_{\tau}^1(j; M_2):=&\{M_1\in\mathbb{D}_{\tau}: (M_1, M_2)\in \mathbb{S}_{\tau}(j)\},\\ \mathbb{S}_{\tau}^2(j; M_1):=&\{M_2\in\mathbb{D}_{\tau}: (M_1, M_2)\in \mathbb{S}_{\tau}(j)\}. \end{align*} $$
7.4 Changing scale estimates
In our next step, we will have to change the scale (or more precisely, we will truncate the size of denominators of fractions in
![]() $\Sigma _{\le l^{\beta }(M_2)}$
) to make the approximation estimates with respect to the first variable possible.
$\Sigma _{\le l^{\beta }(M_2)}$
) to make the approximation estimates with respect to the first variable possible.
We formulate the change of scale argument as follows.
Claim 7.21. For every
![]() $1\le j<r$
and for every
$1\le j<r$
and for every
![]() $M_1\in \mathbb {S}_{\tau }^1(j)$
, one has
$M_1\in \mathbb {S}_{\tau }^1(j)$
, one has
with
![]() $\alpha $
as in (7.9), where
$\alpha $
as in (7.9), where
 $$ \begin{align} \begin{aligned} g_{M_1, M_2}^N & :=m_{M_1, M_2}\Delta_{\le l^{\beta}(N), \le -n_{M_1, M_2}^{v_j,\beta}(N)}, \qquad N\ge1,\\ h_{M_1, M_2}^{N}(\xi) & :=\sum_{m_1\in{\mathbb{Z}}}\Phi_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}^{\Sigma_{\le l^{\beta}(N)}}[G_{m_1}^1, \mathfrak m_{m_1, M_2}^1](\xi)\chi_{M_1}(m_1) , \qquad N\ge1. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} g_{M_1, M_2}^N & :=m_{M_1, M_2}\Delta_{\le l^{\beta}(N), \le -n_{M_1, M_2}^{v_j,\beta}(N)}, \qquad N\ge1,\\ h_{M_1, M_2}^{N}(\xi) & :=\sum_{m_1\in{\mathbb{Z}}}\Phi_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}^{\Sigma_{\le l^{\beta}(N)}}[G_{m_1}^1, \mathfrak m_{m_1, M_2}^1](\xi)\chi_{M_1}(m_1) , \qquad N\ge1. \end{aligned} \end{align} $$
The same estimate holds when
![]() $j=r=1$
, as long as
$j=r=1$
, as long as
![]() $\log M_1\le \log M_2$
.
$\log M_1\le \log M_2$
.
The case
![]() $j=r\ge 2$
requires a minor modification. Keeping in mind that
$j=r\ge 2$
requires a minor modification. Keeping in mind that
![]() $\log M_2\lesssim \log M_1$
, it suffices to establish an analogue of (7.22). Namely, for every
$\log M_2\lesssim \log M_1$
, it suffices to establish an analogue of (7.22). Namely, for every
![]() $M_2\in \mathbb {S}_{\tau }^2(j)$
, one has
$M_2\in \mathbb {S}_{\tau }^2(j)$
, one has
We only present the proof of (7.22); inequality (7.24) can be proved in a similar way.
Proof of Claim 7.21
The proof will proceed in several steps.
Step 1. Using (7.16) from Lemma 7.14, we have
Hence, by (7.25), it suffices to prove (with
![]() $\alpha $
as in (7.9)) that for every
$\alpha $
as in (7.9)) that for every
![]() $M_1\in \mathbb {S}_{\tau }^1(j)$
, one has
$M_1\in \mathbb {S}_{\tau }^1(j)$
, one has
Step 2. To prove (7.26), we define for any
![]() $s\in \mathbb {N}$
a new multiplier by
$s\in \mathbb {N}$
a new multiplier by
In view of (7.8), we may assume that
![]() $l^{\beta }(M_1)< l^{\beta }(M_2)$
. Then one can write
$l^{\beta }(M_1)< l^{\beta }(M_2)$
. Then one can write
 $$ \begin{align*} h_{M_1, M_2}^{M_2}(\xi)-h_{M_1, M_2}^{M_1}(\xi)=&\sum_{0\le s\le l^{\beta}(M_1)}\big(h_{M_1, M_2, s}^{M_2}(\xi)-h_{M_1, M_2, s}^{M_1}(\xi)\big)+\sum_{l^{\beta}(M_1)< s\le l^{\beta}(M_2)}h_{M_1, M_2, s}^{M_2}(\xi). \end{align*} $$
$$ \begin{align*} h_{M_1, M_2}^{M_2}(\xi)-h_{M_1, M_2}^{M_1}(\xi)=&\sum_{0\le s\le l^{\beta}(M_1)}\big(h_{M_1, M_2, s}^{M_2}(\xi)-h_{M_1, M_2, s}^{M_1}(\xi)\big)+\sum_{l^{\beta}(M_1)< s\le l^{\beta}(M_2)}h_{M_1, M_2, s}^{M_2}(\xi). \end{align*} $$
For sufficiently large
![]() $s\in \mathbb {N}$
, if
$s\in \mathbb {N}$
, if
![]() $l^{\beta }(M_1)\ge s$
, then by (7.8) we have
$l^{\beta }(M_1)\ge s$
, then by (7.8) we have
![]() $\log _{\tau }M_2\ge K_j^{-1}2^{s/\beta }\ge 2^{s/(2\beta )}$
. Similarly, if
$\log _{\tau }M_2\ge K_j^{-1}2^{s/\beta }\ge 2^{s/(2\beta )}$
. Similarly, if
![]() $l^{\beta }(M_2)\ge s$
, then
$l^{\beta }(M_2)\ge s$
, then
![]() $\log _{\tau }M_2\ge 2^{s/(2\beta )}$
. Thus, we set
$\log _{\tau }M_2\ge 2^{s/(2\beta )}$
. Thus, we set
![]() $N_s:=\tau ^{2^{s/(2\beta )}}$
for any
$N_s:=\tau ^{2^{s/(2\beta )}}$
for any
![]() $s\in \mathbb {N}$
and let
$s\in \mathbb {N}$
and let
The proof will be finished if we can show (with
![]() $\alpha $
and
$\alpha $
and
![]() $\delta $
as in (7.9)) that for every
$\delta $
as in (7.9)) that for every
![]() $f\in \ell ^2({\mathbb {Z}})$
and for every
$f\in \ell ^2({\mathbb {Z}})$
and for every
![]() $M_1\in \mathbb {S}_{\tau }^1(j)$
, and
$M_1\in \mathbb {S}_{\tau }^1(j)$
, and
![]() $0\le s\le l^{\beta }(M_1)$
, one has
$0\le s\le l^{\beta }(M_1)$
, one has
 $$ \begin{align} \|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}-h_{M_1, M_2, s}^{M_1}]f|\|_{\ell^2({\mathbb{Z}})} \lesssim_{\tau} 2^{-\delta s}(\log M_1)^{-\alpha}\|f\|_{\ell^2({\mathbb{Z}})}, \end{align} $$
$$ \begin{align} \|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}-h_{M_1, M_2, s}^{M_1}]f|\|_{\ell^2({\mathbb{Z}})} \lesssim_{\tau} 2^{-\delta s}(\log M_1)^{-\alpha}\|f\|_{\ell^2({\mathbb{Z}})}, \end{align} $$
and moreover, for every
![]() $s\in \mathbb {N}$
, one also has
$s\in \mathbb {N}$
, one also has
 $$ \begin{align} \|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}]f|\|_{\ell^2({\mathbb{Z}})} \lesssim_{\tau} s2^{-\delta s}\|f\|_{\ell^2({\mathbb{Z}})}. \end{align} $$
$$ \begin{align} \|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}]f|\|_{\ell^2({\mathbb{Z}})} \lesssim_{\tau} s2^{-\delta s}\|f\|_{\ell^2({\mathbb{Z}})}. \end{align} $$
Then summing (7.29) over
![]() $s\ge l^{\beta }(M_1)$
, we obtain the desired claim by (7.9).
$s\ge l^{\beta }(M_1)$
, we obtain the desired claim by (7.9).
Step 3. We now establish (7.28). If
![]() $N\in \{M_1, M_2\}$
and
$N\in \{M_1, M_2\}$
and
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
, then for
$(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
, then for
![]() $M_2\ge N_s$
, we note that
$M_2\ge N_s$
, we note that
 $$ \begin{align} \begin{split} \eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}(\xi)&=\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}(\xi)\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)+1}(\xi)\\ &=\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}(\xi)\eta_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}(\xi), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}(\xi)&=\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}(\xi)\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)+1}(\xi)\\ &=\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}(\xi)\eta_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}(\xi), \end{split} \end{align} $$
since
![]() $1\le j<r$
and
$1\le j<r$
and
![]() $v_{j, 2}\neq 0$
. Using (7.30), we may write
$v_{j, 2}\neq 0$
. Using (7.30), we may write
 $$ \begin{align} \begin{split} &\Phi_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}^{\Sigma_{s}}[G_{m_1}^1, \mathfrak m_{m_1, M_2}^1](\xi)\\ &\quad =\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak m_{m_1, M_2}^1\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}](\xi) \times\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1](\xi), \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\Phi_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}^{\Sigma_{s}}[G_{m_1}^1, \mathfrak m_{m_1, M_2}^1](\xi)\\ &\quad =\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak m_{m_1, M_2}^1\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}](\xi) \times\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1](\xi), \end{split} \end{align} $$
for sufficiently large s such that
![]() $0\le s\le l^{\beta }(M_1)$
, which in turn guarantees that
$0\le s\le l^{\beta }(M_1)$
, which in turn guarantees that
![]() $M_2> N_{s}$
as we have seen in the previous step. Denote
$M_2> N_{s}$
as we have seen in the previous step. Denote
 $$ \begin{gather*} I(m_1, M_2):= T_{{\mathbb{Z}}}\left[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}\Big[1, \sum_{N=l^{\beta}(M_1)}^{l^{\beta}(M_2)-1}\mathfrak m_{m_1, M_2}^1\mathrm{D}_N\big(\eta_{\le -n_{M_1, M_2}^{v_j}(N)}\big)\Big]\right], \end{gather*} $$
$$ \begin{gather*} I(m_1, M_2):= T_{{\mathbb{Z}}}\left[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}\Big[1, \sum_{N=l^{\beta}(M_1)}^{l^{\beta}(M_2)-1}\mathfrak m_{m_1, M_2}^1\mathrm{D}_N\big(\eta_{\le -n_{M_1, M_2}^{v_j}(N)}\big)\Big]\right], \end{gather*} $$
where (see definitions (7.3) and (7.4))
Using the factorization from (7.31), one sees
 $$ \begin{align*} &\|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}-h_{M_1, M_2, s}^{M_1}]f|\|_{\ell^2({\mathbb{Z}})}\\ &\quad \le\sum_{m_1\in{\mathbb{Z}}}\|I(m_1, M_2)\|_{\ell^2({\mathbb{Z}})\to\ell^2({\mathbb{Z}}; \ell^{\infty}_{M_2}(\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)))}\chi_{M_1}(m_1)\Big\| T_{{\mathbb{Z}}}\big[\Phi_{ \le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1]\big]f\Big\|_{\ell^2({\mathbb{Z}})}. \end{align*} $$
$$ \begin{align*} &\|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}-h_{M_1, M_2, s}^{M_1}]f|\|_{\ell^2({\mathbb{Z}})}\\ &\quad \le\sum_{m_1\in{\mathbb{Z}}}\|I(m_1, M_2)\|_{\ell^2({\mathbb{Z}})\to\ell^2({\mathbb{Z}}; \ell^{\infty}_{M_2}(\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)))}\chi_{M_1}(m_1)\Big\| T_{{\mathbb{Z}}}\big[\Phi_{ \le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1]\big]f\Big\|_{\ell^2({\mathbb{Z}})}. \end{align*} $$
Using the Ionescu–Wainger multiplier theory (see Theorem 6.5), we conclude that
with
![]() $\alpha $
as in (7.9), since using standard square function continuous arguments we have
$\alpha $
as in (7.9), since using standard square function continuous arguments we have
 $$ \begin{align*} \begin{gathered} \bigg\|\bigg(\sum_{M_2\in \tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)} \Big|T_{\mathbb{R}}\Big[\sum_{N=l^{\beta}(M_1)}^{l^{\beta}(M_2)-1}\mathfrak m_{m_1, M_2}^1\mathrm{D}_N\big(\eta_{\le -n_{M_1, M_2}^{v_j}(N)}\big)\Big]f\Big|^2\bigg)^{1/2} \bigg\|_{L^2(\mathbb{R})} \lesssim (\log M_1)^{-\alpha}\|f\|_{L^2(\mathbb{R})}. \end{gathered} \end{align*} $$
$$ \begin{align*} \begin{gathered} \bigg\|\bigg(\sum_{M_2\in \tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)} \Big|T_{\mathbb{R}}\Big[\sum_{N=l^{\beta}(M_1)}^{l^{\beta}(M_2)-1}\mathfrak m_{m_1, M_2}^1\mathrm{D}_N\big(\eta_{\le -n_{M_1, M_2}^{v_j}(N)}\big)\Big]f\Big|^2\bigg)^{1/2} \bigg\|_{L^2(\mathbb{R})} \lesssim (\log M_1)^{-\alpha}\|f\|_{L^2(\mathbb{R})}. \end{gathered} \end{align*} $$
Thus, by the Cauchy–Schwarz inequality, Plancherel’s theorem and inequality (5.48), we obtain
 $$ \begin{align*} &\|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}-h_{M_1, M_2, s}^{M_1}]f|\|_{\ell^2({\mathbb{Z}})}\\ &\quad \lesssim (\log M_1)^{-\alpha} \Big\|\Big(\sum_{m_1\in{\mathbb{Z}}}\chi_{M_1}(m_1) \big|T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1]\big]f\big|^2\Big)^{1/2}\Big\|_{\ell^2({\mathbb{Z}})} \\ &\quad \lesssim_{\tau} 2^{-\delta s}(\log M_1)^{-\alpha}\|f\|_{\ell^2({\mathbb{Z}})} \end{align*} $$
$$ \begin{align*} &\|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{M_2}-h_{M_1, M_2, s}^{M_1}]f|\|_{\ell^2({\mathbb{Z}})}\\ &\quad \lesssim (\log M_1)^{-\alpha} \Big\|\Big(\sum_{m_1\in{\mathbb{Z}}}\chi_{M_1}(m_1) \big|T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1]\big]f\big|^2\Big)^{1/2}\Big\|_{\ell^2({\mathbb{Z}})} \\ &\quad \lesssim_{\tau} 2^{-\delta s}(\log M_1)^{-\alpha}\|f\|_{\ell^2({\mathbb{Z}})} \end{align*} $$
with
![]() $\alpha $
and
$\alpha $
and
![]() $\delta $
as in (7.9), which yields (7.28).
$\delta $
as in (7.9), which yields (7.28).
Step 4. We now establish (7.29). Using notation from the previous step and denoting
 $$ \begin{gather*} J(m_1, M_2):= T_{{\mathbb{Z}}}\Big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}\big[1, \mathfrak m_{m_1, M_2}^1\eta_{\le n_{M_1, M_2}^{v_j, \beta}(M_2)}\big)\big]\Big], \end{gather*} $$
$$ \begin{gather*} J(m_1, M_2):= T_{{\mathbb{Z}}}\Big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}\big[1, \mathfrak m_{m_1, M_2}^1\eta_{\le n_{M_1, M_2}^{v_j, \beta}(M_2)}\big)\big]\Big], \end{gather*} $$
and again using the factorization from (7.31), one sees
 $$ \begin{align*} \|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{ M_2}]f|\|_{\ell^2({\mathbb{Z}})} &\le\sum_{m_1\in{\mathbb{Z}}}\|J(m_1, M_2)\|_{\ell^2({\mathbb{Z}})\to\ell^2({\mathbb{Z}}; \ell^{\infty}_{M_2}(\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)))}\chi_{M_1}(m_1)\\ &\quad \times \Big\| T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1]\big]f\Big\|_{\ell^2({\mathbb{Z}})}. \end{align*} $$
$$ \begin{align*} \|\sup_{M_2\in\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)}|T_{{\mathbb{Z}}}[h_{M_1, M_2, s}^{ M_2}]f|\|_{\ell^2({\mathbb{Z}})} &\le\sum_{m_1\in{\mathbb{Z}}}\|J(m_1, M_2)\|_{\ell^2({\mathbb{Z}})\to\ell^2({\mathbb{Z}}; \ell^{\infty}_{M_2}(\tilde{\mathbb{S}}_{\tau, M_1}^2(j; s)))}\chi_{M_1}(m_1)\\ &\quad \times \Big\| T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G_{m_1}^1, 1]\big]f\Big\|_{\ell^2({\mathbb{Z}})}. \end{align*} $$
Using the Ionescu–Wainger multiplier theory (see Theorem 6.14), we conclude that
Then proceeding as in the previous step, we obtain (7.29). This completes the proof of Claim 7.21.
7.5 Transition estimates
Our aim will be to understand the final approximation, which will allow us to apply the oscillation Ionescu–Wainger theory (see Theorem 6.37) from Section 6.
Claim 7.32. For every
![]() $1\le j<r$
and for every
$1\le j<r$
and for every
![]() $M_1\in \mathbb {S}_{\tau }^1(j)$
, one has
$M_1\in \mathbb {S}_{\tau }^1(j)$
, one has
with
![]() $\alpha $
as in (7.9), where
$\alpha $
as in (7.9), where
![]() $h_{M_1, M_2}^{N}$
was defined in (7.23) and
$h_{M_1, M_2}^{N}$
was defined in (7.23) and
 $$ \begin{align} \tilde{h}_{M_1, M_2}^{N}:=\Phi_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}^{\Sigma_{\le l^{\beta}(N)}}[G, \mathfrak m_{M_1, M_2}], \qquad N\ge1. \end{align} $$
$$ \begin{align} \tilde{h}_{M_1, M_2}^{N}:=\Phi_{\le -n_{M_1, M_2}^{v_j, \beta}(N)}^{\Sigma_{\le l^{\beta}(N)}}[G, \mathfrak m_{M_1, M_2}], \qquad N\ge1. \end{align} $$
The same estimate holds when
![]() $j=r=1$
, as long as
$j=r=1$
, as long as
![]() $\log M_1\le \log M_2$
.
$\log M_1\le \log M_2$
.
The case
![]() $j=r\ge 2$
requires a minor modification. Keeping in mind that
$j=r\ge 2$
requires a minor modification. Keeping in mind that
![]() $\log M_2\lesssim \log M_1$
, it suffices to establish an analogue of (7.33). Namely, one has
$\log M_2\lesssim \log M_1$
, it suffices to establish an analogue of (7.33). Namely, one has
We only present the proof of (7.33); inequality (7.35) can be proved in a similar way.
Proof of Claim 7.32
The proof will proceed in several steps as before. Write
 $$ \begin{align*} h_{M_1, M_2}^{M_1}-\tilde{h}_{M_1, M_2}^{M_1}=\sum_{0\le s\le l^{\beta}(M_1)}h_{M_1, M_2, s}^{M_1}-\tilde{h}_{M_1, M_2, s}^{M_1}, \end{align*} $$
$$ \begin{align*} h_{M_1, M_2}^{M_1}-\tilde{h}_{M_1, M_2}^{M_1}=\sum_{0\le s\le l^{\beta}(M_1)}h_{M_1, M_2, s}^{M_1}-\tilde{h}_{M_1, M_2, s}^{M_1}, \end{align*} $$
where
![]() $h_{M_1, M_2, s}^{M_1}$
was defined in (7.27) and
$h_{M_1, M_2, s}^{M_1}$
was defined in (7.27) and
Then it suffices to show that for sufficiently large s such that
![]() $0\le s\le l^{\beta }(M_1)$
, we have
$0\le s\le l^{\beta }(M_1)$
, we have
with
![]() $\alpha $
and
$\alpha $
and
![]() $\delta $
as in (7.9), which will clearly imply (7.33).
$\delta $
as in (7.9), which will clearly imply (7.33).
Step 1. Using (7.30), in a similar way as in (7.31), we may write
where
By Theorem 6.14, we may conclude
 $$ \begin{align} \begin{gathered} \Big\|T_{{\mathbb{Z}}}\Big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \widetilde{\mathfrak m}_{M_1, M_2}]\Big]\Big\|_{\ell^2({\mathbb{Z}})\to \ell^2({\mathbb{Z}}); \ell^{\infty}_{M_2}(\mathbb{S}_{\tau}^2(j;M_1))} \lesssim_{\tau} s. \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} \Big\|T_{{\mathbb{Z}}}\Big[\Phi_{\le -n_{M_1, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \widetilde{\mathfrak m}_{M_1, M_2}]\Big]\Big\|_{\ell^2({\mathbb{Z}})\to \ell^2({\mathbb{Z}}); \ell^{\infty}_{M_2}(\mathbb{S}_{\tau}^2(j;M_1))} \lesssim_{\tau} s. \end{gathered} \end{align} $$
By Plancherel’s theorem and inequality (5.47), we obtain
 $$ \begin{align} \Big\|T_{{\mathbb{Z}}}\Big[\Phi_{ \le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G, 1]\Big]f\Big\|_{\ell^2({\mathbb{Z}})} \lesssim_{\tau} 2^{-\delta s}\|f\|_{\ell^2({\mathbb{Z}})}. \end{align} $$
$$ \begin{align} \Big\|T_{{\mathbb{Z}}}\Big[\Phi_{ \le -n_{M_1, N_s}^{v_j, \beta}(N_s)+1}^{\Sigma_{s}}[G, 1]\Big]f\Big\|_{\ell^2({\mathbb{Z}})} \lesssim_{\tau} 2^{-\delta s}\|f\|_{\ell^2({\mathbb{Z}})}. \end{align} $$
Inequalities (7.40) and (7.41) and (7.38) imply
Step 2. We now establish (7.37). For
![]() $0\le s\le l^{\beta }(M_1)$
, we note that
$0\le s\le l^{\beta }(M_1)$
, we note that
 $$ \begin{align*} h_{M_1, M_2, s}^{M_1}(\xi) &=\sum_{a/q\in \Sigma_{s}}\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(M_1)}(\xi-a/q)\sum_{r_1=1}^qG_{r_1}^1(a/q)\\ &\quad \times \sum_{m_1\in{\mathbb{Z}}} \mathfrak m_{qm_1+r_1, M_2}^1(\xi-a/q) \chi_{M_1}(qm_1+r_1). \end{align*} $$
$$ \begin{align*} h_{M_1, M_2, s}^{M_1}(\xi) &=\sum_{a/q\in \Sigma_{s}}\eta_{\le -n_{M_1, M_2}^{v_j, \beta}(M_1)}(\xi-a/q)\sum_{r_1=1}^qG_{r_1}^1(a/q)\\ &\quad \times \sum_{m_1\in{\mathbb{Z}}} \mathfrak m_{qm_1+r_1, M_2}^1(\xi-a/q) \chi_{M_1}(qm_1+r_1). \end{align*} $$
Introducing
![]() $\theta :=\xi -a/q$
,
$\theta :=\xi -a/q$
,
![]() $U_1:=\frac {\tau ^{-1}M_1-r_1}{q}$
and
$U_1:=\frac {\tau ^{-1}M_1-r_1}{q}$
and
![]() $V_1:=\frac {M_1-r_1}{q}$
, one can expand
$V_1:=\frac {M_1-r_1}{q}$
, one can expand
 $$ \begin{align*} \mathfrak m_{qm_1+r_1, M_2}^1(\theta)=\frac{1}{1-\tau^{-1}} \int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qm_1+r_1, M_2y_2))dy_2, \end{align*} $$
$$ \begin{align*} \mathfrak m_{qm_1+r_1, M_2}^1(\theta)=\frac{1}{1-\tau^{-1}} \int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qm_1+r_1, M_2y_2))dy_2, \end{align*} $$
and by the fundamental theorem of calculus, one can write
 $$ \begin{align*} &\sum_{\lfloor U_1\rfloor<m_1\le \lfloor V_1\rfloor}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qm_1+r_1, M_2y_2))dy_2-\int_{U_1}^{V_1}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))dy_2dy_1\\ &\qquad=\sum_{\lfloor U_1\rfloor<m_1\le \lfloor V_1\rfloor}\int_{m_1-1}^{m_1}\int_{y_1}^{m_1}\int_{\tau^{-1}}^12\pi i q\theta(\partial_1P)(qt+r_1, M_2 y_2)\boldsymbol{e}(P_{\theta}(qt+r_1, M_2y_2))dy_2dtdy_1\\ &\qquad\quad+\Big(\int_{\lfloor U_1\rfloor}^{U_1}-\int_{\lfloor V_1\rfloor}^{V_1}\Big)\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))dy_2dy_1. \end{align*} $$
$$ \begin{align*} &\sum_{\lfloor U_1\rfloor<m_1\le \lfloor V_1\rfloor}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qm_1+r_1, M_2y_2))dy_2-\int_{U_1}^{V_1}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))dy_2dy_1\\ &\qquad=\sum_{\lfloor U_1\rfloor<m_1\le \lfloor V_1\rfloor}\int_{m_1-1}^{m_1}\int_{y_1}^{m_1}\int_{\tau^{-1}}^12\pi i q\theta(\partial_1P)(qt+r_1, M_2 y_2)\boldsymbol{e}(P_{\theta}(qt+r_1, M_2y_2))dy_2dtdy_1\\ &\qquad\quad+\Big(\int_{\lfloor U_1\rfloor}^{U_1}-\int_{\lfloor V_1\rfloor}^{V_1}\Big)\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))dy_2dy_1. \end{align*} $$
By the change of variable, we have
 $$ \begin{align*} \int_{U_1}^{V_1}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))dy_2dy_1=\frac{M_1(1-\tau^{-1})^2}{q}\mathfrak m_{M_1, M_2}(\theta). \end{align*} $$
$$ \begin{align*} \int_{U_1}^{V_1}\int_{\tau^{-1}}^1\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))dy_2dy_1=\frac{M_1(1-\tau^{-1})^2}{q}\mathfrak m_{M_1, M_2}(\theta). \end{align*} $$
We now define new multipliers
 $$ \begin{align*} & \mathfrak g_{M_1, M_2}^{r_1, 1}(\theta)\\ &\! :=\sum_{\lfloor U_1\rfloor<m_1\le \lfloor V_1\rfloor}\int_{m_1-1}^{m_1}\int_{y_1}^{m_1}\int_{\tau^{-1}}^1\frac{2\pi i q(\log M_1)^{\beta}(\partial_1P)(qt+r_1, M_2y_2)\boldsymbol{e}(P_{\theta}(qt+r_1, M_2y_2))}{(1-\tau^{-1})M_1^{v_{j, 1}}M_2^{v_{j,2}}|(\tau^{-1}M_1, M_1]\cap{\mathbb{Z}}|}dy_2dtdy_1, \end{align*} $$
$$ \begin{align*} & \mathfrak g_{M_1, M_2}^{r_1, 1}(\theta)\\ &\! :=\sum_{\lfloor U_1\rfloor<m_1\le \lfloor V_1\rfloor}\int_{m_1-1}^{m_1}\int_{y_1}^{m_1}\int_{\tau^{-1}}^1\frac{2\pi i q(\log M_1)^{\beta}(\partial_1P)(qt+r_1, M_2y_2)\boldsymbol{e}(P_{\theta}(qt+r_1, M_2y_2))}{(1-\tau^{-1})M_1^{v_{j, 1}}M_2^{v_{j,2}}|(\tau^{-1}M_1, M_1]\cap{\mathbb{Z}}|}dy_2dtdy_1, \end{align*} $$
and finally
 $$ \begin{align*} \mathfrak g_{M_1, M_2}^{r_1,2}(\theta):= \Big(\int_{\lfloor U_1\rfloor}^{U_1}-\int_{\lfloor V_1\rfloor}^{V_1}\Big)\int_{\tau^{-1}}^1\frac{\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))}{(1-\tau^{-1})|(\tau^{-1}M_1, M_1]\cap{\mathbb{Z}}|}dy_2dy_1. \end{align*} $$
$$ \begin{align*} \mathfrak g_{M_1, M_2}^{r_1,2}(\theta):= \Big(\int_{\lfloor U_1\rfloor}^{U_1}-\int_{\lfloor V_1\rfloor}^{V_1}\Big)\int_{\tau^{-1}}^1\frac{\boldsymbol{e}(P_{\theta}(qy_1+r_1, M_2y_2))}{(1-\tau^{-1})|(\tau^{-1}M_1, M_1]\cap{\mathbb{Z}}|}dy_2dy_1. \end{align*} $$
Then with these definitions, we can write
 $$ \begin{align*} h_{M_1, M_2, s}^{M_1}(\xi)-\tilde{h}_{M_1, M_2,s}^{M_1}(\xi)= \gamma_{\tau, M_1}\tilde{h}_{M_1, M_2,s}^{M_1}(\xi) +\sum_{\ell\in[2]}\sum_{a/q\in \Sigma_{s}}\sum_{r_1=1}^q G_{r_1}^1(a/q) \mathfrak h_{M_1, M_2}^{r_1, \ell}(\xi-a/q), \end{align*} $$
$$ \begin{align*} h_{M_1, M_2, s}^{M_1}(\xi)-\tilde{h}_{M_1, M_2,s}^{M_1}(\xi)= \gamma_{\tau, M_1}\tilde{h}_{M_1, M_2,s}^{M_1}(\xi) +\sum_{\ell\in[2]}\sum_{a/q\in \Sigma_{s}}\sum_{r_1=1}^q G_{r_1}^1(a/q) \mathfrak h_{M_1, M_2}^{r_1, \ell}(\xi-a/q), \end{align*} $$
where
![]() $\gamma _{\tau , M_1}:=\frac {\{M_1\}-\{\tau ^{-1}M_1\}}{|(\tau ^{-1}M_1, M_1]\cap {\mathbb {Z}}|}$
and
$\gamma _{\tau , M_1}:=\frac {\{M_1\}-\{\tau ^{-1}M_1\}}{|(\tau ^{-1}M_1, M_1]\cap {\mathbb {Z}}|}$
and
and
![]() $\varrho _{\le n}(\theta ):=(2^{-n}\theta )\eta _{\le n}(\theta )$
. For
$\varrho _{\le n}(\theta ):=(2^{-n}\theta )\eta _{\le n}(\theta )$
. For
![]() $\ell \in [2]$
, we have
$\ell \in [2]$
, we have
Finally, using Theorem 6.14 for each
![]() $\ell \in [2]$
, we conclude
$\ell \in [2]$
, we conclude
 $$ \begin{align*} \Big\|\sup_{M_2\in\mathbb{S}_{\tau}^2(j;M_1)}\Big|T_{{\mathbb{Z}}}\Big[\sum_{\ell\in[2]}\sum_{a/q\in \Sigma_{s}}\sum_{r_1=1}^q G_{r_1}^1(a/q) \mathfrak h_{M_1, M_2}^{r_1, \ell}(\cdot-a/q)\Big]f\Big|\Big\|_{\ell^2({\mathbb{Z}})}\lesssim 2^{-\delta s} M_1^{-3/4}\|f\|_{\ell^2({\mathbb{Z}})}. \end{align*} $$
$$ \begin{align*} \Big\|\sup_{M_2\in\mathbb{S}_{\tau}^2(j;M_1)}\Big|T_{{\mathbb{Z}}}\Big[\sum_{\ell\in[2]}\sum_{a/q\in \Sigma_{s}}\sum_{r_1=1}^q G_{r_1}^1(a/q) \mathfrak h_{M_1, M_2}^{r_1, \ell}(\cdot-a/q)\Big]f\Big|\Big\|_{\ell^2({\mathbb{Z}})}\lesssim 2^{-\delta s} M_1^{-3/4}\|f\|_{\ell^2({\mathbb{Z}})}. \end{align*} $$
This in turn, combined with (7.42), implies (7.37), and the proof of Claim 7.32 is established.
7.6 All together: Proof of Theorem 7.6
We begin with a useful auxiliary lemma.
Lemma 7.43. For every
![]() $p\in (1, \infty )$
and every
$p\in (1, \infty )$
and every
![]() $j\in [r]$
, there exists a constant
$j\in [r]$
, there exists a constant
![]() $\delta _p\in (0, 1)$
such that for every
$\delta _p\in (0, 1)$
such that for every
![]() $f\in \ell ^p({\mathbb {Z}})$
and
$f\in \ell ^p({\mathbb {Z}})$
and
![]() $s\in \mathbb {N}$
, one has
$s\in \mathbb {N}$
, one has
where
![]() $N_s:=\tau ^{2^{s/(2\beta )}}$
for any
$N_s:=\tau ^{2^{s/(2\beta )}}$
for any
![]() $s\in \mathbb {N}$
, and
$s\in \mathbb {N}$
, and
![]() $\Pi _s^{\beta }(\xi ):=\prod _{u\in S_P}\eta _{\le -n_{N_s, N_s}^{u, \beta }(N_s)+1}(\xi )$
with
$\Pi _s^{\beta }(\xi ):=\prod _{u\in S_P}\eta _{\le -n_{N_s, N_s}^{u, \beta }(N_s)+1}(\xi )$
with
![]() $\beta>0$
from (7.9).
$\beta>0$
from (7.9).
Proof. We may assume that
![]() $s\ge 0$
is large; otherwise, there is nothing to prove. Inequality (7.44) for
$s\ge 0$
is large; otherwise, there is nothing to prove. Inequality (7.44) for
![]() $p=2$
with
$p=2$
with
![]() $\delta _2=\delta $
as in Proposition 5.46 follows by Plancherel’s theorem from inequality (5.47) and the disjointness of supports of
$\delta _2=\delta $
as in Proposition 5.46 follows by Plancherel’s theorem from inequality (5.47) and the disjointness of supports of
![]() $\Pi _s^{\beta }(\xi -a/q)$
whenever
$\Pi _s^{\beta }(\xi -a/q)$
whenever
![]() $a/q\in \Sigma _{s}$
.
$a/q\in \Sigma _{s}$
.
We now prove (7.44) for
![]() $p\neq 2$
. We shall proceed in four steps.
$p\neq 2$
. We shall proceed in four steps.
Step 1. Let
![]() $M\simeq 2^{10C_{\rho }2^{10\rho s}}$
define
$M\simeq 2^{10C_{\rho }2^{10\rho s}}$
define
By the Ionescu–Wainger multiplier theorem (see Theorem 6.5), one has
whenever
![]() $u\in \{p_0, p_0'\}$
. We will prove
$u\in \{p_0, p_0'\}$
. We will prove
and
Assuming momentarily that (7.46) and (7.47) hold, then (7.45) and the triangle inequality yield
whenever
![]() $u\in \{p_0, p_0'\}$
. Then interpolation between (7.44) for
$u\in \{p_0, p_0'\}$
. Then interpolation between (7.44) for
![]() $p=2$
(that we have shown with
$p=2$
(that we have shown with
![]() $\delta _2=\delta $
) and (7.48) gives (7.44) for all
$\delta _2=\delta $
) and (7.48) gives (7.44) for all
![]() $p\in (1, \infty )$
.
$p\in (1, \infty )$
.
Step 2. We now establish (7.46). For
![]() $p=2$
, it will suffice to show that
$p=2$
, it will suffice to show that
Then by (7.49) and Plancherel’s theorem, we obtain for sufficiently large
![]() $s\in \mathbb {N}$
that
$s\in \mathbb {N}$
that
Moreover, for
![]() $u\in \{p_0, p_0'\}$
, we have the trivial estimate
$u\in \{p_0, p_0'\}$
, we have the trivial estimate
due to (6.4). Interpolating (7.50) and (7.51) gives (7.46).
Step 3. To prove (7.49), we proceed as in the proof of Lemma 7.14 and show that
whenever
![]() $a/q\in \Sigma _s$
and
$a/q\in \Sigma _s$
and
![]() $|\xi -{a}/{q}|\le \min _{u\in S_P}\{(\log _{\tau } N_s)^{\beta }N_s^{-u_1}N_s^{-u_2}\}.$
Then (7.52) immediately gives (7.49), since
$|\xi -{a}/{q}|\le \min _{u\in S_P}\{(\log _{\tau } N_s)^{\beta }N_s^{-u_1}N_s^{-u_2}\}.$
Then (7.52) immediately gives (7.49), since
![]() $q \le 2^{C_{\rho }2^{\rho s}}$
if
$q \le 2^{C_{\rho }2^{\rho s}}$
if
![]() $a/q\in \Sigma _s$
. To verify (7.52), we use Lemma 2.7 twice, which can be applied, since the derivatives
$a/q\in \Sigma _s$
. To verify (7.52), we use Lemma 2.7 twice, which can be applied, since the derivatives
![]() $\partial _{m_1}f$
and
$\partial _{m_1}f$
and
![]() $\partial _{m_2}f$
of
$\partial _{m_2}f$
of
![]() $f(m_1, m_2)=P_{\xi -a/q}(qm_1+r_1, qm_2+r_2)$
satisfy
$f(m_1, m_2)=P_{\xi -a/q}(qm_1+r_1, qm_2+r_2)$
satisfy
for sufficiently large
![]() $s\in \mathbb {N}$
, since
$s\in \mathbb {N}$
, since
![]() $M\le N_s^{1/5}$
,
$M\le N_s^{1/5}$
,
![]() $q \le 2^{C_{\rho }2^{\rho s}}$
and
$q \le 2^{C_{\rho }2^{\rho s}}$
and
![]() $\rho \beta \le 1/10$
by (7.10), and we are done.
$\rho \beta \le 1/10$
by (7.10), and we are done.
Step 4. We now establish (7.47). Assume that
![]() $p=2$
and observe that
$p=2$
and observe that
for sufficiently large
![]() $s\in \mathbb {N}$
, since
$s\in \mathbb {N}$
, since
![]() $M\simeq 2^{10C_{\rho }2^{10\rho s}}$
, and
$M\simeq 2^{10C_{\rho }2^{10\rho s}}$
, and
![]() $\rho \beta < 1/1000$
. Using this bound and Plancherel’s theorem, we see that
$\rho \beta < 1/1000$
. Using this bound and Plancherel’s theorem, we see that
Moreover, by (6.4), for
![]() $u\in \{p_0, p_0'\}$
, we have the trivial estimate
$u\in \{p_0, p_0'\}$
, we have the trivial estimate
Interpolation between (7.53) and (7.54) yields (7.47), and the proof of Lemma 7.43 is complete.
Recalling the definition of
![]() $\tilde {h}_{M_1, M_2}^{M_1}$
from (7.34), we now prove the following claim:
$\tilde {h}_{M_1, M_2}^{M_1}$
from (7.34), we now prove the following claim:
Claim 7.55. For every
![]() $p\in (1, \infty )$
and every
$p\in (1, \infty )$
and every
![]() $1\le j<r$
and for every
$1\le j<r$
and for every
![]() $f\in \ell ^p({\mathbb {Z}})$
, one has
$f\in \ell ^p({\mathbb {Z}})$
, one has
The same estimate holds when
![]() $j=r=1$
, as long as
$j=r=1$
, as long as
![]() $\log M_1\le \log M_2$
.
$\log M_1\le \log M_2$
.
When
![]() $j=r\ge 2$
, in view of (7.35), we will be able to reduce the problem to the following:
$j=r\ge 2$
, in view of (7.35), we will be able to reduce the problem to the following:
We will only prove (7.56); the proof of (7.57) will follow in a similar way. We omit details.
Proof of Claim 7.55
The proof will consist of two steps to make the argument clear.
Step 1. Similarly as in Claim 7.21, we define
![]() $N_s:=\tau ^{2^{s/(2\beta )}}$
for any
$N_s:=\tau ^{2^{s/(2\beta )}}$
for any
![]() $s\in \mathbb {N}$
and introduce
$s\in \mathbb {N}$
and introduce
For each
![]() $(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
, we have
$(M_1, M_2)\in \mathbb {S}_{\tau }(j)$
, we have
![]() $M_1^{v_{j, 1}}M_2^{v_{j, 2}}\ge M_1^{u_{1}}M_2^{u_{2}}$
for every
$M_1^{v_{j, 1}}M_2^{v_{j, 2}}\ge M_1^{u_{1}}M_2^{u_{2}}$
for every
![]() $u=(u_1, u_2)\in S_P$
. Hence,
$u=(u_1, u_2)\in S_P$
. Hence,
 $$ \begin{align} \begin{split} \eta_{\le -n_{M_1, M_2}^{v_{j}, \beta}(M_1)}(\xi)&=\eta_{\le -n_{M_1, M_2}^{v_{j}, \beta}(M_1)}(\xi)\prod_{u\in S_P}\eta_{\le -n_{M_1, M_2}^{u, \beta}(M_1)+1}(\xi)\\ &=\eta_{\le -n_{M_1, M_2}^{v_{j}, \beta}(M_1)}(\xi)\Pi_s^{\beta}(\xi) \end{split} \end{align} $$
$$ \begin{align} \begin{split} \eta_{\le -n_{M_1, M_2}^{v_{j}, \beta}(M_1)}(\xi)&=\eta_{\le -n_{M_1, M_2}^{v_{j}, \beta}(M_1)}(\xi)\prod_{u\in S_P}\eta_{\le -n_{M_1, M_2}^{u, \beta}(M_1)+1}(\xi)\\ &=\eta_{\le -n_{M_1, M_2}^{v_{j}, \beta}(M_1)}(\xi)\Pi_s^{\beta}(\xi) \end{split} \end{align} $$
holds for sufficiently large
![]() $s\in \mathbb {N}$
so that
$s\in \mathbb {N}$
so that
![]() $0\le s\le l^{\beta }(M_1)$
, where
$0\le s\le l^{\beta }(M_1)$
, where
![]() $\Pi _s^{\beta }$
was defined in Lemma 7.43.
$\Pi _s^{\beta }$
was defined in Lemma 7.43.
The proof of (7.56) will be completed if we show (with
![]() $\tilde {h}_{M_1, M_2, s}^{M_1}$
defined in (7.36)) that for every
$\tilde {h}_{M_1, M_2, s}^{M_1}$
defined in (7.36)) that for every
![]() $p\in (1, \infty )$
, there is
$p\in (1, \infty )$
, there is
![]() $\delta _p\in (0, 1)$
such that for all
$\delta _p\in (0, 1)$
such that for all
![]() $f\in \ell ^p({\mathbb {Z}})$
, we have
$f\in \ell ^p({\mathbb {Z}})$
, we have
Using
![]() $\widetilde {\mathfrak m}_{M_1, M_2}$
from (7.39) and (7.58), we may write
$\widetilde {\mathfrak m}_{M_1, M_2}$
from (7.39) and (7.58), we may write
By Lemma 7.43, for sufficiently large
![]() $s\in \mathbb {N}$
, we have
$s\in \mathbb {N}$
, we have
Using factorization (7.60) and (7.61), it suffices to prove that
 $$ \begin{align*} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\tilde{\mathbb{S}}_{\tau}(j,s))} \|O_{I, J}(T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \widetilde{\mathfrak m}_{M_1, M_2}]\big]f & : (M_1, M_2)\in\tilde{\mathbb{S}}_{\tau}(j,s))\|_{\ell^p({\mathbb{Z}})}\\ & \lesssim_{p, \tau} s\|f\|_{\ell^p({\mathbb{Z}})}, \end{align*} $$
$$ \begin{align*} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\tilde{\mathbb{S}}_{\tau}(j,s))} \|O_{I, J}(T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \widetilde{\mathfrak m}_{M_1, M_2}]\big]f & : (M_1, M_2)\in\tilde{\mathbb{S}}_{\tau}(j,s))\|_{\ell^p({\mathbb{Z}})}\\ & \lesssim_{p, \tau} s\|f\|_{\ell^p({\mathbb{Z}})}, \end{align*} $$
which will readily imply (7.59).
Step 2. Appealing to the Ionescu–Wainger multiplier theory (see Theorem 6.37) for oscillation semi-norms developed in the previous section, we see that
 $$ \begin{align*} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\tilde{\mathbb{S}}_{\tau}(j,s))}\|O_{I, J}(T_{{\mathbb{Z}}}[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak m_{M_1, M_2}]]f & : (M_1, M_2)\in\tilde{\mathbb{S}}_{\tau}(j,s))\|_{\ell^p({\mathbb{Z}})} \\ &\lesssim_{p, \tau} s\|f\|_{\ell^p({\mathbb{Z}})}. \end{align*} $$
$$ \begin{align*} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\tilde{\mathbb{S}}_{\tau}(j,s))}\|O_{I, J}(T_{{\mathbb{Z}}}[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak m_{M_1, M_2}]]f & : (M_1, M_2)\in\tilde{\mathbb{S}}_{\tau}(j,s))\|_{\ell^p({\mathbb{Z}})} \\ &\lesssim_{p, \tau} s\|f\|_{\ell^p({\mathbb{Z}})}. \end{align*} $$
Hence, the last inequality from the previous step will be proved if we establish
 $$ \begin{align} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\tilde{\mathbb{S}}_{\tau}(j,s))}\|O_{I, J}(T_{{\mathbb{Z}}}[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak g_{M_1, M_2}]]f & : (M_1, M_2)\in\tilde{\mathbb{S}}_{\tau}(j,s))\|_{\ell^p({\mathbb{Z}})} \nonumber\\ &\lesssim_{p, \tau} \|f\|_{\ell^p({\mathbb{Z}})}, \end{align} $$
$$ \begin{align} \sup_{J\in{\mathbb{Z}}_+}\sup_{I\in\mathfrak S_J(\tilde{\mathbb{S}}_{\tau}(j,s))}\|O_{I, J}(T_{{\mathbb{Z}}}[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak g_{M_1, M_2}]]f & : (M_1, M_2)\in\tilde{\mathbb{S}}_{\tau}(j,s))\|_{\ell^p({\mathbb{Z}})} \nonumber\\ &\lesssim_{p, \tau} \|f\|_{\ell^p({\mathbb{Z}})}, \end{align} $$
with
![]() $\mathfrak g_{M_1, M_2}=\widetilde {\mathfrak m}_{M_1, M_2}-\mathfrak m_{M_1, M_2}$
. By the van der Corput estimate (Proposition 2.6) for
$\mathfrak g_{M_1, M_2}=\widetilde {\mathfrak m}_{M_1, M_2}-\mathfrak m_{M_1, M_2}$
. By the van der Corput estimate (Proposition 2.6) for
![]() $\mathfrak m_{M_1, M_2}$
, there exists
$\mathfrak m_{M_1, M_2}$
, there exists
![]() $\delta _0>0$
(in fact,
$\delta _0>0$
(in fact,
![]() $\delta _0\simeq (\deg P)^{-1}$
) such that
$\delta _0\simeq (\deg P)^{-1}$
) such that
for
![]() $(M_1, M_2)\in \tilde {\mathbb {S}}_{\tau }(j)$
, since
$(M_1, M_2)\in \tilde {\mathbb {S}}_{\tau }(j)$
, since
Then by Plancherel’s theorem combined with a simple interpolation and Theorem 6.5, we conclude that for every
![]() $p\in (1, \infty )$
, there is
$p\in (1, \infty )$
, there is
![]() $\alpha _p>10$
such that for every
$\alpha _p>10$
such that for every
![]() $f\in \ell ^p({\mathbb {Z}})$
, one has
$f\in \ell ^p({\mathbb {Z}})$
, one has
 $$ \begin{align*} \bigg\|\Big(\sum_{M_2\in \tilde{\mathbb{S}}_{\tau}^2(j;M_1)}\big|T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak g_{M_1, M_2}]\big]f\big|^2\Big)^{1/2}\bigg\|_{\ell^p({\mathbb{Z}})} \lesssim_{p, \tau} (\log M_1)^{-\alpha_p}\|f\|_{\ell^p({\mathbb{Z}})}, \end{align*} $$
$$ \begin{align*} \bigg\|\Big(\sum_{M_2\in \tilde{\mathbb{S}}_{\tau}^2(j;M_1)}\big|T_{{\mathbb{Z}}}\big[\Phi_{\le -n_{N_s, N_s}^{v_j, \beta}(N_s)+2}^{\Sigma_{\le s}}[1, \mathfrak g_{M_1, M_2}]\big]f\big|^2\Big)^{1/2}\bigg\|_{\ell^p({\mathbb{Z}})} \lesssim_{p, \tau} (\log M_1)^{-\alpha_p}\|f\|_{\ell^p({\mathbb{Z}})}, \end{align*} $$
completing the proof of (7.62).
Proof of Theorem 7.6
We fix
![]() $1\le j< r$
as before. To prove (7.7), in view of (7.56) and (2.12), it suffices to show that
$1\le j< r$
as before. To prove (7.7), in view of (7.56) and (2.12), it suffices to show that
 $$ \begin{align} \sum_{M_1\in \mathbb{S}_{\tau}^1(j)}\big\|\sup_{M_2\in\mathbb{S}_{\tau}^2(j;M_1)}|T_{{\mathbb{Z}}}[m_{M_1, M_2}-\tilde{h}_{M_1, M_2}^{M_1}]f|\big\|_{\ell^p({\mathbb{Z}})}\lesssim_{p, \tau}\|f\|_{\ell^p({\mathbb{Z}})}. \end{align} $$
$$ \begin{align} \sum_{M_1\in \mathbb{S}_{\tau}^1(j)}\big\|\sup_{M_2\in\mathbb{S}_{\tau}^2(j;M_1)}|T_{{\mathbb{Z}}}[m_{M_1, M_2}-\tilde{h}_{M_1, M_2}^{M_1}]f|\big\|_{\ell^p({\mathbb{Z}})}\lesssim_{p, \tau}\|f\|_{\ell^p({\mathbb{Z}})}. \end{align} $$
For
![]() $u\in \{p_0, p_0'\}$
by the one-parameter theory, which produces bounds independent of the coefficients of the underlying polynomials (see, for instance, [Reference Mirek, Stein and Zorin-Kranich52, Reference Mirek, Slomian and Szarek47]), we may conclude
$u\in \{p_0, p_0'\}$
by the one-parameter theory, which produces bounds independent of the coefficients of the underlying polynomials (see, for instance, [Reference Mirek, Stein and Zorin-Kranich52, Reference Mirek, Slomian and Szarek47]), we may conclude
and by (2.17) combined with (7.56), we also have
On the one hand, combining (7.64) and (7.65), we deduce that
On the other hand, inequalities (7.12), (7.22) and (7.33) imply for every
![]() $M_1\in \mathbb {S}_{\tau }^1(j)$
that
$M_1\in \mathbb {S}_{\tau }^1(j)$
that
with the parameter
![]() $\alpha>0$
as in (7.9). Simple interpolation between (7.66) and (7.67) yields (7.63), and this completes the proof of Theorem 7.6.
$\alpha>0$
as in (7.9). Simple interpolation between (7.66) and (7.67) yields (7.63), and this completes the proof of Theorem 7.6.
Acknowledgements
We thank Mei-Chu Chang and Elly Stein who supported the idea of completing this work. We thank Terry Tao for a fruitful discussion in February 2015 about the estimates for multi-parameter exponential sums and writing a very helpful blog on this subject [Reference Tao60]. We also thank Agnieszka Hejna, Dariusz Kosz and Bartosz Langowski for careful reading of earlier versions of this manuscript and their helpful comments and corrections. Finally, we thank the referees for careful reading of the manuscript and useful remarks that led to the improvement of the presentation.
Competing interest
The authors have no competing interest to declare.
Financial support
Jean Bourgain was supported by NSF grant DMS-1800640. Mariusz Mirek was partially supported by NSF grant DMS-2154712, and by the National Science Centre in Poland, grant Opus 2018/31/B/ST1/00204. Elias M. Stein was partially supported by NSF grant DMS-1265524.