Hostname: page-component-55f67697df-twqc4 Total loading time: 0 Render date: 2025-05-12T14:43:22.411Z Has data issue: false hasContentIssue false
  • English
  • Français

The symplectic geometry of higher Auslander algebras: Symmetric products of disks

Part of: Higher algebraic $K$-theory Symplectic geometry, contact geometry Representation theory of rings and algebras

Published online by Cambridge University Press:  01 February 2021

Tobias Dyckerhoff ,
Gustavo Jasso  and
Yankι Lekili
Tobias Dyckerhoff
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Bundesstraße 55, 20146Hamburg, Germany; E-mail: tobias.dyckerhoff@uni-hamburg.de
Gustavo Jasso
Affiliation:
Mathematisches Institut, Rheinische Friedrich-Wilhelms-Universität Bonn, Endenicher Allee 60, 53115Bonn, Germany; E-mail: gjasso@math.uni-bonn.de
Yankι Lekili
Affiliation:
Department of Mathematics, King’s College London, Strand, LondonWC2R 2LS, United Kingdom; E-mail: yanki.lekili@kcl.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the perfect derived categories of Iyama’s d-dimensional Auslander algebras of type 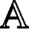${\mathbb {A}}$ are equivalent to the partially wrapped Fukaya categories of the d-fold symmetric product of the 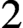$2$-dimensional unit disk with finitely many stops on its boundary. Furthermore, we observe that Koszul duality provides an equivalence between the partially wrapped Fukaya categories associated to the d-fold symmetric product of the disk and those of its 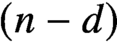$(n-d)$-fold symmetric product; this observation leads to a symplectic proof of a theorem of Beckert concerning the derived Morita equivalence between the corresponding higher Auslander algebras of type 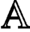${\mathbb {A}}$. As a by-product of our results, we deduce that the partially wrapped Fukaya categories associated to the d-fold symmetric product of the disk organise into a paracyclic object equivalent to the d-dimensional Waldhausen 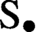$\text {S}_{\bullet }$-construction, a simplicial space whose geometric realisation provides the d-fold delooping of the connective algebraic K-theory space of the ring of coefficients.

MSC classification

Primary: 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers
Secondary: 19D99: None of the above, but in this section 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e10
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - SA
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Amiot, C., Plamondon, P.-G. and Schroll, S., ‘A complete derived invariant for gentle algebras via winding numbers and arf invariants’, Preprint, 2019, arXiv:1904.02555.Google Scholar
Abouzaid, M. and Seidel, P., ‘An open string analogue of Viterbo functoriality’, Geom. Topol. 14(2) (2010), 627–718.10.2140/gt.2010.14.627CrossRefGoogle Scholar
Auroux, D., ‘Fukaya categories and bordered Heegaard-Floer homology’, in Proceedings of the International Congress of Mathematicians, Vol. II, (Hindustan Book Agency, New Delhi, 2010), 917–941.Google Scholar
Auroux, D., ‘Fukaya categories of symmetric products and bordered Heegaard-Floer homology’, J. Gökova Geom. Topol. GGT 4 (2010), 1–54.Google Scholar
Auslander, M., ‘Representation Dimension of Artin Algebras’ Queen Mary College Math. Notes, Queen Mary College, London (1971) reprinted in: Selected Works of Maurice Auslander, part 1, edited and with a foreword by Idun Reiten, Sverre O. Smalø, and Øyvind Solberg, Amer. Math. Soc., Providence, 1999Google Scholar
Björner, A. and Brenti, F., Combinatorics of Coxeter Groups, Graduate Texts in Mathematics, 231 (Springer, New York, 2005).Google Scholar
Beckert, F., The Bivariant Parasimplicial ${S}_{\bullet }$-construction, Ph.D. thesis, Bergische Universität Wuppertal, 2018.Google Scholar
, A. J. Blumberg, Gepner, D. and Tabuada, G., ‘A universal characterization of higher algebraic $K$-theory’, Geom. Topol. 17(2) (2013), 733–838.10.2140/gt.2013.17.733CrossRefGoogle Scholar
Bocklandt, R., ‘Noncommutative mirror symmetry for punctured surfaces’, Trans. Amer. Math. Soc. 368(1) (2016), 429–469. With an appendix by M. Abouzaid.10.1090/tran/6375CrossRefGoogle Scholar
Cohn, L., ‘Differential graded categories are k-linear stable infinity categories’. Preprint, 2013, arXiv:1308.2587.Google Scholar
Dyckerhoff, T., Jasso, G. and Walde, T., ‘Simplicial structures in higher Auslander–Reiten theory’, Adv. Math. 355 (2019), 106762.10.1016/j.aim.2019.106762CrossRefGoogle Scholar
Dyckerhoff, T. and Kapranov, M., ‘Triangulated surfaces in triangulated categories’, J. Eur. Math. Soc. (JEMS) 20(6) (2018), 1473–1524.10.4171/JEMS/791CrossRefGoogle Scholar
De Loera, J. A., Rambau, J. and Santos, F., Triangulations: Structures for Algorithms and Applications, Algorithms and Computation in Mathematics, 25 (Springer-Verlag, Berlin, 2010).Google Scholar
Drinfeld, V., ‘DG quotients of DG categories’, J. Algebra 272(2) (2004), 643–691.10.1016/j.jalgebra.2003.05.001CrossRefGoogle Scholar
Dyckerhoff, T., ‘${A}^1$-homotopy invariants of topological Fukaya categories of surfaces’, Compos. Math. 153(8) (2017), 1673–1705.10.1112/S0010437X17007205CrossRefGoogle Scholar
Dyckerhoff, T., ‘A categorified Dold–Kan correspondence’. Preprint, 2017, arXiv:1710.08356.Google Scholar
Fiedorowicz, Z. and Loday, J.-L., ‘Crossed simplicial groups and their associated homology’, Trans. Amer. Math. Soc. 326(1) (1991), 57–87.10.1090/S0002-9947-1991-0998125-4CrossRefGoogle Scholar
Grant, J. and Iyama, O., ‘Higher preprojective algebras, Koszul algebras, and superpotentials’, Compos. Math., to appear. Preprint, 2019, arXiv:1902.07878.Google Scholar
Getzler, E. and Jones, J. D. S., ‘The cyclic homology of crossed product algebras’, J. Reine Angew. Math. 445 (1993), 161–174.Google Scholar
Geiss, C., Keller, B. and Oppermann, S., ‘$n$-angulated categories’, J. Reine Angew. Math. 675 (2013), 101–120.Google Scholar
Ganatra, S., Pardon, J. and Shende, V., ‘Structural results in wrapped Floer theory’, Preprint, 2018, arXiv:1809.03427.Google Scholar
Ganatra, S., Pardon, J. and Shende, V., ‘Covariantly functorial wrapped Floer theory on Liouville sectors’, Publications mathématiques de l’IHÉS 131 (2020), 73–200.10.1007/s10240-019-00112-xCrossRefGoogle Scholar
Happel, D., Triangulated Categories in the Representation Theory of Finite-Dimensional Algebras, London Mathematical Society Lecture Note Series, 119 (Cambridge University Press, Cambridge, 1988).Google Scholar
Herschend, M. and Iyama, O., ‘$n$-representation-finite algebras and twisted fractionally Calabi-Yau algebras’, Bull. Lond. Math. Soc. 43(3) (2011), 449–466.10.1112/blms/bdq101CrossRefGoogle Scholar
Herschend, M., Iyama, O. and Oppermann, S., ‘$n$-representation infinite algebras’, Adv. Math. 252 (2014), 292–342.10.1016/j.aim.2013.09.023CrossRefGoogle Scholar
Haiden, F., Katzarkov, L. and Kontsevich, M., ‘Flat surfaces and stability structures’, Publ. Math. Inst. Hautes Études Sci. 126(1) (2017), 247–318.10.1007/s10240-017-0095-yCrossRefGoogle Scholar
Iyama, O. and Jasso, G., ‘Higher Auslander correspondence for dualizing $R-$varieties’, Algebr. Represent. Theory 20(2) (2017), 335–354.10.1007/s10468-016-9645-0CrossRefGoogle Scholar
Iyama and, O. Oppermann, S., ‘$n$-representation-finite algebras and $n$-APR tilting’, Trans. Amer. Math. Soc. 363(12) (2011), 6575–6614.10.1090/S0002-9947-2011-05312-2CrossRefGoogle Scholar
Iyama, O. and Oppermann, S., ‘Stable categories of higher preprojective algebras’, Adv. Math. 244 (2013), 23–68.10.1016/j.aim.2013.03.013CrossRefGoogle Scholar
Iyama, O., ‘Auslander correspondence’, Adv. Math. 210(1) (2007), 51–82.10.1016/j.aim.2006.06.003CrossRefGoogle Scholar
Iyama, O., ‘Higher-dimensional Auslander-Reiten theory on maximal orthogonal subcategories’, Adv. Math. 210(1) (2007), 22–50.10.1016/j.aim.2006.06.002CrossRefGoogle Scholar
Iyama, O., ‘Cluster tilting for higher Auslander algebras’, Adv. Math. 226(1) (2011), 1–61.10.1016/j.aim.2010.03.004CrossRefGoogle Scholar
Jasso, G., ‘$n$-abelian and $n$-exact categories’, Math. Z. 283(3–4) (2016), 703–759.10.1007/s00209-016-1619-8CrossRefGoogle Scholar
Jasso, G. and Külshammer, J., ‘Higher Nakayama algebras I: Construction’, Adv. Math. 351 (2019), 1139–1200. With an appendix by J. Külshammer and Ch. Psaroudakis and an appendix by S. Kvamme.10.1016/j.aim.2019.05.026CrossRefGoogle Scholar
Keller, B., ‘Deriving DG categories’, Ann. Sci. Éc. Norm. Supér. (4) 27(1) (1994), 63–102.10.24033/asens.1689CrossRefGoogle Scholar
Keller, B., ‘On differential graded categories’, in International Congress of Mathematicians, Vol. II, (European Mathematical Society, Zürich, 2006), 151–190.Google Scholar
Khovanov, M., ‘How to categorify one-half of quantum $\mathrm{gl}\left(1|2\right)$’, in Knots in Poland III. Part III, Banach Center Publications, 103 (Institute of Mathematics of the Polish Academy of Sciences, Warsaw, 2014), 211–232.Google Scholar
Kontsevich, M., ‘Symplectic geometry of homological algebra’ (2009). URL: http://www.ihes.fr/~maxim/TEXTS/Symplectic_AT2009.pdf.Google Scholar
Lipshitz, R., Ozsváth, P. S. and Thurston, D. P., ‘Bimodules in bordered Heegaard Floer homology’, Geom. Topol. 19(2) (2015), 525–724.10.2140/gt.2015.19.525CrossRefGoogle Scholar
Lipshitz, R., Ozsváth, P. S. and Thurston, D. P., ‘Bordered Heegaard Floer homology’, Mem. Amer. Math. Soc. 254(1216) (2018), viii+279.Google Scholar
Lekili, Y. and Polishchuk, A., ‘Auslander orders over nodal stacky curves and partially wrapped Fukaya categories’, J. Topol. 11(3) (2018), 615–644.10.1112/topo.12064CrossRefGoogle Scholar
Lekili, Y. and Polishchuk, A., ‘Derived equivalences of gentle algebras via Fukaya categories’, Math. Ann. 376(1–2) (2020), 187–225.10.1007/s00208-019-01894-5CrossRefGoogle Scholar
Lekili, Y. and Polishchuk, A., ‘Homological mirror symmetry for higher-dimensional pairs of pants’, Compos. Math. 156(7) (2020), 1310–1347.10.1112/S0010437X20007150CrossRefGoogle Scholar
Lunts, V. A. and Schnürer, O. M., ‘Smoothness of equivariant derived categories’, Proc. Lond. Math. Soc. (3) 108(5) (2014), 1226–1276.10.1112/plms/pdt053CrossRefGoogle Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, 170 (Princeton University Press, Princeton, NJ, 2009).Google Scholar
Lurie, J., ‘Higher algebra’ (May 2017). URL: http://www.math.harvard.edu/~lurie/.Google Scholar
Miyashita, Y., ‘Tilting modules of finite projective dimension’, Math. Z. 193(1) (1986), 113–146.10.1007/BF01163359CrossRefGoogle Scholar
Nistor, V., ‘Group cohomology and the cyclic cohomology of crossed products’, Invent. Math. 99(2) (1990), 411–424.10.1007/BF01234426CrossRefGoogle Scholar
Opper, S., ‘On auto-equivalences and complete derived invariants of gentle algebras’, Preprint, 2019, arXiv:1904.04859.Google Scholar
Oppermann, S. and Thomas, H., ‘Higher-dimensional cluster combinatorics and representation theory’, J. Eur. Math. Soc. (JEMS) 14(6) (2012), 1679–1737.10.4171/JEMS/345CrossRefGoogle Scholar
Perutz, T., ‘Hamiltonian handleslides for Heegaard Floer homology’, in Proceedings of Gökova Geometry-Topology Conference 2007 (International Press, Gökova, 2008), 15–35.Google Scholar
Poguntke, T., ‘Higher Segal structures in algebraic $K$-theory’, Preprint, 2017, arXiv:1709.06510.Google Scholar
Quillen, D., ‘Higher algebraic $K$-theory. I’, Lecture Notes in Math. 341 (1973), 85–147.10.1007/BFb0067053CrossRefGoogle Scholar
Rambau, J., ‘Triangulations of cyclic polytopes and higher Bruhat orders’, Mathematika 44(1) (1997), 162–194.10.1112/S0025579300012055CrossRefGoogle Scholar
Seidel, P., ‘Graded Lagrangian submanifolds’, Bull. Soc. Math. France 128(1) (2000), 103–149.10.24033/bsmf.2365CrossRefGoogle Scholar
Seidel, P., ‘Fukaya categories and Picard-Lefschetz theory’, Zurich Lectures in Advanced Mathematics (European Mathematical Society, Zürich, 2008).10.4171/063CrossRefGoogle Scholar
Sylvan, Z., ‘On partially wrapped Fukaya categories’, J. Topol. 12(2) (2019), 372–441.10.1112/topo.12088CrossRefGoogle Scholar
Sylvan, Z., ‘Orlov and Viterbo functors in partially wrapped Fukaya categories’, Preprint, 2019, arXiv:1908.02317.10.1112/topo.12088CrossRefGoogle Scholar
Tachikawa, H., ‘On dominant dimensions of QF-3 algebras’, Trans. Amer. Math. Soc. 112 (1964), 249–266.Google Scholar
Tanaka, H. L., ‘Cyclic structures and broken cycles’, Preprint, 2019, arXiv:1907.03301.Google Scholar
Toën, B. and Vaquié, M., ‘Moduli of objects in dg-categories’, Ann. Sci. Éc. Norm. Supér. (4) 40(3) (2007), 387–444.10.1016/j.ansens.2007.05.001CrossRefGoogle Scholar
Waldhausen, F., ‘Algebraic $K$-theory of spaces’, in Algebraic and Geometric Topology (New Brunswick, N.J., 1983), Lecture Notes in Math., 1126 (Springer, Berlin, 1985), 318–419.Google Scholar