Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-10T23:47:19.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Thinness of some hypergeometric groups in $\mathrm{Sp}(6)$

Part of: Singularities Lie groups

Published online by Cambridge University Press:  02 May 2024

Sandip Singh  and
Shashank Vikram Singh
Sandip Singh*
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Mumbai, India
Shashank Vikram Singh
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Mumbai, India
*
Corresponding author: Sandip Singh; Email: sandip@math.iitb.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We show the thinness of 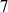$7$ of the 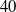$40$ hypergeometric groups having a maximally unipotent monodromy in 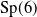$\mathrm{Sp}(6)$.

Keywords

Hypergeometric groupMonodromy representationSymplectic groupThin groupFree group

MSC classification

Primary: 22E40: Discrete subgroups of Lie groups
Secondary: 32S40: Monodromy; relations with differential equations and $D$-modules 33C80: Connections with groups and algebras, and related topics
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bajpai, J., Dona, D., Singh, S. and Singh, S. V., Symplectic hypergeometric groups of degree six, J. Algebra 575 (2021), 256–273.CrossRefGoogle Scholar
Bajpai, J., Dona, D. and Nitsche, M., Arithmetic and thin monodromy in Sp(6), arXiv:2112.12111.Google Scholar
Bajpai, J. and Singh, S., On orthogonal hypergeometric groups of degree five, Trans. Am. Math. Soc. 372(11) (2019), 7541–7572.CrossRefGoogle Scholar
Benson, D., Campagnolo, C., Ranicki, A. and Rovi, C., Cohomology of symplectic groups and Meyer’s signature theorem, Algebr. Geom. Topol. 18(7) (2018), 4069–4091.CrossRefGoogle Scholar
Beukers, F. and Heckman, G., Monodromy for the hypergeometric function $_n{F}_{n-1}$ , Invent. Math. 95(2) (1989), 325–354.CrossRefGoogle Scholar
Brav, C. and Thomas, H., Thin monodromy in Sp(4), Compos. Math. 150(3) (2014), 333–343.CrossRefGoogle Scholar
Detinko, A. S., Flannery, D. L. and Hulpke, A., Experimenting with symplectic hypergeometric monodromy groups, Exp. Math. 32(1) (2021), 88–96. DOI: 10.1080/10586458.2020.1780516.CrossRefGoogle Scholar
Fuchs, E., The ubiquity of thin groups. Thin groups and superstrong approximation, Math. Sci. Res. Inst. Publ., vol. 61 (Cambridge University Press, Cambridge, 2014), 73–92,Google Scholar
Fuchs, E., Meiri, C. and Sarnak, P., Hyperbolic monodromy groups for the hypergeometric equation and Cartan involutions, J. Eur. Math. Soc. (JEMS) 16(8) (2014), 1617–1671.CrossRefGoogle Scholar
Hofmann, J. and van Straten, D., Some monodromy groups of finite index in Sp4 (Z) math, arXiv:1312.3063.Google Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial group theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 89 (Springer, Berlin, 1977).Google Scholar
Sarnak, P., Notes on thin matrix groups. Thin groups and superstrong approximation, Math. Sci. Res. Inst. Publ., vol. 61 (Cambridge University Press, Cambridge, 2014), 343–362.Google Scholar
Singh, S., Arithmeticity of four hypergeometric monodromy groups associated to Calabi-Yau threefolds, Int. Math. Res. Not. (IMRN) 2015(18) (2015), 8874–8889.CrossRefGoogle Scholar
Singh, S., Orthogonal hypergeometric groups with a maximally unipotent monodromy, Exp. Math. 24(4) (2015), 449–459.CrossRefGoogle Scholar
Singh, S., Arithmeticity of some hypergeometric monodromy groups in Sp(4, J. Algebra 473 (2017), 142–165.CrossRefGoogle Scholar
Singh, S. and Venkataramana, T. N., Arithmeticity of certain symplectic hypergeometric groups, Duke Math. J. 163(3) (2014), 591–617.CrossRefGoogle Scholar
Swan, R. G., Groups of cohomological dimension one, J. Algebra 12(4) (1969), 585–610.CrossRefGoogle Scholar
Venkataramana, T. N., Image of the Burau Representation at $d$ -th roots of unity, Ann. Math. 179(3) (2014), 1041–1083.CrossRefGoogle Scholar
Venkataramana, T. N., Hypergeometric groups of orthogonal type, J. Eur. Math. Soc. (JEMS) 19(2) (2017), 581–599.CrossRefGoogle Scholar