Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-18T05:54:13.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Random selective advantages of a gene in a finite population

Published online by Cambridge University Press:  14 July 2016

Louis Jensen  and
Edward Pollak
Louis Jensen
Affiliation:
Iowa State University, Ames, Iowa
Edward Pollak
Affiliation:
Iowa State University, Ames, Iowa
Get access Rights & Permissions [Opens in a new window]

Extract

A problem of interest to many population geneticists is the process of change in a gene frequency. A popular model used to describe the change in a gene frequency involves the assumption that the gene frequency is Markovian. The probabilities in a Markov process can be approximated by the solution of a partial differential equation known as the Fokker-Planck equation or the forward Kolmogorov equation. 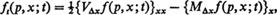Mathematically this equation is where subscripts indicate partial differentiation. In this equation, f(p, x; t) is the probability density that the frequency of a gene is x at time t, given that the frequency was p at time t = o. The expressions MΔX and VΔx are, respectively, the first and second moments of the change in the gene frequency during one generation. A rigorous derivation of this equation was given by Kolmogorov (1931).

Type
Research Papers
Information
Journal of Applied Probability , Volume 6 , Issue 1 , April 1969 , pp. 19 - 37
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Courant, R. and Hilbert, D. (1937) Methods of Mathematical Physics. Vol. I. Interscience Publishers, Inc., New York.Google Scholar
Fisher, R. A. (1922) On the dominance ratio. Proc. Roy. Soc. Edin. 42, 321–341.Google Scholar
Fisher, R. A. (1930) The distribution of gene ratios for rare mutations. Proc. Roy. Soc. Edin. 50, 205–220.Google Scholar
Fisher, R. A. and Ford, E. B. (1947) The spread of a gene in natural conditions in a colony of the moth Panaxia Dominula L. Heredity 1, 143–174.Google Scholar
Kantorovich, L. V. and Krylov, V. I. (1958) Approximate Methods of Higher Analysis. Interscience Publishers, Inc., New York.Google Scholar
Jensen, L. (1967) Some effects of random selective advantages of a gene in a finite population. M.S. thesis (Unpublished). Iowa State University.Google Scholar
Kimura, M. (1954) Process leading to quasi-fixation of genes in natural populations due to random fluctuation of selection intensities. Genetics 39, 280–295.Google Scholar
Kimura, M. (1955a) Stochastic processes and distribution of gene frequencies under natural selection. Cold Spring Harbor Symp. 20, 33–53.Google Scholar
Kimura, M. (1955b) Solution of a process of random genetic drift with a continuous model. Proc. Nat. Acad. Sci. 41, 144–150.Google Scholar
Kimura, M. (1964) Diffusion models in population genetics. J. Appl. Prob. 1, 177–232.Google Scholar
Kolmogorov, A. (1931) Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung. Math. Ann. 104, 415–458.CrossRefGoogle Scholar
MaléCot, G. (1944) Sur une problème de probabilités en chaîne que pose la génétique. C. R. Acad. Sci. 219, 379–381.Google Scholar
Morse, P. M. and Feshbach, H. (1953) Methods of Theoretical Physics. Part I. McGraw-Hill Book Co., Inc., New York.Google Scholar
Wright, S. (1931) Evolution in Mendelian populations. Genetics 16, 97–159.Google Scholar
Wright, S. (1948) On the role of directed and random changes in gene frequency in the genetics of populations. Evolution 2, 279–294.Google Scholar