1. Introduction
The fundamental singularities of free-surface flows are usually associated with pinch-off or coalescence (Eggers Reference Eggers1997; Eggers & Fontelos Reference Eggers and Fontelos2015). The pinch-off of an inviscid liquid thread shows self-similar capillary–inertial dynamics (Day, Hinch & Lister Reference Day, Hinch and Lister1998), while a bubble pinches off in a purely inertial motion and the surface tension becomes irrelevant during the final stage of collapse (Burton, Waldrep & Taborek Reference Burton, Waldrep and Taborek2005; Keim et al. Reference Keim, Møller, Zhang and Nagel2006; Eggers et al. Reference Eggers, Fontelos, Leppinen and Snoeijer2007; Thoroddsen, Etoh & Takehara Reference Thoroddsen, Etoh and Takehara2007a; Schmidt et al. Reference Schmidt, Keim, Zhang and Nagel2009). Singular jets also occur from oscillating drops, both in free fall (Thoroddsen, Etoh & Takehara Reference Thoroddsen, Etoh and Takehara2007b) as well as during the impact and rebounding of a drop from a superhydrophobic surface (Bartolo, Josserand & Bonn Reference Bartolo, Josserand and Bonn2006). Such jetting from the drop apex has been shown to affect the impact force on the solid (Zhang et al. Reference Zhang, Sanjay, Shi, Zhao, Lv, Feng and Lohse2022).
A related singularity occurs when a free-surface crater in a pool rebounds by gravity or surface tension. Such craters can be generated by critical Faraday waves or bursting of bubbles resting under a free surface. The fine jetting emerges from a dimple at the crater bottom and has been suggested to arise from a capillary–inertial singularity modified by viscosity (Zeff et al. Reference Zeff, Kleber, Fineberg and Lathrop2000; Duchemin et al. Reference Duchemin, Popinet, Josserand and Zaleski2002; Das & Hopfinger Reference Das and Hopfinger2008; Deike et al. Reference Deike, Ghabache, Liger-Belair, Das, Zaleski, Popinet and Séon2018; Lai, Eggers & Deike Reference Lai, Eggers and Deike2018; Gañán-Calvo & López-Herrera Reference Gañán-Calvo and López-Herrera2021). However, experiments show this not to be correct during the final stages of collapse of a drop-impact crater, where the dimple dynamics is purely inertial (Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018; Yang, Tian & Thoroddsen Reference Yang, Tian and Thoroddsen2020). One might expect that the radially accelerating collision of the cylindrical walls of the dimple would create the largest impulsive pressure to drive the jets (Oguz & Prosperetti Reference Oguz and Prosperetti1990; Pumphrey & Elmore Reference Pumphrey and Elmore1990; Prosperetti & Oguz Reference Prosperetti and Oguz1993), akin to the spherical collapse of a cavitation bubble. However, somewhat counter-intuitively, the fastest jets occur, not when the dimple pinches off a small bubble, but rather when the narrowest dimple retracts vertically just before pinch-off (Zeff et al. Reference Zeff, Kleber, Fineberg and Lathrop2000; Yang et al. Reference Yang, Tian and Thoroddsen2020). Thoroddsen et al. (Reference Thoroddsen, Takehara, Nguyen and Etoh2018) used ultra-high-speed imaging to show that this occurs without any curvature singularity at the tip of the dimple.
Questions remain: How does the crossover from the radial collapse to vertical jetting occur? What is the largest jet velocity and is there an upper bound? Furthermore, why is the jetting speed so sensitive to the boundary or initial conditions? Why do the fastest singular jets not follow the proposed viscous scaling (Gañán-Calvo Reference Gañán-Calvo2017; Yang et al. Reference Yang, Tian and Thoroddsen2020; Gañán-Calvo & López-Herrera Reference Gañán-Calvo and López-Herrera2021)? Herein we will reveal a conical jetting mechanism that can answer all of these questions.
The dynamical importance of the surrounding air in free-surface flows was conclusively demonstrated by Xu, Zhang & Nagel (Reference Xu, Zhang and Nagel2005), who showed that impact splashing can be suppressed by reducing the ambient pressure. Ambient air pressure has also been shown to affect the evolution of ejecta sheets (Yarin Reference Yarin2006; Thoroddsen et al. Reference Thoroddsen, Thoraval, Takehara and Etoh2011; Marcotte et al. Reference Marcotte, Michon, Séon and Josserand2019). The observations of microbubbles near the most singular jetting, from drop-impact craters, suggested air entrainment or even possible cavitation (Tran et al. Reference Tran, Lee, Lee, Woo, Han, Kim and Hwang2016; Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018). This motivated us to conduct a set of experiments, under reduced ambient pressures, to pinpoint the role of the gas on the jetting. This also serves a second purpose, to correct the jetting speed for the air drag experienced by the tip of the jet before it emerges out of the crater. Below, we show how a cylindrical air sheet is pulled in from the corner of the bottom dimple to play an unexpected role in promoting the fastest jets.
2. Methods
2.1. Experimental set-up
The experimental configuration is shown in figure 1 and is similar to that used in our previous work (Li et al. Reference Li, Langley, Tian, Hicks and Thoroddsen2017; Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018; Yang et al. Reference Yang, Tian and Thoroddsen2020), while now the impacts are performed inside an acrylic vacuum chamber (Tian Reference Tian2020). The dimple evolution is viewed through the glass-walled pool, using a long-distance microscope (Leica Z16 APO) with adjustable magnification and aperture, at pixel (px) resolution down to ![]() $1.1\ \mathrm {\mu }{\rm m}\ {\rm px}^{-1}$. The rapid motions demand observations with an ultra-high-speed video camera (Kirana-05M, Specialized Imaging, Tring, UK), which acquires 180 frames at up to 5 million frames per second with full-frame resolution of 924 px
$1.1\ \mathrm {\mu }{\rm m}\ {\rm px}^{-1}$. The rapid motions demand observations with an ultra-high-speed video camera (Kirana-05M, Specialized Imaging, Tring, UK), which acquires 180 frames at up to 5 million frames per second with full-frame resolution of 924 px ![]() $\times$ 768 px irrespective of the frame rate used. Illumination is provided by 180 diode lasers (SI-LUX640), one for each frame. The pulse duration is between 30 and 170 ns to eliminate any motion smearing. A second video camera (Phantom V2511) captures the jet rising out of the crater to measure its speed and width. Triggering is electronic, started when the falling drop cuts the light to a dedicated line sensor (SI-OT3). The drop has a fixed diameter
$\times$ 768 px irrespective of the frame rate used. Illumination is provided by 180 diode lasers (SI-LUX640), one for each frame. The pulse duration is between 30 and 170 ns to eliminate any motion smearing. A second video camera (Phantom V2511) captures the jet rising out of the crater to measure its speed and width. Triggering is electronic, started when the falling drop cuts the light to a dedicated line sensor (SI-OT3). The drop has a fixed diameter ![]() $D\simeq 3.64$ mm, using water/glycerine mixtures, to cover a small range of viscosities of
$D\simeq 3.64$ mm, using water/glycerine mixtures, to cover a small range of viscosities of ![]() $\mu = 7.3$, 9.5, 12.7 and 14.7 cP, impacting the pool at velocity
$\mu = 7.3$, 9.5, 12.7 and 14.7 cP, impacting the pool at velocity ![]() $U$. The surface tension
$U$. The surface tension ![]() $\sigma \simeq 68\ {\rm mN}\ {\rm m}^{-1}$. The impacts are characterized by Weber, Froude and Reynolds numbers,
$\sigma \simeq 68\ {\rm mN}\ {\rm m}^{-1}$. The impacts are characterized by Weber, Froude and Reynolds numbers, ![]() $We =\rho D U^2/\sigma$,
$We =\rho D U^2/\sigma$, ![]() $Fr= U^2/(gD)$ and
$Fr= U^2/(gD)$ and ![]() $Re = \rho D U/\mu$, respectively, where we use the effective diameter
$Re = \rho D U/\mu$, respectively, where we use the effective diameter ![]() $D = (D_H^2 D_V)^{1/3}$ at impact, as monitored by the upper camera. Here
$D = (D_H^2 D_V)^{1/3}$ at impact, as monitored by the upper camera. Here ![]() $D_H$ and
$D_H$ and ![]() $D_V$ stand for the horizontal and vertical diameter of the drop at impact.
$D_V$ stand for the horizontal and vertical diameter of the drop at impact.
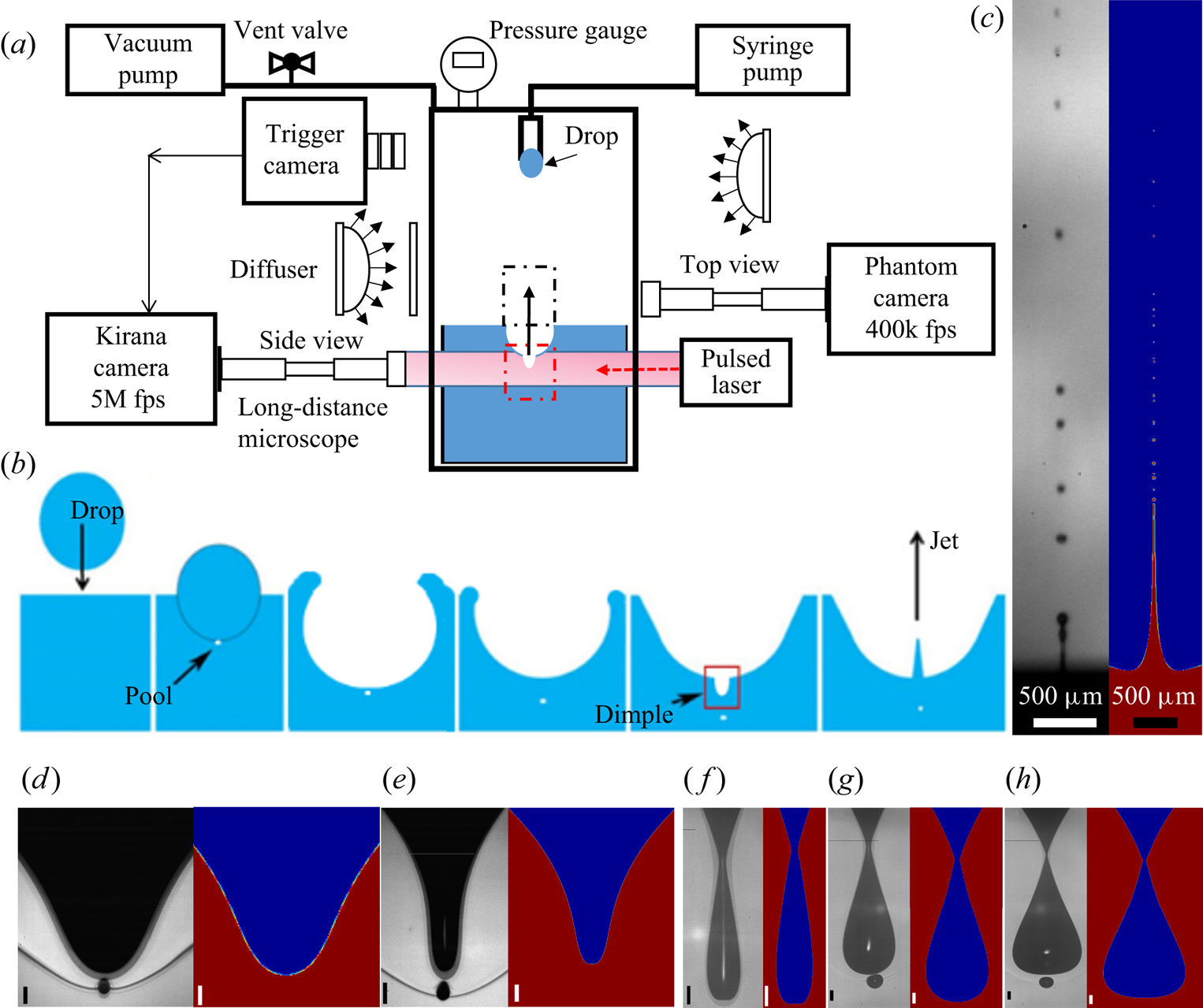
Figure 1. (a) Experimental set-up used to study crater collapse inside a vacuum chamber. (b) Sketch of typical drop-impact crater evolution, bubble entrapment, rebound and jetting. (c) Overall singular jet shape and small fine droplets shooting from the drop-impact crater. (d–h) Comparison between experiments and numerics of different dimple geometries and pinch-offs, under identical conditions with liquid viscosity ![]() $\mu =7.3$ cP and
$\mu =7.3$ cP and ![]() $D=3.64$ mm, for: (d)
$D=3.64$ mm, for: (d) ![]() $U = 1.30\ {\rm m}\ {\rm s}^{-1}$,
$U = 1.30\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 100$,
$We = 100$, ![]() $Fr = 49$,
$Fr = 49$, ![]() $Re=727$; (e)
$Re=727$; (e) ![]() $U = 1.38\ {\rm m}\ {\rm s}^{-1}$,
$U = 1.38\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 113$,
$We = 113$, ![]() $Fr = 55$,
$Fr = 55$, ![]() $Re=773$; (f)
$Re=773$; (f) ![]() $U = 1.45\ {\rm m}\ {\rm s}^{-1}$,
$U = 1.45\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 127$,
$We = 127$, ![]() $Fr = 59$,
$Fr = 59$, ![]() $Re=820$; (g)
$Re=820$; (g) ![]() $U = 1.49\ {\rm m}\ {\rm s}^{-1}$,
$U = 1.49\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 134$,
$We = 134$, ![]() $Fr = 63$,
$Fr = 63$, ![]() $Re=842$; and (h)
$Re=842$; and (h) ![]() $U = 1.54\ {\rm m}\ {\rm s}^{-1}$,
$U = 1.54\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 143$,
$We = 143$, ![]() $Fr = 67$,
$Fr = 67$, ![]() $Re=870$. The unmarked scale bars are
$Re=870$. The unmarked scale bars are ![]() $50\ \mathrm {\mu }{\rm m}$. For the subsequent evolution of the bubbles, please refer to the movies in the supplementary material available at https://doi.org/10.1017/jfm.2022.1085 and sequences in Thoroddsen et al. (Reference Thoroddsen, Takehara, Nguyen and Etoh2018).
$50\ \mathrm {\mu }{\rm m}$. For the subsequent evolution of the bubbles, please refer to the movies in the supplementary material available at https://doi.org/10.1017/jfm.2022.1085 and sequences in Thoroddsen et al. (Reference Thoroddsen, Takehara, Nguyen and Etoh2018).
2.2. Numerical simulations
The axisymmetric numerical simulations use the open-source volume-of-fluid Gerris software (Popinet Reference Popinet2009, Reference Popinet2018), which solves the incompressible Navier–Stokes equations in both the gas and liquid, using exact densities, viscosities and surface tension as in the experiments. To capture the fine air sheets, the code uses extreme grid refinement near the free surface, starting at refinement levels of 12, increasing to 16 or 18 close to the start of jetting (see supplementary material). At the finest level of 18, the effective number of mesh cells across the radius of the initial drop is equivalent to 26 000 of the smallest cells.
For the finest resolution, the grid spacing is only 70 nm. The large density ratio between the two phases limits the simulations to the ambient pressure case. We remove the initial entrapped bubble during the first contact of the drop with the pool, to reduce the computational burden to allow the extreme refinement during the final dimple dynamics. We note that this central bubble is absent during singular jetting from bursting bubbles and supercritical Faraday waves (Zeff et al. Reference Zeff, Kleber, Fineberg and Lathrop2000; Das & Hopfinger Reference Das and Hopfinger2008; Raja, Das & Hopfinger Reference Raja, Das and Hopfinger2019) and was often not even observed in previous experiments on drop-impact craters. We do not believe removing this small bubble changes the dimple collapse in the simulations.
3. Results
Figure 1(d–h) compares experiments and simulations of a series of close-up dimple shapes at the bottom of the drop-impact craters near the singular collapse, as well as for dimple pinch-offs. The agreement is quite good, with the pinched-off volume slightly smaller in the experiments; but keep in mind that in the experiments the gas compresses by the larger collision pressure, while the simulations are incompressible. The compression of the gas and subsequent oscillation of the bubble are clearly seen in Thoroddsen et al. (Reference Thoroddsen, Takehara, Nguyen and Etoh2018). The corresponding jet velocities in figure 2(a,b) show a familiar trend, with isolated peaks occurring over a very narrow range of ![]() $We$ numbers (Zeff et al. Reference Zeff, Kleber, Fineberg and Lathrop2000; Michon, Josserand & Séon Reference Michon, Josserand and Séon2017; Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018; Yang et al. Reference Yang, Tian and Thoroddsen2020). This sensitivity to impact conditions has meant the singular jets being branded as ‘barely reproducible’ by Michon et al. (Reference Michon, Josserand and Séon2017). Reducing the ambient pressure shifts this critical
$We$ numbers (Zeff et al. Reference Zeff, Kleber, Fineberg and Lathrop2000; Michon, Josserand & Séon Reference Michon, Josserand and Séon2017; Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018; Yang et al. Reference Yang, Tian and Thoroddsen2020). This sensitivity to impact conditions has meant the singular jets being branded as ‘barely reproducible’ by Michon et al. (Reference Michon, Josserand and Séon2017). Reducing the ambient pressure shifts this critical ![]() $We_c$ from 121 to 127, and we observe a general trend of higher jetting velocity for lower air pressure, reaching the maximum measured velocity of
$We_c$ from 121 to 127, and we observe a general trend of higher jetting velocity for lower air pressure, reaching the maximum measured velocity of ![]() $137\pm 4\ {\rm m}\ {\rm s}^{-1}$.
$137\pm 4\ {\rm m}\ {\rm s}^{-1}$.
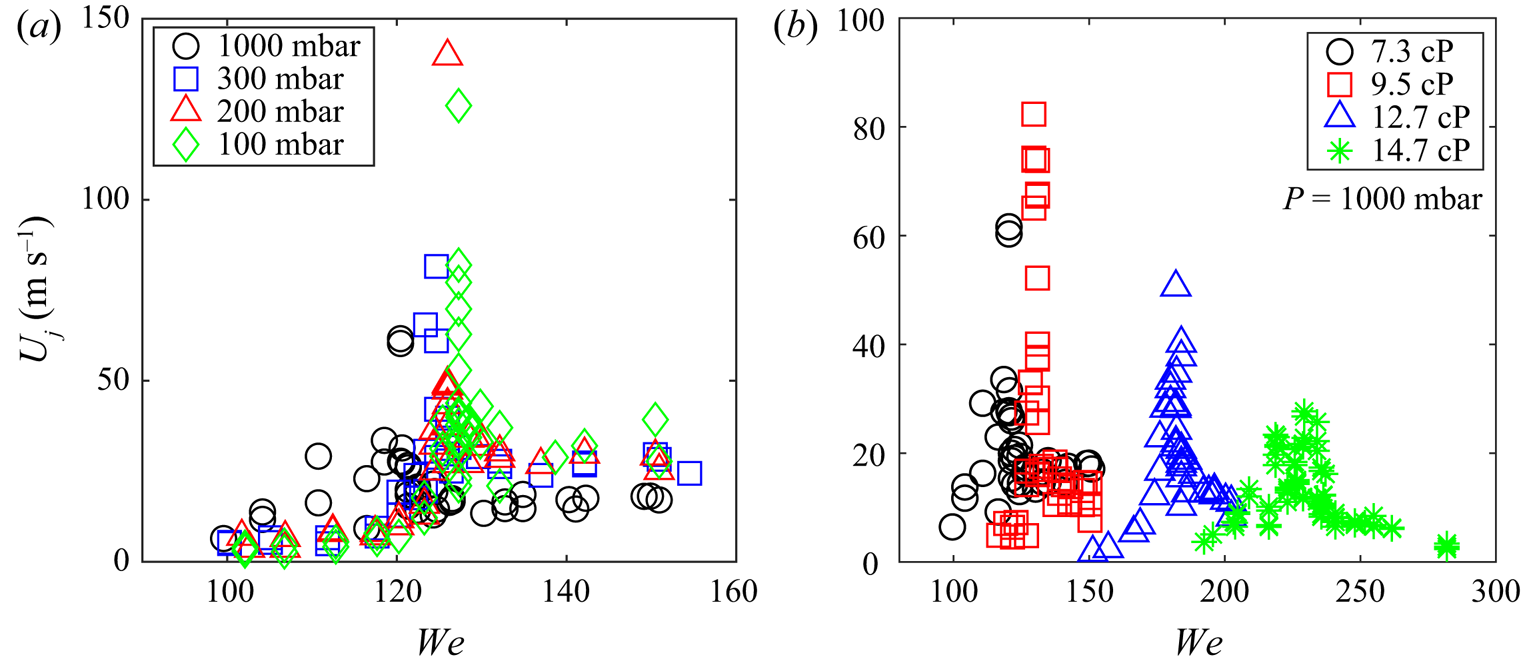
Figure 2. Experimental results for jetting speed ![]() $U_j$ versus impact Weber number
$U_j$ versus impact Weber number ![]() $We$ for (a) different ambient pressures, for liquid viscosity
$We$ for (a) different ambient pressures, for liquid viscosity ![]() $\mu =7.3$ cP, and (b) different liquid viscosities, at 1 atmosphere ambient pressure.
$\mu =7.3$ cP, and (b) different liquid viscosities, at 1 atmosphere ambient pressure.
Increasing the liquid viscosity (figure 2b) at atmospheric pressure shifts ![]() $We_c$ to higher values (
$We_c$ to higher values (![]() $We_c = 182$ for
$We_c = 182$ for ![]() $\mu = 12.7$ cP), but the character of the curves remains the same until
$\mu = 12.7$ cP), but the character of the curves remains the same until ![]() $\mu = 14.7$ cP, where the peak jetting velocity is much weaker and the peak becomes broader. Viscosity below this value does not seem to control the nature of the jetting process, but rather will modify the phase and amplitude of the capillary waves travelling down the crater towards the bottom dimple (Liow Reference Liow2001; Yang et al. Reference Yang, Tian and Thoroddsen2020). The fastest measured jets are indeed observed for
$\mu = 14.7$ cP, where the peak jetting velocity is much weaker and the peak becomes broader. Viscosity below this value does not seem to control the nature of the jetting process, but rather will modify the phase and amplitude of the capillary waves travelling down the crater towards the bottom dimple (Liow Reference Liow2001; Yang et al. Reference Yang, Tian and Thoroddsen2020). The fastest measured jets are indeed observed for ![]() $\mu =9.5$ cP slightly higher than for the 7.3 cP.
$\mu =9.5$ cP slightly higher than for the 7.3 cP.
The maximum jetting velocity for reduced ambient pressure, in figure 2(a), can partly be explained by the reduced air drag acting on the tip of the jet, which often pinches off a small droplet before it emerges out of the crater, as these droplets are travelling orders of magnitude faster than their terminal velocity (Thoroddsen, Takehara & Etoh Reference Thoroddsen, Takehara and Etoh2012). In the inertial regime, this drag force scales linearly with the air density. In figure 3(a) we have accounted for this drag and extrapolated the tip velocity back to the emergence position at the dimple. Assuming that the minute detached jet droplet remains spherical during its motion, the deceleration is caused by both the drag and gravitational force without considering the air flow.
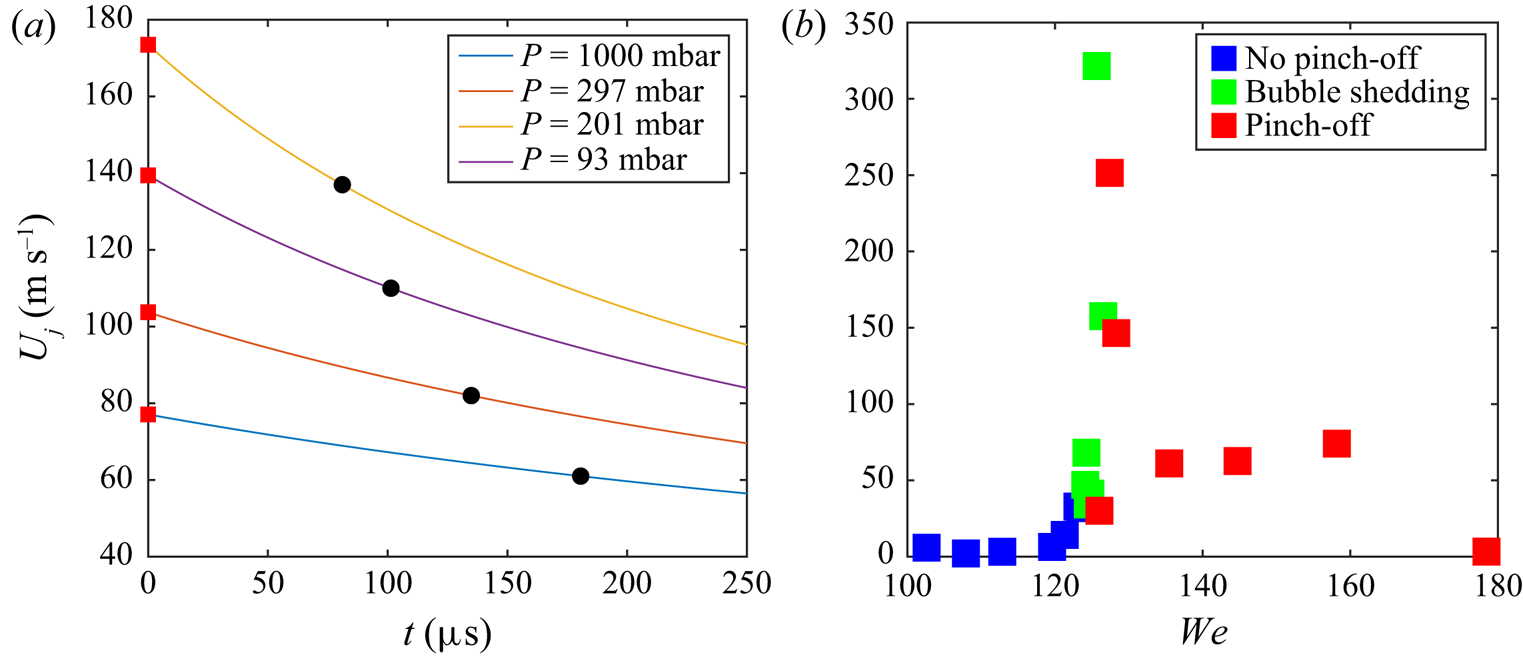
Figure 3. (a) Extrapolation of jetting velocity to emergence, from the observed speed (black circles) coming out of the crater, accounting for the air drag. (b) Results for ![]() $U_j$, at emergence from the dimple, from the Gerris simulations for
$U_j$, at emergence from the dimple, from the Gerris simulations for ![]() $\mu =7.3$ cP at atmospheric pressure.
$\mu =7.3$ cP at atmospheric pressure.
A simple model can be derived, ![]() $ma = -F_d-mg$, where
$ma = -F_d-mg$, where ![]() $F_d = \frac {1}{2}C_D\rho _aAU_j^2$, with cross-sectional area
$F_d = \frac {1}{2}C_D\rho _aAU_j^2$, with cross-sectional area ![]() $A = {\rm \pi}R^2$, where
$A = {\rm \pi}R^2$, where ![]() $R$ is the droplet radius. Then it yields
$R$ is the droplet radius. Then it yields ![]() $U_j'=-CU_j^2-g$, where the droplet rising velocity
$U_j'=-CU_j^2-g$, where the droplet rising velocity ![]() $U(t)$ is a function of time,
$U(t)$ is a function of time, ![]() $g$ is the gravitational acceleration and
$g$ is the gravitational acceleration and ![]() $C=3C_D\rho _a/(8\rho _dR)$ is a constant, with
$C=3C_D\rho _a/(8\rho _dR)$ is a constant, with ![]() $\rho _a$ and
$\rho _a$ and ![]() $\rho _d$ being the air and droplet densities. The drag coefficient,
$\rho _d$ being the air and droplet densities. The drag coefficient, ![]() $C_D$, is assumed to be 0.47 for a spherical droplet, since the local Reynolds number is within
$C_D$, is assumed to be 0.47 for a spherical droplet, since the local Reynolds number is within ![]() $10^3$–
$10^3$–![]() $10^4$. The deceleration by the drag force is assumed to surpass that of the gravitational force. Therefore, the theoretical solution without the gravitational term is
$10^4$. The deceleration by the drag force is assumed to surpass that of the gravitational force. Therefore, the theoretical solution without the gravitational term is ![]() $U_j=1/(Ct+C_1)$, where
$U_j=1/(Ct+C_1)$, where ![]() $C_1$ is a constant of integration.
$C_1$ is a constant of integration.
The initial velocity of the rising droplet can be derived from the solution with two boundary conditions: (1) the measured droplet velocity at the free surface, and (2) the travelling distance equal to the crater depth ![]() $H$, which is calculated as
$H$, which is calculated as ![]() $H =0.727 (Fr/3)^{1/4}D$ from Liow (Reference Liow2001). The measured velocities of the singular jet coming out of the crater, for the different ambient pressures, are marked on each curve in figure 3(a), with the black circle. The effective deceleration of the drag force is of the order of
$H =0.727 (Fr/3)^{1/4}D$ from Liow (Reference Liow2001). The measured velocities of the singular jet coming out of the crater, for the different ambient pressures, are marked on each curve in figure 3(a), with the black circle. The effective deceleration of the drag force is of the order of ![]() $O(10^5\unicode{x2013}10^6)\ {\rm m}\ {\rm s}^{-2}$, which is four orders of magnitude more than the gravitational acceleration. Therefore, the simplification of the equation neglecting the effect of gravity is justified. This suggests the largest initial jet velocity of
$O(10^5\unicode{x2013}10^6)\ {\rm m}\ {\rm s}^{-2}$, which is four orders of magnitude more than the gravitational acceleration. Therefore, the simplification of the equation neglecting the effect of gravity is justified. This suggests the largest initial jet velocity of ![]() $U_j \simeq 175\ {\rm m}\ {\rm s}^{-1}$. This is likely to be an upper bound for the velocity, as air flow can precede the liquid jet (Thoroddsen et al. Reference Thoroddsen, Etoh and Takehara2007b; Gekle et al. Reference Gekle, Peters, Gordillo, van der Meer and Lohse2010), reducing the relative velocity and thereby the drag.
$U_j \simeq 175\ {\rm m}\ {\rm s}^{-1}$. This is likely to be an upper bound for the velocity, as air flow can precede the liquid jet (Thoroddsen et al. Reference Thoroddsen, Etoh and Takehara2007b; Gekle et al. Reference Gekle, Peters, Gordillo, van der Meer and Lohse2010), reducing the relative velocity and thereby the drag.
The experiments do not show measurably narrower dimples as ambient pressure is reduced. Figure 4 shows the video frames closest to the singular collapse, and there is no trend in the dimple width, whereas the size of the initial entrapped bubble clearly becomes smaller at lower ambient pressures, as in the case for impact on a solid (Li et al. Reference Li, Langley, Tian, Hicks and Thoroddsen2017).

Figure 4. The singular dimple shape at different ambient pressures. All images are selected at ![]() $t = 1\ \mathrm {\mu } {\rm s}$ prior to the end of dimple collapse for each case. The scale bar is
$t = 1\ \mathrm {\mu } {\rm s}$ prior to the end of dimple collapse for each case. The scale bar is ![]() $100\ \mathrm {\mu }{\rm m}$.
$100\ \mathrm {\mu }{\rm m}$.
Figure 3(b) shows ![]() $U_j$ from the Gerris simulations, reproducing the very narrow range of
$U_j$ from the Gerris simulations, reproducing the very narrow range of ![]() $We_c\simeq 125$ where the largest jetting velocities are observed. The fastest speed of
$We_c\simeq 125$ where the largest jetting velocities are observed. The fastest speed of ![]() $320\ {\rm m}\ {\rm s}^{-1}$ occurs without dimple pinch-off, but when microbubbles or the air sheet is pulled out of the bottom corner of the dimple, which plays a crucial role in the jetting mechanism we propose below. But why is there such a large range of jet velocities for the green data points without pinch-off?
$320\ {\rm m}\ {\rm s}^{-1}$ occurs without dimple pinch-off, but when microbubbles or the air sheet is pulled out of the bottom corner of the dimple, which plays a crucial role in the jetting mechanism we propose below. But why is there such a large range of jet velocities for the green data points without pinch-off?
Figure 5(e–g) shows the shape at emergence for the second-highest-speed jet, which has a broad mushroom-like tip. Such broader tips are visible, inside the dimple, in some of the experiments (figure 5h). This configuration leaves a minuscule wedge-shaped air sheet, which has a conical shape in three dimensions. The resemblance of the air sheet to that which has been observed in isolated experiments shown in figure 5(b) hints at the same formation process. Yang et al. (Reference Yang, Tian and Thoroddsen2020) also observed similar microbubble shedding for immiscible impact as shown in figure 5(d). Note that, even though there is no experimental observation of this microscopic air sheet, these two cases supply indirect proof for their presence and possible breakup. Future X-ray imaging could clarify their formation and dynamics.
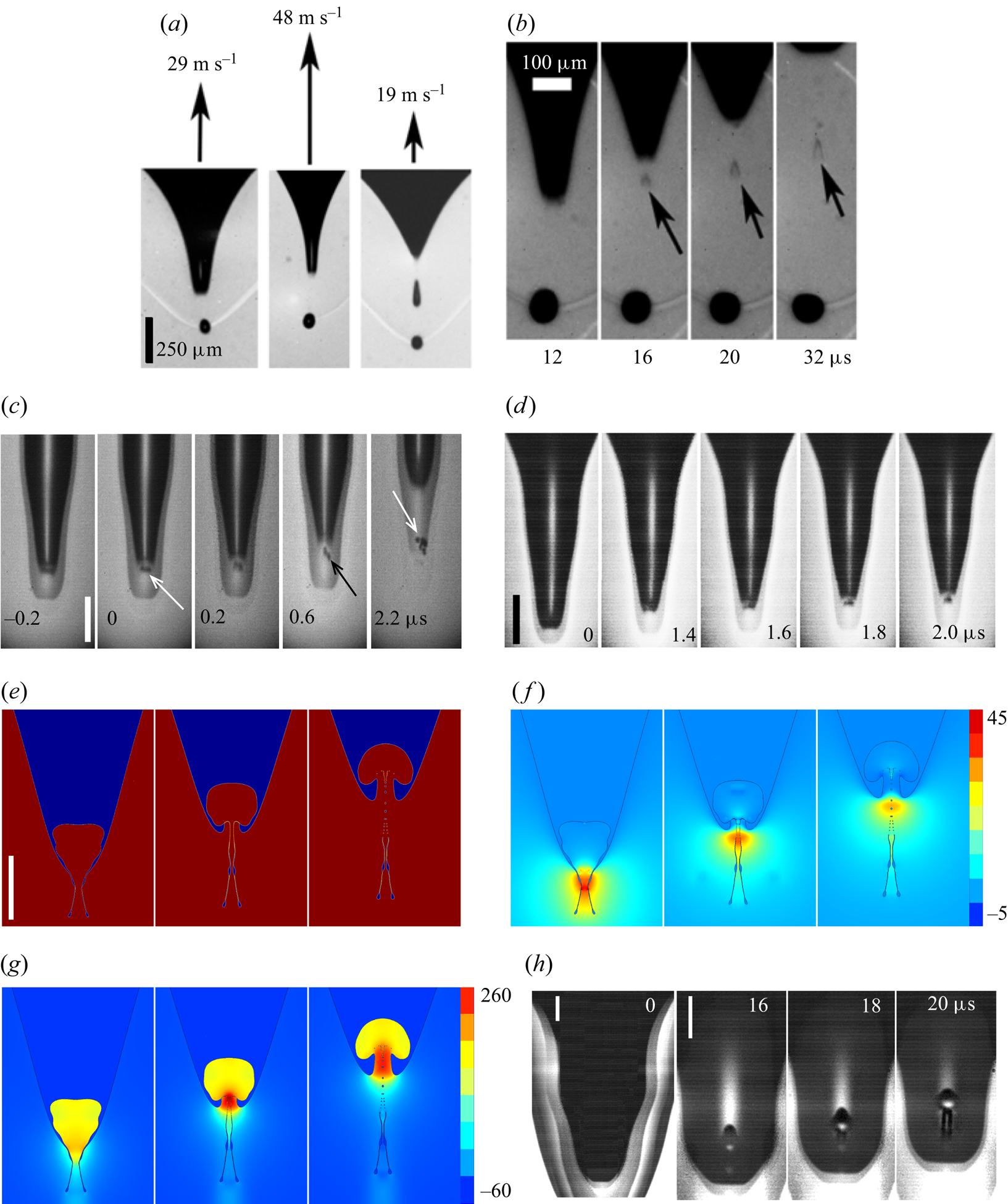
Figure 5. (a) Dimple shapes and the corresponding jet speeds. (b) The wedge-shaped microbubbles shed from the tip of the dimple; modified from Thoroddsen et al. (Reference Thoroddsen, Takehara, Nguyen and Etoh2018). The small bubble in all of the frames comes from the initial air disc entrapped under the drop when it first hits the pool surface (Peck & Sigurdson Reference Peck and Sigurdson1994; Thoroddsen, Etoh & Takehara Reference Thoroddsen, Etoh and Takehara2003; Jian et al. Reference Jian, Channa, Kherbeche, Chizari, Thoroddsen and Thoraval2020a). This bubble is removed in the numerical simulations. (c,d) Microbubble entrapment at the edge of the dimple; modified from Yang et al. (Reference Yang, Tian and Thoroddsen2020). (e–g) Simulation results from the second-highest green square in figure 3(b), showing the broad jet tip shape (e), pressure field (f) and vertical velocity (g). Images are spaced by ![]() $0.76\ \mathrm {\mu }{\rm s}$. (h) Example experimental results, with similar thick jet tip visible inside the dimple. The unmarked scale bars are
$0.76\ \mathrm {\mu }{\rm s}$. (h) Example experimental results, with similar thick jet tip visible inside the dimple. The unmarked scale bars are ![]() $50\ \mathrm {\mu }{\rm m}$.
$50\ \mathrm {\mu }{\rm m}$.
Figure 6 shows the overall shape evolution of the crater for impact conditions near, above and below the singular jet, while figure 7 highlights the small range of impact velocities where the narrowest dimple is formed in the simulations. From the first appearance of air sheets to the pinch-off of the dimple, to form a large bubble, the impact velocity changes only from ![]() $U=1.430$ to
$U=1.430$ to ![]() $1.450\ {\rm m}\ {\rm s}^{-1}$, or a change in the Weber number of less than 3 %.
$1.450\ {\rm m}\ {\rm s}^{-1}$, or a change in the Weber number of less than 3 %.
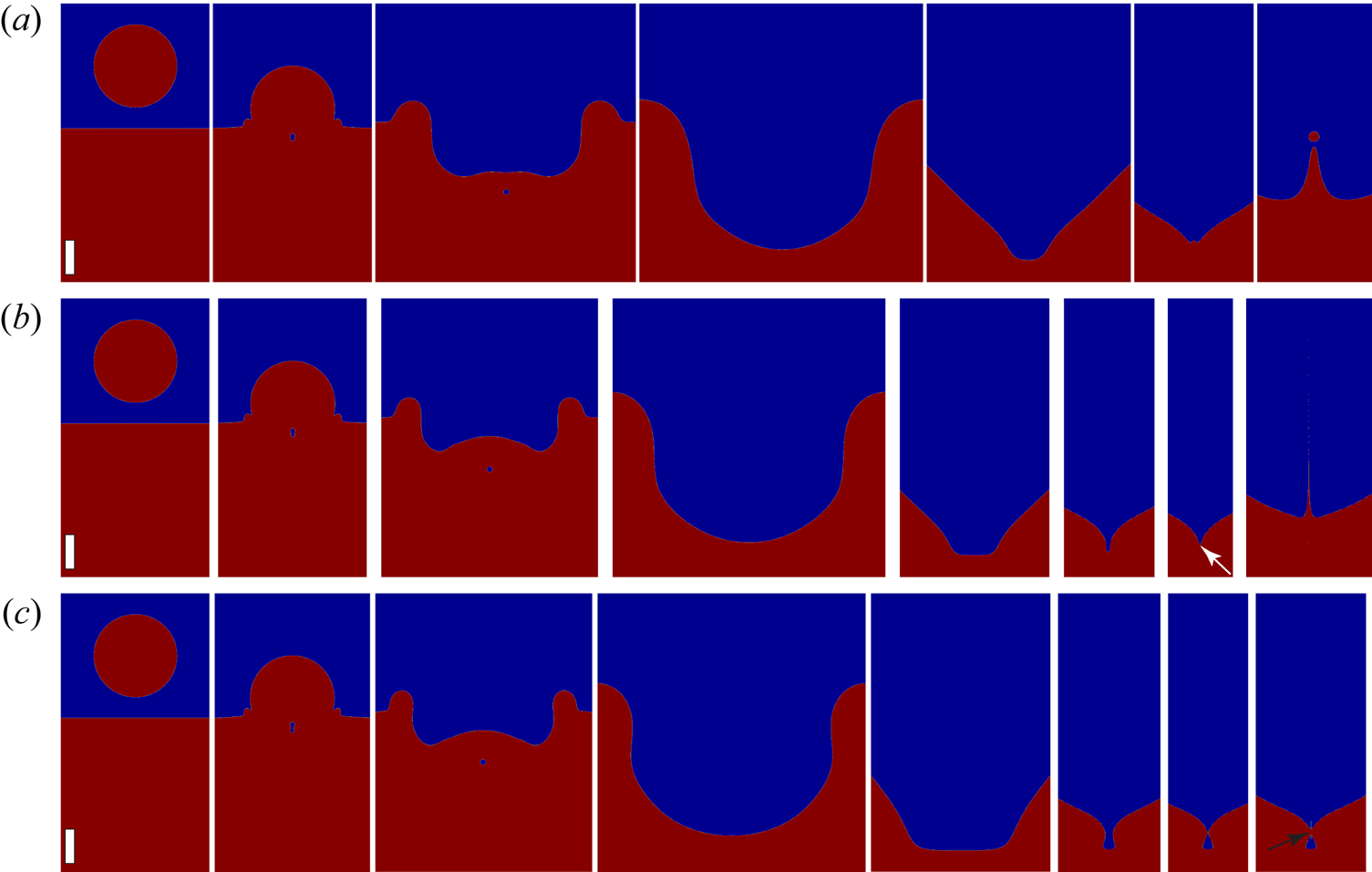
Figure 6. The entire process of the drop impact till the jet emission from the Gerris simulations: (a) low-speed Worthington jet, ![]() $We = 108$,
$We = 108$, ![]() $Re = 756$; (b) singular jet with bubble shedding,
$Re = 756$; (b) singular jet with bubble shedding, ![]() $We = 125$,
$We = 125$, ![]() $Re = 815$; and (c) bubble pinch-off from the dimple,
$Re = 815$; and (c) bubble pinch-off from the dimple, ![]() $We = 145$,
$We = 145$, ![]() $Re = 875$. The white arrow in panel (b) indicates the air sheet generated in the singular case. The scale bars are 1.5 mm.
$Re = 875$. The white arrow in panel (b) indicates the air sheet generated in the singular case. The scale bars are 1.5 mm.
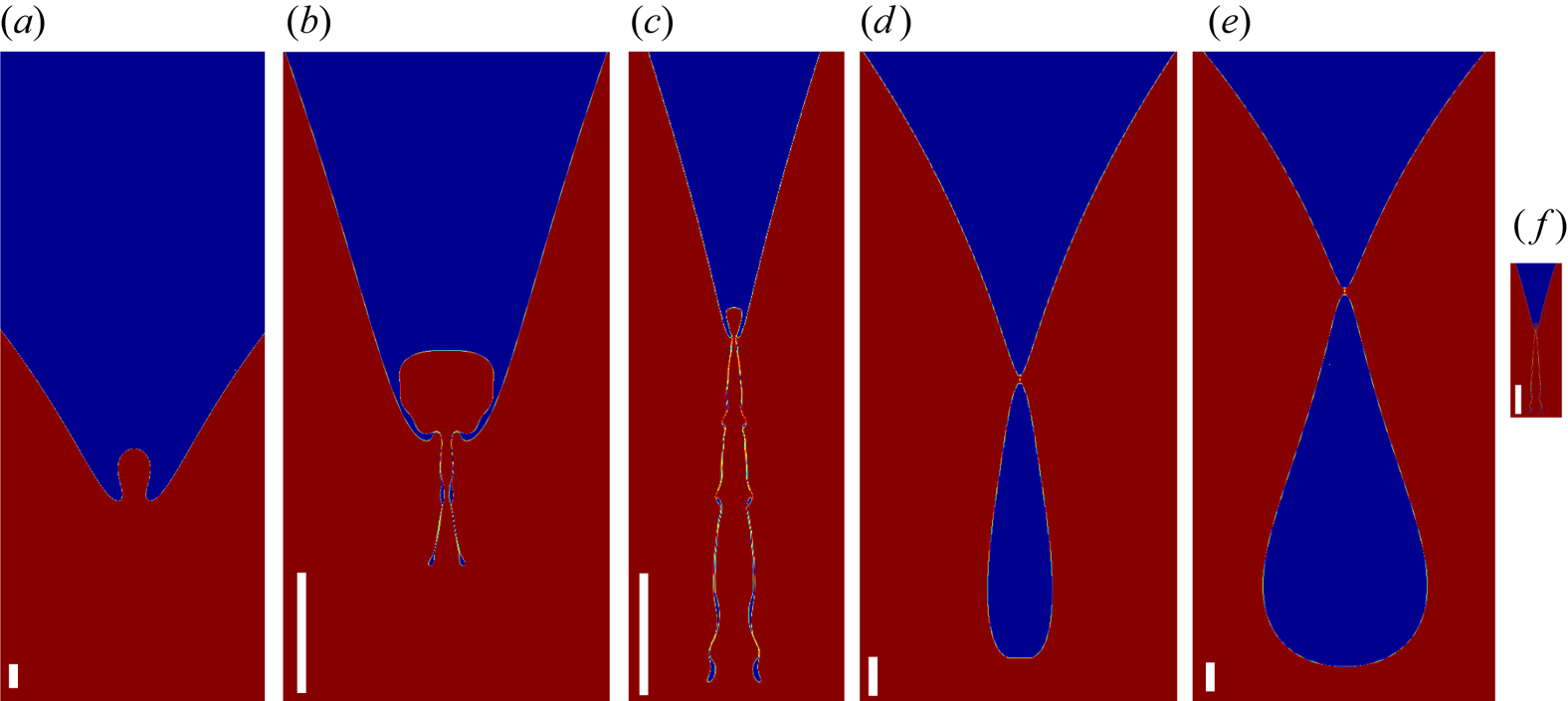
Figure 7. Distinctively different dimple shapes within a narrow range of impact velocities. The drop diameter and liquid viscosity in the simulations are identical to those in our experiments, ![]() $D = 3.6$ mm and
$D = 3.6$ mm and ![]() $\mu = 7.3$ cP. The impact velocity and corresponding
$\mu = 7.3$ cP. The impact velocity and corresponding ![]() $We$ and
$We$ and ![]() $Re$ for each simulation are: (a)
$Re$ for each simulation are: (a) ![]() $U=1.410\ {\rm m}\ {\rm s}^{-1}$,
$U=1.410\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 121.3$,
$We = 121.3$, ![]() $Re = 801.5$; (b)
$Re = 801.5$; (b) ![]() $U=1.430\ {\rm m}\ {\rm s}^{-1}$,
$U=1.430\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 124.8$,
$We = 124.8$, ![]() $Re = 812.9$; (c)
$Re = 812.9$; (c) ![]() $U=1.435\ {\rm m}\ {\rm s}^{-1}$,
$U=1.435\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 125.4$,
$We = 125.4$, ![]() $Re = 814.0$; (d)
$Re = 814.0$; (d) ![]() $U=1.450\ {\rm m}\ {\rm s}^{-1}$,
$U=1.450\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 128.3$,
$We = 128.3$, ![]() $Re = 824.2$; and (e)
$Re = 824.2$; and (e) ![]() $U=1.490\ {\rm m}\ {\rm s}^{-1}$,
$U=1.490\ {\rm m}\ {\rm s}^{-1}$, ![]() $We = 135.5$,
$We = 135.5$, ![]() $Re = 847.0$. The scale bars shown on the snapshots are all
$Re = 847.0$. The scale bars shown on the snapshots are all ![]() $50\ \mathrm {\mu }{\rm m}$. Note the strong zoom-in for the panels with the air sheets. For direct comparison, we have in panel (f) duplicated the conical air sheet from (c), but now used the same scale as in (e). This shows that the length of the air sheet is much smaller than the pinched-off bubble.
$50\ \mathrm {\mu }{\rm m}$. Note the strong zoom-in for the panels with the air sheets. For direct comparison, we have in panel (f) duplicated the conical air sheet from (c), but now used the same scale as in (e). This shows that the length of the air sheet is much smaller than the pinched-off bubble.
Figure 8 reveals the mechanism driving the fastest jets, during the rapid vertical ‘retraction’ of the bottom of the cylindrical dimple. An air sheet is pulled from the corner of the air dimple and the liquid is forced up into the cylindrical air cavity, while maintaining a thin air sheet between the radially converging dimple and the vertically moving squeezed jet. Even though the air is thin (![]() ${\sim }1\ \mathrm {\mu }{\rm m}$), it provides a free-slip boundary protecting the jet from viscous stress from the outer liquid. The liquid is thereby shot out of a ‘barrel’, which narrows in the direction of motion, as well as in time. The phase of these two motions, radial and axial, determines the final diameter and velocity of the jet, as it emerges out of the dimple. This mechanism is sketched in figure 9.
${\sim }1\ \mathrm {\mu }{\rm m}$), it provides a free-slip boundary protecting the jet from viscous stress from the outer liquid. The liquid is thereby shot out of a ‘barrel’, which narrows in the direction of motion, as well as in time. The phase of these two motions, radial and axial, determines the final diameter and velocity of the jet, as it emerges out of the dimple. This mechanism is sketched in figure 9.
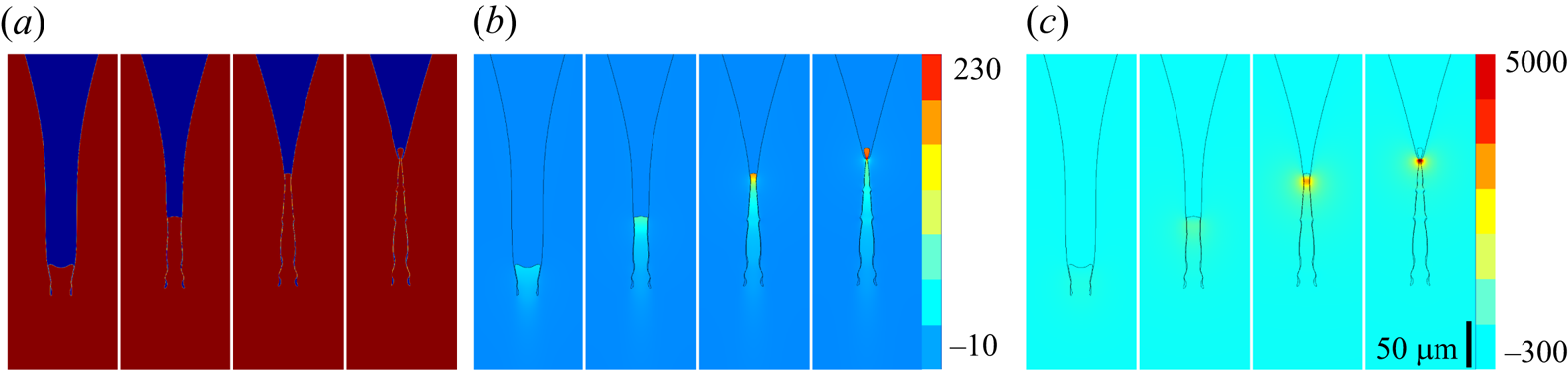
Figure 8. The cone focusing mechanism driving out the fastest narrow jet, at ![]() $U_j=320\ {\rm m}\ {\rm s}^{-1}$, emerging under the conditions of
$U_j=320\ {\rm m}\ {\rm s}^{-1}$, emerging under the conditions of ![]() $D=3.64$ mm and
$D=3.64$ mm and ![]() $U=1.435\ {\rm m}\ {\rm s}^{-1}$, giving
$U=1.435\ {\rm m}\ {\rm s}^{-1}$, giving ![]() $We= 125$ and
$We= 125$ and ![]() $Fr=58$, for
$Fr=58$, for ![]() $\mu =7.3$ cP and at atmospheric pressure: (a) interface shape; (b) vertical velocity; and (c) dynamic pressure. This entire sequence lasts for a real time of
$\mu =7.3$ cP and at atmospheric pressure: (a) interface shape; (b) vertical velocity; and (c) dynamic pressure. This entire sequence lasts for a real time of ![]() $t=t^*L/U = 1.20\ \mathrm {\mu }{\rm s}$.
$t=t^*L/U = 1.20\ \mathrm {\mu }{\rm s}$.
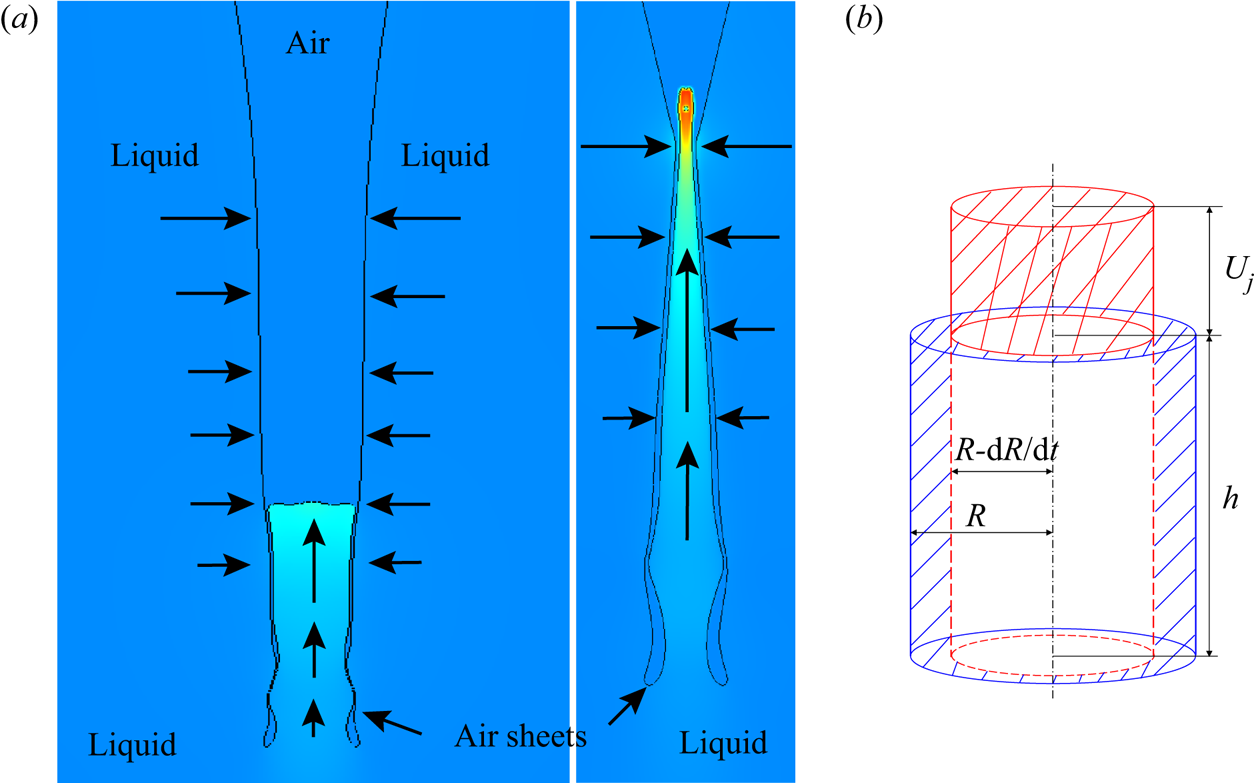
Figure 9. Schematic of the new focusing mechanism. (a) The arrows indicate the local velocity of the liquid. This highlights the decoupling between the radial collapse of the dimple wall and the vertical jetting within the inner cone, with the two regions separated by a thin continuous air layer. The free surfaces are taken from the actual simulation in figure 8. The colour indicates the vertical velocity. The original width of the dimple here is ![]() ${\sim }40\ \mathrm {\mu }{\rm m}$. (b) Sketch showing the evolution of two presumed ‘barrel’ cylinders evolving in time from blue to red, during which the volume is conserved.
${\sim }40\ \mathrm {\mu }{\rm m}$. (b) Sketch showing the evolution of two presumed ‘barrel’ cylinders evolving in time from blue to red, during which the volume is conserved.
Yang et al. (Reference Yang, Tian and Thoroddsen2020) showed that the fastest jets are generated by the narrowest dimple that does not pinch off a bubble, i.e. what they call the ‘telescopic dimple’. Now the reason for this is clear, as the walls must confine, accelerate and direct the fine jet. This follows the simplest possible flow, i.e. that of accelerating towards an axisymmetric sink. Simple volume conservation of a squeezed liquid cylinder inside the dimple, as shown in figure 9, predicts a consistent jet speed,
when we use the height of the dimple ![]() $h=100\ \mathrm {\mu }{\rm m}$ and radial collapse at
$h=100\ \mathrm {\mu }{\rm m}$ and radial collapse at ![]() $15\ {\rm m}\ {\rm s}^{-1}$, estimated from the dimple diameter reducing from 40 to 10
$15\ {\rm m}\ {\rm s}^{-1}$, estimated from the dimple diameter reducing from 40 to 10 ![]() $\mathrm {\mu }$m in
$\mathrm {\mu }$m in ![]() ${\sim }1\ \mathrm {\mu }{\rm s}$. Note that the dimple height
${\sim }1\ \mathrm {\mu }{\rm s}$. Note that the dimple height ![]() $h$, dimple radius
$h$, dimple radius ![]() $R$ and dimple collapse velocity
$R$ and dimple collapse velocity ![]() ${\rm d}R/{\rm d}t$ are measured from our simulations. The local Reynolds number of the
${\rm d}R/{\rm d}t$ are measured from our simulations. The local Reynolds number of the ![]() $d_j=10\ \mathrm {\mu }{\rm m}$ jet is
$d_j=10\ \mathrm {\mu }{\rm m}$ jet is ![]() $Re_j = d_j U_j/\nu \simeq 400$, suggesting that viscosity has not limited this velocity. The local Weber number,
$Re_j = d_j U_j/\nu \simeq 400$, suggesting that viscosity has not limited this velocity. The local Weber number, ![]() $We_j = \rho U_j^2 d_j/\sigma \sim {O}(10^4)$, suggests that there is no capillary contribution either. With perfect alignment, we do not see why these jets cannot be even thinner and faster, i.e. when the radial collapse has reached an even smaller diameter at the exact time of jet emergence.
$We_j = \rho U_j^2 d_j/\sigma \sim {O}(10^4)$, suggests that there is no capillary contribution either. With perfect alignment, we do not see why these jets cannot be even thinner and faster, i.e. when the radial collapse has reached an even smaller diameter at the exact time of jet emergence.
4. Discussion and conclusions
The most unexpected aspect of this jetting mechanism is the effective slip provided by the conical air film at the outer edge of the base of the jet, which brings to mind other geometries where air films play a key role, e.g. the drag reduction from the vapour layer on a free-falling Leidenfrost sphere, as has been realized over a range of viscosities (Vakarelski et al. Reference Vakarelski, Berry, Chan and Thoroddsen2016); leaping shampoo also glides on a ![]() $0.5\ \mathrm {\mu }{\rm m}$ air film (Lee et al. Reference Lee, Li, Marston, Bonito and Thoroddsen2013). This neutralizing of the viscous shear may explain why our jets (Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018; Yang et al. Reference Yang, Tian and Thoroddsen2020) are much faster than those in the related dimple geometry from bursting bubbles at a pool surface (Walls, Henaux & Bird Reference Walls, Henaux and Bird2015; Gañán-Calvo Reference Gañán-Calvo2017; Séon & Liger-Belair Reference Séon and Liger-Belair2017; Brasz et al. Reference Brasz, Bartlett, Walls, Flynn, Yu and Bird2018; Gañán-Calvo Reference Gañán-Calvo2018; Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2018; Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2019). The suggested bubble bursting theories include a viscous length scale, through the Ohnesorge number, but the proposed scaling does not work for our jet velocities; see § 4 in Yang et al. (Reference Yang, Tian and Thoroddsen2020), where their fastest jets were an order of magnitude faster and two orders of magnitude thinner than predicted for the viscous scaling used for bursting bubbles. Figure 10 shows where our fastest jets herein fall in this proposed scaling from Gañán-Calvo (Reference Gañán-Calvo2017). The jet velocity is normalized by the capillary–viscous velocity to form a capillary number, i.e.
$0.5\ \mathrm {\mu }{\rm m}$ air film (Lee et al. Reference Lee, Li, Marston, Bonito and Thoroddsen2013). This neutralizing of the viscous shear may explain why our jets (Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018; Yang et al. Reference Yang, Tian and Thoroddsen2020) are much faster than those in the related dimple geometry from bursting bubbles at a pool surface (Walls, Henaux & Bird Reference Walls, Henaux and Bird2015; Gañán-Calvo Reference Gañán-Calvo2017; Séon & Liger-Belair Reference Séon and Liger-Belair2017; Brasz et al. Reference Brasz, Bartlett, Walls, Flynn, Yu and Bird2018; Gañán-Calvo Reference Gañán-Calvo2018; Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2018; Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2019). The suggested bubble bursting theories include a viscous length scale, through the Ohnesorge number, but the proposed scaling does not work for our jet velocities; see § 4 in Yang et al. (Reference Yang, Tian and Thoroddsen2020), where their fastest jets were an order of magnitude faster and two orders of magnitude thinner than predicted for the viscous scaling used for bursting bubbles. Figure 10 shows where our fastest jets herein fall in this proposed scaling from Gañán-Calvo (Reference Gañán-Calvo2017). The jet velocity is normalized by the capillary–viscous velocity to form a capillary number, i.e. ![]() $Ca = U_j/(\sigma /\mu _l)$. This is predicted to be a power-law function of
$Ca = U_j/(\sigma /\mu _l)$. This is predicted to be a power-law function of ![]() $\psi =(Oh^*/Oh-1)Oh^{-1}$, which includes the Ohnesorge number
$\psi =(Oh^*/Oh-1)Oh^{-1}$, which includes the Ohnesorge number ![]() $Oh=\mu _l/\sqrt {\sigma \rho R}$. The fastest jets are about a factor of 10 higher speed and do not show any convincing power law. One might conclude that perhaps the final collapse differs between drop-impact craters and bursting bubbles, with air sheets absent in the lower Reynolds numbers for the latter.
$Oh=\mu _l/\sqrt {\sigma \rho R}$. The fastest jets are about a factor of 10 higher speed and do not show any convincing power law. One might conclude that perhaps the final collapse differs between drop-impact craters and bursting bubbles, with air sheets absent in the lower Reynolds numbers for the latter.
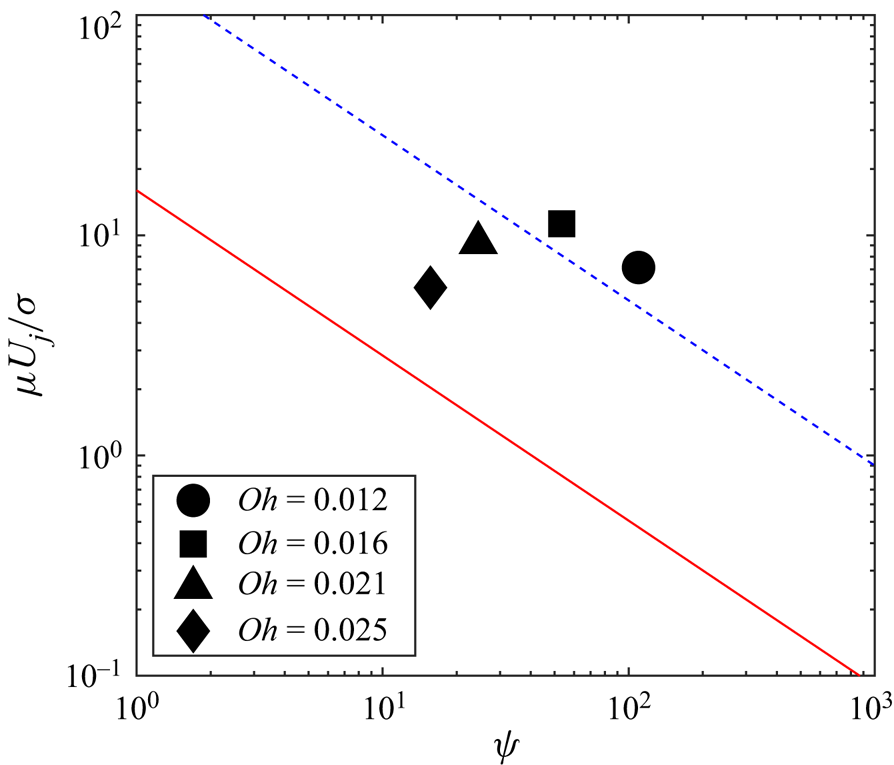
Figure 10. Plot of ![]() $Ca$ versus
$Ca$ versus ![]() $\psi$ for singular jets;
$\psi$ for singular jets; ![]() $Ca$ is the capillary number of the fastest secondary droplet, and
$Ca$ is the capillary number of the fastest secondary droplet, and ![]() $\psi = (Oh^*/Oh-1)Oh^{-1}$, where
$\psi = (Oh^*/Oh-1)Oh^{-1}$, where ![]() $Oh^* = 0.043$ from Gañán-Calvo (Reference Gañán-Calvo2017). The blue dashed line represents
$Oh^* = 0.043$ from Gañán-Calvo (Reference Gañán-Calvo2017). The blue dashed line represents ![]() $Ca = k\psi ^{-3/4}$, where
$Ca = k\psi ^{-3/4}$, where ![]() $k = 160$. However, this is an order of magnitude larger than the
$k = 160$. However, this is an order of magnitude larger than the ![]() $k = 16$ of Gañán-Calvo (Reference Gañán-Calvo2017), shown by the red solid line).
$k = 16$ of Gañán-Calvo (Reference Gañán-Calvo2017), shown by the red solid line).
The decoupling of the radial and axial motions will not be captured by flows demanding continuous velocity fields (Gekle et al. Reference Gekle, Gordillo, van der Meer and Lohse2009), as the air film acts as a discontinuity in the liquid velocity field, with a huge shear rate of ![]() ${\sim }10^8\ {\rm s}^{-1}$, using
${\sim }10^8\ {\rm s}^{-1}$, using ![]() $100\ {\rm m}\ {\rm s}^{-1}$ over the
$100\ {\rm m}\ {\rm s}^{-1}$ over the ![]() $1\ \mathrm {\mu }{\rm m}$ thickness of the air layer. The presence of the air layer does not provide a fully free-slip boundary condition, owing to the viscosity of the gas. However, for reference, if the air layer were filled with the much-larger-viscosity liquid, the shear stress would increase by a factor of
$1\ \mathrm {\mu }{\rm m}$ thickness of the air layer. The presence of the air layer does not provide a fully free-slip boundary condition, owing to the viscosity of the gas. However, for reference, if the air layer were filled with the much-larger-viscosity liquid, the shear stress would increase by a factor of ![]() $\mu _l/\mu _{air}=428$. Furthermore, the large shear rate across the air layer may help stabilize it from capillary breakup.
$\mu _l/\mu _{air}=428$. Furthermore, the large shear rate across the air layer may help stabilize it from capillary breakup.
How does the air film form? Convergent viscous stress at a free surface can lead to air entrainment, as shown in the seminal paper of Jeong & Moffatt (Reference Jeong and Moffatt1992), where the competition between viscous stress and surface tension leads to cusp formation. Eggers (Reference Eggers2001) showed that the lubrication of the converging air flow pulled along the free surface prevents sharpening of the cusp to counteract the viscous stress and a film of air is pulled in. This work has been extended by Kumar, Das & Mitra (Reference Kumar, Das and Mitra2017a,Reference Kumar, Das and Mitrab) to account for asymmetric shear stress. In contrast, in our configuration, the dimple is first formed by converging capillary waves, whereas the final dynamics is independent of surface tension and the air film is created when the jet is forced into the bottom of the dimple. The structure of the shear is therefore different from the above studies.
The above discussion shows that the appearance of the air sheets circumvents viscous control of the jetting during the final inertial focusing from our earlier studies (Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018; Yang et al. Reference Yang, Tian and Thoroddsen2020). Kayal, Basak & Dasgupta (Reference Kayal, Basak and Dasgupta2022) recently studied a minimal model for converging capillary waves without gravity and viscosity. Their simulations have insufficient resolution to capture possible air sheets, but obtain normalized jetting velocities ![]() $v_n = U_j/\sqrt {\sigma /\rho R} = 489$, which is significantly lower than our value of
$v_n = U_j/\sqrt {\sigma /\rho R} = 489$, which is significantly lower than our value of ![]() $v_n \simeq 1590$, using the maximum radius of our cavity.
$v_n \simeq 1590$, using the maximum radius of our cavity.
How realistic are the Gerris simulations? They are known to capture the finest details of splashing (Thoraval et al. Reference Thoraval, Takehara, Etoh, Popinet, Ray, Josserand, Zaleski and Thoroddsen2012) and here they closely reproduced the dimple shapes and the critical Weber number for singular jets, ![]() $We_c \simeq 125$, with any deviation likely arising from the drop shape, which is kept spherical in the simulations, while it oscillates slightly during the free fall in the experiments. Keep in mind that volume-of-fluid simulations have a finite cutoff where a small bubble or air film is eliminated and smoothed out. The final dynamics of a neck pinch-off is therefore achieved artificially. On the other hand, for the singular cases herein, they occur without pinch-off, bypassing this problem, but also requiring extreme grid refinement. The air films in figure 8 are
$We_c \simeq 125$, with any deviation likely arising from the drop shape, which is kept spherical in the simulations, while it oscillates slightly during the free fall in the experiments. Keep in mind that volume-of-fluid simulations have a finite cutoff where a small bubble or air film is eliminated and smoothed out. The final dynamics of a neck pinch-off is therefore achieved artificially. On the other hand, for the singular cases herein, they occur without pinch-off, bypassing this problem, but also requiring extreme grid refinement. The air films in figure 8 are ![]() ${\sim }1\ \mathrm {\mu }{\rm m}$ thick, which is three orders of magnitude smaller than the crater size, presenting significant challenges to numerical studies, even in the axisymmetric case. Comparison with experiments shows qualitatively similar results, with the fastest measured jet velocities, after accounting for air drag, at up to
${\sim }1\ \mathrm {\mu }{\rm m}$ thick, which is three orders of magnitude smaller than the crater size, presenting significant challenges to numerical studies, even in the axisymmetric case. Comparison with experiments shows qualitatively similar results, with the fastest measured jet velocities, after accounting for air drag, at up to ![]() $175\ {\rm m}\ {\rm s}^{-1}$. The larger simulated velocity of
$175\ {\rm m}\ {\rm s}^{-1}$. The larger simulated velocity of ![]() $320\ {\rm m}\ {\rm s}^{-1}$ can obviously arise from the extreme sensitivity to boundary conditions, or can be affected by two properties of the numerical algorithm.
$320\ {\rm m}\ {\rm s}^{-1}$ can obviously arise from the extreme sensitivity to boundary conditions, or can be affected by two properties of the numerical algorithm.
First, the gas and liquid are both incompressible, whereas the air dimple is known to compress measurably from the high dynamic pressure and then emit sound waves through the Minneart mechanism (Pumphrey & Elmore Reference Pumphrey and Elmore1990; Prosperetti & Oguz Reference Prosperetti and Oguz1993; Phillips, Agarwal & Jordan Reference Phillips, Agarwal and Jordan2018; Thoroddsen et al. Reference Thoroddsen, Takehara, Nguyen and Etoh2018). In the experiments with bubble pinch-off, we have observed volume compression of up to a half, suggesting at least a 1 atmosphere overpressure, which we expect to be even larger for the singular case. One would require compressible simulation to verify this effect, which is beyond the current capability of the Gerris code (Popinet Reference Popinet2018), but could be available soon.
Second, our simulations impose axisymmetry, which prevents the air film from rupturing in the azimuthal direction, or from its edge (Jian, Deng & Thoraval Reference Jian, Deng and Thoraval2020b). The compressibility effects can be prominent, as the Mach number ![]() $Ma=U_j/c$ of the maximum experimental jet speed is
$Ma=U_j/c$ of the maximum experimental jet speed is ![]() $Ma\simeq 0.40$, where
$Ma\simeq 0.40$, where ![]() $c$ is the speed of sound, which is independent of ambient pressure. This may contribute additional drag on the jet tip. The numerics are incompressible, but suggest that even larger
$c$ is the speed of sound, which is independent of ambient pressure. This may contribute additional drag on the jet tip. The numerics are incompressible, but suggest that even larger ![]() $U_j$ are possible, reaching conditions of relevance to forced jets encountered in applications (Thoroddsen et al. Reference Thoroddsen, Takehara, Etoh and Ohl2009; Tagawa et al. Reference Tagawa, Oudalov, Visser, Peters, van der Meer, Sun, Prosperetti and Lohse2012; Rohilla & Marston Reference Rohilla and Marston2020). The stability of the air sheets and jet motion inside the dimple could in the future be studied with X-ray imaging with submicrosecond time resolution, which is beyond current capabilities (Rump et al. Reference Rump, Saade, Sen, Fezzaa, Versluis, Lohse and Segers2022).
$U_j$ are possible, reaching conditions of relevance to forced jets encountered in applications (Thoroddsen et al. Reference Thoroddsen, Takehara, Etoh and Ohl2009; Tagawa et al. Reference Tagawa, Oudalov, Visser, Peters, van der Meer, Sun, Prosperetti and Lohse2012; Rohilla & Marston Reference Rohilla and Marston2020). The stability of the air sheets and jet motion inside the dimple could in the future be studied with X-ray imaging with submicrosecond time resolution, which is beyond current capabilities (Rump et al. Reference Rump, Saade, Sen, Fezzaa, Versluis, Lohse and Segers2022).
Herein, we have identified the missing link between radial dimple collapse and the fastest vertical microjetting. The effective slip from the conical air film decouples the radial and vertical motions, and the freedom in the phase between the two motions explains the extreme sensitivity to initial conditions. It furthermore explains the failure of viscous scaling for the fastest jets as well as their extreme velocities. In addition, it suggests that even faster jetting could be induced.
Supplementary material and movies
Supplementary material and movies are available at https://doi.org/10.1017/jfm.2022.1085.
Funding
This study was supported by King Abdullah University of Science and Technology (KAUST) under URF/1/3727-01-01 and BAS/1/1352-01-01. Y.S.T. is also supported by the Fundamental Research Funds for the Central Universities, CHD (grant no. 300102252109).
Declaration of interests
The authors report no conflict of interest.
Author contributions
Y.S.T and Z.Q.Y. contributed equally to this work.


























































































