Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-16T09:34:30.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Deep reinforcement transfer learning of active control for bluff body flows at high Reynolds number

Published online by Cambridge University Press:  20 October 2023

Zhicheng Wang Open the ORCID record for Zhicheng Wang [Opens in a new window] ,
Dixia Fan Open the ORCID record for Dixia Fan [Opens in a new window] ,
Xiaomo Jiang ,
Michael S. Triantafyllou Open the ORCID record for Michael S. Triantafyllou [Opens in a new window]  and
George Em Karniadakis
Zhicheng Wang
Affiliation:
Laboratory of Ocean Energy Utilization of Ministry of Education, Dalian University of Technology, Dalian 116024, PR China School of Energy and Power Engineering, Dalian University of Technology, Dalian 116024, PR China
Dixia Fan
Affiliation:
School of Engineering, Westlake University, Hangzhou 310024, PR China
Xiaomo Jiang
Affiliation:
School of Energy and Power Engineering, Dalian University of Technology, Dalian 116024, PR China State Key Lab of Structural Analysis, Optimization and CAE Software for Industrial Equipment, Provincial Key Lab of Digital Twin for Industrial Equipment, Dalian University of Technology, Dalian 116024, PR China
Michael S. Triantafyllou*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute Technology, Cambridge, MA 02139, USA MIT Sea Grant College Program, Cambridge, MA 02139, USA
George Em Karniadakis
Affiliation:
Division of Applied Mathematics and School of Engineering, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: mistetri@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

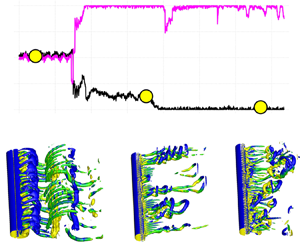
We demonstrate how to accelerate the computationally taxing process of deep reinforcement learning (DRL) in numerical simulations for active control of bluff body flows at high Reynolds number ($Re$) using transfer learning. We consider the canonical flow past a circular cylinder whose wake is controlled by two small rotating cylinders. We first pre-train the DRL agent using data from inexpensive simulations at low $Re$, and subsequently we train the agent with small data from the simulation at high $Re$ (up to $Re=1.4\times 10^5$). We apply transfer learning (TL) to three different tasks, the results of which show that TL can greatly reduce the training episodes, while the control method selected by TL is more stable compared with training DRL from scratch. We analyse for the first time the wake flow at $Re=1.4\times 10^5$ in detail and discover that the hydrodynamic forces on the two rotating control cylinders are not symmetric.

JFM classification

Flow Control: Drag reduction Turbulent Flows: Turbulence simulation Mathematical Foundations: Machine learning
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 973 , 25 October 2023 , A32
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Equal contribution.

References

Achenbach, E. 1968 Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to $Re = 5 \times 10^{6}$. J. Fluid Mech. 34 (4), 625–639.CrossRefGoogle Scholar
Bae, J. & Koumoutsakos, P. 2022 Scientific multi-agent reinforcement learning for wall-models of turbulent flows. Nat. Commun. 13, 1443.CrossRefGoogle ScholarPubMed
Braza, M., Perrin, R. & Hoarau, Y. 2006 Turbulence properties in the cylinder wake at high Reynolds numbers. J. Fluids Struct. 22 (6), 757–771.CrossRefGoogle Scholar
Breuer, M. 2000 A challenging test case for large eddy simulation: high Reynolds number circular cylinder flow. Intl J. Heat Fluid Flow 21 (5), 648–654.CrossRefGoogle Scholar
Bucci, M., Semeraro, O., Allauzen, A., Wisniewski, G., Cordier, L. & Mathelin, L. 2019 Control of chaotic systems by deep reinforcement learning. Proc. R. Soc. Lond. A 475 (2231), 20190351.Google ScholarPubMed
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
Cheng, W., Pullin, D., Samtaney, R., Zhang, W. & Gao, W. 2017 Large-eddy simulation of flow over a cylinder with $Re_{D}$ from $3.9\times 10^{3}$ to $8.5\times 10^{5}$: a skin-friction perspective. J. Fluid Mech. 820, 121–158.CrossRefGoogle Scholar
Colabrese, S., Gustavsson, K., Celani, A. & Biferale, L. 2017 Flow navigation by smart microswimmers via reinforcement learning. Phys. Rev. Lett. 118 (15), 158004.CrossRefGoogle ScholarPubMed
Dong, S., Karniadakis, G.E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.CrossRefGoogle Scholar
Du, Q., Xie, Y., Wang, Z., Jiang, X. & Xie, L. 2023 An entropy viscosity method for large eddy simulation of turbulent thermal flow in a rotor–stator cavity. Phys. Fluids 35 (3), 035126.CrossRefGoogle Scholar
Fan, D., Yang, L., Wang, Z., Triantafyllou, M.S. & Karniadaki, G.E. 2020 Reinforcement learning for bluff body active flow control in experiments and simulations. Proc. Natl Acad. Sci. USA 117 (42), 26091–26098.CrossRefGoogle ScholarPubMed
Fujimoto, S., Hoof, V. & Meger, D. 2018 Addressing function approximation error in actor-critic methods. In International Conference on Machine Learning, pp. 1582–1591.Google Scholar
Gazzola, M., Hejazialhosseini, B. & Koumoutsakos, P. 2014 Reinforcement learning and wavelet adapted vortex methods for simulations of self-propelled swimmers. SIAM J. Sci. Comput. 36 (3), B622–B639.CrossRefGoogle Scholar
Guermond, J.-L., Pasquetti, R. & Popov, B. 2011 a Entropy viscosity method for nonlinear conservation law. J. Comput. Phys. 230 (11), 4248–4267.CrossRefGoogle Scholar
Guermond, J.-L., Pasquetti, R. & Popov, B. 2011 b From suitable weak solutions to entropy viscosity. J. Sci. Comput. 49 (1), 35–50.CrossRefGoogle Scholar
Karniadakis, G.E. & Sherwin, S. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press.CrossRefGoogle Scholar
Kirkpatrick, J., et al. 2017 Overcoming catastrophic forgetting in neural networks. Proc. Natl Acad. Sci. USA 114 (13), 3521–3526.CrossRefGoogle ScholarPubMed
Ma, P., Tian, Y., Pan, Z., Ren, B. & Manocha, D. 2018 Fluid directed rigid body control using deep reinforcement learning. ACM Trans. Graph. 37 (4), 96.CrossRefGoogle Scholar
Morkovin, M. 1964 Flow around circular cylinders: a kaleidoscope of challenging fluid phenomena. In Proceedings of ASME Symposium on Fully Separated Flows, pp. 102–118.Google Scholar
Novati, G., Mahadevan, L. & Koumoutsakos, P. 2019 Controlled gliding and perching through deep-reinforcement-learning. Phys. Rev. Fluids 4 (9), 093902.CrossRefGoogle Scholar
Rabault, J., Kuchta, M., Jensen, A., Réglade, U. & Cerardi, N. 2019 Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 865, 281–302.CrossRefGoogle Scholar
Reddy, G., Celani, A., Sejnowski, T. & Vergassola, M. 2016 Learning to soar in turbulent environments. Proc. Natl Acad. Sci. USA 113 (33), E4877–E4884.CrossRefGoogle ScholarPubMed
Ren, F., Hu, H. & Tang, H. 2020 Active flow control using machine learning: a brief review. J. Hydrodyn. 32 (2), 247–253.CrossRefGoogle Scholar
Ren, F., Rabault, J. & Tang, H. 2021 Applying deep reinforcement learning to active flow control in weakly turbulent conditions. Phys. Fluids 33 (3), 037121.CrossRefGoogle Scholar
Verma, S., Novati, G. & Koumoutsakos, P. 2018 Efficient collective swimming by harnessing vortices through deep reinforcement learning. Proc. Natl Acad. Sci. USA 115 (23), 5849–5854.CrossRefGoogle ScholarPubMed
Viquerat, J., Rabault, J., Kuhnle, A., Ghraieb, H., Larcher, A. & Hachem, E. 2021 Direct shape optimization through deep reinforcement learning. J. Comput. Phys. 428, 110080.CrossRefGoogle Scholar
Wang, Z., Triantafyllou, M.S., Constantinides, Y. & Karniadakis, G.E. 2018 A spectral-element/Fourier smoothed profile method for large-eddy simulations of complex VIV problems. Comput. Fluids 172, 84–96.CrossRefGoogle Scholar
Wang, Z., Triantafyllou, M.S., Constantinides, Y. & Karniadakis, G.E. 2019 An entropy-viscosity large eddy simulation study of turbulent flow in a flexible pipe. J. Fluid Mech. 859, 691–730.CrossRefGoogle Scholar