Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-29T02:32:04.129Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of shear flow on the rotational diffusion of a single axisymmetric particle

Published online by Cambridge University Press:  28 April 2015

Brian D. Leahy ,
Donald L. Koch  and
Itai Cohen
Brian D. Leahy*
Affiliation:
Department of Physics, Cornell University, Ithaca, NY 14853, USA
Donald L. Koch
Affiliation:
Department of Chemical Engineering and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
Itai Cohen
Affiliation:
Department of Physics, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: bdl48@cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Understanding the orientation dynamics of anisotropic colloidal particles is important for suspension rheology and particle self-assembly. However, even for the simplest case of dilute suspensions in shear flow, the orientation dynamics of non-spherical Brownian particles are poorly understood. Here we analytically calculate the time-dependent orientation distributions for non-spherical axisymmetric particles confined to rotate in the flow–gradient plane, in the limit of small but non-zero Brownian diffusivity. 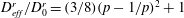For continuous shear, despite the complicated dynamics arising from the particle rotations, we find a coordinate change that maps the orientation dynamics to a diffusion equation with a remarkably simple ratio of the enhanced rotary diffusivity to the zero shear diffusion: $D_{eff}^{r}/D_{0}^{r}=(3/8)(p-1/p)^{2}+1$, where 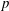$p$ is the particle aspect ratio. For oscillatory shear, the enhanced diffusion becomes orientation dependent and drastically alters the long-time orientation distributions. We describe a general method for solving the time-dependent oscillatory shear distributions and finding the effective diffusion constant. As an illustration, we use this method to solve for the diffusion and distributions in the case of triangle-wave oscillatory shear and find that they depend strongly on the strain amplitude and particle aspect ratio. These results provide new insight into the time-dependent rheology of suspensions of anisotropic particles. For continuous shear, we find two distinct diffusive time scales in the rheology that scale separately with aspect ratio 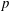$p$, as 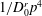$1/D_{0}^{r}p^{4}$ and as 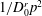$1/D_{0}^{r}p^{2}$ for 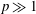$p\gg 1$. For oscillatory shear flows, the intrinsic viscosity oscillates with the strain amplitude. Finally, we show the relevance of our results to real suspensions in which particles can rotate freely. Collectively, the interplay between shear-induced rotations and diffusion has rich structure and strong effects: for a particle with aspect ratio 10, the oscillatory shear intrinsic viscosity varies by a factor of 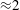${\approx}2$ and the rotational diffusion by a factor of 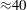${\approx}40$.

JFM classification

Complex Fluids: Colloids Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 42 - 79
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almog, Y. & Frankel, I. 1995 The motion of axisymmetric dipolar particles in homogeneous shear flow. J. Fluid Mech. 289, 243–261.CrossRefGoogle Scholar
Bakhvalov, N. & Panasenko, G. 1989 Homogenisation: Averaging Properties in Periodic Media. Kluwer Academic.CrossRefGoogle Scholar
Balkovsky, E., Falkovich, G. & Fouxon, A. 2001 Intermittent distribution of inertial particles in turbulent flows. Phys. Rev. Lett. 86, 2790–2793.CrossRefGoogle ScholarPubMed
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.CrossRefGoogle Scholar
Bibbo, M. A., Dinh, S. M. & Armstrong, R. C. 1985 Shear flow properties of semiconcentrated fiber suspensions. J. Rheol. 29, 905–929.CrossRefGoogle Scholar
Bird, R. B., Warner, H. R. Jr & Evans, D. C. 1971 Kinetic theory and rheology of dumbbell suspensions with Brownian motion. Adv. Polym. Sci. 8, 1–90.CrossRefGoogle Scholar
Brenner, H. 1974 Rheology of a dilute suspension of axisymmetric Brownian particles. Intl J. Multiphase Flow 1, 195–341.CrossRefGoogle Scholar
Brenner, H. 1979 Taylor dispersion in systems of sedimenting nonspherical Brownian particles I: homogeneous, centrosymmetric, axisymmetric particles. J. Colloid Interface Sci. 71, 189–208.CrossRefGoogle Scholar
Brenner, H., Nadim, A. & Haber, S. 1987 Long-time molecular diffusion, sedimentation and Taylor dispersion of a fluctuating cluster of interacting Brownian particles. J. Fluid Mech. 183, 511–582.CrossRefGoogle Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14, 284–304.CrossRefGoogle Scholar
Brown, A., Clarke, S., Convert, P. & Rennie, A. R. 2000 Orientational order in concentrated dispersions of plate-like kaolinite particles under shear. J. Rheol. 44, 221–233.CrossRefGoogle Scholar
Chaouche, M. & Koch, D. L. 2001 Rheology of non-Brownian rigid fiber suspensions with adhesive contacts. J. Rheol. 45, 369–382.CrossRefGoogle Scholar
Cioranescu, D. & Donato, P. 1999 An Introduction to Homogenization. Oxford University Press.CrossRefGoogle Scholar
Compton, B. G. & Lewis, J. A. 2014 3d-printing of lightweight cellular composites. Adv. Mater. 26, 5930–5935.CrossRefGoogle ScholarPubMed
Corté, L., Chaikin, P. M., Gollub, J. P. & Pine, D. J. 2008 Random organization in periodically driven systems. Nat. Phys. 4, 420–424.CrossRefGoogle Scholar
Datta, S. & Ghosal, S. 2009 Characterizing dispersion in microfluidic channels. Lab on a Chip 9, 2537–2550.CrossRefGoogle ScholarPubMed
Eberle, A., Vélez García, G. M., Baird, D. G. & Wapperom, P. 2010 Fiber orientation kinetics of a concentrated short glass fiber suspension in startup of simple shear flow. J. Non-Newtonian Fluid Mech. 165, 110–119.CrossRefGoogle Scholar
Fallon, M. S., Howell, B. A. & Chauhan, A. 2009 Importance of Taylor dispersion in pharmacokinetic and multiple indicator dilution modeling. Math. Med. Biol. 26, 263–296.CrossRefGoogle Scholar
Férec, J., Heniche, M., Heuzey, M. C., Ausias, G. & Carreau, P. J. 2008 Numerical solution of the Fokker–Planck equation for fiber suspensions: application to the Folgar–Tucker–Lipscomb model. J. Non-Newtonian Fluid Mech. 155, 20–29.CrossRefGoogle Scholar
Fischer, H. 1973 Longitudinal dispersion and turbulent mixing in open-channel flow. Annu. Rev. Fluid Mech. 5, 59–78.CrossRefGoogle Scholar
Folgar, F. & Tucker, C. L. 1984 Orientation behavior of fibers in concentrated suspensions. J. Reinf. Plast. Compos. 3, 98–119.CrossRefGoogle Scholar
Franceschini, A., Filippidi, E., Guazzelli, E. & Pine, D. J. 2011 Transverse alignment of fibers in a periodically sheared suspension: an absorbing phase transition with a slowly varying control parameter. Phys. Rev. Lett. 107, 250603.CrossRefGoogle Scholar
Frankel, I. & Brenner, H. 1989 On the foundations of generalized Taylor dispersion theory. J. Fluid Mech. 204, 97–119.CrossRefGoogle Scholar
Frankel, I. & Brenner, H. 1991 Generalized Taylor dispersion phenomena in unbounded homogeneous shear flows. J. Fluid Mech. 230, 147–181.CrossRefGoogle Scholar
Frankel, I. & Brenner, H. 1993 Taylor dispersion of orientable Brownian particles in unbounded homogeneous shear flows. J. Fluid Mech. 255, 129–156.CrossRefGoogle Scholar
Frattini, P. L. & Fuller, G. G. 1986 Rheo-optical studies of the effect of weak Brownian rotations in sheared suspensions. J. Fluid Mech. 168, 119–150.CrossRefGoogle Scholar
Furry, W. H. 1957 Isotropic rotational Brownian motion. Phys. Rev. 107, 7–13.CrossRefGoogle Scholar
Gason, S. J., Boger, D. V. & Dunstan, D. E. 1999 Rheo-optic measurements on dilute suspensions of hematite rods. Langmuir 15, 7446–7453.CrossRefGoogle Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics: with Special Applications to Particulate Media. Martinus Nijhoff.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1972 The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 52, 683–712.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1973 Time-dependent shear flows of a suspension of particles with weak Brownian rotations. J. Fluid Mech. 57, 753–767.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1976 Constitutive equations in suspension mechanics. Part 2. Approximate forms for a suspension of rigid particles affected by Brownian rotations. J. Fluid Mech. 76, 187–208.CrossRefGoogle Scholar
Hubbard, P. S. 1972 Rotational Brownian motion. Phys. Rev. A 6, 2421–2433.CrossRefGoogle Scholar
Iso, Y., Cohen, C. & Koch, D. L. 1996a Orientation in simple shear flow of semi-dilute fiber suspensions 1. Weakly elastic fluids. J. Non-Newtonian Fluid Mech. 62, 115–134.CrossRefGoogle Scholar
Iso, Y., Cohen, C. & Koch, D. L. 1996b Orientation in simple shear flow of semi-dilute fiber suspensions 2. Highly elastic fluids. J. Non-Newtonian Fluid Mech. 62, 135–153.CrossRefGoogle Scholar
Ivanov, Y., van de Ven, T. G. M. & Mason, S. G. 1982 Damped oscillations in the viscosity of suspensions of rigid rods I: monomodal suspensions. J. Rheol. 26, 213–230.CrossRefGoogle Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Jogun, S. & Zukoski, C. 1999 Rheology and microstructure of dense suspensions of plate-shaped colloidal particles. J. Rheol. 43, 847–871.CrossRefGoogle Scholar
Keim, N. C., Paulsen, J. D. & Nagel, S. R. 2013 Multiple transient memories in sheared suspensions: robustness, structure, and routes to plasticity. Phys. Rev. E 88, 032306.CrossRefGoogle ScholarPubMed
Kim, S. & Fan, X. 1984 A perturbation solution for rigid dumbbell suspensions in steady shear flow. J. Rheol. 28, 117–122.CrossRefGoogle Scholar
Kim, S. & Karrila, S. 2005 Microhydrodynamics: Principles and Selected Applications. Dover.Google Scholar
Krishna Reddy, N., Pérez-Juste, J., Pastoriza-Santos, I., Lang, P. R., Dhont, J. K. G., Liz-Marzán, L. M. & Vermant, J. 2011 Flow dichroism as a reliable method to measure the hydrodynamic aspect ratio of gold nanoparticles. ACS Nano 5, 4935–4944.CrossRefGoogle Scholar
Leahy, B., Cheng, X., Ong, D. C., Liddell-Watson, C. & Cohen, I. 2013 Enhancing rotational diffusion using oscillatory shear. Phys. Rev. Lett. 110, 228301.CrossRefGoogle ScholarPubMed
Leal, L. G. 1975 The slow motion of slender rod-like particles in a second-order fluid. J. Fluid Mech. 69, 305–337.CrossRefGoogle Scholar
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12, 435–476.CrossRefGoogle Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46, 685–703.CrossRefGoogle Scholar
Leal, L. G. & Hinch, E. J. 1972 The rheology of a suspension of nearly spherical particles subject to Brownian rotations. J. Fluid Mech. 55, 745–765.CrossRefGoogle Scholar
Leighton, D. T. 1989 Diffusion from an initial point distribution in an unbounded oscillating simple shear flow. Physico-Chem. Hydrodyn. 11, 377–386.Google Scholar
Okagawa, A., Cox, R. G. & Mason, S. G. 1973 The kinetics of flowing dispersions VI: transient orientation and rheological phenomena of rods and discs in shear flow. J. Colloid Interface Sci. 45, 303–329.CrossRefGoogle Scholar
Okagawa, A. & Mason, S. G. 1973 The kinetics of flowing dispersions VII: oscillatory behavior of rods and discs in shear flow. J. Colloid Interface Sci. 45, 330–358.CrossRefGoogle Scholar
Peterlin, A. 1938 Über die viskosität von verdünnten lösungen und suspensionen in abhängigkeit von der teilchenform. Z. Phys. 111 (3), 232–263.CrossRefGoogle Scholar
Petrich, M., Cohen, C. & Koch, D. L. 2000 An experimental determination of the stress-microstructure relationship in semi-concentrated fiber suspensions. J. Non-Newtonian Fluid Mech. 95, 101–133.CrossRefGoogle Scholar
Pujari, S. et al. 2009 Orientation dynamics in multiwalled carbon nanotube dispersions under shear flow. J. Chem. Phys. 130, 214903.Google ScholarPubMed
Rahnama, M., Koch, D. L. & Shaqfeh, E. S. G. 1995 The effect of hydrodynamic interactions on the orientation distribution in a fiber suspension subject to simple shear flow. Phys. Fluids 7, 487–506.CrossRefGoogle Scholar
Reeks, M. W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 14, 729–739.CrossRefGoogle Scholar
Sanders, J. A., Verhulst, F. & Murdock, J. 2000 Averaging Methods in Nonlinear Dynamical Systems, 2nd edn. Springer.Google Scholar
Scheraga, H. A. 1955 Non-Newtonian viscosity of solutions of ellipsoidal particles. J. Chem. Phys. 23, 1526–1532.CrossRefGoogle Scholar
Shaqfeh, E. S. G. & Fredrickson, G. H. 1990 The hydrodynamic stress in a suspension of rods. Phys. Fluids A 2, 7–24.CrossRefGoogle Scholar
Shaqfeh, E. S. G. & Koch, D. L. 1988 The effect of hydrodynamic interactions on the orientation of axisymmetric particles flowing through a fixed bed of spheres or fibers. Phys. Fluids 31, 728–743.CrossRefGoogle Scholar
Shofner, M. L., Lozano, K., Rodríguez-Macías, F. J. & Barrera, E. V. 2003 Nanofiber-reinforced polymers prepared by fused deposition modeling. J. Appl. Polym. Sci. 89, 3081–3090.CrossRefGoogle Scholar
Stancik, E. J., Gavranovic, G. T., Widenbrant, M. J. O., Laschitsch, A. T., Vermant, J. & Fuller, G. G. 2003 Structure and dynamics of particle monolayers at a liquid–liquid interface subjected to shear flow. Faraday Discuss. 123, 145–156.CrossRefGoogle Scholar
Stasiak, W. & Cohen, C. 1987 Multiple-time scale approach to stress growth in suspensions of rodlike macromolecules. J. Non-Newtonian Fluid Mech. 25, 277–287.CrossRefGoogle Scholar
Stewart, W. E. & Sorensen, J. P. 1972 Hydrodynamic interaction effects in rigid dumbbell suspensions. II. Computations for steady shear flow. Trans. Soc. Rheol. 16, 1–13.CrossRefGoogle Scholar
Stover, C. A. & Cohen, C. 1990 The motion of rodlike particles in the pressure-driven flow between two flat plates. Rheol. Acta 29, 192–203.CrossRefGoogle Scholar
Strand, S. S., Kim, S. & Karrila, S. J. 1987 Computation of rheological properties of suspensions of rigid rods: stress growth after inception of steady shear flow. J. Non-Newtonian Fluid Mech. 24, 311–329.CrossRefGoogle Scholar
Stroock, A. D., Dertinger, S. K. W., Ajdari, A., Mezić, I., Stone, H. A. & Whitesides, G. M. 2002 Chaotic mixer for microchannels. Science 295, 647–651.CrossRefGoogle ScholarPubMed
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.CrossRefGoogle Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Taylor, G. 1954 Conditions under which dispersion of a solute in a stream of solvent can be used to measure molecular diffusion. Proc. R. Soc. Lond. A 225, 473–477.Google Scholar
Vadas, E., Cox, R. G., Goldsmith, H. L. & Mason, S. G. 1976 The microrheology of colloidal dispersions II. Brownian diffusion of doublets of spheres. J. Colloid Interface Sci. 57, 308–326.CrossRefGoogle Scholar
Valiev, K. A. & Ivanov, E. N. 1973 Rotational Brownian motion. Sov. Phys. Uspekhi 16, 1–16.CrossRefGoogle Scholar