We examine the problem of prescribing the macroscale boundary condition to the solute convective–diffusive mass transport equation at a heterogeneous surface consisting of reactive circular disks distributed uniformly on a non-reactive surface. The reaction rate at the disks is characterized by a first-order kinetics. This problem was examined by Shah & Shaqfeh (J. Fluid Mech., vol. 782, 2015, pp. 260–299) who obtained the boundary condition in terms of an effective first-order rate constant, which they determined as a function of the Péclet number 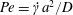$Pe=\dot{\unicode[STIX]{x1D6FE}}a^{2}/D$, the fraction 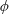$\unicode[STIX]{x1D719}$ of the surface area occupied by the reactive disks and the non-dimensional reaction rate constant 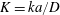$K=ka/D$. Here, $a$ is the radius of the disks, 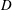$D$ is the solute diffusivity, 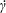$\dot{\unicode[STIX]{x1D6FE}}$ is the wall shear rate and 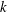$k$ is the first-order surface-reaction rate constant. Their analysis assumed that 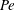$Pe$ and 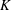$K$ are 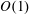$O(1)$ while the ratio of the microscale $a$ to the macroscale 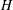$H$ is small. The macroscale transport process is convection–diffusion dominated under these conditions. We examine here the case when the non-dimensional numbers based on the macroscale 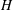$H$ are 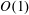$O(1)$. In this limit the microscale transport problem is reaction rate dominated. We find that the boundary condition can be expressed in terms of an effective rate constant only up to 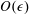$O(\unicode[STIX]{x1D716})$, where 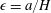$\unicode[STIX]{x1D716}=a/H$. Higher-order expressions for the mass flux involve both the macroscopic concentration and its surface gradient. The 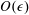$O(\unicode[STIX]{x1D716})$ microscale problem is relatively easy to solve as the convective effects are unimportant and it is possible to obtain analytical expressions for the effective rate constant as a function of 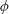$\unicode[STIX]{x1D719}$ for both periodic and random arrangement of the disks without having to solve the boundary integral equation as was done by Shah and Shaqfeh. The results thus obtained are shown to be in good agreement with those obtained numerically by Shah and Shaqfeh for 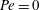$Pe=0$. In a separate study, Shah et al. (J. Fluid Mech., vol. 811, 2017, pp. 372–399) examined the inverse-geometry problem in which the disks are inert and the rest of the surface surrounding them is reactive. We show that the two problems are related when 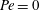$Pe=0$ and 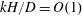$kH/D=O(1)$. Finally, a related problem of determining the current density at a surface consisting of an array of microelectrodes is also examined and the analytical results obtained for the current density are found to agree well with the computed values obtained by solving the integral equation numerically by Lucas et al. (SIAM J. Appl. Maths, vol. 57(6), 1997, pp. 1615–1638) over a wide range of parameters characterizing this problem.