No CrossRef data available.
Article contents
Lagrangian dynamics and regularity of the spin Euler equation
Published online by Cambridge University Press: 24 April 2024
Abstract
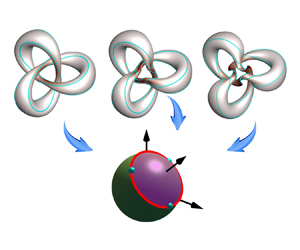
We derive the spin Euler equation for ideal flows by applying the spherical Clebsch mapping. This equation is based on the spin vector, a unit vector field encoding vortex lines, instead of the velocity. The spin Euler equation enables a feasible Lagrangian study of fluid dynamics, as the isosurface of a spin-vector component is a vortex surface and material surface in ideal flows. We establish a non-blowup criterion for the spin Euler equation, suggesting that the Laplacian of the spin vector must diverge if the solution forms a singularity at some finite time. The direct numerical simulations (DNS) of three ideal flows – the vortex knot, the vortex link and the modified Taylor–Green flow – are conducted by solving the spin Euler equation. The evolution of the Lagrangian vortex surface illustrates that the regions with large vorticity are rapidly stretched into spiral sheets. The DNS result exhibits a pronounced double-exponential growth of the maximum norm of Laplacian of the spin vector, showing no evidence of the finite-time singularity formation if the double-exponential growth holds at later times. Moreover, the present criterion with Lagrangian nature appears to be more sensitive than the Beale–Kato–Majda criterion in detecting the flows that are incapable of producing finite-time singularities.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Agafontsev, D.S., Kuznetsov, E.A. & Mailybaev, A.A. 2015 Development of high vorticity structures in incompressible 3D Euler equations. Phys. Fluids 27, 085102.CrossRefGoogle Scholar
Agafontsev, D.S., Kuznetsov, E.A. & Mailybaev, A.A. 2017 Asymptotic solution for high-vorticity regions in incompressible three-dimensional Euler equations. J. Fluid Mech. 813, R1.CrossRefGoogle Scholar
Arnold, B.C. 2015 Pareto Distribution . Wiley Online Library: https://doi.org/10.1002/9781118445112.stat01100.pub2.CrossRefGoogle Scholar
Ayala, D. & Protas, B. 2017 Extreme vortex states and the growth of enstrophy in three-dimensional incompressible flows. J. Fluid Mech. 818, 772–806.CrossRefGoogle Scholar
Beale, J.T., Kato, T. & Majda, A. 1984 Remarks on the breakdown of smooth solutions for the 3-D Euler equations. Commun. Math. Phys. 94, 61–66.CrossRefGoogle Scholar
Boratav, O.N. & Pelz, R.B. 1994 Direct numerical simulation of transition to turbulence from a high-symmetry initial condition. Phys. Fluids 6, 2757–2784.CrossRefGoogle Scholar
Brachet, M.E., Meiron, D.I., Orszag, S.A., Nickel, B.G., Morf, R.H. & Frisch, U. 1983 Small-scale structure of the Taylor–Green vortex. J. Fluid Mech. 130, 411–452.CrossRefGoogle Scholar
Brachet, M.E., Meneguzzi, M., Vincent, A., Politano, H. & Sulem, P.L. 1992 Numerical evidence of smooth self-similar dynamics and possibility of subsequent collapse for three-dimensional ideal flows. Phys. Fluids A 4, 2845–2854.CrossRefGoogle Scholar
Bustamante, M.D. & Brachet, M. 2012 Interplay between the Beale–Kato–Majda theorem and the analyticity-strip method to investigate numerically the incompressible Euler singularity problem. Phys. Rev. E 86, 066302.CrossRefGoogle ScholarPubMed
Bustamante, M.D. & Kerr, R.M. 2008 3D Euler about a 2D symmetry plane. Physica D 237, 1912–1920.CrossRefGoogle Scholar
Campolina, C.S. & Mailybaev, A.A. 2018 Chaotic blowup in the 3D incompressible Euler equations on a logarithmic lattice. Phys. Rev. Lett. 121, 064501.CrossRefGoogle ScholarPubMed
Chae, D. 2008 Incompressible Euler equations: the blow-up problem and related results. In Handbook of Differential Equations: Evolutionary Equations (ed. C.M. Dafermos & M. Pokorny), vol. 4, pp. 1–55. Elsevier.CrossRefGoogle Scholar
Chern, A. 2017 Fluid dynamics with incompressible Schrödinger flow. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Chern, A., Knöppel, F., Pinkall, U. & Schröder, P. 2017 Inside fluids: Clebsch maps for visualization and processing. ACM Trans. Graph. 36, 1–11.CrossRefGoogle Scholar
Chern, A., Knöppel, F., Pinkall, U., Schröder, P. & Weißmann, S. 2016 Schrödinger's smoke. ACM Trans. Graph. 35, 1–13.CrossRefGoogle Scholar
Chorin, A.J. 1994 Vortex phase transitions in 2
$\frac {1}{2}$ dimensions. J. Stat. Phys. 76, 835–856.CrossRefGoogle Scholar
$\frac {1}{2}$ dimensions. J. Stat. Phys. 76, 835–856.CrossRefGoogle ScholarConstantin, P. 2001 a An Eulerian–Lagrangian approach for incompressible fluids: local theory. J. Am. Math. Soc. 14, 263–278.CrossRefGoogle Scholar
Constantin, P. 2001 b An Eulerian–Lagrangian approach to the Navier–Stokes equations. Commun. Math. Phys. 216, 663–686.CrossRefGoogle Scholar
Constantin, P., Fefferman, C. & Majda, A.J. 1996 Geometric constraints on potentially singular solutions for the 3-D Euler equations. Commun. Part. Diff. Equ. 21, 559–571.Google Scholar
Deng, J., Hou, T.Y. & Yu, X. 2005 A level set formulation for the 3D incompressible Euler equations. Meth. Appl. Anal. 12, 427–440.CrossRefGoogle Scholar
Doering, C.R. 2009 The 3D Navier–Stokes problem. Annu. Rev. Fluid Mech. 41, 109–128.CrossRefGoogle Scholar
Drivas, T.D. & Elgindi, T.M. 2023 Singularity formation in the incompressible Euler equation in finite and infinite time. EMS Surv. Math. Sci. 10 (1), 1–100.CrossRefGoogle Scholar
Elgindi, T.M. 2021 Finite-time singularity formation for $C^{1,\alpha }$ solutions to the incompressible Euler equations on $\mathbb {R}^3$. Ann. Maths 194, 647–727.CrossRefGoogle Scholar
$C^{1,\alpha }$ solutions to the incompressible Euler equations on 
$\mathbb {R}^3$. Ann. Maths 194, 647–727.CrossRefGoogle ScholarFaddeev, L.D. 1976 Some comments on the many-dimensional solitons. Lett. Math. Phys. 1, 289–293.CrossRefGoogle Scholar
Fefferman, C. 2001 Existence and smoothness of the Navier–Stokes equation. The Millennium Prize Problems 57, 67. Clay Mathematics Institute.Google Scholar
Gibbon, J.D. 2008 The three-dimensional Euler equations: where do we stand? Physica D 237, 1894–1904.CrossRefGoogle Scholar
Gibbon, J.D. & Holm, D.D. 2007 Lagrangian particle paths and ortho-normal quaternion frames. Nonlinearity 20, 1745–1759.CrossRefGoogle Scholar
Grafke, T., Homann, H., Dreher, J. & Grauer, R. 2008 Numerical simulations of possible finite time singularities in the incompressible Euler equations: comparison of numerical methods. Physica D 237, 1932–1936.CrossRefGoogle Scholar
Grauer, R., Marliani, C. & Germaschewski, K. 1998 Adaptive mesh refinement for singular solutions of the incompressible Euler equations. Phys. Rev. Lett. 80, 4177–4180.CrossRefGoogle Scholar
Hopf, H. 1931 Über die Abbildungen der Dreidimensionalen Sphäre auf die Kugelfläche. Math. Ann. 104, 637–665.CrossRefGoogle Scholar
Hou, T.Y. 2009 Blow-up or no blow-up? A unified computational and analytic approach to 3D incompressible Euler and Navier–Stokes equations. Acta Numerica 18, 277–346.CrossRefGoogle Scholar
Hou, T.Y. & Li, R. 2007 Computing nearly singular solutions using pseudo-spectral methods. J. Comput. Phys. 226, 379–397.CrossRefGoogle Scholar
Hou, T.Y. & Li, R. 2008 Blowup or no blowup? The interplay between theory and numerics. Physica D 237, 1937–1944.CrossRefGoogle Scholar
Kamppeter, T., Leonel, S.A., Mertens, F.G., Gouvêa, M.E., Pires, A.S.T. & Kovalev, A.S. 2001 Topological and dynamical excitations in a classical 2D easy-axis Heisenberg model. Eur. Phys. J. B 21, 93–102.CrossRefGoogle Scholar
Kedia, H., Foster, D., Dennis, M.R. & Irvine, W.T.M. 2016 Weaving knotted vector fields with tunable helicity. Phys. Rev. Lett. 117, 274501.CrossRefGoogle ScholarPubMed
Kerr, R.M. 1993 Evidence for a singularity of the three-dimensional, incompressible Euler equations. Phys. Fluids A 5, 1725–1746.CrossRefGoogle Scholar
Kerr, R.M. 2005 Velocity and scaling of collapsing Euler vortices. Phys. Fluids 17, 075103.CrossRefGoogle Scholar
Kerr, R.M. 2013 Bounds for Euler from vorticity moments and line divergence. J. Fluid Mech. 729, R2.CrossRefGoogle Scholar
Kida, S. 1985 Three-dimensional periodic flows with high-symmetry. J. Phys. Soc. Japan 54, 2132–2136.CrossRefGoogle Scholar
Kivotides, D. & Leonard, A. 2021 Helicity spectra and topological dynamics of vortex links at high Reynolds numbers. J. Fluid Mech. 911, A25.CrossRefGoogle Scholar
Kuznetsov, E.A. & Mikhailov, A.V. 1980 On the topological meaning of canonical Clebsch variables. Phys. Lett. A 77, 37–38.CrossRefGoogle Scholar
Lakshmanan, M. & Porsezian, K. 1990 Planar radially symmetric Heisenberg spin system and generalized nonlinear Schrödinger equation: gauge equivalence, Bäcklund transformations and explicit solutions. Phys. Lett. A 146, 329–334.CrossRefGoogle Scholar
Landau, L. & Lifshitz, E. 1935 On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Zeitsch. Sow. 8, 153–169.Google Scholar
Majda, A.J. & Bertozzi, A.L. 2002 Vorticity and Incompressible Flow. Cambridge University Press.Google Scholar
Meng, Z., Shen, W. & Yang, Y. 2023 Evolution of dissipative fluid flows with imposed helicity conservation. J. Fluid Mech. 954, A36.CrossRefGoogle Scholar
Meng, Z. & Yang, Y. 2023 Quantum computing of fluid dynamics using the hydrodynamic Schrödinger equation. Phys. Rev. Res. 5, 033182.CrossRefGoogle Scholar
Moffatt, H.K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.CrossRefGoogle Scholar
Moffatt, H.K. & Tsinober, A. 1992 Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24, 281–312.CrossRefGoogle Scholar
Moreau, J.J. 1961 Constantes d'un îlot tourbillonnaire en fluide parfait barotrope. C. R. Acad. Sci. Paris 252, 2810–2812.Google Scholar
Nabizadeh, M.S., Wang, S., Ramamoorthi, R. & Chern, A. 2022 Covector fluids. ACM Trans. Graph. 41, 1–16.CrossRefGoogle Scholar
Orlandi, P., Pirozzoli, S. & Carnevale, G.F. 2012 Vortex events in Euler and Navier–Stokes simulations with smooth initial conditions. J. Fluid Mech. 690, 288–320.CrossRefGoogle Scholar
Pelz, R.B. 2001 Symmetry and the hydrodynamic blow-up problem. J. Fluid Mech. 444, 299–320.CrossRefGoogle Scholar
Planchon, F. 2003 An extension of the Beale–Kato–Majda criterion for the Euler equations. Commun. Math. Phys. 232, 319–326.CrossRefGoogle Scholar
Poincaré, H. 1890 Sur le problème des trois corps et les équations de la dynamique. Acta Mathematica 13, 1–270.Google Scholar
Porsezian, K. & Lakshmanan, M. 1991 On the dynamics of the radially symmetric Heisenberg ferromagnetic spin system. J. Math. Phys. 32, 2923–2928.CrossRefGoogle Scholar
Pumir, A. & Siggia, E. 1990 Collapsing solutions to the 3-D Euler equations. Phys. Fluids A 2, 220–241.CrossRefGoogle Scholar
Ricca, R.L., Samuels, D.C. & Barenghi, C.F. 1999 Evolution of vortex knots. J. Fluid Mech. 391, 29–44.CrossRefGoogle Scholar
Shen, W., Yao, J., Hussain, F. & Yang, Y. 2023 Role of internal structures within a vortex in helicity dynamics. J. Fluid Mech. 970, A26.CrossRefGoogle Scholar
Tao, R., Ren, H., Tong, Y. & Xiong, S. 2021 Construction and evolution of knotted vortex tubes in incompressible Schrödinger flow. Phys. Fluids 33, 077112.CrossRefGoogle Scholar
Taylor, G.I. & Green, A.E. 1937 Mechanism of the production of small eddies from large ones. Proc. R. Soc. Lond. A 158, 499–521.Google Scholar
Wei, D. 2016 Regularity criterion to the axially symmetric Navier–Stokes equations. J. Math. Anal. Applics. 435, 402–413.CrossRefGoogle Scholar
Xiong, S., Wang, Z., Wang, M. & Zhu, B. 2022 A Clebsch method for free-surface vortical flow simulation. ACM Trans. Graph. 41, 116.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2019 Identifying the tangle of vortex tubes in homogeneous isotropic turbulence. J. Fluid Mech. 874, 952–978.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2020 Effects of twist on the evolution of knotted magnetic flux tubes. J. Fluid Mech. 895, A28.CrossRefGoogle Scholar
Yang, S., Xiong, S., Zhang, Y., Feng, F., Liu, J. & Zhu, B. 2021 Clebsch gauge fluid. ACM Trans. Graph. 40, 1–11.Google Scholar
Yang, Y. & Pullin, D.I. 2010 On Lagrangian and vortex-surface fields for flows with Taylor–Green and Kida–Pelz initial conditions. J. Fluid Mech. 661, 446–481.CrossRefGoogle Scholar
Yang, Y. & Pullin, D.I. 2011 Evolution of vortex-surface fields in viscous Taylor–Green and Kida–Pelz flows. J. Fluid Mech. 685, 146–164.CrossRefGoogle Scholar
Yang, Y., Xiong, S. & Lu, Z. 2023 Applications of the vortex-surface field to flow visualization, modelling and simulation. Flow 3, E33.CrossRefGoogle Scholar
Yao, J. & Hussain, F. 2022 Vortex reconnection and turbulence cascade. Annu. Rev. Fluid Mech. 54, 317–347.CrossRefGoogle Scholar
Yao, J., Shen, W., Yang, Y. & Hussain, F. 2022 Helicity dynamics in viscous vortex links. J. Fluid Mech. 944, A41.CrossRefGoogle Scholar
Yao, J., Yang, Y. & Hussain, F. 2021 Dynamics of a trefoil knotted vortex. J. Fluid Mech. 923, A19.CrossRefGoogle Scholar
Yudovich, V.I. 1963 Non-stationary flows of an ideal incompressible fluid. Z. Vychisl. Mat. i Mat. Fiz. 3, 1032–1066.Google Scholar
Zhao, X. & Scalo, C. 2021 Helicity dynamics in reconnection events of topologically complex vortex flows. J. Fluid Mech. 920, A30.CrossRefGoogle Scholar
Zhao, X., Yu, Z., Chapelier, J. & Scalo, C. 2021 Direct numerical and large-eddy simulation of trefoil knotted vortices. J. Fluid Mech. 910, A31.CrossRefGoogle Scholar
Zhou, Y. & Lei, Z. 2013 Logarithmically improved criteria for Euler and Navier–Stokes equations. Commun. Pure Appl. Anal. 12, 2715–2719.CrossRefGoogle Scholar