Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-01T08:45:38.965Z Has data issue: false hasContentIssue false
  • English
  • Français

Modification of flow transition for a vortex ring by a bubble released at the axis

Published online by Cambridge University Press:  19 July 2023

Lingxin Zhang ,
Jian Deng Open the ORCID record for Jian Deng [Opens in a new window]  and
Xueming Shao
Lingxin Zhang
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Department of Mechanics, Zhejiang University, Hangzhou 310027, PR China
Jian Deng*
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Department of Mechanics, Zhejiang University, Hangzhou 310027, PR China
Xueming Shao
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Department of Mechanics, Zhejiang University, Hangzhou 310027, PR China
*
†Email address for correspondence: zjudengjian@zju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

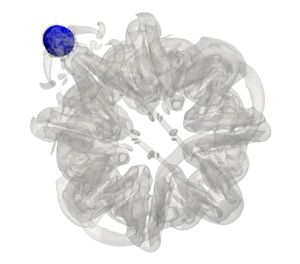
The interactions between a vortex ring and a gas bubble released at the axis are studied numerically, which shed light on understanding more complicated bubble–turbulence coupling. We fix the Reynolds number at $Re_{\tau }=7500$ and consider various Weber numbers in the range of $We=130\unicode{x2013}870$. We find that the translating speed of the vortex ring is substantially lower than the case of the vortex ring without a bubble. It is explained with two different mechanisms, depending on the Weber number. In the low-$We$ range, the reduction of translating speed of the ring is due to the capture of bubbles into the ring core, leading to significant changes in the vorticity distribution within the core. In the high-$We$ range, the repeatedly generated secondary vortex rings perturb the primary one, which bring about an earlier flow transition, thereby reducing the translating speed of the vortex ring. On the other hand, the evolution of a gas bubble is also affected by the presence of the vortex ring. In the low-$We$ range, we observe binary breakup of the bubble after it is captured by the primary vortex ring. In contrast, in the high-$We$ range, it is interesting to find that the bubble experiences sequentially stretching, spreading and breakup stages. In the high-$We$ range, the numbers of smaller bubbles predicted by the classical Rayleigh–Plateau instability of a stretched cylindrical bubble agree well with our numerical simulations. Consistent with the previous experiments, this number keeps unchanged at 16 as $We$ further increases. An additional comparison is made between two higher Reynolds numbers, indicating that the finer eddies in a vortical field with a higher Reynolds number tend to tear the bubble into more fragments.

JFM classification

Drops and Bubbles: Bubble dynamics Instability: Transition to turbulence Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 967 , 25 July 2023 , A28
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archer, P.J., Thomas, T.G. & Coleman, G.N. 2008 Direct numerical simulation of vortex ring evolution from the laminar to the early turbulent regime. J. Fluid Mech. 598, 201–226.CrossRefGoogle Scholar
van den Berg, T.H., van Gils, D.P.M., Lathrop, D.P. & Lohse, D. 2007 Bubbly turbulent drag reduction is a boundary layer effect. Phys. Rev. Lett. 98 (8), 084501.CrossRefGoogle ScholarPubMed
Van den Berg, T.H., Luther, S., Lathrop, D.P. & Lohse, D. 2005 Drag reduction in bubbly Taylor-Couette turbulence. Phys. Rev. Lett. 94 (4), 044501.CrossRefGoogle ScholarPubMed
Bergdorf, M., Koumoutsakos, P. & Leonard, A. 2007 Direct numerical simulations of vortex rings at $re \gamma = 7500$. J. Fluid Mech. 581, 495–505.CrossRefGoogle Scholar
Biswas, S. & Govardhan, R.N. 2020 Effect of single and multiple bubbles on a thin vortex ring. J. Flow Visual. Image Process. 27 (1), 1–27.CrossRefGoogle Scholar
Brackbill, J.U., Kothe, D.B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100 (2), 335–354.CrossRefGoogle Scholar
Ceccio, S.L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–203.CrossRefGoogle Scholar
Dazin, A., Dupont, P. & Stanislas, M. 2006 a Experimental characterization of the instability of the vortex ring. Part I: linear phase. Exp. Fluids 40 (3), 383–399.CrossRefGoogle Scholar
Dazin, A., Dupont, P. & Stanislas, M. 2006 b Experimental characterization of the instability of the vortex rings. Part II: non-linear phase. Exp. Fluids 41 (3), 401–413.CrossRefGoogle Scholar
Deng, J. & Caulfield, C.-C.P. 2018 Horizontal locomotion of a vertically flapping oblate spheroid. J. Fluid Mech. 840, 688–708.CrossRefGoogle Scholar
Elbing, B.R., Mäkiharju, S., Wiggins, A., Perlin, M., Dowling, D.R. & Ceccio, S.L. 2013 On the scaling of air layer drag reduction. J. Fluid Mech. 717, 484–513.CrossRefGoogle Scholar
Elbing, B.R., Winkel, E.S., Lay, K.A., Ceccio, S.L., Dowling, D.R. & Perlin, M. 2008 Bubble-induced skin-friction drag reduction and the abrupt transition to air-layer drag reduction. J. Fluid Mech. 612, 201–236.CrossRefGoogle Scholar
Elghobashi, S. 2019 Direct numerical simulation of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 51, 217–244.CrossRefGoogle Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.CrossRefGoogle Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.CrossRefGoogle Scholar
Ferziger, J.H., Perić, M. & Street, R.L. 2002 Computational Methods for Fluid Dynamics, vol. 3. Springer.CrossRefGoogle Scholar
Foronda-Trillo, F.J., Rodríguez-Rodríguez, J., Gutiérrez-Montes, C. & Martínez-Bazán, C. 2021 Deformation and breakup of bubbles interacting with single vortex rings. Intl J. Multiphase Flow 142, 103734.CrossRefGoogle Scholar
Fukumoto, Y. & Moffatt, H.K. 2008 Kinematic variational principle for motion of vortex rings. Phys. D: Nonlinear Phenom. 237 (14–17), 2210–2217.CrossRefGoogle Scholar
van Gils, D.P.M., Guzman, D.N., Sun, C. & Lohse, D. 2013 The importance of bubble deformability for strong drag reduction in bubbly turbulent Taylor–Couette flow. J. Fluid Mech. 722, 317–347.CrossRefGoogle Scholar
Hinze, J.O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1 (3), 289–295.CrossRefGoogle Scholar
Jha, N.K. & Govardhan, R.N. 2015 Interaction of a vortex ring with a single bubble: bubble and vorticity dynamics. J. Fluid Mech. 773, 460–497.CrossRefGoogle Scholar
Kolmogorov, A. 1949 On the breakage of drops in a turbulent flow. In Doklady Akademii Nauk SSSR, vol. 66, pp. 825–828.Google Scholar
Lauterborn, W. & Kurz, T. 2010 Physics of bubble oscillations. Rep. Prog. Phys. 73 (10), 106501.CrossRefGoogle Scholar
Lu, J., Fernández, A. & Tryggvason, G. 2005 The effect of bubbles on the wall drag in a turbulent channel flow. Phys. Fluids 17 (9), 095102.CrossRefGoogle Scholar
L'vov, V.S., Pomyalov, A., Procaccia, I. & Tiberkevich, V. 2005 Drag reduction by microbubbles in turbulent flows: the limit of minute bubbles. Phys. Rev. Lett. 94 (17), 174502.CrossRefGoogle ScholarPubMed
Mao, X. & Hussain, F. 2017 Optimal transient growth on a vortex ring and its transition via cascade of ringlets. J. Fluid Mech. 832, 269–286.CrossRefGoogle Scholar
Martínez-Bazán, C. 2015 About bubbles and vortex rings. J. Fluid Mech. 780, 1–4.CrossRefGoogle Scholar
Martínez-Bazán, C., Montanes, J.L. & Lasheras, J.C. 1999 a On the breakup of an air bubble injected into a fully developed turbulent flow. Part 1. Breakup frequency. J. Fluid Mech. 401, 157–182.CrossRefGoogle Scholar
Martínez-Bazán, C., Montanes, J.L. & Lasheras, J.C. 1999 b On the breakup of an air bubble injected into a fully developed turbulent flow. Part 2. Size PDF of the resulting daughter bubbles. J. Fluid Mech. 401, 183–207.CrossRefGoogle Scholar
Murai, Y. 2014 Frictional drag reduction by bubble injection. Exp. Fluids 55 (7), 1–28.CrossRefGoogle Scholar
Oweis, G.F., Van der Hout, I.E., Iyer, C., Tryggvason, G. & Ceccio, S.L. 2005 Capture and inception of bubbles near line vortices. Phys. Fluids 17 (2), 022105.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Risso, F. 2000 The mechanisms of deformation and breakup of drops and bubbles. Multiphase Sci. Technol. 12 (1).CrossRefGoogle Scholar
Risso, F. & Fabre, J. 1998 Oscillations and breakup of a bubble immersed in a turbulent field. J. Fluid Mech. 372, 323–355.CrossRefGoogle Scholar
Rodgar, M., Scolan, H., Marié, J.-L., Doppler, D. & Matas, J.-P. 2021 Bubble behaviour in a horizontal high-speed solid-body rotating flow. J. Fluid Mech. 925, A34.CrossRefGoogle Scholar
Roenby, J., Bredmose, H. & Jasak, H. 2016 A computational method for sharp interface advection. R. Soc. Open Sci. 3 (11), 160405.CrossRefGoogle ScholarPubMed
Saffman, P.G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49 (4), 371–380.CrossRefGoogle Scholar
Spandan, V., Verzicco, R. & Lohse, D. 2018 Physical mechanisms governing drag reduction in turbulent taylor–couette flow with finite-size deformable bubbles. J. Fluid Mech. 849, R3.CrossRefGoogle Scholar
Tripathi, M.K., Sahu, K.C. & Govindarajan, R. 2015 Dynamics of an initially spherical bubble rising in quiescent liquid. Nat. Commun. 6 (1), 1–9.CrossRefGoogle ScholarPubMed
Verschoof, R.A., Van Der Veen, R.C.A., Sun, C. & Lohse, D. 2016 Bubble drag reduction requires large bubbles. Phys. Rev. Lett. 117 (10), 104502.CrossRefGoogle ScholarPubMed
Weigand, A. & Gharib, M. 1994 On the decay of a turbulent vortex ring. Phys. Fluids 6 (12), 3806–3808.CrossRefGoogle Scholar
Zednikova, M., Stanovsky, P., Travnickova, T., Orvalho, S., Holub, L. & Vejrazka, J. 2019 Experiments on bubble breakup induced by collision with a vortex ring. Chem. Engng Technol. 42 (4), 843–850.CrossRefGoogle Scholar
Supplementary material: Image

Zhang et al. Supplementary Movie

MovieSee "Zhang et al. Supplementary Movie Caption"

Download Zhang et al. Supplementary Movie(Image)
Image 7.1 MB
Supplementary material: File

Zhang et al. Supplementary Movie Caption

Zhang et al. Supplementary Movie Caption

Download Zhang et al. Supplementary Movie Caption(File)
File 340 Bytes