Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-01T13:44:36.234Z Has data issue: false hasContentIssue false
  • English
  • Français

On the normalized dissipation parameter 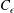$C_{\unicode[STIX]{x1D716}}$ in decaying turbulence

Published online by Cambridge University Press:  15 March 2017

L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window] ,
N. Lefeuvre ,
M. Kamruzzaman  and
R. A. Antonia
L. Djenidi*
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
N. Lefeuvre
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
M. Kamruzzaman
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
R. A. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
*
†Email address for correspondence: lyazid.djenidi@newcastle.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

The Reynolds number dependence of the non-dimensional mean turbulent kinetic energy dissipation rate 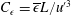$C_{\unicode[STIX]{x1D716}}=\overline{\unicode[STIX]{x1D716}}L/u^{\prime 3}$ (where $\unicode[STIX]{x1D716}$ is the mean turbulent kinetic energy dissipation rate, 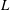$L$ is an integral length scale and 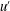$u^{\prime }$ is the velocity root-mean-square) is investigated in decaying turbulence. Expressions for $C_{\unicode[STIX]{x1D716}}$ in homogeneous isotropic turbulent (HIT), as approximated by grid turbulence, and in local HIT, as on the axis of the far field of a turbulent round jet, are developed from the Navier–Stokes equations within the framework of a scale-by-scale energy budget. The analysis shows that when turbulence decays/evolves in compliance with self-preservation (SP), $C_{\unicode[STIX]{x1D716}}$ remains constant for a given flow condition, e.g. a given initial Reynolds number. Measurements in grid turbulence, which does not satisfy SP, and on the axis in the far field of a round jet, which does comply with SP, show that $C_{\unicode[STIX]{x1D716}}$ decreases in the former case and remains constant in the latter, thus supporting the theoretical results. 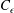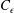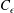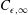Further, while $C_{\unicode[STIX]{x1D716}}$ can remain constant during the decay for a given initial Reynolds number, both the theory and measurements show that it decreases towards a constant, $C_{\unicode[STIX]{x1D716},\infty }$ , as 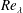$Re_{\unicode[STIX]{x1D706}}$ increases. This trend, in agreement with existing data, is not inconsistent with the possibility that $C_{\unicode[STIX]{x1D716}}$ tends to a universal constant.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 817 , 25 April 2017 , pp. 61 - 79
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Anselmet, F. & Chambers, A. J. 1986 Assessment of local isotropy using measurements in a turbulent plane jet. J. Fluid Mech. 163, 365–391.CrossRefGoogle Scholar
Antonia, R. A., Satyaprakash, B. R. & Hussain, A. K. M. F. 1980 Measurements of dissipation rate and some other characteristics of turbulent plane and circular jets. Phys. Fluids 23, 695–700.Google Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2003 Similarity of energy structure functions in decaying homogeneous isotropic turbulence. J. Fluid Mech. 487, 245–269.Google Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.Google Scholar
Barenblatt, G. J. & Gavrilov, A. A. 1974 On the theory of self-similar degeneracy of homogeneous isotropic turbulence. Sov. Phys. JETP 38, 399–402.Google Scholar
Batchelor, G. K. 1948 Energy decay and self-preserving correlation functions in isotropic turbulence. Q. Appl. Maths 6, 97–116.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1947 Decay of vorticity in isotropic turbulence. Proc. R. Soc. Lond. A 190, 534–550.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005a Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101–025115.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2005b On the normalized dissipation energy rate. Phys. Fluids 17, 98103.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 1999 A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.Google Scholar
Darisse, A., Lemay, J. & Benaissa, A. 2015 Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet. J. Fluid Mech. 774, 95–142.Google Scholar
Djenidi, L. & Antonia, R. A. 2014 Transport equation for the mean turbulent energy dissipation rate in low-R 𝜆 grid turbulence. J. Fluid Mech. 747, 288–315.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R. A. 2015 A general self-preservation analysis for decaying homogeneous isotropic turbulence. J. Fluid Mech. 773, 345–365.Google Scholar
Djenidi, L., Antonia, R. A., Lefeuvre, N. & Lemay, J. 2016 Complete self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 790, 57–70.Google Scholar
Djenidi, L., Kamruzzaman, M. & Antonia, R. A. 2015 Power-law exponent in the transition period of decay in grid turbulence. J. Fluid Mech. 779, 544–555.Google Scholar
Djenidi, L., Tardu, S. F., Antonia, R. A. & Danaila, L. 2014 Breakdown of Kolmogorov’s first similarity hypothesis in grid turbulence. J. Turbul. 15, 596–610.Google Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2005 Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J. Fluid Mech. 532, 199–216.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2012 Particle image velocimetry study of fractal-generated turbulence. J. Fluid Mech. 711, 306–336.CrossRefGoogle Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.CrossRefGoogle Scholar
Kaneda, Y., Ishihara, T., Yokokawa, M., Itakura, K. & Uni, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box. Phys. Fluids 15, L21–L24.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941a The locally structure of structure in incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, (see also Proc. R. Soc. Lond. A (1991), 434, 9–13).Google Scholar
Kolmogorov, A. N. 1941b On degeneration of isotropic turbulence in an incompressible viscous liquid. Dokl. Akad. Nauk SSSR 31 (6), 538–541; (see also Selected works of A. N. Kolmogorov, in Mathematics and its applications (Soviet Series) vol. 25, pp 319–323).Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Krogstad, P.-Å. & Davidson, P. A. 2011 Freely decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.Google Scholar
Lee, S. K., Djenidi, L., Antonia, R. A. & Danaila, L. 2013 On the destruction coefficients for slightly heated decaying grid turbulence. Intl J. Heat Fluid Flow 43, 129–136.Google Scholar
Lohse, D. 1994 Crossover from high to low Reynolds number turbulence. Phys. Rev. Lett. 73, 3223–3226.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22, 075101.CrossRefGoogle Scholar
McComb, W. D. 2014 Homogeneous, Isotropic Turbulence, Phenomenology, Renormalization and Statistical Closures. Oxford University Press.CrossRefGoogle Scholar
McComb, W. D., Berera, A., Salewski, M. & Yoffe, S. 2010 Taylor’s (1935) dissipation surrogate reinterpreted. Phys. Fluids 22, 061704.Google Scholar
McComb, W. D., Berera, A., Yoffe, S. R. & Linkmann, M. F. 2015 Energy transfer and dissipation in forced isotropic turbulence. Phys. Rev. E 91, 043013.Google Scholar
Meldi, M. & Sagaut, P. 2013 Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.Google Scholar
Monin, A. S. & Yaglom, A. M. 2007 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. II (Republication). Dover.Google Scholar
Pearson, B. R. & Antonia, R. A. 2001 Reynolds-number dependence of turbulent velocity and pressure increments. J. Fluid Mech. 444, 343–382.Google Scholar
Pearson, B. R., Krogstad, P.-Å. & van de Water, W. 2002 Measurements of the turbulent energy dissipation rate. Phys. Fluids 14, 1288–1290.Google Scholar
Sinhuber, M., Bodenschatz, E. & Bewley, G. P. 2015 Decay of turbulence at high Reynolds numbers. Phy. Rev. Lett. 114, 034501.Google Scholar
Sreenivasan, K. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27, 1048–1058.Google Scholar
Sreenivasan, K. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.Google Scholar
Succi, S. 2001 The lattice Boltzmann equation for fluid dynamics and beyond. In Numerical Mathematics and Scientific Computation, Oxford University Press.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Abe, H., Zhou., T., Danaila, L. & Zhou, Y. 2015a Transport equation for the meant turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.CrossRefGoogle Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015b Complete self-preservation along the axis of a circular cylinder far wake. J. Fluid Mech. 786, 253–274.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015c Transport equation for the meant turbulent energy dissipation rate in the far-wake of a circular cylinder. J. Fluid Mech. 784, 109–129.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 141, 421–444.Google Scholar
Tennekes, I. & Lumley, J. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Wang, L. P., Chen, S., Brasseur, J. G. & Wyngaard, J. C. 1996 Examination of hypotheses in the kolmogorov refined turbulence theory through high-resolution simulations. Part I. Velocity field. J. Fluid Mech. 309, 113–156.Google Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2012 Dissipation, enstrophy and pressure statistics in turbulence simulations at high Reynolds numbers. J. Fluid Mech. 700, 5–15.CrossRefGoogle Scholar
Zhou, T., Pearson, B. R. & Antonia, R. A. 2001 Comparison between temporal and spatial transverse velocity increments in a turbulent plane jet. Fluid Dyn. Res. 28, 127–138.CrossRefGoogle Scholar