Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-02T19:32:10.837Z Has data issue: false hasContentIssue false
  • English
  • Français

A study of longitudinal processes and interactions in compressible viscous flows

Published online by Cambridge University Press:  23 April 2020

F. Mao ,
L. L. Kang ,
J. Z. Wu Open the ORCID record for J. Z. Wu [Opens in a new window] ,
J.-L. Yu ,
A. K. Gao ,
W. D. Su  and
X.-Y. Lu Open the ORCID record for X.-Y. Lu [Opens in a new window]
F. Mao
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing100871, PR China Shenzhen Qingfengxi Technology Limited, Shenzhen518055, Guangdong, PR China
L. L. Kang
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing100871, PR China
J. Z. Wu
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing100871, PR China
J.-L. Yu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, Anhui, PR China
A. K. Gao
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing100871, PR China
W. D. Su
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing100871, PR China
X.-Y. Lu*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, Anhui, PR China
*
†Email address for correspondence: xlu@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Fluid motion has two well-known fundamental processes: the vector transverse process characterized by vorticity, and the scalar longitudinal process consisting of a sound mode and an entropy mode, characterized by dilatation and thermodynamic variables. The existing theories for the sound mode involve the multi-variable issue and its associated difficulty of source identification. 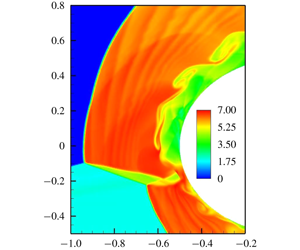In this paper, we define the source of sound inside the fluid by the objective causality inherent in dynamic equations relevant to a longitudinal process, which naturally favours the material time-rate operator $D/Dt$ rather than the local time-rate operator $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t$, and describes the sound mode by inhomogeneous advective wave equations. The sources of sound physical production inside the fluid are then examined at two levels. For the conventional formulation in terms of thermodynamic variables at the first level, we show that the universal kinematic source can be condensed to a scalar invariant of the surface deformation tensor. Further, in the formulation in terms of dilatation at the second level, we find that the sound mode in viscous and heat-conducting flow has sources from rich nonlinear couplings of vorticity, entropy and surface deformation, which cannot be disclosed at the first level. Preliminary numerical demonstration of the theoretical findings is made for two typical compressible flows, i.e. the interaction of two corotating Gaussian vortices and the unsteady type IV shock/shock interaction. The results obtained in this study provide a new theoretical basis for, and physical insight into, understanding various nonlinear longitudinal processes and the interactions therein.

JFM classification

Compressible Flows: Compressible Flows Mathematical Foundations: Mathematical Foundations
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , A23
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blokhintzev, D. 1946 The propagation of sound in an inhomogeneous and moving medium I. J. Acoust. Soc. Am. 18 (2), 322–328.CrossRefGoogle Scholar
Chu, B. T. & Kovásznay, L. S. 1958 Non-linear interactions in a viscous heat-conducting compressible gas. J. Fluid Mech. 3 (5), 494–514.CrossRefGoogle Scholar
Chu, Y. B. & Lu, X. Y. 2012 Characteristics of unsteady type IV shock/shock interaction. Shock Waves 22 (3), 225–235.CrossRefGoogle Scholar
Chu, Y. B. & Lu, X. Y. 2013 Topological evolution in compressible turbulent boundary layers. J. Fluid Mech. 733, 414–438.CrossRefGoogle Scholar
Colonius, T., Lele, S. K. & Moin, P. 1994 The scattering of sound waves by a vortex: numerical simulations and analytical solutions. J. Fluid Mech. 260, 271–298.CrossRefGoogle Scholar
Courant, R. & Friedrichs, K. O. 1948 Supersonic Flow and Shock Waves, Pure and Applied Mathematics, a Series of Texts and Monographs, vol. 1. Interscience.Google Scholar
Eldredge, J. D., Colonius, T. & Leonard, A. 2002 A vortex particle method for two-dimensional compressible flow. J. Comput. Phys. 179 (2), 371–399.CrossRefGoogle Scholar
Emmons, H. W.(Ed.) 1958 Fundamentals of Gas Dynamics, High Speed Aerodynamics and Jet Propulsion, vol. III. Princeton University Press.CrossRefGoogle Scholar
Enflo, B. O. & Hedberg, C. M. 2002 Theory of Nonlinear Acoustics in Fluids, 1st edn. Springer.Google Scholar
Eyink, G. L. & Drivas, T. D. 2018 Cascades and dissipative anomalies in compressible fluid turbulence. Phys. Rev. X 8, 011022.Google Scholar
Ffowcs Williams, J. E. 1977 Aeroacoustics. Annu. Rev. Fluid Mech. 9 (1), 447–468.CrossRefGoogle Scholar
Goldstein, M. E. 1976 Aeroacoustics. McGraw-Hill.Google Scholar
González, D. R., Speth, R. L., Gaitonde, D. V. & Lewis, M. J. 2016 Finite-time Lyapunov exponent-based analysis for compressible flows. Chaos 26 (8), 083112.CrossRefGoogle ScholarPubMed
Haller, G. 2001 Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149 (4), 248–277.CrossRefGoogle Scholar
Han, S., Luo, Y. & Zhang, S. 2019 The relation between finite-time Lyapunov exponent and acoustic wave. AIAA J. 57 (12), 5114–5125.CrossRefGoogle Scholar
Howe, M. S. 1975 Contributions to the theory of aerodynamic sound, with application to excess jet noise and the theory of the flute. J. Fluid Mech. 71, 625–673.CrossRefGoogle Scholar
Howe, M. S. 1998 Acoustics of Fluid-Structure Interactions, Cambridge Monographs on Mechanics, vol. 1. Cambridge University Press.CrossRefGoogle Scholar
Jiang, G. S. & Shu, C. W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Jordan, P. & Gervais, Y. 2008 Subsonic jet aeroacoustics: associating experiment, modelling and simulation. Exp. Fluids 44 (1), 1–21.Google Scholar
Kovásznay, L. S. 1953 Turbulence in supersonic flow. J. Aeronaut. Sci. 20 (10), 657–674.Google Scholar
Lagerstrom, P. A. 1964 Laminar flow theory. In The Theory of Laminar Flows (ed. Moore, F. K.), High Speed Aerodynamics and Jet Propulsion Series, vol. 4. Princeton University Press.Google Scholar
Lagerstrom, P. A., Cole, J. D. & Trilling, L.1949 Problems in the theory of viscous compressible fluids. Tech. Rep. 6. GALCIT.Google Scholar
Liepmann, H. W. & Roshko, A. 1957 Elements of Gasdynamics. Dover.CrossRefGoogle Scholar
Lighthill, M. J. 1952 On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. A 211 (1107), 564–587.Google Scholar
Lighthill, M. J. 1956 Viscosity effects in sound waves of finite amplitude. In Surveys in Mechanics (ed. Batchelor, G. K. & Davies, R. M.), pp. 250–351. Cambridge University Press.Google Scholar
Lighthill, M. J. 1978 Waves in Fluids, Cambridge University Press.Google Scholar
Lilley, G. M. 1974 On the noise from air jets. In Noise Mechanisms, AGARD-CP-131, pp. 13.1–13.12.Google Scholar
Liu, L. Q. 2018 Unified Theoretical Foundations of Lift and Drag in Viscous and Compressible External Flows. Springer.CrossRefGoogle Scholar
Mao, F., Shi, Y. P., Xuan, L. J., Su, W. D. & Wu, J. Z. 2011 On the governing equations for the compressing process and its coupling with other processes. Sci. China Phys., Mech. Astronomy 54 (6), 1154–1168.CrossRefGoogle Scholar
Mao, F., Shi, Y. P. & Wu, J. Z. 2010 On a general theory for compressing process and aeroacoustics: linear analysis. Acta Mechanica Sin. 26 (3), 355–364.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43 (1), 219–245.CrossRefGoogle Scholar
Mitchell, B. E., Lele, S. K. & Moin, P. 1995 Direct computation of the sound from a compressible co-rotating vortex pair. J. Fluid Mech. 285, 181–202.CrossRefGoogle Scholar
Ostashev, V. 1997 Acoustics in Moving Inhomogeneous Media. CRC Press.Google Scholar
Phillips, O. M. 1960 On the generation of sound by supersonic turbulent shear layers. J. Fluid Mech. 9 (1), 1–28.CrossRefGoogle Scholar
Pierce, A. D. 1981 Acoustics: An Introduction to Its Physical Principles and Applications. Springer.Google Scholar
Serrin, J. B. 1959 Mathematical principles of classical fluid mechanics. In Fluid Dynamics I/Strömungsmechanik I (ed. Flugge, S. & Truesdell, C.), Encyclopedia of Physics Book Series, vol. 8, pp. 125–263. Springer.CrossRefGoogle Scholar
Tam, C. K., Webb, J. C. & Dong, Z. 1993 A study of the short wave components in computational acoustics. J. Comput. Acoust. 1 (1), 1–30.CrossRefGoogle Scholar
Truesdell, C. 1954 The Kinematics of Vorticity. Indiana University Press.Google Scholar
Wang, M., Freund, J. B. & Lele, S. K. 2006 Computational prediction of flow-generated sound. Annu. Rev. Fluid Mech. 38 (1), 483–512.CrossRefGoogle Scholar
Wang, L. & Lu, X. Y. 2012 Flow topology in compressible turbulent boundary layer. J. Fluid Mech. 703, 255–278.CrossRefGoogle Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves, John Wiley & Sons.Google Scholar
Wilczek, M. & Meneveau, C. 2014 Pressure Hessian and viscous contributions to velocity gradient statistics based on gaussian random fields. J. Fluid Mech. 756, 191–225.CrossRefGoogle Scholar
Wu, T. Y. 1956 Small perturbations in the unsteady flow of a compressible viscous and heat-conducting fluid. J. Math. Phys. 35 (1–4), 13–27.CrossRefGoogle Scholar
Wu, J. Z., Liu, L. Q. & Liu, T. S. 2018 Fundamental theories of aerodynamic force in viscous and compressible complex flows. Prog. Aerosp. Sci. 99, 27–63.CrossRefGoogle Scholar
Wu, J. Z., Ma, H. Y. & Zhou, M. D. 2015 Vortical Flows. Springer.CrossRefGoogle Scholar
Wu, J. Z., Zhou, Y. & Fan, M. 1999 A note on kinetic energy, dissipation and enstrophy. Phys. Fluids 11 (2), 503–505.CrossRefGoogle Scholar
Zhang, S. H., Li, H., Liu, X. L., Zhang, H. X. & Shu, C. W. 2013 Classification and sound generation of two-dimensional interaction of two Taylor vortices. Phys. Fluids 25 (5), 056103.CrossRefGoogle Scholar
Zhu, Y. D., Chen, X., Wu, J. Z., Chen, S. Y., Lee, C. B. & Gad-el Hak, M. 2018 Aerodynamic heating in transitional hypersonic boundary layers: role of second-mode instability. Phys. Fluids 30 (1), 011701.CrossRefGoogle Scholar