Introduction
The presence of a debris layer on the surface of a glacier can have a significant influence upon its expected lifespan, even though the layer may be just a few centimetres thick (Reference Mihalcea, Mayer, Diolaiuti, Lambrecht, Smiraglia and TartariMihalcea and others, 2006). As shown in Figure 1, debris can become embedded within glacial ice by various mechanisms, including rock wall collapse and wind-blown particles within the snow accumulation zone. As the glacier flows into the ablation zone, the buried debris is liberated by the gradual melting of the overlying ice and contributes to the surface debris layer (e.g. Reference Stokes, Popovnin, Aleynikov, Gurney and ShahgedanovaStokes and others, 2007). If enough debris cover is created, it can significantly affect the interaction between the glacial ice and the atmosphere (e.g. by changing the surface albedo and insulation effects). Despite the debris layer’s importance to the energy balance of a glacier, there are still many uncertainties regarding the underlying physical processes (Reference Collier, Nicholson, Brock, Maussion, Essery and BushCollier and others, 2014). It is the purpose of this paper to help close this gap and thereby offer insight into the relationship between glacial debris cover and glacial melt rates.

Fig. 1. A schematic diagram showing some of the processes by which debris can become embedded and transported within (and upon) a mountain glacier, causing the debris content of the glacier surface to increase towards the snout.
Field studies of debris-covered glaciers have revealed many of the important mechanisms that contribute to the energy flux balance, and these have allowed melt-rate computations to be conducted (e.g. Reference Benn and EvansBenn and Evans, 2010). However, a disparity appears to exist between current model predictions and field observations. Existing models of glaciers that are fully covered by debris predict that their melt rate decreases monotonically with increasing debris thickness (e.g. Reference Nicholson and BennNicholson and Benn, 2006). Yet the well-known experimentally measured Østrem curve (Reference ØstremØstrem, 1959), which plots melt rates against debris thickness (Fig. 2), shows that a thickening of the debris layer can initially enhance melting up to a critical depth, after which the melt rate decreases due to insulation effects (Reference Reid, Carenzo, Pellicciotti and BrockReid and others, 2012). Reference Reid and BrockReid and Brock (2010) noted this discrepancy within their debris energy-balance model (which assumed perfect debris coverage) stating that ‘there is no sign that [the melt rate] reaches a maximum and then decreases […] as the debris thickness tends to zero’. They argue that the disparity may be due to the ‘patchiness’ of debris cover for thin non-uniform debris layers, whereby the melt rate increases as the proportion of glacier that is debris-covered increases. Whilst the patchiness of the debris cover certainly affects the rising limb of the Østrem curve, experiments show that it can still be produced on fully covered ice (e.g. Reference Adhikary, Nakawo, Seko and ShakyaAdhikary and others, 2000). Current theoretical models lack a mechanism that could account for this discrepancy.
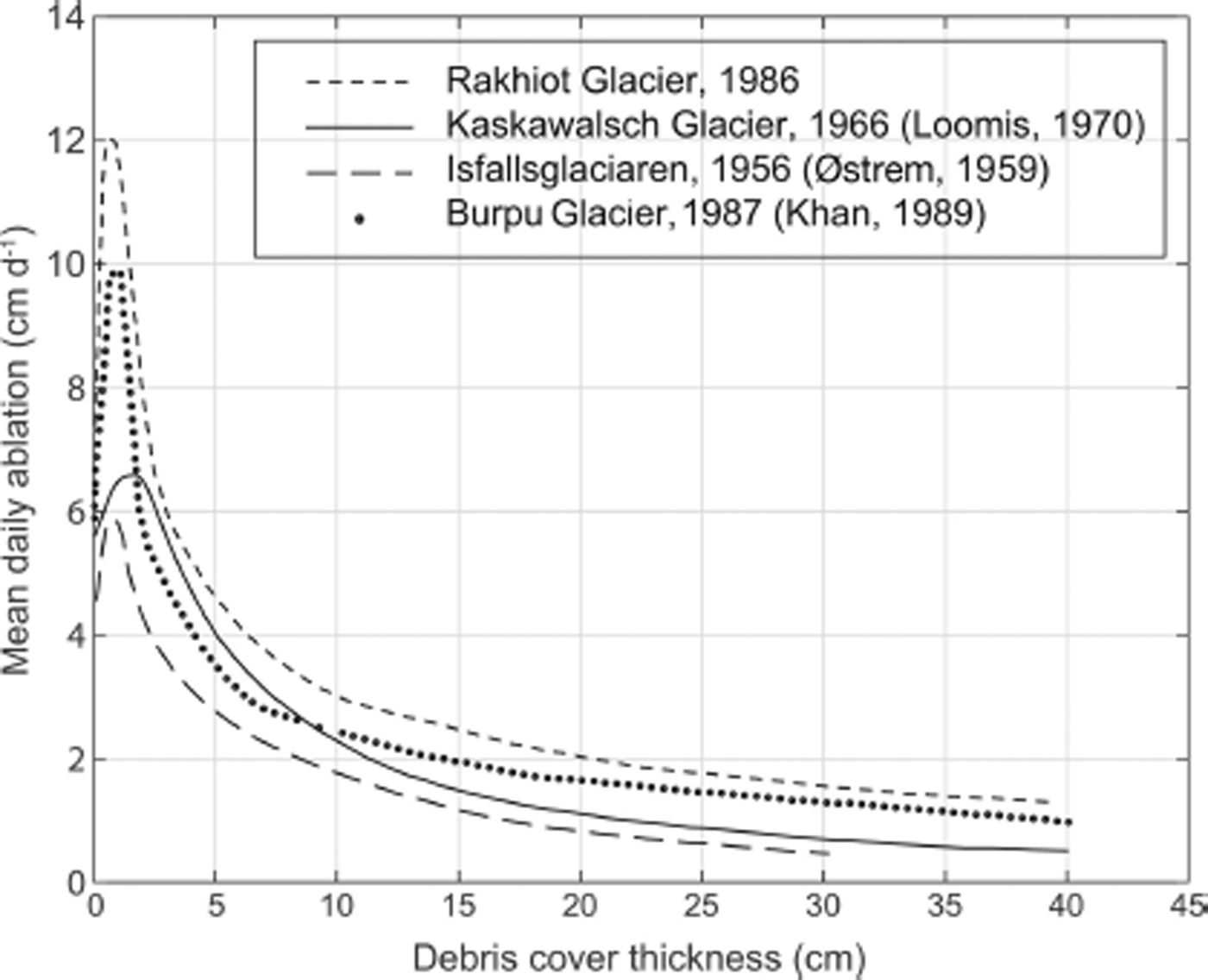
Fig. 2. A selection of measured Østrem curves, showing ice melt rates versus debris thickness. This figure is taken from Reference Mattson, Gardner and YoungMattson and others (1993).
The present paper builds upon previous theoretical models, primarily by Reference Bozhinskiy, Krass and PopovninBozhinskiy and others (1986), Reference Nicholson and BennNicholson and Benn (2006) and Reference Reid and BrockReid and Brock (2010), but incorporates the important fact that glacial debris is porous (Reference Nicholson and BennNicholson and Benn, 2012), thus allowing air to flow through the debris layer. This enables our model to take account of the heat energy exchange between the moving air and the ice at the bottom of the debris layer. The airflow within the debris layer is heavily attenuated with depth (Reference Beavers and JosephBeavers and Joseph, 1967), causing the energy exchange between the moving air and underlying ice (and hence energy available for evaporation) to diminish rapidly as the debris layer thickens. It is this reduction in (latent) energy to evaporation that is presented, and quantified, as a potential cause for the increasing melt rate in the Østrem curve for uniformly covered glaciers.
The outline of the paper is as follows. We start by examining the energy balance of a debris-covered glacier, paying particular attention to the dependence of the evaporative heat flux on the debris-layer thickness. We use the energy-balance equations to derive an explicit prediction of the glacier’s melt rate for the case of a spatially uniform, continuous debris cover and then extend the model to the case of patchy debris cover. We show that our predictions for the melt rate agree well with experimental data obtained by Reference Nicholson and BennNicholson and Benn (2006), and then study the effect of various physical quantities on the development of the maximum in the Østrem curve. Finally, we demonstrate how the meltout of debris particles from the glacier contributes to the thickness of the debris layer, and show that this has a strong effect on the long-term evolution of the glacier.
The Model Problem and Energy Considerations
The model configuration is shown in the schematic diagram of Figure 3, where we consider a small section of a debris-laden glacier. We denote the volume (packing) fraction of solid debris within the porous debris layer by φ, and the volume fraction of debris embedded in the ice by φ. The ice/ debris interface is located at z = h, where z is measured positive downwards, with z = 0 indicating the initial position of the ice surface. The interface between the debris layer and the atmosphere is located at z = s, so that the debris thickness is h s. Both h and s will, in general, vary over different horizontal locations on the glacier. Assuming that these variations are sufficiently gentle at a local scale (i.e. within the small glacial section of interest), we neglect such spatial dependence in our analysis and assume that h and s are functions of time, t, only. Of course, this may affect the absolute value of the melt rate, but the approximation significantly simplifies the analysis and will not undermine the principle of the processes to be discussed here.

Fig. 3. Schematic diagram of a portion of a debris-laden and debris-covered glacier.
The main aim of this paper is to determine the rate of melting of glacial ice. To determine this it is necessary to study the energy fluxes at z = s and z = h and to evaluate the temperature, T (°C), throughout the debris layer. For the sake of clarity it will be assumed that the ice layer under investigation is at the melting point, T = 0°C. This implies there is no heat flux into the ice across its surface at z = h. For simplicity we neglect energy input due to precipitation and condensation (we explore this further in the Discussion section). We also assume that all meltwater that is not evaporated runs off without pooling and does not influence the energy exchange processes. Similar assumptions are made by Reference Bozhinskiy, Krass and PopovninBozhinskiy and others (1986), Reference Nicholson and BennNicholson and Benn (2006), Reference Reid and BrockReid and Brock (2010) and Reference Lejeune, Bertrand, Wagnon and MorinLejeune and others (2013), although the latter does include a snow layer overlying the top of the debris surface. The energy flux in the system then has the following components:
Shortwave energy flux
During daylight hours, there is shortwave solar irradiation of the glacier. It is assumed that throughout the day the incoming shortwave radiation reaches the surface at an average rate of Q (W m−2), which will vary with time; however, a certain fraction, α, is reflected back into the atmosphere. The parameter α (the albedo) depends upon the material in question (and could vary with moisture) and we denote the broadband albedo of debris and bare ice by α d and α i, respectively. Thus, for a section of glacier completely covered by debris, the shortwave energy flux supplied to the debris layer is
Longwave energy flux
The debris layer emits longwave radiation, which increases with its surface temperature, T(z = s), via the Stefan–Boltzmann law: ![]() , where is the Stefan–Boltzmann constant and
, where is the Stefan–Boltzmann constant and ![]() is 273 K. In practice, the emitted longwave energy flux depends on the thermal emissivity, ∊, of the debris (i.e. its ability to emit radiation compared with a perfect black body at the same temperature). This outgoing radiation is offset by a component l*
(W m−2), comprised of incoming long-wave radiation from the atmosphere (e.g. overlying cloud layers and air particles (Reference Liston, Bruland, Elvehøy and SandListon and others, 1999)). This implies that the total longwave energy flux to the debris layer is
is 273 K. In practice, the emitted longwave energy flux depends on the thermal emissivity, ∊, of the debris (i.e. its ability to emit radiation compared with a perfect black body at the same temperature). This outgoing radiation is offset by a component l*
(W m−2), comprised of incoming long-wave radiation from the atmosphere (e.g. overlying cloud layers and air particles (Reference Liston, Bruland, Elvehøy and SandListon and others, 1999)). This implies that the total longwave energy flux to the debris layer is
Sensible heat flux
The sensible heat flux at the upper debris surface represents the rate at which thermal energy is transferred across the surface from the air and into the debris layer. The (downwards) vertical flux of sensible heat, Q SH, at that location depends upon the temperature gradient of the air at the debris surface (z = s) and can be modelled as
where c a is the specific heat of air, ρ a is the air density and K h is the eddy diffusivity for heat (assuming that heat transfer is dominated by turbulent mixing rather than molecular diffusion).
Heat flux due to evaporation at the ice surface
Spatial variations in the absolute humidity, q (the mass of water vapour per unit volume of air), result in a diffusive (mass) flux of water vapour at a rate that is proportional to its gradient, ∂q/∂z. Assuming again that this diffusive transport process is dominated by turbulent mixing, the mass flux of vapour is given by −K w∂q/∂z where K w is the eddy diffusivity for water vapour. At the ice surface, this mass flux is balanced by the creation of water vapour via evaporation, a process that extracts energy from the system at a rate
where L v is the latent heat of evaporation. The dimensions of Q V are the same as those of a heat flux (W m−2), therefore we refer to it as the evaporative heat flux (also known as the latent heat flux).
Latent heat of melting
The energy flux required to melt (pure) ice at a rate dh/dt is given by L mρi dh/dt, where L m is the latent heat of melting and ρ i is the density of the ice. For a glacier with debris volume fraction φ, the flux of energy, Q M, required to melt the glacier at the same rate is therefore given by
Heat flux within the debris layer
The debris layer is a randomly distributed air-filled porous medium, which, for ease of analysis in this paper, will have its thermal properties represented by a single conductivity, k, which should be a suitably averaged mixture of the thermal conductivities of rock(s), moisture and air that comprise the layer. Consequently, the debris mantle’s heat flux automatically takes account of the sensible heat exchange between rock and air within the debris. The heat flux downwards through the debris is then given by Fourier’s law
which also holds at both the upper and lower debris surfaces. Note that, for convenience, we have assumed that k has no spatial variation. Conservation of energy within the debris layer then implies that the temperature distribution is governed by the heat equation
where κ = k / (ρ d c d) is the thermal diffusivity, expressed in terms of the debris layer’s average density, ρ d, and its average specific heat, c d. Since our interest is the development of the debris layer over a long time, it is reasonable to assume that the melt rate is slow enough for daily fluctuations in the temperature to be averaged out, allowing us to neglect the time-derivative in Eqn (7). The temperature distribution in the debris layer is then governed by the steady heat equation,
With these energy fluxes, the energy balance at the upper and lower surfaces of the debris layer can now be written. Assuming that the ice is perfectly covered by debris (an assumption we later relax), the energy balance at the top of the debris surface (at z = s) is
and at the bottom surface of the debris cover, where it makes contact with the ice (at z = h), we have
We stress that these energy fluxes also form the basis of many other theoretical models of glacial melting (Reference Cuffey and PatersonCuffey and Paterson (2010) provide a discussion in the context of clean ice; Reference Nicholson and BennNicholson and Benn (2006) and Reference Reid and BrockReid and Brock (2010) discuss the case of debris-covered glaciers). However, the novel feature of our model is that the evaporative heat flux, Q V, is evaluated at the bottom of the debris layer, which is where the melting takes place. The fact that this makes Q V dependent upon the wind dynamics within the debris layer will turn out to be a key feature that allows us to explain the maximum in the Østrem curve.
Determination of the Sensible and Evaporative Heat Fluxes
To make further progress, it is necessary to derive expressions for the sensible and evaporative heat fluxes, Q SH and Q V, in terms of quantities that are, at least in principle, easy to measure (Reference GarrattGarratt, 1992). A key element for the forthcoming discussion will be the turbulent flow of air both in the atmosphere above the debris and in the debris layer itself. The model will partition these distinct flow regions, and the height z = r (where r < s) denotes the separation, or switching, surface between the two (see Fig. 4). That is, for z < r it is assumed that the wind-speed profile resembles the usual turbulent boundary layer flow over a surface, whereas for z > r the wind-speed profile is dominated by the debris properties and so a porous flow model must be employed (Reference BrutsaertBrutsaert (1982), gives an analysis of the related problem of flow through canopies and vegetation). The height, s − r = x r, say, can be thought of as an effective surface roughness length scale (Fig. 3), which is related to the average particle size and packing configuration of the debris at the top surface of the layer.

Fig. 4. Schematic diagram of the wind-speed profile above, and within, a debris layer. At any depth, z = h, within the porous flow region, the overlying debris depth is h − s. In the atmospheric region the wind speed can be thought of as obeying a logarithmic flow profile and in the porous region it obeys an exponential decay profile (Reference BrutsaertBrutsaert, 1982).
Evaporative heat flux
As stated in Eqn (4), the evaporative heat flux, Q V, is determined by the humidity gradient in the air and the eddy diffusivity of water vapour, K w. Since the flux of water vapour must be conserved throughout the system, the spatial variation in humidity, q, is governed by the diffusion equation
where we have again assumed that the timescales involved are sufficiently slow for time-derivatives to be neglected. To solve this equation within the atmosphere and the porous debris layer, appropriate forms for K w are required in each region. To simplify matters, it is reasonable to assume that the eddy diffusivity, K w (i.e. the rate at which vapour disperses), is the same as the eddy viscosity of the air, K say (i.e. the rate at which momentum disperses). Thus, the ratio K w/K, which resembles an eddy Prandtl number, is taken as unity in both regions (Reference Cuffey and PatersonCuffey and Paterson, 2010). The eddy viscosity is defined by the relation
where τ is a turbulent shear stress and u is the mean horizontal wind speed at height z. It can be expected that the variation of u and τ with z will be quite different within the debris mantle or above it in the atmosphere. In order to determine τ and u it is necessary to postulate the fluid mechanical behaviour in each region.
In the atmosphere above the surface roughness height z = r it is possible to follow the approach employed by, among others, Reference Cuffey and PatersonCuffey and Paterson (2010), who assume that the flow within the atmospheric dynamic sublayer obeys the classical log-law velocity profile (e.g. Landau and Lifshitz,
with a constant turbulent shear stress
where u * is a constant friction velocity and k * is the von Kármán constant. Substitution into Eqn (12) gives the atmospheric eddy viscosity as
Crucially, Eqn (13) introduces a nonzero slip velocity, u r, at the switching surface z = r, which we will match to the flow within the debris. While the slip velocity is, in principle, yet another parameter that has to be measured, Reference Landau and LifshitzLandau and Lifshitz (1987) state that the slip velocity is equal to the friction velocity multiplied by a ‘constant of the order of unity’. For simplicity we will therefore assume that u r ≈ u *. We note that in many previous studies where the porosity of the debris layer was neglected (e.g. Reference Nicholson and BennNicholson and Benn, 2006), the slip velocity was set to zero. While this only has a small effect on the velocity field at sufficiently large distances above the debris surface (i.e. for s − z ≫x r), u r cannot be neglected close to the debris surface (i.e. when the distance becomes comparable with the roughness height, x r). In fact, it is important to note that a nonzero slip velocity is a feature of any turbulent flow above a rough surface, whether porous or not (Reference Spurk and AkselSpurk and Aksel, 2008); we shall make use of this when we consider the melting of a bare-ice surface.
Within the debris layer, it can be expected that the wind speed is heavily attenuated with depth. Analogies to the present model occur in many other porous media flow models, such as wind flow through crops. Reference BrutsaertBrutsaert (1982) provides a detailed description of such similar models, which themselves are based on general physical principles from dimensional analysis, and are therefore appropriate to a wide range of porous media. In particular, Brutsaert presents two assumptions by which τ and u can be determined explicitly. These assumptions are (1) that flow within the porous layer is given by the momentum-balance equation
where A is the average ratio of a debris particle’s surface area to the volume of air (1 − φ) in the debris layer, and C D is the drag coefficient on a typical debris particle; and (2) that the flow is turbulent with a constant mixing length,
x d, implying
By solving the coupled Eqns (12), (16) and (17), and ensuring continuity of wind speed across the switching surface, z = r, it can be shown that
for z ≥ r, where

Finally, it is necessary to determine the mixing length, x d, which is obtained by satisfying continuity of shear stress across z = r:
The above relation allows γ to be written in the more convenient form
where the final approximation follows from our assumption that u r ≈ u *. These descriptions for τ, u and K confirm two important empirical observations: horizontal wind speed within a porous medium decays exponentially with depth (Reference BrutsaertBrutsaert, 1982), and evaporative heat transfer is proportional to wind speed (because K, and hence K w, is directly proportional to u) (Reference Cuffey and PatersonCuffey and Paterson, 2010). The fact that this derivation confirms these observations is encouraging, although clearly heuristic arguments could have been employed from the outset without having to involve mixing length theory. But what the present derivation provides, which an observational approach does not, is a quantifiable link between debris geometry (captured by A and C D) and the exponential decay rate, γ, of the wind speed. That said, it is clear that in practice, debris geometry, drag and packing fraction will be difficult to measure, and thus A and C D will be extremely hard to determine robustly. Thus, it may actually be easier to employ direct values for γ found by experiment, supported by the knowledge that there is a physical justification for doing so.
With expressions for K w = K(z) derived in both regions (Eqns (15) and (20)), it is now possible to determine the humidity, q(z), via Eqn (11). This, in turn, enables the simple step of calculating the evaporative heat flux at the ice surface (z = h) from Eqn (4). To solve Eqn (11) in the two regions, four boundary conditions for q are needed. First, continuity of humidity and vapour flux, respectively, at the switching surface require that
where ![]() denotes the difference in the given quantity either side of a boundary. Next, the humidity level at the ice/debris interface is taken to be that for saturated air, q
h,
denotes the difference in the given quantity either side of a boundary. Next, the humidity level at the ice/debris interface is taken to be that for saturated air, q
h,
which is justified by the melting conditions at the ice surface. We further assume that measurements at z = m, which is at a height x m above the mean surface of the debris layer, z = s, have determined the humidity level and wind speed as q m and u m, respectively, i.e.
Solving for q in Eqn (11) is straightforward, and the vapour flux within the debris layer can be written as
in which Eqns (22) and (23) have been used to eliminate x d. With some slight rearrangement and use of Eqns (13) and (18), this result yields the evaporative heat flux (Eqn (4)) at the ice/debris interface as
The presence of the ice surface wind speed, u(h), within Eqn (29) means that this energy flux will rapidly tend to zero as the debris depth increases, thereby offering a mechanism by which the Østrem curve can be reproduced.
It is of note that one can transform the above equation, in terms of absolute humidity, to one in terms of another water vapour measure (e.g. specific humidity, relative humidity or water vapour pressure).
Sensible heat flux
The flux of sensible heat may be treated in a similar manner. Fortunately its value is required only at the debris/ atmosphere interface, where it interacts with the overlying atmosphere. The flux of sensible heat is again taken as quasi-steady, implying
and K h, the eddy diffusivity of heat, is taken to be the eddy viscosity, K, i.e. the eddy Prandtl number is again assumed to be unity. In the surface roughness region, r < z < s, the diffusivity is given by Eqn (20), whereas above this, in z < r, it takes the linear profile given by Eqn (15). Hence Eqn (30) may be integrated, ensuring continuity of temperature and heat flux across z = r, to yield
where T m is the temperature measured at z = m.
Note that if we were to set the slip velocity, u r, to zero then the wind speed throughout the debris layer vanishes. If we then express u m via Eqn (13), evaluated at z = m, the heat flux at the top of the debris layer becomes
This agrees with the expression used by Reference Cuffey and PatersonCuffey and Paterson (2010) for an impermeable debris layer, and this form of sensible heat flux is utilized in several other studies, including Reference Nicholson and BennNicholson and Benn (2006).
Governing Equations
Complete, spatially uniform debris cover
We are now in a position to derive an equation for the melt rate at the ice surface and will first consider the case where the debris cover is complete and spatially uniform. For this purpose we split the spatially one-dimensional model of debris-covered ice shown in Figure 1 into three regions: the atmosphere, the debris and the ice. The debris-layer depth, h − s, can be determined by consideration of the rate at which it grows due to the fraction of debris (e.g. rocks, silt or sand), φ, liberated as the ice melts, and any supraglacial source terms of debris, g (e.g. via rock avalanches or the addition or loss of wind-blown particles so that g can be positive or negative). Thus, as the ice melts at a rate dh/dt, it creates additional debris at the rate φ dh/dt and hence the pile grows at the rate φ/φ dh/dt due to the debris packing fraction, φ. Similarly, the supraglacial debris deposition leads to an additional debris-pile growth rate of g/φ, and hence the debris-layer growth equation is
If we assume, for simplicity, that φ, g and φ are locally constant then Eqn (33) can be integrated to give the instantaneous position of the debris surface level as
where −d 0 is the initial position of the debris surface (at time t = 0) as h(0) = 0, and therefore the initial debris thickness is d 0. We shall take d 0 = 0 in what follows, but will assume that the glacier has an initial debris cover that, although infinitesimally thin, perfectly covers the ice. Hence, the glacier’s surface albedo remains a constant, α d, for all time; however, in the following subsection we extend the model to allow the glacier to have an initially bare-ice surface.
The temperature distribution in the debris layer (for s(t) < z < h(t)) is governed by the steady heat equation, Eqn (8), subject to boundary conditions for the temperature,
the energy flux balance at the ice/debris interface,
where Q V is given by Eqn (29), and the energy flux balance at the atmosphere/debris interface

where Q SH is given by Eqn (31). The +/− subscript indicates the limiting value of the specified quantity as s is approached from below/above respectively. Equations (8–37) constitute a free-boundary problem – a so-called ‘Stefan problem’ – whose solution determines the melt rate and the evolution of the debris-layer thickness.
Integration of the steady heat equation (Eqn (8)), subject to the temperate ice condition (Eqn (35)) at the lower interface, z = h(t), yields the temperature distribution within the debris
To make further progress, we assume that the variations in temperature at the debris surface are sufficiently small (compared with ![]() ) to allow the longwave radiation term, Eqn (2), to be linearized in T. This simplifies the analysis but does not qualitatively alter the results. Employing the derived expressions for the evaporative heat flux, Q
V, at the ice surface, Eqn (29), and the sensible heat flux, Q
SH at the upper surface of the debris layer, Eqn (31), the boundary conditions Eqns (36) and (37) reduce to
) to allow the longwave radiation term, Eqn (2), to be linearized in T. This simplifies the analysis but does not qualitatively alter the results. Employing the derived expressions for the evaporative heat flux, Q
V, at the ice surface, Eqn (29), and the sensible heat flux, Q
SH at the upper surface of the debris layer, Eqn (31), the boundary conditions Eqns (36) and (37) reduce to
on z = h(t), and
on z = s(t), where the constants are defined as
and
By construction, it is physically reasonable to assume that all of these constants take positive values whilst the ice is melting.
Differentiating Eqn (38) allows the heat flux to be written in terms of the temperature at the debris surface, T(s). So, by eliminating T(s) between Eqns (39) and (40) it is straightforward to show that the solution to this free-boundary problem is determined by the ice surface evolution equation
in which the debris surface location, s, is given by Eqn (34). For completeness, the vertical debris temperature profile is
The original Stefan problem has thus been reduced to the simple nonlinear first-order ordinary differential (Eqn (46)) for h(t) as a function for time, solutions to which are readily computable. The debris-layer temperature may be solved directly from the linear Eqn (47), which does not rely on a spatial discretization. Most importantly, Eqn (46) shows clearly why the present model can produce a melt-rate curve of the form measured by Østrem: the second term on the right-hand side is associated with the energy loss due to evaporation and rapidly decays to zero as the debris-layer thickness (h − s) increases, thus increasing the melt rate (due to the negative sign). However, as time progresses, the first term on the right-hand side also gets smaller, due to increased insulation of the ice via the debris, thereby reducing the rate of melt from its peak. Thus, Eqn (46) appears to resolve a long-standing problem regarding dynamic ablation due to debris from ice. The model includes new physical elements not used in previous studies, yet is still easily solvable, and so it seems appropriate to term Eqn (46) the ‘dynamic ablation due to debris from ice (DADDI) equation’.
Modifications for thin, patchy debris cover
So far we have assumed that the debris layer is sufficiently thick to be able to form a spatially uniform covering over the ice. This assumption is questionable during the very early stages of the formation of the debris mantle, when the thickness of this layer is comparable to the typical grain width, 2x g, say. In this regime the debris cover is likely to be patchy and we denote the fraction of the ice surface that is debris-covered by, p, say. To determine this time-varying (and probabilistic) debris-coverage fraction, we have to make certain assumptions about how the grains accumulate and distribute (Reference Kirkbride and DelineKirkbride and Deline (2013) provide a discussion of this issue). We will assume that while the debris cover is incomplete, the debris arrives at the glacier surface to form a layer that is a single grain thick. After reaching complete debris coverage (p = 1) we then assume that the debris thickness increases uniformly over the entire surface.
For a (horizontal) unit area of ice, the total rate of increase in volume of the debris deposited from melting and supraglacial sources is, from Eqn (33),
where now dH/dt is the weighted average melt rate of bare and covered ice, i.e.
where b is the surface elevation of the bare-ice proportion (itself an average). The evolution equation for h is given by Eqn (46) and b is found by substituting h = s into Eqn (46) to give
where ![]() is given by Eqn (41) but using the albedo of ice, α
i.
is given by Eqn (41) but using the albedo of ice, α
i.
We can finally close the system by integrating Eqn (48) (with initial condition H(0) = 0) to get the accumulated volume of debris in a unit area of ice, and hence dividing by the average grain size yields the surface debris fraction
The numerical solution of Eqn (49) is straightforward, using p from Eqn (51), h from Eqn (46) and b from Eqn (50). Given this model’s relation to the DADDI (Eqn (46)) and its consideration of bare ice, we term Eqn (49) the DADDI-BARE equation.
Results
To illustrate the capabilities of our model, we start by comparing the instantaneous melt rate predicted by Eqn (46) with field measurements obtained by Reference Nicholson and BennNicholson and Benn (2006) on Larsbreen, Svalbard. The parameter values of Reference Nicholson and BennNicholson and Benn (2006) are listed in Table 1, which themselves are 24 hour means from a dry debris layer. We choose to apply these particular parameter values to our model as they provide, to the best of our knowledge, the most comprehensive parameter set yet published. In doing so, they leave us to specify only two remaining parameter values, both of which arise out of the novel aspects of our own modelling: the volume fraction of debris in the ice, φ, and the wind-speed attenuation constant, γ. The former only has a small effect on the instantaneous melt rate (but see Fig. 10 for an illustration of how variations in φ affect a glacier’s long-term evolution) and was set to 1%. A value for γ can be obtained via estimates for the parameters A and C D which feature in Eqn (23). The parameter A is the average ratio of the debris surface area to the volume of air in the debris layer. We can obtain a rough estimate of this quantity by assuming that the debris is composed of identical spheres of radius x g (the typical grain size) and packed into a body-centred cubic arrangement with volume fraction φ. It is then straightforward to show that A is given by
which yields A = 188 m−1 for a grain radius of x g = 4 mm. To estimate the drag coefficient, C D, we use data from Reference Reddy and JoshiReddy and Joshi (2008), who performed experiments on flow through a rigid body-centred cubic arrangement of spheres over a range of Reynolds numbers and packing fractions. For the parameter regime of interest here, C D ≈ 5, which yields the estimate γ = 234 m−1. We note that the dependence of A (and thus, via Eqn (23), also γ) on x g in Eqn (52) is consistent with the empirical findings of Reference Harris and PedersenHarris and Pedersen (1998), who showed that wind can transfer heat energy through large blocky debris (larger x g thus smaller γ) much more easily than it can through fine-grained material (smaller x g thus larger γ). Our estimate for γ is nevertheless very crude and any attempt to directly measure this quantity in field experiments (e.g. by fitting the exponentially decaying profile, Eqn (18), to the flow speed measured within the debris layer, using micro-anemometers; see Reference Juliussen and HumlumJuliussen and Humlum, 2008) would therefore be valuable.
Table 1. Parameter values taken from Reference Nicholson and BennNicholson and Benn (2006) for their measurements on Larsbreen, Svalbard. The lower eight parameters take non-site-specific values

Figure 5 shows that, with these parameter values, our predictions for the melt rate (solid curve) against debris-layer thickness are in excellent agreement with Reference Nicholson and BennNicholson and Benn’s (2006) field measurements (symbols) which were averaged over an 11 day measurement period. The figure also shows the predictions from Nicholson and Benn’s own computations (dash-dotted curve), in which the time-derivative in the diffusion equation (Eqn (7)) for the temperature was retained. The agreement between the three datasets indicates that our quasi-steady model, which is based on time-averaged heat fluxes and a homogenized debris layer, adequately describes the melt process. The figure also shows that the presence of a thin debris layer increases the melt rate above that of clean ice (shown by the dashed line), because the debris layer has a smaller albedo than clean ice and therefore absorbs a larger fraction of the incoming shortwave radiation. Neither of the datasets shows any evidence of a maximum in the melt rate at small debris-layer thicknesses, suggesting that in this particular parameter regime the evaporative heat flux is small and only plays a minor role in the overall energy balance. The shape of that curve is therefore determined predominantly by the insulating effect of the debris layer, resulting in a continuous decrease in the melt rate with an increase in debris-layer thickness. The only effect of the evaporative heat flux is the slight reduction in the slope of the melt-rate curve for very small debris-layer thicknesses.
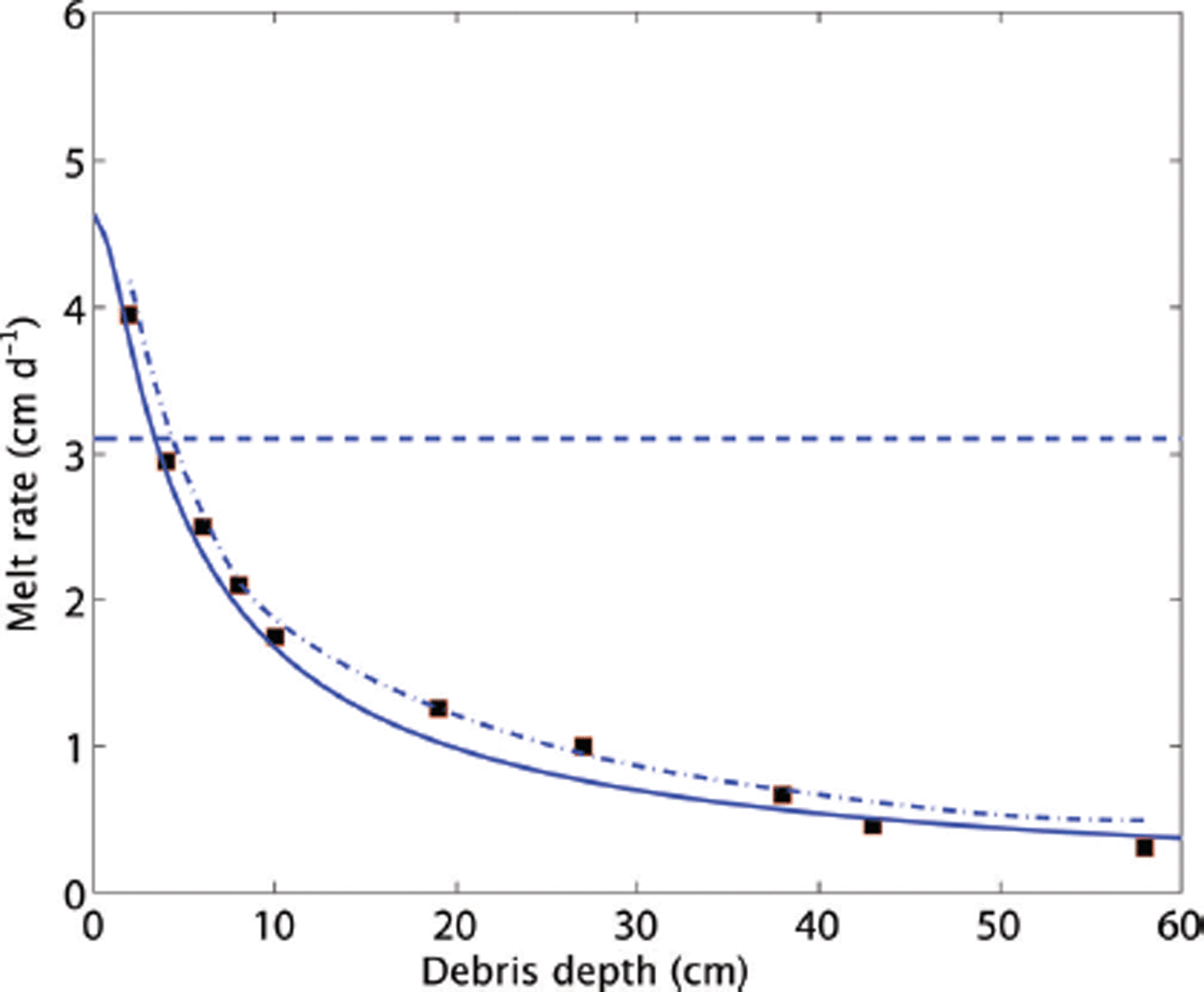
Fig. 5. Instantaneous melt rate plotted against debris-layer thickness, with parameters from Table 1. Solid curve: the Østrem curve predicted by the DADDI equation (Eqn (46)) (at the y-intercept, the debris layer is assumed infinitesimally thin); square markers: Reference Nicholson and BennNicholson and Benn (2006) field measurements; dash-dotted curve: spline fit to predictions from Reference Nicholson and BennNicholson and Benn’s (2006) computational model; dashed line: melt rate for bare ice from Eqn (50).
Figure 6 shows a plot of the temperature, T(s), at the top of the debris layer versus thickness of the debris layer. The figure shows that the surface temperature initially increases rapidly with the debris-layer thickness, before ultimately approaching an asymptotic limit of ∼14.6°C. This value, which is indicated by the dashed line, may be obtained by taking the limit of Eqn (47) for large values of h − s. Physically, the limit corresponds to the situation in which the debris layer has become thick enough for heat conduction into the debris to have become negligible, so that the surface temperature is simply determined by the energy balance between shortwave and longwave energies, and the sensible heat flux.

Fig. 6. Plot of temperature at the top of the debris layer, T(s), as a function of the debris-layer thickness, for the parameter values in Table 1. The dashed line shows the theoretical limit for an infinitely thick debris layer.
Evaporation is driven by humidity gradients (Eqn (4)), therefore the relative importance of the evaporative heat flux on the overall energy balance depends strongly on the atmospheric humidity, q m. This is illustrated in Figure 7b, which shows that a decrease in q m (from 0.74q h to 0.5q h and 0.25q h while keeping all other parameters constant) increases the evaporative heat flux, Q v, significantly. The associated reduction in the amount of energy available for melting results in a noticeable decrease in the melt rate (Fig. 7a). This implies that the reduction in Q v caused by an increase in debris-layer thickness now has an appreciable effect on the energy balance, and manifests itself in the clearly defined maximum in the Østrem curve at modest debris-layer thicknesses. The maximum in the melt rate arises for debris-layer thicknesses of the order of a few centimetres, consistent with the field measurements shown in Figure 2.

Fig. 7. (a) Instantaneous melt rate and (b) evaporative heat flux, plotted against debris-layer thickness, for different humidities (q m = 0.74q h, 0.5q h and 0.25q h, decreasing in the direction of the arrow). Other parameters as in Table 1.
Figure 8 illustrates the effect of variations in the attenuation coefficient, γ, which is a key parameter in our model. Here the reference γ (234 m−1) is varied by ±33%. An increase in γ corresponds to an increase in the drag experienced by the flow in the porous debris layer (Eqn (23)) and therefore reduces the wind speed at the ice surface. The associated reduction in the evaporative heat flux, shown in Figure 8b, again increases the amount of energy available for melting and therefore increases the melt rate (Fig. 8a). Interestingly, the maximum in the melt-rate curve only develops for sufficiently large values of γ. To explain this we note that the debris-layer depth beyond which the evaporative heat flux becomes so small that it only plays a minor role in the overall energy balance decreases with increasing γ. An increase in γ therefore increases the initial slopes of the curves in Figure 8b, which represent the rate at which an increase in the debris-layer depth reduces the evaporative heat flux, Q v. The maximum in the melt-rate curve develops only for values of γ for which the rate at which Q v decreases with an increase in the debris-layer thickness outweighs the reduction in the melt rate due the concomitant increase in the insulating effect of the debris layer. See the Appendix for a more detailed analysis of the conditions under which the turning point in the Østrem curve arises.

Fig. 8. (a) Instantaneous melt rate and (b) evaporative heat flux, plotted against debris-layer thickness, for different values of the attenuation parameter (γ = 155, 234 and 311 m−1, increasing in the direction of the arrow) and q m = 0.5q h. Other parameters as in Table 1.
The results presented so far were obtained from Eqn (46), which is based on the assumption that the debris cover remains continuous as its thickness approaches zero. This assumption implies that the melt rate for a (nominally) zero debris-layer thickness exceeds that of bare ice (see, e.g., Fig. 5), because the albedo of the debris is lower than that of the bare-ice surface. (All other effects associated with the presence of the debris layer vanish as the layer thickness goes to zero.) As discussed above, this is clearly an artefact of the model, since it ignores the fact that very thin debris layers are inevitably patchy and thus provide only a partial cover to the underlying ice. Figure 9 shows the melt rate predicted by our revised model, Eqn (49), which offers a simple way to incorporate the transition from bare ice to complete debris cover in the model. The three curves in the figure show the instantaneous melt rate as a function of the debris-layer thickness for different values of the debris albedo, α d, which increases in the direction of the arrow (α d = 0.07, 0.24, 0.4). The humidity was set to q m = 0.5q h, the value for which the original model predicts a turning point in the melt-rate curve (Fig. 7) due to the reduction of the evaporative heat flux with increasing debris-layer thickness. The topmost curve in Figure 9 shows the melt rate for α d = 0.07, which is the value used in the previous computations. For a sufficiently thick debris layer (for which we assume the debris cover to be continuous), the melt rate therefore agrees with that already shown in Figure 7. Once the debris-layer thickness drops below the average grain width, 2x g (8 mm), the reduction in the debris coverage, p (modelled crudely by Eqn (51)), reduces the overall shortwave energy input and thus reduces the average melt rate until, for zero debris-layer thickness, it reaches that of bare ice. Patchiness therefore contributes to the maximum in the Østrem curve – a point also noticed by Reference Reid and BrockReid and Brock (2010). The additional curves in Figure 9 show that its importance (relative to the reduction in evaporative heat flux) depends on the difference in the albedo of ice and debris. If α i and α d are very similar (or if the incoming shortwave energy is small) the effect of partial debris cover on the melt rate is modest. This is shown by the bottommost curve in Figure 9, where we set the debris albedo to that of bare ice, α d = α i = 0.4. In this extreme case the maximum in the Østrem curve is entirely due to the variations in the evaporative heat flux with the debris-layer thickness, while patchiness only plays a very minor role.

Fig. 9. Instantaneous melt rate predicted by Eqn (51), plotted against debris-layer thickness, for different values of the debris albedo (α d = 0.07, 0.24 and 0.4, increasing in the direction of the arrow), where the measured humidity is set as q m = 0.5q h. The dashed line represents the melt rate of bare ice.
So far our discussion has focused on the dependence of the melt rate, dh/dt, on the instantaneous debris-layer thickness. To determine the total thickness of ice melted over a given period of time, it is important to account for the fact that the meltout of debris particles that are embedded in the ice leads to a continuous increase in the debris-layer thickness. Within our model, this effect is represented by the dependence of the melt rate on the volume fraction of debris in the ice, φ, via the parameters ν 1 and μ 1 (Eqns (41) and (44), respectively). Using a highly simplified, yet useful, assumption of constant energy fluxes, Figure 10 shows a plot of the thickness of ice melted as a function of time for three different values of φ: φ = 0 (clean ice), φ = 0.01 and φ = 0.1. The data were produced by time-integrating Eqn (46). Whilst this estimate is not intended to reflect diurnal/annual effects, it does demonstrate that the depth of ice melted is clearly very sensitive to the debris volume fraction, confirming that debris content can have a dramatic effect on the lifespan of ice masses (Reference Jansson and FredinJansson and Fredin, 2002).

Fig. 10. Thickness of ice melted as a function of time for three different values of the volume fraction of debris embedded in the ice: φ = 0, 0.01 and 0.1, increasing in the direction of the arrow. Other parameters are as in Table 1.
Discussion and Conclusions
We have developed a simple model for determining the melt rate of a debris-laden glacier. Solutions to the model, given by Eqn (46), are able to capture the experimentally observed features of the Østrem curve, most notably the turning point in the melt rate for debris-layer thicknesses of a few centimetres (consistent with the observations shown in Fig. 2). More specifically, model solutions are in close agreement with field data from Reference Nicholson and BennNicholson and Benn (2006).
Our model provides a simple explanation for the observed increase in the melt rate for thin debris layers: as the debris layer thickens (either via meltout of englacial debris or supraglacial source terms), the wind speed at the ice/debris interface decreases. This reduces the rate of evaporation, which increases the energy available for melting. Once a sufficiently thick debris layer has been created, the wind speed at the ice/debris interface becomes negligible, allowing the thermodynamics of the system to become dominated by the insulating effect of the debris layer. A further increase in the thickness of the debris layer then reduces the melt rate. For a sufficiently thin debris layer, the patchiness of the debris cover makes an additional contribution to the maximum in the melt-rate curve, and we showed that the relative importance of the two effects depends on the difference in the albedo of the ice and the debris cover. Note that the results for the initial patchy phase of the melting are rather dependent on the assumed form of the debris distribution, Eqn (51), and are a useful area for future investigation.
The consideration of the debris layer’s porosity introduced a crucial new parameter, γ, which appears explicitly within the DADDI equation (Eqn (46)). This parameter captures the attenuation of the wind speed within the debris layer and we estimated it to take a value of ∼234 m−1 for the parameters listed in Table 1. We showed that the evaporative heat flux’s overall behaviour is fairly robust to variations in γ, although a 50% reduction in was able to suppress the turning point in the Østrem curve. It will be interesting to assess its value in field experiments, particularly when measured against a variety of debris media compositions.
The relative simplicity of our model allowed us to perform a detailed analysis of a small number of key physical effects, while neglecting a large number of others. For instance, our model deliberately ignores a sub-zero temperature distribution in the glacier, energy exchange with rain and snow, the effect of refreezing moisture within the debris layer, spatial variations in the particle size distribution and capillary effects, to name but a few. Some of these effects could easily be incorporated into a more complex version of our model. For instance, in a fine-grained debris cover, capillary effects are likely to create a thin, water-saturated layer of debris directly above the ice surface. The inclusion of this feature will require the evaluation of the evaporative heat flux at the (elevated) air/water interface. While this is likely to change the precise details of the model’s predictions, the main effect studied in this paper, namely the increase in melt rate due to the reduction of wind speed within the non-saturated porous debris layer above the saturated region, is likely to remain a key feature. Likewise, including a sub-zero ice temperature (i.e. a nonzero temperature gradient) is an easy extension to the model, although, again, it would not have added much insight into the dynamics this paper focused on (and would have been inconsistent with Reference Nicholson and BennNicholson and Benn, 2006).
However, there exist other physical effects whose inclusion will require a considerable amount of additional modelling. There are two such aspects we believe to be particularly important. The first concerns the development of a more detailed description of the spatio-temporal evolution of the (highly inhomogeneous) debris layer. Methods that can appropriately take account of this complexity and offer estimates of a debris layer’s time- and depth-varying thermal conductivity, and wind speed attenuation, will be desirable. Secondly, the time-varying effect of moisture (and its phase changes) within a debris layer should be explored. Evidence of its importance has been provided; for example, Reference Brock, Mihalcea, Kirkbride, Diolaiuti, Cutler and SmiragliaBrock and others (2010) and Reference Collier, Nicholson, Brock, Maussion, Essery and BushCollier and others (2014) measured a positive evaporative heat flux over reasonably deep debris layers. This is in contrast to our dry debris-layer model, which assumed these fluxes to be negligible. Both these future areas of work will require an array of mathematical models, field trials and laboratory experiments to be implemented. In doing so, a fuller quantitative understanding of a debris-covered glacier’s evolution could be produced, paving the way for more accurate glacier mass-balance forecasts.
Acknowledgements
This paper is the result of a workshop held in Karthaus, Süd-Tirol, 3–9 June 2012. Funding for the workshop was provided by the Engineering and Physical Sciences Research Council, UK, via the MAPLE Platform Grant EP/I01912X/1. A.C.F. acknowledges the support of the Science Foundation Ireland mathematics initiative grant 12/1A/1683, and I.D.A. undertook part of this work whilst in receipt of a Royal Society Wolfson Research Merit Award. We are also extremely grateful to reviewers of this paper for detailed and helpful comments.
Appendix
The maximum predicted melt rate can be determined by differentiating Eqn (46) with respect to the debris depth, X = h − s. Although the Østrem curve has a single interior (X > 0) turning point that is the maximum melt rate, it is necessary to explore the possibility of multiple (or zero) local maxima and minima melt rates. The turning points of Eqn (46) are found by setting the derivative to zero, and hence they are given by the roots of
where use has been made of the fact that only positive values of X are of interest.
Analytical insight may be gained by examining the functional form of g(X). Clearly, g(X) is large and positive as X → ±∞, and thus interior turning points must exist, and one of them will be a global minimum. Differentiation of g(X) reveals that there is one, and only one, turning point (minimum) at
at which point
So, when g(X min) > 0, there will be no turning points of Eqn (46) and hence the melt-rate curve will be monotonic decreasing in X ≥ 0. In the case g(X min) = 0 then there will be a single (interior) maximum to the curve of dh/dt if X min > 0.
When g(X min) < 0, the curve of g(X) crosses the X-axis twice; however, these crossings may occur for two positive X values, a single positive X value, or for no positive X values. To discern this number, it is necessary to find the point at which g(0) = 0, i.e. when zero is a root of Eqn (A1):
A new parameter, J D, say, may be introduced as
which can be rearranged from Eqn (A4) so that J D = 0 corresponds to g(0) = 0. So, it is easy to conclude that two positive roots occur if X min > 0 and g(0) > 0, and two non-positive roots when X min < 0 and g(0) > 0. Finally one, and only one, positive root occurs at the parameter values corresponding to g(0) ≤ 0. This may be summarized as follows.
Zero roots: the melt rate monotonically decreases for all debris thicknesses. In this case the parameter values satisfy either:
-
(1) g(X min) > 0, or
-
(2) g(X min) ≤ 0, X min ≤ 0 and J D ≤ 0.
One root: the melt rate will qualitatively behave as the Østrem curve, with an interior maximum melt rate occurring at a positive debris depth. In this case the conditions are
-
(1) g(X min) = 0, X min > 0, or
-
(2) g(X min) < 0, and J D > 0.
Two roots: The melt rate will have a local maximum and minimum (where X min < X max). The conditions for this novel scenario are given by g(X min) < 0, X min > 0 and J D < 0.
It can be easily shown that J D is actually the slope of the melt-rate curve at X = 0; thus, as the function dh/dt tends to zero for large debris thickness, there must be a maximum, and the above analysis has shown this to be a single turning point. When the initial slope is zero or negative, then for X > 0 it has been shown that there can be two, or zero, turning points. As a final point, it is a physical requirement of the system that the melt rate is always positive; thus, from Eqn (46) it is seen that the parameters obey the inequality













