Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-02T19:07:16.549Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse cascade based on nonlinear Schrödinger equation analysis with nonlinear feedback control

Published online by Cambridge University Press:  24 July 2023

Shaoyan Cui Open the ORCID record for Shaoyan Cui [Opens in a new window] ,
Xin Hu ,
Peng Xie ,
Jialin Yang  and
Shuwen Feng
Shaoyan Cui*
Affiliation:
School of Mathematics and Statistics Science, Ludong University, Yantai, Shandong, 264025, PR China
Xin Hu
Affiliation:
School of Mathematics and Statistics Science, Ludong University, Yantai, Shandong, 264025, PR China
Peng Xie
Affiliation:
School of Mathematics and Statistics Science, Ludong University, Yantai, Shandong, 264025, PR China
Jialin Yang
Affiliation:
School of Mathematics and Statistics Science, Ludong University, Yantai, Shandong, 264025, PR China
Shuwen Feng
Affiliation:
School of Mathematics and Statistics Science, Ludong University, Yantai, Shandong, 264025, PR China
*
†Email address for correspondence: shycui@ldu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper focuses on the wave inverse cascade instability analysis with self-regulating feedback control for a fixed external potential field and a highly localized finite-amplitude initial pulse. The wave inverse cascade instability analysis is carried out by solving the corresponding two-dimensional generalized nonlinear Schrödinger equation. The wave field firstly suffers from the modulation instability, followed by collapse into turbulence containing the shortest-wavelength modes in the system. This is followed by inverse cascade of the shortest wavelength modes back to the longer-wavelength ones, until a statistical stationary turbulent state is reached. It is found that the inverse cascade is limited to the shorter-wavelength modes with the wavenumber $\left |k\right |\geq 100$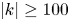. This shows that the viscous damping $p_i$ 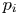acts like a control switch to the inverse cascade, and the feedback control can also regulate the intensity of the inverse cascade mode.

Keywords

plasma instabilitiesplasma nonlinear phenomenaplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 89 , Issue 4 , August 2023 , 905890407
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aranson, I.S. & Kramer, L. 2002 The world of the complex Ginzburg–Landau equation. Rev. Mod. Phys. 74, 99–143.CrossRefGoogle Scholar
Bernatz, R.A. 2010 Fourier Series and Numerical Methods for Partial Differential Equations, pp. 98–101. Wiley.CrossRefGoogle Scholar
Conway, J.M. & Riecke, H. 2007 Quasipatterns in a model for chemical oscillations forced at multiple resonance frequencies. Phys. Rev. Lett. 99 (21), 218301.CrossRefGoogle Scholar
Cui, S.Y., Lv, X.X. & Xin, J. 2016 Wave slump and its evolution described by generalized nonlinear Schrödinger equation. Acta Phys. Sin. 65, 040201.Google Scholar
Cui, S.Y., Yu, M.Y. & Zhao, D. 2013 Collapse, decay, and single-$|k|$ turbulence from a generalized nonlinear Schrödinger equation. Phys. Rev. E 87 (5), 053104.CrossRefGoogle ScholarPubMed
Goldman, M.V. 1984 Strong turbulence of plasma waves. Rev. Mod. Phys. 56, 709–735.CrossRefGoogle Scholar
Grimes, C.C. & Adams, G. 1979 Evidence for a liquid-to-crystal phase transition in a classical, two-dimensional sheet of electrons. Phys. Rev. Lett. 42, 795–798.CrossRefGoogle Scholar
Grindrod, P. 1966 The Theory and Applications of Reaction–Diffusion Equations, pp. 35–39. Oxford University Press.Google Scholar
Gupta, M.R., Som, B.K. & Dasgupta, B. 1981 Coupled nonlinear Schrödinger equations for Langmuir and elecromagnetic waves and extension of their modulational instability domain. J. Plasma Phys. 25 (3), 499–507.CrossRefGoogle Scholar
Kivshar, Y.S. & Pelinovsky, D.E. 2000 Self-focusing and transverse instabilities of solitary waves. Phys. Rep. 331 (4), 117–195.CrossRefGoogle Scholar
Liao, Y., Kelley, D.H. & Ouellette, N.T. 2012 Effects of forcing geometry on two-dimensional weak turbulence. Phys. Rev. E 86 (3), 036306.CrossRefGoogle ScholarPubMed
Mendonça, J.T. & Bingham, R. 2002 Plasmon beam instability and plasmon landau damping of ion acoustic waves. Phys. Plasmas 9 (6), 2604–2608.CrossRefGoogle Scholar
Mendonça, J.T. & Hizanidis, K.R. 2011 Improved model of quasi-particle turbulence (with applications to alfvén and drift wave turbulence). Phys. Plasmas 18 (11), C61.CrossRefGoogle Scholar
Murray, C.A., Sprenger, W.O. & Wenk, R.A. 1990 Comparison of melting in three and two dimensions: microscopy of colloidal spheres. Phys. Rev. B 42, 688–703.CrossRefGoogle ScholarPubMed
Murray, J.D. 1993 Mathematical Biology. Springer.CrossRefGoogle Scholar
Musher, S.L., Rubenchik, A.M. & Zakharov, V.E. 1995 Weak Langmuir turbulence. Phys. Rep. 252 (4), 177–274.CrossRefGoogle Scholar
Nie, J. & Li, Q. 2020 Multiplicity of sign changing solutions for a supercritical nonlinear Schrdinger equation. Appl. Maths Lett. 109, 106569.CrossRefGoogle Scholar
Pereira, N.R. & Stenflo, L. 1977 Nonlinear Shrodinger equation including growth and dumping. Phys. Fluids 20 (10), 1733–1734.CrossRefGoogle Scholar
Porras, M.A. 2010 A dissipative attractor in the spatiotemporal collapse of ultrashort light pulses. Opt. Express 18 (7), 7376–7383.CrossRefGoogle ScholarPubMed
Reis, P.M., Ingale, R.A. & Shattuck, M.D. 2006 Crystallization of a quasi two-dimensional granular fluid. Phys. Rev. Lett. 96, 258001.CrossRefGoogle ScholarPubMed
Robinson, P.A. 1997 Nonlinear wave collapse strong turbulence. Rev. Mod. Phys. 69, 507–573.CrossRefGoogle Scholar
Sagdeev, R.Z. & Galeev, A.A. 1969 Nonlinear Plasma Theory. Benjamin.Google Scholar
Shukla, P.K., Bingham, R., Phelps, A.D.R. & Stenflo, L. 2009 Dark and grey electromagnetic electron-cyclotron envelope solitons in an electron-positron magnetoplasma. J. Plasma Phys. 75 (5), 575–580.CrossRefGoogle Scholar
Silberberg, Y. 1990 Collapse of optical pulses. Opt. Lett. 15, 1282–1284.CrossRefGoogle ScholarPubMed
Skarka, V., Aleksic, N.B. & Leblond, H. 2010 The variety of stable vortical solitons in Ginzburg–Landau media with radially inhomogeneous losses. Phys. Rev. Lett. 105 (21), 213901.CrossRefGoogle ScholarPubMed
Stenflo, L. 1994 Resonant three-wave interactions in plasmas. Phys. Scr. T50, 15–19.CrossRefGoogle Scholar
Sulem, C. & Sulem, P.L. 1999 The Nonlinear Schrödinger Equation, pp. 102–103. Springer.Google Scholar
Yu, M.Y., Cui, S.Y. & Zhao, D. 2015 Feedback control of collapse-induced turbulent condensation of Langmuir waves. Europhys. Lett. 109 (6), 65001.CrossRefGoogle Scholar
Zakharov, V.E. 1972 Collapse of Langmuir waves. Sov. Phys. JETP 35, 908–914.Google Scholar
Zakharov, V.E., Musher, S.L. & Rubenchik, A.M. 1985 Hamiltonian approach to the description of non-linear plasma phenomena. Phys. Rep. 129 (5), 285–366.CrossRefGoogle Scholar
Zhao, D., Tian, L.P., Cui, S.Y. & Yu, M.Y. 2012 Instability and energy cascade in isotropic and anisotropic media. Phys. Scr. 86 (3), 471–473.CrossRefGoogle Scholar
Zhao, D. & Yu, M.Y. 2011 A generalized nonlinear Schrödinger equation as model for turbulence, collapse, and inverse cascade. Phys. Rev. E 83 (3), 036405.CrossRefGoogle ScholarPubMed