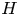1. Introduction
1.1. Background
Electromagnetic waves are present in plasmas naturally, and they are also launched into plasmas using external antennas, for example, for plasma heating and current drive (Fisch Reference Fisch1987; Stix Reference Stix1992; Pinsker Reference Pinsker2001). Nonlinear effects produced by these waves are often modelled within the quasilinear (QL) approximation, meaning that the nonlinearities are retained in the low-frequency (‘average’) dynamics but neglected in the high-frequency dynamics. Two separate paradigms exist within this approach.
In the first paradigm, commonly known as ‘the’ QL theory (QLT), the focus is on resonant interactions. Non-resonant particles are considered as a background that is homogeneous in spatial (Vedenov, Velikhov & Sagdeev Reference Vedenov, Velikhov and Sagdeev1961; Drummond & Pines Reference Drummond and Pines1962; Kennel & Engelmann Reference Kennel and Engelmann1966; Rogister & Oberman Reference Rogister and Oberman1968, Reference Rogister and Oberman1969) or generalized coordinates (Kaufman Reference Kaufman1972; Eriksson & Helander Reference Eriksson and Helander1994; Catto, Lee & Ram Reference Catto, Lee and Ram2017); then, the oscillating fields can be described in terms of global modes. This approach has the advantage of simplicity, but its applications are limited in that real plasmas are never actually homogeneous in any predefined variables (and, furthermore, tend to exhibit nonlinear instabilities in the presence of intense waves). The ‘ponderomotive’ dynamics determined by the gradients of the wave and plasma parameters is lost in this approach; then, spurious effects can emerge and have to be dealt with (Lee et al. Reference Lee, Smithe, Wright and Bonoli2018).
The second paradigm successfully captures the ponderomotive dynamics by introducing effective Hamiltonians for the particle average motion (Gaponov & Miller Reference Gaponov and Miller1958; Motz & Watson Reference Motz and Watson1967; Cary & Kaufman Reference Cary and Kaufman1981; Kaufman Reference Kaufman1987; Dodin Reference Dodin2014). But, as usual in perturbation theory (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1992), those Hamiltonians are by default singular for resonant interactions. Thus, such models have limited reach as well, and remarkable subtleties are still found even in basic QL problems. For example, it is still debated (Ochs & Fisch Reference Ochs and Fisch2021a; Ochs Reference Ochs2021) to which extent the QL effects that remove resonant particles while capturing their energy (Fisch & Rax Reference Fisch and Rax1992) also remove charge along with the resonant particles, thereby driving plasma rotation (Fetterman & Fisch Reference Fetterman and Fisch2008). This state of affairs means, arguably, that a clear comprehensive theory of QL wave–plasma interactions remains to be developed – a challenge that must be faced.
The first framework that subsumed both resonant and non-resonant interactions in inhomogeneous plasmas was proposed by Dewar (Reference Dewar1973) for electrostatic turbulence in non-magnetized plasma and is known as ‘oscillation-centre’ (OC) QLT. It was later extended by McDonald, Grebogi & Kaufman (Reference McDonald, Grebogi and Kaufman1985) to non-relativistic magnetized plasma. However, both of these models are partly heuristic and limited in several respects. For example, they are bounded by the limitations of the variational approach used therein, and they separate resonant particles from non-resonant particles somewhat arbitrarily (see also Ye & Kaufman Reference Ye and Kaufman1992). Both models also assume specific particle Hamiltonians and require that waves be governed by a QL wave-kinetic equation (WKE), i.e. be only weakly dissipative, or ‘on-shell’. (Somewhat similar formulations were also proposed, independently and without references to the OC formalism, in Weibel Reference Weibel1981; Yasseen Reference Yasseen1983; Yasseen & Vaclavik Reference Yasseen and Vaclavik1986.) This means that collisions and microscopic fluctuations are automatically excluded. Attempts to merge QLT and the WKE with the theory of plasma collisions were made (Rogister & Oberman Reference Rogister and Oberman1968; Schlickeiser & Yoon Reference Schlickeiser and Yoon2014; Yoon et al. Reference Yoon, Ziebell, Kontar and Schlickeiser2016) but have not yielded a local theory applicable to inhomogeneous plasma. In particular, the existing models rely on global-mode decompositions and treat complex frequencies heuristically. Thus, the challenge stands.
Related problems are also of interest in the context of gravitostatic interactions (Chavanis Reference Chavanis2012; Hamilton Reference Hamilton2020; Magorrian Reference Magorrian2021), where inhomogeneity of the background fields cannot be neglected in principle (Binney & Tremaine Reference Binney and Tremaine2008). (To our knowledge, OC QLT analogues have not been considered in this field.) Similar challenges also arise in QLT of dispersive gravitational waves (Garg & Dodin Reference Garg and Dodin2020, Reference Garg and Dodin2021a). Hence, one cannot help but wonder whether a specific form of the particle Hamiltonian really matters for developing QLT or it is irrelevant and therefore should not be assumed. Since basic theory of linear waves is independent of Maxwell's equations (Dodin & Fisch Reference Dodin and Fisch2012; Tracy et al. Reference Tracy, Brizard, Richardson and Kaufman2014; Dodin, Zhmoginov & Ruiz Reference Dodin, Zhmoginov and Ruiz2017), a general QLT might be possible too, and it might be easier to develop than a zoo of problem-specific models.
1.2. Outline
Here, we propose a general QLT that allows for plasma inhomogeneity and is not restricted to any particular Hamiltonian or interaction field. By starting with the Klimontovich equation, we derive a model that captures QL diffusion, interaction with background fields and ponderomotive effects simultaneously. The local diffusion coefficient in this model is manifestly positive-semidefinite. Waves are allowed to be off-shell, and a collision integral of the Balescu–Lenard type emerges for general Hamiltonian interactions. This operator conserves particles, momentum and energy, and it also satisfies the ![]() $\smash {H}$-theorem, as usual. As a spin-off, a general expression for the spectrum of microscopic fluctuations of the interaction field is derived. For on-shell waves governed by the WKE, the theory conserves the momentum and energy of the wave–plasma system. The action of non-resonant waves is also conserved, unlike in the standard version of QLT.Footnote 1 Dewar's OC QLT of electrostatic turbulence (Dewar Reference Dewar1973) is proven formally as a particular case and given a concise formulation. Also discussed as examples are relativistic electromagnetic and gravitational interactions, and QLT for gravitational waves is proposed. Overall, our formulation interconnects many known results that in the past were derived independently and reproduces them within a unifying framework.
$\smash {H}$-theorem, as usual. As a spin-off, a general expression for the spectrum of microscopic fluctuations of the interaction field is derived. For on-shell waves governed by the WKE, the theory conserves the momentum and energy of the wave–plasma system. The action of non-resonant waves is also conserved, unlike in the standard version of QLT.Footnote 1 Dewar's OC QLT of electrostatic turbulence (Dewar Reference Dewar1973) is proven formally as a particular case and given a concise formulation. Also discussed as examples are relativistic electromagnetic and gravitational interactions, and QLT for gravitational waves is proposed. Overall, our formulation interconnects many known results that in the past were derived independently and reproduces them within a unifying framework.
This progress is made by giving up the traditional Fourier–Laplace approach. The author takes the stance that the global-mode language is unnatural for inhomogeneous-plasma problems (i.e. all real-plasma problems). A fundamental theory must be local. Likewise, the variational approach that is used sometimes in QL calculations is not universally advantageous, especially for describing dissipation. Instead of those methods, we use operator analysis and the Weyl symbol calculus, as has also been proven fruitful in other recent studies of ponderomotive effects and turbulence (Ruiz Reference Ruiz2017; Ruiz & Dodin Reference Ruiz and Dodin2017b; Zhu & Dodin Reference Zhu and Dodin2021) and linear-wave theory (Dodin et al. Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019). No logical leaps are made in this paper other than assuming the QL approximation per se and a certain ordering.Footnote 2 In a nutshell, we treat the commonly known QL-diffusion coefficient as a non-local operator, and we systematically approximate it using the Weyl symbol calculus. It is the non-locality of this operator that gives rise to ponderomotive effects and ensures the proper conservation laws. The existing concept of ‘adiabatic diffusion’ (Galeev & Sagdeev Reference Galeev and Sagdeev1985; Stix Reference Stix1992) captures some of that, but systematic application of operator analysis yields a more general, more accurate and more rigorous theory.
The author hopes not that this paper is an entertaining read. However, the paper was intended as self-contained, maximally structured and easily searchable, so readers interested in specific questions could find and understand answers without having to read the whole paper. The text is organized as follows. In § 2, we present a primer on the Weyl symbol calculus and the associated notation. In § 3, we formulate our general model. In § 4, we introduce the necessary auxiliary theorems. In § 5, we derive a QL model for plasma interacting with prescribed waves. The waves may or may not be on-shell or self-consistent. (Their origin and dynamics are not addressed in § 5.) In § 6, we consider interactions with self-consistent waves. In particular, we separate out microscopic fluctuations, calculate their average distribution and derive the corresponding collision operator. In § 7, we assume that the remaining macroscopic waves are on-shell, rederive the WKE, and show that our QL model combined with the WKE is conservative. In § 8, we discuss the general properties that our model predicts for plasmas in thermal equilibrium. In § 9, we show how to apply our theory to non-relativistic electrostatic interactions, relativistic electromagnetic interactions, Newtonian gravity and relativistic gravity. In § 10, we summarize our results. Auxiliary calculations are presented in Appendices A–D, and Appendix G summarizes our notation. This notation is extensive and may not be particularly intuitive. Thus, readers are encouraged to occasionally scout § 9 for examples even before fully absorbing the preceding sections.
An impatient reader can also skip calculations entirely and consult only the summaries of the individual sections (2.3, 3.4, 4.4, 5.6, 6.9, 7.6 and 8.5; they are mostly self-contained) and then proceed to the examples in § 9. However, the main point of this work is not just the final results per se (surely, some readers will find them obvious) but also that they are derived with minimal assumptions and rigorously, which makes them reliable. A reader may also notice that we rederive some known results along the way, for example, basic linear-wave theory and the WKE. This is done for completeness and, more importantly, with the goal to present all pieces of the story within a unified notation.
2. A math primer
Here, we summarize the machinery to be used in the next sections. This machinery is not new, but a brief overview is in order at least to introduce the necessary notation. A more comprehensive summary, with proofs, can be found in Dodin et al. (Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019, supplementary material). For extended discussions, see Tracy et al. (Reference Tracy, Brizard, Richardson and Kaufman2014), Ruiz (Reference Ruiz2017), McDonald (Reference McDonald1988) and Littlejohn (Reference Littlejohn1986).
2.1. Weyl symbol calculus on spacetime
2.1.1. Basic notation
We denote the time variable as ![]() $t$, space coordinates as
$t$, space coordinates as ![]() ${\boldsymbol {x}} \equiv (x^1, x^2, \ldots, x^n)$, spacetime coordinates as
${\boldsymbol {x}} \equiv (x^1, x^2, \ldots, x^n)$, spacetime coordinates as ![]() ${\boldsymbol {\mathsf {x}}} \equiv ({\mathsf {x}}^0, {\mathsf {x}}^1, \ldots, {\mathsf {x}}^n)$, where
${\boldsymbol {\mathsf {x}}} \equiv ({\mathsf {x}}^0, {\mathsf {x}}^1, \ldots, {\mathsf {x}}^n)$, where ![]() ${\mathsf {x}}^0 \doteq t$ and
${\mathsf {x}}^0 \doteq t$ and ![]() ${\mathsf {x}}^i \doteq x^i$. The symbol
${\mathsf {x}}^i \doteq x^i$. The symbol ![]() $\doteq$ denotes definitions, and Latin indices from the middle of the alphabet (
$\doteq$ denotes definitions, and Latin indices from the middle of the alphabet (![]() $i, j, \ldots$) range from 1 to
$i, j, \ldots$) range from 1 to ![]() $n$ unless specified otherwise. We assume the spacetime-coordinate domain to be
$n$ unless specified otherwise. We assume the spacetime-coordinate domain to be ![]() $\smash {\mathbb {R}^{{\mathsf {n}}}}$.Footnote 3 Functions on
$\smash {\mathbb {R}^{{\mathsf {n}}}}$.Footnote 3 Functions on ![]() ${\boldsymbol {\mathsf {x}}}$ form a Hilbert space
${\boldsymbol {\mathsf {x}}}$ form a Hilbert space ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ with an inner product that we define as
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ with an inner product that we define as
The symbol ![]() $^*$ denotes complex conjugate,
$^*$ denotes complex conjugate,
(a similar convention is assumed also for other multi-dimensional variables used below), and integrals in this paper are taken over ![]() $(-\infty, \infty )$ unless specified otherwise. Operators on
$(-\infty, \infty )$ unless specified otherwise. Operators on ![]() $\mathscr {H}_{{{\mathsf {x}}}}$ will be denoted with carets, and we will use indexes
$\mathscr {H}_{{{\mathsf {x}}}}$ will be denoted with carets, and we will use indexes ![]() $_\text {H}$ and
$_\text {H}$ and ![]() $_\text {A}$ to denote their Hermitian and anti-Hermitian parts. For a given operator
$_\text {A}$ to denote their Hermitian and anti-Hermitian parts. For a given operator ![]() $\smash {\widehat {{\mathsf {A}}}}$, one has
$\smash {\widehat {{\mathsf {A}}}}$, one has ![]() $\smash {\widehat {{\mathsf {A}}}=\widehat {{\mathsf {A}}}_\text {H} + \mathrm {i} \widehat {{\mathsf {A}}}_\text {A}}$,
$\smash {\widehat {{\mathsf {A}}}=\widehat {{\mathsf {A}}}_\text {H} + \mathrm {i} \widehat {{\mathsf {A}}}_\text {A}}$,
where ![]() $^{{\dagger}}$ denotes the Hermitian adjoint with respect to the inner product (2.1). The case of a more general inner product is detailed in Dodin et al. (Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019, supplementary material).
$^{{\dagger}}$ denotes the Hermitian adjoint with respect to the inner product (2.1). The case of a more general inner product is detailed in Dodin et al. (Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019, supplementary material).
2.1.2. Vector fields
For multi-component fields ![]() $\smash {{\boldsymbol {\psi }} \equiv (\psi ^1, \psi ^2, \ldots, \psi ^M)}$
$\smash {{\boldsymbol {\psi }} \equiv (\psi ^1, \psi ^2, \ldots, \psi ^M)}$![]() ${}^{\intercal }$ (our
${}^{\intercal }$ (our ![]() $\smash {^\intercal }$ denotes the matrix trans pose), or ‘row vectors’ (actually, tuples), we define the dual ‘column vectors’
$\smash {^\intercal }$ denotes the matrix trans pose), or ‘row vectors’ (actually, tuples), we define the dual ‘column vectors’ ![]() $\smash {{\boldsymbol {\psi }}^{{\dagger}} \equiv (\psi _1^*, \psi _2^*, \ldots, \psi _M^*)^\intercal }$ via
$\smash {{\boldsymbol {\psi }}^{{\dagger}} \equiv (\psi _1^*, \psi _2^*, \ldots, \psi _M^*)^\intercal }$ via ![]() $\smash {{\boldsymbol {\psi }}^{{\dagger}} \doteq \boldsymbol{\mathsf {g}}{\boldsymbol {\psi }}^*}$. The matrix
$\smash {{\boldsymbol {\psi }}^{{\dagger}} \doteq \boldsymbol{\mathsf {g}}{\boldsymbol {\psi }}^*}$. The matrix ![]() $\boldsymbol{\mathsf {g}}$ is assumed to be real, diagonal, invertible and constant; other than that, it can be chosen as suits a specific problem. (For example, a unit matrix may suffice.) This induces the standard rule of index manipulation
$\boldsymbol{\mathsf {g}}$ is assumed to be real, diagonal, invertible and constant; other than that, it can be chosen as suits a specific problem. (For example, a unit matrix may suffice.) This induces the standard rule of index manipulation
where ![]() $\smash {{\mathsf {g}}_{ij}}$ are elements of
$\smash {{\mathsf {g}}_{ij}}$ are elements of ![]() $\boldsymbol{\mathsf {g}}$ and
$\boldsymbol{\mathsf {g}}$ and ![]() $\smash {{\mathsf {g}}^{ij}}$ are elements of
$\smash {{\mathsf {g}}^{ij}}$ are elements of ![]() $\boldsymbol{\mathsf {g}}^{-1}$. Summation over repeating indices is assumed. The rules of matrix multiplication apply to row and column vectors as usual. Then, for
$\boldsymbol{\mathsf {g}}^{-1}$. Summation over repeating indices is assumed. The rules of matrix multiplication apply to row and column vectors as usual. Then, for ![]() $\smash {{\boldsymbol {\psi }} \equiv (\psi ^1, \psi ^2, \ldots, \psi ^M)}$
$\smash {{\boldsymbol {\psi }} \equiv (\psi ^1, \psi ^2, \ldots, \psi ^M)}$![]() ${}^{\intercal }$ and
${}^{\intercal }$ and ![]() $\smash {{\boldsymbol {\xi }} \equiv (\xi ^1, \xi ^2, \ldots, \xi ^M)^{\intercal }}$, the quantity
$\smash {{\boldsymbol {\xi }} \equiv (\xi ^1, \xi ^2, \ldots, \xi ^M)^{\intercal }}$, the quantity ![]() $\smash {{\boldsymbol {\psi }}{\boldsymbol {\xi }}}$ is a matrix with elements
$\smash {{\boldsymbol {\psi }}{\boldsymbol {\xi }}}$ is a matrix with elements ![]() $\smash {\psi ^i\xi ^j}$,
$\smash {\psi ^i\xi ^j}$, ![]() $\smash {{\boldsymbol {\psi }}{\boldsymbol {\xi }}^{{\dagger}} }$ is a matrix with elements
$\smash {{\boldsymbol {\psi }}{\boldsymbol {\xi }}^{{\dagger}} }$ is a matrix with elements ![]() $\smash {\psi ^i\xi _j^*}$ and
$\smash {\psi ^i\xi _j^*}$ and ![]() $\smash {{\boldsymbol {\xi }}^{{\dagger}} {\boldsymbol {\psi }}}$ is its scalar trace:Footnote 4
$\smash {{\boldsymbol {\xi }}^{{\dagger}} {\boldsymbol {\psi }}}$ is its scalar trace:Footnote 4
(Similarly, for ![]() $\smash {{\boldsymbol {\chi }} \equiv (\chi _1, \chi _2, \ldots, \chi _M)}$ and
$\smash {{\boldsymbol {\chi }} \equiv (\chi _1, \chi _2, \ldots, \chi _M)}$ and ![]() $\smash {{\boldsymbol {\eta }} \equiv (\eta _1, \eta _2, \ldots, \eta _M)}$,
$\smash {{\boldsymbol {\eta }} \equiv (\eta _1, \eta _2, \ldots, \eta _M)}$, ![]() $\smash {{\boldsymbol {\eta }}{\boldsymbol {\chi }}}$ is a matrix with elements
$\smash {{\boldsymbol {\eta }}{\boldsymbol {\chi }}}$ is a matrix with elements ![]() $\smash {\eta _i \chi _j}$.) We use (2.5) to define a Hilbert space
$\smash {\eta _i \chi _j}$.) We use (2.5) to define a Hilbert space ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}^M}$ of
$\smash {\mathscr {H}_{{{\mathsf {x}}}}^M}$ of ![]() $\smash {M}$-dimensional vector fields on
$\smash {M}$-dimensional vector fields on ![]() ${\boldsymbol {\mathsf {x}}}$, specifically, by adopting the inner product
${\boldsymbol {\mathsf {x}}}$, specifically, by adopting the inner product
Below, the distinction between ![]() $\mathscr {H}_{{{\mathsf {x}}}}^M$ and
$\mathscr {H}_{{{\mathsf {x}}}}^M$ and ![]() $\mathscr {H}_{{{\mathsf {x}}}}$ will be assumed but not emphasized. Also note that (2.5) yields
$\mathscr {H}_{{{\mathsf {x}}}}$ will be assumed but not emphasized. Also note that (2.5) yields
for any ![]() $\smash {{\boldsymbol {\xi }}}$ and
$\smash {{\boldsymbol {\xi }}}$ and ![]() $\smash {{\boldsymbol {\psi }}}$. Thus, dyadic matrices of the form
$\smash {{\boldsymbol {\psi }}}$. Thus, dyadic matrices of the form ![]() $\smash {{\boldsymbol {\psi }}{\boldsymbol {\psi }}^{{\dagger}} }$ are positive-semidefinite, even though
$\smash {{\boldsymbol {\psi }}{\boldsymbol {\psi }}^{{\dagger}} }$ are positive-semidefinite, even though ![]() $\smash {{\boldsymbol {\psi }}^{{\dagger}} {\boldsymbol {\psi }}}$ may be negative (when
$\smash {{\boldsymbol {\psi }}^{{\dagger}} {\boldsymbol {\psi }}}$ may be negative (when ![]() $\boldsymbol{\mathsf {g}}$ is not positive-definite).
$\boldsymbol{\mathsf {g}}$ is not positive-definite).
For general matrices, the indices can be raised and lowered using ![]() $\boldsymbol{\mathsf {g}}$ and
$\boldsymbol{\mathsf {g}}$ and ![]() $\boldsymbol{\mathsf {g}}^{-1}$ as usual. The Hermitian adjoint
$\boldsymbol{\mathsf {g}}^{-1}$ as usual. The Hermitian adjoint ![]() $\smash {{{\boldsymbol {\mathsf {A}}}}^{{\dagger}} }$ for a given matrix
$\smash {{{\boldsymbol {\mathsf {A}}}}^{{\dagger}} }$ for a given matrix ![]() $\smash {{\boldsymbol {\mathsf {A}}}}$ is defined such that
$\smash {{\boldsymbol {\mathsf {A}}}}$ is defined such that ![]() $\smash {({{\boldsymbol {\mathsf {A}}}}^{{\dagger}} {\boldsymbol {\xi }})^{{\dagger}} {\boldsymbol {\psi }} = {\boldsymbol {\xi }}^{{\dagger}} ({{\boldsymbol {\mathsf {A}}}}{\boldsymbol {\psi }})}$ for any
$\smash {({{\boldsymbol {\mathsf {A}}}}^{{\dagger}} {\boldsymbol {\xi }})^{{\dagger}} {\boldsymbol {\psi }} = {\boldsymbol {\xi }}^{{\dagger}} ({{\boldsymbol {\mathsf {A}}}}{\boldsymbol {\psi }})}$ for any ![]() $\smash {{\boldsymbol {\psi }}}$ and
$\smash {{\boldsymbol {\psi }}}$ and ![]() $\smash {{\boldsymbol {\xi }}}$, which means
$\smash {{\boldsymbol {\xi }}}$, which means
The Hermitian and anti-Hermitian parts are defined as
so ![]() $\smash {{{\boldsymbol {\mathsf {A}}}} = {{\boldsymbol {\mathsf {A}}}}_\text {H} + \mathrm {i} {{\boldsymbol {\mathsf {A}}}}_\text {A}}$. For one-dimensional matrices (scalars), one has
$\smash {{{\boldsymbol {\mathsf {A}}}} = {{\boldsymbol {\mathsf {A}}}}_\text {H} + \mathrm {i} {{\boldsymbol {\mathsf {A}}}}_\text {A}}$. For one-dimensional matrices (scalars), one has ![]() ${{\boldsymbol {\mathsf {A}}}} = {\mathsf {A}}$,
${{\boldsymbol {\mathsf {A}}}} = {\mathsf {A}}$,
where ![]() $\smash {\operatorname {re}}$ and
$\smash {\operatorname {re}}$ and ![]() $\smash {\operatorname {im}}$ denote the real part and the imaginary part, respectively. We also define matrix operators
$\smash {\operatorname {im}}$ denote the real part and the imaginary part, respectively. We also define matrix operators ![]() $\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}}}$ as matrices of the corresponding operators
$\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}}}$ as matrices of the corresponding operators ![]() $\smash {\widehat {{\mathsf {A}}}^{\,\,i}_j}$. Because
$\smash {\widehat {{\mathsf {A}}}^{\,\,i}_j}$. Because ![]() $\boldsymbol{\mathsf {g}}$ is constant, index manipulation applies as usual. Also as usual, one has
$\boldsymbol{\mathsf {g}}$ is constant, index manipulation applies as usual. Also as usual, one has
and ![]() $\,\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}} = \widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}}_\text {H} + \mathrm {i} \widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}}_\text {A}}$, where
$\,\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}} = \widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}}_\text {H} + \mathrm {i} \widehat {\boldsymbol {{\boldsymbol {\mathsf {A}}}}}_\text {A}}$, where ![]() $^{{\dagger}}$ is the Hermitian adjoint with respect to the inner product (2.6).
$^{{\dagger}}$ is the Hermitian adjoint with respect to the inner product (2.6).
2.1.3. Bra–ket notation
Let us define the following operators that are Hermitian under the inner product (2.1):
where ![]() $\partial _0 \equiv \partial _t \doteq \partial /\partial x^0$ and
$\partial _0 \equiv \partial _t \doteq \partial /\partial x^0$ and ![]() $\partial _i \doteq \partial /\partial x^i$. Accordingly,
$\partial _i \doteq \partial /\partial x^i$. Accordingly,
are understood as the spacetime-position operator and the corresponding wavevector operator, which will also be expressed as follows:
Also note the commutation property, where ![]() $\smash {\delta _i^j}$ is the Kronecker symbol:Footnote 5
$\smash {\delta _i^j}$ is the Kronecker symbol:Footnote 5
The eigenvectors of the operators (2.14) will be denoted as ‘kets’ ![]() $\smash {\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}$ and
$\smash {\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}$ and ![]() $\smash {\left. {\boldsymbol {\mathsf {|k}}} \right\rangle}$:Footnote 6
$\smash {\left. {\boldsymbol {\mathsf {|k}}} \right\rangle}$:Footnote 6
and we assume the usual normalization
where ![]() $\delta$ is the Dirac delta function. Both sets
$\delta$ is the Dirac delta function. Both sets ![]() $\lbrace {\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}, {\boldsymbol {\mathsf {x}}} \in \mathbb {R}^{{\mathsf {n}}} \rbrace$ and
$\lbrace {\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}, {\boldsymbol {\mathsf {x}}} \in \mathbb {R}^{{\mathsf {n}}} \rbrace$ and ![]() $\lbrace {\left. {\boldsymbol {\mathsf {|k}}} \right\rangle}, {\boldsymbol {\mathsf {k}}} \in \mathbb {R}^{{\mathsf {n}}} \rbrace$, where
$\lbrace {\left. {\boldsymbol {\mathsf {|k}}} \right\rangle}, {\boldsymbol {\mathsf {k}}} \in \mathbb {R}^{{\mathsf {n}}} \rbrace$, where ![]() ${{\mathsf {n}}} \doteq n + 1$, form a complete basis on
${{\mathsf {n}}} \doteq n + 1$, form a complete basis on ![]() $\mathscr {H}_{{{\mathsf {x}}}}$, and the eigenvalues of these operators form an extended real phase space
$\mathscr {H}_{{{\mathsf {x}}}}$, and the eigenvalues of these operators form an extended real phase space ![]() $({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$, where
$({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$, where
The notation ![]() $\smash {{\boldsymbol {\mathsf {k}}} \cdot {\boldsymbol {\mathsf {s}}} \doteq -\omega \tau + {\boldsymbol {k}} \cdot {\boldsymbol {s}}}$ will be assumed for any
$\smash {{\boldsymbol {\mathsf {k}}} \cdot {\boldsymbol {\mathsf {s}}} \doteq -\omega \tau + {\boldsymbol {k}} \cdot {\boldsymbol {s}}}$ will be assumed for any ![]() ${\boldsymbol {\mathsf {s}}} \equiv (\tau, {\boldsymbol {s}})$ and
${\boldsymbol {\mathsf {s}}} \equiv (\tau, {\boldsymbol {s}})$ and ![]() $\smash {{\boldsymbol {k}} \cdot {\boldsymbol {s}} \doteq k_i s^i}$. In particular, for any
$\smash {{\boldsymbol {k}} \cdot {\boldsymbol {s}} \doteq k_i s^i}$. In particular, for any ![]() $\psi$ and constant
$\psi$ and constant ![]() ${\boldsymbol {\mathsf {s}}}$, one has
${\boldsymbol {\mathsf {s}}}$, one has
as seen from comparing the Taylor expansions in ![]() ${\boldsymbol {\mathsf{s}}}$ of the latter two expressions. (A generalization of this formula is discussed in § 4.1.) Also,
${\boldsymbol {\mathsf{s}}}$ of the latter two expressions. (A generalization of this formula is discussed in § 4.1.) Also,
and
Here, ‘bra’ ![]() ${\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\mathsf{x|}}}}}}} \right.}$ is the one-form dual to
${\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\mathsf{x|}}}}}}} \right.}$ is the one-form dual to ![]() ${\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}$,
${\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}$, ![]() ${\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\mathsf{k|}}}}}}} \right.}$ is the one-form dual to
${\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\mathsf{k|}}}}}}} \right.}$ is the one-form dual to ![]() ${\left. {\boldsymbol {\mathsf {|k}}} \right\rangle}$, and
${\left. {\boldsymbol {\mathsf {|k}}} \right\rangle}$, and ![]() $\widehat {{\mathsf {1}}}$ is the unit operator. Any field
$\widehat {{\mathsf {1}}}$ is the unit operator. Any field ![]() $\psi$ on
$\psi$ on ![]() ${\boldsymbol {\mathsf {x}}}$ can be viewed as the
${\boldsymbol {\mathsf {x}}}$ can be viewed as the ![]() ${\boldsymbol {\mathsf {x}}}$ representation (‘coordinate representation’) of
${\boldsymbol {\mathsf {x}}}$ representation (‘coordinate representation’) of ![]() ${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle}$, i.e. the projection of an abstract ket vector
${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle}$, i.e. the projection of an abstract ket vector ![]() ${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle} \in \mathscr {H}_{{{\mathsf {x}}}}$ on
${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle} \in \mathscr {H}_{{{\mathsf {x}}}}$ on ![]() $\smash {\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}$:
$\smash {\left. {\boldsymbol {\mathsf {|x}}} \right\rangle}$:
Similarly, ![]() $\left\langle {{\boldsymbol {\mathsf {k}}}|\psi }\right\rangle$ is the
$\left\langle {{\boldsymbol {\mathsf {k}}}|\psi }\right\rangle$ is the ![]() ${\boldsymbol {\mathsf {k}}}$ representation (‘spectral representation’) of
${\boldsymbol {\mathsf {k}}}$ representation (‘spectral representation’) of ![]() ${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle}$, or the Fourier image of
${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle}$, or the Fourier image of ![]() $\psi$:
$\psi$:
2.1.4. Wigner–Weyl transform
For a given operator ![]() $\widehat {{\mathsf {A}}}$ and a given field
$\widehat {{\mathsf {A}}}$ and a given field ![]() $\psi$,
$\psi$, ![]() $\widehat {{\mathsf {A}}}\psi$ can be expressed in the integral form
$\widehat {{\mathsf {A}}}\psi$ can be expressed in the integral form
where ![]() ${\left\langle {\boldsymbol {\mathsf {x}}}|\widehat {{\mathsf {A}}}|{\boldsymbol {\mathsf {x}}}'\right\rangle}$ is a function of
${\left\langle {\boldsymbol {\mathsf {x}}}|\widehat {{\mathsf {A}}}|{\boldsymbol {\mathsf {x}}}'\right\rangle}$ is a function of ![]() $({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {x}}}')$. This is called the
$({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {x}}}')$. This is called the ![]() ${\boldsymbol {\mathsf {x}}}$ representation (‘coordinate representation’) of
${\boldsymbol {\mathsf {x}}}$ representation (‘coordinate representation’) of ![]() $\smash {\widehat {{\mathsf {A}}}}$. Equivalently,
$\smash {\widehat {{\mathsf {A}}}}$. Equivalently, ![]() $\widehat {{\mathsf {A}}}$ can be given a phase-space, or Weyl, representation, i.e. expressed through a function of the phase-space coordinates,
$\widehat {{\mathsf {A}}}$ can be given a phase-space, or Weyl, representation, i.e. expressed through a function of the phase-space coordinates, ![]() ${\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$Footnote 7:
${\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$Footnote 7:
The function ![]() ${\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$, called the Weyl symbol (or just ‘symbol’) of
${\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$, called the Weyl symbol (or just ‘symbol’) of ![]() $\widehat {{\mathsf {A}}}$, is given by
$\widehat {{\mathsf {A}}}$, is given by
The ![]() ${\boldsymbol {\mathsf {x}}}$ and phase-space representations are connected by the Fourier transform:
${\boldsymbol {\mathsf {x}}}$ and phase-space representations are connected by the Fourier transform:
This also leads to the following notable properties of Weyl symbols:
An operator unambiguously determines its symbol, and vice versa. We denote this isomorphism as ![]() $\smash {\widehat {{\mathsf {A}}} \leftrightarrow {\mathsf {A}}}$. The mapping
$\smash {\widehat {{\mathsf {A}}} \leftrightarrow {\mathsf {A}}}$. The mapping ![]() $\smash {\widehat {{\mathsf {A}}} \mapsto {\mathsf {A}}}$ is called the Wigner transform, and
$\smash {\widehat {{\mathsf {A}}} \mapsto {\mathsf {A}}}$ is called the Wigner transform, and ![]() $\smash {{\mathsf {A}} \mapsto \widehat {{\mathsf {A}}}}$ is called the Weyl transform. For uniformity, we call them the direct and inverse Wigner–Weyl transform. The isomorphism
$\smash {{\mathsf {A}} \mapsto \widehat {{\mathsf {A}}}}$ is called the Weyl transform. For uniformity, we call them the direct and inverse Wigner–Weyl transform. The isomorphism ![]() $\smash {\leftrightarrow }$ is natural in that it has the following properties:
$\smash {\leftrightarrow }$ is natural in that it has the following properties:
where ![]() $h$ is any function and
$h$ is any function and ![]() $\smash {\widehat {{\mathsf {A}}}}$ is any operator. The product of two operators maps to the so-called Moyal product, or star product, of their symbols (Moyal Reference Moyal1949):
$\smash {\widehat {{\mathsf {A}}}}$ is any operator. The product of two operators maps to the so-called Moyal product, or star product, of their symbols (Moyal Reference Moyal1949):
which is associative:
Here, ![]() $\smash {\widehat {\mathcal {L}}_{{\mathsf {x}}} \doteq \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {\mathsf {x}}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {\mathsf {k}}} - \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {\mathsf {k}}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {\mathsf {x}}}}$, and the arrows indicate the directions in which the derivatives act. For example,
$\smash {\widehat {\mathcal {L}}_{{\mathsf {x}}} \doteq \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {\mathsf {x}}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {\mathsf {k}}} - \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {\mathsf {k}}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {\mathsf {x}}}}$, and the arrows indicate the directions in which the derivatives act. For example, ![]() $\smash {{\mathsf {A}}\widehat {\mathcal {L}}_{{\mathsf {x}}}{\mathsf {B}}}$ is just the canonical Poisson bracket on
$\smash {{\mathsf {A}}\widehat {\mathcal {L}}_{{\mathsf {x}}}{\mathsf {B}}}$ is just the canonical Poisson bracket on ![]() $\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$:
$\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$:
These formulas readily yield
also ![]() $h(\widehat {\boldsymbol {{\boldsymbol {\mathsf {k}}}}}) \mathrm {e}^{\mathrm {i}{\boldsymbol {\mathsf {K}}} \cdot \widehat {\boldsymbol {{\boldsymbol {\mathsf {x}}}}}} \leftrightarrow h({\boldsymbol {\mathsf {k}}})\star \mathrm {e}^{\mathrm {i}{\boldsymbol {\mathsf {K}}} \cdot {\boldsymbol {\mathsf {x}}}} = h({\boldsymbol {\mathsf {k}}} + {\boldsymbol {\mathsf {K}}}/2) \mathrm {e}^{\mathrm {i}{\boldsymbol {\mathsf {K}}} \cdot {\boldsymbol {\mathsf {x}}}}$, etc. Another notable formula to be used below, which flows from (2.28) and (2.31), is
$h(\widehat {\boldsymbol {{\boldsymbol {\mathsf {k}}}}}) \mathrm {e}^{\mathrm {i}{\boldsymbol {\mathsf {K}}} \cdot \widehat {\boldsymbol {{\boldsymbol {\mathsf {x}}}}}} \leftrightarrow h({\boldsymbol {\mathsf {k}}})\star \mathrm {e}^{\mathrm {i}{\boldsymbol {\mathsf {K}}} \cdot {\boldsymbol {\mathsf {x}}}} = h({\boldsymbol {\mathsf {k}}} + {\boldsymbol {\mathsf {K}}}/2) \mathrm {e}^{\mathrm {i}{\boldsymbol {\mathsf {K}}} \cdot {\boldsymbol {\mathsf {x}}}}$, etc. Another notable formula to be used below, which flows from (2.28) and (2.31), is
The Moyal product is particularly handy when ![]() $\partial _{{\boldsymbol {\mathsf {x}}}} \partial _{{\boldsymbol {\mathsf {k}}}} \sim \epsilon \ll 1$. Such
$\partial _{{\boldsymbol {\mathsf {x}}}} \partial _{{\boldsymbol {\mathsf {k}}}} \sim \epsilon \ll 1$. Such ![]() $\epsilon$ is often called the geometrical-optics parameter. Since
$\epsilon$ is often called the geometrical-optics parameter. Since ![]() $\widehat {\mathcal {L}}_{{\mathsf {x}}} = \mathcal {O}(\epsilon )$, one can express the Moyal product as an asymptotic series in powers of
$\widehat {\mathcal {L}}_{{\mathsf {x}}} = \mathcal {O}(\epsilon )$, one can express the Moyal product as an asymptotic series in powers of ![]() $\epsilon$:
$\epsilon$:
2.1.5. Weyl expansion of operators
Operators can be approximated by approximating their symbols (McDonald Reference McDonald1988; Dodin et al. Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019). If ![]() $\smash {\widehat {{\mathsf {A}}}}$ is approximately local in
$\smash {\widehat {{\mathsf {A}}}}$ is approximately local in ![]() ${\boldsymbol {\mathsf {x}}}$ (i.e. if
${\boldsymbol {\mathsf {x}}}$ (i.e. if ![]() $\smash {\widehat {{\mathsf {A}}}\psi ({\boldsymbol {\mathsf {x}}})}$ is determined by values
$\smash {\widehat {{\mathsf {A}}}\psi ({\boldsymbol {\mathsf {x}}})}$ is determined by values ![]() $\psi ({\boldsymbol {\mathsf {x}}} + {\boldsymbol {\mathsf {s}}})$ only with small enough
$\psi ({\boldsymbol {\mathsf {x}}} + {\boldsymbol {\mathsf {s}}})$ only with small enough ![]() ${\boldsymbol {\mathsf {s}}}$), its symbol can be adequately represented by the first few terms of the Taylor expansion in
${\boldsymbol {\mathsf {s}}}$), its symbol can be adequately represented by the first few terms of the Taylor expansion in ![]() ${\boldsymbol {\mathsf {k}}}$:
${\boldsymbol {\mathsf {k}}}$:
Application of ![]() $\smash {\text {oper}_{{\mathsf {x}}} }$ to this formula leads to
$\smash {\text {oper}_{{\mathsf {x}}} }$ to this formula leads to
where ![]() $\widehat {\boldsymbol {\Theta }}_0 \doteq {\boldsymbol {\Theta }}_0(\widehat {\,\boldsymbol {{\boldsymbol {\mathsf {x}}}}\,})$. One can also rewrite (2.37) using the commutation property
$\widehat {\boldsymbol {\Theta }}_0 \doteq {\boldsymbol {\Theta }}_0(\widehat {\,\boldsymbol {{\boldsymbol {\mathsf {x}}}}\,})$. One can also rewrite (2.37) using the commutation property
In the ![]() ${\boldsymbol {\mathsf {x}}}$ representation, this leads to
${\boldsymbol {\mathsf {x}}}$ representation, this leads to
The effect of a non-local operator on eikonal (monochromatic or quasimonochromatic) fields can be approximated similarly. Suppose ![]() $\psi = \mathrm {e}^{\mathrm {i}\theta }{\breve {\psi }}$, where the dependence of
$\psi = \mathrm {e}^{\mathrm {i}\theta }{\breve {\psi }}$, where the dependence of ![]() $\overline {{\boldsymbol {\mathsf {k}}}} \doteq \partial _{{\boldsymbol {\mathsf {x}}}}\theta$ and
$\overline {{\boldsymbol {\mathsf {k}}}} \doteq \partial _{{\boldsymbol {\mathsf {x}}}}\theta$ and ![]() ${\breve {\psi }}$ on
${\breve {\psi }}$ on ![]() ${\boldsymbol {\mathsf {x}}}$ is slower than that of
${\boldsymbol {\mathsf {x}}}$ is slower than that of ![]() $\theta$ by factor
$\theta$ by factor ![]() $\epsilon \ll 1$. Then,
$\epsilon \ll 1$. Then, ![]() $\widehat {{\mathsf {A}}}\psi = \mathrm {e}^{\mathrm {i}\theta }\widehat {{\mathsf {A}}}' {\breve {\psi }}$, where
$\widehat {{\mathsf {A}}}\psi = \mathrm {e}^{\mathrm {i}\theta }\widehat {{\mathsf {A}}}' {\breve {\psi }}$, where ![]() $\widehat {{\mathsf {A}}}' \doteq \mathrm {e}^{-\mathrm {i}\theta (\widehat {{\mathsf {x}}})}\widehat {{\mathsf {A}}}\mathrm {e}^{\mathrm {i}\theta (\widehat {{\mathsf {x}}})}$, and the symbol of
$\widehat {{\mathsf {A}}}' \doteq \mathrm {e}^{-\mathrm {i}\theta (\widehat {{\mathsf {x}}})}\widehat {{\mathsf {A}}}\mathrm {e}^{\mathrm {i}\theta (\widehat {{\mathsf {x}}})}$, and the symbol of ![]() $\widehat {{\mathsf {A}}}'$ can be approximated as follows:
$\widehat {{\mathsf {A}}}'$ can be approximated as follows:
By expanding this in ![]() ${\boldsymbol {\mathsf {k}}}$ and applying
${\boldsymbol {\mathsf {k}}}$ and applying ![]() $\smash {\text {oper}_{{\mathsf {x}}} }$, one obtains
$\smash {\text {oper}_{{\mathsf {x}}} }$, one obtains
where ![]() ${\boldsymbol {\Theta }}({\boldsymbol {\mathsf {x}}}) \doteq (\partial _{\boldsymbol {\mathsf {k}}} {\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}}))_{{\boldsymbol {\mathsf {k}}}=\overline {{\boldsymbol {\mathsf {k}}}}({\boldsymbol {\mathsf {x}}})}$. Neglecting the
${\boldsymbol {\Theta }}({\boldsymbol {\mathsf {x}}}) \doteq (\partial _{\boldsymbol {\mathsf {k}}} {\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}}))_{{\boldsymbol {\mathsf {k}}}=\overline {{\boldsymbol {\mathsf {k}}}}({\boldsymbol {\mathsf {x}}})}$. Neglecting the ![]() $\mathcal {O}(\epsilon ^2)$ corrections in this formula leads to what is commonly known as the geometrical-optics approximation (Dodin et al. Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019).
$\mathcal {O}(\epsilon ^2)$ corrections in this formula leads to what is commonly known as the geometrical-optics approximation (Dodin et al. Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019).
2.1.6. Wigner functions
Any ket ![]() ${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle}$ generates a dyadic
${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle}$ generates a dyadic ![]() ${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\mathsf{\psi|}}}}}}} \right.}$. In quantum mechanics, such dyadics are known as density operators (of pure states). For our purposes, though, it is more convenient to define the density operator in a slightly different form, namely, as
${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\mathsf{\psi|}}}}}}} \right.}$. In quantum mechanics, such dyadics are known as density operators (of pure states). For our purposes, though, it is more convenient to define the density operator in a slightly different form, namely, as
The symbol of this operator, ![]() $\smash {{\mathsf {W}}_{\psi } = \text {symb}_{{\mathsf {x}}} \widehat {{\mathsf {W}}}_\psi }$, is a real function called the Wigner function. It is given by
$\smash {{\mathsf {W}}_{\psi } = \text {symb}_{{\mathsf {x}}} \widehat {{\mathsf {W}}}_\psi }$, is a real function called the Wigner function. It is given by
 \begin{align} {\mathsf{W}}_\psi({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) & = \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}} \int \mathrm{d}{\boldsymbol {\mathsf{s}}} \left\langle{{\boldsymbol {\mathsf{x}}} + {\boldsymbol {\mathsf{s}}}/2 | \psi}\right\rangle \left\langle{\psi | {\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{s}}}/2}\right\rangle \mathrm{e}^{-\mathrm{i} {\boldsymbol {\mathsf{k}}} \cdot {\boldsymbol {\mathsf{s}}}} \nonumber\\ & = \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}} \int \mathrm{d}{\boldsymbol {\mathsf{s}}}\, \psi({\boldsymbol {\mathsf{x}}} + {\boldsymbol {\mathsf{s}}}/2) \psi^*({\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{s}}}/2)\,\mathrm{e}^{-\mathrm{i} {\boldsymbol {\mathsf{k}}} \cdot {\boldsymbol {\mathsf{s}}}}, \end{align}
\begin{align} {\mathsf{W}}_\psi({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) & = \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}} \int \mathrm{d}{\boldsymbol {\mathsf{s}}} \left\langle{{\boldsymbol {\mathsf{x}}} + {\boldsymbol {\mathsf{s}}}/2 | \psi}\right\rangle \left\langle{\psi | {\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{s}}}/2}\right\rangle \mathrm{e}^{-\mathrm{i} {\boldsymbol {\mathsf{k}}} \cdot {\boldsymbol {\mathsf{s}}}} \nonumber\\ & = \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}} \int \mathrm{d}{\boldsymbol {\mathsf{s}}}\, \psi({\boldsymbol {\mathsf{x}}} + {\boldsymbol {\mathsf{s}}}/2) \psi^*({\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{s}}}/2)\,\mathrm{e}^{-\mathrm{i} {\boldsymbol {\mathsf{k}}} \cdot {\boldsymbol {\mathsf{s}}}}, \end{align}which is manifestly real and can be understood as the (inverse) Fourier image of
Any function bilinear in ![]() $\smash {\psi }$ and
$\smash {\psi }$ and ![]() $\smash {\psi ^*}$ can be expressed through
$\smash {\psi ^*}$ can be expressed through ![]() $\smash {{\mathsf {W}}_\psi }$. Specifically, for any operators
$\smash {{\mathsf {W}}_\psi }$. Specifically, for any operators ![]() $\smash {\widehat {{\mathsf {L}}}}$ and
$\smash {\widehat {{\mathsf {L}}}}$ and ![]() $\smash {\widehat {{\mathsf {R}}}}$, one has
$\smash {\widehat {{\mathsf {R}}}}$, one has
 \begin{align} (\widehat{{\mathsf{L}}}\psi({\boldsymbol {\mathsf{x}}}))(\widehat{{\mathsf{R}}}\psi({\boldsymbol {\mathsf{x}}}))^* & = \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}}}|\psi}\right\rangle \left\langle{\psi|\widehat{{\mathsf{R}}}^{{\dagger}} |{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = (2{\rm \pi})^{{\mathsf{n}}} \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}}}\,\widehat{{\mathsf{W}}}_\psi\widehat{{\mathsf{R}}}^{{\dagger}}|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = \textstyle \int \mathrm{d}{\boldsymbol {\mathsf{k}}}\,{\mathsf{L}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {\mathsf{W}}_\psi({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {\mathsf{R}}^*({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}), \end{align}
\begin{align} (\widehat{{\mathsf{L}}}\psi({\boldsymbol {\mathsf{x}}}))(\widehat{{\mathsf{R}}}\psi({\boldsymbol {\mathsf{x}}}))^* & = \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}}}|\psi}\right\rangle \left\langle{\psi|\widehat{{\mathsf{R}}}^{{\dagger}} |{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = (2{\rm \pi})^{{\mathsf{n}}} \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}}}\,\widehat{{\mathsf{W}}}_\psi\widehat{{\mathsf{R}}}^{{\dagger}}|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = \textstyle \int \mathrm{d}{\boldsymbol {\mathsf{k}}}\,{\mathsf{L}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {\mathsf{W}}_\psi({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {\mathsf{R}}^*({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}), \end{align}
where ![]() ${\mathsf {L}}$ and
${\mathsf {L}}$ and ![]() ${\mathsf {R}}$ are the corresponding symbols and (2.28) was used along with (2.31). As a corollary, and as also seen from (2.28), one has
${\mathsf {R}}$ are the corresponding symbols and (2.28) was used along with (2.31). As a corollary, and as also seen from (2.28), one has
As a reminder, ![]() $\psi ({\boldsymbol {\mathsf {x}}}) = \left\langle {{\boldsymbol {\mathsf {x}}}|\psi }\right\rangle$ and
$\psi ({\boldsymbol {\mathsf {x}}}) = \left\langle {{\boldsymbol {\mathsf {x}}}|\psi }\right\rangle$ and ![]() $\mathring {\psi }({\boldsymbol {\mathsf {k}}}) \doteq \left\langle {{\boldsymbol {\mathsf {k}}}|\psi }\right\rangle$ is the Fourier image of
$\mathring {\psi }({\boldsymbol {\mathsf {k}}}) \doteq \left\langle {{\boldsymbol {\mathsf {k}}}|\psi }\right\rangle$ is the Fourier image of ![]() $\psi$ (2.23), so
$\psi$ (2.23), so ![]() $\smash {|\psi ({\boldsymbol {\mathsf {x}}})|^2}$ and
$\smash {|\psi ({\boldsymbol {\mathsf {x}}})|^2}$ and ![]() $\smash {|\mathring {\psi }({\boldsymbol {\mathsf {k}}})|^2}$ can be loosely understood as the densities of quanta (associated with the field
$\smash {|\mathring {\psi }({\boldsymbol {\mathsf {k}}})|^2}$ can be loosely understood as the densities of quanta (associated with the field ![]() $\smash {\psi }$) in the
$\smash {\psi }$) in the ![]() $\smash {{\boldsymbol {\mathsf {x}}}}$-space and the
$\smash {{\boldsymbol {\mathsf {x}}}}$-space and the ![]() $\smash {{\boldsymbol {\mathsf {k}}}}$-space, respectively. Because of (2.46),
$\smash {{\boldsymbol {\mathsf {k}}}}$-space, respectively. Because of (2.46), ![]() $\smash {{\mathsf {W}}_\psi }$ is commonly attributed as a quasiprobability distribution of wave quanta in phase space. (The prefix ‘quasi’ is added because
$\smash {{\mathsf {W}}_\psi }$ is commonly attributed as a quasiprobability distribution of wave quanta in phase space. (The prefix ‘quasi’ is added because ![]() $\smash {{\mathsf {W}}_\psi }$ can be negative.) In case of real fields, which satisfy
$\smash {{\mathsf {W}}_\psi }$ can be negative.) In case of real fields, which satisfy ![]() $\left\langle {{\boldsymbol {\mathsf {x}}}|\psi }\right\rangle = \left\langle {\psi |{\boldsymbol {\mathsf {x}}}}\right\rangle$, one also has
$\left\langle {{\boldsymbol {\mathsf {x}}}|\psi }\right\rangle = \left\langle {\psi |{\boldsymbol {\mathsf {x}}}}\right\rangle$, one also has
Of particular importance are Wigner functions averaged over a sufficiently large phase-space volume ![]() $\varDelta {\boldsymbol {\mathsf {x}}}\,\varDelta {\boldsymbol {\mathsf {k}}} \gtrsim 1$. The average Wigner function
$\varDelta {\boldsymbol {\mathsf {x}}}\,\varDelta {\boldsymbol {\mathsf {k}}} \gtrsim 1$. The average Wigner function ![]() $\smash {\overline {{\mathsf {W}}}_\psi }$ is a local property of the field (as opposed to, say, the field's global Fourier spectrum) and satisfies (Appendix A)
$\smash {\overline {{\mathsf {W}}}_\psi }$ is a local property of the field (as opposed to, say, the field's global Fourier spectrum) and satisfies (Appendix A)
2.1.7. Generalization to vector fields
In case of vector (tuple) fields ![]() ${\boldsymbol {\psi }} = (\psi ^1, \psi ^2, \ldots, \psi ^M)^{\intercal }$, kets are column vectors,
${\boldsymbol {\psi }} = (\psi ^1, \psi ^2, \ldots, \psi ^M)^{\intercal }$, kets are column vectors, ![]() ${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle} = ({\left. {\boldsymbol {\mathsf {|\psi ^1}}} \right\rangle} , {\left. {\boldsymbol {\mathsf {|\psi ^2}}} \right\rangle}, \ldots, {\left. {\boldsymbol {\mathsf {|\psi ^M}}} \right\rangle})^{\intercal }$, and bras are row vectors,
${\left. {\boldsymbol {\mathsf {|\psi}}} \right\rangle} = ({\left. {\boldsymbol {\mathsf {|\psi ^1}}} \right\rangle} , {\left. {\boldsymbol {\mathsf {|\psi ^2}}} \right\rangle}, \ldots, {\left. {\boldsymbol {\mathsf {|\psi ^M}}} \right\rangle})^{\intercal }$, and bras are row vectors, ![]() ${\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\psi |}}}}}} \right.} = ({\left\langle {{\boldsymbol {\mathsf {{\psi ^1}|}}}} \right.}, {\left\langle {{\boldsymbol {\mathsf {{\psi ^2}|}}}} \right.}, \ldots, {\left\langle {{\boldsymbol {\mathsf {{\psi ^M}|}}}} \right.})^\intercal$. The operators acting on such kets and bras are matrices of operators. The Weyl symbol of a matrix operator is defined as the matrix of the corresponding symbols. As a result, the symbol of a Hermitian adjoint of a given operator is the Hermitian adjoint of the symbol of that operator:
${\left\langle {{\boldsymbol {\mathsf {{\boldsymbol {\psi |}}}}}} \right.} = ({\left\langle {{\boldsymbol {\mathsf {{\psi ^1}|}}}} \right.}, {\left\langle {{\boldsymbol {\mathsf {{\psi ^2}|}}}} \right.}, \ldots, {\left\langle {{\boldsymbol {\mathsf {{\psi ^M}|}}}} \right.})^\intercal$. The operators acting on such kets and bras are matrices of operators. The Weyl symbol of a matrix operator is defined as the matrix of the corresponding symbols. As a result, the symbol of a Hermitian adjoint of a given operator is the Hermitian adjoint of the symbol of that operator:
and as a corollary, the symbol of a Hermitian matrix operator is a Hermitian matrix.
In particular, the density operator of a given vector field ![]() ${\boldsymbol {\psi }}$ is a matrix operator
${\boldsymbol {\psi }}$ is a matrix operator
The symbol of this operator, ![]() $\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}} = \text {symb}_{{\mathsf {x}}} \widehat {\boldsymbol {{\boldsymbol {\mathsf {W}}}}}_{{\boldsymbol {\psi }}}}$, is a Hermitian matrix functionFootnote 8
$\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}} = \text {symb}_{{\mathsf {x}}} \widehat {\boldsymbol {{\boldsymbol {\mathsf {W}}}}}_{{\boldsymbol {\psi }}}}$, is a Hermitian matrix functionFootnote 8
called the Wigner matrix. (It is also called the ‘Wigner tensor’ when ![]() $\smash {{\boldsymbol {\psi }}}$ is a true vector rather than a tuple.) It can be understood as the (inverse) Fourier image of
$\smash {{\boldsymbol {\psi }}}$ is a true vector rather than a tuple.) It can be understood as the (inverse) Fourier image of
The analogue of (2.45) is (Appendix B.1)
The Wigner matrix averaged over a sufficiently large phase-space volume ![]() $\varDelta {\boldsymbol {\mathsf {x}}}\,\varDelta {\boldsymbol {\mathsf {k}}} \gtrsim 1$ is a local property of the field, and it is positive-semidefinite (Appendix A).
$\varDelta {\boldsymbol {\mathsf {x}}}\,\varDelta {\boldsymbol {\mathsf {k}}} \gtrsim 1$ is a local property of the field, and it is positive-semidefinite (Appendix A).
For real fields, one also has
and (2.53) yields the following corollary at ![]() $\smash {\epsilon \to 0}$, when
$\smash {\epsilon \to 0}$, when ![]() $\smash {\star }$ becomes the usual product (Appendix B.1):
$\smash {\star }$ becomes the usual product (Appendix B.1):
The generalizations of the other formulas from the previous sections are obvious.
2.2. Weyl symbol calculus on phase space
2.2.1. Notation
Consider a Hamiltonian system with coordinates ![]() ${\boldsymbol {x}} \equiv (x^1, x^2, \ldots, x^n)$ and canonical momenta
${\boldsymbol {x}} \equiv (x^1, x^2, \ldots, x^n)$ and canonical momenta ![]() ${\boldsymbol {p}} \equiv (p_1, p_2, \ldots, p_n)$. Together, these variables comprise the phase-space coordinates
${\boldsymbol {p}} \equiv (p_1, p_2, \ldots, p_n)$. Together, these variables comprise the phase-space coordinates ![]() ${\boldsymbol {z}} \equiv ({\boldsymbol {x}}, {\boldsymbol {p}})$, i.e.
${\boldsymbol {z}} \equiv ({\boldsymbol {x}}, {\boldsymbol {p}})$, i.e.
Components of ![]() ${\boldsymbol {z}}$ will be denoted with Greek indices ranging from 1 to
${\boldsymbol {z}}$ will be denoted with Greek indices ranging from 1 to ![]() $2n$.Footnote 9
$2n$.Footnote 9
Hamilton's equations for ![]() $z^\alpha$ can be written as
$z^\alpha$ can be written as ![]() $\dot {z}^{\alpha } = \lbrace z^{\alpha }, H \rbrace$, or equivalently, as
$\dot {z}^{\alpha } = \lbrace z^{\alpha }, H \rbrace$, or equivalently, as
Here, ![]() $H = H(t, {\boldsymbol {z}})$ is a Hamiltonian,
$H = H(t, {\boldsymbol {z}})$ is a Hamiltonian, ![]() $\partial _\beta \doteq \partial /\partial z^\beta$,
$\partial _\beta \doteq \partial /\partial z^\beta$,
is the Poisson bracket on ![]() $\smash {{\boldsymbol {z}}}$, and
$\smash {{\boldsymbol {z}}}$, and ![]() $J^{\alpha \beta }$ is the canonical Poisson structure:
$J^{\alpha \beta }$ is the canonical Poisson structure:
where ![]() ${\boldsymbol {0}}_n$ is an
${\boldsymbol {0}}_n$ is an ![]() $n$-dimensional zero matrix, and
$n$-dimensional zero matrix, and ![]() ${\boldsymbol {1}}_n$ is an
${\boldsymbol {1}}_n$ is an ![]() $n$-dimensional unit matrix. The corresponding equation for the probability distribution
$n$-dimensional unit matrix. The corresponding equation for the probability distribution ![]() $f(t, {\boldsymbol {z}})$ is
$f(t, {\boldsymbol {z}})$ is
Solutions of (2.58) and other functions of the extended-phase-space coordinates ![]() ${\boldsymbol {X}} \equiv (t, {\boldsymbol {z}})$ can be considered as vectors in the Hilbert space
${\boldsymbol {X}} \equiv (t, {\boldsymbol {z}})$ can be considered as vectors in the Hilbert space ![]() $\mathscr {H}_X$ with the usual inner productFootnote 10
$\mathscr {H}_X$ with the usual inner productFootnote 10
Assuming the notation ![]() $N \doteq \dim {\boldsymbol {X}} = 2n + 1$, one has
$N \doteq \dim {\boldsymbol {X}} = 2n + 1$, one has
Let us introduce the position operator on ![]() ${\boldsymbol {z}}$,
${\boldsymbol {z}}$,
and the momentum operator on ![]() ${\boldsymbol {z}}$,
${\boldsymbol {z}}$,
 \begin{equation} \widehat{\boldsymbol{q}} \equiv ( \underbrace{-\mathrm{i} \partial_1, \ldots, -\mathrm{i}\partial_n}_{\widehat{\boldsymbol{k}}}, \underbrace{-\mathrm{i}\partial^1, \ldots, -\mathrm{i}\partial^n}_{\widehat{\boldsymbol{r}}} ), \end{equation}
\begin{equation} \widehat{\boldsymbol{q}} \equiv ( \underbrace{-\mathrm{i} \partial_1, \ldots, -\mathrm{i}\partial_n}_{\widehat{\boldsymbol{k}}}, \underbrace{-\mathrm{i}\partial^1, \ldots, -\mathrm{i}\partial^n}_{\widehat{\boldsymbol{r}}} ), \end{equation}
where ![]() $\partial _i \doteq \partial /\partial x^i$ but
$\partial _i \doteq \partial /\partial x^i$ but ![]() $\partial ^i \doteq \partial /\partial p_i$; that is,
$\partial ^i \doteq \partial /\partial p_i$; that is, ![]() $\widehat {\boldsymbol {z}} = (\widehat {\boldsymbol {x}}, \widehat {\boldsymbol {p}})$,
$\widehat {\boldsymbol {z}} = (\widehat {\boldsymbol {x}}, \widehat {\boldsymbol {p}})$, ![]() $\widehat {\boldsymbol {q}} = (\widehat {\boldsymbol {k}}, \widehat {\boldsymbol {r}}\,)$ and
$\widehat {\boldsymbol {q}} = (\widehat {\boldsymbol {k}}, \widehat {\boldsymbol {r}}\,)$ and
Then, much like in § 2.1, one can also introduce the position and momentum operators on the extended phase space ![]() ${\boldsymbol {X}}$:
${\boldsymbol {X}}$:
Assuming the convention that Latin indices from the beginning of the alphabet ![]() $(a, b, c, \ldots )$ range from 0 to
$(a, b, c, \ldots )$ range from 0 to ![]() $2n$, and
$2n$, and ![]() $\partial _a \doteq \partial /\partial X^a$, one can compactly express this as
$\partial _a \doteq \partial /\partial X^a$, one can compactly express this as
The eigenvectors of these operators will be denoted ![]() ${\left. {\boldsymbol {\mathsf {|X}}} \right\rangle}$ and
${\left. {\boldsymbol {\mathsf {|X}}} \right\rangle}$ and ![]() ${\left. {\boldsymbol {\mathsf {|K}}} \right\rangle}$:
${\left. {\boldsymbol {\mathsf {|K}}} \right\rangle}$:
and we assume the usual normalization
Both sets ![]() $\lbrace {\left. {\boldsymbol {\mathsf {|X}}} \right\rangle}, {\boldsymbol {X}} \in \mathbb {R}^N \rbrace$ and
$\lbrace {\left. {\boldsymbol {\mathsf {|X}}} \right\rangle}, {\boldsymbol {X}} \in \mathbb {R}^N \rbrace$ and ![]() $\lbrace {\left. {\boldsymbol {\mathsf {|K}}} \right\rangle}, {\boldsymbol {K}} \in \mathbb {R}^N \rbrace$ form a complete basis on
$\lbrace {\left. {\boldsymbol {\mathsf {|K}}} \right\rangle}, {\boldsymbol {K}} \in \mathbb {R}^N \rbrace$ form a complete basis on ![]() $\mathscr {H}_X$, and the eigenvalues of these operators form a real extended phase space
$\mathscr {H}_X$, and the eigenvalues of these operators form a real extended phase space ![]() $({\boldsymbol {X}}, {\boldsymbol {K}})$, where
$({\boldsymbol {X}}, {\boldsymbol {K}})$, where
Particularly note the following formula, which will be used below:
2.2.2. Wigner–Weyl transform
One can construct the Weyl symbol calculus on the extended phase space ![]() ${\boldsymbol {X}}$ just like it is done on spacetime
${\boldsymbol {X}}$ just like it is done on spacetime ![]() ${\boldsymbol {\mathsf {x}}}$ in § 2.1, with an obvious modification of the notation. The Wigner–Weyl transform is defined as
${\boldsymbol {\mathsf {x}}}$ in § 2.1, with an obvious modification of the notation. The Wigner–Weyl transform is defined as
 \begin{gather}\displaystyle \widehat{A} = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}\,\mathrm{d}{\boldsymbol{K}}\,\mathrm{d}{\boldsymbol{S}} {\left. {\boldsymbol {\mathsf {|X}}} \right\rangle}+{{\boldsymbol{S}}/2} A({\boldsymbol{X}}, {\boldsymbol{K}}) {\left\langle {{\boldsymbol {\mathsf {X|}}}} \right.} - {{\boldsymbol{S}}/2} \mathrm{e}^{\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}}} \equiv \text{oper}_X A. \end{gather}
\begin{gather}\displaystyle \widehat{A} = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}\,\mathrm{d}{\boldsymbol{K}}\,\mathrm{d}{\boldsymbol{S}} {\left. {\boldsymbol {\mathsf {|X}}} \right\rangle}+{{\boldsymbol{S}}/2} A({\boldsymbol{X}}, {\boldsymbol{K}}) {\left\langle {{\boldsymbol {\mathsf {X|}}}} \right.} - {{\boldsymbol{S}}/2} \mathrm{e}^{\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}}} \equiv \text{oper}_X A. \end{gather}
(Notice the change in the font and in the index compared with (2.26) and (2.25).) The corresponding Moyal product is denoted ![]() $\bigstar$ (as opposed to
$\bigstar$ (as opposed to ![]() $\star$ introduced earlier) and is given by
$\star$ introduced earlier) and is given by
where ![]() $\widehat {\mathcal {L}}_X \doteq \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {X}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {K}} - \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {K}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {X}}$ can be expressed as follows:
$\widehat {\mathcal {L}}_X \doteq \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {X}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {K}} - \overset {{\scriptscriptstyle \leftarrow }}{\partial }_{\boldsymbol {K}} \cdot \overset {{\scriptscriptstyle \rightarrow }}{\partial }_{\boldsymbol {X}}$ can be expressed as follows:
If an operator ![]() $\smash {\widehat {A}}$ is local in
$\smash {\widehat {A}}$ is local in ![]() $\smash {{\boldsymbol {p}}}$, its
$\smash {{\boldsymbol {p}}}$, its ![]() $\smash {{\boldsymbol {X}}}$ representation and
$\smash {{\boldsymbol {X}}}$ representation and ![]() $\smash {{\boldsymbol {\mathsf {x}}}}$ representation satisfy
$\smash {{\boldsymbol {\mathsf {x}}}}$ representation satisfy
and therefore the Weyl symbol of ![]() $\smash {\widehat {A}}$ is the same irrespective of whether the operator is considered on
$\smash {\widehat {A}}$ is the same irrespective of whether the operator is considered on ![]() $\smash {\mathscr {H}_X}$ or on
$\smash {\mathscr {H}_X}$ or on ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$. In this case, we will use a unifying notation
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$. In this case, we will use a unifying notation ![]() $\smash {\text {symb}\,\widehat {A}}$ instead of
$\smash {\text {symb}\,\widehat {A}}$ instead of ![]() $\smash {\text {symb}_X \widehat {A}}$ and
$\smash {\text {symb}_X \widehat {A}}$ and ![]() $\smash {\text {symb}_{{\mathsf {x}}} \widehat {A}}$.
$\smash {\text {symb}_{{\mathsf {x}}} \widehat {A}}$.
2.2.3. Wigner functions and Wigner matrices
The density operator of a given scalar field ![]() $\psi$ is given by
$\psi$ is given by
The symbol of this operator, ![]() $\smash {W_{\psi } = \text {symb}_X \widehat {W}_\psi }$, is a real function called the Wigner function. It is given by
$\smash {W_{\psi } = \text {symb}_X \widehat {W}_\psi }$, is a real function called the Wigner function. It is given by
which can be understood as the (inverse) Fourier image of
In particular, one has
where the right-hand side is ![]() $\smash {{\mathsf {W}}_\psi }$ given by (2.43), with
$\smash {{\mathsf {W}}_\psi }$ given by (2.43), with ![]() ${\boldsymbol {p}}$ treated as a parameter. Also, for real fields,
${\boldsymbol {p}}$ treated as a parameter. Also, for real fields,
The density operator of a given vector field ![]() ${\boldsymbol {\psi }} = (\psi ^1, \psi ^2, \ldots, \psi ^M)$ is a matrix operator
${\boldsymbol {\psi }} = (\psi ^1, \psi ^2, \ldots, \psi ^M)$ is a matrix operator
The symbol of this operator, or the Wigner matrix, is a Hermitian matrix function
which can be understood as the (inverse) Fourier image of
In particular, one has
where the right-hand side is ![]() $\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}}$ given by (2.51), with
$\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}}$ given by (2.51), with ![]() ${\boldsymbol {p}}$ treated as a parameter. Also, for real fields,
${\boldsymbol {p}}$ treated as a parameter. Also, for real fields,
Like those on ![]() $\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$, the Wigner matrices (Wigner functions) on
$\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$, the Wigner matrices (Wigner functions) on ![]() $\smash {({\boldsymbol {X}}, {\boldsymbol {K}})}$ become positive-semidefinite (non-negative), and characterize local properties of the corresponding fields, when averaged over a sufficiently large phase-space volume
$\smash {({\boldsymbol {X}}, {\boldsymbol {K}})}$ become positive-semidefinite (non-negative), and characterize local properties of the corresponding fields, when averaged over a sufficiently large phase-space volume ![]() $\varDelta {\boldsymbol {X}}\,\varDelta {\boldsymbol {K}} \gtrsim 1$.
$\varDelta {\boldsymbol {X}}\,\varDelta {\boldsymbol {K}} \gtrsim 1$.
2.3. Summary of § 2
In summary, we have introduced a generic ![]() $\smash {n}$-dimensional physical space
$\smash {n}$-dimensional physical space ![]() $\smash {{\boldsymbol {x}}}$, the dual
$\smash {{\boldsymbol {x}}}$, the dual ![]() $\smash {n}$-dimensional wavevector space
$\smash {n}$-dimensional wavevector space ![]() $\smash {{\boldsymbol {k}}}$, the corresponding
$\smash {{\boldsymbol {k}}}$, the corresponding ![]() $\smash {{{\mathsf {n}}}}$-dimensional (
$\smash {{{\mathsf {n}}}}$-dimensional (![]() $\smash {{{\mathsf {n}}} = n + 1}$) spacetime
$\smash {{{\mathsf {n}}} = n + 1}$) spacetime ![]() $\smash {{\boldsymbol {\mathsf {x}}} \equiv (t, {\boldsymbol {x}})}$ and the dual
$\smash {{\boldsymbol {\mathsf {x}}} \equiv (t, {\boldsymbol {x}})}$ and the dual ![]() $\smash {{{\mathsf {n}}}}$-dimensional wavevector space
$\smash {{{\mathsf {n}}}}$-dimensional wavevector space ![]() $\smash {{\boldsymbol {\mathsf {k}}} \equiv (-\omega, {\boldsymbol {k}})}$. We have also introduced an
$\smash {{\boldsymbol {\mathsf {k}}} \equiv (-\omega, {\boldsymbol {k}})}$. We have also introduced an ![]() $\smash {n}$-dimensional momentum space
$\smash {n}$-dimensional momentum space ![]() $\smash {{\boldsymbol {p}}}$, the corresponding
$\smash {{\boldsymbol {p}}}$, the corresponding ![]() $\smash {2n}$-dimensional phase space
$\smash {2n}$-dimensional phase space ![]() $\smash {{\boldsymbol {z}} \equiv ({\boldsymbol {x}}, {\boldsymbol {p}})}$, the
$\smash {{\boldsymbol {z}} \equiv ({\boldsymbol {x}}, {\boldsymbol {p}})}$, the ![]() $\smash {N}$-dimensional (
$\smash {N}$-dimensional (![]() $\smash {N = 2n + 1}$) extended space
$\smash {N = 2n + 1}$) extended space ![]() $\smash {{\boldsymbol {X}} \equiv (t, {\boldsymbol {z}}) \equiv (t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ and the dual
$\smash {{\boldsymbol {X}} \equiv (t, {\boldsymbol {z}}) \equiv (t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ and the dual ![]() $\smash {N}$-dimensional wavevector space
$\smash {N}$-dimensional wavevector space ![]() $\smash {{\boldsymbol {K}} \equiv (-\omega, {\boldsymbol {q}}) \equiv (-\omega, {\boldsymbol {k}}, {\boldsymbol {r}})}$, where
$\smash {{\boldsymbol {K}} \equiv (-\omega, {\boldsymbol {q}}) \equiv (-\omega, {\boldsymbol {k}}, {\boldsymbol {r}})}$, where ![]() $\smash {{\boldsymbol {r}}}$ is the
$\smash {{\boldsymbol {r}}}$ is the ![]() $\smash {n}$-dimensional wavevector space dual to
$\smash {n}$-dimensional wavevector space dual to ![]() $\smash {{\boldsymbol {p}}}$. We have also introduced the
$\smash {{\boldsymbol {p}}}$. We have also introduced the ![]() $\smash {2N}$-dimensional phase space
$\smash {2N}$-dimensional phase space ![]() $\smash {({\boldsymbol {X}}, {\boldsymbol {K}})}$. Each of the said variables has a corresponding operator associated with it, which is denoted with a caret. For example,
$\smash {({\boldsymbol {X}}, {\boldsymbol {K}})}$. Each of the said variables has a corresponding operator associated with it, which is denoted with a caret. For example, ![]() $\smash {\widehat {\boldsymbol {x}}}$ is the operator of position in the
$\smash {\widehat {\boldsymbol {x}}}$ is the operator of position in the ![]() $\smash {{\boldsymbol {x}}}$ space, and
$\smash {{\boldsymbol {x}}}$ space, and ![]() $\smash {\widehat {\boldsymbol {k}} = -\mathrm {i}\partial _{{\boldsymbol {x}}}}$ is the corresponding wavevector operator.
$\smash {\widehat {\boldsymbol {k}} = -\mathrm {i}\partial _{{\boldsymbol {x}}}}$ is the corresponding wavevector operator.
Functions on ![]() $\smash {{\boldsymbol {\mathsf {x}}}}$ form a Hilbert space
$\smash {{\boldsymbol {\mathsf {x}}}}$ form a Hilbert space ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$, and the corresponding bra–ket notation is introduced as usual. Any operator
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$, and the corresponding bra–ket notation is introduced as usual. Any operator ![]() $\smash {\widehat {{\mathsf {A}}}}$ on
$\smash {\widehat {{\mathsf {A}}}}$ on ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ can be represented by its Weyl symbol
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ can be represented by its Weyl symbol ![]() $\smash {{\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. The correspondence between operators and their symbols,
$\smash {{\mathsf {A}}({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. The correspondence between operators and their symbols, ![]() $\smash {\widehat {{\mathsf {A}}} \leftrightarrow {\mathsf {A}}}$, is determined by the Wigner–Weyl transform and is natural in the sense that (2.29) is satisfied. In particular,
$\smash {\widehat {{\mathsf {A}}} \leftrightarrow {\mathsf {A}}}$, is determined by the Wigner–Weyl transform and is natural in the sense that (2.29) is satisfied. In particular, ![]() $\smash {\widehat {{\mathsf {A}}}\,\widehat {{\mathsf {B}}} \leftrightarrow {\mathsf {A}} \star {\mathsf {B}}}$, where
$\smash {\widehat {{\mathsf {A}}}\,\widehat {{\mathsf {B}}} \leftrightarrow {\mathsf {A}} \star {\mathsf {B}}}$, where ![]() $\smash {\star }$ is the Moyal product on
$\smash {\star }$ is the Moyal product on ![]() $\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. When the geometrical-optics parameter is negligible (
$\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. When the geometrical-optics parameter is negligible (![]() $\smash {\epsilon \to 0}$), one has
$\smash {\epsilon \to 0}$), one has ![]() $\smash {\widehat {{\mathsf {A}}} = {\mathsf {A}}(\,\widehat {\boldsymbol {{\boldsymbol {\mathsf {x}}}}}, \widehat {\boldsymbol {{\boldsymbol {\mathsf {k}}}}})}$ and the Moyal product becomes the usual product. Similarly, functions on
$\smash {\widehat {{\mathsf {A}}} = {\mathsf {A}}(\,\widehat {\boldsymbol {{\boldsymbol {\mathsf {x}}}}}, \widehat {\boldsymbol {{\boldsymbol {\mathsf {k}}}}})}$ and the Moyal product becomes the usual product. Similarly, functions on ![]() $\smash {{\boldsymbol {X}}}$ form a Hilbert space
$\smash {{\boldsymbol {X}}}$ form a Hilbert space ![]() $\smash {\mathscr {H}_X}$, the corresponding bra–ket notation is also introduced as usual, any operator
$\smash {\mathscr {H}_X}$, the corresponding bra–ket notation is also introduced as usual, any operator ![]() $\smash {\widehat {A}}$ on
$\smash {\widehat {A}}$ on ![]() $\smash {\mathscr {H}_X}$ can be represented by its Weyl symbol
$\smash {\mathscr {H}_X}$ can be represented by its Weyl symbol ![]() $\smash {A({\boldsymbol {X}}, {\boldsymbol {K}})}$, and
$\smash {A({\boldsymbol {X}}, {\boldsymbol {K}})}$, and ![]() $\smash {\widehat {A\,}\widehat {B} \leftrightarrow A \,\bigstar \, B}$. An operator that is local in
$\smash {\widehat {A\,}\widehat {B} \leftrightarrow A \,\bigstar \, B}$. An operator that is local in ![]() $\smash {{\boldsymbol {p}}}$ has the same symbol irrespective of whether it is considered on
$\smash {{\boldsymbol {p}}}$ has the same symbol irrespective of whether it is considered on ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ or on
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ or on ![]() $\smash {\mathscr {H}_X}$.
$\smash {\mathscr {H}_X}$.
Any given field ![]() $\smash {\psi }$ generates the corresponding density operator
$\smash {\psi }$ generates the corresponding density operator ![]() and its symbol called the Wigner function (Wigner matrix, if the field is a vector). If the density operator is considered on
and its symbol called the Wigner function (Wigner matrix, if the field is a vector). If the density operator is considered on ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$, it is denoted
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$, it is denoted ![]() $\smash {\widehat {{\mathsf {W}}}_\psi }$ and the corresponding Wigner function is denoted
$\smash {\widehat {{\mathsf {W}}}_\psi }$ and the corresponding Wigner function is denoted ![]() $\smash {{\mathsf {W}}_\psi ({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. If the density operator is considered on
$\smash {{\mathsf {W}}_\psi ({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. If the density operator is considered on ![]() $\smash {\mathscr {H}_X}$, it is denoted
$\smash {\mathscr {H}_X}$, it is denoted ![]() $\smash {\widehat {W}_\psi }$ and the corresponding Wigner function is denoted
$\smash {\widehat {W}_\psi }$ and the corresponding Wigner function is denoted ![]() $\smash {W_\psi ({\boldsymbol {X}}, {\boldsymbol {K}})}$. The two Wigner functions are related via
$\smash {W_\psi ({\boldsymbol {X}}, {\boldsymbol {K}})}$. The two Wigner functions are related via ![]() $\smash {\int \mathrm {d}{\boldsymbol {r}}\,W_\psi (t, {\boldsymbol {x}}, {\boldsymbol {p}}, \omega, {\boldsymbol {k}}, {\boldsymbol {r}}) = {\mathsf {W}}_\psi (t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}})}$, where
$\smash {\int \mathrm {d}{\boldsymbol {r}}\,W_\psi (t, {\boldsymbol {x}}, {\boldsymbol {p}}, \omega, {\boldsymbol {k}}, {\boldsymbol {r}}) = {\mathsf {W}}_\psi (t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}})}$, where ![]() $\smash {{\boldsymbol {p}}}$ enters
$\smash {{\boldsymbol {p}}}$ enters ![]() $\smash {{\mathsf {W}}_\psi }$ as a parameter, if at all. If averaged over a sufficiently large phase-space volume, the Wigner functions (matrices) are non-negative (positive-semidefinite) and characterize local properties of the corresponding fields.
$\smash {{\mathsf {W}}_\psi }$ as a parameter, if at all. If averaged over a sufficiently large phase-space volume, the Wigner functions (matrices) are non-negative (positive-semidefinite) and characterize local properties of the corresponding fields.
3. Model
Here, we introduce the general assumptions and the key ingredients of our theory.
3.1. Basic assumptions
3.1.1. Ordering
Let us consider particles governed by a Hamiltonian ![]() $H = \overline {H} + \widetilde {H}$ such that
$H = \overline {H} + \widetilde {H}$ such that
In other words, ![]() $\widetilde {H}$ serves as a small perturbation to the leading-order Hamiltonian
$\widetilde {H}$ serves as a small perturbation to the leading-order Hamiltonian ![]() $\overline {H}$. The system will be described in canonical variables
$\overline {H}$. The system will be described in canonical variables ![]() $\smash {{\boldsymbol {z}} \equiv ({\boldsymbol {x}}, {\boldsymbol {p}}) \in \mathbb {R}^{2n}}$. Let us also assume that the system is close to being homogeneous in
$\smash {{\boldsymbol {z}} \equiv ({\boldsymbol {x}}, {\boldsymbol {p}}) \in \mathbb {R}^{2n}}$. Let us also assume that the system is close to being homogeneous in ![]() ${\boldsymbol {x}}$. This includes two conditions. First, we require that the external fields are weak (yet see § 3.1.2), meaning
${\boldsymbol {x}}$. This includes two conditions. First, we require that the external fields are weak (yet see § 3.1.2), meaning
where ![]() $\epsilon \ll 1$ is a small parameter,
$\epsilon \ll 1$ is a small parameter, ![]() $\kappa _x$ and
$\kappa _x$ and ![]() $\kappa _p$ are the characteristic inverse scales in the
$\kappa _p$ are the characteristic inverse scales in the ![]() ${\boldsymbol {x}}$ and
${\boldsymbol {x}}$ and ![]() ${\boldsymbol {p}}$ spaces, respectively, and the bar denotes local averaging.Footnote 11 Hence, the particle momenta
${\boldsymbol {p}}$ spaces, respectively, and the bar denotes local averaging.Footnote 11 Hence, the particle momenta ![]() ${\boldsymbol {p}}$ are close to being local invariants. Second, the statistical properties of
${\boldsymbol {p}}$ are close to being local invariants. Second, the statistical properties of ![]() $\smash {\widetilde {H}}$ are also assumed to vary in
$\smash {\widetilde {H}}$ are also assumed to vary in ![]() ${\boldsymbol {x}}$ slowly. These properties can be characterized using the density operator of the perturbation Hamiltonian,
${\boldsymbol {x}}$ slowly. These properties can be characterized using the density operator of the perturbation Hamiltonian,
and its symbol, the (real) Wigner function, as in (2.43):
Specifically, we will use the average Wigner function, ![]() $\overline {W}$, which represents the Fourier spectrum of the symmetrized autocorrelation function of
$\overline {W}$, which represents the Fourier spectrum of the symmetrized autocorrelation function of ![]() $\widetilde {H}$:
$\widetilde {H}$:
The averaging is performed over sufficiently large volume of ![]() ${\boldsymbol {x}}$ to eliminate rapid oscillations and also over phase-space volumes
${\boldsymbol {x}}$ to eliminate rapid oscillations and also over phase-space volumes ![]() $\varDelta {\boldsymbol {X}}\,\varDelta {\boldsymbol {K}} \gtrsim 1$, which guarantees
$\varDelta {\boldsymbol {X}}\,\varDelta {\boldsymbol {K}} \gtrsim 1$, which guarantees ![]() $\overline {W}$ to be non-negative and local (§ 2.2.3). The function
$\overline {W}$ to be non-negative and local (§ 2.2.3). The function ![]() $\overline {W}$ can be understood as a measure of the phase-space density of wave quanta when the latter is well defined (§ 7).
$\overline {W}$ can be understood as a measure of the phase-space density of wave quanta when the latter is well defined (§ 7).
We will assumeFootnote 12
That said, we will also allow (albeit not require) for oscillations to be constrained by a dispersion relation. In this case, ![]() $\overline {W}\, \propto \, \delta (\omega -\overline {\omega }(t, {\boldsymbol {x}}))$, so (3.6) per se is not satisfied; then we assume a similar ordering for
$\overline {W}\, \propto \, \delta (\omega -\overline {\omega }(t, {\boldsymbol {x}}))$, so (3.6) per se is not satisfied; then we assume a similar ordering for ![]() $\int \mathrm {d}\omega \,\overline {W}$ instead. Also note that in application to the standard QLT of homogeneous turbulence (Stix Reference Stix1992, chapter 16),
$\int \mathrm {d}\omega \,\overline {W}$ instead. Also note that in application to the standard QLT of homogeneous turbulence (Stix Reference Stix1992, chapter 16), ![]() $\epsilon$ is understood as the geometrical-optics parameter characterizing the smallness of the linear-instability growth rates. (We discuss the ordering further in the end of § 3.3.)
$\epsilon$ is understood as the geometrical-optics parameter characterizing the smallness of the linear-instability growth rates. (We discuss the ordering further in the end of § 3.3.)
3.1.2. Quasilinear approximation
The particle-motion equations can be written as
where ![]() $v^{\alpha }$ and
$v^{\alpha }$ and ![]() $u^{\alpha }$ are understood as the unperturbed phase-space velocity and the perturbation to the phase-space velocity, respectively:
$u^{\alpha }$ are understood as the unperturbed phase-space velocity and the perturbation to the phase-space velocity, respectively:
The notation ![]() $v^i$ (with
$v^i$ (with ![]() $i = 1, 2, \ldots n$) will also be used for the spatial part of the phase-space velocity
$i = 1, 2, \ldots n$) will also be used for the spatial part of the phase-space velocity ![]() $v^{\alpha }$, i.e. for the true velocity per se. Likewise,
$v^{\alpha }$, i.e. for the true velocity per se. Likewise, ![]() ${\boldsymbol {v}}$ will be used to denote either the phase-space velocity vector or the spatial velocity vector depending on the context. Also note that a slightly different definition of
${\boldsymbol {v}}$ will be used to denote either the phase-space velocity vector or the spatial velocity vector depending on the context. Also note that a slightly different definition of ![]() ${\boldsymbol {v}}$ will be used starting from § 5.6.
${\boldsymbol {v}}$ will be used starting from § 5.6.
The corresponding Klimontovich equation for the particle distribution ![]() $f(t, {\boldsymbol {z}})$ is
$f(t, {\boldsymbol {z}})$ is
(If collisions are not of interest, (3.9) can as well be understood as the Vlasov equation. Also, a small collision term can be included ad hoc; see the comment in the end of § 3.3.) Let us search for ![]() $f$ in the form
$f$ in the form
The equations for ![]() $\smash {\overline {f}}$ and
$\smash {\overline {f}}$ and ![]() $\smash {\widetilde {f}}$ are obtained as the average and oscillating parts of (3.9), and we neglect the nonlinearity in the equation for
$\smash {\widetilde {f}}$ are obtained as the average and oscillating parts of (3.9), and we neglect the nonlinearity in the equation for ![]() $\smash {\widetilde {f}}$, following the standard QL approximation (Stix Reference Stix1992, chapter 16). Then, one obtains
$\smash {\widetilde {f}}$, following the standard QL approximation (Stix Reference Stix1992, chapter 16). Then, one obtains
A comment is due here regarding plasmas in strong fields and magnetized plasmas in particular. Our formulation can be applied to such plasmas in canonical angle–action variables ![]() $\smash {({{\phi }}, \boldsymbol{\mathsf {J}})}$. For fast angle variables, the ordering (3.2) is not satisfied and the Weyl symbol calculus is inapplicable as is (see the footnote in § 2.1.3). Such systems can be accommodated by representing the distribution function as a Fourier series in
$\smash {({{\phi }}, \boldsymbol{\mathsf {J}})}$. For fast angle variables, the ordering (3.2) is not satisfied and the Weyl symbol calculus is inapplicable as is (see the footnote in § 2.1.3). Such systems can be accommodated by representing the distribution function as a Fourier series in ![]() $\smash {{{\phi }}}$ and treating the individual-harmonic amplitudes separately as slow functions of the remaining coordinates. Then, our averaging procedure subsumes averaging over
$\smash {{{\phi }}}$ and treating the individual-harmonic amplitudes separately as slow functions of the remaining coordinates. Then, our averaging procedure subsumes averaging over ![]() $\smash {{{\phi }}}$, so the averaged quantities are
$\smash {{{\phi }}}$, so the averaged quantities are ![]() $\smash {{{\phi }}}$-independent and (3.2) is reinstated. In particular, magnetized plasmas can be described using guiding-centre variables. Although not canonical by default (Littlejohn Reference Littlejohn1983), they can always be cast in a canonical form, at least in principle (Littlejohn Reference Littlejohn1979). Examples of canonical guiding-centre variables are reviewed in Cary & Brizard (Reference Cary and Brizard2009). To make the connection with the homogeneous-plasma theory, one can also order the canonical pairs of guiding-centre variables such that they would describe the gyromotion, the parallel motion, and the drifts separately (Wong Reference Wong2000). This readily leads to results similar to those in Catto et al. (Reference Catto, Lee and Ram2017). Further discussions on this topic are left to future papers.
$\smash {{{\phi }}}$-independent and (3.2) is reinstated. In particular, magnetized plasmas can be described using guiding-centre variables. Although not canonical by default (Littlejohn Reference Littlejohn1983), they can always be cast in a canonical form, at least in principle (Littlejohn Reference Littlejohn1979). Examples of canonical guiding-centre variables are reviewed in Cary & Brizard (Reference Cary and Brizard2009). To make the connection with the homogeneous-plasma theory, one can also order the canonical pairs of guiding-centre variables such that they would describe the gyromotion, the parallel motion, and the drifts separately (Wong Reference Wong2000). This readily leads to results similar to those in Catto et al. (Reference Catto, Lee and Ram2017). Further discussions on this topic are left to future papers.
3.2. Equation for  ${\widetilde {f}}$
${\widetilde {f}}$
Let us consider solutions of (3.12) as a subclass of solutions of the more general equation
Here, we have introduced an auxiliary second ‘time’ ![]() $\smash {\tau }$, the operator
$\smash {\tau }$, the operator
(here and further, ![]() ${\unicode{x25AA}}$ denotes a placeholder), and
${\unicode{x25AA}}$ denotes a placeholder), and ![]() ${\boldsymbol {V}}({\boldsymbol {X}}) \equiv (1, {\boldsymbol {v}}(t, {\boldsymbol {z}}))$ is the unperturbed velocity in the
${\boldsymbol {V}}({\boldsymbol {X}}) \equiv (1, {\boldsymbol {v}}(t, {\boldsymbol {z}}))$ is the unperturbed velocity in the ![]() ${\boldsymbol {X}}$ space. Note that
${\boldsymbol {X}}$ space. Note that
due to the incompressibility of the phase flow. Hence, ![]() $\smash {[\partial _a, V^a] = 0}$, so
$\smash {[\partial _a, V^a] = 0}$, so ![]() $\smash {\widehat {L}}$ is anti-Hermitian.
$\smash {\widehat {L}}$ is anti-Hermitian.
Let us search for a solution of (3.13) in the formFootnote 13
Then, ![]() $\partial _\tau \widetilde {f} = \widehat {L\,}\,\widetilde {f} + \mathrm {e}^{\widehat {L} \tau }\partial _\tau \xi$, so
$\partial _\tau \widetilde {f} = \widehat {L\,}\,\widetilde {f} + \mathrm {e}^{\widehat {L} \tau }\partial _\tau \xi$, so ![]() $\partial _\tau \xi = \mathrm {e}^{-\widehat {L} \tau }\mathscr {F}({\boldsymbol {X}})$ and therefore
$\partial _\tau \xi = \mathrm {e}^{-\widehat {L} \tau }\mathscr {F}({\boldsymbol {X}})$ and therefore
where ![]() $\smash {\xi _0({\boldsymbol {X}}) \doteq \widetilde {f}(\tau _0, {\boldsymbol {X}})}$. Hence, one obtains
$\smash {\xi _0({\boldsymbol {X}}) \doteq \widetilde {f}(\tau _0, {\boldsymbol {X}})}$. Hence, one obtains
or equivalently, using ![]() $\tau '' \doteq \tau - \tau '$,
$\tau '' \doteq \tau - \tau '$,
Here, ![]() $\smash {g_0}$ is a solution of
$\smash {g_0}$ is a solution of ![]() $\partial _\tau g_0 = \widehat {L} g_0$, specifically,
$\partial _\tau g_0 = \widehat {L} g_0$, specifically,
and we have also introduced
Because ![]() $\smash {\widehat {L}}$ is anti-Hermitian, the operator
$\smash {\widehat {L}}$ is anti-Hermitian, the operator ![]() $\smash {\widehat {T}_\tau }$ is unitary, and comparison with (2.19) shows that it can be recognized as a shift operator. For further details, see § 4.1.
$\smash {\widehat {T}_\tau }$ is unitary, and comparison with (2.19) shows that it can be recognized as a shift operator. For further details, see § 4.1.
Using ![]() $\smash {\widehat {T}_\tau }$, one can express (3.19) as
$\smash {\widehat {T}_\tau }$, one can express (3.19) as
where ![]() $\widehat {\mathscr {G}}$ is the Green's operator understood as the right inverse of the operator
$\widehat {\mathscr {G}}$ is the Green's operator understood as the right inverse of the operator ![]() $\smash {\partial _\tau - \widehat {L}}$, or on the space of
$\smash {\partial _\tau - \widehat {L}}$, or on the space of ![]() $\smash {\tau }$-independent functions,
$\smash {\tau }$-independent functions, ![]() $\smash {\partial _t - \lbrace \overline {H}, {\unicode{x25AA}} \rbrace }$. Let us rewrite this operator as
$\smash {\partial _t - \lbrace \overline {H}, {\unicode{x25AA}} \rbrace }$. Let us rewrite this operator as ![]() $\smash {\widehat {\mathscr {G}} = \widehat {\mathscr {G}}_< + \widehat {\mathscr {G}}_>}$, where
$\smash {\widehat {\mathscr {G}} = \widehat {\mathscr {G}}_< + \widehat {\mathscr {G}}_>}$, where
and ![]() $\nu$ is a positive constant. Note that
$\nu$ is a positive constant. Note that ![]() $\widehat {\mathscr {G}}_<$ is well defined at
$\widehat {\mathscr {G}}_<$ is well defined at ![]() $\tau _0 \to -\infty$, meaning that
$\tau _0 \to -\infty$, meaning that ![]() $\widehat {\mathscr {G}}_<\mathscr {F}$ is well defined for any physical (bounded) field
$\widehat {\mathscr {G}}_<\mathscr {F}$ is well defined for any physical (bounded) field ![]() $\mathscr {F}$.Footnote 14 Thus, so is
$\mathscr {F}$.Footnote 14 Thus, so is ![]() $\smash {g_0 + \widehat {\mathscr {G}}_>\mathscr {F}}$. Let us take
$\smash {g_0 + \widehat {\mathscr {G}}_>\mathscr {F}}$. Let us take ![]() $\tau _0 \to -\infty$ and then take
$\tau _0 \to -\infty$ and then take ![]() $\nu \to 0+$. (Here,
$\nu \to 0+$. (Here, ![]() $0+$ denotes that
$0+$ denotes that ![]() $\nu$ must remain positive, i.e. the upper limit is taken.) Then, (3.22) can be expressed as
$\nu$ must remain positive, i.e. the upper limit is taken.) Then, (3.22) can be expressed as
Here, we introduced an ‘effective’ Green's operator ![]() $\smash {\widehat {G} \doteq \lim _{\nu \to 0+} \lim _{\tau _0 \to -\infty } \widehat {\mathscr {G}}_<}$, i.e.
$\smash {\widehat {G} \doteq \lim _{\nu \to 0+} \lim _{\tau _0 \to -\infty } \widehat {\mathscr {G}}_<}$, i.e.
This operator will be discussed in § 4.2, and ![]() $g$ will be discussed in § 4.3. Meanwhile, note that because
$g$ will be discussed in § 4.3. Meanwhile, note that because ![]() $\smash {\tau }$ is just an auxiliary variable, we will be interested in solutions independent of
$\smash {\tau }$ is just an auxiliary variable, we will be interested in solutions independent of ![]() $\tau$. In particular, this means that
$\tau$. In particular, this means that ![]() $\smash {\widetilde {f}(\tau _0, {\boldsymbol {X}}) = \widetilde {f}({\boldsymbol {X}})}$, so
$\smash {\widetilde {f}(\tau _0, {\boldsymbol {X}}) = \widetilde {f}({\boldsymbol {X}})}$, so ![]() $\smash {\xi _0({\boldsymbol {X}}) = \widetilde {f}({\boldsymbol {X}})}$, so (3.20) leads to
$\smash {\xi _0({\boldsymbol {X}}) = \widetilde {f}({\boldsymbol {X}})}$, so (3.20) leads to
3.3. Equation for  ${\overline {f}}$
${\overline {f}}$
Using (3.22), one can rewrite (3.12) for ![]() $\overline {f}$ as follows:
$\overline {f}$ as follows:
Notice that
and also
 \begin{align} \lbrace \widetilde{H}, \widehat{G}\lbrace \widetilde{H}, \overline{f} \rbrace \rbrace & = \partial_{\beta}( J^{\alpha\beta} (\partial_{\alpha}\widetilde{H}) \widehat{G}\lbrace \widetilde{H}, \overline{f} \rbrace )\nonumber\\ & = \partial_{\beta}(J^{\alpha\beta} (\partial_{\alpha}\widetilde{H}) \widehat{G} (J^{\mu \nu} (\partial_{\mu}\widetilde{H})(\partial_{\nu}\overline{f})))\nonumber\\ & = \partial_{\beta}(u^{\beta}\widehat{G}(u^{\nu}\partial_{\nu}\overline{f})). \end{align}
\begin{align} \lbrace \widetilde{H}, \widehat{G}\lbrace \widetilde{H}, \overline{f} \rbrace \rbrace & = \partial_{\beta}( J^{\alpha\beta} (\partial_{\alpha}\widetilde{H}) \widehat{G}\lbrace \widetilde{H}, \overline{f} \rbrace )\nonumber\\ & = \partial_{\beta}(J^{\alpha\beta} (\partial_{\alpha}\widetilde{H}) \widehat{G} (J^{\mu \nu} (\partial_{\mu}\widetilde{H})(\partial_{\nu}\overline{f})))\nonumber\\ & = \partial_{\beta}(u^{\beta}\widehat{G}(u^{\nu}\partial_{\nu}\overline{f})). \end{align}
The field ![]() $u^\alpha$ enters here as a multiplication factor and can be considered as an operator:
$u^\alpha$ enters here as a multiplication factor and can be considered as an operator:
Then, (3.29) can be compactly represented as
We will also use the notation
This leads to the following equation for ![]() $\overline {f}$:
$\overline {f}$:
where we introduced the following average quantities:
Our goal is to derive explicit approximate expressions for the quantities (3.34) and to rewrite (3.33) in a more tractable form using the assumptions introduced in § 3.1. We will useFootnote 15
and we will keep terms of order ![]() $\epsilon$,
$\epsilon$, ![]() $\varepsilon ^2$ and
$\varepsilon ^2$ and ![]() $\smash {\epsilon \varepsilon ^2}$ in the equation for
$\smash {\epsilon \varepsilon ^2}$ in the equation for ![]() $\smash {\overline {f}}$, while terms of order
$\smash {\overline {f}}$, while terms of order ![]() $\smash {\varepsilon ^4}$,
$\smash {\varepsilon ^4}$, ![]() $\smash {\epsilon ^2 \varepsilon ^2}$ and higher will be neglected. This implies the ordering
$\smash {\epsilon ^2 \varepsilon ^2}$ and higher will be neglected. This implies the ordering
As a reminder, ![]() $\smash {\varepsilon }$ is a linear measure of the characteristic amplitude of oscillations, and
$\smash {\varepsilon }$ is a linear measure of the characteristic amplitude of oscillations, and ![]() $\smash {\epsilon }$ is the geometrical-optics parameter, which is proportional to the inverse scale of the plasma inhomogeneity in spacetime. As usual then, linear dissipation is assumed to be of order
$\smash {\epsilon }$ is the geometrical-optics parameter, which is proportional to the inverse scale of the plasma inhomogeneity in spacetime. As usual then, linear dissipation is assumed to be of order ![]() $\smash {\epsilon }$. This model implies the assumption that collisionless dissipation is much stronger than collisional dissipation, which is to emerge as an effect quadratic in
$\smash {\epsilon }$. This model implies the assumption that collisionless dissipation is much stronger than collisional dissipation, which is to emerge as an effect quadratic in ![]() $\smash {\widetilde {f}}$ (§ 6). Furthermore, the inverse plasma parameterFootnote 16 will be assumed to be of order
$\smash {\widetilde {f}}$ (§ 6). Furthermore, the inverse plasma parameterFootnote 16 will be assumed to be of order ![]() $\smash {\epsilon }$, so the collision operator for
$\smash {\epsilon }$, so the collision operator for ![]() $\smash {\overline {f}}$ (§ 6.8) will be of order
$\smash {\overline {f}}$ (§ 6.8) will be of order ![]() $\smash {\epsilon \varepsilon ^2}$. Within the assumed accuracy, this operator must be retained, while the dynamics of
$\smash {\epsilon \varepsilon ^2}$. Within the assumed accuracy, this operator must be retained, while the dynamics of ![]() $\smash {\widetilde {f}}$ is considered linear and therefore collisionless. Alternatively, one can switch from the Klimontovich description to the Vlasov–Boltzmann description and introduce an ad hoc order-
$\smash {\widetilde {f}}$ is considered linear and therefore collisionless. Alternatively, one can switch from the Klimontovich description to the Vlasov–Boltzmann description and introduce an ad hoc order-![]() $\smash {\epsilon }$ collision operator directly in (3.9). This will alter the Green's operator, but the conceptual formulation would remain the same, so it will not be considered separately in detail.
$\smash {\epsilon }$ collision operator directly in (3.9). This will alter the Green's operator, but the conceptual formulation would remain the same, so it will not be considered separately in detail.
3.4. Summary of § 3
Our QL model is defined as usual, except: (i) we allow for a general particle Hamiltonian ![]() $\smash {H}$; (ii) we use the Klimontovich equation rather than the Vlasov equation to retain collisions; (iii) we use local averaging (denoted with overbar) and allow for weak inhomogeneity of all averaged quantities; (iv) we retain the initial conditions
$\smash {H}$; (ii) we use the Klimontovich equation rather than the Vlasov equation to retain collisions; (iii) we use local averaging (denoted with overbar) and allow for weak inhomogeneity of all averaged quantities; (iv) we retain the initial conditions ![]() $\smash {g}$ for the oscillating part of the distribution function (defined as in (3.24) but yet to be calculated explicitly). Then, the average part of the distribution function satisfies
$\smash {g}$ for the oscillating part of the distribution function (defined as in (3.24) but yet to be calculated explicitly). Then, the average part of the distribution function satisfies
where ![]() $\smash {\widehat {D}^{\alpha \beta } \doteq \overline {\widehat {u}^{\alpha }\widehat {G\,}\widehat {u}^{\beta }}}$,
$\smash {\widehat {D}^{\alpha \beta } \doteq \overline {\widehat {u}^{\alpha }\widehat {G\,}\widehat {u}^{\beta }}}$, ![]() $\smash {\vphantom{\frac{f^l}{f^l}}\varGamma \doteq - \partial _\alpha (\overline {u^{\alpha } g})}$,
$\smash {\vphantom{\frac{f^l}{f^l}}\varGamma \doteq - \partial _\alpha (\overline {u^{\alpha } g})}$, ![]() $\smash {u^{\alpha }}$ is the wave-driven perturbation of the phase-space velocity (see (3.8)),
$\smash {u^{\alpha }}$ is the wave-driven perturbation of the phase-space velocity (see (3.8)), ![]() $\smash {\widehat {u\,\,}^{\alpha }}$ is the same quantity considered as an operator on
$\smash {\widehat {u\,\,}^{\alpha }}$ is the same quantity considered as an operator on ![]() $\smash {\mathscr {H}_X}$ (see (3.30)) and
$\smash {\mathscr {H}_X}$ (see (3.30)) and ![]() $\smash {\widehat {G} }$ is the ‘effective’ Green's operator given by
$\smash {\widehat {G} }$ is the ‘effective’ Green's operator given by
Also, ![]() $\smash {\partial _{\alpha } \equiv \partial /\partial z^\alpha }$, and
$\smash {\partial _{\alpha } \equiv \partial /\partial z^\alpha }$, and ![]() $\smash {\lbrace {\unicode{x25AA}}, {\unicode{x25AA}} \rbrace }$ is the Poisson bracket on the particle phase space
$\smash {\lbrace {\unicode{x25AA}}, {\unicode{x25AA}} \rbrace }$ is the Poisson bracket on the particle phase space ![]() $\smash {{\boldsymbol {z}}}$. The equation for
$\smash {{\boldsymbol {z}}}$. The equation for ![]() $\smash {\overline {f}}$ used in the standard QLT is recovered from (3.37) by neglecting
$\smash {\overline {f}}$ used in the standard QLT is recovered from (3.37) by neglecting ![]() $\smash {\varGamma }$ and the spatial gradients (in particular, the whole Poisson bracket) and also by approximating the operator
$\smash {\varGamma }$ and the spatial gradients (in particular, the whole Poisson bracket) and also by approximating the operator ![]() $\smash {\widehat {D}^{\alpha \beta }}$ with a local function of
$\smash {\widehat {D}^{\alpha \beta }}$ with a local function of ![]() $\smash {{\boldsymbol {z}}}$.
$\smash {{\boldsymbol {z}}}$.
4. Preliminaries
Before we start calculating the functions in (3.37) explicitly, let us get some preliminaries out of the way. In this section, we discuss the shift operators ![]() $\smash {\widehat {T}_\tau }$ (§ 4.1), approximate the operator
$\smash {\widehat {T}_\tau }$ (§ 4.1), approximate the operator ![]() $\smash {\widehat {G}}$ (§ 4.2) and develop a model for the function
$\smash {\widehat {G}}$ (§ 4.2) and develop a model for the function ![]() $g$ that encodes the initial conditions for
$g$ that encodes the initial conditions for ![]() $\smash {\widetilde {f}}$ (§ 4.3).
$\smash {\widetilde {f}}$ (§ 4.3).
4.1. Shift operator
Here, we derive some properties of the shift operator ![]() $\smash {\widehat {T}_\tau }$ introduced in § 3.2.
$\smash {\widehat {T}_\tau }$ introduced in § 3.2.
4.1.1.  ${\widehat {T}_\tau }$ as a shift
${\widehat {T}_\tau }$ as a shift
Here, we formally prove (an admittedly obvious fact) that
where the ‘characteristics’ ![]() $\smash {Y^a}$ solveFootnote 17
$\smash {Y^a}$ solveFootnote 17
and thus ![]() $\ell _{\tau }^{a}$ can be Taylor-expanded in
$\ell _{\tau }^{a}$ can be Taylor-expanded in ![]() $\tau$ as
$\tau$ as
As the first step to proving (4.1), let us Taylor-expand ![]() $V^{a}$ around a fixed point
$V^{a}$ around a fixed point ![]() ${\boldsymbol {X}}_1$:
${\boldsymbol {X}}_1$:
where ![]() $V^a_1 \equiv V^a({\boldsymbol {X}}_1)$. If one neglects the first and higher derivatives of
$V^a_1 \equiv V^a({\boldsymbol {X}}_1)$. If one neglects the first and higher derivatives of ![]() $V^{a}$, one obtains
$V^{a}$, one obtains
By taking the limit ![]() ${\boldsymbol {X}}_1 \to {\boldsymbol {X}}$, which corresponds to
${\boldsymbol {X}}_1 \to {\boldsymbol {X}}$, which corresponds to ![]() ${\boldsymbol {V}}_1 \to {\boldsymbol {V}}$, one obtains
${\boldsymbol {V}}_1 \to {\boldsymbol {V}}$, one obtains
Similarly, if one neglects the second and higher derivatives of ![]() $V^{a}$, one obtainsFootnote 18
$V^{a}$, one obtainsFootnote 18
 \begin{align} \widehat{T}_{\tau}\psi({\boldsymbol{X}}) & = \mathrm{e}^{ - \tau (V^{a}_1 + (\partial_{b}V^{a}_1) \delta X^{b}+\ldots) \partial_{a} } \psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{- \tau (\partial_{b} V^{a}_1) \delta X^{b} \partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1 \partial_{a}} \,\mathrm{e}^{-\frac{1}{2}[ -\tau(\partial_{b}V^{a}_1) \delta X^{b}\partial_{a}, -\tau V^{c}_1\partial_{c} ]} \psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{ -\tau (\partial_{b} V^{a}_1) \delta X^{b} \partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1 \partial_{a}} \,\mathrm{e}^{ \frac{1}{2}\tau^2 V^{c}_1(\partial_{b}V^{a}_1) [\partial_{c}, \delta X^{b}\partial_{a}] }\psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{-\tau (\partial_{b}V^{a}_1)\delta X^{b}\partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1 \partial_{a}} \,\mathrm{e}^{\frac{1}{2}\tau^2 V^{b}_1 (\partial_{b}V^{a}_1) \partial_{a}} \psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{-\tau (\partial_{b}V^{a}_1) \delta X^{b} \partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1\partial_{a} + \frac{1}{2}\tau^2 V^{b}_1(\partial_{b}V^{a}_1)\partial_{a}}\psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{-\tau (\partial_{b}V^{a}_1)\delta X^{b}\partial_{a}} \psi({\boldsymbol{X}} - \tau {\boldsymbol{V}}_1 + \textstyle\frac{1}{2}\,\tau^2 V^{b}_1 \partial_{b}{\boldsymbol{V}}_1). \end{align}
\begin{align} \widehat{T}_{\tau}\psi({\boldsymbol{X}}) & = \mathrm{e}^{ - \tau (V^{a}_1 + (\partial_{b}V^{a}_1) \delta X^{b}+\ldots) \partial_{a} } \psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{- \tau (\partial_{b} V^{a}_1) \delta X^{b} \partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1 \partial_{a}} \,\mathrm{e}^{-\frac{1}{2}[ -\tau(\partial_{b}V^{a}_1) \delta X^{b}\partial_{a}, -\tau V^{c}_1\partial_{c} ]} \psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{ -\tau (\partial_{b} V^{a}_1) \delta X^{b} \partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1 \partial_{a}} \,\mathrm{e}^{ \frac{1}{2}\tau^2 V^{c}_1(\partial_{b}V^{a}_1) [\partial_{c}, \delta X^{b}\partial_{a}] }\psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{-\tau (\partial_{b}V^{a}_1)\delta X^{b}\partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1 \partial_{a}} \,\mathrm{e}^{\frac{1}{2}\tau^2 V^{b}_1 (\partial_{b}V^{a}_1) \partial_{a}} \psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{-\tau (\partial_{b}V^{a}_1) \delta X^{b} \partial_{a}} \,\mathrm{e}^{-\tau V^{a}_1\partial_{a} + \frac{1}{2}\tau^2 V^{b}_1(\partial_{b}V^{a}_1)\partial_{a}}\psi({\boldsymbol{X}}) \nonumber\\ & \approx \mathrm{e}^{-\tau (\partial_{b}V^{a}_1)\delta X^{b}\partial_{a}} \psi({\boldsymbol{X}} - \tau {\boldsymbol{V}}_1 + \textstyle\frac{1}{2}\,\tau^2 V^{b}_1 \partial_{b}{\boldsymbol{V}}_1). \end{align}
In the limit ![]() ${\boldsymbol {X}}_1 \to {\boldsymbol {X}}$, when
${\boldsymbol {X}}_1 \to {\boldsymbol {X}}$, when ![]() $\smash {\mathrm {e}^{-\tau (\partial _{b}V^{a}_1)\delta X^{b} \partial _{a}} \to 1}$ and
$\smash {\mathrm {e}^{-\tau (\partial _{b}V^{a}_1)\delta X^{b} \partial _{a}} \to 1}$ and ![]() ${\boldsymbol {V}}_1 \to {\boldsymbol {V}}$, one obtains
${\boldsymbol {V}}_1 \to {\boldsymbol {V}}$, one obtains
In conjunction with (4.3), equations (4.6) and (4.8) show agreement with the sought result (4.3) within the assumed accuracy. One can also retain ![]() ${\mathsf {m}}$ derivatives of
${\mathsf {m}}$ derivatives of ![]() ${\boldsymbol {V}}$ and derive the corresponding approximations similarly. Then the error will be
${\boldsymbol {V}}$ and derive the corresponding approximations similarly. Then the error will be ![]() $\smash {\mathcal {O}(\tau ^{{\mathsf {m}} + 2})}$.
$\smash {\mathcal {O}(\tau ^{{\mathsf {m}} + 2})}$.
For an order-one time interval ![]() $\tau$, one can split this interval on
$\tau$, one can split this interval on ![]() $N_\tau \gg 1$ subintervals of small duration
$N_\tau \gg 1$ subintervals of small duration ![]() $\tau /N_\tau$ and apply finite-
$\tau /N_\tau$ and apply finite-![]() ${\mathsf {m}}$ formulas (for example, (4.6) or (4.8)) to those. Then the total error scales as
${\mathsf {m}}$ formulas (for example, (4.6) or (4.8)) to those. Then the total error scales as ![]() $\smash {\mathcal {O}(N_\tau ^{-{\mathsf {m}} - 1})}$ and the exact formula (4.1) is obtained at
$\smash {\mathcal {O}(N_\tau ^{-{\mathsf {m}} - 1})}$ and the exact formula (4.1) is obtained at ![]() $N_\tau \to \infty$.
$N_\tau \to \infty$.
4.1.2. Symbol of  ${\widehat {T}_\tau }$
${\widehat {T}_\tau }$
Using the bra–ket notation, (4.1) can be written as
Thus, ![]() $ {{\left\langle {{\boldsymbol {\mathsf {X|}}}} \right.}} \widehat {T}_{\tau } = {\left\langle {{\boldsymbol {\mathsf {X|}}}} \right.} - {\boldsymbol {\ell }}_{\tau }({\boldsymbol {X}})$, so
$ {{\left\langle {{\boldsymbol {\mathsf {X|}}}} \right.}} \widehat {T}_{\tau } = {\left\langle {{\boldsymbol {\mathsf {X|}}}} \right.} - {\boldsymbol {\ell }}_{\tau }({\boldsymbol {X}})$, so
Using (2.70), one obtains the Weyl symbol of ![]() $\smash {\widehat {T}_{\tau }}$ in the form
$\smash {\widehat {T}_{\tau }}$ in the form
From (4.3), one has
 \begin{align} \ell^a_{\tau}({\boldsymbol{X}} + {\boldsymbol{S}}/2) & = \tau V^{a}({\boldsymbol{X}} + {\boldsymbol{S}}/2) - (\tau^2/2)\,V^{b} \partial_{b} V^{a} + \mathcal{O}(\epsilon^2) \nonumber\\ & = \tau V^{a} + (\tau/2) (\partial_b V^{a}) S^b - (\tau^2/2)\,V^{b} \partial_{b} V^{a} + \mathcal{O}(\epsilon^2) \nonumber\\ & = {M^a}_b V^{b}\tau + {m^a}_b S^b + \mathcal{O}(\epsilon^2), \end{align}
\begin{align} \ell^a_{\tau}({\boldsymbol{X}} + {\boldsymbol{S}}/2) & = \tau V^{a}({\boldsymbol{X}} + {\boldsymbol{S}}/2) - (\tau^2/2)\,V^{b} \partial_{b} V^{a} + \mathcal{O}(\epsilon^2) \nonumber\\ & = \tau V^{a} + (\tau/2) (\partial_b V^{a}) S^b - (\tau^2/2)\,V^{b} \partial_{b} V^{a} + \mathcal{O}(\epsilon^2) \nonumber\\ & = {M^a}_b V^{b}\tau + {m^a}_b S^b + \mathcal{O}(\epsilon^2), \end{align}
where we introduced a matrix ![]() $\smash {{\boldsymbol {M}} \doteq {\boldsymbol {1}} - {\boldsymbol {m}}}$, or explicitly,
$\smash {{\boldsymbol {M}} \doteq {\boldsymbol {1}} - {\boldsymbol {m}}}$, or explicitly,
Let us express the term ![]() $\smash {\mathcal {O}(\epsilon ^2)}$ in (4.12) as
$\smash {\mathcal {O}(\epsilon ^2)}$ in (4.12) as ![]() $\smash {-{M^a}_b\mu ^b}$. Then,
$\smash {-{M^a}_b\mu ^b}$. Then,
 \begin{align} \delta ({\boldsymbol{S}} - {\boldsymbol{\ell}}_{\tau}({\boldsymbol{X}} + {\boldsymbol{S}}/2)) & = \delta ({\boldsymbol{S}} - {\boldsymbol{M}}{\boldsymbol{V}}\tau - {\boldsymbol{m}}{\boldsymbol{S}} + {\boldsymbol{M}}{\boldsymbol{\mu}}) \nonumber\\ & = \delta ({\boldsymbol{M}}({\boldsymbol{S}} - {\boldsymbol{V}}\tau + {\boldsymbol{\mu}})) \nonumber\\ & = \delta ({\boldsymbol{S}} - {\boldsymbol{V}}\tau + {\boldsymbol{\mu}})/|\det {\boldsymbol{M}}|. \end{align}
\begin{align} \delta ({\boldsymbol{S}} - {\boldsymbol{\ell}}_{\tau}({\boldsymbol{X}} + {\boldsymbol{S}}/2)) & = \delta ({\boldsymbol{S}} - {\boldsymbol{M}}{\boldsymbol{V}}\tau - {\boldsymbol{m}}{\boldsymbol{S}} + {\boldsymbol{M}}{\boldsymbol{\mu}}) \nonumber\\ & = \delta ({\boldsymbol{M}}({\boldsymbol{S}} - {\boldsymbol{V}}\tau + {\boldsymbol{\mu}})) \nonumber\\ & = \delta ({\boldsymbol{S}} - {\boldsymbol{V}}\tau + {\boldsymbol{\mu}})/|\det {\boldsymbol{M}}|. \end{align}
Because ![]() $\smash {{\boldsymbol {m}} = \mathcal {O}(\epsilon )}$, the well-known formula yields
$\smash {{\boldsymbol {m}} = \mathcal {O}(\epsilon )}$, the well-known formula yields ![]() $\smash {\det {\boldsymbol {M}} = 1 + \operatorname {tr}{\boldsymbol {m}} + \mathcal {O}(\epsilon ^2)}$. But
$\smash {\det {\boldsymbol {M}} = 1 + \operatorname {tr}{\boldsymbol {m}} + \mathcal {O}(\epsilon ^2)}$. But ![]() $\operatorname {tr}{\boldsymbol {m}} = 0$ by (3.15), so
$\operatorname {tr}{\boldsymbol {m}} = 0$ by (3.15), so
The last term ![]() $\smash {\mathcal {O}(\epsilon ^2)}$ is insignificant and can be neglected right away, so (4.11) leads to
$\smash {\mathcal {O}(\epsilon ^2)}$ is insignificant and can be neglected right away, so (4.11) leads to
where we have introduced the following notation:
By definition, ![]() $\smash {{\boldsymbol {\mu }}}$ is a polynomial of
$\smash {{\boldsymbol {\mu }}}$ is a polynomial of ![]() $\smash {\tau }$ with coefficients that are of order
$\smash {\tau }$ with coefficients that are of order ![]() $\smash {\epsilon ^2}$ and therefore small. But because
$\smash {\epsilon ^2}$ and therefore small. But because ![]() $\smash {\tau }$ can be large, and because
$\smash {\tau }$ can be large, and because ![]() $\smash {{\boldsymbol {\mu }}}$ is under the exponent, this makes
$\smash {{\boldsymbol {\mu }}}$ is under the exponent, this makes ![]() $\smash {T_{\tau }}$ potentially sensitive to this term, so we retain it (for now).
$\smash {T_{\tau }}$ potentially sensitive to this term, so we retain it (for now).
4.2. Effective Green's operator
The effective Green's operator (3.25) can be understood as the right inverse of the operator (cf. § 3.2)
so we denote it also as ![]() $\widehat {G} = \widehat {L}^{-1}_\text {eff}$ (which is admittedly abuse of notation). Because
$\widehat {G} = \widehat {L}^{-1}_\text {eff}$ (which is admittedly abuse of notation). Because ![]() $\smash {\widehat {L}_\text {eff}}$ has real
$\smash {\widehat {L}_\text {eff}}$ has real ![]() ${\boldsymbol {X}}$ representation by definition, the
${\boldsymbol {X}}$ representation by definition, the ![]() ${\boldsymbol {X}}$ representation of
${\boldsymbol {X}}$ representation of ![]() $\smash {\widehat {G}}$ is real too. In particular,
$\smash {\widehat {G}}$ is real too. In particular, ![]() $\smash {\left\langle {{\boldsymbol {X}} + {\boldsymbol {S}}/2 | \widehat {G} | {\boldsymbol {X}} - {\boldsymbol {S}}/2}\right\rangle}$ is real, hence
$\smash {\left\langle {{\boldsymbol {X}} + {\boldsymbol {S}}/2 | \widehat {G} | {\boldsymbol {X}} - {\boldsymbol {S}}/2}\right\rangle}$ is real, hence
by definition of the Weyl symbol (2.70). As a corollary, the derivative of ![]() $G({\boldsymbol {X}}, {\boldsymbol {K}})$ with respect to the
$G({\boldsymbol {X}}, {\boldsymbol {K}})$ with respect to the ![]() $a$th component of the whole second argument, denoted
$a$th component of the whole second argument, denoted ![]() $G^{|a}$, satisfies
$G^{|a}$, satisfies
Also note that ![]() $\widehat {G}$ can be expressed as
$\widehat {G}$ can be expressed as
(the notation ‘![]() $\smash {\lim _{\nu \to 0+} A(\omega + \mathrm {i} \nu )}$’ will also be shortened as ‘
$\smash {\lim _{\nu \to 0+} A(\omega + \mathrm {i} \nu )}$’ will also be shortened as ‘![]() $\smash {A(\omega + \mathrm {i} 0)}$’), whence
$\smash {A(\omega + \mathrm {i} 0)}$’), whence
Due to (4.16), the leading-order approximation of the symbol of the operator (3.25) is ![]() $G({\boldsymbol {X}}, {\boldsymbol {K}}) = G_0(\varOmega ({\boldsymbol {X}}, {\boldsymbol {K}}))$, where
$G({\boldsymbol {X}}, {\boldsymbol {K}}) = G_0(\varOmega ({\boldsymbol {X}}, {\boldsymbol {K}}))$, where
and the (standard) notation ![]() $\operatorname {pv} (1/\varOmega )$ is defined as follows:
$\operatorname {pv} (1/\varOmega )$ is defined as follows:
This means, in particular, that for any ![]() $A$, one has
$A$, one has
 \begin{align} \mathcal{J}[A, G_0] & \doteq \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})) \nonumber\\ & ={\rm \pi} \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) \delta(\varOmega ({\boldsymbol{X}}, {\boldsymbol{K}})) + \mathrm{i} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{A({\boldsymbol{X}}, {\boldsymbol{K}})}{\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})}, \end{align}
\begin{align} \mathcal{J}[A, G_0] & \doteq \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})) \nonumber\\ & ={\rm \pi} \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) \delta(\varOmega ({\boldsymbol{X}}, {\boldsymbol{K}})) + \mathrm{i} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{A({\boldsymbol{X}}, {\boldsymbol{K}})}{\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})}, \end{align}
where ![]() ${\unicode{x2A0F}}$ is a principal-value integral. Also usefully,
${\unicode{x2A0F}}$ is a principal-value integral. Also usefully, ![]() $\smash {\overline {G}_0 = G_0}$ and
$\smash {\overline {G}_0 = G_0}$ and
 \begin{align} \partial_a \mathcal{J}[A, G_0] & = \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0'(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}}))\,\partial_a\varOmega({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & ={-}(\partial_a V^b({\boldsymbol{X}})) \int \mathrm{d}{\boldsymbol{K}}\,K_b A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0'(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})) \nonumber\\ & ={-}(\partial_a V^b({\boldsymbol{X}}))\,\frac{\eth}{\partial \varOmega} \int \mathrm{d}{\boldsymbol{K}}\,K_b A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0(\varOmega ({\boldsymbol{X}}, {\boldsymbol{K}})), \end{align}
\begin{align} \partial_a \mathcal{J}[A, G_0] & = \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0'(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}}))\,\partial_a\varOmega({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & ={-}(\partial_a V^b({\boldsymbol{X}})) \int \mathrm{d}{\boldsymbol{K}}\,K_b A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0'(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})) \nonumber\\ & ={-}(\partial_a V^b({\boldsymbol{X}}))\,\frac{\eth}{\partial \varOmega} \int \mathrm{d}{\boldsymbol{K}}\,K_b A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0(\varOmega ({\boldsymbol{X}}, {\boldsymbol{K}})), \end{align}
where the notation ![]() $\eth /\partial \lambda \equiv \eth _\lambda$ is defined, for any
$\eth /\partial \lambda \equiv \eth _\lambda$ is defined, for any ![]() $\smash {\lambda }$ and
$\smash {\lambda }$ and ![]() $Q$, as follows:
$Q$, as follows:
Now let us reinstate the term ![]() ${\boldsymbol {\mu }}$ in (4.16). It is readily seen (Appendix B.2) that, although
${\boldsymbol {\mu }}$ in (4.16). It is readily seen (Appendix B.2) that, although ![]() ${\boldsymbol {\mu }}$ may significantly affect
${\boldsymbol {\mu }}$ may significantly affect ![]() $\smash {T_{\tau }}$ per se, its effect on
$\smash {T_{\tau }}$ per se, its effect on ![]() $\mathcal {J}[A, G]$ is small, namely,
$\mathcal {J}[A, G]$ is small, namely,
Below, we apply this formulation to ![]() $\smash {A = \mathcal {O}(\varepsilon ^2)}$, in which case (4.28) becomes
$\smash {A = \mathcal {O}(\varepsilon ^2)}$, in which case (4.28) becomes ![]() $\smash {\mathcal {J}[A, G] - \mathcal {J}[A, G_0] = \mathcal {O}(\epsilon ^2\varepsilon ^2)}$. Such corrections are negligible within our model, so from now on we adopt
$\smash {\mathcal {J}[A, G] - \mathcal {J}[A, G_0] = \mathcal {O}(\epsilon ^2\varepsilon ^2)}$. Such corrections are negligible within our model, so from now on we adopt
4.3. Initial conditions
Consider the function ![]() $g$ from (3.24). Using (3.26), the latter can be written as follows:
$g$ from (3.24). Using (3.26), the latter can be written as follows:
Because ![]() $(1 - \mathrm {e}^{-\nu \tau })$ is smooth and
$(1 - \mathrm {e}^{-\nu \tau })$ is smooth and ![]() $\smash {\widehat {T}_{\tau }\mathscr {F}}$ is rapidly oscillating, the second term in the external parenthesis is an oscillatory function of
$\smash {\widehat {T}_{\tau }\mathscr {F}}$ is rapidly oscillating, the second term in the external parenthesis is an oscillatory function of ![]() $\tau _0$ with the average negligible at
$\tau _0$ with the average negligible at ![]() $\smash {\nu \to 0}$. But the whole expression in these parenthesis is independent of
$\smash {\nu \to 0}$. But the whole expression in these parenthesis is independent of ![]() $\tau _0$ at large
$\tau _0$ at large ![]() $\tau _0$ (§ 3.2). Thus, it can be replaced with its own average over
$\tau _0$ (§ 3.2). Thus, it can be replaced with its own average over ![]() $\tau _0$, denoted
$\tau _0$, denoted ![]() $\smash {\langle \ldots \rangle _{\tau _0}}$. Because there is no
$\smash {\langle \ldots \rangle _{\tau _0}}$. Because there is no ![]() $\smash {\nu }$-dependence left in this case, one can also omit
$\smash {\nu }$-dependence left in this case, one can also omit ![]() $\smash {\lim _{\nu \to 0+}}$. That gives
$\smash {\lim _{\nu \to 0+}}$. That gives
Using
where the sum is taken over individual particles, one can writeFootnote 19
where ![]() $\smash {{\boldsymbol {z}}_\sigma \doteq {\boldsymbol {z}}_\sigma - \overline {{\boldsymbol {z}}}_\sigma }$ are the
$\smash {{\boldsymbol {z}}_\sigma \doteq {\boldsymbol {z}}_\sigma - \overline {{\boldsymbol {z}}}_\sigma }$ are the ![]() $\smash {\widetilde {H}}$-driven small deviations from the particle unperturbed trajectories
$\smash {\widetilde {H}}$-driven small deviations from the particle unperturbed trajectories ![]() $\smash {\overline {{\boldsymbol {z}}}_\sigma }$. Then,
$\smash {\overline {{\boldsymbol {z}}}_\sigma }$. Then, ![]() $\smash {\overline {f} = \overline {\mathfrak {f}}({\boldsymbol {X}})}$, and the linearized perturbation
$\smash {\overline {f} = \overline {\mathfrak {f}}({\boldsymbol {X}})}$, and the linearized perturbation ![]() $\smash {\widetilde {f} \doteq f - \overline {f}}$ is given by
$\smash {\widetilde {f} \doteq f - \overline {f}}$ is given by
 \begin{equation} \textstyle \widetilde{f}({\boldsymbol{X}}) = \underbrace{\, \mathfrak{f}({\boldsymbol{X}}) -\overline{\mathfrak{f}}({\boldsymbol{X}}) }_{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\widetilde{f}}} \underbrace{\textstyle - \sum_\sigma \widetilde{{\boldsymbol{z}}}_\sigma({\boldsymbol{X}}) \partial_{{\boldsymbol{z}}}\delta({\boldsymbol{z}} - \overline{{\boldsymbol{z}}}_\sigma({\boldsymbol{X}})) }_{\underline{\widetilde{f}}}. \end{equation}
\begin{equation} \textstyle \widetilde{f}({\boldsymbol{X}}) = \underbrace{\, \mathfrak{f}({\boldsymbol{X}}) -\overline{\mathfrak{f}}({\boldsymbol{X}}) }_{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\widetilde{f}}} \underbrace{\textstyle - \sum_\sigma \widetilde{{\boldsymbol{z}}}_\sigma({\boldsymbol{X}}) \partial_{{\boldsymbol{z}}}\delta({\boldsymbol{z}} - \overline{{\boldsymbol{z}}}_\sigma({\boldsymbol{X}})) }_{\underline{\widetilde{f}}}. \end{equation} By definition, the unperturbed trajectories ![]() $\smash {\overline {{\boldsymbol {z}}}_\sigma }$ satisfy
$\smash {\overline {{\boldsymbol {z}}}_\sigma }$ satisfy ![]() $\smash {\widehat {L} \delta ({\boldsymbol {z}} - \overline {{\boldsymbol {z}}}_\sigma ({\boldsymbol {X}})) = 0}$, where
$\smash {\widehat {L} \delta ({\boldsymbol {z}} - \overline {{\boldsymbol {z}}}_\sigma ({\boldsymbol {X}})) = 0}$, where ![]() $\smash {\widehat {L}}$ as in (3.14); thus,
$\smash {\widehat {L}}$ as in (3.14); thus,
Also, ![]() $\smash {\langle \widehat {T}_{\tau - \tau _0} \underline {\widetilde {f}} \rangle _{\tau _0} = 0}$, because
$\smash {\langle \widehat {T}_{\tau - \tau _0} \underline {\widetilde {f}} \rangle _{\tau _0} = 0}$, because ![]() $\smash {\widetilde {{\boldsymbol {z}}}_\sigma }$ are oscillatory functions of
$\smash {\widetilde {{\boldsymbol {z}}}_\sigma }$ are oscillatory functions of ![]() ${\boldsymbol {X}}$ that is slowly evolved by
${\boldsymbol {X}}$ that is slowly evolved by ![]() $\smash {\widehat {T}_{\tau - \tau _0}}$. Hence,
$\smash {\widehat {T}_{\tau - \tau _0}}$. Hence, ![]() $\smash {g}$ is the microscopic part of the unperturbed distribution function:
$\smash {g}$ is the microscopic part of the unperturbed distribution function:
This indicates that the term ![]() $\smash {\varGamma }$ defined in (3.34) is due to collisional effects. We postpone discussing these effects until § 6, so
$\smash {\varGamma }$ defined in (3.34) is due to collisional effects. We postpone discussing these effects until § 6, so ![]() $\smash {\varGamma }$ will be ignored for now.
$\smash {\varGamma }$ will be ignored for now.
4.4. Summary of § 4
The main result of this section is that the Weyl symbol of the effective Green's operator ![]() $\smash {\widehat {G}}$ can be approximated within the assumed accuracy as follows:
$\smash {\widehat {G}}$ can be approximated within the assumed accuracy as follows:
Here, ![]() $\smash {{\boldsymbol {V}}}$ is the unperturbed velocity in the
$\smash {{\boldsymbol {V}}}$ is the unperturbed velocity in the ![]() $\smash {{\boldsymbol {X}}}$ space, so
$\smash {{\boldsymbol {X}}}$ space, so ![]() $\smash {\varOmega ({\boldsymbol {X}}, {\boldsymbol {K}}) = \omega - {\boldsymbol {k}} \cdot {\boldsymbol {v}} + \mathcal {O}(\epsilon )}$, where
$\smash {\varOmega ({\boldsymbol {X}}, {\boldsymbol {K}}) = \omega - {\boldsymbol {k}} \cdot {\boldsymbol {v}} + \mathcal {O}(\epsilon )}$, where ![]() $\smash {{\boldsymbol {v}}}$ is the unperturbed velocity in the
$\smash {{\boldsymbol {v}}}$ is the unperturbed velocity in the ![]() $\smash {{\boldsymbol {x}}}$ space, and
$\smash {{\boldsymbol {x}}}$ space, and
We also show that the term ![]() $\smash {\varGamma }$ defined in (3.34) is due to collisional effects. We postpone discussing these effects until § 6, so
$\smash {\varGamma }$ defined in (3.34) is due to collisional effects. We postpone discussing these effects until § 6, so ![]() $\smash {\varGamma }$ will be ignored for now.
$\smash {\varGamma }$ will be ignored for now.
5. Interaction with prescribed fields
In this section, we explore the effect of the diffusion operator ![]() $\smash {\widehat {D}^{\alpha \beta }}$. The oscillations will be described by
$\smash {\widehat {D}^{\alpha \beta }}$. The oscillations will be described by ![]() $\smash {\overline {W}}$ as a prescribed function, so they are allowed (yet not required) to be ‘off-shell’, i.e. do not have to be constrained by a dispersion relation. Examples of off-shell fluctuations include driven near-field oscillations, evanescent waves and microscopic fluctuations (see also § 6). We will first derive the symbol of
$\smash {\overline {W}}$ as a prescribed function, so they are allowed (yet not required) to be ‘off-shell’, i.e. do not have to be constrained by a dispersion relation. Examples of off-shell fluctuations include driven near-field oscillations, evanescent waves and microscopic fluctuations (see also § 6). We will first derive the symbol of ![]() $\smash {\widehat {D}^{\alpha \beta }}$ and, using this symbol, approximate the diffusion operator with a differential operator (§ 5.1). Then, we will calculate the coefficients in the approximate expression for
$\smash {\widehat {D}^{\alpha \beta }}$ and, using this symbol, approximate the diffusion operator with a differential operator (§ 5.1). Then, we will calculate the coefficients in the approximate expression for ![]() $\smash {\widehat {D}^{\alpha \beta }}$ (§§ 5.2 and 5.3). Finally, we will introduce the concept of the OC distribution (§ 5.4) and summarize and simplify the resulting equations (§ 5.6).
$\smash {\widehat {D}^{\alpha \beta }}$ (§§ 5.2 and 5.3). Finally, we will introduce the concept of the OC distribution (§ 5.4) and summarize and simplify the resulting equations (§ 5.6).
5.1. Expansion of the dispersion operator
The (effective) Green's operator can be represented through its symbol ![]() $G$ using (2.71):
$G$ using (2.71):
The corresponding representation of ![]() $\widehat {u\,\,}^\alpha$ is even simpler, because the symbol of
$\widehat {u\,\,}^\alpha$ is even simpler, because the symbol of ![]() $\widehat {u\,\,}^\alpha$ is independent of
$\widehat {u\,\,}^\alpha$ is independent of ![]() ${\boldsymbol {K}}$:Footnote 20
${\boldsymbol {K}}$:Footnote 20
Let us also introduce the Wigner matrix of ![]() $u^\alpha$, denoted
$u^\alpha$, denoted ![]() $\smash {W_{{\boldsymbol {u}}}^{\alpha \beta }}$, and its inverse Fourier transform
$\smash {W_{{\boldsymbol {u}}}^{\alpha \beta }}$, and its inverse Fourier transform ![]() $\smash {C_{{\boldsymbol {u}}}^{\alpha \beta }}$ as in § 2.2.3. Using these together with (2.67), one obtains
$\smash {C_{{\boldsymbol {u}}}^{\alpha \beta }}$ as in § 2.2.3. Using these together with (2.67), one obtains

Then, by taking ![]() $\smash {\text {symb}_X }$ of (
$\smash {\text {symb}_X }$ of (
), one finds that the symbol of ![]() $\smash {\widehat {D}^{\alpha \beta }}$ is a convolution of
$\smash {\widehat {D}^{\alpha \beta }}$ is a convolution of ![]() $\smash {\overline {W}_{{\boldsymbol {u}}}^{\alpha \beta }}$ and
$\smash {\overline {W}_{{\boldsymbol {u}}}^{\alpha \beta }}$ and ![]() $\smash {G}$ (Appendix B.3):
$\smash {G}$ (Appendix B.3):
Let us Taylor-expand the symbol (5.4) in ![]() ${\boldsymbol {K}}$:
${\boldsymbol {K}}$:
 \begin{align} D^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}) &\approx \int \mathrm{d}{\boldsymbol{K}}'\, \overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G({\boldsymbol{X}}, -{\boldsymbol{K}}')\nonumber\\ &\quad + K_c \int \mathrm{d}{\boldsymbol{K}}'\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G^{|c}({\boldsymbol{X}}, -{\boldsymbol{K}}') +\mathcal{O}(K_a K_b G^{|ab}). \end{align}
\begin{align} D^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}) &\approx \int \mathrm{d}{\boldsymbol{K}}'\, \overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G({\boldsymbol{X}}, -{\boldsymbol{K}}')\nonumber\\ &\quad + K_c \int \mathrm{d}{\boldsymbol{K}}'\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G^{|c}({\boldsymbol{X}}, -{\boldsymbol{K}}') +\mathcal{O}(K_a K_b G^{|ab}). \end{align}
As a reminder, ![]() $G^{|a}({\boldsymbol {X}}, -{\boldsymbol {K}}) = - \partial ^a G({\boldsymbol {X}}, -{\boldsymbol {K}})$ denotes the derivative of
$G^{|a}({\boldsymbol {X}}, -{\boldsymbol {K}}) = - \partial ^a G({\boldsymbol {X}}, -{\boldsymbol {K}})$ denotes the derivative of ![]() $G$ with respect to (the
$G$ with respect to (the ![]() $a$th component of) the whole second argument,
$a$th component of) the whole second argument, ![]() $-K_a$, and
$-K_a$, and
Upon application of ![]() $\smash {\text {oper}_X }$,
$\smash {\text {oper}_X }$, ![]() $\omega$ gets replaced (roughly) with
$\omega$ gets replaced (roughly) with ![]() $\mathrm {i} \partial _t = \mathcal {O}(\epsilon )$ and
$\mathrm {i} \partial _t = \mathcal {O}(\epsilon )$ and ![]() $k_i$ gets replaced (also roughly) with
$k_i$ gets replaced (also roughly) with ![]() $-\mathrm {i}\partial _i = \mathcal {O}(\epsilon )$. By (4.22), the last term in (5.6) is of order
$-\mathrm {i}\partial _i = \mathcal {O}(\epsilon )$. By (4.22), the last term in (5.6) is of order ![]() $\epsilon$ too. This means that the contribution of the whole
$\epsilon$ too. This means that the contribution of the whole ![]() $\smash {K_a \partial ^a G}$ term to the equation for
$\smash {K_a \partial ^a G}$ term to the equation for ![]() $\smash {\overline {f}}$ is of order
$\smash {\overline {f}}$ is of order ![]() $\epsilon$. The standard QLT neglects this contribution entirely, i.e. adopts
$\epsilon$. The standard QLT neglects this contribution entirely, i.e. adopts ![]() $\smash {D^{\alpha \beta }({\boldsymbol {X}}, {\boldsymbol {K}}) \approx D^{\alpha \beta }({\boldsymbol {X}}, {\boldsymbol {0}})}$, in which case the diffusion operator becomes just a local function of phase-space variables,
$\smash {D^{\alpha \beta }({\boldsymbol {X}}, {\boldsymbol {K}}) \approx D^{\alpha \beta }({\boldsymbol {X}}, {\boldsymbol {0}})}$, in which case the diffusion operator becomes just a local function of phase-space variables, ![]() $\smash {\widehat {D}^{\alpha \beta } \approx D^{\alpha \beta }({\boldsymbol {X}}, {\boldsymbol {0}})}$. In this work, we retain corrections to the first order in
$\smash {\widehat {D}^{\alpha \beta } \approx D^{\alpha \beta }({\boldsymbol {X}}, {\boldsymbol {0}})}$. In this work, we retain corrections to the first order in ![]() ${\boldsymbol {X}}$, i.e. keep the second term in (5.5) as well, while neglecting the higher-order terms as usual.
${\boldsymbol {X}}$, i.e. keep the second term in (5.5) as well, while neglecting the higher-order terms as usual.
Within this model, one can rewrite (5.5) as follows:
Here, we used (4.19) and introduced
which satisfy (Appendix B.4)
The first-order Weyl expansion of ![]() $\smash {\widehat {D}^{\alpha \beta }}$ is obtained by applying
$\smash {\widehat {D}^{\alpha \beta }}$ is obtained by applying ![]() $\smash {\text {oper}_X }$ to (5.7). Namely, for any
$\smash {\text {oper}_X }$ to (5.7). Namely, for any ![]() $\psi$, one has (cf. § 2.1.5)
$\psi$, one has (cf. § 2.1.5)
What remains now is to calculate the functions ![]() $\smash {D_0^{\alpha \beta }}$ and
$\smash {D_0^{\alpha \beta }}$ and ![]() $\smash {\varTheta ^{\alpha \beta c}}$ explicitly.
$\smash {\varTheta ^{\alpha \beta c}}$ explicitly.
5.2. Wigner matrix of the velocity oscillations
To express ![]() $\smash {\widehat {D}^{\alpha \beta }}$ through the Wigner function
$\smash {\widehat {D}^{\alpha \beta }}$ through the Wigner function ![]() $W$ of the perturbation Hamiltonian (§ 3.1.1), we need to express
$W$ of the perturbation Hamiltonian (§ 3.1.1), we need to express ![]() $\smash {W_{{\boldsymbol {u}}}^{\alpha \beta }}$ through
$\smash {W_{{\boldsymbol {u}}}^{\alpha \beta }}$ through ![]() $W$. Recall that
$W$. Recall that ![]() $\smash {W_{{\boldsymbol {u}}}^{\alpha \beta }}$ is the symbol of the density operator
$\smash {W_{{\boldsymbol {u}}}^{\alpha \beta }}$ is the symbol of the density operator ![]() (§ 2.2.3). By definition (3.8), one has
(§ 2.2.3). By definition (3.8), one has ![]() $\smash {u^{\alpha } = \mathrm {i} J^{\alpha \mu } \widehat {q}_{\mu } \widetilde {H}}$, where
$\smash {u^{\alpha } = \mathrm {i} J^{\alpha \mu } \widehat {q}_{\mu } \widetilde {H}}$, where ![]() $\smash {\widehat {q}_\alpha \doteq - \mathrm {i}\partial _\alpha }$ (§ 2.2.1). Then,
$\smash {\widehat {q}_\alpha \doteq - \mathrm {i}\partial _\alpha }$ (§ 2.2.1). Then,
where ![]() $\widehat {W}$ is the density operator whose symbol is
$\widehat {W}$ is the density operator whose symbol is ![]() $W$. By applying
$W$. By applying ![]() $\smash {\text {symb}_X }$, one obtains
$\smash {\text {symb}_X }$, one obtains
where ![]() $\bigstar$ is the Moyal product (2.72). Using formulas analogous to (2.33) in the
$\bigstar$ is the Moyal product (2.72). Using formulas analogous to (2.33) in the ![]() $\smash {({\boldsymbol {X}}, {\boldsymbol {K}})}$ space, one obtains
$\smash {({\boldsymbol {X}}, {\boldsymbol {K}})}$ space, one obtains
 \begin{align} q_{\mu} \,\bigstar\, W \,\bigstar \,q_{\nu} & = \left(q_{\mu} W -\frac{\mathrm{i}}{2} \frac{\partial W}{\partial z^{\mu}} \right) \,\bigstar \,q_{\nu} \nonumber\\ & = q_{\mu}q_{\nu} W - \frac{\mathrm{i}}{2}\,q_{\nu}\,\frac{\partial W}{\partial z^{\mu}} + \frac{\mathrm{i}}{2} \frac{\partial}{\partial z^{\nu}} \left(q_{\mu} W_h - \frac{\mathrm{i}}{2}\frac{\partial W}{\partial z^{\mu}}\right) \nonumber\\ & = q_{\mu}q_{\nu} W_h + \frac{\mathrm{i}}{2} \left(q_{\mu}\frac{\partial W}{\partial z^{\nu}} - q_{\nu}\frac{\partial W}{\partial z^{\mu}}\right) + \frac{1}{4}\frac{\partial^2 W}{\partial z^{\mu}\partial z^{\nu}}. \end{align}
\begin{align} q_{\mu} \,\bigstar\, W \,\bigstar \,q_{\nu} & = \left(q_{\mu} W -\frac{\mathrm{i}}{2} \frac{\partial W}{\partial z^{\mu}} \right) \,\bigstar \,q_{\nu} \nonumber\\ & = q_{\mu}q_{\nu} W - \frac{\mathrm{i}}{2}\,q_{\nu}\,\frac{\partial W}{\partial z^{\mu}} + \frac{\mathrm{i}}{2} \frac{\partial}{\partial z^{\nu}} \left(q_{\mu} W_h - \frac{\mathrm{i}}{2}\frac{\partial W}{\partial z^{\mu}}\right) \nonumber\\ & = q_{\mu}q_{\nu} W_h + \frac{\mathrm{i}}{2} \left(q_{\mu}\frac{\partial W}{\partial z^{\nu}} - q_{\nu}\frac{\partial W}{\partial z^{\mu}}\right) + \frac{1}{4}\frac{\partial^2 W}{\partial z^{\mu}\partial z^{\nu}}. \end{align}
Hence, ![]() $W_{{\boldsymbol {u}}}^{\alpha \beta }$ and
$W_{{\boldsymbol {u}}}^{\alpha \beta }$ and ![]() $W$ are connected via the following exact formula:
$W$ are connected via the following exact formula:
5.3. Nonlinear potentials
Due to (5.10), one has ![]() $D_0^{\alpha \beta } = \operatorname {re} D_0^{\alpha \beta }$. Using this together with (5.8), (5.15), (4.29), and (4.23), one obtains
$D_0^{\alpha \beta } = \operatorname {re} D_0^{\alpha \beta }$. Using this together with (5.8), (5.15), (4.29), and (4.23), one obtains
 \begin{align} D_0^{\alpha\beta} = J^{\alpha \mu}J^{\beta \nu} \operatorname{re} &\int \mathrm{d}{\boldsymbol{K}} \left({\rm \pi}\,\delta(\varOmega) - \mathrm{i}\, \operatorname{pv}\frac{1}{\varOmega}\right). \nonumber\\ & \qquad \times\left( q_{\mu} q_{\nu} \overline{W} - \frac{\mathrm{i}}{2}\left( q_{\nu}\,\frac{\partial\overline{W}}{\partial z^{\mu}} - q_{\mu}\,\frac{\partial\overline{W}}{\partial z^{\nu}} \right) + \frac{1}{4} \frac{\partial^2\overline{W}}{\partial z^{\mu}\partial z^{\nu}} \right), \end{align}
\begin{align} D_0^{\alpha\beta} = J^{\alpha \mu}J^{\beta \nu} \operatorname{re} &\int \mathrm{d}{\boldsymbol{K}} \left({\rm \pi}\,\delta(\varOmega) - \mathrm{i}\, \operatorname{pv}\frac{1}{\varOmega}\right). \nonumber\\ & \qquad \times\left( q_{\mu} q_{\nu} \overline{W} - \frac{\mathrm{i}}{2}\left( q_{\nu}\,\frac{\partial\overline{W}}{\partial z^{\mu}} - q_{\mu}\,\frac{\partial\overline{W}}{\partial z^{\nu}} \right) + \frac{1}{4} \frac{\partial^2\overline{W}}{\partial z^{\mu}\partial z^{\nu}} \right), \end{align}
with notation as in (2.10). This can be written as ![]() $\smash {D_0^{\alpha \beta } = {\mathsf {D}}^{\alpha \beta } + \varrho ^{\alpha \beta } + \varsigma ^{\alpha \beta }}$, where
$\smash {D_0^{\alpha \beta } = {\mathsf {D}}^{\alpha \beta } + \varrho ^{\alpha \beta } + \varsigma ^{\alpha \beta }}$, where
and we also introduced
As shown in Appendix B.5, the contributions of these two functions to (3.33) are
Thus, ![]() $\smash {\varrho ^{\alpha \beta }}$ must be retained and
$\smash {\varrho ^{\alpha \beta }}$ must be retained and ![]() $\smash {\varsigma ^{\alpha \beta }}$ must be neglected, which leads to
$\smash {\varsigma ^{\alpha \beta }}$ must be neglected, which leads to
The function ![]() $\smash {\varTheta ^{\alpha \beta c} = \mathrm {i}\, \operatorname {im} \varTheta ^{\alpha \beta c}}$ can be written as follows:
$\smash {\varTheta ^{\alpha \beta c} = \mathrm {i}\, \operatorname {im} \varTheta ^{\alpha \beta c}}$ can be written as follows:
where we introduced
and ![]() $\smash {\eth }$ is defined as in (4.27). Then finally, one can rewrite (5.11) as follows:
$\smash {\eth }$ is defined as in (4.27). Then finally, one can rewrite (5.11) as follows:
 \begin{align} \widehat{D}^{\alpha\beta}\psi & \approx ({\mathsf{D}}^{\alpha\beta} + \varrho^{\alpha\beta})\psi -\Theta^{\alpha\beta} V^c \partial_c\psi - \frac{1}{2}\,V^c(\partial_c\Theta^{\alpha\beta})\psi \nonumber\\ & = ({\mathsf{D}}^{\alpha\beta} + \varrho^{\alpha\beta})\psi - \Theta^{\alpha\beta} (\partial_t + v^{\lambda}\partial_{\lambda})\psi -\frac{1}{2}\,((\partial_t+v^{\lambda}\partial_{\lambda})\Theta^{\alpha\beta})\psi, \end{align}
\begin{align} \widehat{D}^{\alpha\beta}\psi & \approx ({\mathsf{D}}^{\alpha\beta} + \varrho^{\alpha\beta})\psi -\Theta^{\alpha\beta} V^c \partial_c\psi - \frac{1}{2}\,V^c(\partial_c\Theta^{\alpha\beta})\psi \nonumber\\ & = ({\mathsf{D}}^{\alpha\beta} + \varrho^{\alpha\beta})\psi - \Theta^{\alpha\beta} (\partial_t + v^{\lambda}\partial_{\lambda})\psi -\frac{1}{2}\,((\partial_t+v^{\lambda}\partial_{\lambda})\Theta^{\alpha\beta})\psi, \end{align}where we used (3.15). With some algebra (Appendix B.6), and assuming the notation
one finds that (5.23) leads to
Hence, (3.33) becomes (to the extent that ![]() $\varGamma$ is negligible; see § 6.7)
$\varGamma$ is negligible; see § 6.7)
The functions ![]() $\smash {\Theta ^{\alpha \beta }}$,
$\smash {\Theta ^{\alpha \beta }}$, ![]() $\smash {\varPhi }$ and
$\smash {\varPhi }$ and ![]() $\smash {{\mathsf {D}}^{\alpha \beta }}$ that determine the coefficients in this equation are fundamental and, for the lack of a better term, will be called nonlinear potentials.
$\smash {{\mathsf {D}}^{\alpha \beta }}$ that determine the coefficients in this equation are fundamental and, for the lack of a better term, will be called nonlinear potentials.
5.4. Oscillation-centre distribution
Let us introduce
Then, using (5.25), one can rewrite (5.26) asFootnote 21
where corrections ![]() $\mathcal {O}(\varepsilon ^4)$ have been neglected and we introduced
$\mathcal {O}(\varepsilon ^4)$ have been neglected and we introduced ![]() $\smash {\mathcal {H} \doteq \overline {H} + \varPhi }$. As a reminder, the nonlinear potentials in (5.28) are as follows:
$\smash {\mathcal {H} \doteq \overline {H} + \varPhi }$. As a reminder, the nonlinear potentials in (5.28) are as follows:
Equations (5.27)–(5.31) form a closed model that describes the evolution of the average distribution ![]() $\smash {\overline {f}}$ in turbulence with prescribed
$\smash {\overline {f}}$ in turbulence with prescribed ![]() $\overline {W}$. In particular, (5.28) can be interpreted as a Liouville-type equation for
$\overline {W}$. In particular, (5.28) can be interpreted as a Liouville-type equation for ![]() $F$ as an effective, or ‘dressed’, distribution. The latter can be understood as the distribution of ‘dressed’ particles called OCs. Then,
$F$ as an effective, or ‘dressed’, distribution. The latter can be understood as the distribution of ‘dressed’ particles called OCs. Then, ![]() $\mathcal {H}$ serves as the OC Hamiltonian,
$\mathcal {H}$ serves as the OC Hamiltonian, ![]() $\smash {{\mathsf {D}}^{\alpha \beta }}$ is the phase-space diffusion coefficient,
$\smash {{\mathsf {D}}^{\alpha \beta }}$ is the phase-space diffusion coefficient, ![]() $\smash {\varPhi }$ is the ponderomotive energy,
$\smash {\varPhi }$ is the ponderomotive energy, ![]() $\smash {\varOmega = \omega - q_\alpha v^\alpha }$ and
$\smash {\varOmega = \omega - q_\alpha v^\alpha }$ and ![]() $\smash {v^\alpha \doteq J^{\alpha \beta }\partial _\beta \overline {H}}$. Within the assumed accuracy, one can redefine
$\smash {v^\alpha \doteq J^{\alpha \beta }\partial _\beta \overline {H}}$. Within the assumed accuracy, one can redefine ![]() $\smash {v^\alpha }$ to be the OC velocity rather than the particle velocity; specifically,Footnote 22
$\smash {v^\alpha }$ to be the OC velocity rather than the particle velocity; specifically,Footnote 22
Then, the presence of ![]() $\smash {\delta (\varOmega )}$ in (5.29) signifies that OCs diffuse in phase space in response to waves they are resonant with. Below, we use the terms ‘OCs’ and ‘particles’ interchangeably except where specified otherwise.
$\smash {\delta (\varOmega )}$ in (5.29) signifies that OCs diffuse in phase space in response to waves they are resonant with. Below, we use the terms ‘OCs’ and ‘particles’ interchangeably except where specified otherwise.
That said, the interpretation of OCs as particle-like objects is limited. Single-OC motion equations are not introduced in our approach. (They would have been singular for resonant interactions.) Accordingly, the transformation (5.27) of the distribution function ![]() $\smash {\overline {f} \mapsto F}$ is not derived from a coordinate transformation but rather is fundamental. As a result, particles and OCs live in the same phase space, but the ‘dynamics of OCs’ can be irreversible (§ 5.5). This qualitatively distinguishes our approach from the traditional OC theory (Dewar Reference Dewar1973) and from the conceptually similar gyrokinetic theory (Littlejohn Reference Littlejohn1981; Cary & Brizard Reference Cary and Brizard2009), where coordinate transformations are central.
$\smash {\overline {f} \mapsto F}$ is not derived from a coordinate transformation but rather is fundamental. As a result, particles and OCs live in the same phase space, but the ‘dynamics of OCs’ can be irreversible (§ 5.5). This qualitatively distinguishes our approach from the traditional OC theory (Dewar Reference Dewar1973) and from the conceptually similar gyrokinetic theory (Littlejohn Reference Littlejohn1981; Cary & Brizard Reference Cary and Brizard2009), where coordinate transformations are central.
5.5.  ${H}$-theorem
${H}$-theorem
Because ![]() $\smash {\overline {W}}$ is non-negative (§ 2.1.6),
$\smash {\overline {W}}$ is non-negative (§ 2.1.6), ![]() $\smash {{\mathsf {D}}^{\alpha \beta }}$ is positive-semidefinite; that is,
$\smash {{\mathsf {D}}^{\alpha \beta }}$ is positive-semidefinite; that is,
for any real ![]() $\smash {\psi }$. This leads to the following theorem. Consider the OC entropy defined as
$\smash {\psi }$. This leads to the following theorem. Consider the OC entropy defined as
According to (5.28), ![]() $\smash {\mathscr {S}}$ satisfies
$\smash {\mathscr {S}}$ satisfies
 \begin{align} \frac{\mathrm{d}\mathscr{S}}{\mathrm{d} t} & ={-} \int \mathrm{d}{\boldsymbol{z}}\,\frac{\mathrm{d}(F \ln F)}{\mathrm{d} F}\left( \lbrace \mathcal{H}, F \rbrace + \partial_{\alpha}({\mathsf{D}}^{\alpha \beta} \partial_{\beta} F) \right)\nonumber\\ & ={-} \int \mathrm{d}{\boldsymbol{z}}\,\frac{\mathrm{d}(F \ln F)}{\mathrm{d} F}\,J^{\alpha\beta}(\partial_\alpha \mathcal{H})(\partial_\beta F) - \int \mathrm{d}{\boldsymbol{z}}\,(1 + \ln F)\,\partial_{\alpha}({\mathsf{D}}^{\alpha \beta} \partial_{\beta} F) \nonumber\\ & ={-} \int \mathrm{d}{\boldsymbol{z}}\,J^{\alpha\beta}(\partial_\alpha \mathcal{H}) \partial_\beta(F \ln F) - \int \mathrm{d}{\boldsymbol{z}}\,\ln F\,\partial_{\alpha}({\mathsf{D}}^{\alpha \beta} \partial_{\beta} F) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{z}}\,(J^{\alpha\beta} \partial^2_{\alpha\beta} \mathcal{H})\,F \ln F + \int \mathrm{d}{\boldsymbol{z}}\,{\mathsf{D}}^{\alpha \beta} (\partial_\alpha\ln F) (\partial_{\beta} \ln F) F. \end{align}
\begin{align} \frac{\mathrm{d}\mathscr{S}}{\mathrm{d} t} & ={-} \int \mathrm{d}{\boldsymbol{z}}\,\frac{\mathrm{d}(F \ln F)}{\mathrm{d} F}\left( \lbrace \mathcal{H}, F \rbrace + \partial_{\alpha}({\mathsf{D}}^{\alpha \beta} \partial_{\beta} F) \right)\nonumber\\ & ={-} \int \mathrm{d}{\boldsymbol{z}}\,\frac{\mathrm{d}(F \ln F)}{\mathrm{d} F}\,J^{\alpha\beta}(\partial_\alpha \mathcal{H})(\partial_\beta F) - \int \mathrm{d}{\boldsymbol{z}}\,(1 + \ln F)\,\partial_{\alpha}({\mathsf{D}}^{\alpha \beta} \partial_{\beta} F) \nonumber\\ & ={-} \int \mathrm{d}{\boldsymbol{z}}\,J^{\alpha\beta}(\partial_\alpha \mathcal{H}) \partial_\beta(F \ln F) - \int \mathrm{d}{\boldsymbol{z}}\,\ln F\,\partial_{\alpha}({\mathsf{D}}^{\alpha \beta} \partial_{\beta} F) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{z}}\,(J^{\alpha\beta} \partial^2_{\alpha\beta} \mathcal{H})\,F \ln F + \int \mathrm{d}{\boldsymbol{z}}\,{\mathsf{D}}^{\alpha \beta} (\partial_\alpha\ln F) (\partial_{\beta} \ln F) F. \end{align}
The first integral vanishes due to ![]() $\smash {J^{\alpha \beta } \partial ^2_{\alpha \beta } = 0}$. The second integral is non-negative due to (5.33). Thus,
$\smash {J^{\alpha \beta } \partial ^2_{\alpha \beta } = 0}$. The second integral is non-negative due to (5.33). Thus,
which is recognized as the ![]() $\smash {H}$-theorem (Lifshitz & Pitaevskii Reference Lifshitz and Pitaevskii1981, § 4) for QL OC dynamics.
$\smash {H}$-theorem (Lifshitz & Pitaevskii Reference Lifshitz and Pitaevskii1981, § 4) for QL OC dynamics.
5.6. Summary of § 5
From now on, we assume that the right-hand side of (5.28) scales not as ![]() $\smash {\mathcal {O}(\varepsilon ^2)}$ but as
$\smash {\mathcal {O}(\varepsilon ^2)}$ but as ![]() $\smash {\mathcal {O}(\epsilon \varepsilon ^2)}$, either due to the scarcity of resonant particles or, for QL diffusion driven by microscopic fluctuations (§ 6), due to the plasma parameter's being large. Also, the spatial derivatives can be neglected within the assumed accuracy in the definition of
$\smash {\mathcal {O}(\epsilon \varepsilon ^2)}$, either due to the scarcity of resonant particles or, for QL diffusion driven by microscopic fluctuations (§ 6), due to the plasma parameter's being large. Also, the spatial derivatives can be neglected within the assumed accuracy in the definition of ![]() $F$ (5.27) and on the right-hand side of (5.28). Using this together with (2.69), and with (2.56) for the Poisson bracket, our results can be summarized as follows.
$F$ (5.27) and on the right-hand side of (5.28). Using this together with (2.69), and with (2.56) for the Poisson bracket, our results can be summarized as follows.
QL evolution of a particle distribution in a prescribed wave field is governed byFootnote 23
The OC distribution ![]() $\smash {F}$ is defined as
$\smash {F}$ is defined as
so the density of OCs is the same as the locally averaged density of the true particles:
The function ![]() $\smash {\mathcal {H}}$ is understood as the OC Hamiltonian. It is given by
$\smash {\mathcal {H}}$ is understood as the OC Hamiltonian. It is given by
where ![]() $\smash {\overline {H}}$ is the average Hamiltonian, which may include interaction with background fields, and
$\smash {\overline {H}}$ is the average Hamiltonian, which may include interaction with background fields, and ![]() $\smash {\varPhi }$ is the ponderomotive potential. The nonlinear potentials that enter (5.37) can be calculated to the zeroth order in
$\smash {\varPhi }$ is the ponderomotive potential. The nonlinear potentials that enter (5.37) can be calculated to the zeroth order in ![]() $\epsilon$ and are given byFootnote 24
$\epsilon$ and are given byFootnote 24
where ![]() $\smash {{\boldsymbol {k}} {\boldsymbol {k}}}$ is a dyadic matrix with two lower indices, and the same conventions apply as in § 2.1.2. Also,
$\smash {{\boldsymbol {k}} {\boldsymbol {k}}}$ is a dyadic matrix with two lower indices, and the same conventions apply as in § 2.1.2. Also, ![]() $\smash {{\boldsymbol {v}}}$ is hereby redefined as the OC spatial velocity, namely,
$\smash {{\boldsymbol {v}}}$ is hereby redefined as the OC spatial velocity, namely,
The function ![]() $\smash {\overline {{\mathsf {W}}}}$ is defined as
$\smash {\overline {{\mathsf {W}}}}$ is defined as
where ![]() $\overline {W}$ is the average Wigner function (3.4) of the perturbation Hamiltonian, i.e. the spectrum of its symmetrized autocorrelation function (3.5). Due to (2.78), it can be understood as the average of
$\overline {W}$ is the average Wigner function (3.4) of the perturbation Hamiltonian, i.e. the spectrum of its symmetrized autocorrelation function (3.5). Due to (2.78), it can be understood as the average of ![]() $\smash {{\mathsf {W}} \doteq \text {symb}_{{\mathsf {x}}} \widehat {{\mathsf {W}}}}$ (where
$\smash {{\mathsf {W}} \doteq \text {symb}_{{\mathsf {x}}} \widehat {{\mathsf {W}}}}$ (where ![]() $\smash {\widehat {{\mathsf {W}}}}$ is defined in (3.3)), i.e. as the Wigner function of the perturbation Hamiltonian with
$\smash {\widehat {{\mathsf {W}}}}$ is defined in (3.3)), i.e. as the Wigner function of the perturbation Hamiltonian with ![]() $\smash {{\boldsymbol {p}}}$ treated as a parameter. As such,
$\smash {{\boldsymbol {p}}}$ treated as a parameter. As such, ![]() $\smash {\overline {{\mathsf {W}}}}$ is non-negative, so
$\smash {\overline {{\mathsf {W}}}}$ is non-negative, so ![]() $\smash {{{\boldsymbol {\mathsf {D}}}}}$ is positive-semidefinite. This leads to an
$\smash {{{\boldsymbol {\mathsf {D}}}}}$ is positive-semidefinite. This leads to an ![]() $\smash {H}$-theorem (proven similarly to (5.36)) for the entropy density
$\smash {H}$-theorem (proven similarly to (5.36)) for the entropy density ![]() $\smash {\sigma \doteq - \int \mathrm {d}{\boldsymbol {p}}\,F\ln F}$:
$\smash {\sigma \doteq - \int \mathrm {d}{\boldsymbol {p}}\,F\ln F}$:
Also note that for homogeneous turbulence in particular, where ![]() $\smash {\overline {{\mathsf {W}}}}$ is independent of
$\smash {\overline {{\mathsf {W}}}}$ is independent of ![]() $\smash {{\boldsymbol {x}}}$, (2.46) yields that
$\smash {{\boldsymbol {x}}}$, (2.46) yields that
where ![]() $\smash {\mathscr {V}_n}$ is the plasma volume (the index
$\smash {\mathscr {V}_n}$ is the plasma volume (the index ![]() $\smash {n}$ denotes the number of spatial dimensions) and
$\smash {n}$ denotes the number of spatial dimensions) and ![]() $\smash {\mathring {\widetilde {H}}}$ is the spatial spectrum of
$\smash {\mathring {\widetilde {H}}}$ is the spatial spectrum of ![]() $\smash {\widetilde {H}}$ as defined in (2.23).
$\smash {\widetilde {H}}$ as defined in (2.23).
Equation (5.37) can be used to calculate the ponderomotive force ![]() $\smash {\partial _t\int \mathrm {d}{\boldsymbol {p}}\,\overline {f}}$ that a given wave field imparts on a plasma. This potentially resolves the controversies mentioned in Kentwell & Jones (Reference Kentwell and Jones1987). We will revisit this subject for on-shell waves in § 7.5.
$\smash {\partial _t\int \mathrm {d}{\boldsymbol {p}}\,\overline {f}}$ that a given wave field imparts on a plasma. This potentially resolves the controversies mentioned in Kentwell & Jones (Reference Kentwell and Jones1987). We will revisit this subject for on-shell waves in § 7.5.
6. Interaction with self-consistent fields
Here, we explain how to calculate the function ![]() $\overline {{\mathsf {W}}}$ in the presence of microscopic fluctuations (non-zero
$\overline {{\mathsf {W}}}$ in the presence of microscopic fluctuations (non-zero ![]() $g$). In particular, we reinstate the term
$g$). In particular, we reinstate the term ![]() $\smash {\varGamma }$ that was omitted in § 5. We also show that a collision operator of the Balescu–Lenard type emerges from our theory within a general interaction model. This calculation can be considered as a generalization of that in Rogister & Oberman (Reference Rogister and Oberman1968) for homogeneous plasmas. Another related calculation was proposed in Chavanis (Reference Chavanis2012) in application to potential interactions in inhomogeneous systems using action–angle variables, with global averaging over the angles. (See also Mynick (Reference Mynick1988) for a related calculation in action–angle variables based on the Fokker–Planck approach.) In contrast, our model holds for any Hamiltonian interactions via any vector fields and allows for weak inhomogeneities in canonical coordinates.
$\smash {\varGamma }$ that was omitted in § 5. We also show that a collision operator of the Balescu–Lenard type emerges from our theory within a general interaction model. This calculation can be considered as a generalization of that in Rogister & Oberman (Reference Rogister and Oberman1968) for homogeneous plasmas. Another related calculation was proposed in Chavanis (Reference Chavanis2012) in application to potential interactions in inhomogeneous systems using action–angle variables, with global averaging over the angles. (See also Mynick (Reference Mynick1988) for a related calculation in action–angle variables based on the Fokker–Planck approach.) In contrast, our model holds for any Hamiltonian interactions via any vector fields and allows for weak inhomogeneities in canonical coordinates.
6.1. Interaction model
Let us assume that particles interact via an ![]() $M$-component real field
$M$-component real field ![]() ${\boldsymbol {\varPsi }} \equiv (\varPsi ^1, \varPsi ^2, \ldots, \varPsi ^M)^\intercal$. It is treated below as a column vector; hence the index
${\boldsymbol {\varPsi }} \equiv (\varPsi ^1, \varPsi ^2, \ldots, \varPsi ^M)^\intercal$. It is treated below as a column vector; hence the index ![]() $\smash {^\intercal }$. (A complex field can be accommodated by considering its real and imaginary parts as separate components.) We split this field into the average part
$\smash {^\intercal }$. (A complex field can be accommodated by considering its real and imaginary parts as separate components.) We split this field into the average part ![]() $\smash {\overline {{\boldsymbol {\varPsi }}}}$ and the oscillating part
$\smash {\overline {{\boldsymbol {\varPsi }}}}$ and the oscillating part ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$. The former is considered given. For the latter, we assume the action integral of this field without plasma in the form
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$. The former is considered given. For the latter, we assume the action integral of this field without plasma in the form
(see § 9 for examples), where ![]() $\smash {\widehat {\boldsymbol {\varXi }}_0}$ is a Hermitian operatorFootnote 25 and
$\smash {\widehat {\boldsymbol {\varXi }}_0}$ is a Hermitian operatorFootnote 25 and ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}^{{\dagger}} = \smash {\widetilde {{\boldsymbol {\varPsi }}}}^\intercal }$ is a row vector dual to
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}^{{\dagger}} = \smash {\widetilde {{\boldsymbol {\varPsi }}}}^\intercal }$ is a row vector dual to ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$. Plasma is allowed to consist of multiple species, henceforth denoted with index
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$. Plasma is allowed to consist of multiple species, henceforth denoted with index ![]() $\smash {s}$. Because
$\smash {s}$. Because ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ is assumed small, the generic Hamiltonian for each species
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ is assumed small, the generic Hamiltonian for each species ![]() $\smash {s}$ can be Taylor-expanded in
$\smash {s}$ can be Taylor-expanded in ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ and represented in a generic form
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ and represented in a generic form
(see § 9 for examples), which can be considered as a second-order Taylor expansion of the full Hamiltonian in ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$. Here,
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$. Here, ![]() $\smash {H_{0s} \equiv H_{0s}(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ is independent of
$\smash {H_{0s} \equiv H_{0s}(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ is independent of ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}} \equiv \widetilde {{\boldsymbol {\varPsi }}}(t, {\boldsymbol {x}})}$,
$\smash {\widetilde {{\boldsymbol {\varPsi }}} \equiv \widetilde {{\boldsymbol {\varPsi }}}(t, {\boldsymbol {x}})}$, ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s \equiv (\widehat {\alpha }_{s,1}, \widehat {\alpha }_{s,2}, \ldots, \widehat {\alpha }_{s,M})^\intercal }$ is a column vector whose elements
$\smash {\widehat {\boldsymbol {\alpha }}_s \equiv (\widehat {\alpha }_{s,1}, \widehat {\alpha }_{s,2}, \ldots, \widehat {\alpha }_{s,M})^\intercal }$ is a column vector whose elements ![]() $\smash {\widehat {\alpha }_{s,i}}$ are linear operators on
$\smash {\widehat {\alpha }_{s,i}}$ are linear operators on ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$. The dagger is added so that
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$. The dagger is added so that ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s^{{\dagger}} }$ could be understood as a row vector whose elements
$\smash {\widehat {\boldsymbol {\alpha }}_s^{{\dagger}} }$ could be understood as a row vector whose elements ![]() $\smash {\widehat {\alpha }_{s,i}^{{\dagger}} }$ act on the individual components of the field; i.e.
$\smash {\widehat {\alpha }_{s,i}^{{\dagger}} }$ act on the individual components of the field; i.e. ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s^{{\dagger}} \widetilde {{\boldsymbol {\varPsi }}} \equiv \widehat {\alpha }^{{\dagger}} _{s,i}\widetilde {\varPsi }^i}$. We let
$\smash {\widehat {\boldsymbol {\alpha }}_s^{{\dagger}} \widetilde {{\boldsymbol {\varPsi }}} \equiv \widehat {\alpha }^{{\dagger}} _{s,i}\widetilde {\varPsi }^i}$. We let ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s}$ be non-local in
$\smash {\widehat {\boldsymbol {\alpha }}_s}$ be non-local in ![]() $t$ and
$t$ and ![]() ${\boldsymbol {x}}$ (for example,
${\boldsymbol {x}}$ (for example, ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s}$ can be a spacetime derivative or a spacetime integral), and we also let
$\smash {\widehat {\boldsymbol {\alpha }}_s}$ can be a spacetime derivative or a spacetime integral), and we also let ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s}$ depend on
$\smash {\widehat {\boldsymbol {\alpha }}_s}$ depend on ![]() $\smash {{\boldsymbol {p}}}$ parametrically so
$\smash {{\boldsymbol {p}}}$ parametrically so
The matrix operators ![]() $\smash {\widehat {\boldsymbol {L}}_s}$ and
$\smash {\widehat {\boldsymbol {L}}_s}$ and ![]() $\smash {\widehat {\boldsymbol {R}}_s}$ and their symbols
$\smash {\widehat {\boldsymbol {R}}_s}$ and their symbols ![]() $\smash {{\boldsymbol {L}}_s}$ and
$\smash {{\boldsymbol {L}}_s}$ and ![]() $\smash {{\boldsymbol {R}}_s}$ are understood similarly.
$\smash {{\boldsymbol {R}}_s}$ are understood similarly.
The Lagrangian density of the oscillating-field–plasma system is
where the sum is taken over individual particles. Note that
 \begin{align} \sum_{\sigma_s} H_s(t, {\boldsymbol{x}}_{\sigma_s}, {\boldsymbol{p}}_{\sigma_s}) \delta({\boldsymbol{x}} - {\boldsymbol{x}}_{\sigma_s}(t)) & = \int \mathrm{d}{\boldsymbol{p}}\, \sum_{\sigma_s} \delta({\boldsymbol{z}} - {\boldsymbol{z}}_{\sigma_s}(t)) H_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{p}}\, f_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}) H_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}), \end{align}
\begin{align} \sum_{\sigma_s} H_s(t, {\boldsymbol{x}}_{\sigma_s}, {\boldsymbol{p}}_{\sigma_s}) \delta({\boldsymbol{x}} - {\boldsymbol{x}}_{\sigma_s}(t)) & = \int \mathrm{d}{\boldsymbol{p}}\, \sum_{\sigma_s} \delta({\boldsymbol{z}} - {\boldsymbol{z}}_{\sigma_s}(t)) H_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{p}}\, f_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}) H_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}), \end{align}
so the ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$-dependent part of the system action can be written as
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$-dependent part of the system action can be written as ![]() $\smash {S = \int \mathrm {d}{\boldsymbol {\mathsf {x}}}\,\mathfrak {L}}$ with
$\smash {S = \int \mathrm {d}{\boldsymbol {\mathsf {x}}}\,\mathfrak {L}}$ with
(The contribution of ![]() $\smash {\widetilde {f}_s}$ to the second term in (6.6) has been omitted because it averages to zero at integration over spacetime and thus does not contribute to
$\smash {\widetilde {f}_s}$ to the second term in (6.6) has been omitted because it averages to zero at integration over spacetime and thus does not contribute to ![]() $\smash {S}$.) This ‘abridged’ action is not sufficient to describe the particle motion, but it is sufficient to describe the dynamics of
$\smash {S}$.) This ‘abridged’ action is not sufficient to describe the particle motion, but it is sufficient to describe the dynamics of ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ at given
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ at given ![]() $\smash {f_s}$, as discussed below. The operator
$\smash {f_s}$, as discussed below. The operator ![]() $\smash {\widehat {\boldsymbol {\varXi }}_p}$ can be considered Hermitian without loss of generality, because its anti-Hermitian part does not contribute to
$\smash {\widehat {\boldsymbol {\varXi }}_p}$ can be considered Hermitian without loss of generality, because its anti-Hermitian part does not contribute to ![]() $\smash {S}$. Also, we assume that unless either of
$\smash {S}$. Also, we assume that unless either of ![]() $\smash {\widehat {\boldsymbol {L}}}$ and
$\smash {\widehat {\boldsymbol {L}}}$ and ![]() $\smash {\widehat {\boldsymbol {R}}}$ is zero, the high-frequency field has no three-wave resonances, so terms cubic in
$\smash {\widehat {\boldsymbol {R}}}$ is zero, the high-frequency field has no three-wave resonances, so terms cubic in ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ can be neglected in
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ can be neglected in ![]() $\smash {S}$;Footnote 26 then,
$\smash {S}$;Footnote 26 then,
Using the same assumption, one can also adopt
because in the absence of three-wave resonances, the oscillating part of ![]() $\smash {(\widehat {\boldsymbol {L}}_s\widetilde {{\boldsymbol {\varPsi }}})^{{\dagger}} (\widehat {\boldsymbol {R}}_s\widetilde {{\boldsymbol {\varPsi }}})}$ contributes only
$\smash {(\widehat {\boldsymbol {L}}_s\widetilde {{\boldsymbol {\varPsi }}})^{{\dagger}} (\widehat {\boldsymbol {R}}_s\widetilde {{\boldsymbol {\varPsi }}})}$ contributes only ![]() $\smash {\mathcal {O}(\varepsilon ^4)}$ terms to the equation for
$\smash {\mathcal {O}(\varepsilon ^4)}$ terms to the equation for ![]() $\smash {F_s}$.
$\smash {F_s}$.
6.2. Field equations
The Euler–Lagrange equation for ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ derived from (6.6) is
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ derived from (6.6) is
Then, to the extent that the linear approximation for ![]() $\smash {\tilde {f}_s}$ is sufficient (see below), one finds that the oscillating part of the field satisfies
$\smash {\tilde {f}_s}$ is sufficient (see below), one finds that the oscillating part of the field satisfies
where we used (3.24). Note that the right-hand side of (6.11) is determined by microscopic fluctuations ![]() $g_s(t, {\boldsymbol {x}}, {\boldsymbol {p}})$ (§ 4.3). Equation (6.11) can also be expressed as
$g_s(t, {\boldsymbol {x}}, {\boldsymbol {p}})$ (§ 4.3). Equation (6.11) can also be expressed as
where ![]() $\smash {\widehat {\boldsymbol {\varXi }}}$ is understood as the plasma dispersion operator and is given by
$\smash {\widehat {\boldsymbol {\varXi }}}$ is understood as the plasma dispersion operator and is given by
where ![]() $\smash {{\unicode{x25AA}} }$ is a placeholder. The general solution of (6.12) can be written as
$\smash {{\unicode{x25AA}} }$ is a placeholder. The general solution of (6.12) can be written as
Here, ![]() $\smash {\smash {\widehat {\boldsymbol {\varXi }}}^{-1}}$ is the right inverse of
$\smash {\smash {\widehat {\boldsymbol {\varXi }}}^{-1}}$ is the right inverse of ![]() $\smash {\widehat {\boldsymbol {\varXi }}}$ (specifically,
$\smash {\widehat {\boldsymbol {\varXi }}}$ (specifically, ![]() $\smash {\widehat {\boldsymbol {\varXi }} \smash {\widehat {\boldsymbol {\varXi }}}^{-1} = \widehat {\boldsymbol {1}}}$ yet
$\smash {\widehat {\boldsymbol {\varXi }} \smash {\widehat {\boldsymbol {\varXi }}}^{-1} = \widehat {\boldsymbol {1}}}$ yet ![]() $\smash {\smash {\widehat {\boldsymbol {\varXi }}}^{-1}\widehat {\boldsymbol {\varXi }} \ne \widehat {\boldsymbol {1}}}$) such that
$\smash {\smash {\widehat {\boldsymbol {\varXi }}}^{-1}\widehat {\boldsymbol {\varXi }} \ne \widehat {\boldsymbol {1}}}$) such that ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$ vanishes at zero
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$ vanishes at zero ![]() $g$.Footnote 27 The rest of the solution,
$g$.Footnote 27 The rest of the solution, ![]() $\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$, is the macroscopic field that satisfies
$\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$, is the macroscopic field that satisfies
In the special case when the dispersion operator is Hermitian (![]() $\smash {\widehat {\boldsymbol {\varXi }} = \widehat {\boldsymbol {\varXi }}_\text {H}}$), (6.15) also flows from the ‘adiabatic’ macroscopic part of the action
$\smash {\widehat {\boldsymbol {\varXi }} = \widehat {\boldsymbol {\varXi }}_\text {H}}$), (6.15) also flows from the ‘adiabatic’ macroscopic part of the action ![]() $\smash {S}$, namely,
$\smash {S}$, namely,
Because we have assumed a linear model for ![]() $\smash {f_s}$ in (6.11),
$\smash {f_s}$ in (6.11), ![]() $\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ is decoupled from
$\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ is decoupled from ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$, and hence the dynamics of
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$, and hence the dynamics of ![]() $\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ turns out to be collisionless. This is justified, because collisional dissipation is assumed to be much slower that collisionless dissipation (§ 3.3). One can reinstate collisions in (6.15) by modifying
$\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ turns out to be collisionless. This is justified, because collisional dissipation is assumed to be much slower that collisionless dissipation (§ 3.3). One can reinstate collisions in (6.15) by modifying ![]() $\smash {\widehat {G}_s}$ ad hoc, if necessary. Alternatively, one can avoid separating
$\smash {\widehat {G}_s}$ ad hoc, if necessary. Alternatively, one can avoid separating ![]() $\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ and
$\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ and ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$ and, instead, derive an equation for the average Wigner matrix of the whole
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$ and, instead, derive an equation for the average Wigner matrix of the whole ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ (McDonald Reference McDonald1991). However, this approach is beyond QLT, so it is not considered in this paper.
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ (McDonald Reference McDonald1991). However, this approach is beyond QLT, so it is not considered in this paper.
6.3. Dispersion matrix
As readily seen from the definition (6.13), the operator ![]() $\smash {\widehat {\boldsymbol {\varXi }}}$ can be expressed as
$\smash {\widehat {\boldsymbol {\varXi }}}$ can be expressed as
The corrections caused by non-zero ![]() $\epsilon$ and
$\epsilon$ and ![]() $\varepsilon$ in this formula will be insignificant for our purposes, so they will be neglected. In particular, this means that
$\varepsilon$ in this formula will be insignificant for our purposes, so they will be neglected. In particular, this means that ![]() $\smash {G_s \doteq \text {symb}_X \widehat {G}_s}$ can be adopted in the form independent of
$\smash {G_s \doteq \text {symb}_X \widehat {G}_s}$ can be adopted in the form independent of ![]() $\smash {{\boldsymbol {r}}}$ (§ 4.2):
$\smash {{\boldsymbol {r}}}$ (§ 4.2):
Then, ![]() $\smash {\widehat {G}_s}$ can be considered as an operator on
$\smash {\widehat {G}_s}$ can be considered as an operator on ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ with
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ with ![]() ${\boldsymbol {p}}$ as a parameter, and
${\boldsymbol {p}}$ as a parameter, and ![]() $\smash {\text{symb}\, \widehat {G}_s = G_s(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}})}$. Also,
$\smash {\text{symb}\, \widehat {G}_s = G_s(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}})}$. Also,
This readily yields the ‘dispersion matrix’ ![]() $\smash {{\boldsymbol {\varXi }} \doteq \text {symb}_{{\mathsf {x}}} \widehat {\boldsymbol {\varXi }}}$:
$\smash {{\boldsymbol {\varXi }} \doteq \text {symb}_{{\mathsf {x}}} \widehat {\boldsymbol {\varXi }}}$:
 \begin{gather} \displaystyle {\boldsymbol{\varXi}}(\omega, {\boldsymbol{k}}) \approx {\boldsymbol{\varXi}}_p(\omega, {\boldsymbol{k}}) + \sum_s \int \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0}\, {\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \end{gather}
\begin{gather} \displaystyle {\boldsymbol{\varXi}}(\omega, {\boldsymbol{k}}) \approx {\boldsymbol{\varXi}}_p(\omega, {\boldsymbol{k}}) + \sum_s \int \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0}\, {\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \end{gather}
(see § 9 for examples). Here, ![]() $\smash {{\boldsymbol {\alpha }}_s {\boldsymbol {\alpha }}_s^{{\dagger}} }$ is a dyadic matrix, and the arguments
$\smash {{\boldsymbol {\alpha }}_s {\boldsymbol {\alpha }}_s^{{\dagger}} }$ is a dyadic matrix, and the arguments ![]() $t$ and
$t$ and ![]() ${\boldsymbol {x}}$ are henceforth omitted for brevity. Also, we introduced the operators
${\boldsymbol {x}}$ are henceforth omitted for brevity. Also, we introduced the operators ![]() $\smash {\widehat {\boldsymbol {\wp }}_s = \widehat {\boldsymbol {\wp }}_s^{{\dagger}} }$ and their symbols
$\smash {\widehat {\boldsymbol {\wp }}_s = \widehat {\boldsymbol {\wp }}_s^{{\dagger}} }$ and their symbols ![]() $\smash {{\boldsymbol {\wp }}_s = {\boldsymbol {\wp }}_s^{{\dagger}} }$ as
$\smash {{\boldsymbol {\wp }}_s = {\boldsymbol {\wp }}_s^{{\dagger}} }$ as
The appearance of ![]() $+ \mathrm {i} 0$ in the denominator in (6.20) is related to the Landau rule. (Remember that as arguments of Weyl symbols,
$+ \mathrm {i} 0$ in the denominator in (6.20) is related to the Landau rule. (Remember that as arguments of Weyl symbols, ![]() $\omega$ and
$\omega$ and ![]() ${\boldsymbol {k}}$ are real by definition.) The Hermitian and anti-Hermitian parts of the dispersion matrix are
${\boldsymbol {k}}$ are real by definition.) The Hermitian and anti-Hermitian parts of the dispersion matrix are
 \begin{align} {\boldsymbol{\varXi}}_\text{H}(\omega, {\boldsymbol{k}}) & \approx {\boldsymbol{\varXi}}_p(\omega, {\boldsymbol{k}}) + \sum_s {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, {\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \end{align}
\begin{align} {\boldsymbol{\varXi}}_\text{H}(\omega, {\boldsymbol{k}}) & \approx {\boldsymbol{\varXi}}_p(\omega, {\boldsymbol{k}}) + \sum_s {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, {\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \end{align}
Assuming the notation ![]() $\smash {{\boldsymbol {\varXi }}^{-{{\dagger}} } \doteq ({\boldsymbol {\varXi }}^{{\dagger}} )^{-1}}$, the inverse dispersion matrix can be expressed as
$\smash {{\boldsymbol {\varXi }}^{-{{\dagger}} } \doteq ({\boldsymbol {\varXi }}^{{\dagger}} )^{-1}}$, the inverse dispersion matrix can be expressed as
Because ![]() $\smash {{\boldsymbol {\varXi }}^{-{{\dagger}} } = ({\boldsymbol {\varXi }}^{-1})^{{\dagger}} }$, this leads to the following formulas, which we will need later:
$\smash {{\boldsymbol {\varXi }}^{-{{\dagger}} } = ({\boldsymbol {\varXi }}^{-1})^{{\dagger}} }$, this leads to the following formulas, which we will need later:
6.4. Spectrum of microscopic fluctuations
Other objects to be used below are the density operators of the oscillating fields:
and the corresponding average Wigner matrices on ![]() $\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. The former,
$\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$. The former, ![]() $\smash {{{\boldsymbol {\mathsf {U}}}} \doteq \overline {{{\boldsymbol {\mathsf {W}}}}}_{\underline {\widetilde {{\boldsymbol {\varPsi }}}}}}$, is readily found by definition (2.51), and the latter,
$\smash {{{\boldsymbol {\mathsf {U}}}} \doteq \overline {{{\boldsymbol {\mathsf {W}}}}}_{\underline {\widetilde {{\boldsymbol {\varPsi }}}}}}$, is readily found by definition (2.51), and the latter, ![]() $\smash {{\boldsymbol {\mathfrak {W}}} \doteq \overline {{{\boldsymbol {\mathsf {W}}}}}_{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}}$, is calculated as follows. Let us consider
$\smash {{\boldsymbol {\mathfrak {W}}} \doteq \overline {{{\boldsymbol {\mathsf {W}}}}}_{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}}$, is calculated as follows. Let us consider ![]() $\smash {g_s(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ as a ket in
$\smash {g_s(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ as a ket in ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$, with
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$, with ![]() $\smash {{\boldsymbol {p}}}$ as a parameter. Then, (6.14) readily yields
$\smash {{\boldsymbol {p}}}$ as a parameter. Then, (6.14) readily yields
By applying ![]() $\smash {\text {symb}_{{\mathsf {x}}} }$ to this, one obtains
$\smash {\text {symb}_{{\mathsf {x}}} }$ to this, one obtains
 \begin{equation} {\boldsymbol{\mathfrak{W}}}= \sum_{s,s'} \int \mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, {\boldsymbol{\varXi}}^{{-}1} \star {\boldsymbol{\alpha}}_s({\boldsymbol{p}}) \star {\boldsymbol{\mathfrak{G}}}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \star {\boldsymbol{\alpha}}^{{\dagger}}_{s'}({\boldsymbol{p}}') \star {\boldsymbol{\varXi}}^{-{{\dagger}}}, \end{equation}
\begin{equation} {\boldsymbol{\mathfrak{W}}}= \sum_{s,s'} \int \mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, {\boldsymbol{\varXi}}^{{-}1} \star {\boldsymbol{\alpha}}_s({\boldsymbol{p}}) \star {\boldsymbol{\mathfrak{G}}}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \star {\boldsymbol{\alpha}}^{{\dagger}}_{s'}({\boldsymbol{p}}') \star {\boldsymbol{\varXi}}^{-{{\dagger}}}, \end{equation}where most arguments are omitted for brevity and (Appendix B.7)
 \begin{align} \mathfrak{G}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') & \doteq \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}} \int \mathrm{d}{\boldsymbol {\mathsf{s}}}\,\mathrm{e}^{- \mathrm{i}{\boldsymbol {\mathsf{k}}}\cdot{\boldsymbol {\mathsf{s}}}}\, \overline{g_{s}({\boldsymbol {\mathsf{x}}} + {\boldsymbol {\mathsf{s}}}/2, {\boldsymbol{p}})\, g_{s'}({\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{s}}}/2, {\boldsymbol{p}}')} \nonumber\\ & \approx \frac{1}{(2{\rm \pi})^n}\,\delta_{ss'}\delta({\boldsymbol{p}} - {\boldsymbol{p}}') \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)F_s({\boldsymbol{p}}), \end{align}
\begin{align} \mathfrak{G}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') & \doteq \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}} \int \mathrm{d}{\boldsymbol {\mathsf{s}}}\,\mathrm{e}^{- \mathrm{i}{\boldsymbol {\mathsf{k}}}\cdot{\boldsymbol {\mathsf{s}}}}\, \overline{g_{s}({\boldsymbol {\mathsf{x}}} + {\boldsymbol {\mathsf{s}}}/2, {\boldsymbol{p}})\, g_{s'}({\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{s}}}/2, {\boldsymbol{p}}')} \nonumber\\ & \approx \frac{1}{(2{\rm \pi})^n}\,\delta_{ss'}\delta({\boldsymbol{p}} - {\boldsymbol{p}}') \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)F_s({\boldsymbol{p}}), \end{align}assuming corrections due to inter-particle correlations are negligible. Then, (6.29) gives
 \begin{align} {\boldsymbol{\mathfrak{W}}}(\omega, {\boldsymbol{k}}) = \frac{1}{(2{\rm \pi})^{n}} \sum_{s'}\int \mathrm{d}{\boldsymbol{p}}'\,&\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})F_{s'}({\boldsymbol{p}}') \nonumber\\ & \times {\boldsymbol{\varXi}}^{{-}1}(\omega, {\boldsymbol{k}}) ({\boldsymbol{\alpha}}_{s'}{\boldsymbol{\alpha}}_{s'}^{{\dagger}})(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') {\boldsymbol{\varXi}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}), \end{align}
\begin{align} {\boldsymbol{\mathfrak{W}}}(\omega, {\boldsymbol{k}}) = \frac{1}{(2{\rm \pi})^{n}} \sum_{s'}\int \mathrm{d}{\boldsymbol{p}}'\,&\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})F_{s'}({\boldsymbol{p}}') \nonumber\\ & \times {\boldsymbol{\varXi}}^{{-}1}(\omega, {\boldsymbol{k}}) ({\boldsymbol{\alpha}}_{s'}{\boldsymbol{\alpha}}_{s'}^{{\dagger}})(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') {\boldsymbol{\varXi}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}), \end{align}
where ![]() $\smash {{\boldsymbol {v}}'_{s'} \doteq {\boldsymbol {v}}_{s'}(t, {\boldsymbol {x}}, {\boldsymbol {p}}')}$. It is readily seen from (6.31) that
$\smash {{\boldsymbol {v}}'_{s'} \doteq {\boldsymbol {v}}_{s'}(t, {\boldsymbol {x}}, {\boldsymbol {p}}')}$. It is readily seen from (6.31) that ![]() $\smash {{\boldsymbol {\mathfrak {W}}}}$ is positive-semidefinite. One can also recognize (6.31) as a manifestation of the dressed-particle superposition principle (Rostoker Reference Rostoker1964). Specifically, (6.31) shows that the contributions of individual OCs to
$\smash {{\boldsymbol {\mathfrak {W}}}}$ is positive-semidefinite. One can also recognize (6.31) as a manifestation of the dressed-particle superposition principle (Rostoker Reference Rostoker1964). Specifically, (6.31) shows that the contributions of individual OCs to ![]() $\smash {{\boldsymbol {\mathfrak {W}}}}$ are additive and affected by the plasma collective response, i.e. by the difference between
$\smash {{\boldsymbol {\mathfrak {W}}}}$ are additive and affected by the plasma collective response, i.e. by the difference between ![]() $\smash {{\boldsymbol {\varXi }}}$ and the vacuum dispersion matrix
$\smash {{\boldsymbol {\varXi }}}$ and the vacuum dispersion matrix ![]() $\smash {{\boldsymbol {\varXi }}_0}$.
$\smash {{\boldsymbol {\varXi }}_0}$.
Using (6.31), one can also find other averages quadratic in the field via (cf. (2.53a))
where ![]() $\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {L}}}}}}$ and
$\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {L}}}}}}$ and ![]() $\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {R}}}}}}$ are any linear operators and
$\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {R}}}}}}$ are any linear operators and ![]() $\smash {{{\boldsymbol {\mathsf {L}}}}}$ and
$\smash {{{\boldsymbol {\mathsf {L}}}}}$ and ![]() $\smash {{{\boldsymbol {\mathsf {R}}}}}$ are their symbols; for example,
$\smash {{{\boldsymbol {\mathsf {R}}}}}$ are their symbols; for example,
Because of this, we loosely attribute ![]() $\smash {{\boldsymbol {\mathfrak {W}}}}$ as the spectrum of microscopic oscillations, but see also § 8.2, where an alternative notation is introduced and a fluctuation–dissipation theorem is derived from (6.31) for plasma in thermal equilibrium. See also § 9 for specific examples.
$\smash {{\boldsymbol {\mathfrak {W}}}}$ as the spectrum of microscopic oscillations, but see also § 8.2, where an alternative notation is introduced and a fluctuation–dissipation theorem is derived from (6.31) for plasma in thermal equilibrium. See also § 9 for specific examples.
6.5. Nonlinear potentials
From (6.14), the oscillating part of the Hamiltonian (6.9) can be split into the macroscopic part and the microscopic part as ![]() $\smash {\widetilde {H}_s = \underline {\widetilde {H}}_s + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {H}}_s}$,
$\smash {\widetilde {H}_s = \underline {\widetilde {H}}_s + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {H}}_s}$, ![]() $\smash {\underline {\widetilde {H}}_s = \widehat {\boldsymbol {\alpha }}_s^{{\dagger}} \underline {\widetilde {{\boldsymbol {\varPsi }}}}}$, and
$\smash {\underline {\widetilde {H}}_s = \widehat {\boldsymbol {\alpha }}_s^{{\dagger}} \underline {\widetilde {{\boldsymbol {\varPsi }}}}}$, and
Here, ![]() $\smash {\widehat {\mathcal {X}}_{ss'}}$ is an operator on
$\smash {\widehat {\mathcal {X}}_{ss'}}$ is an operator on ![]() $\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ given by
$\smash {\mathscr {H}_{{{\mathsf {x}}}}}$ given by
with the symbol
(see § 9 for examples). The corresponding average Wigner functions on ![]() $\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$ are
$\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$ are ![]() $\smash {\overline {{\mathsf {W}}}_s = \overline {{\mathsf {W}}}_s^{\text {(m)}} + \overline {{\mathsf {W}}}_s^{(\mu )}}$, where the index ‘m’ stands for ‘macroscopic’ and the index ‘
$\smash {\overline {{\mathsf {W}}}_s = \overline {{\mathsf {W}}}_s^{\text {(m)}} + \overline {{\mathsf {W}}}_s^{(\mu )}}$, where the index ‘m’ stands for ‘macroscopic’ and the index ‘![]() $\smash {\mu }$’ stands for ‘microscopic’. Because the dependence on
$\smash {\mu }$’ stands for ‘microscopic’. Because the dependence on ![]() $\smash {t}$ and
$\smash {t}$ and ![]() $\smash {{\boldsymbol {x}}}$ is slow, one can approximate them as follows:
$\smash {{\boldsymbol {x}}}$ is slow, one can approximate them as follows:
The matrix ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ is positive-semidefinite as an average Wigner tensor (§ 2.1.7), and so is
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ is positive-semidefinite as an average Wigner tensor (§ 2.1.7), and so is ![]() $\smash {{\boldsymbol {\mathfrak {W}}}}$ (§ 6.4). Hence, both
$\smash {{\boldsymbol {\mathfrak {W}}}}$ (§ 6.4). Hence, both ![]() $\smash {\overline {{\mathsf {W}}}_s^{\text {(m)}}}$ and
$\smash {\overline {{\mathsf {W}}}_s^{\text {(m)}}}$ and ![]() $\smash {\overline {{\mathsf {W}}}_s^{(\mu )}}$ are non-negative. Using (6.31), one can also rewrite the Wigner function of
$\smash {\overline {{\mathsf {W}}}_s^{(\mu )}}$ are non-negative. Using (6.31), one can also rewrite the Wigner function of ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {H}}_s}$ more compactly as
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {H}}_s}$ more compactly as
Now we can represent the nonlinear potentials (5.41)–(5.43) as
Here, the index ![]() $\smash {^{\text {(m)}}}$ denotes contributions from
$\smash {^{\text {(m)}}}$ denotes contributions from ![]() $\smash {\overline {{\mathsf {W}}}_s^{\text {(m)}}}$ and the index
$\smash {\overline {{\mathsf {W}}}_s^{\text {(m)}}}$ and the index ![]() $\smash {^{(\mu )}}$ denotes contributions from
$\smash {^{(\mu )}}$ denotes contributions from ![]() $\smash {\overline {{\mathsf {W}}}_s^{(\mu )}}$. Specifically,
$\smash {\overline {{\mathsf {W}}}_s^{(\mu )}}$. Specifically,
 \begin{align} {\boldsymbol{\Theta}}_s^{\text{(m)}} & =\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}} \overline{{\mathsf{W}}}_s^{\text{(m)}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}, \end{align}
\begin{align} {\boldsymbol{\Theta}}_s^{\text{(m)}} & =\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}} \overline{{\mathsf{W}}}_s^{\text{(m)}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}, \end{align} \begin{align} \varPhi_s^{\text{(m)}} & = \frac{1}{2}\frac{\partial}{\partial {\boldsymbol{p}}} \cdot {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\frac{{\boldsymbol{k}} \overline{{\mathsf{W}}}_s^{\text{(m)}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}. \end{align}
\begin{align} \varPhi_s^{\text{(m)}} & = \frac{1}{2}\frac{\partial}{\partial {\boldsymbol{p}}} \cdot {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\frac{{\boldsymbol{k}} \overline{{\mathsf{W}}}_s^{\text{(m)}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}. \end{align}
Here, ![]() $\smash {\overline {{\mathsf {W}}}_s^{\text {(m)}}}$ is a non-negative function (6.37a), so
$\smash {\overline {{\mathsf {W}}}_s^{\text {(m)}}}$ is a non-negative function (6.37a), so ![]() $\smash {{{\boldsymbol {\mathsf {D}}}}_s^{\text {(m)}}}$ is positive-semidefinite and leads to an
$\smash {{{\boldsymbol {\mathsf {D}}}}_s^{\text {(m)}}}$ is positive-semidefinite and leads to an ![]() $\smash {H}$-theorem similar to (5.46). One also has
$\smash {H}$-theorem similar to (5.46). One also has
 \begin{align} {\boldsymbol{\Theta}}_s^{(\mu)} &= \sum_{s'} \frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}} F_{s'}({\boldsymbol{p}}')}{{\boldsymbol{k}} \cdot ({\boldsymbol{v}}'_{s'} - {\boldsymbol{v}}_s) + \vartheta}\, |\mathcal{X}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') |^2 \right|_{\vartheta=0}, \end{align}
\begin{align} {\boldsymbol{\Theta}}_s^{(\mu)} &= \sum_{s'} \frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}} F_{s'}({\boldsymbol{p}}')}{{\boldsymbol{k}} \cdot ({\boldsymbol{v}}'_{s'} - {\boldsymbol{v}}_s) + \vartheta}\, |\mathcal{X}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') |^2 \right|_{\vartheta=0}, \end{align}
The functions ![]() $\smash {{\boldsymbol {\Theta }}_s^{(\mu )}}$ and
$\smash {{\boldsymbol {\Theta }}_s^{(\mu )}}$ and ![]() $\smash {\varPhi _s^{(\mu )}}$ scale as
$\smash {\varPhi _s^{(\mu )}}$ scale as ![]() $\smash {\overline {{\mathsf {W}}}_s^{(\mu )}}$, i.e. as
$\smash {\overline {{\mathsf {W}}}_s^{(\mu )}}$, i.e. as ![]() $\smash {\epsilon \varepsilon ^2}$ (§ 3.3). Their contribution to (5.37) is of order
$\smash {\epsilon \varepsilon ^2}$ (§ 3.3). Their contribution to (5.37) is of order ![]() $\smash {\epsilon {\boldsymbol {\Theta }}_s^{(\mu )}}$ and
$\smash {\epsilon {\boldsymbol {\Theta }}_s^{(\mu )}}$ and ![]() $\smash {\epsilon \varPhi _s^{(\mu )}}$, respectively, so it scales as
$\smash {\epsilon \varPhi _s^{(\mu )}}$, respectively, so it scales as ![]() $\smash {\epsilon ^2\varepsilon ^2}$ and therefore is negligible within our model. In contrast,
$\smash {\epsilon ^2\varepsilon ^2}$ and therefore is negligible within our model. In contrast, ![]() $\smash {{{\boldsymbol {\mathsf {D}}}}_s^{(\mu )}}$ must be retained alongside with
$\smash {{{\boldsymbol {\mathsf {D}}}}_s^{(\mu )}}$ must be retained alongside with ![]() $\smash {{{\boldsymbol {\mathsf {D}}}}_s^{\text {(m)}}}$. This is because although weak, macroscopic fluctuations can resonate with particles from the bulk distribution, while the stronger macroscopic fluctuations are assumed to resonate only with particles from the tail distribution, which are few.
$\smash {{{\boldsymbol {\mathsf {D}}}}_s^{\text {(m)}}}$. This is because although weak, macroscopic fluctuations can resonate with particles from the bulk distribution, while the stronger macroscopic fluctuations are assumed to resonate only with particles from the tail distribution, which are few.
6.6. Oscillation-centre Hamiltonian
Within the assumed accuracy, the OC Hamiltonian is ![]() $\smash {\mathcal {H}_s = \overline {H}_s + \varPhi _s^{\text {(m)}}}$, and
$\smash {\mathcal {H}_s = \overline {H}_s + \varPhi _s^{\text {(m)}}}$, and ![]() $\smash {\overline {H}_s}$ is given by (6.9). Combined with the general theorem (2.53c), the latter readily yields
$\smash {\overline {H}_s}$ is given by (6.9). Combined with the general theorem (2.53c), the latter readily yields ![]() $\smash {\overline {H}_s = H_{0s} + \phi _s}$, where
$\smash {\overline {H}_s = H_{0s} + \phi _s}$, where
and the contribution of ![]() $\smash {{\boldsymbol {\mathfrak {W}}}}$ has been neglected. Because both
$\smash {{\boldsymbol {\mathfrak {W}}}}$ has been neglected. Because both ![]() $\smash {\varPhi _s^{\text {(m)}}}$ and
$\smash {\varPhi _s^{\text {(m)}}}$ and ![]() $\smash {\phi _s}$ are quadratic in
$\smash {\phi _s}$ are quadratic in ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ and enter
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ and enter ![]() $\smash {\mathcal {H}_s}$ only in the combination
$\smash {\mathcal {H}_s}$ only in the combination ![]() $\smash {\varDelta _s \doteq \varPhi _s^{\text {(m)}} + \phi _s}$, it is convenient to attribute the latter as the ‘total’ ponderomotive energy. Using (6.42) in combination with (6.37a), one can express it as follows:
$\smash {\varDelta _s \doteq \varPhi _s^{\text {(m)}} + \phi _s}$, it is convenient to attribute the latter as the ‘total’ ponderomotive energy. Using (6.42) in combination with (6.37a), one can express it as follows:
(see § 9 for examples). Notably,
where ![]() $\smash {\delta /\delta F_s}$ denotes a functional derivative and
$\smash {\delta /\delta F_s}$ denotes a functional derivative and ![]() $\smash {S_{\text {ad}}}$ is the adiabatic action defined in (6.16). Equation (6.48) is a generalization of the well-known ‘
$\smash {S_{\text {ad}}}$ is the adiabatic action defined in (6.16). Equation (6.48) is a generalization of the well-known ‘![]() $\smash {K}$–
$\smash {K}$–![]() $\smash {\chi }$ theorem’ (Kaufman & Holm Reference Kaufman and Holm1984; Kaufman Reference Kaufman1987). Loosely speaking, it says that the coefficient connecting
$\smash {\chi }$ theorem’ (Kaufman & Holm Reference Kaufman and Holm1984; Kaufman Reference Kaufman1987). Loosely speaking, it says that the coefficient connecting ![]() $\smash {\varDelta _s}$ with
$\smash {\varDelta _s}$ with ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ is proportional to the linear polarizability of an individual particle of type
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ is proportional to the linear polarizability of an individual particle of type ![]() $\smash {s}$ (Dodin et al. Reference Dodin, Zhmoginov and Ruiz2017; Dodin & Fisch Reference Dodin and Fisch2010a) (‘
$\smash {s}$ (Dodin et al. Reference Dodin, Zhmoginov and Ruiz2017; Dodin & Fisch Reference Dodin and Fisch2010a) (‘![]() $\smash {K}$’ in the name of this theorem is the same as our
$\smash {K}$’ in the name of this theorem is the same as our ![]() $\smash {\varDelta _s}$, and ‘
$\smash {\varDelta _s}$, and ‘![]() $\smash {\chi }$’ is the linear susceptibility). Also, the OC Hamiltonian and the OC velocity can be expressed as
$\smash {\chi }$’ is the linear susceptibility). Also, the OC Hamiltonian and the OC velocity can be expressed as
6.7. Polarization drag
Within the assumed accuracy, the OC distribution can be expressed as
and (5.37) becomes
where we have reinstated the term ![]() $\smash {\varGamma _s}$ introduced in § 3.3. As a collisional term,
$\smash {\varGamma _s}$ introduced in § 3.3. As a collisional term, ![]() $\smash {\varGamma _s}$ is needed only to the zeroth order in
$\smash {\varGamma _s}$ is needed only to the zeroth order in ![]() $\smash {\epsilon }$, so
$\smash {\epsilon }$, so
Correlating with ![]() $\smash {g_s}$ is only the microscopic part of
$\smash {g_s}$ is only the microscopic part of ![]() $\smash {\widetilde {H}_s}$, so using (6.34) one obtains
$\smash {\widetilde {H}_s}$, so using (6.34) one obtains
Next, let us use (2.28) and ![]() $\smash {{\boldsymbol {\zeta }} = \operatorname {re} {\boldsymbol {\zeta }}}$ to express this result as follows:
$\smash {{\boldsymbol {\zeta }} = \operatorname {re} {\boldsymbol {\zeta }}}$ to express this result as follows:
 \begin{align} {\boldsymbol{\zeta}}_s & = \mathrm{i} \sum_{s'} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}'\,{\boldsymbol{k}} \star \mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}, {\boldsymbol{p}}, {\boldsymbol{p}}') \star {\boldsymbol{\mathfrak{G}}}_{s's}(\omega, {\boldsymbol{k}}, {\boldsymbol{p}}', {\boldsymbol{p}})\nonumber\\ & \approx \mathrm{i} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}'\,{\boldsymbol{k}} \mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}, {\boldsymbol{p}}, {\boldsymbol{p}}') \,(2{\rm \pi})^{{-}n}\delta({\boldsymbol{p}} - {\boldsymbol{p}}')\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,F_s({\boldsymbol{p}}) \nonumber\\ & ={-} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,{\boldsymbol{k}} \operatorname{im} \mathcal{X}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}, {\boldsymbol{p}}, {\boldsymbol{p}})\,F_s({\boldsymbol{p}}), \end{align}
\begin{align} {\boldsymbol{\zeta}}_s & = \mathrm{i} \sum_{s'} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}'\,{\boldsymbol{k}} \star \mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}, {\boldsymbol{p}}, {\boldsymbol{p}}') \star {\boldsymbol{\mathfrak{G}}}_{s's}(\omega, {\boldsymbol{k}}, {\boldsymbol{p}}', {\boldsymbol{p}})\nonumber\\ & \approx \mathrm{i} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}'\,{\boldsymbol{k}} \mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}, {\boldsymbol{p}}, {\boldsymbol{p}}') \,(2{\rm \pi})^{{-}n}\delta({\boldsymbol{p}} - {\boldsymbol{p}}')\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,F_s({\boldsymbol{p}}) \nonumber\\ & ={-} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,{\boldsymbol{k}} \operatorname{im} \mathcal{X}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}, {\boldsymbol{p}}, {\boldsymbol{p}})\,F_s({\boldsymbol{p}}), \end{align}
where we have approximated ![]() $\smash {\star }$ with the usual product and substituted (6.30). Hence,
$\smash {\star }$ with the usual product and substituted (6.30). Hence,
where ![]() $\smash {{\boldsymbol {\mathfrak {F}}}_s}$ can be interpreted as the polarization drag (i.e. the average force that is imposed on an OC by its dress) and is given by
$\smash {{\boldsymbol {\mathfrak {F}}}_s}$ can be interpreted as the polarization drag (i.e. the average force that is imposed on an OC by its dress) and is given by
Using (6.36), one also rewrite this as follows:
where we have substituted (6.26) for ![]() $\smash {({\boldsymbol {\varXi }}^{-1})_\text {A}}$. With (6.24) for
$\smash {({\boldsymbol {\varXi }}^{-1})_\text {A}}$. With (6.24) for ![]() $\smash {{\boldsymbol {\varXi }}_\text {A}}$, this yields
$\smash {{\boldsymbol {\varXi }}_\text {A}}$, this yields
 \begin{align} {\boldsymbol{\mathfrak{F}}}_s \approx \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi}\,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\,{\boldsymbol{k}}{\boldsymbol{k}}\cdot\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \nonumber\\ & \times {\boldsymbol{\alpha}}_s^{{\dagger}}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}) {\boldsymbol{\varXi}}^{{-}1}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}') \nonumber\\ & \times {\boldsymbol{\alpha}}_{s'}^{{\dagger}}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}') {\boldsymbol{\varXi}}^{-{{\dagger}}}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_s({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}). \end{align}
\begin{align} {\boldsymbol{\mathfrak{F}}}_s \approx \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi}\,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\,{\boldsymbol{k}}{\boldsymbol{k}}\cdot\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \nonumber\\ & \times {\boldsymbol{\alpha}}_s^{{\dagger}}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}) {\boldsymbol{\varXi}}^{{-}1}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}') \nonumber\\ & \times {\boldsymbol{\alpha}}_{s'}^{{\dagger}}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}') {\boldsymbol{\varXi}}^{-{{\dagger}}}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_s({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}). \end{align}
The product of the last two lines equals ![]() $\smash {|\mathcal {X}_{ss'}({\boldsymbol {k}} \cdot {\boldsymbol {v}}_{s}, {\boldsymbol {k}}; {\boldsymbol {p}}, {\boldsymbol {p}}')|^2}$. Hence,
$\smash {|\mathcal {X}_{ss'}({\boldsymbol {k}} \cdot {\boldsymbol {v}}_{s}, {\boldsymbol {k}}; {\boldsymbol {p}}, {\boldsymbol {p}}')|^2}$. Hence,
6.8. Collision operator
By combining (6.56) for ![]() $\smash {\varGamma _s}$ with (6.43) for
$\smash {\varGamma _s}$ with (6.43) for ![]() $\smash {{{\boldsymbol {\mathsf {D}}}}_s^{(\mu )}}$, one can express
$\smash {{{\boldsymbol {\mathsf {D}}}}_s^{(\mu )}}$, one can express ![]() $\smash {\mathcal {C}_s}$ as
$\smash {\mathcal {C}_s}$ as
 \begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}}\cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi} \,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, |\mathcal{X}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')|^2 \nonumber\\ &\times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right), \end{align}
\begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}}\cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi} \,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, |\mathcal{X}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')|^2 \nonumber\\ &\times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right), \end{align}
where ![]() $\mathcal {X}_{ss'}$ is given by (6.36). One can recognize this as a generalization of the Balescu–Lenard collision operator (Krall & Trivelpiece Reference Krall and Trivelpiece1973, § 11.11) to interactions via a general multi-component field
$\mathcal {X}_{ss'}$ is given by (6.36). One can recognize this as a generalization of the Balescu–Lenard collision operator (Krall & Trivelpiece Reference Krall and Trivelpiece1973, § 11.11) to interactions via a general multi-component field ![]() ${\boldsymbol {\varPsi }}$. Specific examples can be found in § 9.
${\boldsymbol {\varPsi }}$. Specific examples can be found in § 9.
It is readily seen that ![]() $\smash {\mathcal {C}_s}$ conserves particles, i.e.
$\smash {\mathcal {C}_s}$ conserves particles, i.e.
and vanishes in thermal equilibrium (§ 8.1). Other properties of ![]() $\smash {\mathcal {C}_s}$ are determined by the properties of the coupling coefficient
$\smash {\mathcal {C}_s}$ are determined by the properties of the coupling coefficient ![]() $\smash {\mathcal {X}_{ss'}}$, which are as follows. Note that
$\smash {\mathcal {X}_{ss'}}$, which are as follows. Note that
where we introduced
To calculate ![]() $\smash {\mathcal {R}_{ss'}}$, note that (6.36) yields
$\smash {\mathcal {R}_{ss'}}$, note that (6.36) yields
 \begin{align} |\mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')|^2 & \approx |{\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) {\boldsymbol{\varXi}}^{{-}1}(\omega, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}')|^2,\nonumber\\ |\mathcal{X}_{s's}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}', {\boldsymbol{p}})|^2 & \approx |{\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) {\boldsymbol{\varXi}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}')|^2, \end{align}
\begin{align} |\mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')|^2 & \approx |{\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) {\boldsymbol{\varXi}}^{{-}1}(\omega, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}')|^2,\nonumber\\ |\mathcal{X}_{s's}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}', {\boldsymbol{p}})|^2 & \approx |{\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) {\boldsymbol{\varXi}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}')|^2, \end{align}whence one obtains
 \begin{align} \mathcal{R}_{ss'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \approx 4\operatorname{im}\big(&{\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) ({\boldsymbol{\varXi}}^{{-}1})_\text{H}(\omega, {\boldsymbol{k}}){\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}')\nonumber\\ & {\boldsymbol{\alpha}}_{s'}^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') ({\boldsymbol{\varXi}}^{{-}1})_\text{A}(\omega, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') \big). \end{align}
\begin{align} \mathcal{R}_{ss'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \approx 4\operatorname{im}\big(&{\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) ({\boldsymbol{\varXi}}^{{-}1})_\text{H}(\omega, {\boldsymbol{k}}){\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}')\nonumber\\ & {\boldsymbol{\alpha}}_{s'}^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') ({\boldsymbol{\varXi}}^{{-}1})_\text{A}(\omega, {\boldsymbol{k}}) {\boldsymbol{\alpha}}_{s'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') \big). \end{align}
The operators ![]() $\smash {({\boldsymbol {\varXi }}^{-1})_\text {H}}$,
$\smash {({\boldsymbol {\varXi }}^{-1})_\text {H}}$, ![]() $\smash {({\boldsymbol {\varXi }}^{-1})_\text {A}}$ and
$\smash {({\boldsymbol {\varXi }}^{-1})_\text {A}}$ and ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s}$ (for all
$\smash {\widehat {\boldsymbol {\alpha }}_s}$ (for all ![]() $\smash {s}$) have been introduced for real fields, so their matrix elements in the coordinate representation are real. Then, the corresponding symbols satisfy
$\smash {s}$) have been introduced for real fields, so their matrix elements in the coordinate representation are real. Then, the corresponding symbols satisfy ![]() $\smash {{\boldsymbol {A}}(-\omega, -{\boldsymbol {k}}) = {\boldsymbol {A}}^*(\omega, {\boldsymbol {k}})}$, where
$\smash {{\boldsymbol {A}}(-\omega, -{\boldsymbol {k}}) = {\boldsymbol {A}}^*(\omega, {\boldsymbol {k}})}$, where ![]() $\smash {{\boldsymbol {A}}}$ is any of the three symbols. This gives
$\smash {{\boldsymbol {A}}}$ is any of the three symbols. This gives
Because the rest of the integrand in (6.61) is even in ![]() $\smash {{\boldsymbol {k}}}$, (6.68) signifies that
$\smash {{\boldsymbol {k}}}$, (6.68) signifies that ![]() $\smash {\mathcal {R}_{ss'}}$ does not contribute to
$\smash {\mathcal {R}_{ss'}}$ does not contribute to ![]() $\smash {\mathcal {C}_s}$. Thus,
$\smash {\mathcal {C}_s}$. Thus, ![]() $\smash {\mathcal {X}_{ss'}}$ in (6.61) can also be replaced with
$\smash {\mathcal {X}_{ss'}}$ in (6.61) can also be replaced with ![]() $\smash {\mathcal {Q}_{ss'}}$:
$\smash {\mathcal {Q}_{ss'}}$:
 \begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi} \,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, \mathcal{Q}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & \times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right). \end{align}
\begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi} \,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, \mathcal{Q}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & \times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right). \end{align}
In this representation, the coupling coefficient in ![]() $\smash {\mathcal {C}_s}$ is manifestly symmetric,
$\smash {\mathcal {C}_s}$ is manifestly symmetric,
which readily leads to momentum and energy conservation (Appendix C):Footnote 28
The collision operator ![]() $\smash {\mathcal {C}_s}$ also satisfies the
$\smash {\mathcal {C}_s}$ also satisfies the ![]() $\smash {H}$-theorem (Appendix C.3):
$\smash {H}$-theorem (Appendix C.3):
where the entropy density ![]() $\smash {\sigma }$ is defined as
$\smash {\sigma }$ is defined as
and ![]() $\smash {(\partial _t F_s)_{\text {coll}} \doteq \mathcal {C}_s}$. Note that these properties are not restricted to any particular
$\smash {(\partial _t F_s)_{\text {coll}} \doteq \mathcal {C}_s}$. Note that these properties are not restricted to any particular ![]() $\smash {\mathcal {H}_s}$. Also note that if applied in proper variables (§ 3.1.2), our formula (6.69) can describe collisions in strong background fields. This topic, including comparison with the relevant literature, is left to future work.
$\smash {\mathcal {H}_s}$. Also note that if applied in proper variables (§ 3.1.2), our formula (6.69) can describe collisions in strong background fields. This topic, including comparison with the relevant literature, is left to future work.
6.9. Summary of § 6
Let us summarize the above general results (for examples, see § 9). We consider species ![]() $\smash {s}$ governed by a Hamiltonian of the form
$\smash {s}$ governed by a Hamiltonian of the form
where ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ is a real oscillating field (of any dimension
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ is a real oscillating field (of any dimension ![]() $\smash {M}$), which generally consists of a macroscopic part
$\smash {M}$), which generally consists of a macroscopic part ![]() $\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ and a microscopic part
$\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}}}$ and a microscopic part ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$. The term
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$. The term ![]() $\smash {H_{0s}}$ is independent of
$\smash {H_{0s}}$ is independent of ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$, and the operators
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$, and the operators ![]() $\smash {\smash {\widehat {\boldsymbol {\alpha }}}_s^{{\dagger}} }$,
$\smash {\smash {\widehat {\boldsymbol {\alpha }}}_s^{{\dagger}} }$, ![]() $\smash {\widehat {\boldsymbol {L}}_s}$ and
$\smash {\widehat {\boldsymbol {L}}_s}$ and ![]() $\smash {\widehat {\boldsymbol {R}}_s}$ may be non-local in
$\smash {\widehat {\boldsymbol {R}}_s}$ may be non-local in ![]() $t$ and
$t$ and ![]() ${\boldsymbol {x}}$ and may depend on the momentum
${\boldsymbol {x}}$ and may depend on the momentum ![]() ${\boldsymbol {p}}$ parametrically. The dynamics of this system averaged over the fast oscillations can be described in terms of the OC distribution function
${\boldsymbol {p}}$ parametrically. The dynamics of this system averaged over the fast oscillations can be described in terms of the OC distribution function
(the index ![]() $\smash {^{\text {(m)}}}$ is henceforth omitted for brevity), which is governed by the following equation of the Fokker–Planck type:
$\smash {^{\text {(m)}}}$ is henceforth omitted for brevity), which is governed by the following equation of the Fokker–Planck type:
Here, ![]() $\smash {\mathcal {H}_s = H_{0s} + \varDelta _s}$ is the OC Hamiltonian,
$\smash {\mathcal {H}_s = H_{0s} + \varDelta _s}$ is the OC Hamiltonian, ![]() $\smash {{\boldsymbol {\Theta }}_s}$ is the dressing function and
$\smash {{\boldsymbol {\Theta }}_s}$ is the dressing function and ![]() $\smash {\varDelta _s}$ is the total ponderomotive energy (i.e. the part of the OC Hamiltonian that is quadratic in
$\smash {\varDelta _s}$ is the total ponderomotive energy (i.e. the part of the OC Hamiltonian that is quadratic in ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$), so
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$), so ![]() $\smash {{\boldsymbol {v}}_s(t, {\boldsymbol {x}}, {\boldsymbol {p}}) \doteq \partial _{\boldsymbol {p}}\mathcal {H}_s}$ is the OC velocity. Specifically,
$\smash {{\boldsymbol {v}}_s(t, {\boldsymbol {x}}, {\boldsymbol {p}}) \doteq \partial _{\boldsymbol {p}}\mathcal {H}_s}$ is the OC velocity. Specifically,
 \begin{align} \varDelta_s & = \frac{1}{2}\frac{\partial}{\partial {\boldsymbol{p}}} \cdot {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,{\boldsymbol{k}}\,\frac{\overline{{\mathsf{W}}}_s(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \nonumber\\ & \quad +\frac{1}{2}\int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\operatorname{tr}\big({{\boldsymbol {\mathsf{U}}}}{\boldsymbol{\wp}}_s\big)(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}; {\boldsymbol{p}}). \end{align}
\begin{align} \varDelta_s & = \frac{1}{2}\frac{\partial}{\partial {\boldsymbol{p}}} \cdot {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,{\boldsymbol{k}}\,\frac{\overline{{\mathsf{W}}}_s(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}; {\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \nonumber\\ & \quad +\frac{1}{2}\int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\operatorname{tr}\big({{\boldsymbol {\mathsf{U}}}}{\boldsymbol{\wp}}_s\big)(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}; {\boldsymbol{p}}). \end{align}
Here, ![]() $\smash {\overline {{\mathsf {W}}}_s = {\boldsymbol {\alpha }}_s^{{\dagger}} {{\boldsymbol {\mathsf {U}}}} {\boldsymbol {\alpha }}_s}$ is a scalar function, the average Wigner matrix
$\smash {\overline {{\mathsf {W}}}_s = {\boldsymbol {\alpha }}_s^{{\dagger}} {{\boldsymbol {\mathsf {U}}}} {\boldsymbol {\alpha }}_s}$ is a scalar function, the average Wigner matrix ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ is understood as the Fourier spectrum of the symmetrized autocorrelation matrix of the macroscopic oscillations:
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ is understood as the Fourier spectrum of the symmetrized autocorrelation matrix of the macroscopic oscillations:
with ![]() $\smash {n \doteq \dim {\boldsymbol {x}}}$. Also, the vector
$\smash {n \doteq \dim {\boldsymbol {x}}}$. Also, the vector ![]() $\smash {{\boldsymbol {\alpha }}_s(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}})}$ is the Weyl symbol of
$\smash {{\boldsymbol {\alpha }}_s(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}})}$ is the Weyl symbol of ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s}$ as defined in (2.26),
$\smash {\widehat {\boldsymbol {\alpha }}_s}$ as defined in (2.26), ![]() $\smash {{\boldsymbol {\wp }}_s(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}}) \approx ({\boldsymbol {L}}_s^{{\dagger}} {\boldsymbol {R}}_s)_\text {H}}$,
$\smash {{\boldsymbol {\wp }}_s(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}; {\boldsymbol {p}}) \approx ({\boldsymbol {L}}_s^{{\dagger}} {\boldsymbol {R}}_s)_\text {H}}$, ![]() $\smash {{\boldsymbol {L}}_s}$ and
$\smash {{\boldsymbol {L}}_s}$ and ![]() $\smash {{\boldsymbol {R}}_s}$ are the Weyl symbols of
$\smash {{\boldsymbol {R}}_s}$ are the Weyl symbols of ![]() $\smash {\widehat {\boldsymbol {L}}_s}$ and
$\smash {\widehat {\boldsymbol {L}}_s}$ and ![]() $\smash {\widehat {\boldsymbol {R}}_s}$, respectively, and
$\smash {\widehat {\boldsymbol {R}}_s}$, respectively, and ![]() $\smash {_\text {H}}$ denotes the Hermitian part. The matrix
$\smash {_\text {H}}$ denotes the Hermitian part. The matrix ![]() $\smash {{{\boldsymbol {\mathsf {D}}}}_s}$ is positive-semidefinite and satisfies an
$\smash {{{\boldsymbol {\mathsf {D}}}}_s}$ is positive-semidefinite and satisfies an ![]() $\smash {H}$-theorem of the form (5.46). Also,
$\smash {H}$-theorem of the form (5.46). Also, ![]() $\smash {\varDelta _s}$ satisfies the ‘
$\smash {\varDelta _s}$ satisfies the ‘![]() $\smash {K}$–
$\smash {K}$–![]() $\smash {\chi }$ theorem’
$\smash {\chi }$ theorem’
The matrix ![]() ${\boldsymbol {\varXi }}$ characterizes the collective plasma response to the field
${\boldsymbol {\varXi }}$ characterizes the collective plasma response to the field ![]() $\widetilde {{\boldsymbol {\varPsi }}}$ and is given by
$\widetilde {{\boldsymbol {\varPsi }}}$ and is given by
 \begin{equation} {\boldsymbol{\varXi}}\approx {\boldsymbol{\varXi}}_0 + \sum_s \int \mathrm{d}{\boldsymbol{p}}\, \Bigg( \frac{{\boldsymbol{\alpha}}_s({\boldsymbol{p}})\,{\boldsymbol{\alpha}}_s^{{\dagger}}({\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s({\boldsymbol{p}}) + \mathrm{i} 0}\, {\boldsymbol{k}}\cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}} - {\boldsymbol{\wp}}_s({\boldsymbol{p}})F_s({\boldsymbol{p}}) \Bigg). \end{equation}
\begin{equation} {\boldsymbol{\varXi}}\approx {\boldsymbol{\varXi}}_0 + \sum_s \int \mathrm{d}{\boldsymbol{p}}\, \Bigg( \frac{{\boldsymbol{\alpha}}_s({\boldsymbol{p}})\,{\boldsymbol{\alpha}}_s^{{\dagger}}({\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s({\boldsymbol{p}}) + \mathrm{i} 0}\, {\boldsymbol{k}}\cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}} - {\boldsymbol{\wp}}_s({\boldsymbol{p}})F_s({\boldsymbol{p}}) \Bigg). \end{equation}
Here, the arguments ![]() $\smash {(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})}$ are omitted for brevity,
$\smash {(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})}$ are omitted for brevity, ![]() $\smash {{\boldsymbol {\alpha }}_s{\boldsymbol {\alpha }}_s^{{\dagger}} }$ is a dyadic matrix and
$\smash {{\boldsymbol {\alpha }}_s{\boldsymbol {\alpha }}_s^{{\dagger}} }$ is a dyadic matrix and ![]() $\smash {{\boldsymbol {\varXi }}_0}$ is the symbol of the Hermitian dispersion operator
$\smash {{\boldsymbol {\varXi }}_0}$ is the symbol of the Hermitian dispersion operator ![]() $\smash {\widehat {\boldsymbol {\varXi }}_0}$ that governs the field
$\smash {\widehat {\boldsymbol {\varXi }}_0}$ that governs the field ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ in the absence of plasma. Specifically,
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ in the absence of plasma. Specifically, ![]() $\smash {\widehat {\boldsymbol {\varXi }}_0}$ is defined such that the field Lagrangian density without plasma is
$\smash {\widehat {\boldsymbol {\varXi }}_0}$ is defined such that the field Lagrangian density without plasma is ![]() $\smash {\mathfrak {L}_0 = \smash {\widetilde {{\boldsymbol {\varPsi }}}}^{{\dagger}} \widehat {\boldsymbol {\varXi }}_0 \widetilde {{\boldsymbol {\varPsi }}}/2}$.
$\smash {\mathfrak {L}_0 = \smash {\widetilde {{\boldsymbol {\varPsi }}}}^{{\dagger}} \widehat {\boldsymbol {\varXi }}_0 \widetilde {{\boldsymbol {\varPsi }}}/2}$.
The spectrum of microscopic fluctuations (specifically, the spectrum of the symmetrized autocorrelation function of the microscopic field ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$) is a positive-semidefinite matrix function and given by
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}}$) is a positive-semidefinite matrix function and given by
 \begin{align} {\boldsymbol{\mathfrak{W}}}(\omega, {\boldsymbol{k}}) = \frac{1}{(2{\rm \pi})^{n}} \sum_{s'}\int \mathrm{d}{\boldsymbol{p}}'\,&\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})F_{s'}({\boldsymbol{p}}') \nonumber\\ &\times {\boldsymbol{\varXi}}^{{-}1}(\omega, {\boldsymbol{k}}) ({\boldsymbol{\alpha}}_{s'}{\boldsymbol{\alpha}}_{s'}^{{\dagger}})(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') {\boldsymbol{\varXi}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}), \end{align}
\begin{align} {\boldsymbol{\mathfrak{W}}}(\omega, {\boldsymbol{k}}) = \frac{1}{(2{\rm \pi})^{n}} \sum_{s'}\int \mathrm{d}{\boldsymbol{p}}'\,&\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})F_{s'}({\boldsymbol{p}}') \nonumber\\ &\times {\boldsymbol{\varXi}}^{{-}1}(\omega, {\boldsymbol{k}}) ({\boldsymbol{\alpha}}_{s'}{\boldsymbol{\alpha}}_{s'}^{{\dagger}})(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}') {\boldsymbol{\varXi}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}), \end{align}
where ![]() $\smash {{\boldsymbol {v}}'_{s'} \doteq {\boldsymbol {v}}_{s'}({\boldsymbol {p}}')}$. (The dependence on t and
$\smash {{\boldsymbol {v}}'_{s'} \doteq {\boldsymbol {v}}_{s'}({\boldsymbol {p}}')}$. (The dependence on t and ![]() $\boldsymbol{x}$ is assumed too but not emphasized.) The microscopic fluctuations give rise to a collision operator of the Balescu–Lenard type:
$\boldsymbol{x}$ is assumed too but not emphasized.) The microscopic fluctuations give rise to a collision operator of the Balescu–Lenard type:
 \begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}}\cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi} \,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, \mathcal{Q}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')\nonumber\\ &\times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right), \end{align}
\begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}}\cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\, &{\rm \pi} \,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, \mathcal{Q}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s}, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')\nonumber\\ &\times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right), \end{align}
where the coupling coefficient ![]() $\smash {\mathcal {Q}_{ss'}(\omega, {\boldsymbol {k}}; {\boldsymbol {p}}, {\boldsymbol {p}}') = \mathcal {Q}_{s's}(\omega, {\boldsymbol {k}}; {\boldsymbol {p}}', {\boldsymbol {p}})}$ is given by
$\smash {\mathcal {Q}_{ss'}(\omega, {\boldsymbol {k}}; {\boldsymbol {p}}, {\boldsymbol {p}}') = \mathcal {Q}_{s's}(\omega, {\boldsymbol {k}}; {\boldsymbol {p}}', {\boldsymbol {p}})}$ is given by
The operator ![]() $\smash {\mathcal {C}_s}$ satisfies the
$\smash {\mathcal {C}_s}$ satisfies the ![]() $\smash {H}$-theorem and conserves particles, momentum and energy
$\smash {H}$-theorem and conserves particles, momentum and energy
7. Interaction with on-shell waves
Here, we discuss QL interaction of plasma with ‘on-shell’ waves, i.e. waves constrained by dispersion relations. To motivate the assumptions that will be adopted, and also to systematically introduce our notation, we start with briefly overviewing theory of linear waves in dispersive media (Whitham Reference Whitham1974; Tracy et al. Reference Tracy, Brizard, Richardson and Kaufman2014), including monochromatic waves (§ 7.1), conservative eikonal waves (§ 7.2), general eikonal waves (§ 7.3) and general broadband waves described by the WKE (§ 7.4). After that, we derive conservation laws for the total momentum and energy, which are exact within our model (§ 7.5). All waves in this section are considered macroscopic, so we adopt a simplified notation ![]() $\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}} \equiv \widetilde {{\boldsymbol {\varPsi }}}}$ and the index
$\smash {\underline {\widetilde {{\boldsymbol {\varPsi }}}} \equiv \widetilde {{\boldsymbol {\varPsi }}}}$ and the index ![]() $\smash {^{(\text {m})}}$ will be omitted.
$\smash {^{(\text {m})}}$ will be omitted.
7.1. Monochromatic waves
Conservative (non-dissipative) waves can be described using the least-action principle ![]() $\delta S = 0$. Assuming the notation as in § 6.2, the action integral can be expressed as
$\delta S = 0$. Assuming the notation as in § 6.2, the action integral can be expressed as ![]() $S = \int \mathrm {d}{\boldsymbol {\mathsf {x}}}\,\mathfrak {L}$ with the Lagrangian density given by
$S = \int \mathrm {d}{\boldsymbol {\mathsf {x}}}\,\mathfrak {L}$ with the Lagrangian density given by
First, let us assume a homogeneous stationary medium, so ![]() $\smash {{\boldsymbol {\varXi }}_\text {H}(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}) = {\boldsymbol {\varXi }}_\text {H}(\omega, {\boldsymbol {k}})}$. Because we assume real fields,Footnote 29
$\smash {{\boldsymbol {\varXi }}_\text {H}(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}) = {\boldsymbol {\varXi }}_\text {H}(\omega, {\boldsymbol {k}})}$. Because we assume real fields,Footnote 29 ![]() $\smash {\left\langle {t_1, {\boldsymbol {x}}_1 |\widehat {\boldsymbol {\varXi }}|t_2, {\boldsymbol {x}}_2}\right\rangle}$ is real for all
$\smash {\left\langle {t_1, {\boldsymbol {x}}_1 |\widehat {\boldsymbol {\varXi }}|t_2, {\boldsymbol {x}}_2}\right\rangle}$ is real for all ![]() $\smash {(t_1, {\boldsymbol {x}}_1, t_2, {\boldsymbol {x}}_2)}$, one also has
$\smash {(t_1, {\boldsymbol {x}}_1, t_2, {\boldsymbol {x}}_2)}$, one also has
where the latter equality is due to ![]() $\smash {{\boldsymbol {\varXi }}_\text {H}^{{\dagger}} (\omega, {\boldsymbol {k}}) = {\boldsymbol {\varXi }}_\text {H}(\omega, {\boldsymbol {k}})}$.
$\smash {{\boldsymbol {\varXi }}_\text {H}^{{\dagger}} (\omega, {\boldsymbol {k}}) = {\boldsymbol {\varXi }}_\text {H}(\omega, {\boldsymbol {k}})}$.
Because ![]() ${\boldsymbol {\varXi }}_\text {H}(\omega, {\boldsymbol {k}})$ is Hermitian, it has
${\boldsymbol {\varXi }}_\text {H}(\omega, {\boldsymbol {k}})$ is Hermitian, it has ![]() $M \doteq \dim {\boldsymbol {\varXi }}_\text {H}$ orthonormal eigenvectors
$M \doteq \dim {\boldsymbol {\varXi }}_\text {H}$ orthonormal eigenvectors ![]() ${\boldsymbol {\eta }}_b$:
${\boldsymbol {\eta }}_b$:
Here, ![]() $\smash {\varLambda _b}$ are the corresponding eigenvalues, which are real and satisfy
$\smash {\varLambda _b}$ are the corresponding eigenvalues, which are real and satisfy
Due to (7.2), one has
where ![]() $\text {eigv}_b$ stands for the
$\text {eigv}_b$ stands for the ![]() $b$th eigenvalue. Using this together with (7.2), one obtains from (7.3) that
$b$th eigenvalue. Using this together with (7.2), one obtains from (7.3) that
whence
Let us consider a monochromatic wave of the form
with real frequency ![]() $\overline {\omega }$, real wavevector
$\overline {\omega }$, real wavevector ![]() $\overline {{\boldsymbol {k}}}$ and complex amplitude
$\overline {{\boldsymbol {k}}}$ and complex amplitude ![]() ${\breve {{\boldsymbol {\varPsi }}}}$. For such a wave, the action integral can be expressed as
${\breve {{\boldsymbol {\varPsi }}}}$. For such a wave, the action integral can be expressed as ![]() $\smash {S = \int \mathrm {d}{\boldsymbol {\mathsf {x}}}\,\overline {\mathfrak {L}}}$, where the average Lagrangian density
$\smash {S = \int \mathrm {d}{\boldsymbol {\mathsf {x}}}\,\overline {\mathfrak {L}}}$, where the average Lagrangian density ![]() $\overline {\mathfrak {L}}$ is given byFootnote 30
$\overline {\mathfrak {L}}$ is given byFootnote 30
Let us decompose ![]() ${\breve {{\boldsymbol {\varPsi }}}}$ in the basis formed by the eigenvectors
${\breve {{\boldsymbol {\varPsi }}}}$ in the basis formed by the eigenvectors ![]() $\smash {{\boldsymbol {\eta }}_b}$, that is, as
$\smash {{\boldsymbol {\eta }}_b}$, that is, as
Then, (7.9) becomes
The real and imaginary parts of the amplitudes ![]() ${\breve {a}}^b$ can be treated as independent variables. This is equivalent to treating
${\breve {a}}^b$ can be treated as independent variables. This is equivalent to treating ![]() ${\breve {a}}^{b*}$ and
${\breve {a}}^{b*}$ and ![]() ${\breve {a}}^b$ as independent variables, so one arrives at the following Euler–Lagrange equations:
${\breve {a}}^b$ as independent variables, so one arrives at the following Euler–Lagrange equations:
Hence the ![]() $b$th mode with a non-zero amplitude
$b$th mode with a non-zero amplitude ![]() ${\breve {a}}^b$ satisfies the dispersion relation
${\breve {a}}^b$ satisfies the dispersion relation
Equation (7.13) determines a dispersion surface in the ![]() ${\boldsymbol {\mathsf {k}}}$ space where the waves can have non-zero amplitude. This surface is sometimes called a shell, so waves constrained by a dispersion relation are called on-shell. Also note that combining (7.13) with (7.3) yields that on-shell waves satisfy
${\boldsymbol {\mathsf {k}}}$ space where the waves can have non-zero amplitude. This surface is sometimes called a shell, so waves constrained by a dispersion relation are called on-shell. Also note that combining (7.13) with (7.3) yields that on-shell waves satisfy
which are two mutually adjoint representations of the same equation.
Below, we consider the case when (7.13) is satisfied only for one mode at a time, so summation over ![]() $b$ and the index
$b$ and the index ![]() $b$ itself can be omitted. (A more general case is discussed, for example, in Dodin et al. (Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019).) Then,
$b$ itself can be omitted. (A more general case is discussed, for example, in Dodin et al. (Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019).) Then, ![]() $\smash {{\breve {{\boldsymbol {\varPsi }}}} = {\boldsymbol {\eta }}(\overline {\omega }, \overline {{\boldsymbol {k}}}){\breve {a}}}$,
$\smash {{\breve {{\boldsymbol {\varPsi }}}} = {\boldsymbol {\eta }}(\overline {\omega }, \overline {{\boldsymbol {k}}}){\breve {a}}}$,
and ![]() $\overline {\omega }$ is connected with
$\overline {\omega }$ is connected with ![]() $\overline {{\boldsymbol {k}}}$ via
$\overline {{\boldsymbol {k}}}$ via ![]() $\smash {\overline {\omega } = w(\overline {{\boldsymbol {k}}})}$, where
$\smash {\overline {\omega } = w(\overline {{\boldsymbol {k}}})}$, where ![]() $w({\boldsymbol {k}}) = -w(-{\boldsymbol {k}})$ is the function that solves
$w({\boldsymbol {k}}) = -w(-{\boldsymbol {k}})$ is the function that solves ![]() $\varLambda (w({\boldsymbol {k}}), {\boldsymbol {k}}) = 0$. Also importantly, (7.14) ensures that
$\varLambda (w({\boldsymbol {k}}), {\boldsymbol {k}}) = 0$. Also importantly, (7.14) ensures that
 \begin{align} \partial_{\unicode{x25AA}} \varLambda(\overline{\omega}, \overline{{\boldsymbol{k}}}) & = ((\partial_{\unicode{x25AA}} {\boldsymbol{\eta}}^{{\dagger}}) {\boldsymbol{\varXi}}_\text{H}{\boldsymbol{\eta}} + {\boldsymbol{\eta}}^{{\dagger}}(\partial_{\unicode{x25AA}} {\boldsymbol{\varXi}}_\text{H}){\boldsymbol{\eta}} + {\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\varXi}}_\text{H}(\partial_{\unicode{x25AA}} {\boldsymbol{\eta}}))\big|_{(\omega, {\boldsymbol{k}}) = (\overline{\omega}, \overline{{\boldsymbol{k}}})} \nonumber\\ & = ({\boldsymbol{\eta}}^{{\dagger}}(\partial_{\unicode{x25AA}} {\boldsymbol{\varXi}}_\text{H}){\boldsymbol{\eta}})\big|_{(\omega, {\boldsymbol{k}}) = (\overline{\omega}, \overline{{\boldsymbol{k}}})}, \end{align}
\begin{align} \partial_{\unicode{x25AA}} \varLambda(\overline{\omega}, \overline{{\boldsymbol{k}}}) & = ((\partial_{\unicode{x25AA}} {\boldsymbol{\eta}}^{{\dagger}}) {\boldsymbol{\varXi}}_\text{H}{\boldsymbol{\eta}} + {\boldsymbol{\eta}}^{{\dagger}}(\partial_{\unicode{x25AA}} {\boldsymbol{\varXi}}_\text{H}){\boldsymbol{\eta}} + {\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\varXi}}_\text{H}(\partial_{\unicode{x25AA}} {\boldsymbol{\eta}}))\big|_{(\omega, {\boldsymbol{k}}) = (\overline{\omega}, \overline{{\boldsymbol{k}}})} \nonumber\\ & = ({\boldsymbol{\eta}}^{{\dagger}}(\partial_{\unicode{x25AA}} {\boldsymbol{\varXi}}_\text{H}){\boldsymbol{\eta}})\big|_{(\omega, {\boldsymbol{k}}) = (\overline{\omega}, \overline{{\boldsymbol{k}}})}, \end{align}
where ![]() $\smash {{\unicode{x25AA}} }$ can be replaced with any variable.
$\smash {{\unicode{x25AA}} }$ can be replaced with any variable.
7.2. Conservative eikonal waves
7.2.1. Basic properties
In case of a quasimonochromatic eikonal wave and, possibly, inhomogeneous non-stationary plasma, one can apply the same arguments as in § 7.1 except the above equalities are now satisfied up to ![]() $\smash {\mathcal {O}(\epsilon )}$. For a single-mode wave, one has
$\smash {\mathcal {O}(\epsilon )}$. For a single-mode wave, one has
where the local frequency and the wavevector,
are slow functions of ![]() $\smash {(t, {\boldsymbol {x}})}$, and so is
$\smash {(t, {\boldsymbol {x}})}$, and so is ![]() $\smash {{\boldsymbol {\eta }}(t, {\boldsymbol {x}}) \doteq {\boldsymbol {\eta }}(t, {\boldsymbol {x}}, \overline {\omega }(t, {\boldsymbol {x}}), \overline {{\boldsymbol {k}}}(t, {\boldsymbol {x}}))}$, which satisfies (7.3). Then,
$\smash {{\boldsymbol {\eta }}(t, {\boldsymbol {x}}) \doteq {\boldsymbol {\eta }}(t, {\boldsymbol {x}}, \overline {\omega }(t, {\boldsymbol {x}}), \overline {{\boldsymbol {k}}}(t, {\boldsymbol {x}}))}$, which satisfies (7.3). Then,
Within the leading-order theory, the term ![]() $\smash {\mathcal {O}(\epsilon )}$ is neglected.Footnote 31 Then, the least-action principle
$\smash {\mathcal {O}(\epsilon )}$ is neglected.Footnote 31 Then, the least-action principle
leads to the same (but now local) dispersion relation as for monochromatic waves, ![]() $\smash {\varLambda (t, {\boldsymbol {x}}, \overline {\omega }, \overline {{\boldsymbol {k}}}) = 0}$. This shows that quasimonochromatic waves are also on-shell, and thus they satisfy (7.16) as well. Also notice that the dispersion relation can now be understood as a Hamilton–Jacobi equation for the eikonal phase
$\smash {\varLambda (t, {\boldsymbol {x}}, \overline {\omega }, \overline {{\boldsymbol {k}}}) = 0}$. This shows that quasimonochromatic waves are also on-shell, and thus they satisfy (7.16) as well. Also notice that the dispersion relation can now be understood as a Hamilton–Jacobi equation for the eikonal phase ![]() $\smash {\theta }$:
$\smash {\theta }$:
Like in the previous section, let us introduce the function ![]() $\smash {w}$ that solves
$\smash {w}$ that solves
and therefore satisfies
Differentiating (7.22) with respect to ![]() $t$,
$t$, ![]() ${\boldsymbol {x}}$ and
${\boldsymbol {x}}$ and ![]() ${\boldsymbol {k}}$ leads to
${\boldsymbol {k}}$ leads to
where the derivatives of ![]() $\varLambda$ are evaluated at
$\varLambda$ are evaluated at ![]() $\smash {(t, {\boldsymbol {x}}, w(t, {\boldsymbol {x}}, {\boldsymbol {k}}), {\boldsymbol {k}})}$. In particular, (7.24c) gives
$\smash {(t, {\boldsymbol {x}}, w(t, {\boldsymbol {x}}, {\boldsymbol {k}}), {\boldsymbol {k}})}$. In particular, (7.24c) gives
for the group velocity ![]() $\smash {{\boldsymbol {v}}_{\text {g}}}$, whose physical meaning is to be specified shortly.
$\smash {{\boldsymbol {v}}_{\text {g}}}$, whose physical meaning is to be specified shortly.
Because ![]() $\theta$ is now an additional dynamical variable, one also obtains an additional Euler–Lagrange equation
$\theta$ is now an additional dynamical variable, one also obtains an additional Euler–Lagrange equation
where ![]() $\mathcal {I}$ is called the action density and
$\mathcal {I}$ is called the action density and ![]() ${\boldsymbol {\mathcal {J}}}$ is the action flux density:
${\boldsymbol {\mathcal {J}}}$ is the action flux density:
where we used (7.16) and the derivatives are evaluated on ![]() $\smash {(t, {\boldsymbol {x}}, w(t, {\boldsymbol {x}}, \overline {{\boldsymbol {k}}}(t, {\boldsymbol {x}})), \overline {{\boldsymbol {k}}}(t, {\boldsymbol {x}}))}$. Using (7.25), one can also rewrite (7.28) as
$\smash {(t, {\boldsymbol {x}}, w(t, {\boldsymbol {x}}, \overline {{\boldsymbol {k}}}(t, {\boldsymbol {x}})), \overline {{\boldsymbol {k}}}(t, {\boldsymbol {x}}))}$. Using (7.25), one can also rewrite (7.28) as
(The arguments ![]() $(t, {\boldsymbol {x}})$ will be omitted from now on for brevity. We will also use
$(t, {\boldsymbol {x}})$ will be omitted from now on for brevity. We will also use ![]() $({\boldsymbol {k}})$ as a shorthand for
$({\boldsymbol {k}})$ as a shorthand for ![]() $(w({\boldsymbol {k}}), {\boldsymbol {k}})$ where applicable.) Then, (7.26) becomes
$(w({\boldsymbol {k}}), {\boldsymbol {k}})$ where applicable.) Then, (7.26) becomes
which can be a understood as a continuity equation for quasiparticles (‘photons’ or, more generally, ‘wave quanta’) with density ![]() $\smash {\mathcal {I}}$ and fluid velocity
$\smash {\mathcal {I}}$ and fluid velocity ![]() $\smash {\overline {{\boldsymbol {v}}}_{\text {g}}}$ (see also § 7.2.2). Thus, if an eikonal wave satisfies the least-action principle, its total action
$\smash {\overline {{\boldsymbol {v}}}_{\text {g}}}$ (see also § 7.2.2). Thus, if an eikonal wave satisfies the least-action principle, its total action ![]() $\smash {\int \mathrm {d}{\boldsymbol {x}}\,\mathcal {I}}$ (‘number of quanta’) is an invariant. This conservation law can be attributed to the fact that the wave Lagrangian density
$\smash {\int \mathrm {d}{\boldsymbol {x}}\,\mathcal {I}}$ (‘number of quanta’) is an invariant. This conservation law can be attributed to the fact that the wave Lagrangian density ![]() $\smash {\overline {\mathfrak {L}}}$ depends on derivatives of
$\smash {\overline {\mathfrak {L}}}$ depends on derivatives of ![]() $\smash {\theta }$ but not on
$\smash {\theta }$ but not on ![]() $\smash {\theta }$ per se.
$\smash {\theta }$ per se.
Also notice the following. By expanding (7.19) in ![]() $\smash {\partial _t \theta }$ around
$\smash {\partial _t \theta }$ around ![]() $\smash {\partial _t \theta = -w(t, {\boldsymbol {x}}, \partial _{{\boldsymbol {x}}}\theta )}$, which is satisfied on any solution, one obtains
$\smash {\partial _t \theta = -w(t, {\boldsymbol {x}}, \partial _{{\boldsymbol {x}}}\theta )}$, which is satisfied on any solution, one obtains
where we used that ![]() $\smash {\overline {\mathfrak {L}}(t, {\boldsymbol {x}}, -\partial _t\theta, \partial _{{\boldsymbol {x}}}\theta ) = 0}$ due to (7.21). Then, one arrives at the canonical form of the action integral (Hayes Reference Hayes1973)
$\smash {\overline {\mathfrak {L}}(t, {\boldsymbol {x}}, -\partial _t\theta, \partial _{{\boldsymbol {x}}}\theta ) = 0}$ due to (7.21). Then, one arrives at the canonical form of the action integral (Hayes Reference Hayes1973)
From here, ![]() $\smash {\delta _{\mathcal {I}} S = 0}$ yields the dispersion relation in the Hamilton–Jacobi form
$\smash {\delta _{\mathcal {I}} S = 0}$ yields the dispersion relation in the Hamilton–Jacobi form ![]() $\smash {\partial _t \theta + w(t, {\boldsymbol {x}}, {\boldsymbol {k}}) = 0}$, and
$\smash {\partial _t \theta + w(t, {\boldsymbol {x}}, {\boldsymbol {k}}) = 0}$, and ![]() $\smash {\delta _{\theta} S = 0}$ yields the action conservation (7.30).
$\smash {\delta _{\theta} S = 0}$ yields the action conservation (7.30).
7.2.2. Ray equations
By (7.18), one has the so-called consistency relations
These lead to
 \begin{align} \bigg(\frac{\partial}{\partial t} & + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\bigg) \overline{k}_i(t, {\boldsymbol{x}}) ={-} \frac{\partial w(t, {\boldsymbol{x}}, \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}}))}{\partial x^i} + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial \overline{k}_i(t, {\boldsymbol{x}})}{\partial {\boldsymbol{x}}} \nonumber\\ & ={-} \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i} \right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})} - \overline{v}_{\text{g}}^j\,\frac{\partial \overline{k}_j(t, {\boldsymbol{x}})}{\partial x^i} + \overline{v}_{\text{g}}^j\, \frac{\partial \overline{k}_i(t, {\boldsymbol{x}})}{\partial x^j} \nonumber\\ & ={-} \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}, \end{align}
\begin{align} \bigg(\frac{\partial}{\partial t} & + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\bigg) \overline{k}_i(t, {\boldsymbol{x}}) ={-} \frac{\partial w(t, {\boldsymbol{x}}, \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}}))}{\partial x^i} + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial \overline{k}_i(t, {\boldsymbol{x}})}{\partial {\boldsymbol{x}}} \nonumber\\ & ={-} \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i} \right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})} - \overline{v}_{\text{g}}^j\,\frac{\partial \overline{k}_j(t, {\boldsymbol{x}})}{\partial x^i} + \overline{v}_{\text{g}}^j\, \frac{\partial \overline{k}_i(t, {\boldsymbol{x}})}{\partial x^j} \nonumber\\ & ={-} \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}, \end{align}and similarly,
 \begin{align} \bigg(\frac{\partial}{\partial t} & + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\bigg) \overline{\omega}(t, {\boldsymbol{x}}) = \bigg(\frac{\partial}{\partial t} + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\bigg) w(t, {\boldsymbol{x}}, \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})) \nonumber\\ & = \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial t} + \overline{v}_{\text{g}}^i\, \frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})} + \overline{v}_{\text{g}}^i \left(\frac{\partial}{\partial t}+ \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\right) \overline{k}_i(t, {\boldsymbol{x}})\nonumber\\ & = \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial t}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}, \end{align}
\begin{align} \bigg(\frac{\partial}{\partial t} & + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\bigg) \overline{\omega}(t, {\boldsymbol{x}}) = \bigg(\frac{\partial}{\partial t} + \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\bigg) w(t, {\boldsymbol{x}}, \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})) \nonumber\\ & = \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial t} + \overline{v}_{\text{g}}^i\, \frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})} + \overline{v}_{\text{g}}^i \left(\frac{\partial}{\partial t}+ \overline{{\boldsymbol{v}}}_{\text{g}} \cdot \frac{\partial}{\partial {\boldsymbol{x}}}\right) \overline{k}_i(t, {\boldsymbol{x}})\nonumber\\ & = \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial t}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}, \end{align}where we used (7.34). Using the convective derivative associated with the group velocity,
one can rewrite these compactly as
 \begin{equation} \frac{\mathrm{d}\overline{k}_i(t, {\boldsymbol{x}})}{\mathrm{d} t} ={-} \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}, \quad \frac{\mathrm{d}\overline{\omega}(t, {\boldsymbol{x}})}{\mathrm{d} t} = \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial t}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}. \end{equation}
\begin{equation} \frac{\mathrm{d}\overline{k}_i(t, {\boldsymbol{x}})}{\mathrm{d} t} ={-} \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial x^i}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}, \quad \frac{\mathrm{d}\overline{\omega}(t, {\boldsymbol{x}})}{\mathrm{d} t} = \left(\frac{\partial w(t, {\boldsymbol{x}}, {\boldsymbol{k}})}{\partial t}\right)_{{\boldsymbol{k}} = \overline{{\boldsymbol{k}}}(t, {\boldsymbol{x}})}. \end{equation}
One can also represent (7.37) as ordinary differential equations for ![]() $\smash {\overline {{\boldsymbol {k}}}(t) \doteq \overline {{\boldsymbol {k}}}(t, \overline {{\boldsymbol {x}}}(t))}$ and
$\smash {\overline {{\boldsymbol {k}}}(t) \doteq \overline {{\boldsymbol {k}}}(t, \overline {{\boldsymbol {x}}}(t))}$ and ![]() $\smash {\overline {\omega }(t) \doteq \overline {\omega }(t, \overline {{\boldsymbol {x}}}(t))}$, where
$\smash {\overline {\omega }(t) \doteq \overline {\omega }(t, \overline {{\boldsymbol {x}}}(t))}$, where ![]() $\smash {\overline {{\boldsymbol {x}}}(t)}$ are the ‘ray trajectories’ governed by
$\smash {\overline {{\boldsymbol {x}}}(t)}$ are the ‘ray trajectories’ governed by
Specifically, together with (7.38), equations (7.37) become Hamilton's equations also known as the ray equations:
where ![]() $\smash {\overline {{\boldsymbol {x}}}}$ is the coordinate,
$\smash {\overline {{\boldsymbol {x}}}}$ is the coordinate, ![]() $\smash {\hbar \overline {{\boldsymbol {k}}}}$ is the momentum,
$\smash {\hbar \overline {{\boldsymbol {k}}}}$ is the momentum, ![]() $\smash {\hbar \overline {\omega }}$ is the energy,
$\smash {\hbar \overline {\omega }}$ is the energy, ![]() $\smash {\hbar w}$ is the Hamiltonian and the constant factor
$\smash {\hbar w}$ is the Hamiltonian and the constant factor ![]() $\smash {\hbar }$ can be anything. If
$\smash {\hbar }$ can be anything. If ![]() $\smash {\hbar }$ is chosen to be the Planck constant, then (7.39) can be interpreted as the motion equations of individual wave quanta, for example, photons. Hamilton's equations for ‘true’ particles, such as electrons and ions, are also subsumed under (7.39) in that they can be understood as the ray equations of the particles considered as quantum-matter waves in the semiclassical limit.
$\smash {\hbar }$ is chosen to be the Planck constant, then (7.39) can be interpreted as the motion equations of individual wave quanta, for example, photons. Hamilton's equations for ‘true’ particles, such as electrons and ions, are also subsumed under (7.39) in that they can be understood as the ray equations of the particles considered as quantum-matter waves in the semiclassical limit.
Also notably, (7.39) can be obtained by considering the point-particle limit of (7.32) (Ruiz & Dodin Reference Ruiz and Dodin2015b). Specifically, adopting ![]() $\smash {\mathcal {I}(t, {\boldsymbol {x}}) \,\propto \, \delta ({\boldsymbol {x}} - \overline {{\boldsymbol {x}}}(t))}$ and taking the integral in (7.32) by parts leads to a canonical action
$\smash {\mathcal {I}(t, {\boldsymbol {x}}) \,\propto \, \delta ({\boldsymbol {x}} - \overline {{\boldsymbol {x}}}(t))}$ and taking the integral in (7.32) by parts leads to a canonical action ![]() $\smash {S\, \propto \, \int \mathrm {d} t\,(\overline {{\boldsymbol {k}}} \cdot \dot {\overline {{\boldsymbol {x}}}} - w(t, \overline {{\boldsymbol {x}}}, \overline {{\boldsymbol {k}}}))}$, whence Hamilton's equations follow as usual.
$\smash {S\, \propto \, \int \mathrm {d} t\,(\overline {{\boldsymbol {k}}} \cdot \dot {\overline {{\boldsymbol {x}}}} - w(t, \overline {{\boldsymbol {x}}}, \overline {{\boldsymbol {k}}}))}$, whence Hamilton's equations follow as usual.
7.2.3. Wave momentum and energy
Using (7.30) and (7.36), one arrives at the following equality for any given field ![]() $\smash {{\mathsf {X}}}$:
$\smash {{\mathsf {X}}}$:
 \begin{align} \partial_t({\mathsf{X}} \mathcal{I})+\partial_{\boldsymbol{x}} \cdot ({\mathsf{X}} \mathcal{I} \overline{{\boldsymbol{v}}}_{\text{g}}) & =(\partial_t{\mathsf{X}})\mathcal{I}+{\mathsf{X}}(\partial_t\mathcal{I})+[\partial_{\boldsymbol{x}} \cdot (\mathcal{I} \overline{{\boldsymbol{v}}}_{\text{g}})]{\mathsf{X}}+\mathcal{I}(\overline{{\boldsymbol{v}}}_{\text{g}}\cdot \partial_{\boldsymbol{x}} ){\mathsf{X}} \nonumber\\ &=\mathcal{I}[\partial_t+(\overline{{\boldsymbol{v}}}_{\text{g}}\cdot \partial_{\boldsymbol{x}})]{\mathsf{X}}+{\mathsf{X}}[\partial_t\mathcal{I}+\partial_{\boldsymbol{x}} \cdot (\mathcal{I}\overline{{\boldsymbol{v}}}_{\text{g}})] \nonumber\\ &=\mathcal{I}\,\mathrm{d}_t{\mathsf{X}}. \end{align}
\begin{align} \partial_t({\mathsf{X}} \mathcal{I})+\partial_{\boldsymbol{x}} \cdot ({\mathsf{X}} \mathcal{I} \overline{{\boldsymbol{v}}}_{\text{g}}) & =(\partial_t{\mathsf{X}})\mathcal{I}+{\mathsf{X}}(\partial_t\mathcal{I})+[\partial_{\boldsymbol{x}} \cdot (\mathcal{I} \overline{{\boldsymbol{v}}}_{\text{g}})]{\mathsf{X}}+\mathcal{I}(\overline{{\boldsymbol{v}}}_{\text{g}}\cdot \partial_{\boldsymbol{x}} ){\mathsf{X}} \nonumber\\ &=\mathcal{I}[\partial_t+(\overline{{\boldsymbol{v}}}_{\text{g}}\cdot \partial_{\boldsymbol{x}})]{\mathsf{X}}+{\mathsf{X}}[\partial_t\mathcal{I}+\partial_{\boldsymbol{x}} \cdot (\mathcal{I}\overline{{\boldsymbol{v}}}_{\text{g}})] \nonumber\\ &=\mathcal{I}\,\mathrm{d}_t{\mathsf{X}}. \end{align}
For ![]() $\smash {{\mathsf {X}} = \overline {k}_i}$ and
$\smash {{\mathsf {X}} = \overline {k}_i}$ and ![]() $\smash {{\mathsf {X}} = \overline {\omega }}$, (7.40) yields, respectively,
$\smash {{\mathsf {X}} = \overline {\omega }}$, (7.40) yields, respectively,
where we used (7.37) and introduced the following notation:
When a medium is homogeneous along ![]() $\smash {x^i}$, (7.41a) yields
$\smash {x^i}$, (7.41a) yields ![]() $\smash {\int \mathrm {d}{\boldsymbol {x}}\,P_{\text {w},i} = \text {const}}$. Likewise, when a medium is stationary, (7.41b) yields
$\smash {\int \mathrm {d}{\boldsymbol {x}}\,P_{\text {w},i} = \text {const}}$. Likewise, when a medium is stationary, (7.41b) yields ![]() $\smash {\int \mathrm {d}{\boldsymbol {x}}\,\mathcal {E}_{\text {w}} = \text {const}}$. Hence, by definition,
$\smash {\int \mathrm {d}{\boldsymbol {x}}\,\mathcal {E}_{\text {w}} = \text {const}}$. Hence, by definition, ![]() $\smash {{\boldsymbol {P}}_{\text {w}}}$ and
$\smash {{\boldsymbol {P}}_{\text {w}}}$ and ![]() $\smash {\mathcal {E}_{\text {w}}}$ are the densities of the wave canonical momentum and energy, at least up to a constant factor
$\smash {\mathcal {E}_{\text {w}}}$ are the densities of the wave canonical momentum and energy, at least up to a constant factor ![]() $\smash {\kappa }$.Footnote 32 A proof that
$\smash {\kappa }$.Footnote 32 A proof that ![]() $\smash {\kappa = 1}$ can be found, for example, in Dodin & Fisch (Reference Dodin and Fisch2012). In § 7.5, we will show this using different arguments.
$\smash {\kappa = 1}$ can be found, for example, in Dodin & Fisch (Reference Dodin and Fisch2012). In § 7.5, we will show this using different arguments.
7.3. Non-conservative eikonal waves
In a medium with non-zero ![]() $\smash {{\boldsymbol {\varXi }}_\text {A}}$, where waves are non-conservative, the wave properties are defined as in the previous section but the wave action evolves differently. The variational principle is not easy to apply in this case (however, see Dodin et al. Reference Dodin, Zhmoginov and Ruiz2017), so a different approach will be used to derive the action equation. A more straightforward but less intuitive approach can be found in Dodin et al. (Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019) and McDonald (Reference McDonald1988).
$\smash {{\boldsymbol {\varXi }}_\text {A}}$, where waves are non-conservative, the wave properties are defined as in the previous section but the wave action evolves differently. The variational principle is not easy to apply in this case (however, see Dodin et al. Reference Dodin, Zhmoginov and Ruiz2017), so a different approach will be used to derive the action equation. A more straightforward but less intuitive approach can be found in Dodin et al. (Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019) and McDonald (Reference McDonald1988).
7.3.1. Monochromatic waves
First, consider a homogeneous stationary medium and a ‘monochromatic’ (exponentially growing at a constant rate) wave field in the form
where the constants ![]() $\smash {\overline {\omega }}$ and
$\smash {\overline {\omega }}$ and ![]() $\smash {\overline {{\boldsymbol {k}}}}$ are, as usual, the real frequency and wavenumber, and
$\smash {\overline {{\boldsymbol {k}}}}$ are, as usual, the real frequency and wavenumber, and ![]() $\smash {\overline {\gamma }}$ is the linear growth rate, which can have either sign. Then, (6.15) becomes
$\smash {\overline {\gamma }}$ is the linear growth rate, which can have either sign. Then, (6.15) becomes
where we assume that ![]() $\smash {{\boldsymbol {\varXi }}}$ is a smooth function of
$\smash {{\boldsymbol {\varXi }}}$ is a smooth function of ![]() $\smash {\omega }$ and also that both
$\smash {\omega }$ and also that both ![]() $\smash {{\boldsymbol {\varXi }}_\text {A}}$ and
$\smash {{\boldsymbol {\varXi }}_\text {A}}$ and ![]() $\smash {\overline {\gamma }}$ are
$\smash {\overline {\gamma }}$ are ![]() $\smash {\mathcal {O}(\epsilon )}$. Like in § 7.2.1, we adopt
$\smash {\mathcal {O}(\epsilon )}$. Like in § 7.2.1, we adopt ![]() $\smash {{\breve {{\boldsymbol {\varPsi }}}}_{\text {c}} = {\boldsymbol {\eta }}{\breve {a}} + \mathcal {O}(\epsilon )}$, where the polarization vector
$\smash {{\breve {{\boldsymbol {\varPsi }}}}_{\text {c}} = {\boldsymbol {\eta }}{\breve {a}} + \mathcal {O}(\epsilon )}$, where the polarization vector ![]() $\smash {{\boldsymbol {\eta }}}$ is the relevant eigenvector of
$\smash {{\boldsymbol {\eta }}}$ is the relevant eigenvector of ![]() $\smash {{\boldsymbol {\varXi }}_\text {H}}$. Then, by projecting (7.44) on
$\smash {{\boldsymbol {\varXi }}_\text {H}}$. Then, by projecting (7.44) on ![]() $\smash {{\boldsymbol {\eta }}}$, one obtains
$\smash {{\boldsymbol {\eta }}}$, one obtains
where ![]() $\smash {\varLambda = {\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\varXi }}_\text {H}{\boldsymbol {\eta }}}$ is the corresponding eigenvalue of
$\smash {\varLambda = {\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\varXi }}_\text {H}{\boldsymbol {\eta }}}$ is the corresponding eigenvalue of ![]() $\smash {{\boldsymbol {\varXi }}_\text {H}}$ and we used (7.16). Let us neglect
$\smash {{\boldsymbol {\varXi }}_\text {H}}$ and we used (7.16). Let us neglect ![]() $\smash {\mathcal {O}(\epsilon ^2)}$, divide (7.45) by
$\smash {\mathcal {O}(\epsilon ^2)}$, divide (7.45) by ![]() $\smash {{\breve {a}}}$ and consider the real and imaginary parts of the resulting equation separately:
$\smash {{\breve {a}}}$ and consider the real and imaginary parts of the resulting equation separately:
The former is the same dispersion relation for ![]() $\smash {\overline {\omega }}$ as for conservative waves, and the latter yields
$\smash {\overline {\omega }}$ as for conservative waves, and the latter yields ![]() $\overline {\gamma } = \gamma ({\boldsymbol {\overline {k}}})$, where
$\overline {\gamma } = \gamma ({\boldsymbol {\overline {k}}})$, where
Because ![]() $\smash {|{\breve {a}}|\, \propto \, \mathrm {e}^{\overline {\gamma }t}}$, one can write the amplitude equation as
$\smash {|{\breve {a}}|\, \propto \, \mathrm {e}^{\overline {\gamma }t}}$, one can write the amplitude equation as
One can also define the action density ![]() $\smash {\mathcal {I}}$ as in § 7.2.1 and rewrite (7.48) in terms of that. Because
$\smash {\mathcal {I}}$ as in § 7.2.1 and rewrite (7.48) in terms of that. Because ![]() $\smash {\mathcal {I} = |{\breve {a}}|^2 \times \text {const}}$, one obtains
$\smash {\mathcal {I} = |{\breve {a}}|^2 \times \text {const}}$, one obtains
7.3.2. Non-monochromatic waves
When weak inhomogeneity and weak dissipation coexist, their effect on the action density is additive, so (7.30) and (7.49) merge into a general equation
(A formal derivation of (7.50), which uses the Weyl expansion (2.41) and projection of the field equation on the polarization vector, can be found in Dodin et al. Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019.) Then, (7.40) is modified as follows:
and the equations (7.41) for the wave momentum and energy (7.42) become
A comment is due here regarding the relation between (7.50) and the amplitude equation (7.48) that is commonly used in the standard QLT for homogeneous plasma (for example, see (2.21) in Drummond & Pines Reference Drummond and Pines1962). In a nutshell, the latter is incorrect, even when ![]() $\smash {\partial _{\boldsymbol {x}} = 0}$. Because
$\smash {\partial _{\boldsymbol {x}} = 0}$. Because ![]() $\smash {\overline {f}}$ is time-dependent, waves do not grow or decay exponentially. Rather, they can be considered as geometrical-optics (WKB) waves, and unlike in § 7.3.1, the ratio
$\smash {\overline {f}}$ is time-dependent, waves do not grow or decay exponentially. Rather, they can be considered as geometrical-optics (WKB) waves, and unlike in § 7.3.1, the ratio ![]() $\smash {|{\breve {a}}|^2/\mathcal {I}}$ generally evolves at a rate comparable to
$\smash {|{\breve {a}}|^2/\mathcal {I}}$ generally evolves at a rate comparable to ![]() $\smash {\overline {\gamma }}$. The standard QLT remains conservative only because it also incorrectly replaces (3.19) with its stationary-plasma limit (
$\smash {\overline {\gamma }}$. The standard QLT remains conservative only because it also incorrectly replaces (3.19) with its stationary-plasma limit (![]() $\smash {\epsilon = 0}$) and the two errors cancel each other. These issues are less of a problem for waves in not-too-hot plasmas (e.g. Langmuir waves), because in such plasmas, changing the distribution functions does not significantly affect the dispersion relations and thus
$\smash {\epsilon = 0}$) and the two errors cancel each other. These issues are less of a problem for waves in not-too-hot plasmas (e.g. Langmuir waves), because in such plasmas, changing the distribution functions does not significantly affect the dispersion relations and thus ![]() $\smash {|{\breve {a}}|^2/\mathcal {I}}$ does in fact approximately remain constant. See also the discussion in § 9.1.4.
$\smash {|{\breve {a}}|^2/\mathcal {I}}$ does in fact approximately remain constant. See also the discussion in § 9.1.4.
7.4. General waves
Let us now discuss a more general case that includes broadband waves. The evolution of such waves can be described statistically in terms of their average Wigner matrix ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$. This matrix also determines the function
$\smash {{{\boldsymbol {\mathsf {U}}}}}$. This matrix also determines the function ![]() $\smash {\overline {{\mathsf {W}}}_s}$ that is given by (6.37a) and enters the nonlinear potentials (6.77). Below, we derive the general form of
$\smash {\overline {{\mathsf {W}}}_s}$ that is given by (6.37a) and enters the nonlinear potentials (6.77). Below, we derive the general form of ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ in terms of the phase-space action density
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ in terms of the phase-space action density ![]() $\smash {J}$ and the governing equation for
$\smash {J}$ and the governing equation for ![]() $\smash {J}$ (§§ 7.4.1–7.4.3). Then, we also express the function
$\smash {J}$ (§§ 7.4.1–7.4.3). Then, we also express the function ![]() $\smash {\overline {{\mathsf {W}}}_s}$ through
$\smash {\overline {{\mathsf {W}}}_s}$ through ![]() $\smash {J}$ (§ 7.4.4). Related calculations can also be found in McDonald & Kaufman (Reference McDonald and Kaufman1985) and Ruiz (Reference Ruiz2017).
$\smash {J}$ (§ 7.4.4). Related calculations can also be found in McDonald & Kaufman (Reference McDonald and Kaufman1985) and Ruiz (Reference Ruiz2017).
7.4.1. Average Wigner matrix of an eikonal-wave field
Let us start with calculating the average Wigner matrix of an eikonal field ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ of the form (7.17) (see also Appendix A.2). Using
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ of the form (7.17) (see also Appendix A.2). Using ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}} = (\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}} + \smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^*)/2}$, it can be readily expressed through the average Wigner functions of the complexified fieldFootnote 33
$\smash {\widetilde {{\boldsymbol {\varPsi }}} = (\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}} + \smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^*)/2}$, it can be readily expressed through the average Wigner functions of the complexified fieldFootnote 33 ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}}$ and of its complex conjugate:
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}}$ and of its complex conjugate:
For ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}} = {\breve {a}}{\boldsymbol {\eta }}(\overline {\omega }, \overline {{\boldsymbol {k}}})\mathrm {e}^{\mathrm {i} \theta }}$, where the arguments
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}} = {\breve {a}}{\boldsymbol {\eta }}(\overline {\omega }, \overline {{\boldsymbol {k}}})\mathrm {e}^{\mathrm {i} \theta }}$, where the arguments ![]() $(t, {\boldsymbol {x}})$ are omitted for brevity, one has
$(t, {\boldsymbol {x}})$ are omitted for brevity, one has
where we neglected the dependence of ![]() $\smash {{\breve {a}}}$ and
$\smash {{\breve {a}}}$ and ![]() $\smash {{\boldsymbol {\eta }}}$ on
$\smash {{\boldsymbol {\eta }}}$ on ![]() $\smash {(t, {\boldsymbol {x}})}$ because it is weak compared with that of
$\smash {(t, {\boldsymbol {x}})}$ because it is weak compared with that of ![]() $\smash {\mathrm {e}^{\pm \mathrm {i}\theta }}$. By Taylor-expanding
$\smash {\mathrm {e}^{\pm \mathrm {i}\theta }}$. By Taylor-expanding ![]() $\smash {\theta }$, one obtains
$\smash {\theta }$, one obtains
For ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^* = {\breve {a}}^*{\boldsymbol {\eta }}^*(\overline {\omega }, \overline {{\boldsymbol {k}}})\mathrm {e}^{-\mathrm {i} \theta }}$, which can also be written as
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^* = {\breve {a}}^*{\boldsymbol {\eta }}^*(\overline {\omega }, \overline {{\boldsymbol {k}}})\mathrm {e}^{-\mathrm {i} \theta }}$, which can also be written as ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^* = {\breve {a}}^*{\boldsymbol {\eta }}(-\overline {\omega }, -\overline {{\boldsymbol {k}}})\mathrm {e}^{-\mathrm {i} \theta }}$ due to (7.7), the result is the same up to replacing
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^* = {\breve {a}}^*{\boldsymbol {\eta }}(-\overline {\omega }, -\overline {{\boldsymbol {k}}})\mathrm {e}^{-\mathrm {i} \theta }}$ due to (7.7), the result is the same up to replacing ![]() $\smash {\overline {\omega } \to - \overline {\omega }}$ and
$\smash {\overline {\omega } \to - \overline {\omega }}$ and ![]() $\smash {\overline {{\boldsymbol {k}}} \to -\overline {{\boldsymbol {k}}}}$. Also notice that
$\smash {\overline {{\boldsymbol {k}}} \to -\overline {{\boldsymbol {k}}}}$. Also notice that
 \begin{align} \delta(\omega \mp \overline{\omega}) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}) & = \delta(\omega \mp w(\overline{{\boldsymbol{k}}})) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}) \nonumber\\ & = \delta(\omega \mp w({\pm} {\boldsymbol{k}})) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}) \nonumber\\ & = \delta(\omega - w({\boldsymbol{k}})) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}), \end{align}
\begin{align} \delta(\omega \mp \overline{\omega}) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}) & = \delta(\omega \mp w(\overline{{\boldsymbol{k}}})) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}) \nonumber\\ & = \delta(\omega \mp w({\pm} {\boldsymbol{k}})) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}) \nonumber\\ & = \delta(\omega - w({\boldsymbol{k}})) \delta({\boldsymbol{k}} \mp \overline{{\boldsymbol{k}}}), \end{align}
so one can rewrite ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}\pm }}$ as follows:
$\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}\pm }}$ as follows:
where ![]() $\smash {({\boldsymbol {k}}) \equiv (w({\boldsymbol {k}}), {\boldsymbol {k}})}$. Thus finally,
$\smash {({\boldsymbol {k}}) \equiv (w({\boldsymbol {k}}), {\boldsymbol {k}})}$. Thus finally,
7.4.2. Average Wigner matrix of a general wave
Assuming the background medium is sufficiently smooth, a general wave field can be represented as a superposition of eikonal fields
As a quadratic functional, its average Wigner matrix ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ equals the sum of the average Wigner matrices
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ equals the sum of the average Wigner matrices ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}_\sigma }$ of the individual eikonal waves:
$\smash {{{\boldsymbol {\mathsf {U}}}}_\sigma }$ of the individual eikonal waves:
where ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}_{\sigma,\text {c}+} \equiv {{\boldsymbol {\mathsf {U}}}}_{\sigma,\text {c}}}$ and
$\smash {{{\boldsymbol {\mathsf {U}}}}_{\sigma,\text {c}+} \equiv {{\boldsymbol {\mathsf {U}}}}_{\sigma,\text {c}}}$ and ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}_{\sigma,\text {c}-}}$ are the average Wigner matrices of
$\smash {{{\boldsymbol {\mathsf {U}}}}_{\sigma,\text {c}-}}$ are the average Wigner matrices of ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\sigma,\text {c}}}$ and
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\sigma,\text {c}}}$ and ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\sigma,\text {c}}^*}$, respectively,
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\sigma,\text {c}}^*}$, respectively,
Equation (7.59) can also be expressed as
where ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}\pm }}$ are the average Wigner matrices of
$\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}\pm }}$ are the average Wigner matrices of ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}}$ and
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}}$ and ![]() $\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^*}$, respectively,
$\smash {\smash {\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}^*}$, respectively,
Because ![]() $\smash {h_{\text {c}-}({\boldsymbol {k}}) = h_{\text {c}+}(-{\boldsymbol {k}}) \equiv h_{\text {c}}(-{\boldsymbol {k}})}$, the matrix
$\smash {h_{\text {c}-}({\boldsymbol {k}}) = h_{\text {c}+}(-{\boldsymbol {k}}) \equiv h_{\text {c}}(-{\boldsymbol {k}})}$, the matrix ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ can also be written as follows:
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ can also be written as follows:
where ![]() $\smash {h({\boldsymbol {k}}) \doteq h_{\text {c}}({\boldsymbol {k}})/4}$ is given by
$\smash {h({\boldsymbol {k}}) \doteq h_{\text {c}}({\boldsymbol {k}})/4}$ is given by
This shows that, for broadband waves comprised of eikonal waves, ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ has the same form as for an eikonal wave except
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ has the same form as for an eikonal wave except ![]() ${h({\boldsymbol {k}})}$ is not necessarily delta-shaped.
${h({\boldsymbol {k}})}$ is not necessarily delta-shaped.
7.4.3. Phase-space action density and the WKE
The wave equation for the complexified field ![]() ${{\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}}$ can be written in the invariant form as
${{\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}}$ can be written in the invariant form as ![]() ${\widehat {\boldsymbol {\varXi }}{\left. {\boldsymbol {\mathsf {{\widetilde {{\boldsymbol {|\varPsi }}}}_{\text {c}}}}} \right\rangle}= {\left. {\boldsymbol {\mathsf {\widehat {\boldsymbol {|0}}}}} \right\rangle}}$. Multiplying it by
${\widehat {\boldsymbol {\varXi }}{\left. {\boldsymbol {\mathsf {{\widetilde {{\boldsymbol {|\varPsi }}}}_{\text {c}}}}} \right\rangle}= {\left. {\boldsymbol {\mathsf {\widehat {\boldsymbol {|0}}}}} \right\rangle}}$. Multiplying it by ![]() $ {\left. {\boldsymbol {\mathsf {{\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}|}}} \right\rangle}$ from the right leads to
$ {\left. {\boldsymbol {\mathsf {{\widetilde {{\boldsymbol {\varPsi }}}}_{\text {c}}|}}} \right\rangle}$ from the right leads to
This readily yields an equation for the Wigner matrix: ![]() $\smash {{\boldsymbol {\varXi }} \star {{\boldsymbol {\mathsf {U}}}}_{\text {c}} = {\boldsymbol {0}}}$. Let us integrate this equation over
$\smash {{\boldsymbol {\varXi }} \star {{\boldsymbol {\mathsf {U}}}}_{\text {c}} = {\boldsymbol {0}}}$. Let us integrate this equation over ![]() $\smash {\omega }$ to make the left-hand side a smooth function of
$\smash {\omega }$ to make the left-hand side a smooth function of ![]() $\smash {(t, {\boldsymbol {x}}, {\boldsymbol {k}})}$. Let us also take the trace of the resulting equation to put it in a scalar form
$\smash {(t, {\boldsymbol {x}}, {\boldsymbol {k}})}$. Let us also take the trace of the resulting equation to put it in a scalar form
As usual, we assume ![]() ${\boldsymbol {\varXi }} = {\boldsymbol {\varXi }}_\text {H} + \mathrm {i} {\boldsymbol {\varXi }}_\text {A}$ with
${\boldsymbol {\varXi }} = {\boldsymbol {\varXi }}_\text {H} + \mathrm {i} {\boldsymbol {\varXi }}_\text {A}$ with ![]() ${\boldsymbol {\varXi }}_\text {A} = \mathcal {O}(\epsilon ) \ll {\boldsymbol {\varXi }}_\text {H} = \mathcal {O}(1)$ for generic
${\boldsymbol {\varXi }}_\text {A} = \mathcal {O}(\epsilon ) \ll {\boldsymbol {\varXi }}_\text {H} = \mathcal {O}(1)$ for generic ![]() $({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$. The integrand in (7.66) can be written as
$({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})$. The integrand in (7.66) can be written as ![]() $\smash {{\boldsymbol {\varXi }} \star {{\boldsymbol {\mathsf {U}}}}_{\text {c}} = {\boldsymbol {\varXi }}\mathrm {e}^{\mathrm {i}\widehat {\mathcal {L}}_{{\mathsf {x}}}/2}{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$, and its expansion in the differential operator
$\smash {{\boldsymbol {\varXi }} \star {{\boldsymbol {\mathsf {U}}}}_{\text {c}} = {\boldsymbol {\varXi }}\mathrm {e}^{\mathrm {i}\widehat {\mathcal {L}}_{{\mathsf {x}}}/2}{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$, and its expansion in the differential operator ![]() $\smash {\widehat {\mathcal {L}}_{{\mathsf {x}}}}$ (2.32) contains derivatives of all orders. High-order derivatives on
$\smash {\widehat {\mathcal {L}}_{{\mathsf {x}}}}$ (2.32) contains derivatives of all orders. High-order derivatives on ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$ are not negligible per se, because for on-shell waves this function is delta-shaped. However, using integration by parts, one can reapply all derivatives with respect to
$\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$ are not negligible per se, because for on-shell waves this function is delta-shaped. However, using integration by parts, one can reapply all derivatives with respect to ![]() $\smash {\omega }$ to
$\smash {\omega }$ to ![]() $\smash {{\boldsymbol {\varXi }}}$ and take the remaining derivatives (with respect to
$\smash {{\boldsymbol {\varXi }}}$ and take the remaining derivatives (with respect to ![]() $\smash {t}$,
$\smash {t}$, ![]() $\boldsymbol{x}$ and
$\boldsymbol{x}$ and ![]() $\boldsymbol{k}$) outside the integral. Then it is seen that each power
$\boldsymbol{k}$) outside the integral. Then it is seen that each power ![]() $\smash {m}$ of
$\smash {m}$ of ![]() $\smash {\widehat {\mathcal {L}}_{{\mathsf {x}}}}$ in the expansion of
$\smash {\widehat {\mathcal {L}}_{{\mathsf {x}}}}$ in the expansion of ![]() $\smash {{\boldsymbol {\varXi }}\mathrm {e}^{\mathrm {i}\widehat {\mathcal {L}}_{{\mathsf {x}}}/2}{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$ contributes
$\smash {{\boldsymbol {\varXi }}\mathrm {e}^{\mathrm {i}\widehat {\mathcal {L}}_{{\mathsf {x}}}/2}{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$ contributes ![]() $\smash {\mathcal {O}(\epsilon ^m)}$ to the integral. Let us neglect terms with
$\smash {\mathcal {O}(\epsilon ^m)}$ to the integral. Let us neglect terms with ![]() $\smash {m \geqslant 2}$ and use (7.62). Hence, one obtainsFootnote 34
$\smash {m \geqslant 2}$ and use (7.62). Hence, one obtainsFootnote 34
 \begin{align} 0 & \approx \operatorname{tr} \int \mathrm{d}\omega\,\left({\boldsymbol{\varXi}}_\text{H} {{\boldsymbol {\mathsf{U}}}}_{\text{c}} + \mathrm{i} {\boldsymbol{\varXi}}_\text{A} {{\boldsymbol {\mathsf{U}}}}_{\text{c}} + \frac{\mathrm{i}}{2}\,\lbrace {\boldsymbol{\varXi}}_\text{H}, {{\boldsymbol {\mathsf{U}}}}_{\text{c}} \rbrace_{{{\mathsf{x}}}}\right) \nonumber\\ & \approx ({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_\text{H} {\boldsymbol{\eta}} + \mathrm{i} {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_\text{A} {\boldsymbol{\eta}})h_{\text{c}} + \frac{\mathrm{i}}{2}\,\operatorname{tr} \int \mathrm{d}\omega\left( \frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial {\mathsf{x}}^i}\frac{\partial {{\boldsymbol {\mathsf{U}}}}_{\text{c}}}{\partial {\mathsf{k}}_i} - \frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial {\mathsf{k}}_i}\frac{\partial {{\boldsymbol {\mathsf{U}}}}_{\text{c}}}{\partial {\mathsf{x}}^i} \right). \end{align}
\begin{align} 0 & \approx \operatorname{tr} \int \mathrm{d}\omega\,\left({\boldsymbol{\varXi}}_\text{H} {{\boldsymbol {\mathsf{U}}}}_{\text{c}} + \mathrm{i} {\boldsymbol{\varXi}}_\text{A} {{\boldsymbol {\mathsf{U}}}}_{\text{c}} + \frac{\mathrm{i}}{2}\,\lbrace {\boldsymbol{\varXi}}_\text{H}, {{\boldsymbol {\mathsf{U}}}}_{\text{c}} \rbrace_{{{\mathsf{x}}}}\right) \nonumber\\ & \approx ({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_\text{H} {\boldsymbol{\eta}} + \mathrm{i} {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_\text{A} {\boldsymbol{\eta}})h_{\text{c}} + \frac{\mathrm{i}}{2}\,\operatorname{tr} \int \mathrm{d}\omega\left( \frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial {\mathsf{x}}^i}\frac{\partial {{\boldsymbol {\mathsf{U}}}}_{\text{c}}}{\partial {\mathsf{k}}_i} - \frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial {\mathsf{k}}_i}\frac{\partial {{\boldsymbol {\mathsf{U}}}}_{\text{c}}}{\partial {\mathsf{x}}^i} \right). \end{align}Let us also re-express this as follows, using (7.4) and (7.47):
 \begin{align} 0 & \approx \left(\varLambda - \mathrm{i}\gamma\, \frac{\partial\varLambda}{\partial\omega}\right)h_{\text{c}} - \frac{\mathrm{i}}{2} \operatorname{tr} \int \mathrm{d}\omega\,\frac{\partial}{\partial \omega}\left(\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial t}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}}\right) + \frac{\mathrm{i}}{2}\frac{\partial}{\partial t}\operatorname{tr}\int \mathrm{d}\omega\,\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial \omega}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}} \nonumber\\ & \hspace{1.25in} + \frac{\mathrm{i}}{2}\frac{\partial}{\partial k_i} \operatorname{tr} \int \mathrm{d}\omega\,\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial x^i}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}} - \frac{\mathrm{i}}{2}\frac{\partial}{\partial x^i}\operatorname{tr}\int \mathrm{d}\omega\,\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial k_i}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}}. \end{align}
\begin{align} 0 & \approx \left(\varLambda - \mathrm{i}\gamma\, \frac{\partial\varLambda}{\partial\omega}\right)h_{\text{c}} - \frac{\mathrm{i}}{2} \operatorname{tr} \int \mathrm{d}\omega\,\frac{\partial}{\partial \omega}\left(\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial t}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}}\right) + \frac{\mathrm{i}}{2}\frac{\partial}{\partial t}\operatorname{tr}\int \mathrm{d}\omega\,\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial \omega}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}} \nonumber\\ & \hspace{1.25in} + \frac{\mathrm{i}}{2}\frac{\partial}{\partial k_i} \operatorname{tr} \int \mathrm{d}\omega\,\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial x^i}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}} - \frac{\mathrm{i}}{2}\frac{\partial}{\partial x^i}\operatorname{tr}\int \mathrm{d}\omega\,\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial k_i}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}}. \end{align}Clearly,
To simplify the remaining terms, we proceed as follows. As a Hermitian matrix, ![]() $\smash {{\boldsymbol {\varXi }}_\text {H}}$ can be represented in terms of its eigenvalues
$\smash {{\boldsymbol {\varXi }}_\text {H}}$ can be represented in terms of its eigenvalues ![]() $\smash {\varLambda _b}$ and eigenvectors
$\smash {\varLambda _b}$ and eigenvectors ![]() $\smash {{\boldsymbol {\eta }}_b }$ as
$\smash {{\boldsymbol {\eta }}_b }$ as ![]() $\smash {{\boldsymbol {\varXi }}_\text {H} = \varLambda _b {\boldsymbol {\eta }}_b {\boldsymbol {\eta }}_b^{{\dagger}} }$. For
$\smash {{\boldsymbol {\varXi }}_\text {H} = \varLambda _b {\boldsymbol {\eta }}_b {\boldsymbol {\eta }}_b^{{\dagger}} }$. For ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$, let us use (7.62) again, where
$\smash {{{\boldsymbol {\mathsf {U}}}}_{\text {c}}}$, let us use (7.62) again, where ![]() $\smash {{\boldsymbol {\eta }}}$ is one of the vectors
$\smash {{\boldsymbol {\eta }}}$ is one of the vectors ![]() $\smash {{\boldsymbol {\eta }}_b}$, say,
$\smash {{\boldsymbol {\eta }}_b}$, say, ![]() $\smash {{\boldsymbol {\eta }} \equiv {\boldsymbol {\eta }}_0}$. (Accordingly,
$\smash {{\boldsymbol {\eta }} \equiv {\boldsymbol {\eta }}_0}$. (Accordingly, ![]() $\smash {\varLambda \equiv \varLambda _0}$.) Then, for any
$\smash {\varLambda \equiv \varLambda _0}$.) Then, for any ![]() $\smash {{\unicode{x25AA}} \in \lbrace \omega, x^i, k_i \rbrace }$, one has
$\smash {{\unicode{x25AA}} \in \lbrace \omega, x^i, k_i \rbrace }$, one has
 \begin{align} \operatorname{tr}\int \mathrm{d}\omega \left(\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial {\unicode{x25AA}}}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}}\right) & = \frac{\partial \varLambda_b}{\partial {\unicode{x25AA}}}\, |{\boldsymbol{\eta}}_b^{{\dagger}} {\boldsymbol{\eta}}|^2 h_{\text{c}} + \varLambda_b\,\Big({\boldsymbol{\eta}}^{{\dagger}}\frac{\partial {\boldsymbol{\eta}}_b}{\partial{\unicode{x25AA}}}\Big)({\boldsymbol{\eta}}_b^{{\dagger}}{\boldsymbol{\eta}})h_{\text{c}} + \varLambda_b\,({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\eta}}_b)\Big(\frac{\partial {\boldsymbol{\eta}}_b^{{\dagger}}}{\partial{\unicode{x25AA}}}\,{\boldsymbol{\eta}}\Big)h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda_b}{\partial {\unicode{x25AA}}}\,(\delta_{b,0})^2h_{\text{c}} + \varLambda_b\,\Big({\boldsymbol{\eta}}^{{\dagger}}\frac{\partial {\boldsymbol{\eta}}_b}{\partial{\unicode{x25AA}}}\Big)\delta_{b,0} h_{\text{c}} + \varLambda_b\,\delta_{b,0}\Big(\frac{\partial {\boldsymbol{\eta}}_b^{{\dagger}}}{\partial{\unicode{x25AA}}}\,{\boldsymbol{\eta}}\Big)h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda}{\partial {\unicode{x25AA}}}\,h_{\text{c}} + \Big({\boldsymbol{\eta}}^{{\dagger}}\frac{\partial{\boldsymbol{\eta}}}{\partial{\unicode{x25AA}}} + \frac{\partial {\boldsymbol{\eta}}^{{\dagger}}}{\partial{\unicode{x25AA}}}\,{\boldsymbol{\eta}}\Big)\,\varLambda h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda}{\partial {\unicode{x25AA}}}\,h_{\text{c}} + \frac{\partial({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\eta}})}{\partial{\unicode{x25AA}}}\,\varLambda h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda}{\partial {\unicode{x25AA}}}\,h_{\text{c}}, \end{align}
\begin{align} \operatorname{tr}\int \mathrm{d}\omega \left(\frac{\partial {\boldsymbol{\varXi}}_\text{H}}{\partial {\unicode{x25AA}}}\,{{\boldsymbol {\mathsf{U}}}}_{\text{c}}\right) & = \frac{\partial \varLambda_b}{\partial {\unicode{x25AA}}}\, |{\boldsymbol{\eta}}_b^{{\dagger}} {\boldsymbol{\eta}}|^2 h_{\text{c}} + \varLambda_b\,\Big({\boldsymbol{\eta}}^{{\dagger}}\frac{\partial {\boldsymbol{\eta}}_b}{\partial{\unicode{x25AA}}}\Big)({\boldsymbol{\eta}}_b^{{\dagger}}{\boldsymbol{\eta}})h_{\text{c}} + \varLambda_b\,({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\eta}}_b)\Big(\frac{\partial {\boldsymbol{\eta}}_b^{{\dagger}}}{\partial{\unicode{x25AA}}}\,{\boldsymbol{\eta}}\Big)h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda_b}{\partial {\unicode{x25AA}}}\,(\delta_{b,0})^2h_{\text{c}} + \varLambda_b\,\Big({\boldsymbol{\eta}}^{{\dagger}}\frac{\partial {\boldsymbol{\eta}}_b}{\partial{\unicode{x25AA}}}\Big)\delta_{b,0} h_{\text{c}} + \varLambda_b\,\delta_{b,0}\Big(\frac{\partial {\boldsymbol{\eta}}_b^{{\dagger}}}{\partial{\unicode{x25AA}}}\,{\boldsymbol{\eta}}\Big)h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda}{\partial {\unicode{x25AA}}}\,h_{\text{c}} + \Big({\boldsymbol{\eta}}^{{\dagger}}\frac{\partial{\boldsymbol{\eta}}}{\partial{\unicode{x25AA}}} + \frac{\partial {\boldsymbol{\eta}}^{{\dagger}}}{\partial{\unicode{x25AA}}}\,{\boldsymbol{\eta}}\Big)\,\varLambda h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda}{\partial {\unicode{x25AA}}}\,h_{\text{c}} + \frac{\partial({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\eta}})}{\partial{\unicode{x25AA}}}\,\varLambda h_{\text{c}} \nonumber\\ & = \frac{\partial \varLambda}{\partial {\unicode{x25AA}}}\,h_{\text{c}}, \end{align}
where we used ![]() $\smash {{\boldsymbol {\eta }}_b^{{\dagger}} {\boldsymbol {\eta }} = \delta _{b,0}}$ and, in particular,
$\smash {{\boldsymbol {\eta }}_b^{{\dagger}} {\boldsymbol {\eta }} = \delta _{b,0}}$ and, in particular, ![]() $\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\eta }} = 1}$. Then, (7.68) can be written as
$\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\eta }} = 1}$. Then, (7.68) can be written as
where
The real part of (7.71) gives ![]() $\smash {\varLambda = 0}$, which is the dispersion relation. The imaginary part of (7.71) gives
$\smash {\varLambda = 0}$, which is the dispersion relation. The imaginary part of (7.71) gives ![]() $\smash {\mathscr {E} = 0}$. To understand this equation, let us rewrite
$\smash {\mathscr {E} = 0}$. To understand this equation, let us rewrite ![]() $\smash {\mathscr {E}}$ as
$\smash {\mathscr {E}}$ as
Here, we introduced
which, according to (7.24), satisfy
Note that using (7.64), one can also express ![]() $\smash {J}$ as
$\smash {J}$ as
where ![]() $\smash {\mathcal {I}_\sigma }$ are the action densities (7.27) of the individual eikonal waves that comprise the total wave field (§ 7.4.2). In particular,
$\smash {\mathcal {I}_\sigma }$ are the action densities (7.27) of the individual eikonal waves that comprise the total wave field (§ 7.4.2). In particular, ![]() $\smash {\int \mathrm {d}{\boldsymbol {k}}\,J = \sum _\sigma \mathcal {I}_\sigma }$, which is the total action density. Therefore, the function
$\smash {\int \mathrm {d}{\boldsymbol {k}}\,J = \sum _\sigma \mathcal {I}_\sigma }$, which is the total action density. Therefore, the function ![]() $\smash {J}$ can be interpreted as the phase-space action density. In terms of
$\smash {J}$ can be interpreted as the phase-space action density. In terms of ![]() $\smash {J}$, the equation
$\smash {J}$, the equation ![]() $\smash {\mathscr {E} = 0}$ can be written as
$\smash {\mathscr {E} = 0}$ can be written as
This equation, called the WKE, serves the same role in QL wave-kinetic theory as the Vlasov equation serves in plasma kinetic theory.Footnote 35 Unlike the field equation used in the standard QLT (Drummond & Pines Reference Drummond and Pines1962), (7.77) exactly conserves the action of non-resonant waves, i.e. those with ![]() $\smash {\gamma = 0}$. Also note that (7.50) for eikonal waves can be deduced from (7.77) as a particular case by assuming the ansatz
$\smash {\gamma = 0}$. Also note that (7.50) for eikonal waves can be deduced from (7.77) as a particular case by assuming the ansatz
and integrating over ![]() $\smash {{\boldsymbol {k}}}$. In other words, eikonal-wave theory can be understood as the ‘cold-fluid’ limit of wave-kinetic theory.
$\smash {{\boldsymbol {k}}}$. In other words, eikonal-wave theory can be understood as the ‘cold-fluid’ limit of wave-kinetic theory.
7.4.4. Function  ${\overline {\mathsf{{W}}}}_s$ in terms of
${\overline {\mathsf{{W}}}}_s$ in terms of  ${J}$
${J}$
Here we explicitly calculate the function (6.37a) that determines the nonlinear potentials (6.77). Using (7.63), one obtains
where ![]() $\smash {({\boldsymbol {k}}; {\boldsymbol {p}}) \equiv (w({\boldsymbol {k}}), {\boldsymbol {k}}; {\boldsymbol {p}})}$. By definition of
$\smash {({\boldsymbol {k}}; {\boldsymbol {p}}) \equiv (w({\boldsymbol {k}}), {\boldsymbol {k}}; {\boldsymbol {p}})}$. By definition of ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s}$, the function
$\smash {\widehat {\boldsymbol {\alpha }}_s}$, the function ![]() $\smash {\left\langle {t_1, {\boldsymbol {x}}_1 | \widehat {\boldsymbol {\alpha }}_s |t_2, {\boldsymbol {x}}_2}\right\rangle}$ is real for all
$\smash {\left\langle {t_1, {\boldsymbol {x}}_1 | \widehat {\boldsymbol {\alpha }}_s |t_2, {\boldsymbol {x}}_2}\right\rangle}$ is real for all ![]() $\smash {(t_1, {\boldsymbol {x}}_1)}$ and
$\smash {(t_1, {\boldsymbol {x}}_1)}$ and ![]() $\smash {(t_2, {\boldsymbol {x}}_2)}$, so
$\smash {(t_2, {\boldsymbol {x}}_2)}$, so ![]() $\smash {{\boldsymbol {\alpha }}_s(-\omega, -{\boldsymbol {k}}) = {\boldsymbol {\alpha }}_s^*(\omega, {\boldsymbol {k}})}$ by definition of the Weyl symbol (2.26). Together with (7.7), this gives
$\smash {{\boldsymbol {\alpha }}_s(-\omega, -{\boldsymbol {k}}) = {\boldsymbol {\alpha }}_s^*(\omega, {\boldsymbol {k}})}$ by definition of the Weyl symbol (2.26). Together with (7.7), this gives ![]() $\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2(\omega, {\boldsymbol {k}}; {\boldsymbol {p}})} = \smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2(-\omega, -{\boldsymbol {k}}; {\boldsymbol {p}})}$, so
$\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2(\omega, {\boldsymbol {k}}; {\boldsymbol {p}})} = \smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2(-\omega, -{\boldsymbol {k}}; {\boldsymbol {p}})}$, so
and similarly,
This also means that ![]() $\smash {\overline {{\mathsf {W}}}_s(\omega, {\boldsymbol {k}}; {\boldsymbol {p}})} = \smash {\overline {{\mathsf {W}}}_s(-\omega, -{\boldsymbol {k}}; {\boldsymbol {p}})}$. Then finally, using (7.74), one can express this function through the phase-space action density:
$\smash {\overline {{\mathsf {W}}}_s(\omega, {\boldsymbol {k}}; {\boldsymbol {p}})} = \smash {\overline {{\mathsf {W}}}_s(-\omega, -{\boldsymbol {k}}; {\boldsymbol {p}})}$. Then finally, using (7.74), one can express this function through the phase-space action density:
7.5. Conservation laws
Let us rewrite (7.77) together with (6.76) in the ‘divergence’ form
Using (7.62), the diffusion matrix ![]() $\smash {{\mathsf {D}}_{s,ij}}$ can be represented as follows:
$\smash {{\mathsf {D}}_{s,ij}}$ can be represented as follows:
Also, by substituting (6.24) into (7.47), one finds
 \begin{equation} \gamma = {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\,\frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda({\boldsymbol{k}})}\, \delta(w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s({\boldsymbol{p}}))\,{\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}. \end{equation}
\begin{equation} \gamma = {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\,\frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda({\boldsymbol{k}})}\, \delta(w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s({\boldsymbol{p}}))\,{\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}. \end{equation}
Together with (7.75), these yield the following notable corollaries. First of all, if ![]() $\smash {{\boldsymbol {\varXi }}_0}$,
$\smash {{\boldsymbol {\varXi }}_0}$, ![]() $\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and
$\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and ![]() $\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of
$\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of ![]() $\smash {{\boldsymbol {x}}}$,Footnote 36 one has for each
$\smash {{\boldsymbol {x}}}$,Footnote 36 one has for each ![]() $\smash {l}$ that (Appendix D.1)
$\smash {l}$ that (Appendix D.1)
 \begin{align} \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,p_l F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l J \right) &+ \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, p_l v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l v_{\text{g}}^i J \right)\nonumber\\ &+ \frac{\partial}{\partial x^l}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s F_s ={-}\sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial x^l}\,F_s. \end{align}
\begin{align} \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,p_l F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l J \right) &+ \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, p_l v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l v_{\text{g}}^i J \right)\nonumber\\ &+ \frac{\partial}{\partial x^l}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s F_s ={-}\sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial x^l}\,F_s. \end{align}
This can be viewed as a momentum-conservation theorem, because at ![]() $\smash {\partial _l H_{0s} = 0}$, one has
$\smash {\partial _l H_{0s} = 0}$, one has
Also, the ponderomotive force on a plasma is readily found from (7.87) as the sum of the terms quadratic in the wave amplitude (after ![]() $\smash {F_s}$ has been expressed through
$\smash {F_s}$ has been expressed through ![]() $\smash {\overline {f}_s}$). Similarly, if
$\smash {\overline {f}_s}$). Similarly, if ![]() $\smash {{\boldsymbol {\varXi }}_0}$,
$\smash {{\boldsymbol {\varXi }}_0}$, ![]() $\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and
$\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and ![]() $\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of
$\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of ![]() $\smash {t}$, one has (Appendix D.2)
$\smash {t}$, one has (Appendix D.2)
 \begin{align} \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \int \mathrm{d}{\boldsymbol{k}}\,w J \right)& + \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, H_{0s} v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J \right)\nonumber\\ & + \frac{\partial}{\partial x^i}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s v_s^i F_s = \sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s. \end{align}
\begin{align} \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \int \mathrm{d}{\boldsymbol{k}}\,w J \right)& + \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, H_{0s} v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J \right)\nonumber\\ & + \frac{\partial}{\partial x^i}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s v_s^i F_s = \sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s. \end{align}
This can be viewed as an energy-conservation theorem, because at ![]() $\smash {\partial _t H_{0s} = 0}$, one has
$\smash {\partial _t H_{0s} = 0}$, one has
Related equations are also discussed in Dodin & Fisch (Reference Dodin and Fisch2012) and Dewar (Reference Dewar1977).
The individual terms in (7.87) and (7.89) can be interpreted as described in table 1. The results of § 7.2.3 are reproduced as a particular case for the eikonal-wave ansatz (7.78).Footnote 37 In particular, note that electrostatic waves carry non-zero momentum density ![]() $\smash {\int \mathrm {d}{\boldsymbol {k}}\,{\boldsymbol {k}} J}$ just like any other waves, even though an electrostatic field of these waves carries no momentum. The momentum is stored in the particle motion in this case (§ 9.1.3), and it is pumped there via either temporal dependence (Liu & Dodin Reference Liu and Dodin2015, § II.2) or spatial dependence (Ochs & Fisch Reference Ochs and Fisch2021b, Reference Ochs and Fisch2022) of the wave amplitude. This shows that homogeneous-plasma models that ignore ponderomotive effects cannot adequately describe the energy–momentum transfer between waves and plasma even when resonant absorption per se occurs in a homogeneous-plasma region. The OC formalism presented here provides means to describe such processes rigorously, generally, and without cumbersome calculations.
$\smash {\int \mathrm {d}{\boldsymbol {k}}\,{\boldsymbol {k}} J}$ just like any other waves, even though an electrostatic field of these waves carries no momentum. The momentum is stored in the particle motion in this case (§ 9.1.3), and it is pumped there via either temporal dependence (Liu & Dodin Reference Liu and Dodin2015, § II.2) or spatial dependence (Ochs & Fisch Reference Ochs and Fisch2021b, Reference Ochs and Fisch2022) of the wave amplitude. This shows that homogeneous-plasma models that ignore ponderomotive effects cannot adequately describe the energy–momentum transfer between waves and plasma even when resonant absorption per se occurs in a homogeneous-plasma region. The OC formalism presented here provides means to describe such processes rigorously, generally, and without cumbersome calculations.
Table 1. Interpretation of the individual terms in (7.87) and (7.89). The wave energy–momentum is understood as the canonical (‘Minkowski’) energy–momentum, which must not be confused with the kinetic (‘Abraham’) energy–momentum (Dewar Reference Dewar1977; Dodin & Fisch Reference Dodin and Fisch2012). Whether the terms with ![]() $\smash {\varDelta _s F_s}$ should be attributed to OCs or to the wave is a matter of convention, because
$\smash {\varDelta _s F_s}$ should be attributed to OCs or to the wave is a matter of convention, because ![]() $\smash {\varDelta _s F_s}$ scales linearly both with
$\smash {\varDelta _s F_s}$ scales linearly both with ![]() $\smash {F_s}$ and with
$\smash {F_s}$ and with ![]() $\smash {J}$. In contrast, the wave energy density is defined unambiguously as
$\smash {J}$. In contrast, the wave energy density is defined unambiguously as ![]() $\smash {\mathcal {E}_s \doteq \int \mathrm {d}{\boldsymbol {p}}\,H_{0s} F_s}$ and does not contain
$\smash {\mathcal {E}_s \doteq \int \mathrm {d}{\boldsymbol {p}}\,H_{0s} F_s}$ and does not contain ![]() $\smash {\varDelta _s}$. This is because
$\smash {\varDelta _s}$. This is because ![]() $\smash {\int \mathrm {d}{\boldsymbol {p}}\,\varDelta _s F_s}$ is a part of the wave energy density
$\smash {\int \mathrm {d}{\boldsymbol {p}}\,\varDelta _s F_s}$ is a part of the wave energy density ![]() $\smash {\mathcal {E}_{\text {w}}}$ (Dodin & Fisch Reference Dodin and Fisch2010a). Similarly,
$\smash {\mathcal {E}_{\text {w}}}$ (Dodin & Fisch Reference Dodin and Fisch2010a). Similarly, ![]() $\smash {\int \mathrm {d}{\boldsymbol {p}}\,(\partial _{{\boldsymbol {v}}_s}\varDelta _s) F_s}$ is a part of the wave momentum density (Dodin & Fisch Reference Dodin and Fisch2012).
$\smash {\int \mathrm {d}{\boldsymbol {p}}\,(\partial _{{\boldsymbol {v}}_s}\varDelta _s) F_s}$ is a part of the wave momentum density (Dodin & Fisch Reference Dodin and Fisch2012).

7.6. Summary of § 7
In summary, we have considered plasma interaction with general broadband single-mode on-shell waves (for examples, see § 9). Assuming a general response matrix ![]() $\smash {{\boldsymbol {\varXi }}}$, these waves have a dispersion function
$\smash {{\boldsymbol {\varXi }}}$, these waves have a dispersion function ![]() $\smash {\varLambda (t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})}$ and polarization
$\smash {\varLambda (t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})}$ and polarization ![]() ${\boldsymbol {\eta }}(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})$ determined by
${\boldsymbol {\eta }}(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})$ determined by
where the normalization ![]() $\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\eta }} = 1}$ is assumed. Specifically for
$\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\eta }} = 1}$ is assumed. Specifically for ![]() $\smash {{\boldsymbol {\varXi }}}$ given by (6.80), one has
$\smash {{\boldsymbol {\varXi }}}$ given by (6.80), one has
 \begin{align} \varLambda(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}) = {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_0 {\boldsymbol{\eta}} & - \sum_s \int \mathrm{d}{\boldsymbol{p}}\, {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\wp}}_s({\boldsymbol{p}}){\boldsymbol{\eta}}\,F_s({\boldsymbol{p}}) \nonumber\\ &+ \sum_s {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{|{\boldsymbol{\alpha}}_s^{{{\dagger}}}{\boldsymbol{\eta}}|^2 ({\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s({\boldsymbol{p}})}\, {\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \end{align}
\begin{align} \varLambda(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}) = {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_0 {\boldsymbol{\eta}} & - \sum_s \int \mathrm{d}{\boldsymbol{p}}\, {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\wp}}_s({\boldsymbol{p}}){\boldsymbol{\eta}}\,F_s({\boldsymbol{p}}) \nonumber\\ &+ \sum_s {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{|{\boldsymbol{\alpha}}_s^{{{\dagger}}}{\boldsymbol{\eta}}|^2 ({\boldsymbol{p}})}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s({\boldsymbol{p}})}\, {\boldsymbol{k}} \cdot \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \end{align}
where the arguments ![]() $\smash {(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})}$ are omitted for brevity. (Some notation is summarized in § 6.9.) The wave frequency
$\smash {(t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}})}$ are omitted for brevity. (Some notation is summarized in § 6.9.) The wave frequency ![]() $\smash {\omega = w(t, {\boldsymbol {x}}, {\boldsymbol {k}})}$ satisfies
$\smash {\omega = w(t, {\boldsymbol {x}}, {\boldsymbol {k}})}$ satisfies
and ![]() $\smash {w(t, {\boldsymbol {x}}, -{\boldsymbol {k}}) = -w(t, {\boldsymbol {x}}, {\boldsymbol {k}})}$, where
$\smash {w(t, {\boldsymbol {x}}, -{\boldsymbol {k}}) = -w(t, {\boldsymbol {x}}, {\boldsymbol {k}})}$, where ![]() $w$ is a real function at real arguments. The wave local linear growth rate
$w$ is a real function at real arguments. The wave local linear growth rate ![]() $\smash {\gamma }$, which is assumed to be small in this section, is
$\smash {\gamma }$, which is assumed to be small in this section, is
 \begin{equation} \gamma (t, {\boldsymbol{x}}, {\boldsymbol{k}}) ={-}\left( \frac{{\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_\text{A} {\boldsymbol{\eta}}}{\partial_{\omega}\varLambda} \right)_{(t, {\boldsymbol{x}}, w(t, {\boldsymbol{x}}, {\boldsymbol{k}}), {\boldsymbol{k}})}, \end{equation}
\begin{equation} \gamma (t, {\boldsymbol{x}}, {\boldsymbol{k}}) ={-}\left( \frac{{\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{\varXi}}_\text{A} {\boldsymbol{\eta}}}{\partial_{\omega}\varLambda} \right)_{(t, {\boldsymbol{x}}, w(t, {\boldsymbol{x}}, {\boldsymbol{k}}), {\boldsymbol{k}})}, \end{equation}or explicitly,
 \[ \gamma (t, {\boldsymbol{x}}, {\boldsymbol{k}}) = {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda(t, {\boldsymbol{x}}, w, {\boldsymbol{k}})}\, \delta(w - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}))\,{\boldsymbol{k}} \cdot \frac{\partial F_s(t, {\boldsymbol{x}}, {\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \]
\[ \gamma (t, {\boldsymbol{x}}, {\boldsymbol{k}}) = {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda(t, {\boldsymbol{x}}, w, {\boldsymbol{k}})}\, \delta(w - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s(t, {\boldsymbol{x}}, {\boldsymbol{p}}))\,{\boldsymbol{k}} \cdot \frac{\partial F_s(t, {\boldsymbol{x}}, {\boldsymbol{p}})}{\partial {\boldsymbol{p}}}, \]
where ![]() $w \equiv w(t, {\boldsymbol {x}}, {\boldsymbol {k}})$ and
$w \equiv w(t, {\boldsymbol {x}}, {\boldsymbol {k}})$ and ![]() $\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2 \equiv |{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2(t, {\boldsymbol {x}}, w, {\boldsymbol {k}}; {\boldsymbol {p}})}$. The nonlinear potentials (6.77) are expressed through the scalar function
$\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2 \equiv |{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2(t, {\boldsymbol {x}}, w, {\boldsymbol {k}}; {\boldsymbol {p}})}$. The nonlinear potentials (6.77) are expressed through the scalar function
where ![]() $\smash {\varsigma _{{\boldsymbol {k}}} \doteq \operatorname {sgn}(\partial _{\omega }\varLambda (t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}))}$ is evaluated at
$\smash {\varsigma _{{\boldsymbol {k}}} \doteq \operatorname {sgn}(\partial _{\omega }\varLambda (t, {\boldsymbol {x}}, \omega, {\boldsymbol {k}}))}$ is evaluated at ![]() $\omega = w(t, {\boldsymbol {x}}, {\boldsymbol {k}})$; see also (7.82). The function
$\omega = w(t, {\boldsymbol {x}}, {\boldsymbol {k}})$; see also (7.82). The function ![]() $J$ is the phase-space action density governed by the WKE
$J$ is the phase-space action density governed by the WKE
where ![]() $\smash {\partial _{\boldsymbol {k}} w = {\boldsymbol {v}}_{\text {g}}}$ is the group velocity. Collisional dissipation is assumed small compared with collisionless dissipation, so it is neglected in (7.96) but can be reintroduced by an ad hoc modification of
$\smash {\partial _{\boldsymbol {k}} w = {\boldsymbol {v}}_{\text {g}}}$ is the group velocity. Collisional dissipation is assumed small compared with collisionless dissipation, so it is neglected in (7.96) but can be reintroduced by an ad hoc modification of ![]() $\smash {\gamma }$ (§ 6.2). Unlike the field equation used in the standard QLT, (7.96) exactly conserves the action of non-resonant waves, i.e. those with
$\smash {\gamma }$ (§ 6.2). Unlike the field equation used in the standard QLT, (7.96) exactly conserves the action of non-resonant waves, i.e. those with ![]() $\smash {\gamma = 0}$. The WKE must be solved together with the QL equation for the OC distribution
$\smash {\gamma = 0}$. The WKE must be solved together with the QL equation for the OC distribution ![]() $F_s$,
$F_s$,
because ![]() $F_s$ determines the coefficients in (7.96) and
$F_s$ determines the coefficients in (7.96) and ![]() $\smash {J}$ determines the coefficients in (7.97). When
$\smash {J}$ determines the coefficients in (7.97). When ![]() $\smash {{\boldsymbol {\varXi }}_0}$ and
$\smash {{\boldsymbol {\varXi }}_0}$ and ![]() $\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ are independent of
$\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ are independent of ![]() $\smash {t}$ and
$\smash {t}$ and ![]() $\smash {{\boldsymbol {x}}}$, (7.96) and (7.97) conserve the total momentum and energy of the system; specifically,
$\smash {{\boldsymbol {x}}}$, (7.96) and (7.97) conserve the total momentum and energy of the system; specifically,
Here, the notation is as in table 1, or see (7.87) and (7.89) instead.
8. Thermal equilibrium
In this section, we discuss, for completeness, the properties of plasmas in thermal equilibrium.
8.1. Boltzmann–Gibbs distribution
As discussed in § 6.8, collisions conserve the density of each species, the total momentum density and the total energy density, while the plasma total entropy density ![]() $\smash {\sigma }$ either grows or remains constant. Let us search for equilibrium states in particular. At least one of the states in which
$\smash {\sigma }$ either grows or remains constant. Let us search for equilibrium states in particular. At least one of the states in which ![]() $\smash {\sigma }$ remains constant is the one that maximizes the entropy density at fixed
$\smash {\sigma }$ remains constant is the one that maximizes the entropy density at fixed ![]() $\smash {\int \mathrm {d}{\boldsymbol {p}}\,F_s}$,
$\smash {\int \mathrm {d}{\boldsymbol {p}}\,F_s}$, ![]() $\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,{\boldsymbol {p}}F_s}$ and
$\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,{\boldsymbol {p}}F_s}$ and ![]() $\smash {\sum _s\int \mathrm {d}{\boldsymbol {p}}\,\mathcal {H}_s F_s}$. This ‘state of thermal equilibrium’ can be found as an extremizer of
$\smash {\sum _s\int \mathrm {d}{\boldsymbol {p}}\,\mathcal {H}_s F_s}$. This ‘state of thermal equilibrium’ can be found as an extremizer of
considered as a functional of all ![]() $\smash {F_s}$, where
$\smash {F_s}$, where ![]() $\smash {\lambda _s^{(\mathcal {N})}}$,
$\smash {\lambda _s^{(\mathcal {N})}}$, ![]() $\smash {{\boldsymbol {\lambda }}^{({\boldsymbol {P}})}}$ and
$\smash {{\boldsymbol {\lambda }}^{({\boldsymbol {P}})}}$ and ![]() $\smash {\lambda ^{(\mathcal {H})}}$ are Lagrange multipliers. Using (6.73), one finds that extremizers of
$\smash {\lambda ^{(\mathcal {H})}}$ are Lagrange multipliers. Using (6.73), one finds that extremizers of ![]() $\smash {\sigma '}$ satisfy
$\smash {\sigma '}$ satisfy
whence
The pre-exponential constant is determined by the given density of species ![]() $\smash {s}$, while
$\smash {s}$, while ![]() $\smash {{\boldsymbol {\lambda }}^{({\boldsymbol {P}})}}$ and
$\smash {{\boldsymbol {\lambda }}^{({\boldsymbol {P}})}}$ and ![]() $\smash {\lambda ^{(\mathcal {H})}}$ can be expressed through the densities of the plasma momentum and energy stored in the whole distribution. Because
$\smash {\lambda ^{(\mathcal {H})}}$ can be expressed through the densities of the plasma momentum and energy stored in the whole distribution. Because
the matrix ![]() $\smash {\delta ^2 \sigma '/\delta F_s \delta F_{s'}}$ is positive-definite, so the entropy is maximal (as opposed to minimal) at the extremizer (8.3).
$\smash {\delta ^2 \sigma '/\delta F_s \delta F_{s'}}$ is positive-definite, so the entropy is maximal (as opposed to minimal) at the extremizer (8.3).
The distribution (8.3) is known as the Boltzmann–Gibbs distribution, with ![]() $\smash {T \doteq ~1/\lambda ^{(\mathcal {H})}}$ being the temperature (common for all species). Also, let us introduce a new, rescaled Lagrange multiplier
$\smash {T \doteq ~1/\lambda ^{(\mathcal {H})}}$ being the temperature (common for all species). Also, let us introduce a new, rescaled Lagrange multiplier ![]() $\smash {{\boldsymbol {\mathfrak {u}}}}$ via
$\smash {{\boldsymbol {\mathfrak {u}}}}$ via ![]() $\smash {{\boldsymbol {\lambda }}^{({\boldsymbol {P}})} = -{\boldsymbol {\mathfrak {u}}}/T}$. Then,
$\smash {{\boldsymbol {\lambda }}^{({\boldsymbol {P}})} = -{\boldsymbol {\mathfrak {u}}}/T}$. Then,
where ![]() $\smash {F_s^{(0)}}$ is independent of
$\smash {F_s^{(0)}}$ is independent of ![]() $\smash {{\boldsymbol {p}}}$. Correspondingly,
$\smash {{\boldsymbol {p}}}$. Correspondingly,
where we used (5.44). From (8.6), one obtains
 \begin{align} &\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, {\boldsymbol{k}}\cdot \left(\frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'}\right)\nonumber\\ &\quad ={-} \frac{1}{T}\,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, ({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, F_s({\boldsymbol{p}})F_{s'}({\boldsymbol{p}}')\nonumber\\ &\quad = 0, \end{align}
\begin{align} &\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, {\boldsymbol{k}}\cdot \left(\frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'}\right)\nonumber\\ &\quad ={-} \frac{1}{T}\,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, ({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'})\, F_s({\boldsymbol{p}})F_{s'}({\boldsymbol{p}}')\nonumber\\ &\quad = 0, \end{align}
where ![]() $\smash {\mathcal {H}'_{s'} \doteq \mathcal {H}_{s'}({\boldsymbol {p}}')}$. Then, (6.61) yields that the collision operator vanishes on the Boltzmann–Gibbs distribution, and thus, expectedly,
$\smash {\mathcal {H}'_{s'} \doteq \mathcal {H}_{s'}({\boldsymbol {p}}')}$. Then, (6.61) yields that the collision operator vanishes on the Boltzmann–Gibbs distribution, and thus, expectedly, ![]() $\smash {(\mathrm {d}\sigma /\mathrm {d} t)_{\text {coll}} = 0}$. One can also show that the Boltzmann–Gibbs distribution is the only distribution (strictly speaking, a class of distributions parameterized by
$\smash {(\mathrm {d}\sigma /\mathrm {d} t)_{\text {coll}} = 0}$. One can also show that the Boltzmann–Gibbs distribution is the only distribution (strictly speaking, a class of distributions parameterized by ![]() $\smash {T}$ and
$\smash {T}$ and ![]() $\smash {{\boldsymbol {\mathfrak {u}}}}$) for which the entropy density is conserved (Appendix E).
$\smash {{\boldsymbol {\mathfrak {u}}}}$) for which the entropy density is conserved (Appendix E).
The property (8.6) of the thermal-equilibrium state also leads to other notable results that we derive below. In doing so, we will assume the reference frame where ![]() $\smash {{\boldsymbol {\mathfrak {u}}} = 0}$, so the Boltzmann–Gibbs distribution has a better known form
$\smash {{\boldsymbol {\mathfrak {u}}} = 0}$, so the Boltzmann–Gibbs distribution has a better known form
(For ![]() $\smash {\mathcal {H}_s}$ isotropic in
$\smash {\mathcal {H}_s}$ isotropic in ![]() $\smash {{\boldsymbol {p}}}$, this is the frame where the plasma total momentum density
$\smash {{\boldsymbol {p}}}$, this is the frame where the plasma total momentum density ![]() $\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,{\boldsymbol {p}}F_s}$ is zero.) The generalizations to arbitrary
$\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,{\boldsymbol {p}}F_s}$ is zero.) The generalizations to arbitrary ![]() $\smash {{\boldsymbol {\mathfrak {u}}}}$ are straightforward.
$\smash {{\boldsymbol {\mathfrak {u}}}}$ are straightforward.
8.2. Fluctuation–dissipation theorem
Let us describe microscopic fluctuations in equilibrium plasmas in terms of ![]() $\smash {{{\boldsymbol {\mathsf {S}}}}(\omega, {\boldsymbol {k}}) \doteq (2{\rm \pi} )^{{{\mathsf {n}}}}\,{\boldsymbol {\mathfrak {W}}}(\omega, {\boldsymbol {k}})}$, i.e.
$\smash {{{\boldsymbol {\mathsf {S}}}}(\omega, {\boldsymbol {k}}) \doteq (2{\rm \pi} )^{{{\mathsf {n}}}}\,{\boldsymbol {\mathfrak {W}}}(\omega, {\boldsymbol {k}})}$, i.e.
which can also be represented in terms of the Fourier image ![]() $\smash {\mathring {{\boldsymbol {\varPsi }}}(\omega, {\boldsymbol {k}})}$ of the microscopic field
$\smash {\mathring {{\boldsymbol {\varPsi }}}(\omega, {\boldsymbol {k}})}$ of the microscopic field ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}(t, {\boldsymbol {x}})}$:
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {{\boldsymbol {\varPsi }}}}(t, {\boldsymbol {x}})}$:
 \begin{equation} {{\boldsymbol {\mathsf{S}}}}(\omega, {\boldsymbol{k}}) = \frac{\overline{ \mathring{{\boldsymbol{\varPsi}}}(\omega, {\boldsymbol{k}}) \smash{\mathring{{\boldsymbol{\varPsi}}}}^{{\dagger}}(\omega, {\boldsymbol{k}}) }}{\mathscr{T}\mathscr{V}_n}. \end{equation}
\begin{equation} {{\boldsymbol {\mathsf{S}}}}(\omega, {\boldsymbol{k}}) = \frac{\overline{ \mathring{{\boldsymbol{\varPsi}}}(\omega, {\boldsymbol{k}}) \smash{\mathring{{\boldsymbol{\varPsi}}}}^{{\dagger}}(\omega, {\boldsymbol{k}}) }}{\mathscr{T}\mathscr{V}_n}. \end{equation}
For statistically homogeneous fields that persist on time ![]() $\smash {\mathscr {T} \to \infty }$ within volume
$\smash {\mathscr {T} \to \infty }$ within volume ![]() $\smash {\mathscr {V}_n \to \infty }$, the Fourier transform is formally divergent; hence the appearance of the factors
$\smash {\mathscr {V}_n \to \infty }$, the Fourier transform is formally divergent; hence the appearance of the factors ![]() $\smash {\mathscr {T}}$ and
$\smash {\mathscr {T}}$ and ![]() $\smash {\mathscr {V}_n}$ in (8.10).Footnote 38 Also, as seen from (6.32), any quadratic function of the microscopic field can be expressed through
$\smash {\mathscr {V}_n}$ in (8.10).Footnote 38 Also, as seen from (6.32), any quadratic function of the microscopic field can be expressed through ![]() $\smash {{{\boldsymbol {\mathsf {S}}}}}$ via
$\smash {{{\boldsymbol {\mathsf {S}}}}}$ via
where ![]() $\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {L}}}}}}$ and
$\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {L}}}}}}$ and ![]() $\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {R}}}}}}$ are any linear operators and
$\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {R}}}}}}$ are any linear operators and ![]() $\smash {{{\boldsymbol {\mathsf {L}}}}}$ and
$\smash {{{\boldsymbol {\mathsf {L}}}}}$ and ![]() $\smash {{{\boldsymbol {\mathsf {R}}}}}$ are their symbols.
$\smash {{{\boldsymbol {\mathsf {R}}}}}$ are their symbols.
From (6.31), one finds that, in general,
For a thermal distribution in particular, which satisfies (8.8), one can rewrite (6.24) as follows:
 \begin{align} {\boldsymbol{\varXi}}_\text{A}(\omega, {\boldsymbol{k}}) & \approx \frac{\rm \pi}{T} \sum_s \int \mathrm{d}{\boldsymbol{p}}\, {\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) F_s({\boldsymbol{p}}) \nonumber\\ & = \frac{{\rm \pi} \omega}{T} \sum_s \int \mathrm{d}{\boldsymbol{p}}\, {\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) F_s({\boldsymbol{p}}). \end{align}
\begin{align} {\boldsymbol{\varXi}}_\text{A}(\omega, {\boldsymbol{k}}) & \approx \frac{\rm \pi}{T} \sum_s \int \mathrm{d}{\boldsymbol{p}}\, {\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) F_s({\boldsymbol{p}}) \nonumber\\ & = \frac{{\rm \pi} \omega}{T} \sum_s \int \mathrm{d}{\boldsymbol{p}}\, {\boldsymbol{\alpha}}_s(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}){\boldsymbol{\alpha}}_s^{{\dagger}}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}) \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) F_s({\boldsymbol{p}}). \end{align}By comparing this with (8.12), one also finds that
Due to (6.26), this leads to the fluctuation–dissipation theorem in the following form:
For examples of ![]() $\smash {{\boldsymbol {\varXi }}}$ for specific systems, see § 9.
$\smash {{\boldsymbol {\varXi }}}$ for specific systems, see § 9.
8.3. Kirchhoff's law
Consider the power deposition via polarization drag
Using (6.58a) for ![]() $\smash {{\boldsymbol {\mathfrak {F}}}_s}$, (8.13) for
$\smash {{\boldsymbol {\mathfrak {F}}}_s}$, (8.13) for ![]() $\smash {{\boldsymbol {\varXi }}_\text {A}}$ and (8.15) for
$\smash {{\boldsymbol {\varXi }}_\text {A}}$ and (8.15) for ![]() $\smash {{{\boldsymbol {\mathsf {S}}}}}$, this can also be expressed as follows:
$\smash {{{\boldsymbol {\mathsf {S}}}}}$, this can also be expressed as follows:
 \begin{align} \mathfrak{P} & \approx \sum_s \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\, ({\boldsymbol{\alpha}}_s^{{\dagger}} ({\boldsymbol{\varXi}}^{{-}1})_\text{A} {\boldsymbol{\alpha}}_s)({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}) F_s({\boldsymbol{p}}) \nonumber\\ & = \sum_s\int \frac{\mathrm{d}\omega}{2{\rm \pi}} \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\, 2{\rm \pi}\omega\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) ({\boldsymbol{\alpha}}_s^{{\dagger}} ({\boldsymbol{\varXi}}^{{-}1})_\text{A} {\boldsymbol{\alpha}}_s)(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})F_s({\boldsymbol{p}}) \nonumber\\ & = 2T \int \frac{\mathrm{d}\omega}{2{\rm \pi}} \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n} \operatorname{tr}\bigg(({\boldsymbol{\varXi}}^{{-}1})_\text{A} \frac{{\rm \pi} \omega}{T}\, \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) ({\boldsymbol{\alpha}}_s{\boldsymbol{\alpha}}_s^{{\dagger}})(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})F_s({\boldsymbol{p}})\bigg) \nonumber\\ & ={-}\int \frac{\mathrm{d}\omega}{2{\rm \pi}}\,\frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\omega \operatorname{tr}({{\boldsymbol {\mathsf{S}}}}{\boldsymbol{\varXi}}_\text{A})(\omega, {\boldsymbol{k}}). \end{align}
\begin{align} \mathfrak{P} & \approx \sum_s \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\, ({\boldsymbol{\alpha}}_s^{{\dagger}} ({\boldsymbol{\varXi}}^{{-}1})_\text{A} {\boldsymbol{\alpha}}_s)({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}) F_s({\boldsymbol{p}}) \nonumber\\ & = \sum_s\int \frac{\mathrm{d}\omega}{2{\rm \pi}} \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\, 2{\rm \pi}\omega\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) ({\boldsymbol{\alpha}}_s^{{\dagger}} ({\boldsymbol{\varXi}}^{{-}1})_\text{A} {\boldsymbol{\alpha}}_s)(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})F_s({\boldsymbol{p}}) \nonumber\\ & = 2T \int \frac{\mathrm{d}\omega}{2{\rm \pi}} \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n} \operatorname{tr}\bigg(({\boldsymbol{\varXi}}^{{-}1})_\text{A} \frac{{\rm \pi} \omega}{T}\, \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) ({\boldsymbol{\alpha}}_s{\boldsymbol{\alpha}}_s^{{\dagger}})(\omega, {\boldsymbol{k}}; {\boldsymbol{p}})F_s({\boldsymbol{p}})\bigg) \nonumber\\ & ={-}\int \frac{\mathrm{d}\omega}{2{\rm \pi}}\,\frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\omega \operatorname{tr}({{\boldsymbol {\mathsf{S}}}}{\boldsymbol{\varXi}}_\text{A})(\omega, {\boldsymbol{k}}). \end{align}Thus, the spectral density of the power deposition via polarization drag is given by
which is a restatement of Kirchhoff's law (Krall & Trivelpiece Reference Krall and Trivelpiece1973, § 11.4). For examples of ![]() $\smash {{\boldsymbol {\varXi }}}$ for specific systems, see § 9.
$\smash {{\boldsymbol {\varXi }}}$ for specific systems, see § 9.
8.4. Equipartition theorem
As flows from § 7.5, the energy of on-shell waves of a field ![]() $\smash {{\boldsymbol {\widetilde {\varPsi }}}}$ in a homogeneous
$\smash {{\boldsymbol {\widetilde {\varPsi }}}}$ in a homogeneous ![]() $\smash {n}$-dimensional plasma of a given volume
$\smash {n}$-dimensional plasma of a given volume ![]() $\smash {\mathscr {V}_n}$ can be written as
$\smash {\mathscr {V}_n}$ can be written as
 \begin{align} \mathscr{V}_n\mathcal{E}_{\text{w}} & = \int \mathrm{d}{\boldsymbol{k}}\,\mathscr{V}_n w({\boldsymbol{k}})J({\boldsymbol{k}}) \nonumber\\ & = (2{\rm \pi})^n\int \frac{\mathscr{V}_n \mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\int_0^\infty \mathrm{d}\omega\, \omega\,\partial_\omega\varLambda(\omega, {\boldsymbol{k}})\,h({\boldsymbol{k}})\,\delta(\omega - w({\boldsymbol{k}})) \nonumber\\ & = (2{\rm \pi})^n \sum_{{\boldsymbol{k}}} \int^{\infty}_0 \mathrm{d}\omega\,\omega\, \partial_\omega\varLambda(\omega, {\boldsymbol{k}})\, ({\boldsymbol{\eta}}^{{\dagger}}{{\boldsymbol {\mathsf{U}}}}{\boldsymbol{\eta}})(\omega, {\boldsymbol{k}}). \end{align}
\begin{align} \mathscr{V}_n\mathcal{E}_{\text{w}} & = \int \mathrm{d}{\boldsymbol{k}}\,\mathscr{V}_n w({\boldsymbol{k}})J({\boldsymbol{k}}) \nonumber\\ & = (2{\rm \pi})^n\int \frac{\mathscr{V}_n \mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\int_0^\infty \mathrm{d}\omega\, \omega\,\partial_\omega\varLambda(\omega, {\boldsymbol{k}})\,h({\boldsymbol{k}})\,\delta(\omega - w({\boldsymbol{k}})) \nonumber\\ & = (2{\rm \pi})^n \sum_{{\boldsymbol{k}}} \int^{\infty}_0 \mathrm{d}\omega\,\omega\, \partial_\omega\varLambda(\omega, {\boldsymbol{k}})\, ({\boldsymbol{\eta}}^{{\dagger}}{{\boldsymbol {\mathsf{U}}}}{\boldsymbol{\eta}})(\omega, {\boldsymbol{k}}). \end{align}
To apply this to microscopic fluctuations, one can replace ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$ with
$\smash {{{\boldsymbol {\mathsf {U}}}}}$ with ![]() $\smash {{\boldsymbol {\mathfrak {W}}}}$ and substitute
$\smash {{\boldsymbol {\mathfrak {W}}}}$ and substitute ![]() $\smash {{\boldsymbol {\mathfrak {W}}} = (2{\rm \pi} )^{-(n+1)}{{\boldsymbol {\mathsf {S}}}}}$. Then, the total energy of a mode with given wavevector
$\smash {{\boldsymbol {\mathfrak {W}}} = (2{\rm \pi} )^{-(n+1)}{{\boldsymbol {\mathsf {S}}}}}$. Then, the total energy of a mode with given wavevector ![]() $\smash {{\boldsymbol {k}}}$ and polarization
$\smash {{\boldsymbol {k}}}$ and polarization ![]() $\smash {{\boldsymbol {\eta }}}$ can be expressed as
$\smash {{\boldsymbol {\eta }}}$ can be expressed as
where the arguments ![]() $\smash {(\omega, {\boldsymbol {k}})}$ are omitted for brevity. For thermal equilibrium, one can substitute (8.15) for
$\smash {(\omega, {\boldsymbol {k}})}$ are omitted for brevity. For thermal equilibrium, one can substitute (8.15) for ![]() $\smash {{{\boldsymbol {\mathsf {S}}}}}$; then,
$\smash {{{\boldsymbol {\mathsf {S}}}}}$; then,
The integrand peaks at ![]() $\smash {\omega = w({\boldsymbol {k}})}$, where the mode eigenvalue
$\smash {\omega = w({\boldsymbol {k}})}$, where the mode eigenvalue ![]() $\smash {\varLambda }$ is small. Due to damping, the actual zero of
$\smash {\varLambda }$ is small. Due to damping, the actual zero of ![]() $\smash {\varLambda }$ is slightly below the real axis in the complex-frequency space. Then, at infinitesimally small damping,
$\smash {\varLambda }$ is slightly below the real axis in the complex-frequency space. Then, at infinitesimally small damping, ![]() $\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\varXi }}^{-1} {\boldsymbol {\eta }}}$ can be approximated near
$\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\varXi }}^{-1} {\boldsymbol {\eta }}}$ can be approximated near ![]() $\smash {\omega = w({\boldsymbol {k}})}$ as
$\smash {\omega = w({\boldsymbol {k}})}$ as
This leads to the well-known equipartition theorem
Note that, according to (8.23), the sum ![]() $\smash {\mathscr {V}_n\mathcal {E}_{\text {w}} = \sum _{{\boldsymbol {k}}, {\boldsymbol {\eta }}}\mathcal {E}_{{\boldsymbol {k}}, {\boldsymbol {\eta }}}}$ is divergent. This indicates that not all modes can be classical and on-shell (weakly damped) simultaneously.
$\smash {\mathscr {V}_n\mathcal {E}_{\text {w}} = \sum _{{\boldsymbol {k}}, {\boldsymbol {\eta }}}\mathcal {E}_{{\boldsymbol {k}}, {\boldsymbol {\eta }}}}$ is divergent. This indicates that not all modes can be classical and on-shell (weakly damped) simultaneously.
8.5. Summary of § 8
In thermal equilibrium, when all species have Boltzmann–Gibbs distributions with common temperature ![]() $\smash {T}$, the collision operator vanishes, the entropy is conserved and the spectrum of microscopic fluctuations (8.9) satisfies the fluctuation–dissipation theorem
$\smash {T}$, the collision operator vanishes, the entropy is conserved and the spectrum of microscopic fluctuations (8.9) satisfies the fluctuation–dissipation theorem
where ![]() $\smash {{\boldsymbol {\varXi }}}$ is the dispersion matrix (6.80) and
$\smash {{\boldsymbol {\varXi }}}$ is the dispersion matrix (6.80) and ![]() $\smash {_\text {A}}$ denotes the anti-Hermitian part (or the imaginary part in case of scalar fields). From here, it is shown that the spectral density of the power deposition via polarization drag is given by
$\smash {_\text {A}}$ denotes the anti-Hermitian part (or the imaginary part in case of scalar fields). From here, it is shown that the spectral density of the power deposition via polarization drag is given by ![]() $\smash {\mathfrak {P}_{\omega, {\boldsymbol {k}}} = - \omega \operatorname {tr}({{\boldsymbol {\mathsf {S}}}}{\boldsymbol {\varXi }}_\text {A})}$, which is a restatement of Kirchhoff's law. For on-shell waves, (8.24) reduces to the equipartition theorem, which says that the energy per mode equals
$\smash {\mathfrak {P}_{\omega, {\boldsymbol {k}}} = - \omega \operatorname {tr}({{\boldsymbol {\mathsf {S}}}}{\boldsymbol {\varXi }}_\text {A})}$, which is a restatement of Kirchhoff's law. For on-shell waves, (8.24) reduces to the equipartition theorem, which says that the energy per mode equals ![]() $\smash {T}$. Applications to specific systems are discussed in § 9.
$\smash {T}$. Applications to specific systems are discussed in § 9.
9. Examples
In this section, we show how to apply our general formulation to non-relativistic electrostatic interactions (§ 9.1), relativistic electromagnetic interactions (§ 9.2), Newtonian gravity (§ 9.3) and relativistic gravity, including gravitational waves (§ 9.4).
9.1. Non-relativistic electrostatic interactions
9.1.1. Main equations
Let us show how our general formulation reproduces (and generalizes) the well-known results for electrostatic turbulence in non-magnetized non-relativistic plasma. In this case,
where ![]() $e_s$ is the electric charge,
$e_s$ is the electric charge, ![]() $\varphi$ is the electrostatic potential and
$\varphi$ is the electrostatic potential and ![]() $\smash {\overline {\varphi }}$ and
$\smash {\overline {\varphi }}$ and ![]() $\smash {\widetilde {\varphi }}$ are its average and oscillating parts, respectively. Then,
$\smash {\widetilde {\varphi }}$ are its average and oscillating parts, respectively. Then, ![]() $\smash {H_{0s} = \overline {H}_s = p^2/(2m_s) + e_s \overline {\varphi }}$,
$\smash {H_{0s} = \overline {H}_s = p^2/(2m_s) + e_s \overline {\varphi }}$, ![]() $\smash {\widetilde {H}_s = e_s \widetilde {\varphi }}$,
$\smash {\widetilde {H}_s = e_s \widetilde {\varphi }}$, ![]() $\smash {\widehat {\boldsymbol {\alpha }}_s = e_s}$ and
$\smash {\widehat {\boldsymbol {\alpha }}_s = e_s}$ and ![]() $\smash {\widehat {\boldsymbol {L}}_s = \widehat {\boldsymbol {R}}_s = \widehat {\boldsymbol {0}}}$, so
$\smash {\widehat {\boldsymbol {L}}_s = \widehat {\boldsymbol {R}}_s = \widehat {\boldsymbol {0}}}$, so ![]() $\smash {{\boldsymbol {\wp }}_s = {\boldsymbol {0}}}$. The matrix (6.78) is a scalar (Wigner function) given by
$\smash {{\boldsymbol {\wp }}_s = {\boldsymbol {0}}}$. The matrix (6.78) is a scalar (Wigner function) given by
(Underlining denotes the macroscopic part, ![]() $\smash {n \doteq \dim {\boldsymbol {x}}}$, and the arguments
$\smash {n \doteq \dim {\boldsymbol {x}}}$, and the arguments ![]() $\smash {(t, {\boldsymbol {x}})}$ will be omitted from now on.) Correspondingly,
$\smash {(t, {\boldsymbol {x}})}$ will be omitted from now on.) Correspondingly,
and also
The Lagrangian density of a free electrostatic field is
The first term on the right-hand side does not contribute to the field action ![]() $\smash {S_0}$ and thus can be ignored. The second term is of the form (6.1) with
$\smash {S_0}$ and thus can be ignored. The second term is of the form (6.1) with ![]() $\smash {M = 1}$,
$\smash {M = 1}$, ![]() $\smash {{\boldsymbol {\mathsf {g}}}} = 1$ (§ 2.1.2) and
$\smash {{\boldsymbol {\mathsf {g}}}} = 1$ (§ 2.1.2) and ![]() $\smash {\widehat {\boldsymbol {\varXi }}_0 = \widehat {k}^2/(4{\rm \pi} )}$, so
$\smash {\widehat {\boldsymbol {\varXi }}_0 = \widehat {k}^2/(4{\rm \pi} )}$, so ![]() $\smash {{\boldsymbol {\varXi }}_0 (\omega, {\boldsymbol {k}}) = k^2/(4{\rm \pi} )}$, where
$\smash {{\boldsymbol {\varXi }}_0 (\omega, {\boldsymbol {k}}) = k^2/(4{\rm \pi} )}$, where ![]() $\smash {k^2 \equiv {\boldsymbol {k}}^2 \equiv \delta ^{ij}k_i k_j}$. Then, (6.20) gives
$\smash {k^2 \equiv {\boldsymbol {k}}^2 \equiv \delta ^{ij}k_i k_j}$. Then, (6.20) gives
where the arguments ![]() $\smash {t}$ and
$\smash {t}$ and ![]() $\smash {{\boldsymbol {x}}}$ are omitted for brevity and
$\smash {{\boldsymbol {x}}}$ are omitted for brevity and ![]() $\smash {\epsilon _\parallel }$ is the parallel permittivity,
$\smash {\epsilon _\parallel }$ is the parallel permittivity,
 \begin{equation} \epsilon_\parallel(\omega, {\boldsymbol{k}}) = 1 + \sum_s \frac{4{\rm \pi} e_s^2}{k^2} \int \mathrm{d}{\boldsymbol{p}}\,\frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}}. \end{equation}
\begin{equation} \epsilon_\parallel(\omega, {\boldsymbol{k}}) = 1 + \sum_s \frac{4{\rm \pi} e_s^2}{k^2} \int \mathrm{d}{\boldsymbol{p}}\,\frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}}. \end{equation}9.1.2. Collisions and fluctuations
By (8.12), the spectrum of microscopic oscillations of ![]() $\smash {\widetilde {\varphi }}$ is a scalar given by
$\smash {\widetilde {\varphi }}$ is a scalar given by
 \begin{equation} {\mathsf{S}}(\omega, {\boldsymbol{k}}) = 2{\rm \pi}\sum_{s} \left(\frac{4{\rm \pi} e_s}{k^2 |\epsilon_\parallel (\omega, {\boldsymbol{k}})|}\right)^2 \int \mathrm{d}{\boldsymbol{p}}\, \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s})F_{s}({\boldsymbol{p}}), \end{equation}
\begin{equation} {\mathsf{S}}(\omega, {\boldsymbol{k}}) = 2{\rm \pi}\sum_{s} \left(\frac{4{\rm \pi} e_s}{k^2 |\epsilon_\parallel (\omega, {\boldsymbol{k}})|}\right)^2 \int \mathrm{d}{\boldsymbol{p}}\, \delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s})F_{s}({\boldsymbol{p}}), \end{equation}
where we substituted ![]() $n = 3$ for three-dimensional plasma. For thermal equilibrium, (8.15) leads to the well-known formula (Lifshitz & Pitaevskii Reference Lifshitz and Pitaevskii1981, § 51)
$n = 3$ for three-dimensional plasma. For thermal equilibrium, (8.15) leads to the well-known formula (Lifshitz & Pitaevskii Reference Lifshitz and Pitaevskii1981, § 51)
The spectrum ![]() $\smash {{\mathsf {S}}_\rho }$ of charge-density fluctuations is found using Poisson's equation
$\smash {{\mathsf {S}}_\rho }$ of charge-density fluctuations is found using Poisson's equation ![]() $\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {\rho }} = \widehat {k}^2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {\varphi }}/4{\rm \pi} }$, whence
$\smash {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {\rho }} = \widehat {k}^2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}} {\widetilde {\varphi }}/4{\rm \pi} }$, whence ![]() $\smash {{\mathsf {S}}_\rho \approx (k^2/4{\rm \pi} )^2{\mathsf {S}}}$. Fluctuations of other fields are found similarly. Also, (6.36) leads to
$\smash {{\mathsf {S}}_\rho \approx (k^2/4{\rm \pi} )^2{\mathsf {S}}}$. Fluctuations of other fields are found similarly. Also, (6.36) leads to
 \begin{equation} |\mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')|^2 = \left(\frac{4{\rm \pi} e_s e_{s'}}{k^2 |\epsilon_\parallel(\omega, {\boldsymbol{k}})|}\right)^2. \end{equation}
\begin{equation} |\mathcal{X}_{ss'}(\omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}')|^2 = \left(\frac{4{\rm \pi} e_s e_{s'}}{k^2 |\epsilon_\parallel(\omega, {\boldsymbol{k}})|}\right)^2. \end{equation}Then, (6.61) yields the standard Balescu–Lenard collision operator
 \begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^3}\,\mathrm{d}{\boldsymbol{p}}'\, &\frac{{\rm \pi} {\boldsymbol{k}}{\boldsymbol{k}}}{|\epsilon_\parallel({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}})|^2}\, \left(\frac{4{\rm \pi} e_s e_{s'}}{k^2}\right)^2 \delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) \nonumber\\ & \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right). \end{align}
\begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \sum_{s'}\int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^3}\,\mathrm{d}{\boldsymbol{p}}'\, &\frac{{\rm \pi} {\boldsymbol{k}}{\boldsymbol{k}}}{|\epsilon_\parallel({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}})|^2}\, \left(\frac{4{\rm \pi} e_s e_{s'}}{k^2}\right)^2 \delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) \nonumber\\ & \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right). \end{align}
(As a reminder, the distribution functions are normalized such that ![]() $\int \mathrm {d}{\boldsymbol {p}}\,F_s$ is the local average density of species
$\int \mathrm {d}{\boldsymbol {p}}\,F_s$ is the local average density of species ![]() $\smash {s}$ (5.39).)
$\smash {s}$ (5.39).)
9.1.3. On-shell waves
For on-shell waves, (7.63) gives ![]() $\smash {{\mathsf {U}}(\omega, {\boldsymbol {k}}) = (h({\boldsymbol {k}}) + h(-{\boldsymbol {k}}))\delta (\omega - w({\boldsymbol {k}}))}$, where
$\smash {{\mathsf {U}}(\omega, {\boldsymbol {k}}) = (h({\boldsymbol {k}}) + h(-{\boldsymbol {k}}))\delta (\omega - w({\boldsymbol {k}}))}$, where ![]() $\smash {w({\boldsymbol {k}})}$ is determined by the dispersion relation
$\smash {w({\boldsymbol {k}})}$ is determined by the dispersion relation
and ![]() $\smash {\epsilon _{\parallel \text {H}} \equiv \operatorname {re} \epsilon _\parallel }$ is given by
$\smash {\epsilon _{\parallel \text {H}} \equiv \operatorname {re} \epsilon _\parallel }$ is given by
 \begin{equation} \epsilon_{{\parallel}\text{H}}(\omega, {\boldsymbol{k}}) = 1 + \sum_s \frac{4{\rm \pi} e_s^2}{k^2} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\,\frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}}. \end{equation}
\begin{equation} \epsilon_{{\parallel}\text{H}}(\omega, {\boldsymbol{k}}) = 1 + \sum_s \frac{4{\rm \pi} e_s^2}{k^2} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\,\frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}}. \end{equation}The phase-space density of the wave action, defined in (7.74), is
and the dressing function (9.4) is given by
 \begin{align} {\boldsymbol{\Theta}}_{s} & = e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}\nonumber\\ & = 2e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}}) \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}. \end{align}
\begin{align} {\boldsymbol{\Theta}}_{s} & = e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}\nonumber\\ & = 2e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}}) \left. \frac{{\boldsymbol{k}} {\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}. \end{align}Using these, one obtains (Appendix F.1.1)
so the conserved quantity (7.88) is the average momentum of the plasma (while the electrostatic field carries no momentum, naturally). Also (Appendix F.1.2),
so, expectedly, the conserved quantity (7.90) is the average particle energy plus the energy of the electrostatic field. In combination with our equations for ![]() $\smash {F_s}$ and
$\smash {F_s}$ and ![]() $\smash {J}$ (§ 7.6), these results can be considered as a generalization and concise restatement of the OC QLT by Dewar (Reference Dewar1973), which is rigorously reproduced from our general formulation as a particular case.
$\smash {J}$ (§ 7.6), these results can be considered as a generalization and concise restatement of the OC QLT by Dewar (Reference Dewar1973), which is rigorously reproduced from our general formulation as a particular case.
9.1.4. Eikonal waves
As a particular case, let us consider an eikonal wave
which may or may not be on-shell. As seen from § 7.4.1,
 \begin{equation} {\mathsf{U}} \approx \frac{|{\breve{\varphi}}|^2}{4}\,\sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}}). \end{equation}
\begin{equation} {\mathsf{U}} \approx \frac{|{\breve{\varphi}}|^2}{4}\,\sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}}). \end{equation}For non-resonant particles, the dressing function is well defined is found as follows:
 \begin{align} {\boldsymbol{\Theta}}_s & \approx{-} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, \frac{e_s^2 {\boldsymbol{k}}{\boldsymbol{k}}|{\breve{\varphi}}|^2}{4(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)^2}\,\sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}})\nonumber\\ & ={-} \frac{e_s^2 \overline{{\boldsymbol{k}}}\,\overline{{\boldsymbol{k}}} |{\breve{\varphi}}|^2}{2(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}. \end{align}
\begin{align} {\boldsymbol{\Theta}}_s & \approx{-} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, \frac{e_s^2 {\boldsymbol{k}}{\boldsymbol{k}}|{\breve{\varphi}}|^2}{4(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)^2}\,\sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}})\nonumber\\ & ={-} \frac{e_s^2 \overline{{\boldsymbol{k}}}\,\overline{{\boldsymbol{k}}} |{\breve{\varphi}}|^2}{2(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}. \end{align}Similarly, the ponderomotive energy for non-resonant particles is
 \begin{align} \varDelta_s & \approx \frac{e_s^2 |{\breve{\varphi}}|^2}{8m_s} \frac{\partial}{\partial {\boldsymbol{v}}_s} \cdot \int \mathrm{d}{\omega}\,\mathrm{d}{\boldsymbol{k}}\, \frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}}) \nonumber\\ & = \frac{e_s^2 |{\breve{\varphi}}|^2}{8m_s} \int \mathrm{d}{\omega}\,\mathrm{d}{\boldsymbol{k}}\, \frac{k^2}{(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)^2} \sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}}) \nonumber\\ & = \frac{e_s^2 \overline{k}^2 |{\breve{\varphi}}|^2}{4m_s(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}, \end{align}
\begin{align} \varDelta_s & \approx \frac{e_s^2 |{\breve{\varphi}}|^2}{8m_s} \frac{\partial}{\partial {\boldsymbol{v}}_s} \cdot \int \mathrm{d}{\omega}\,\mathrm{d}{\boldsymbol{k}}\, \frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}}) \nonumber\\ & = \frac{e_s^2 |{\breve{\varphi}}|^2}{8m_s} \int \mathrm{d}{\omega}\,\mathrm{d}{\boldsymbol{k}}\, \frac{k^2}{(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)^2} \sum_{{\pm}} \delta(\omega \pm \overline{\omega})\,\delta({\boldsymbol{k}} \pm \overline{{\boldsymbol{k}}}) \nonumber\\ & = \frac{e_s^2 \overline{k}^2 |{\breve{\varphi}}|^2}{4m_s(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}, \end{align}
in agreement with Dewar (Reference Dewar1972) and Cary & Kaufman (Reference Cary and Kaufman1977). One can also express these functions in terms of the electric-field envelope ![]() $\smash {{\breve {{\boldsymbol {E}}}} \approx -\mathrm {i} \overline {{\boldsymbol {k}}} {\breve {\varphi }}}$:
$\smash {{\breve {{\boldsymbol {E}}}} \approx -\mathrm {i} \overline {{\boldsymbol {k}}} {\breve {\varphi }}}$:
 \begin{equation} {\boldsymbol{\Theta}}_{s} \approx{-}\frac{e_s^2{\breve{{\boldsymbol{E}}}}\smash{{\breve{{\boldsymbol{E}}}}}^{{\dagger}}}{2(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}, \qquad \varDelta_s \approx \frac{e_s^2 |\smash{{\breve{{\boldsymbol{E}}}}}|^2}{4m_s (\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}. \end{equation}
\begin{equation} {\boldsymbol{\Theta}}_{s} \approx{-}\frac{e_s^2{\breve{{\boldsymbol{E}}}}\smash{{\breve{{\boldsymbol{E}}}}}^{{\dagger}}}{2(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}, \qquad \varDelta_s \approx \frac{e_s^2 |\smash{{\breve{{\boldsymbol{E}}}}}|^2}{4m_s (\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}. \end{equation} For on-shell in particular, one can use (9.16) together with ![]() $\smash {h({\boldsymbol {k}}) = \frac {1}{4} |{\breve {\varphi }}|^2 \delta ({\boldsymbol {k}} - \overline {{\boldsymbol {k}}})}$ (cf. (7.64)) to obtain the well-known expression for the wave action density
$\smash {h({\boldsymbol {k}}) = \frac {1}{4} |{\breve {\varphi }}|^2 \delta ({\boldsymbol {k}} - \overline {{\boldsymbol {k}}})}$ (cf. (7.64)) to obtain the well-known expression for the wave action density ![]() $\smash {\mathcal {I} \doteq \int \mathrm {d}{\boldsymbol {k}}\,J}$:
$\smash {\mathcal {I} \doteq \int \mathrm {d}{\boldsymbol {k}}\,J}$:
For not-too-hot plasma, one has ![]() $\smash {\epsilon _{\parallel \text {H}}(\omega, {\boldsymbol {k}}) \approx 1 - \omega _p^2/\omega ^2}$, where
$\smash {\epsilon _{\parallel \text {H}}(\omega, {\boldsymbol {k}}) \approx 1 - \omega _p^2/\omega ^2}$, where ![]() $\smash {\omega _p \doteq \sum _s 4{\rm \pi} \mathcal {N}_s e_s^2/m_s}$ is the plasma frequency. The corresponding waves are Langmuir waves. Their dispersion relation is
$\smash {\omega _p \doteq \sum _s 4{\rm \pi} \mathcal {N}_s e_s^2/m_s}$ is the plasma frequency. The corresponding waves are Langmuir waves. Their dispersion relation is ![]() $\smash {w(\overline {{\boldsymbol {k}}}) \approx \pm \omega _p}$, so
$\smash {w(\overline {{\boldsymbol {k}}}) \approx \pm \omega _p}$, so ![]() $\smash {\mathcal {I} \approx \pm |{\breve {{\boldsymbol {E}}}}|^2/(8{\rm \pi} \omega _p)}$ (and accordingly, the wave energy density is
$\smash {\mathcal {I} \approx \pm |{\breve {{\boldsymbol {E}}}}|^2/(8{\rm \pi} \omega _p)}$ (and accordingly, the wave energy density is ![]() $\smash {\mathcal {E}_{\text {w}} = w\mathcal {I} \geqslant 0}$ for either sign). Remember, though, that this expression is only approximate. Using it instead of (9.25) can result in violation of the exact conservation laws of QLT. Conservation of the Langmuir-wave action in non-stationary plasmas beyond the cold-plasma approximation is also discussed in Dodin, Geyko & Fisch (Reference Dodin, Geyko and Fisch2009), Dodin & Fisch (Reference Dodin and Fisch2010b) and Schmit, Dodin & Fisch (Reference Schmit, Dodin and Fisch2010).
$\smash {\mathcal {E}_{\text {w}} = w\mathcal {I} \geqslant 0}$ for either sign). Remember, though, that this expression is only approximate. Using it instead of (9.25) can result in violation of the exact conservation laws of QLT. Conservation of the Langmuir-wave action in non-stationary plasmas beyond the cold-plasma approximation is also discussed in Dodin, Geyko & Fisch (Reference Dodin, Geyko and Fisch2009), Dodin & Fisch (Reference Dodin and Fisch2010b) and Schmit, Dodin & Fisch (Reference Schmit, Dodin and Fisch2010).
9.1.5. Homogeneous plasma
In homogeneous ![]() $n$-dimensional plasma of a given volume
$n$-dimensional plasma of a given volume ![]() $\mathscr {V}_n$, the Wigner function (9.2) has the form
$\mathscr {V}_n$, the Wigner function (9.2) has the form ![]() $\smash {{\mathsf {U}} = \mathcal {U}(t, {\boldsymbol {k}}) \delta (\omega - w(t, {\boldsymbol {k}}))}$. The function
$\smash {{\mathsf {U}} = \mathcal {U}(t, {\boldsymbol {k}}) \delta (\omega - w(t, {\boldsymbol {k}}))}$. The function ![]() $\mathcal {U}$ is readily found using (5.47):
$\mathcal {U}$ is readily found using (5.47):
Then,
This coincides with the well-known formula for the QL-diffusion coefficient in homogeneous electrostatic plasma.Footnote 39 The functions ![]() $\smash {{\boldsymbol {\Theta }}_{s}}$ and
$\smash {{\boldsymbol {\Theta }}_{s}}$ and ![]() $\smash {\varDelta _s}$ are also important in homogeneous turbulence in that they ensure the proper energy–momentum conservation; for example, see Stix (Reference Stix1992, § 16.3) and Liu & Dodin (Reference Liu and Dodin2015, § II.2). These functions can be expressed through
$\smash {\varDelta _s}$ are also important in homogeneous turbulence in that they ensure the proper energy–momentum conservation; for example, see Stix (Reference Stix1992, § 16.3) and Liu & Dodin (Reference Liu and Dodin2015, § II.2). These functions can be expressed through ![]() $\smash {\mathring {\underline {\widetilde {\varphi }}}}$ too. However, they have a simpler representation in terms of the Wigner function
$\smash {\mathring {\underline {\widetilde {\varphi }}}}$ too. However, they have a simpler representation in terms of the Wigner function ![]() $\smash {{\mathsf {U}}}$, as in (9.4) and (9.5), respectively. This is because
$\smash {{\mathsf {U}}}$, as in (9.4) and (9.5), respectively. This is because ![]() $\smash {{\mathsf {U}}}$ is a local property of the field, which makes it more fundamental than the amplitudes of global Fourier harmonics commonly used in the literature.
$\smash {{\mathsf {U}}}$ is a local property of the field, which makes it more fundamental than the amplitudes of global Fourier harmonics commonly used in the literature.
9.2. Relativistic electromagnetic interactions
9.2.1. Main equations
Let us extend the above results to relativistic electromagnetic interactions. In this case,
where ![]() $\smash {c}$ is the speed of light and
$\smash {c}$ is the speed of light and ![]() $\smash {{\boldsymbol {A}}}$ is the vector potential. Let us adopt the Weyl gauge for the oscillating part of the electromagnetic field (
$\smash {{\boldsymbol {A}}}$ is the vector potential. Let us adopt the Weyl gauge for the oscillating part of the electromagnetic field (![]() $\smash {\widetilde {\varphi } = 0}$) and Taylor-expand
$\smash {\widetilde {\varphi } = 0}$) and Taylor-expand ![]() $\smash {H_s}$ to the second order in
$\smash {H_s}$ to the second order in ![]() $\smash {\widetilde {{\boldsymbol {A}}}}$. This leads to
$\smash {\widetilde {{\boldsymbol {A}}}}$. This leads to
(although plasma is assumed non-magnetized, a weak average magnetic field ![]() $\smash {\overline {{\boldsymbol {B}}} = \nabla \times \overline {{\boldsymbol {A}}}}$ is allowed, so
$\smash {\overline {{\boldsymbol {B}}} = \nabla \times \overline {{\boldsymbol {A}}}}$ is allowed, so ![]() $\smash {\overline {{\boldsymbol {A}}}}$ can be order-one and thus generally must be retained), where
$\smash {\overline {{\boldsymbol {A}}}}$ can be order-one and thus generally must be retained), where
and ![]() $\smash {\gamma _s \doteq (1-\beta _s^2)^{-1/2}}$. In the equations presented below,
$\smash {\gamma _s \doteq (1-\beta _s^2)^{-1/2}}$. In the equations presented below, ![]() $\smash {{\boldsymbol {\beta }}_s = {\boldsymbol {v}}_s/c}$ (where
$\smash {{\boldsymbol {\beta }}_s = {\boldsymbol {v}}_s/c}$ (where ![]() $\smash {{\boldsymbol {v}}_s}$ is the OC velocity) is a sufficiently accurate approximation. Also,
$\smash {{\boldsymbol {v}}_s}$ is the OC velocity) is a sufficiently accurate approximation. Also, ![]() $\smash {{\boldsymbol {\mu }}_s \equiv (\partial ^2_{{\boldsymbol {p}}{\boldsymbol {p}}} H_{0s})^{-1}}$ can be interpreted as the relativistic-mass tensor.
$\smash {{\boldsymbol {\mu }}_s \equiv (\partial ^2_{{\boldsymbol {p}}{\boldsymbol {p}}} H_{0s})^{-1}}$ can be interpreted as the relativistic-mass tensor.
Let us choose the field ![]() $\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ of our general theory to be the oscillating electric field
$\smash {\widetilde {{\boldsymbol {\varPsi }}}}$ of our general theory to be the oscillating electric field ![]() $\smash {\widetilde {{\boldsymbol {E}}} = \mathrm {i} \widehat {\omega }\widetilde {{\boldsymbol {A}}}/c}$; then (cf. (6.2)),
$\smash {\widetilde {{\boldsymbol {E}}} = \mathrm {i} \widehat {\omega }\widetilde {{\boldsymbol {A}}}/c}$; then (cf. (6.2)),
(Other ways to identify ![]() $\smash {\widehat {\boldsymbol {L}}_s}$ and
$\smash {\widehat {\boldsymbol {L}}_s}$ and ![]() $\smash {\widehat {\boldsymbol {R}}_s}$ are also possible and lead to the same results.) Then,
$\smash {\widehat {\boldsymbol {R}}_s}$ are also possible and lead to the same results.) Then,
The average Wigner matrix of ![]() $\smash {\widetilde {{\boldsymbol {E}}}}$ is
$\smash {\widetilde {{\boldsymbol {E}}}}$ is
(the arguments ![]() $\smash {t}$ and
$\smash {t}$ and ![]() $\smash {{\boldsymbol {x}}}$ are henceforth omitted), and the nonlinear potentials are
$\smash {{\boldsymbol {x}}}$ are henceforth omitted), and the nonlinear potentials are
When plasma is non-relativistic and the field is electrostatic (so ![]() $\smash {{{\boldsymbol {\mathsf {U}}}} = {\boldsymbol {k}}{\boldsymbol {k}}^{{\dagger}} {\mathsf {U}}_\varphi }$, where
$\smash {{{\boldsymbol {\mathsf {U}}}} = {\boldsymbol {k}}{\boldsymbol {k}}^{{\dagger}} {\mathsf {U}}_\varphi }$, where ![]() $\smash {{\mathsf {U}}_\varphi }$ is scalar), (9.35) gives the same
$\smash {{\mathsf {U}}_\varphi }$ is scalar), (9.35) gives the same ![]() $\smash {{{\boldsymbol {\mathsf {D}}}}_s}$ as (9.3) and (9.37) gives the same
$\smash {{{\boldsymbol {\mathsf {D}}}}_s}$ as (9.3) and (9.37) gives the same ![]() $\smash {\varDelta _s}$ as (9.5). For
$\smash {\varDelta _s}$ as (9.5). For ![]() $\smash {{\boldsymbol {\Theta }}_s}$, the equivalence between (9.36) and (9.4) should not be expected because
$\smash {{\boldsymbol {\Theta }}_s}$, the equivalence between (9.36) and (9.4) should not be expected because ![]() $\smash {{\boldsymbol {\Theta }}_s}$ is a part of a distribution function, which is not gauge-invariant. (Canonical momenta in the Weyl gauge are different from those in the electrostatic gauge.) But it is precisely the dressing function (9.36) that leads to the correct expressions for the momentum and energy stored in the OC distribution (§ 9.2.3).
$\smash {{\boldsymbol {\Theta }}_s}$ is a part of a distribution function, which is not gauge-invariant. (Canonical momenta in the Weyl gauge are different from those in the electrostatic gauge.) But it is precisely the dressing function (9.36) that leads to the correct expressions for the momentum and energy stored in the OC distribution (§ 9.2.3).
The Lagrangian density of a free electromagnetic field is
From Faraday's law, one has ![]() $\smash {\widetilde {{\boldsymbol {B}}} = \widehat {\omega }^{-1}c(\widehat {\boldsymbol {k}} \times {\boldsymbol {E}})}$.Footnote 40 Then,
$\smash {\widetilde {{\boldsymbol {B}}} = \widehat {\omega }^{-1}c(\widehat {\boldsymbol {k}} \times {\boldsymbol {E}})}$.Footnote 40 Then, ![]() $\smash {- \smash {\widetilde {{\boldsymbol {B}}}}^{{\dagger}} \widetilde {{\boldsymbol {B}}}/c^2}$ can be represented as follows (up to a divergence, which is insignificant):
$\smash {- \smash {\widetilde {{\boldsymbol {B}}}}^{{\dagger}} \widetilde {{\boldsymbol {B}}}/c^2}$ can be represented as follows (up to a divergence, which is insignificant):
 \begin{align} (\widetilde{{\boldsymbol{E}}} \times \widehat{\omega}^{{-}1}\widehat{\boldsymbol{k}}) \cdot (\widehat{\omega}^{{-}1}\widehat{\boldsymbol{k}} \times \widetilde{{\boldsymbol{E}}}) & = \widetilde{{\boldsymbol{E}}} \cdot \widehat{\omega}^{{-}2}(\widehat{\boldsymbol{k}} \times (\widehat{\boldsymbol{k}} \times \widetilde{{\boldsymbol{E}}})) \nonumber\\ & = \smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widehat{\omega}^{{-}2}(\widehat{\boldsymbol{k}}(\widehat{\boldsymbol{k}} \cdot \widetilde{{\boldsymbol{E}}}) - \widetilde{{\boldsymbol{E}}} \widehat{k}^2) \nonumber\\ & = \smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widehat{\omega}^{{-}2}(\widehat{\boldsymbol{k}\,}\smash{\widehat{\boldsymbol{k}}}^{{\dagger}} - {\boldsymbol{1}}\widehat{k\,}^2)\widetilde{{\boldsymbol{E}}}. \end{align}
\begin{align} (\widetilde{{\boldsymbol{E}}} \times \widehat{\omega}^{{-}1}\widehat{\boldsymbol{k}}) \cdot (\widehat{\omega}^{{-}1}\widehat{\boldsymbol{k}} \times \widetilde{{\boldsymbol{E}}}) & = \widetilde{{\boldsymbol{E}}} \cdot \widehat{\omega}^{{-}2}(\widehat{\boldsymbol{k}} \times (\widehat{\boldsymbol{k}} \times \widetilde{{\boldsymbol{E}}})) \nonumber\\ & = \smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widehat{\omega}^{{-}2}(\widehat{\boldsymbol{k}}(\widehat{\boldsymbol{k}} \cdot \widetilde{{\boldsymbol{E}}}) - \widetilde{{\boldsymbol{E}}} \widehat{k}^2) \nonumber\\ & = \smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widehat{\omega}^{{-}2}(\widehat{\boldsymbol{k}\,}\smash{\widehat{\boldsymbol{k}}}^{{\dagger}} - {\boldsymbol{1}}\widehat{k\,}^2)\widetilde{{\boldsymbol{E}}}. \end{align}Then, the vacuum dispersion operator can be written as (cf. (6.1))
The total dispersion matrix is readily found to be
where ![]() $\smash {{\boldsymbol {\epsilon }}}$ (not to be confused with the small parameter
$\smash {{\boldsymbol {\epsilon }}}$ (not to be confused with the small parameter ![]() $\smash {\epsilon }$ that we introduced earlier) is the dielectric tensor
$\smash {\epsilon }$ that we introduced earlier) is the dielectric tensor
 \begin{equation} {\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}) = {\boldsymbol{1}} - \frac{{\boldsymbol{\mathfrak{w}}}_p}{\omega^2} + \sum_s \frac{4{\rm \pi} e_s^2}{\omega^2}\int \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0}\,{\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial{\boldsymbol{p}}}. \end{equation}
\begin{equation} {\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}) = {\boldsymbol{1}} - \frac{{\boldsymbol{\mathfrak{w}}}_p}{\omega^2} + \sum_s \frac{4{\rm \pi} e_s^2}{\omega^2}\int \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0}\,{\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial{\boldsymbol{p}}}. \end{equation}
Here, ![]() $\smash {{\boldsymbol {\mathfrak {w}}}_p}$ is the squared relativistic plasma frequency, which is a matrix, because the ‘masses’
$\smash {{\boldsymbol {\mathfrak {w}}}_p}$ is the squared relativistic plasma frequency, which is a matrix, because the ‘masses’ ![]() $\smash {{\boldsymbol {\mu }}_s}$ are matrices:
$\smash {{\boldsymbol {\mu }}_s}$ are matrices:
9.2.2. Collisions and fluctuations
By (8.12), the spectrum of microscopic oscillations of ![]() $\smash {\widetilde {{\boldsymbol {E}}}}$ is a matrix given by
$\smash {\widetilde {{\boldsymbol {E}}}}$ is a matrix given by
 \begin{equation} {{\boldsymbol {\mathsf{S}}}}(\omega, {\boldsymbol{k}}) = 2{\rm \pi}\, \sum_s \left(\frac{4\pi e_s}{\omega}\right)^2 \int \mathrm{d}{\boldsymbol{p}}\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s})F_{s}({\boldsymbol{p}}) {\boldsymbol{\epsilon}}^{{-}1}(\omega, {\boldsymbol{k}})\, {\boldsymbol{v}}_{s}{\boldsymbol{v}}_{s}^{{\dagger}}\, {\boldsymbol{\epsilon}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}). \end{equation}
\begin{equation} {{\boldsymbol {\mathsf{S}}}}(\omega, {\boldsymbol{k}}) = 2{\rm \pi}\, \sum_s \left(\frac{4\pi e_s}{\omega}\right)^2 \int \mathrm{d}{\boldsymbol{p}}\,\delta(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_{s})F_{s}({\boldsymbol{p}}) {\boldsymbol{\epsilon}}^{{-}1}(\omega, {\boldsymbol{k}})\, {\boldsymbol{v}}_{s}{\boldsymbol{v}}_{s}^{{\dagger}}\, {\boldsymbol{\epsilon}}^{-{{\dagger}}}(\omega, {\boldsymbol{k}}). \end{equation}
In the electrostatic limit, one can replace ![]() $\smash {{\boldsymbol {\epsilon }}^{-1}}$ with
$\smash {{\boldsymbol {\epsilon }}^{-1}}$ with ![]() $\smash {\epsilon _\parallel ^{-1}{\boldsymbol {k}}{\boldsymbol {k}}^{{\dagger}} /k^2}$, where
$\smash {\epsilon _\parallel ^{-1}{\boldsymbol {k}}{\boldsymbol {k}}^{{\dagger}} /k^2}$, where ![]() $\smash {\epsilon _\parallel }$ is the relativistic generalization of (9.9); then (9.44) leads to (9.10) as a particular case. For thermal equilibrium, one can also use (8.15) and the following form of
$\smash {\epsilon _\parallel }$ is the relativistic generalization of (9.9); then (9.44) leads to (9.10) as a particular case. For thermal equilibrium, one can also use (8.15) and the following form of ![]() $\smash {{\boldsymbol {\epsilon }}^{-1}}$ for isotropic plasma:
$\smash {{\boldsymbol {\epsilon }}^{-1}}$ for isotropic plasma:
 \begin{equation} {\boldsymbol{\epsilon}}^{{-}1} = \frac{1}{\epsilon_\perp}\bigg({\boldsymbol{1}} - \frac{{\boldsymbol{k}}{\boldsymbol{k}}^{{\dagger}}}{k^2}\bigg) + \frac{1}{\epsilon_\parallel}\frac{{\boldsymbol{k}}{\boldsymbol{k}}^{{\dagger}}}{k^2}, \end{equation}
\begin{equation} {\boldsymbol{\epsilon}}^{{-}1} = \frac{1}{\epsilon_\perp}\bigg({\boldsymbol{1}} - \frac{{\boldsymbol{k}}{\boldsymbol{k}}^{{\dagger}}}{k^2}\bigg) + \frac{1}{\epsilon_\parallel}\frac{{\boldsymbol{k}}{\boldsymbol{k}}^{{\dagger}}}{k^2}, \end{equation}
where ![]() $\smash {\epsilon _\perp }$ is the (scalar) transverse permittivity. Also, (6.36) leads to
$\smash {\epsilon _\perp }$ is the (scalar) transverse permittivity. Also, (6.36) leads to
Then the collision operator (6.61) is obtained in the form
 \begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}}\cdot \sum_{s'} 2 e_s^2 e_{s'}^2 \int & \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^3}\,\mathrm{d}{\boldsymbol{p}}'\, \frac{|{\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\epsilon}}^{{-}1}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}) {\boldsymbol{v}'}_{s'}|^2}{({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)^4}\, \delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) \nonumber\\ & \times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right), \end{align}
\begin{align} \mathcal{C}_s = \frac{\partial}{\partial {\boldsymbol{p}}}\cdot \sum_{s'} 2 e_s^2 e_{s'}^2 \int & \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^3}\,\mathrm{d}{\boldsymbol{p}}'\, \frac{|{\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\epsilon}}^{{-}1}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}) {\boldsymbol{v}'}_{s'}|^2}{({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)^4}\, \delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) \nonumber\\ & \times {\boldsymbol{k}}{\boldsymbol{k}} \cdot \left( \frac{\partial F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right), \end{align}
which is in agreement with (Silin Reference Silin1961; Hizanidis, Molvig & Swartz Reference Hizanidis, Molvig and Swartz1983). Replacing ![]() $\smash {{\boldsymbol {\epsilon }}^{-1}}$ with
$\smash {{\boldsymbol {\epsilon }}^{-1}}$ with ![]() $\smash {\epsilon _\parallel ^{-1}{\boldsymbol {k}}{\boldsymbol {k}}^{{\dagger}} /k^2}$ leads to the standard Balescu–Lenard operator (9.13) as a particular case.
$\smash {\epsilon _\parallel ^{-1}{\boldsymbol {k}}{\boldsymbol {k}}^{{\dagger}} /k^2}$ leads to the standard Balescu–Lenard operator (9.13) as a particular case.
9.2.3. On-shell waves
Electromagnetic on-shell waves satisfy
where ![]() $\smash {{\breve {{\boldsymbol {E}}}}}$ is the complex envelope vector parallel to the polarization vector
$\smash {{\breve {{\boldsymbol {E}}}}}$ is the complex envelope vector parallel to the polarization vector ![]() $\smash {{\boldsymbol {\eta }}}$; also,
$\smash {{\boldsymbol {\eta }}}$; also,
This yields (see (9.39))
Then, the phase-space density of the wave action (7.74) can be cast in the form
(cf. Dodin et al. Reference Dodin, Ruiz, Yanagihara, Zhou and Kubo2019), and the dressing function (9.36) is given by
 \begin{align} {\boldsymbol{\Theta}}_s & = e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \left. \frac{{\boldsymbol{k}}{\boldsymbol{k}}}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}} {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s)}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0} \nonumber\\ & = 2e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}}) \left. \frac{{\boldsymbol{k}}{\boldsymbol{k}}}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}})}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}. \end{align}
\begin{align} {\boldsymbol{\Theta}}_s & = e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \left. \frac{{\boldsymbol{k}}{\boldsymbol{k}}}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}} {\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s)}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0} \nonumber\\ & = 2e_s^2\,\frac{\partial}{\partial \vartheta} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}}) \left. \frac{{\boldsymbol{k}}{\boldsymbol{k}}}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}})}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} \right|_{\vartheta=0}. \end{align}Using these, one obtains (Appendix F.2.1)
 \begin{equation} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,{\boldsymbol{p}} F_s + \int \mathrm{d}{\boldsymbol{k}}\,{\boldsymbol{k}} J = {\boldsymbol{\mathcal{P}}}^{(\text{kin})} + \frac{\overline{\widetilde{{\boldsymbol{E}}} \times \widetilde{{\boldsymbol{B}}}}}{4{\rm \pi} c}, \end{equation}
\begin{equation} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,{\boldsymbol{p}} F_s + \int \mathrm{d}{\boldsymbol{k}}\,{\boldsymbol{k}} J = {\boldsymbol{\mathcal{P}}}^{(\text{kin})} + \frac{\overline{\widetilde{{\boldsymbol{E}}} \times \widetilde{{\boldsymbol{B}}}}}{4{\rm \pi} c}, \end{equation}
where ![]() $\smash {{\boldsymbol {\mathcal {P}}}^{(\text {kin})}}$ is the average density of the plasma kinetic (up to
$\smash {{\boldsymbol {\mathcal {P}}}^{(\text {kin})}}$ is the average density of the plasma kinetic (up to ![]() $\smash {\overline {{\boldsymbol {A}}}}$) momentum,
$\smash {\overline {{\boldsymbol {A}}}}$) momentum,
the functions ![]() $\smash {f_s^{\text {(kin)}}({\boldsymbol {p}}) \doteq f_s({\boldsymbol {p}} + e_s \widetilde {{\boldsymbol {A}}}/c)}$ are the distributions of kinetic (up to
$\smash {f_s^{\text {(kin)}}({\boldsymbol {p}}) \doteq f_s({\boldsymbol {p}} + e_s \widetilde {{\boldsymbol {A}}}/c)}$ are the distributions of kinetic (up to ![]() $\smash {\overline {{\boldsymbol {A}}}}$) momenta, and the second term in (9.53) is the well-known average momentum of electromagnetic field. Similarly (Appendix F.2.2),
$\smash {\overline {{\boldsymbol {A}}}}$) momenta, and the second term in (9.53) is the well-known average momentum of electromagnetic field. Similarly (Appendix F.2.2),
where ![]() $\smash {\mathcal {K}^{(\text {kin})}}$ is given by
$\smash {\mathcal {K}^{(\text {kin})}}$ is given by
In other words, the total momentum and energy of the system in the OC–wave representation are the same as those in the original particle–field variables.
9.2.4. Eikonal waves
As a particular case, let us consider an eikonal wave
which may or may not be on-shell. Then, (9.36) and (9.37) lead to (cf. § 9.1.4)
 $$\begin{gather} \displaystyle {\boldsymbol{\Theta}}_s ={-} \frac{\overline{{\boldsymbol{k}}}\,\overline{{\boldsymbol{k}}}}{\overline{\omega}^2} \frac{e_s^2 |{\boldsymbol{v}}_s^{{\dagger}} {\breve{{\boldsymbol{E}}}}|^2}{2(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}, \end{gather}$$
$$\begin{gather} \displaystyle {\boldsymbol{\Theta}}_s ={-} \frac{\overline{{\boldsymbol{k}}}\,\overline{{\boldsymbol{k}}}}{\overline{\omega}^2} \frac{e_s^2 |{\boldsymbol{v}}_s^{{\dagger}} {\breve{{\boldsymbol{E}}}}|^2}{2(\overline{\omega} - \overline{{\boldsymbol{k}}} \cdot {\boldsymbol{v}}_s)^2}, \end{gather}$$For on-shell waves in particular, one also obtains the action density in the form
 \begin{align} \mathcal{I} & = \frac{1}{16{\rm \pi}\omega^2}\, \smash{{\breve{{\boldsymbol{E}}}}}^{{\dagger}}\, \frac{\partial(\omega^2{\boldsymbol{\epsilon}}_{\text{H}}(\omega, {\boldsymbol{k}}))}{\partial \omega}\, {\breve{{\boldsymbol{E}}}}\,\Big|_{\omega = w(\overline{{\boldsymbol{k}}})} \nonumber\\ & = \frac{1}{16{\rm \pi}\omega}\left( \smash{{\breve{{\boldsymbol{E}}}}}^{{\dagger}}\, \frac{\partial(\omega {\boldsymbol{\epsilon}}_{\text{H}}(\omega, {\boldsymbol{k}}))}{\partial \omega}\, {\breve{{\boldsymbol{E}}}} + \smash{{\breve{{\boldsymbol{B}}}}}^{{\dagger}} {\breve{{\boldsymbol{B}}}} \right)\Big|_{\omega = w(\overline{{\boldsymbol{k}}})}, \end{align}
\begin{align} \mathcal{I} & = \frac{1}{16{\rm \pi}\omega^2}\, \smash{{\breve{{\boldsymbol{E}}}}}^{{\dagger}}\, \frac{\partial(\omega^2{\boldsymbol{\epsilon}}_{\text{H}}(\omega, {\boldsymbol{k}}))}{\partial \omega}\, {\breve{{\boldsymbol{E}}}}\,\Big|_{\omega = w(\overline{{\boldsymbol{k}}})} \nonumber\\ & = \frac{1}{16{\rm \pi}\omega}\left( \smash{{\breve{{\boldsymbol{E}}}}}^{{\dagger}}\, \frac{\partial(\omega {\boldsymbol{\epsilon}}_{\text{H}}(\omega, {\boldsymbol{k}}))}{\partial \omega}\, {\breve{{\boldsymbol{E}}}} + \smash{{\breve{{\boldsymbol{B}}}}}^{{\dagger}} {\breve{{\boldsymbol{B}}}} \right)\Big|_{\omega = w(\overline{{\boldsymbol{k}}})}, \end{align}where we used (9.50).
9.3. Newtonian gravity
For Newtonian interactions governed by a gravitostatic potential ![]() $\smash {\varphi _g}$, one has
$\smash {\varphi _g}$, one has
where ![]() $\smash {{\mathsf {G}}}$ is the gravitational constant. This system is identical to that considered in § 9.1 for non-relativistic electrostatic interactions up to coefficients. Specifically,
$\smash {{\mathsf {G}}}$ is the gravitational constant. This system is identical to that considered in § 9.1 for non-relativistic electrostatic interactions up to coefficients. Specifically, ![]() $\smash {e_s}$ are replaced with
$\smash {e_s}$ are replaced with ![]() $\smash {m_s}$, a factor
$\smash {m_s}$, a factor ![]() $\smash {-{\mathsf {G}}^{-1}}$ appears in
$\smash {-{\mathsf {G}}^{-1}}$ appears in ![]() $\smash {{\boldsymbol {\varXi }}_0}$, and the dispersion matrix becomes
$\smash {{\boldsymbol {\varXi }}_0}$, and the dispersion matrix becomes
Thus, ![]() $\smash {\epsilon _\parallel }$ is replaced with
$\smash {\epsilon _\parallel }$ is replaced with ![]() $\smash {-\epsilon _g/{\mathsf {G}}}$, where
$\smash {-\epsilon _g/{\mathsf {G}}}$, where ![]() $\smash {\epsilon _g}$ is the gravitostatic permittivity given by
$\smash {\epsilon _g}$ is the gravitostatic permittivity given by
 \begin{equation} \epsilon_g(\omega, {\boldsymbol{k}}) = 1 - \sum_s \frac{4{\rm \pi} {\mathsf{G}} m_s^2}{k^2} \int \mathrm{d}{\boldsymbol{p}}\,\frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}}. \end{equation}
\begin{equation} \epsilon_g(\omega, {\boldsymbol{k}}) = 1 - \sum_s \frac{4{\rm \pi} {\mathsf{G}} m_s^2}{k^2} \int \mathrm{d}{\boldsymbol{p}}\,\frac{{\boldsymbol{k}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \mathrm{i} 0} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}}. \end{equation}
This readily yields, for example, the kinetic theory of the Jeans instability (Trigger et al. Reference Trigger, Ershkovich, van Heijst and Schram2004), whose dispersion relation is given by ![]() $\smash {\epsilon _g(\omega, {\boldsymbol {k}}) = 0}$ (modulo the usual analytic continuation of the permittivity to modes with
$\smash {\epsilon _g(\omega, {\boldsymbol {k}}) = 0}$ (modulo the usual analytic continuation of the permittivity to modes with ![]() $\smash {\operatorname {im}\omega < 0}$).
$\smash {\operatorname {im}\omega < 0}$).
9.4. Relativistic gravity
9.4.1. Main equations
The dynamics of a relativistic neutral particle with mass ![]() $\smash {m}$ in a spacetime metric
$\smash {m}$ in a spacetime metric ![]() $\smash {g_{\alpha \beta }}$ with signature
$\smash {g_{\alpha \beta }}$ with signature ![]() $\smash {(-+++)}$ is governed by a covariant Hamiltonian (see, for example, Garg & Dodin Reference Garg and Dodin2020)
$\smash {(-+++)}$ is governed by a covariant Hamiltonian (see, for example, Garg & Dodin Reference Garg and Dodin2020)
Here, ![]() $\smash {{\boldsymbol {\mathsf {x}}} \equiv (x^0, {\boldsymbol {x}})}$, and
$\smash {{\boldsymbol {\mathsf {x}}} \equiv (x^0, {\boldsymbol {x}})}$, and ![]() $\smash {x^0 = t}$, as usual. Also,
$\smash {x^0 = t}$, as usual. Also, ![]() $\smash {{\boldsymbol {\mathsf {p}}} \equiv (p_0, {\boldsymbol {p}})}$ is the index-free notation for the four-momentum
$\smash {{\boldsymbol {\mathsf {p}}} \equiv (p_0, {\boldsymbol {p}})}$ is the index-free notation for the four-momentum ![]() $\smash {p_\alpha }$,
$\smash {p_\alpha }$, ![]() $\smash {g^{\alpha \beta }}$ is the inverse metric,
$\smash {g^{\alpha \beta }}$ is the inverse metric, ![]() $\smash {{\boldsymbol {g}}}$ is the index-free notation for
$\smash {{\boldsymbol {g}}}$ is the index-free notation for ![]() $\smash {g^{\alpha \beta }}$, the units are such that
$\smash {g^{\alpha \beta }}$, the units are such that ![]() $\smash {c = 1}$ and the species index is omitted.Footnote 41 The corresponding Hamilton's equations, with
$\smash {c = 1}$ and the species index is omitted.Footnote 41 The corresponding Hamilton's equations, with ![]() $\smash {\tau }$ the proper time, are
$\smash {\tau }$ the proper time, are
This dynamics is constrained to the shell ![]() $\smash {p_0 = P_0(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$, where
$\smash {p_0 = P_0(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$, where ![]() $\smash {P_0}$ is the (negative) solution of
$\smash {P_0}$ is the (negative) solution of
This means that the particle distribution in the ![]() $\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {p}}})}$ space is delta-shaped and thus does not satisfy (3.35). Hence, we will consider particles in the six-dimensional space
$\smash {({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {p}}})}$ space is delta-shaped and thus does not satisfy (3.35). Hence, we will consider particles in the six-dimensional space ![]() $\smash {({\boldsymbol {x}}, {\boldsymbol {p}})}$ instead. The corresponding dynamics is governed by the Hamiltonian
$\smash {({\boldsymbol {x}}, {\boldsymbol {p}})}$ instead. The corresponding dynamics is governed by the Hamiltonian
This is seen from the fact that
where ![]() $\smash {{\unicode{x25AA}} \in \lbrace t, {\boldsymbol {x}}, {\boldsymbol {p}} \rbrace }$, so Hamilton's equations obtained from (9.67) are equivalent to (9.65):
$\smash {{\unicode{x25AA}} \in \lbrace t, {\boldsymbol {x}}, {\boldsymbol {p}} \rbrace }$, so Hamilton's equations obtained from (9.67) are equivalent to (9.65):
Let us decompose the metric into the average part and oscillations, ![]() $\smash {g_{\alpha \beta } = \overline {g}_{\alpha \beta } + \widetilde {g}_{\alpha \beta }}$, and approximate the inverse metric to the second order in
$\smash {g_{\alpha \beta } = \overline {g}_{\alpha \beta } + \widetilde {g}_{\alpha \beta }}$, and approximate the inverse metric to the second order in ![]() $\smash {\widetilde {{\boldsymbol {g}}}}$:
$\smash {\widetilde {{\boldsymbol {g}}}}$:
where the indices of ![]() $\smash {\widetilde {{\boldsymbol {g}}}}$ are manipulated using the background metric
$\smash {\widetilde {{\boldsymbol {g}}}}$ are manipulated using the background metric ![]() $\smash {\overline {g}_{\alpha \beta }}$. This gives
$\smash {\overline {g}_{\alpha \beta }}$. This gives
The Hamiltonian (9.67) is expanded in ![]() $\smash {\widetilde {{\boldsymbol {g}}}}$ as follows:
$\smash {\widetilde {{\boldsymbol {g}}}}$ as follows:
where ![]() $\smash {P_0}$ and the derivatives on the right-hand side are evaluated on
$\smash {P_0}$ and the derivatives on the right-hand side are evaluated on ![]() $\smash {(\overline {{\boldsymbol {g}}}, {\boldsymbol {\mathsf {p}}})}$. To calculate these derivatives, let us differentiate (9.66) and use (9.71) for
$\smash {(\overline {{\boldsymbol {g}}}, {\boldsymbol {\mathsf {p}}})}$. To calculate these derivatives, let us differentiate (9.66) and use (9.71) for ![]() $\smash {{\mathsf {H}}}$. This gives
$\smash {{\mathsf {H}}}$. This gives
where the derivatives with respect to the oscillating metric are taken at fixed ![]() $\smash {p_\alpha }$ and at
$\smash {p_\alpha }$ and at ![]() $\smash {\widetilde {{\boldsymbol {g}}} \to 0}$, and
$\smash {\widetilde {{\boldsymbol {g}}} \to 0}$, and ![]() $\smash {P^0 \equiv P^0({\boldsymbol {g}}, {\boldsymbol {\mathsf {p}}}) = \overline {g}^{0\alpha }p_\alpha }$; thus,
$\smash {P^0 \equiv P^0({\boldsymbol {g}}, {\boldsymbol {\mathsf {p}}}) = \overline {g}^{0\alpha }p_\alpha }$; thus,
Similarly, differentiating (9.66) twice gives
 \begin{align*} 0 & = \frac{\partial^2{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial{\mathsf{H}}}{\partial p_0}\frac{\partial^2P_0}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}}\frac{\partial}{\partial p_0} \frac{\partial {\mathsf{H}}}{\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial}{\partial p_0}\left( \frac{\partial{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}} + \frac{\partial{\mathsf{H}}}{\partial p_0}\frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}} \right)\frac{\partial P_0}{\partial g^{\gamma\delta}} \nonumber\\ & = \frac{\partial^2{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial{\mathsf{H}}}{\partial p_0} \frac{\partial^2P_0}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}}\frac{\partial}{\partial p_0}\frac{\partial {\mathsf{H}}}{\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial P_0}{\partial \widetilde{g}^{\gamma\delta}}\frac{\partial}{\partial p_0} \frac{\partial{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}} + \frac{\partial^2{\mathsf{H}}}{\partial p_0\partial p_0}\frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}}\frac{\partial P_0}{\partial \widetilde{g}^{\gamma\delta}} \nonumber\\ & = \frac{1}{2m}\left(\overline{g}_{\beta\gamma}p_\alpha p_\delta + \overline{g}_{\delta\alpha} p_\gamma p_\beta + 2P^0 \frac{\partial^2P_0}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} - \frac{1}{2P^0}\frac{\partial(p_\alpha p_\beta p_\gamma p_\delta)}{\partial p_0} + \overline{g}^{00}\,\frac{p_\alpha p_\beta p_\gamma p_\delta}{2(P^0)^2}\right),\nonumber \end{align*}
\begin{align*} 0 & = \frac{\partial^2{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial{\mathsf{H}}}{\partial p_0}\frac{\partial^2P_0}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}}\frac{\partial}{\partial p_0} \frac{\partial {\mathsf{H}}}{\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial}{\partial p_0}\left( \frac{\partial{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}} + \frac{\partial{\mathsf{H}}}{\partial p_0}\frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}} \right)\frac{\partial P_0}{\partial g^{\gamma\delta}} \nonumber\\ & = \frac{\partial^2{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial{\mathsf{H}}}{\partial p_0} \frac{\partial^2P_0}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}}\frac{\partial}{\partial p_0}\frac{\partial {\mathsf{H}}}{\partial \widetilde{g}^{\gamma\delta}} + \frac{\partial P_0}{\partial \widetilde{g}^{\gamma\delta}}\frac{\partial}{\partial p_0} \frac{\partial{\mathsf{H}}}{\partial \widetilde{g}^{\alpha\beta}} + \frac{\partial^2{\mathsf{H}}}{\partial p_0\partial p_0}\frac{\partial P_0}{\partial \widetilde{g}^{\alpha\beta}}\frac{\partial P_0}{\partial \widetilde{g}^{\gamma\delta}} \nonumber\\ & = \frac{1}{2m}\left(\overline{g}_{\beta\gamma}p_\alpha p_\delta + \overline{g}_{\delta\alpha} p_\gamma p_\beta + 2P^0 \frac{\partial^2P_0}{\partial \widetilde{g}^{\alpha\beta}\partial \widetilde{g}^{\gamma\delta}} - \frac{1}{2P^0}\frac{\partial(p_\alpha p_\beta p_\gamma p_\delta)}{\partial p_0} + \overline{g}^{00}\,\frac{p_\alpha p_\beta p_\gamma p_\delta}{2(P^0)^2}\right),\nonumber \end{align*}whence
Then, (9.72) yields
where we introduced ![]() $\smash {H_0 = - P_0}$,
$\smash {H_0 = - P_0}$, ![]() $\smash {\alpha ^{\alpha \beta } = p^\alpha p^\beta /(2P^0)}$ and
$\smash {\alpha ^{\alpha \beta } = p^\alpha p^\beta /(2P^0)}$ and
9.4.2. Nonlinear potentials
Let us treat ![]() $\smash {\widetilde {{\boldsymbol {g}}}}$ as a 16-dimensional vector (Garg & Dodin Reference Garg and Dodin2021b), so
$\smash {\widetilde {{\boldsymbol {g}}}}$ as a 16-dimensional vector (Garg & Dodin Reference Garg and Dodin2021b), so ![]() $\smash {\alpha _{\alpha \beta }}$ serves as
$\smash {\alpha _{\alpha \beta }}$ serves as ![]() $\smash {{\boldsymbol {\alpha }}^{{\dagger}} }$ and
$\smash {{\boldsymbol {\alpha }}^{{\dagger}} }$ and ![]() $\smash {\wp ^{\alpha \beta }{}_{\gamma \delta }}$ serves as
$\smash {\wp ^{\alpha \beta }{}_{\gamma \delta }}$ serves as ![]() $\smash {{\boldsymbol {\wp }}}$. (Because these operators happen to be local in the
$\smash {{\boldsymbol {\wp }}}$. (Because these operators happen to be local in the ![]() $\smash {{\boldsymbol {\mathsf {x}}}}$ representation, here we do not distinguish them from their symbols.) Let us also introduce
$\smash {{\boldsymbol {\mathsf {x}}}}$ representation, here we do not distinguish them from their symbols.) Let us also introduce
and notice that ![]() $\smash {v^i \approx \dot {x}^i = p^i/p^0}$ (see (9.69)), so
$\smash {v^i \approx \dot {x}^i = p^i/p^0}$ (see (9.69)), so ![]() $\smash {\omega - {\boldsymbol {k}} \cdot {\boldsymbol {v}} = - k_\rho p^\rho /P^0}$ and
$\smash {\omega - {\boldsymbol {k}} \cdot {\boldsymbol {v}} = - k_\rho p^\rho /P^0}$ and ![]() $\smash {\delta (\omega - {\boldsymbol {k}} \cdot {\boldsymbol {v}})} = \smash {P^0\delta (k^\rho p_\rho )}$. Then, one finds from (6.77) that (Appendix B.8)
$\smash {\delta (\omega - {\boldsymbol {k}} \cdot {\boldsymbol {v}})} = \smash {P^0\delta (k^\rho p_\rho )}$. Then, one finds from (6.77) that (Appendix B.8)
Equation (9.80) (where one takes ![]() $\smash {p_0 = P_0}$ after the differentiation) is in agreement with the result that was obtained for quasimonochromatic waves in Garg & Dodin (Reference Garg and Dodin2020). The derivation of the dispersion matrix
$\smash {p_0 = P_0}$ after the differentiation) is in agreement with the result that was obtained for quasimonochromatic waves in Garg & Dodin (Reference Garg and Dodin2020). The derivation of the dispersion matrix ![]() $\smash {{\boldsymbol {\varXi }}}$ for relativistic gravitational interactions in matter is cumbersome, so it is not presented here, but see Garg & Dodin (Reference Garg and Dodin2022). The collision integral and fluctuations for relativistic gravitational interactions are straightforward to obtain from the general formulas presented in §§ 6.9 and 8. This can be used to describe QL interactions of gravitational waves, including not only the usual vacuum modesFootnote 42 but also waves coupled with matter, for example, the relativistic Jeans mode.
$\smash {{\boldsymbol {\varXi }}}$ for relativistic gravitational interactions in matter is cumbersome, so it is not presented here, but see Garg & Dodin (Reference Garg and Dodin2022). The collision integral and fluctuations for relativistic gravitational interactions are straightforward to obtain from the general formulas presented in §§ 6.9 and 8. This can be used to describe QL interactions of gravitational waves, including not only the usual vacuum modesFootnote 42 but also waves coupled with matter, for example, the relativistic Jeans mode.
Also notice that the OC Hamiltonian ![]() $\smash {\mathcal {H} = H_0 + \varDelta }$ can be put in a covariant form as follows. Like in the original system (§ 9.4.1),
$\smash {\mathcal {H} = H_0 + \varDelta }$ can be put in a covariant form as follows. Like in the original system (§ 9.4.1), ![]() $\smash {\mathcal {H}}$ determines the ponderomotively modified shell
$\smash {\mathcal {H}}$ determines the ponderomotively modified shell ![]() $\smash {p_0 = \mathcal {P}_0(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ via
$\smash {p_0 = \mathcal {P}_0(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ via ![]() $\smash {\mathcal {H} = -\mathcal {P}_0}$. On one hand, the covariant OC Hamiltonian
$\smash {\mathcal {H} = -\mathcal {P}_0}$. On one hand, the covariant OC Hamiltonian ![]() $\smash {\mathcal {H}'}$ vanishes on this shell,Footnote 43 so it can be Taylor-expanded as follows:
$\smash {\mathcal {H}'}$ vanishes on this shell,Footnote 43 so it can be Taylor-expanded as follows:
On the other hand, it can also be represented as ![]() $\smash {\mathcal {H}' = {\mathsf {H}}(\overline {{\boldsymbol {g}}}, {\boldsymbol {\mathsf {p}}}) + \varDelta '}$ (here
$\smash {\mathcal {H}' = {\mathsf {H}}(\overline {{\boldsymbol {g}}}, {\boldsymbol {\mathsf {p}}}) + \varDelta '}$ (here ![]() $\smash {\varDelta '}$ is the ponderomotive term yet to be found) and Taylor-expanded around the unperturbed shell
$\smash {\varDelta '}$ is the ponderomotive term yet to be found) and Taylor-expanded around the unperturbed shell ![]() $\smash {p_0 = P_0(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ as
$\smash {p_0 = P_0(t, {\boldsymbol {x}}, {\boldsymbol {p}})}$ as
By comparing (9.81) with (9.82), one finds that ![]() $\smash {\varDelta ' = \lambda \varDelta }$. Because
$\smash {\varDelta ' = \lambda \varDelta }$. Because ![]() $\smash {\lambda = P^0/m}$, this leads to the following covariant Hamiltonian for OCs:
$\smash {\lambda = P^0/m}$, this leads to the following covariant Hamiltonian for OCs:
9.4.3. Gauge invariance
As shown in Garg & Dodin (Reference Garg and Dodin2021a, Reference Garg and Dodinb) adiabatic QL interactions via gravitational waves (i.e. those determined by ![]() $\smash {{\boldsymbol {\Theta }}}$ and
$\smash {{\boldsymbol {\Theta }}}$ and ![]() $\smash {\varDelta }$) can be formulated in a form invariant with respect to gauge transformations
$\smash {\varDelta }$) can be formulated in a form invariant with respect to gauge transformations
where ![]() $\smash {\nabla }$ is the covariant derivative associated with the background metric
$\smash {\nabla }$ is the covariant derivative associated with the background metric ![]() $\smash {\overline {{\boldsymbol {g}}}}$,
$\smash {\overline {{\boldsymbol {g}}}}$, ![]() $\smash {\widetilde {\xi }^\mu }$ is an arbitrary vector field and
$\smash {\widetilde {\xi }^\mu }$ is an arbitrary vector field and ![]() $\smash {\psi ^{(\alpha } \eta ^{\beta )}} \equiv \smash {(\psi ^{\alpha } \eta ^{\beta } + \psi ^{\beta } \eta ^{\alpha })/2}$. Let us show that this also extends to resonant interactions. Recall that within the assumed accuracy the nonlinear potentials are supposed to be calculated only to the zeroth order in the geometrical-optics parameter. Then, the modification of the average Wigner matrix of the metric oscillations under the transformation (9.85) can be written as
$\smash {\psi ^{(\alpha } \eta ^{\beta )}} \equiv \smash {(\psi ^{\alpha } \eta ^{\beta } + \psi ^{\beta } \eta ^{\alpha })/2}$. Let us show that this also extends to resonant interactions. Recall that within the assumed accuracy the nonlinear potentials are supposed to be calculated only to the zeroth order in the geometrical-optics parameter. Then, the modification of the average Wigner matrix of the metric oscillations under the transformation (9.85) can be written as
 \begin{align} {\mathsf{U}}'^{\alpha\beta\gamma\delta} - {\mathsf{U}}^{\alpha\beta\gamma\delta} & = \text{symb}_{{\mathsf{x}}} \Big( \mathrm{i} \widehat{k}^{(\alpha}\, \overline{{\left. {\boldsymbol {\mathsf {|\widetilde{{\boldsymbol{\xi}^{\beta}}} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde{g}^{\gamma\delta}}|}}}} \right.}} -\mathrm{i} \overline{{\left. {\boldsymbol {\mathsf {|\widetilde{g}^{\alpha\beta} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde{\xi}^{(\gamma}}|}}}} \right.}}\, \widehat{k}^{\delta)} + \widehat{k}^{(\alpha} \overline{{\left. {\boldsymbol {\mathsf {|{\widetilde{\xi}^{\beta)}} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde{\xi}^{(\gamma}}|}}}} \right.}} \,\widehat{k}^{\delta)} \Big) \nonumber\\ & = \mathrm{i} k^{(\alpha} \mathcal{W}^{\beta)\gamma\delta} - \mathrm{i} k^{(\delta} \mathcal{W}^{\gamma)\alpha\beta *} + k^{(\alpha} {\mathsf{W}}_{\widetilde{\xi}}^{\beta)(\gamma} k^{\delta)}, \end{align}
\begin{align} {\mathsf{U}}'^{\alpha\beta\gamma\delta} - {\mathsf{U}}^{\alpha\beta\gamma\delta} & = \text{symb}_{{\mathsf{x}}} \Big( \mathrm{i} \widehat{k}^{(\alpha}\, \overline{{\left. {\boldsymbol {\mathsf {|\widetilde{{\boldsymbol{\xi}^{\beta}}} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde{g}^{\gamma\delta}}|}}}} \right.}} -\mathrm{i} \overline{{\left. {\boldsymbol {\mathsf {|\widetilde{g}^{\alpha\beta} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde{\xi}^{(\gamma}}|}}}} \right.}}\, \widehat{k}^{\delta)} + \widehat{k}^{(\alpha} \overline{{\left. {\boldsymbol {\mathsf {|{\widetilde{\xi}^{\beta)}} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde{\xi}^{(\gamma}}|}}}} \right.}} \,\widehat{k}^{\delta)} \Big) \nonumber\\ & = \mathrm{i} k^{(\alpha} \mathcal{W}^{\beta)\gamma\delta} - \mathrm{i} k^{(\delta} \mathcal{W}^{\gamma)\alpha\beta *} + k^{(\alpha} {\mathsf{W}}_{\widetilde{\xi}}^{\beta)(\gamma} k^{\delta)}, \end{align}
where ![]() $\smash {\mathcal {W}^{\beta \gamma \delta } \doteq \overline {\text {symb}_{{\mathsf {x}}} {\left. {\boldsymbol {\mathsf {|{\widetilde {\xi }^{\beta }} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde {g}^{\gamma \delta }}|}}}} \right.}}}$ and
$\smash {\mathcal {W}^{\beta \gamma \delta } \doteq \overline {\text {symb}_{{\mathsf {x}}} {\left. {\boldsymbol {\mathsf {|{\widetilde {\xi }^{\beta }} }}} \right\rangle} {\left\langle {{\boldsymbol {\mathsf {{\widetilde {g}^{\gamma \delta }}|}}}} \right.}}}$ and ![]() $\smash {{\mathsf {W}}_{\widetilde {\xi }}^{\beta \gamma }}$ is the average Wigner matrix of
$\smash {{\mathsf {W}}_{\widetilde {\xi }}^{\beta \gamma }}$ is the average Wigner matrix of ![]() $\smash {\widetilde {\xi }^\alpha }$. The corresponding change of
$\smash {\widetilde {\xi }^\alpha }$. The corresponding change of ![]() $\smash {\mathfrak {E}}$ is
$\smash {\mathfrak {E}}$ is
Then, the difference in the diffusion coefficients (9.78) is
because ![]() $\smash {\delta (k^\rho p_\rho )\,(k^\rho p_\rho ) = 0}$. In particular, this rules out QL diffusion via ‘coordinate waves’.
$\smash {\delta (k^\rho p_\rho )\,(k^\rho p_\rho ) = 0}$. In particular, this rules out QL diffusion via ‘coordinate waves’.
9.4.4. Lorenz gauge and effective metric
Let us consider gravitational waves in the Lorenz gauge, ![]() $\smash {\nabla _\alpha \widetilde {g}^{\alpha \beta } = 0}$. In this case,
$\smash {\nabla _\alpha \widetilde {g}^{\alpha \beta } = 0}$. In this case,
and thus ![]() $\smash {k_\lambda \partial \mathfrak {E}/\partial p^\lambda = 0}$. Then,
$\smash {k_\lambda \partial \mathfrak {E}/\partial p^\lambda = 0}$. Then,
This simplifies the expression (9.80) for ![]() $\smash {\varDelta }$ and (9.83) for
$\smash {\varDelta }$ and (9.83) for ![]() $\smash {\mathcal {H}'}$. Furthermore, if the waves are not significantly affected by matter, so the vacuum dispersion
$\smash {\mathcal {H}'}$. Furthermore, if the waves are not significantly affected by matter, so the vacuum dispersion ![]() $\smash {k_\lambda k^\lambda = 0}$ can be assumed, the term (9.89) vanishes completely. Then, (9.83) becomes
$\smash {k_\lambda k^\lambda = 0}$ can be assumed, the term (9.89) vanishes completely. Then, (9.83) becomes
and QL diffusion disappears, because particles cannot resonate with waves. This shows that the only average QL effect of vacuum gravitational waves on particles is the modification of the spacetime metric by ![]() $\smash {\int \mathrm {d}{\boldsymbol {\mathsf {k}}}\,{\mathsf {U}}_{\alpha \gamma }{}^{\gamma }{}_{\beta } = \mathcal {O}(\varepsilon ^2)}$. For quasimonochromatic waves, this effect is discussed in further detail in Garg & Dodin (Reference Garg and Dodin2020).
$\smash {\int \mathrm {d}{\boldsymbol {\mathsf {k}}}\,{\mathsf {U}}_{\alpha \gamma }{}^{\gamma }{}_{\beta } = \mathcal {O}(\varepsilon ^2)}$. For quasimonochromatic waves, this effect is discussed in further detail in Garg & Dodin (Reference Garg and Dodin2020).
10. Summary
In summary, we have presented QLT for classical plasma interacting with inhomogeneous turbulence in the presence of background fields. Because we use the Weyl symbol calculus, global-mode decomposition is not invoked, so our formulation is local and avoids the usual issues with complex-frequency modes. Also, the particle Hamiltonian is kept general, so the results are equally applicable to relativistic, electromagnetic, and even non-electromagnetic (for example, gravitational) interactions. Because our approach is not bounded by the limitations of variational analysis either, effects caused by collisional and collisionless dissipation are also included naturally.
Our main results are summarized in §§ 5.6, 6.9, 7.6 and 8.5 and are as follows. Starting from the Klimontovich equation, we derive a Fokker–Planck model for the dressed OC distribution. This model captures QL diffusion, interaction with the background fields and ponderomotive effects simultaneously. The local diffusion coefficient is manifestly positive-semidefinite. Waves are allowed to be off-shell (not constrained by a dispersion relation), and a collision integral of the Balescu–Lenard type emerges in a form that is not restricted to any particular Hamiltonian. This operator conserves particles, momentum and energy, and it also satisfies the ![]() $\smash {H}$-theorem, as usual. As a spin-off, a general expression for the spectrum (average Wigner matrix) of microscopic fluctuations of the interaction field is derived. For on-shell waves, which satisfy a QL WKE, our theory conserves the momentum and energy of the wave–plasma system. Dewar's OC QLT of electrostatic turbulence (Dewar Reference Dewar1973) is proven formally as a particular case and given a concise formulation. Also discussed as examples are relativistic electromagnetic and gravitational interactions, and QLT for gravitational waves is proposed.
$\smash {H}$-theorem, as usual. As a spin-off, a general expression for the spectrum (average Wigner matrix) of microscopic fluctuations of the interaction field is derived. For on-shell waves, which satisfy a QL WKE, our theory conserves the momentum and energy of the wave–plasma system. Dewar's OC QLT of electrostatic turbulence (Dewar Reference Dewar1973) is proven formally as a particular case and given a concise formulation. Also discussed as examples are relativistic electromagnetic and gravitational interactions, and QLT for gravitational waves is proposed.
Aside from having the aesthetic appeal of a rigorous local theory, our formulation can help, for example, better understand and model QL plasma heating and current drive. First of all, it systematically accounts for the wave-driven evolution of the non-resonant particle distribution and for the ponderomotive effects caused by plasma inhomogeneity in both time and space. As discussed above (§ 7.5), this is generally important for adequately calculating the energy–momentum transfer between waves and plasma even when resonant absorption per se occurs in a homogeneous-plasma region. Second, our formulation provides general formulas that equally hold in any canonical variables and for any Hamiltonians that satisfy our basic assumptions (§ 3.1). Therefore, our results can be applied to various plasma models immediately. This eliminates the need for ad hoc calculations, which can be especially cumbersome beyond the homogeneous-plasma approximation. Discussing specific models of applied interest, however exciting, is beyond the scope of this paper and is left to future work.
Acknowledgements
Editor Alex Schekochihin and the author thank the referees for their advice in evaluating this article.
Funding
This work was supported by the U.S. DOE through Contract DE-AC02-09CH11466. It is also based upon the work supported by National Science Foundation under the grant No. PHY 1903130.
Declaration of interests
The author reports no conflict of interest.
Appendix A. Average Wigner matrices
A.1 Positive-semidefinitness
As known from Cartwright (Reference Cartwright1976), the average Wigner function of any scalar field on the real axis is non-negative if the averaging is done over a sufficiently large phase-space volume. Here, we extend this theorem to average Wigner matrices of vector fields in a multi-dimensional space, ![]() $\smash {{\boldsymbol {\psi }}({\boldsymbol {\mathsf {x}}})}$, and show that such matrices are positive-semidefinite.
$\smash {{\boldsymbol {\psi }}({\boldsymbol {\mathsf {x}}})}$, and show that such matrices are positive-semidefinite.
For any given function ![]() $\smash {h({\boldsymbol {z}}) \equiv h({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$, we define its local phase-space average as the following convolution integral:Footnote 44
$\smash {h({\boldsymbol {z}}) \equiv h({\boldsymbol {\mathsf {x}}}, {\boldsymbol {\mathsf {k}}})}$, we define its local phase-space average as the following convolution integral:Footnote 44
with a Gaussian window function
and positive constants ![]() $\smash {\sigma _{{\mathsf {x}}}}$ and
$\smash {\sigma _{{\mathsf {x}}}}$ and ![]() $\smash {\sigma _{{\mathsf {k}}}}$ yet to be specified. Unlike in § 2.1.1, the following notation will be assumed for the ‘scalar product’ for variables with upper, lower and mixed indices:
$\smash {\sigma _{{\mathsf {k}}}}$ yet to be specified. Unlike in § 2.1.1, the following notation will be assumed for the ‘scalar product’ for variables with upper, lower and mixed indices:
(The Latin indices in this appendix range from 0 to ![]() $\smash {n}$,
$\smash {n}$, ![]() $\smash {\delta _{ij}}$ and
$\smash {\delta _{ij}}$ and ![]() $\smash {\delta ^{ij}}$ are unit matrices, and summation over repeating indices is assumed.) In particular, note that
$\smash {\delta ^{ij}}$ are unit matrices, and summation over repeating indices is assumed.) In particular, note that ![]() $\smash {|{\boldsymbol {\mathsf {x}}}|^2 \doteq {\boldsymbol {\mathsf {x}}} \cdot {\boldsymbol {\mathsf {x}}} \geqslant 0}$ and must not be confused with the squared spacetime interval, which can have either sign. Likewise,
$\smash {|{\boldsymbol {\mathsf {x}}}|^2 \doteq {\boldsymbol {\mathsf {x}}} \cdot {\boldsymbol {\mathsf {x}}} \geqslant 0}$ and must not be confused with the squared spacetime interval, which can have either sign. Likewise, ![]() $\smash {|{\boldsymbol {\mathsf {k}}}|^2 \doteq {\boldsymbol {\mathsf {k}}} \cdot {\boldsymbol {\mathsf {k}}} \geqslant 0}$ must not be confused with
$\smash {|{\boldsymbol {\mathsf {k}}}|^2 \doteq {\boldsymbol {\mathsf {k}}} \cdot {\boldsymbol {\mathsf {k}}} \geqslant 0}$ must not be confused with ![]() $\smash {{\mathsf {k}}_i{\mathsf {k}}^i = -\omega ^2 + {\boldsymbol {k}}^2}$.
$\smash {{\mathsf {k}}_i{\mathsf {k}}^i = -\omega ^2 + {\boldsymbol {k}}^2}$.
The average Wigner matrix of any given vector field ![]() $\smash {{\boldsymbol {\psi }}}$ is given by
$\smash {{\boldsymbol {\psi }}}$ is given by
 \begin{align} \overline{{{\boldsymbol {\mathsf{W}}}}}_{{\boldsymbol{\psi}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) = \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}}\frac{1}{(2{\rm \pi} \sigma_{{\mathsf{x}}} \sigma_{{\mathsf{k}}})^{{\mathsf{n}}}} \int &\mathrm{d}{\boldsymbol {\mathsf{s}}}\,\mathrm{d}{\boldsymbol {\mathsf{x}}}'\,\mathrm{d}{\boldsymbol {\mathsf{k}}}'\, {\boldsymbol{\psi}}({\boldsymbol {\mathsf{x}}}' + {\boldsymbol {\mathsf{s}}}/2) {\boldsymbol{\psi}}^{{\dagger}}({\boldsymbol {\mathsf{x}}}' - {\boldsymbol {\mathsf{s}}}/2) \nonumber\\ &\times \exp\left(-\frac{|{\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{x}}}'|^2}{2\sigma_{{\mathsf{x}}}^2} - \frac{|{\boldsymbol {\mathsf{k}}} - {\boldsymbol {\mathsf{k}}}'|^2}{2\sigma_{{\mathsf{k}}}^2}-\mathrm{i} {\boldsymbol {\mathsf{k}}}' \cdot {\boldsymbol {\mathsf{s}}}\right). \end{align}
\begin{align} \overline{{{\boldsymbol {\mathsf{W}}}}}_{{\boldsymbol{\psi}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) = \frac{1}{(2{\rm \pi})^{{\mathsf{n}}}}\frac{1}{(2{\rm \pi} \sigma_{{\mathsf{x}}} \sigma_{{\mathsf{k}}})^{{\mathsf{n}}}} \int &\mathrm{d}{\boldsymbol {\mathsf{s}}}\,\mathrm{d}{\boldsymbol {\mathsf{x}}}'\,\mathrm{d}{\boldsymbol {\mathsf{k}}}'\, {\boldsymbol{\psi}}({\boldsymbol {\mathsf{x}}}' + {\boldsymbol {\mathsf{s}}}/2) {\boldsymbol{\psi}}^{{\dagger}}({\boldsymbol {\mathsf{x}}}' - {\boldsymbol {\mathsf{s}}}/2) \nonumber\\ &\times \exp\left(-\frac{|{\boldsymbol {\mathsf{x}}} - {\boldsymbol {\mathsf{x}}}'|^2}{2\sigma_{{\mathsf{x}}}^2} - \frac{|{\boldsymbol {\mathsf{k}}} - {\boldsymbol {\mathsf{k}}}'|^2}{2\sigma_{{\mathsf{k}}}^2}-\mathrm{i} {\boldsymbol {\mathsf{k}}}' \cdot {\boldsymbol {\mathsf{s}}}\right). \end{align}
The integral over ![]() $\smash {{\boldsymbol {\mathsf {k}}}'}$ can be readily taken:
$\smash {{\boldsymbol {\mathsf {k}}}'}$ can be readily taken:
Then, using the variables ![]() $\smash {{\boldsymbol {\mathsf {x}}}_{1,2} \doteq {\boldsymbol {\mathsf {x}}}' \pm {\boldsymbol {\mathsf {s}}}/2}$, one can rewrite (A4) as follows:
$\smash {{\boldsymbol {\mathsf {x}}}_{1,2} \doteq {\boldsymbol {\mathsf {x}}}' \pm {\boldsymbol {\mathsf {s}}}/2}$, one can rewrite (A4) as follows:
The function ![]() $\smash {\phi }$ can also be expressed as
$\smash {\phi }$ can also be expressed as ![]() $\smash {\phi = |{\boldsymbol {\mathsf {x}}}|^2/(2\sigma _{{\mathsf {x}}}^2) + \phi ({\boldsymbol {\mathsf {x}}}_1) + \phi ^*({\boldsymbol {\mathsf {x}}}_2) - \lambda {\boldsymbol {\mathsf {x}}}_1 \cdot {\boldsymbol {\mathsf {x}}}_2}$, where
$\smash {\phi = |{\boldsymbol {\mathsf {x}}}|^2/(2\sigma _{{\mathsf {x}}}^2) + \phi ({\boldsymbol {\mathsf {x}}}_1) + \phi ^*({\boldsymbol {\mathsf {x}}}_2) - \lambda {\boldsymbol {\mathsf {x}}}_1 \cdot {\boldsymbol {\mathsf {x}}}_2}$, where
and ![]() $\smash {\lambda \doteq \sigma _{{\mathsf {k}}}^2 - (4\sigma _{{\mathsf {x}}}^2)^{-1}}$. Then, using
$\smash {\lambda \doteq \sigma _{{\mathsf {k}}}^2 - (4\sigma _{{\mathsf {x}}}^2)^{-1}}$. Then, using ![]() $\smash {{\boldsymbol {\xi }}({\boldsymbol {\mathsf {y}}}) \doteq {\boldsymbol {\psi }}({\boldsymbol {\mathsf {y}}})\mathrm {e}^{-\phi ({\boldsymbol {\mathsf {y}}})}}$, one obtains from (A6) that
$\smash {{\boldsymbol {\xi }}({\boldsymbol {\mathsf {y}}}) \doteq {\boldsymbol {\psi }}({\boldsymbol {\mathsf {y}}})\mathrm {e}^{-\phi ({\boldsymbol {\mathsf {y}}})}}$, one obtains from (A6) that
By Taylor-expanding ![]() $\smash {\mathrm {e}^{\lambda {\boldsymbol {\mathsf {x}}}_1 \cdot {\boldsymbol {\mathsf {x}}}_2}}$, one obtains
$\smash {\mathrm {e}^{\lambda {\boldsymbol {\mathsf {x}}}_1 \cdot {\boldsymbol {\mathsf {x}}}_2}}$, one obtains
 \begin{equation} \overline{{{\boldsymbol {\mathsf{W}}}}}_{{\boldsymbol{\psi}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) = \frac{\mathrm{e}^{-|{\boldsymbol {\mathsf{x}}}|^2/(2\sigma_{{\mathsf{x}}}^2)}}{(2{\rm \pi})^{3{{\mathsf{n}}}/2}\sigma_{{\mathsf{x}}}^{{\mathsf{n}}}} \sum_{m=0}^\infty\frac{\lambda^m}{m!}\,{{\boldsymbol {\mathsf{J}}}}_m, \end{equation}
\begin{equation} \overline{{{\boldsymbol {\mathsf{W}}}}}_{{\boldsymbol{\psi}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) = \frac{\mathrm{e}^{-|{\boldsymbol {\mathsf{x}}}|^2/(2\sigma_{{\mathsf{x}}}^2)}}{(2{\rm \pi})^{3{{\mathsf{n}}}/2}\sigma_{{\mathsf{x}}}^{{\mathsf{n}}}} \sum_{m=0}^\infty\frac{\lambda^m}{m!}\,{{\boldsymbol {\mathsf{J}}}}_m, \end{equation}
where ![]() $\smash {{{\boldsymbol {\mathsf {J}}}}_m \doteq \int \mathrm {d}{\boldsymbol {\mathsf {x}}}_1\,\mathrm {d}{\boldsymbol {\mathsf {x}}}_2\,({\boldsymbol {\mathsf {x}}}_1 \cdot {\boldsymbol {\mathsf {x}}}_2)^m {\boldsymbol {\xi }}({\boldsymbol {\mathsf {x}}}_1) {\boldsymbol {\xi }}^{{\dagger}} ({\boldsymbol {\mathsf {x}}}_2)}$. Note that
$\smash {{{\boldsymbol {\mathsf {J}}}}_m \doteq \int \mathrm {d}{\boldsymbol {\mathsf {x}}}_1\,\mathrm {d}{\boldsymbol {\mathsf {x}}}_2\,({\boldsymbol {\mathsf {x}}}_1 \cdot {\boldsymbol {\mathsf {x}}}_2)^m {\boldsymbol {\xi }}({\boldsymbol {\mathsf {x}}}_1) {\boldsymbol {\xi }}^{{\dagger}} ({\boldsymbol {\mathsf {x}}}_2)}$. Note that
 \begin{equation} ({\boldsymbol {\mathsf{x}}}_1 \cdot {\boldsymbol {\mathsf{x}}}_2)^m = \sum_{{\boldsymbol{\mu}}(m)} \prod_{i=1}^{{{\mathsf{n}}}} ({\mathsf{x}}_1^i{\mathsf{x}}^i_2)^{m_i}, \end{equation}
\begin{equation} ({\boldsymbol {\mathsf{x}}}_1 \cdot {\boldsymbol {\mathsf{x}}}_2)^m = \sum_{{\boldsymbol{\mu}}(m)} \prod_{i=1}^{{{\mathsf{n}}}} ({\mathsf{x}}_1^i{\mathsf{x}}^i_2)^{m_i}, \end{equation}
where the summation is performed over all combinations ![]() ${\boldsymbol {\mu }}(m) \equiv \{m_1, m_2, \ldots, m_{{\mathsf {n}}}\}$ of integers
${\boldsymbol {\mu }}(m) \equiv \{m_1, m_2, \ldots, m_{{\mathsf {n}}}\}$ of integers ![]() $\smash {m_i \geqslant 0}$ such that
$\smash {m_i \geqslant 0}$ such that ![]() $\smash {\sum _i m_i = m}$. Thus,
$\smash {\sum _i m_i = m}$. Thus,
 \begin{equation} {{\boldsymbol {\mathsf{J}}}}_m = \sum_{{\boldsymbol{\mu}}(m)} {\boldsymbol{\mathcal{J}}}_{{\boldsymbol{\mu}}}{\boldsymbol{\mathcal{J}}}^{{\dagger}}_{{\boldsymbol{\mu}}}, \qquad {\boldsymbol{\mathcal{J}}}_{{\boldsymbol{\mu}}} = \int \mathrm{d}{\boldsymbol {\mathsf{y}}}\,{\boldsymbol{\xi}}({\boldsymbol {\mathsf{y}}})\prod_{i=1}^{{{\mathsf{n}}}}({\mathsf{y}}^i)^{m_i}. \end{equation}
\begin{equation} {{\boldsymbol {\mathsf{J}}}}_m = \sum_{{\boldsymbol{\mu}}(m)} {\boldsymbol{\mathcal{J}}}_{{\boldsymbol{\mu}}}{\boldsymbol{\mathcal{J}}}^{{\dagger}}_{{\boldsymbol{\mu}}}, \qquad {\boldsymbol{\mathcal{J}}}_{{\boldsymbol{\mu}}} = \int \mathrm{d}{\boldsymbol {\mathsf{y}}}\,{\boldsymbol{\xi}}({\boldsymbol {\mathsf{y}}})\prod_{i=1}^{{{\mathsf{n}}}}({\mathsf{y}}^i)^{m_i}. \end{equation}
Because each ![]() $\smash {{{\boldsymbol {\mathsf {J}}}}_m}$ is positive-semidefinite, the Wigner matrix
$\smash {{{\boldsymbol {\mathsf {J}}}}_m}$ is positive-semidefinite, the Wigner matrix ![]() $\smash {\overline {{{\boldsymbol {\mathsf {W}}}}}_{{\boldsymbol {\psi }}}}$ is positive-semidefinite when
$\smash {\overline {{{\boldsymbol {\mathsf {W}}}}}_{{\boldsymbol {\psi }}}}$ is positive-semidefinite when ![]() $\smash {\lambda \geqslant 0}$, or equivalently, when
$\smash {\lambda \geqslant 0}$, or equivalently, when ![]() $\smash {\sigma _{{\mathsf {x}}}\sigma _{{\mathsf {k}}} > 1/2}$. This condition is assumed to be satisfied for the phase-space averaging of
$\smash {\sigma _{{\mathsf {x}}}\sigma _{{\mathsf {k}}} > 1/2}$. This condition is assumed to be satisfied for the phase-space averaging of ![]() $\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}}$ used in the main text. Loosely, this means that the averaging is done over the phase-space volume
$\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}}$ used in the main text. Loosely, this means that the averaging is done over the phase-space volume ![]() $\smash {\varDelta {\boldsymbol {\mathsf {x}}}\,\varDelta {\boldsymbol {\mathsf {k}}} \sim (\sigma _{{\mathsf {x}}}\sigma _{{\mathsf {k}}})^{{\mathsf {n}}} \gtrsim 1}$.
$\smash {\varDelta {\boldsymbol {\mathsf {x}}}\,\varDelta {\boldsymbol {\mathsf {k}}} \sim (\sigma _{{\mathsf {x}}}\sigma _{{\mathsf {k}}})^{{\mathsf {n}}} \gtrsim 1}$.
A.2 Invariant limit for eikonal fields
For eikonal fields (7.17), one has
Here, ![]() $\smash {{\boldsymbol {A}} \doteq {\boldsymbol {\eta }}{\boldsymbol {\eta }}^{{\dagger}} |{\breve {a}}|^2/4}$,
$\smash {{\boldsymbol {A}} \doteq {\boldsymbol {\eta }}{\boldsymbol {\eta }}^{{\dagger}} |{\breve {a}}|^2/4}$, ![]() $\smash {{\boldsymbol {B}} \doteq {\boldsymbol {\eta }}{\boldsymbol {\eta }}^\intercal {\breve {a}}^2/4}$, ‘c.c.’ stands for complex conjugate, we used the linear approximation
$\smash {{\boldsymbol {B}} \doteq {\boldsymbol {\eta }}{\boldsymbol {\eta }}^\intercal {\breve {a}}^2/4}$, ‘c.c.’ stands for complex conjugate, we used the linear approximation ![]() $\smash {\theta ({\boldsymbol {\mathsf {x}}} \pm {\boldsymbol {\mathsf{s}}}/2) \approx \theta ({\boldsymbol {\mathsf {x}}}) \pm \overline {{\boldsymbol {\mathsf {k}}}}({\boldsymbol {\mathsf {x}}})\cdot {\boldsymbol {\mathsf {s}}}/2}$, with
$\smash {\theta ({\boldsymbol {\mathsf {x}}} \pm {\boldsymbol {\mathsf{s}}}/2) \approx \theta ({\boldsymbol {\mathsf {x}}}) \pm \overline {{\boldsymbol {\mathsf {k}}}}({\boldsymbol {\mathsf {x}}})\cdot {\boldsymbol {\mathsf {s}}}/2}$, with ![]() $\smash {\overline {{\boldsymbol {\mathsf {k}}}} \equiv (-\overline {\omega }, \overline {{\boldsymbol {k}}})}$. Then,
$\smash {\overline {{\boldsymbol {\mathsf {k}}}} \equiv (-\overline {\omega }, \overline {{\boldsymbol {k}}})}$. Then,
Let us adopt ![]() $\smash {\sigma _{{\mathsf {x}}} \ll l_c}$, where
$\smash {\sigma _{{\mathsf {x}}} \ll l_c}$, where ![]() $\smash {l_c}$ is the least characteristic scale of
$\smash {l_c}$ is the least characteristic scale of ![]() $\smash {{\breve {a}}}$,
$\smash {{\breve {a}}}$, ![]() $\smash {{\boldsymbol {\eta }}}$ and
$\smash {{\boldsymbol {\eta }}}$ and ![]() $\smash {\overline {{\boldsymbol {\mathsf {k}}}}}$. Then,
$\smash {\overline {{\boldsymbol {\mathsf {k}}}}}$. Then,
Here, ![]() $\smash {\mathcal {G}_{{\mathsf {k}}}({\boldsymbol {\mathsf {k}}})}$ are normalized Gaussians that can be replaced with delta functions if
$\smash {\mathcal {G}_{{\mathsf {k}}}({\boldsymbol {\mathsf {k}}})}$ are normalized Gaussians that can be replaced with delta functions if ![]() $\smash {\sigma _{{\mathsf {k}}}}$ is small compared with any scale of interest in the
$\smash {\sigma _{{\mathsf {k}}}}$ is small compared with any scale of interest in the ![]() $\smash {{\boldsymbol {\mathsf {k}}}}$ space:
$\smash {{\boldsymbol {\mathsf {k}}}}$ space:
Also, the function
can be made exponentially small by adopting ![]() $\smash {\sigma _{{\mathsf {x}}} \gg |\overline {{\boldsymbol {\mathsf {k}}}}|^{-1}}$.Footnote 45 In this limit, the average Wigner matrix of an eikonal field is independent of
$\smash {\sigma _{{\mathsf {x}}} \gg |\overline {{\boldsymbol {\mathsf {k}}}}|^{-1}}$.Footnote 45 In this limit, the average Wigner matrix of an eikonal field is independent of ![]() $\smash {\sigma _{{\mathsf {x}}}}$ and
$\smash {\sigma _{{\mathsf {x}}}}$ and ![]() $\smash {\sigma _{{\mathsf {k}}}}$:
$\smash {\sigma _{{\mathsf {k}}}}$:
This ![]() $\smash {\overline {{{\boldsymbol {\mathsf {W}}}}}_{{\boldsymbol {\psi }}}}$ is also Hermitian and positive-semidefinite (in agreement with the general theory from § A.1), because so are
$\smash {\overline {{{\boldsymbol {\mathsf {W}}}}}_{{\boldsymbol {\psi }}}}$ is also Hermitian and positive-semidefinite (in agreement with the general theory from § A.1), because so are ![]() $\smash {{\boldsymbol {A}}}$ and
$\smash {{\boldsymbol {A}}}$ and ![]() $\smash {{\boldsymbol {A}}^*}$. The same properties pertain to the Wigner matrix of an ensemble of randomly phased eikonal fields, because it equals the sum of the Wigner matrices of the individual components (see also § 7.4).
$\smash {{\boldsymbol {A}}^*}$. The same properties pertain to the Wigner matrix of an ensemble of randomly phased eikonal fields, because it equals the sum of the Wigner matrices of the individual components (see also § 7.4).
Appendix B. Auxiliary proofs
B.1 Proof of (2.53)
Like in the case of (2.45), one finds that
 \begin{align} (\widehat{\boldsymbol{{\boldsymbol {\mathsf{L}}}}}{\boldsymbol{\psi}}({\boldsymbol {\mathsf{x}}}))^i (\widehat{\boldsymbol{{\boldsymbol {\mathsf{R}}}}}{\boldsymbol{\psi}}({\boldsymbol {\mathsf{x}}}))^{*j} & = \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}}\,}^i{}_{i'}|\psi^{i'}}\right\rangle \left\langle{\psi^{j'}|(\widehat{{\mathsf{R}}}^j{}_{j'})^{{\dagger}}|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = (2{\rm \pi})^{{\mathsf{n}}} \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}\,}}^i{}_{i'}\widehat{{\mathsf{W}}}_{{\boldsymbol{\psi}}}^{i'j'}(\widehat{{\mathsf{R}}}^{{\dagger}})_{j'}{}^j|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = (2{\rm \pi})^{{\mathsf{n}}} \left\langle{{\boldsymbol {\mathsf{x}}}|(\widehat{\boldsymbol{{\boldsymbol {\mathsf{L}\,}}}}\widehat{\boldsymbol{{\boldsymbol {\mathsf{W}}}}}_\psi\smash{\widehat{\boldsymbol{{\boldsymbol {\mathsf{R}}}}}}^{{\dagger}})^{ij}|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = \textstyle \int \mathrm{d}{\boldsymbol {\mathsf{k}}}\, \big({{\boldsymbol {\mathsf{L}}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {{\boldsymbol {\mathsf{W}}}}_{{\boldsymbol{\psi}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {{\boldsymbol {\mathsf{R}}}}^{{\dagger}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}})\big)^{ij}. \end{align}
\begin{align} (\widehat{\boldsymbol{{\boldsymbol {\mathsf{L}}}}}{\boldsymbol{\psi}}({\boldsymbol {\mathsf{x}}}))^i (\widehat{\boldsymbol{{\boldsymbol {\mathsf{R}}}}}{\boldsymbol{\psi}}({\boldsymbol {\mathsf{x}}}))^{*j} & = \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}}\,}^i{}_{i'}|\psi^{i'}}\right\rangle \left\langle{\psi^{j'}|(\widehat{{\mathsf{R}}}^j{}_{j'})^{{\dagger}}|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = (2{\rm \pi})^{{\mathsf{n}}} \left\langle{{\boldsymbol {\mathsf{x}}}|\widehat{{\mathsf{L}\,}}^i{}_{i'}\widehat{{\mathsf{W}}}_{{\boldsymbol{\psi}}}^{i'j'}(\widehat{{\mathsf{R}}}^{{\dagger}})_{j'}{}^j|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = (2{\rm \pi})^{{\mathsf{n}}} \left\langle{{\boldsymbol {\mathsf{x}}}|(\widehat{\boldsymbol{{\boldsymbol {\mathsf{L}\,}}}}\widehat{\boldsymbol{{\boldsymbol {\mathsf{W}}}}}_\psi\smash{\widehat{\boldsymbol{{\boldsymbol {\mathsf{R}}}}}}^{{\dagger}})^{ij}|{\boldsymbol {\mathsf{x}}}}\right\rangle \nonumber\\ & = \textstyle \int \mathrm{d}{\boldsymbol {\mathsf{k}}}\, \big({{\boldsymbol {\mathsf{L}}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {{\boldsymbol {\mathsf{W}}}}_{{\boldsymbol{\psi}}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}}) \star {{\boldsymbol {\mathsf{R}}}}^{{\dagger}}({\boldsymbol {\mathsf{x}}}, {\boldsymbol {\mathsf{k}}})\big)^{ij}. \end{align}
This proves (2.53a). At ![]() $\smash {\epsilon \to 0}$, when
$\smash {\epsilon \to 0}$, when ![]() $\smash {\star }$ becomes the usual product, (B1) gives
$\smash {\star }$ becomes the usual product, (B1) gives
and in particular, taking the trace of (B2) yields
Here, ![]() $\smash {{{\boldsymbol {\mathsf {Q}}}} \doteq {{\boldsymbol {\mathsf {R}}}}^{{\dagger}} {{\boldsymbol {\mathsf {L}}}}}$, and we used that
$\smash {{{\boldsymbol {\mathsf {Q}}}} \doteq {{\boldsymbol {\mathsf {R}}}}^{{\dagger}} {{\boldsymbol {\mathsf {L}}}}}$, and we used that ![]() $\smash {\operatorname {tr}({{\boldsymbol {\mathsf {A}}}}{{\boldsymbol {\mathsf {B}}}}) = \operatorname {tr}({{\boldsymbol {\mathsf {B}}}}{{\boldsymbol {\mathsf {A}}}})}$ for any matrices
$\smash {\operatorname {tr}({{\boldsymbol {\mathsf {A}}}}{{\boldsymbol {\mathsf {B}}}}) = \operatorname {tr}({{\boldsymbol {\mathsf {B}}}}{{\boldsymbol {\mathsf {A}}}})}$ for any matrices ![]() $\smash {{{\boldsymbol {\mathsf {A}}}}}$ and
$\smash {{{\boldsymbol {\mathsf {A}}}}}$ and ![]() $\smash {{{\boldsymbol {\mathsf {B}}}}}$.
$\smash {{{\boldsymbol {\mathsf {B}}}}}$.
For real fields, one can also replace the integrand with
where we used ![]() $\smash {\operatorname {tr}{{\boldsymbol {\mathsf {A}}}}^\intercal = \operatorname {tr}{{\boldsymbol {\mathsf {A}}}}}$,
$\smash {\operatorname {tr}{{\boldsymbol {\mathsf {A}}}}^\intercal = \operatorname {tr}{{\boldsymbol {\mathsf {A}}}}}$, ![]() $\smash {({{\boldsymbol {\mathsf {A}}}}{{\boldsymbol {\mathsf {B}}}})^\intercal = {{\boldsymbol {\mathsf {B}}}}^\intercal {{\boldsymbol {\mathsf {A}}}}^\intercal }$,
$\smash {({{\boldsymbol {\mathsf {A}}}}{{\boldsymbol {\mathsf {B}}}})^\intercal = {{\boldsymbol {\mathsf {B}}}}^\intercal {{\boldsymbol {\mathsf {A}}}}^\intercal }$, ![]() $\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}^{{\dagger}} = {{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}}$ and, again,
$\smash {{{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}^{{\dagger}} = {{\boldsymbol {\mathsf {W}}}}_{{\boldsymbol {\psi }}}}$ and, again, ![]() $\smash {\operatorname {tr}({{\boldsymbol {\mathsf {A}}}}{{\boldsymbol {\mathsf {B}}}}) = \operatorname {tr}({{\boldsymbol {\mathsf {B}}}}{{\boldsymbol {\mathsf {A}}}})}$, respectively. In summary then,
$\smash {\operatorname {tr}({{\boldsymbol {\mathsf {A}}}}{{\boldsymbol {\mathsf {B}}}}) = \operatorname {tr}({{\boldsymbol {\mathsf {B}}}}{{\boldsymbol {\mathsf {A}}}})}$, respectively. In summary then,
so the anti-Hermitian part of ![]() $\smash {{{\boldsymbol {\mathsf {Q}}}}}$ does not contribute to the integrals. Thus,
$\smash {{{\boldsymbol {\mathsf {Q}}}}}$ does not contribute to the integrals. Thus,
Because ![]() $\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {L}}}}}}$ and
$\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {L}}}}}}$ and ![]() $\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {R}}}}}}$ are arbitrary, they can as well be swapped; then one obtains (2.53c).
$\smash {\widehat {\boldsymbol {{\boldsymbol {\mathsf {R}}}}}}$ are arbitrary, they can as well be swapped; then one obtains (2.53c).
B.2 Proof of (4.28)
Suppose the dominant term in ![]() ${\boldsymbol {\mu }}$ in (4.16) has the form
${\boldsymbol {\mu }}$ in (4.16) has the form ![]() ${\boldsymbol {\mu }}_h \tau ^h$, where
${\boldsymbol {\mu }}_h \tau ^h$, where ![]() $h$ is a natural number and
$h$ is a natural number and ![]() $\smash {\mu _h = \mathcal {O}(\epsilon ^2)}$. (Here,
$\smash {\mu _h = \mathcal {O}(\epsilon ^2)}$. (Here, ![]() $h$ is a power index, so no summation over
$h$ is a power index, so no summation over ![]() $h$ is assumed.) Let us Taylor-expand
$h$ is assumed.) Let us Taylor-expand ![]() $\mathcal {J}[A, G]$ in
$\mathcal {J}[A, G]$ in ![]() $\smash {{\boldsymbol {\mu }}_h}$:
$\smash {{\boldsymbol {\mu }}_h}$:
 \begin{align} \mathcal{J}[A, G] & - \mathcal{J}[A, G_0] - \mathcal{O}(\epsilon^2) \nonumber\\ &\quad \approx {\boldsymbol{\mu}}_h \cdot \frac{\partial}{\partial {\boldsymbol{\mu}}_h}\left( \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) \lim_{\nu\to 0+} \int_0^{\infty}\mathrm{d}\tau\,\mathrm{e}^{-\nu \tau + \mathrm{i} \varOmega \tau + \mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{\mu}}_h \tau^h} \right)_{{\boldsymbol{\mu}}_h = {\boldsymbol{0}}} \nonumber\\ &\quad \approx {\boldsymbol{\mu}}_h \cdot \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) \lim_{\nu \to 0+} \frac{\partial}{\partial {\boldsymbol{\mu}}_h} \left( \int_0^{\infty} \mathrm{d}\tau\,\mathrm{e}^{-\nu \tau + \mathrm{i}\varOmega \tau + \mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{\mu}}_h \tau^h} \right)_{{\boldsymbol{\mu}}_h = {\boldsymbol{0}}} \nonumber\\ &\quad \approx \mathrm{i} {\boldsymbol{\mu}}_h \cdot \int \mathrm{d}{\boldsymbol{K}}\,{\boldsymbol{K}} A({\boldsymbol{X}}, {\boldsymbol{K}}) \lim_{\nu \to 0+}\int_0^{\infty} \mathrm{d}\tau\,\tau^h \mathrm{e}^{-\nu \tau + \mathrm{i} \varOmega \tau} \nonumber\\ &\quad \approx \mathrm{i}^{1-h} {\boldsymbol{\mu}}_h \cdot \int \mathrm{d}{\boldsymbol{K}}\,{\boldsymbol{K}} A({\boldsymbol{X}}, {\boldsymbol{K}}) \,\frac{\mathrm{d}^h G_0(\varOmega ({\boldsymbol{X}}, {\boldsymbol{K}}))}{\mathrm{d}\varOmega^h} \nonumber\\ &\quad \approx \mathrm{i}^{1-h} {\boldsymbol{\mu}}_h \cdot \frac{\eth^h}{\partial \varOmega^h} \int \mathrm{d}{\boldsymbol{K}}\,{\boldsymbol{K}} A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})). \end{align}
\begin{align} \mathcal{J}[A, G] & - \mathcal{J}[A, G_0] - \mathcal{O}(\epsilon^2) \nonumber\\ &\quad \approx {\boldsymbol{\mu}}_h \cdot \frac{\partial}{\partial {\boldsymbol{\mu}}_h}\left( \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) \lim_{\nu\to 0+} \int_0^{\infty}\mathrm{d}\tau\,\mathrm{e}^{-\nu \tau + \mathrm{i} \varOmega \tau + \mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{\mu}}_h \tau^h} \right)_{{\boldsymbol{\mu}}_h = {\boldsymbol{0}}} \nonumber\\ &\quad \approx {\boldsymbol{\mu}}_h \cdot \int \mathrm{d}{\boldsymbol{K}}\,A({\boldsymbol{X}}, {\boldsymbol{K}}) \lim_{\nu \to 0+} \frac{\partial}{\partial {\boldsymbol{\mu}}_h} \left( \int_0^{\infty} \mathrm{d}\tau\,\mathrm{e}^{-\nu \tau + \mathrm{i}\varOmega \tau + \mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{\mu}}_h \tau^h} \right)_{{\boldsymbol{\mu}}_h = {\boldsymbol{0}}} \nonumber\\ &\quad \approx \mathrm{i} {\boldsymbol{\mu}}_h \cdot \int \mathrm{d}{\boldsymbol{K}}\,{\boldsymbol{K}} A({\boldsymbol{X}}, {\boldsymbol{K}}) \lim_{\nu \to 0+}\int_0^{\infty} \mathrm{d}\tau\,\tau^h \mathrm{e}^{-\nu \tau + \mathrm{i} \varOmega \tau} \nonumber\\ &\quad \approx \mathrm{i}^{1-h} {\boldsymbol{\mu}}_h \cdot \int \mathrm{d}{\boldsymbol{K}}\,{\boldsymbol{K}} A({\boldsymbol{X}}, {\boldsymbol{K}}) \,\frac{\mathrm{d}^h G_0(\varOmega ({\boldsymbol{X}}, {\boldsymbol{K}}))}{\mathrm{d}\varOmega^h} \nonumber\\ &\quad \approx \mathrm{i}^{1-h} {\boldsymbol{\mu}}_h \cdot \frac{\eth^h}{\partial \varOmega^h} \int \mathrm{d}{\boldsymbol{K}}\,{\boldsymbol{K}} A({\boldsymbol{X}}, {\boldsymbol{K}}) G_0(\varOmega({\boldsymbol{X}}, {\boldsymbol{K}})). \end{align}
Provided that ![]() $A$ is sufficiently smooth and well behaved, the overall coefficient here is
$A$ is sufficiently smooth and well behaved, the overall coefficient here is ![]() $\mathcal {O}(1)$, so
$\mathcal {O}(1)$, so ![]() $\smash {\mathcal {J}[A, G] - \mathcal {J}[A, G_0] = \mathcal {O}(\mu _h) + \mathcal {O}(\epsilon ^2)}$. Because
$\smash {\mathcal {J}[A, G] - \mathcal {J}[A, G_0] = \mathcal {O}(\mu _h) + \mathcal {O}(\epsilon ^2)}$. Because ![]() $\mu _h = \mathcal {O}(\epsilon ^2)$, this proves (4.28).
$\mu _h = \mathcal {O}(\epsilon ^2)$, this proves (4.28).
B.3 Proof of (5.4)
Here, we show that
 \begin{align} \text {symb}_{{\mathsf {x}}}(&\widehat{u\,}^{\alpha}\widehat{G\,}\widehat{u\,}^{\beta})\nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{S}}\, \mathrm{e}^{-\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}}} \left\langle{{\boldsymbol{X}} + {\boldsymbol{S}}/2 | \widehat{u\,}^{\alpha}\widehat{G\,}\widehat{u\,}^{\beta} | {\boldsymbol{X}} - {\boldsymbol{S}}/2}\right\rangle \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{S}}\,\mathrm{d}{\boldsymbol{S}}'\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}', {\boldsymbol{K}}') G({\boldsymbol{X}}', {\boldsymbol{K}}'')\, \mathrm{e}^{-\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}} + \mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'') \cdot {\boldsymbol{S}}'} \nonumber\\ & \hspace{2cm}\times \delta({\boldsymbol{X}} + {\boldsymbol{S}}/2 - {\boldsymbol{X}}' - {\boldsymbol{S}}'/2) \delta({\boldsymbol{X}} - {\boldsymbol{S}}/2 - {\boldsymbol{X}}' + {\boldsymbol{S}}'/2) \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}'\,\mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{S}}\,\mathrm{d}{\boldsymbol{S}}'\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}', {\boldsymbol{K}}') G({\boldsymbol{X}}', {\boldsymbol{K}}'')\, \mathrm{e}^{-\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}} + \mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'') \cdot {\boldsymbol{S}}'} \nonumber\\ &\hspace{2cm}\times \delta ({\boldsymbol{S}} - {\boldsymbol{S}}') \delta ({\boldsymbol{X}} - {\boldsymbol{S}}/2 - {\boldsymbol{X}}' + {\boldsymbol{S}}'/2) \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}'\,\mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{S}}\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}', {\boldsymbol{K}}') G({\boldsymbol{X}}', {\boldsymbol{K}}'')\, \mathrm{e}^{\mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'' - {\boldsymbol{K}}) \cdot {\boldsymbol{S}}} \delta({\boldsymbol{X}} - {\boldsymbol{X}}') \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{S}}\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G({\boldsymbol{X}}, {\boldsymbol{K}}'')\, \mathrm{e}^{\mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'' - {\boldsymbol{K}}) \cdot {\boldsymbol{S}}} \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}'\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G({\boldsymbol{X}}, {\boldsymbol{K}} - {\boldsymbol{K}}'). \end{align}
\begin{align} \text {symb}_{{\mathsf {x}}}(&\widehat{u\,}^{\alpha}\widehat{G\,}\widehat{u\,}^{\beta})\nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{S}}\, \mathrm{e}^{-\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}}} \left\langle{{\boldsymbol{X}} + {\boldsymbol{S}}/2 | \widehat{u\,}^{\alpha}\widehat{G\,}\widehat{u\,}^{\beta} | {\boldsymbol{X}} - {\boldsymbol{S}}/2}\right\rangle \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{S}}\,\mathrm{d}{\boldsymbol{S}}'\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}', {\boldsymbol{K}}') G({\boldsymbol{X}}', {\boldsymbol{K}}'')\, \mathrm{e}^{-\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}} + \mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'') \cdot {\boldsymbol{S}}'} \nonumber\\ & \hspace{2cm}\times \delta({\boldsymbol{X}} + {\boldsymbol{S}}/2 - {\boldsymbol{X}}' - {\boldsymbol{S}}'/2) \delta({\boldsymbol{X}} - {\boldsymbol{S}}/2 - {\boldsymbol{X}}' + {\boldsymbol{S}}'/2) \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}'\,\mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{S}}\,\mathrm{d}{\boldsymbol{S}}'\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}', {\boldsymbol{K}}') G({\boldsymbol{X}}', {\boldsymbol{K}}'')\, \mathrm{e}^{-\mathrm{i} {\boldsymbol{K}} \cdot {\boldsymbol{S}} + \mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'') \cdot {\boldsymbol{S}}'} \nonumber\\ &\hspace{2cm}\times \delta ({\boldsymbol{S}} - {\boldsymbol{S}}') \delta ({\boldsymbol{X}} - {\boldsymbol{S}}/2 - {\boldsymbol{X}}' + {\boldsymbol{S}}'/2) \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{X}}'\,\mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{S}}\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}', {\boldsymbol{K}}') G({\boldsymbol{X}}', {\boldsymbol{K}}'')\, \mathrm{e}^{\mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'' - {\boldsymbol{K}}) \cdot {\boldsymbol{S}}} \delta({\boldsymbol{X}} - {\boldsymbol{X}}') \nonumber\\ & = \frac{1}{(2{\rm \pi})^N} \int \mathrm{d}{\boldsymbol{K}}'\,\mathrm{d}{\boldsymbol{K}}''\,\mathrm{d}{\boldsymbol{S}}\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G({\boldsymbol{X}}, {\boldsymbol{K}}'')\, \mathrm{e}^{\mathrm{i} ({\boldsymbol{K}}' + {\boldsymbol{K}}'' - {\boldsymbol{K}}) \cdot {\boldsymbol{S}}} \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}'\, {W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}') G({\boldsymbol{X}}, {\boldsymbol{K}} - {\boldsymbol{K}}'). \end{align}B.4 Proof of (5.10)
Using (4.19), (4.20) and (2.84) in application to ![]() $W_{{\boldsymbol {u}}}^{\alpha \beta }$, one finds that
$W_{{\boldsymbol {u}}}^{\alpha \beta }$, one finds that
 \begin{align} D_0^{\alpha\beta}({\boldsymbol{X}}) & \doteq \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}) G^*({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, - {\boldsymbol{K}}) G^*({\boldsymbol{X}},-{\boldsymbol{K}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, - {\boldsymbol{K}}) G({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta *}({\boldsymbol{X}}, {\boldsymbol{K}}) G({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & = (D_0^{\alpha\beta}({\boldsymbol{X}}))^*, \end{align}
\begin{align} D_0^{\alpha\beta}({\boldsymbol{X}}) & \doteq \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}) G^*({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, - {\boldsymbol{K}}) G^*({\boldsymbol{X}},-{\boldsymbol{K}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, - {\boldsymbol{K}}) G({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta *}({\boldsymbol{X}}, {\boldsymbol{K}}) G({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & = (D_0^{\alpha\beta}({\boldsymbol{X}}))^*, \end{align}and also
 \begin{align} \Theta^{\alpha \beta c}({\boldsymbol{X}}) & \doteq{-}\int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}})(G^{|c}({\boldsymbol{X}}, {\boldsymbol{K}}))^* \nonumber\\ & =\int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}) G^{|c}({\boldsymbol{X}}, - {\boldsymbol{K}}) \nonumber\\ & =\int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, - {\boldsymbol{K}}) G^{|c}({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & =\int \mathrm{d}{\boldsymbol{K}}\,(\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}))^* G^{|c}({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & ={-} (\Theta^{\alpha\beta c}({\boldsymbol{X}}))^*. \end{align}
\begin{align} \Theta^{\alpha \beta c}({\boldsymbol{X}}) & \doteq{-}\int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}})(G^{|c}({\boldsymbol{X}}, {\boldsymbol{K}}))^* \nonumber\\ & =\int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}) G^{|c}({\boldsymbol{X}}, - {\boldsymbol{K}}) \nonumber\\ & =\int \mathrm{d}{\boldsymbol{K}}\,\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, - {\boldsymbol{K}}) G^{|c}({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & =\int \mathrm{d}{\boldsymbol{K}}\,(\overline{W}_{{\boldsymbol{u}}}^{\alpha\beta}({\boldsymbol{X}}, {\boldsymbol{K}}))^* G^{|c}({\boldsymbol{X}}, {\boldsymbol{K}}) \nonumber\\ & ={-} (\Theta^{\alpha\beta c}({\boldsymbol{X}}))^*. \end{align}B.5 Proof of (5.20)
Let us estimate
where ![]() $\mathcal {P}_{\mu \nu }^{(1)}$ has the form
$\mathcal {P}_{\mu \nu }^{(1)}$ has the form
First, notice that
 \begin{align} \mathcal{P}_{\mu \nu}^{(1)} & = \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}G - \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}\,\frac{\partial G}{\partial z^{\mu}} \nonumber\\ & = \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}G + \frac{\partial v^{\lambda}}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}q_{\lambda}\overline{W}G' \nonumber\\ & = \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}G + \frac{\partial v^{\lambda}}{\partial z^{\mu}} \frac{\eth}{\partial\varOmega} \int \mathrm{d}{\boldsymbol{K}}\, q_{\nu}q_{\lambda}\overline{W}G \nonumber\\ & \equiv \frac{\partial \mathcal{Q}_{\nu}^{(1)}}{\partial z^{\mu}} + \frac{\partial v^{\lambda}}{\partial z^{\mu}}\,\mathcal{R}_{\lambda \nu}^{(1)}. \end{align}
\begin{align} \mathcal{P}_{\mu \nu}^{(1)} & = \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}G - \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}\,\frac{\partial G}{\partial z^{\mu}} \nonumber\\ & = \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}G + \frac{\partial v^{\lambda}}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}q_{\lambda}\overline{W}G' \nonumber\\ & = \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}G + \frac{\partial v^{\lambda}}{\partial z^{\mu}} \frac{\eth}{\partial\varOmega} \int \mathrm{d}{\boldsymbol{K}}\, q_{\nu}q_{\lambda}\overline{W}G \nonumber\\ & \equiv \frac{\partial \mathcal{Q}_{\nu}^{(1)}}{\partial z^{\mu}} + \frac{\partial v^{\lambda}}{\partial z^{\mu}}\,\mathcal{R}_{\lambda \nu}^{(1)}. \end{align}
Because ![]() $\mathcal {Q}_{\nu }^{(1)}$ and
$\mathcal {Q}_{\nu }^{(1)}$ and ![]() $\mathcal {R}_{\lambda \nu }^{(1)}$ are
$\mathcal {R}_{\lambda \nu }^{(1)}$ are ![]() $\mathcal {O}(\varepsilon ^2)$, one has
$\mathcal {O}(\varepsilon ^2)$, one has ![]() $\smash {\mathcal {P}_{\mu \nu }^{(1)} \sim \kappa _{\mu } \varepsilon ^2}$, where
$\smash {\mathcal {P}_{\mu \nu }^{(1)} \sim \kappa _{\mu } \varepsilon ^2}$, where ![]() $\kappa _{\mu }$ is the characteristic inverse scale along the
$\kappa _{\mu }$ is the characteristic inverse scale along the ![]() $\mu$th phase-space axis. Thus,
$\mu$th phase-space axis. Thus,
where we used (see (2.69) and (3.2))
The first part of (5.20) is obtained by considering ![]() $\operatorname {im}\mathcal {L}^{(1)} \overline {f}$ and using (B14).
$\operatorname {im}\mathcal {L}^{(1)} \overline {f}$ and using (B14).
Let us also estimate
where ![]() $\mathcal {P}_{\mu \nu }^{(2)}$ has the form
$\mathcal {P}_{\mu \nu }^{(2)}$ has the form
First, note that
 \begin{align} \mathcal{P}_{\mu \nu}^{(2)} &= \int \mathrm{d}{\boldsymbol{K}}\,\frac{\partial^2\overline{W}}{\partial z^{\mu}\partial z^{\nu}}\,G \nonumber\\ &= \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,\frac{\partial \overline{W}}{\partial z^{\nu}}\,G - \int \mathrm{d}{\boldsymbol{K}}\,\frac{\partial \overline{W}}{\partial z^{\nu}}\frac{\partial G}{\partial z^{\mu}} \nonumber\\ &= \frac{\partial^2}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\, \overline{W} G - \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\, \frac{\partial G}{\partial z^{\nu}} - \frac{\partial}{\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial G}{\partial z^{\mu}} + \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}} \nonumber\\ &= \frac{\partial^2}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,G - \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,G' \left(- q_{\lambda}\,\frac{\partial v^{\lambda}}{\partial z^{\nu}}\right) \nonumber\\ &\quad - \frac{\partial}{\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,G' \left(- q_{\lambda}\,\frac{\partial v^{\lambda}}{\partial z^{\mu}}\right) + \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}} \nonumber\\ &= \frac{\partial^2}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}G + \frac{\partial}{\partial z^{\mu}} \left(\frac{\partial v^{\lambda}}{\partial z^{\nu}} \frac{\eth}{\partial\varOmega} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W}G\right) \nonumber\\ &\quad + \frac{\partial}{\partial z^{\nu}} \left(\frac{\partial v^{\lambda}}{\partial z^{\mu}} \frac{\eth}{\partial\varOmega} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W}G\right) + \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}}. \end{align}
\begin{align} \mathcal{P}_{\mu \nu}^{(2)} &= \int \mathrm{d}{\boldsymbol{K}}\,\frac{\partial^2\overline{W}}{\partial z^{\mu}\partial z^{\nu}}\,G \nonumber\\ &= \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,\frac{\partial \overline{W}}{\partial z^{\nu}}\,G - \int \mathrm{d}{\boldsymbol{K}}\,\frac{\partial \overline{W}}{\partial z^{\nu}}\frac{\partial G}{\partial z^{\mu}} \nonumber\\ &= \frac{\partial^2}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\, \overline{W} G - \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\, \frac{\partial G}{\partial z^{\nu}} - \frac{\partial}{\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial G}{\partial z^{\mu}} + \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}} \nonumber\\ &= \frac{\partial^2}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,G - \frac{\partial}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,G' \left(- q_{\lambda}\,\frac{\partial v^{\lambda}}{\partial z^{\nu}}\right) \nonumber\\ &\quad - \frac{\partial}{\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,G' \left(- q_{\lambda}\,\frac{\partial v^{\lambda}}{\partial z^{\mu}}\right) + \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}} \nonumber\\ &= \frac{\partial^2}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}G + \frac{\partial}{\partial z^{\mu}} \left(\frac{\partial v^{\lambda}}{\partial z^{\nu}} \frac{\eth}{\partial\varOmega} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W}G\right) \nonumber\\ &\quad + \frac{\partial}{\partial z^{\nu}} \left(\frac{\partial v^{\lambda}}{\partial z^{\mu}} \frac{\eth}{\partial\varOmega} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W}G\right) + \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}}. \end{align}Next, note that
 \begin{align} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}} & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial}{\partial z^{\mu}} \left(- q_{\lambda}G'\frac{\partial v^{\lambda}}{\partial z^{\nu}}\right) \nonumber\\ & ={-} \frac{\partial v^{\lambda}}{\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\, q_{\lambda}\overline{W}\,\frac{\partial G'}{\partial z^{\mu}} - \frac{\partial^2 v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W}G'\nonumber\\ & = \frac{\partial v^{\lambda}}{\partial z^{\nu}} \frac{\partial v^{\delta}}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}q_{\delta} \overline{W} G'' - \frac{\partial^2 v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W} G' \nonumber\\ & = \frac{\partial v^{\lambda}}{\partial z^{\nu}} \frac{\partial v^{\delta}}{\partial z^{\mu}} \frac{\eth^2}{\partial\varOmega^2} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}q_{\delta}\overline{W}G - \frac{\partial^2v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}} \frac{\eth}{\partial\varOmega}\int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W} G. \end{align}
\begin{align} \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial^2G}{\partial z^{\mu}\partial z^{\nu}} & = \int \mathrm{d}{\boldsymbol{K}}\,\overline{W}\,\frac{\partial}{\partial z^{\mu}} \left(- q_{\lambda}G'\frac{\partial v^{\lambda}}{\partial z^{\nu}}\right) \nonumber\\ & ={-} \frac{\partial v^{\lambda}}{\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\, q_{\lambda}\overline{W}\,\frac{\partial G'}{\partial z^{\mu}} - \frac{\partial^2 v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W}G'\nonumber\\ & = \frac{\partial v^{\lambda}}{\partial z^{\nu}} \frac{\partial v^{\delta}}{\partial z^{\mu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}q_{\delta} \overline{W} G'' - \frac{\partial^2 v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W} G' \nonumber\\ & = \frac{\partial v^{\lambda}}{\partial z^{\nu}} \frac{\partial v^{\delta}}{\partial z^{\mu}} \frac{\eth^2}{\partial\varOmega^2} \int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}q_{\delta}\overline{W}G - \frac{\partial^2v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}} \frac{\eth}{\partial\varOmega}\int \mathrm{d}{\boldsymbol{K}}\,q_{\lambda}\overline{W} G. \end{align}Assuming the notation
 \begin{align} \mathcal{S}^{(2)} & \doteq \int \mathrm{d}{\boldsymbol{K}}\, \overline{W} G = \mathcal{O}\left(\varepsilon^2\right), \nonumber\\ \mathcal{Q}_{\lambda}^{(2)} & \doteq \frac{\eth}{\partial\varOmega}\int \mathrm{d}{\boldsymbol{K}}\, q_{\lambda}\overline{W} G = \mathcal{O}\left(\varepsilon^2\right), \nonumber\\ \mathcal{R}_{\lambda \delta}^{(2)} & \doteq \frac{\eth^2}{\partial\varOmega^2} \int \mathrm{d}{\boldsymbol{K}}\, q_{\lambda}q_{\delta}\overline{W}G = \mathcal{O}\left(\varepsilon^2\right), \end{align}
\begin{align} \mathcal{S}^{(2)} & \doteq \int \mathrm{d}{\boldsymbol{K}}\, \overline{W} G = \mathcal{O}\left(\varepsilon^2\right), \nonumber\\ \mathcal{Q}_{\lambda}^{(2)} & \doteq \frac{\eth}{\partial\varOmega}\int \mathrm{d}{\boldsymbol{K}}\, q_{\lambda}\overline{W} G = \mathcal{O}\left(\varepsilon^2\right), \nonumber\\ \mathcal{R}_{\lambda \delta}^{(2)} & \doteq \frac{\eth^2}{\partial\varOmega^2} \int \mathrm{d}{\boldsymbol{K}}\, q_{\lambda}q_{\delta}\overline{W}G = \mathcal{O}\left(\varepsilon^2\right), \end{align}
one can then rewrite ![]() $\mathcal {P}_{\mu \nu }^{(2)}$ as follows:
$\mathcal {P}_{\mu \nu }^{(2)}$ as follows:
 \begin{align*} \mathcal{P}_{\mu \nu}^{(2)} & = \frac{\partial^2\mathcal{S}^{(2)}}{\partial z^{\mu}\partial z^{\nu}} + \frac{\partial}{\partial z^{\mu}}\left(\frac{\partial v^{\lambda}}{\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)}\right) + \frac{\partial}{\partial z^{\nu}}\left(\frac{\partial v^{\lambda}}{\partial z^{\mu}}\,\mathcal{Q}_{\lambda}^{(2)}\right) - \frac{\partial^2v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)} + \frac{\partial v^{\lambda}}{\partial z^{\nu}}\frac{\partial v^{\delta}}{\partial z^{\mu}}\,\mathcal{R}_{\lambda \delta}^{(2)} \\ & = \frac{\partial^2\mathcal{S}^{(2)}}{\partial z^{\mu}\partial z^{\nu}} + \frac{\partial^2 v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)} + \frac{\partial v^{\lambda}}{\partial z^{\nu}}\frac{\partial \mathcal{Q}_{\lambda}^{(2)}}{\partial z^{\mu}} + \frac{\partial v^{\lambda}}{\partial z^{\mu}}\frac{\partial \mathcal{Q}_{\lambda}^{(2)}}{\partial z^{\nu}} + \frac{\partial^2v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)} + \frac{\partial v^{\lambda}}{\partial z^{\nu}}\frac{\partial v^{\delta}}{\partial z^{\mu}}\,\mathcal{R}_{\lambda\delta}^{(2)}. \end{align*}
\begin{align*} \mathcal{P}_{\mu \nu}^{(2)} & = \frac{\partial^2\mathcal{S}^{(2)}}{\partial z^{\mu}\partial z^{\nu}} + \frac{\partial}{\partial z^{\mu}}\left(\frac{\partial v^{\lambda}}{\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)}\right) + \frac{\partial}{\partial z^{\nu}}\left(\frac{\partial v^{\lambda}}{\partial z^{\mu}}\,\mathcal{Q}_{\lambda}^{(2)}\right) - \frac{\partial^2v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)} + \frac{\partial v^{\lambda}}{\partial z^{\nu}}\frac{\partial v^{\delta}}{\partial z^{\mu}}\,\mathcal{R}_{\lambda \delta}^{(2)} \\ & = \frac{\partial^2\mathcal{S}^{(2)}}{\partial z^{\mu}\partial z^{\nu}} + \frac{\partial^2 v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)} + \frac{\partial v^{\lambda}}{\partial z^{\nu}}\frac{\partial \mathcal{Q}_{\lambda}^{(2)}}{\partial z^{\mu}} + \frac{\partial v^{\lambda}}{\partial z^{\mu}}\frac{\partial \mathcal{Q}_{\lambda}^{(2)}}{\partial z^{\nu}} + \frac{\partial^2v^{\lambda}}{\partial z^{\mu}\partial z^{\nu}}\,\mathcal{Q}_{\lambda}^{(2)} + \frac{\partial v^{\lambda}}{\partial z^{\nu}}\frac{\partial v^{\delta}}{\partial z^{\mu}}\,\mathcal{R}_{\lambda\delta}^{(2)}. \end{align*}
Each term on the right-hand side of this equation scales as ![]() $\varepsilon ^2\kappa _{\mu }\kappa _{\nu }$, so
$\varepsilon ^2\kappa _{\mu }\kappa _{\nu }$, so
where we again used (B15). The second part of (5.20) is obtained by considering ![]() $\operatorname {re}\mathcal {L}^{(2)} \overline {f}$ and using (B21).
$\operatorname {re}\mathcal {L}^{(2)} \overline {f}$ and using (B21).
B.6 Proof of (5.25)
Using (5.23) and assuming the notation ![]() $\mathrm {d}_t \doteq \partial _t + v^{\gamma }\partial _{\gamma }$, one finds that
$\mathrm {d}_t \doteq \partial _t + v^{\gamma }\partial _{\gamma }$, one finds that
 \begin{align} \partial_{\alpha}& (\widehat{D}^{\alpha\beta}\partial_{\beta}\overline{f}) - \partial_{\alpha}(({\mathsf{D}}^{\alpha\beta}+\varrho^{\alpha\beta})\partial_{\beta}\overline{f}) \nonumber\\ =\,& {-} \partial_{\alpha}\left(\Theta^{\alpha\beta}\mathrm{d}_t\partial_{\beta}\overline{f} + \frac{1}{2}\,(\mathrm{d}_t\Theta^{\alpha\beta}) \partial_{\beta}\overline{f}\right) \nonumber\\ =\,& {-} \partial_{\alpha} \left( \frac{1}{2}\,\Theta^{\alpha\beta}\mathrm{d}_t \partial_{\beta}\overline{f} + \frac{1}{2}\,\mathrm{d}_t(\Theta^{\alpha\beta}\partial_{\beta}\overline{f}) \right)\nonumber\\ =\, & {-}\partial_{\alpha} \left( \frac{1}{2}\,\Theta^{\alpha\beta}\partial_{\beta}\mathrm{d}_t\overline{f} - \frac{1}{2}\,\Theta^{\alpha\beta}(\partial_{\beta}v^{\gamma})\partial_{\gamma}\overline{f} \right) - \partial_{\alpha}\left( \frac{1}{2}\,\mathrm{d}_t(\Theta^{\alpha\beta}\partial_{\beta}\overline{f}) \right)\nonumber\\ = \,& {-}\partial_{\alpha}\left( \frac{1}{2}\,\Theta^{\alpha\beta}\partial_{\beta}\mathrm{d}_t\overline{f} \right) + \partial_{\alpha}\left(\frac{1}{2}\,\Theta^{\alpha\beta}(\partial_{\beta}v^{\gamma})\partial_{\gamma}\overline{f}\right) \nonumber\\ &{-} \mathrm{d}_t \left( \frac{1}{2}\,\partial_{\alpha}(\Theta^{\alpha\beta}\partial_{\beta}\overline{f}) \right) - (\partial_{\alpha}v^{\gamma}) \partial_{\gamma}\left( \frac{1}{2}\,\Theta^{\alpha\beta}\partial_{\beta}\overline{f} \right). \end{align}
\begin{align} \partial_{\alpha}& (\widehat{D}^{\alpha\beta}\partial_{\beta}\overline{f}) - \partial_{\alpha}(({\mathsf{D}}^{\alpha\beta}+\varrho^{\alpha\beta})\partial_{\beta}\overline{f}) \nonumber\\ =\,& {-} \partial_{\alpha}\left(\Theta^{\alpha\beta}\mathrm{d}_t\partial_{\beta}\overline{f} + \frac{1}{2}\,(\mathrm{d}_t\Theta^{\alpha\beta}) \partial_{\beta}\overline{f}\right) \nonumber\\ =\,& {-} \partial_{\alpha} \left( \frac{1}{2}\,\Theta^{\alpha\beta}\mathrm{d}_t \partial_{\beta}\overline{f} + \frac{1}{2}\,\mathrm{d}_t(\Theta^{\alpha\beta}\partial_{\beta}\overline{f}) \right)\nonumber\\ =\, & {-}\partial_{\alpha} \left( \frac{1}{2}\,\Theta^{\alpha\beta}\partial_{\beta}\mathrm{d}_t\overline{f} - \frac{1}{2}\,\Theta^{\alpha\beta}(\partial_{\beta}v^{\gamma})\partial_{\gamma}\overline{f} \right) - \partial_{\alpha}\left( \frac{1}{2}\,\mathrm{d}_t(\Theta^{\alpha\beta}\partial_{\beta}\overline{f}) \right)\nonumber\\ = \,& {-}\partial_{\alpha}\left( \frac{1}{2}\,\Theta^{\alpha\beta}\partial_{\beta}\mathrm{d}_t\overline{f} \right) + \partial_{\alpha}\left(\frac{1}{2}\,\Theta^{\alpha\beta}(\partial_{\beta}v^{\gamma})\partial_{\gamma}\overline{f}\right) \nonumber\\ &{-} \mathrm{d}_t \left( \frac{1}{2}\,\partial_{\alpha}(\Theta^{\alpha\beta}\partial_{\beta}\overline{f}) \right) - (\partial_{\alpha}v^{\gamma}) \partial_{\gamma}\left( \frac{1}{2}\,\Theta^{\alpha\beta}\partial_{\beta}\overline{f} \right). \end{align}
Because ![]() $\Theta ^{\alpha \beta } = \mathcal {O}(\varepsilon ^2)$ and
$\Theta ^{\alpha \beta } = \mathcal {O}(\varepsilon ^2)$ and ![]() $\mathrm {d}_t \overline {f} = \mathcal {O}(\varepsilon ^2)$, the first term on the right-hand side of (B22) is negligible. Also note that due to (3.15), the factor
$\mathrm {d}_t \overline {f} = \mathcal {O}(\varepsilon ^2)$, the first term on the right-hand side of (B22) is negligible. Also note that due to (3.15), the factor ![]() $\smash {\partial _{\alpha }v^{\gamma }}$ in the last term on the right-hand side of (B22) commutes with
$\smash {\partial _{\alpha }v^{\gamma }}$ in the last term on the right-hand side of (B22) commutes with ![]() $\smash {\partial _\gamma }$. Hence, one obtains
$\smash {\partial _\gamma }$. Hence, one obtains
 \begin{align} \partial_{\alpha} (\widehat{D}^{\alpha\beta}\partial_{\beta}\overline{f}) & - \partial_{\alpha}({\mathsf{D}}^{\alpha\beta}\partial_{\beta}\overline{f}) + \mathrm{d}_t \left(\frac{1}{2}\,\partial_{\alpha}(\Theta^{\alpha \beta}\partial_{\beta}\overline{f})\right) \nonumber\\ & = \partial_{\alpha} \left( \varrho^{\alpha\beta} \partial_{\beta}\overline{f} + \frac{1}{2}\,\Theta^{\alpha\beta} \left(\partial_{\beta}v^{\gamma}\right) \partial_{\gamma}\overline{f} \right) - \partial_{\gamma} \left( \frac{1}{2}\,\Theta^{\alpha\beta} (\partial_{\alpha}v^{\gamma}) \partial_{\beta}\overline{f} \right)\nonumber\\ & = \partial_{\alpha}\left( \varrho^{\alpha\beta} \partial_{\beta} \overline{f} + \frac{1}{2} \left( \Theta^{\alpha \gamma}(\partial_{\gamma}v^{\beta}) -\Theta^{\gamma \beta}(\partial_{\gamma}v^{\alpha}) \right)\partial_{\beta}\overline{f} \right)\nonumber\\ & \equiv \partial_{\alpha} (U^{\alpha\beta} \partial_{\beta}\overline{f}). \end{align}
\begin{align} \partial_{\alpha} (\widehat{D}^{\alpha\beta}\partial_{\beta}\overline{f}) & - \partial_{\alpha}({\mathsf{D}}^{\alpha\beta}\partial_{\beta}\overline{f}) + \mathrm{d}_t \left(\frac{1}{2}\,\partial_{\alpha}(\Theta^{\alpha \beta}\partial_{\beta}\overline{f})\right) \nonumber\\ & = \partial_{\alpha} \left( \varrho^{\alpha\beta} \partial_{\beta}\overline{f} + \frac{1}{2}\,\Theta^{\alpha\beta} \left(\partial_{\beta}v^{\gamma}\right) \partial_{\gamma}\overline{f} \right) - \partial_{\gamma} \left( \frac{1}{2}\,\Theta^{\alpha\beta} (\partial_{\alpha}v^{\gamma}) \partial_{\beta}\overline{f} \right)\nonumber\\ & = \partial_{\alpha}\left( \varrho^{\alpha\beta} \partial_{\beta} \overline{f} + \frac{1}{2} \left( \Theta^{\alpha \gamma}(\partial_{\gamma}v^{\beta}) -\Theta^{\gamma \beta}(\partial_{\gamma}v^{\alpha}) \right)\partial_{\beta}\overline{f} \right)\nonumber\\ & \equiv \partial_{\alpha} (U^{\alpha\beta} \partial_{\beta}\overline{f}). \end{align}Next, notice that
 \begin{align} \varrho^{\alpha\beta} & ={-} \frac{1}{2}\, J^{\alpha \mu}J^{\beta \nu}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\left( q_{\nu}\,\frac{\partial\overline{W}}{\partial z^\mu} - q_{\mu}\,\frac{\partial\overline{W}}{\partial z^\nu} \right) \frac{1}{\varOmega} \nonumber\\ & ={-}\frac{1}{2}\,J^{\alpha \mu}J^{\beta \nu} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\nu}}{\varOmega}\frac{\partial\overline{W}}{\partial z^\mu} + \frac{1}{2}\,J^{\alpha \mu}J^{\nu \beta}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\mu}}{\varOmega}\frac{\partial\overline{W}}{\partial z^\nu} \nonumber\\ & ={-}\frac{1}{2}\,J^{\alpha \mu}J^{\beta\nu}\left( \frac{\partial}{\partial z^\mu}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\nu}\overline{W}}{\varOmega} -{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}\,\frac{\partial}{\partial z^\mu}\frac{1}{\varOmega} \right. \nonumber\\ & \hspace{2.5cm}\left. -\frac{\partial}{\partial z^\nu}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\mu}\overline{W}}{\varOmega} +{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,q_{\mu}\overline{W}\frac{\partial}{\partial z^\nu}\frac{1}{\varOmega}\right) \nonumber\\ & ={-}\frac{1}{2}\,J^{\alpha\mu}J^{\beta \nu} \left( \frac{\partial}{\partial z^\mu} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\nu}\overline{W}}{\varOmega} + \frac{\partial v^{\lambda}}{\partial z^\mu} \frac{\eth}{\partial \varOmega} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\lambda}q_{\nu}\overline{W}}{\varOmega} \right.\nonumber\\ & \hspace{2.5cm}\left. - \frac{\partial}{\partial z^\nu} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\mu}\overline{W}}{\varOmega} - \frac{\partial v^{\lambda}}{\partial z^\nu} \frac{\eth}{\partial \varOmega} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\lambda}q_{\mu}\overline{W}}{\varOmega} \right). \end{align}
\begin{align} \varrho^{\alpha\beta} & ={-} \frac{1}{2}\, J^{\alpha \mu}J^{\beta \nu}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\left( q_{\nu}\,\frac{\partial\overline{W}}{\partial z^\mu} - q_{\mu}\,\frac{\partial\overline{W}}{\partial z^\nu} \right) \frac{1}{\varOmega} \nonumber\\ & ={-}\frac{1}{2}\,J^{\alpha \mu}J^{\beta \nu} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\nu}}{\varOmega}\frac{\partial\overline{W}}{\partial z^\mu} + \frac{1}{2}\,J^{\alpha \mu}J^{\nu \beta}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\mu}}{\varOmega}\frac{\partial\overline{W}}{\partial z^\nu} \nonumber\\ & ={-}\frac{1}{2}\,J^{\alpha \mu}J^{\beta\nu}\left( \frac{\partial}{\partial z^\mu}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\nu}\overline{W}}{\varOmega} -{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,q_{\nu}\overline{W}\,\frac{\partial}{\partial z^\mu}\frac{1}{\varOmega} \right. \nonumber\\ & \hspace{2.5cm}\left. -\frac{\partial}{\partial z^\nu}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\mu}\overline{W}}{\varOmega} +{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,q_{\mu}\overline{W}\frac{\partial}{\partial z^\nu}\frac{1}{\varOmega}\right) \nonumber\\ & ={-}\frac{1}{2}\,J^{\alpha\mu}J^{\beta \nu} \left( \frac{\partial}{\partial z^\mu} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\nu}\overline{W}}{\varOmega} + \frac{\partial v^{\lambda}}{\partial z^\mu} \frac{\eth}{\partial \varOmega} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\lambda}q_{\nu}\overline{W}}{\varOmega} \right.\nonumber\\ & \hspace{2.5cm}\left. - \frac{\partial}{\partial z^\nu} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\,\frac{q_{\mu}\overline{W}}{\varOmega} - \frac{\partial v^{\lambda}}{\partial z^\nu} \frac{\eth}{\partial \varOmega} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{K}}\, \frac{q_{\lambda}q_{\mu}\overline{W}}{\varOmega} \right). \end{align}Assuming the notation
one can rewrite (B24) compactly as follows:
Notice also that ![]() $\Theta ^{\alpha \beta } = 2J^{\alpha \mu }J^{\beta \nu }R_{\mu \nu }$. Hence, for
$\Theta ^{\alpha \beta } = 2J^{\alpha \mu }J^{\beta \nu }R_{\mu \nu }$. Hence, for ![]() $\smash {U^{\alpha \beta }}$ introduced in (B23), one has
$\smash {U^{\alpha \beta }}$ introduced in (B23), one has
 \begin{align} &U ^{\alpha\beta} - J^{\alpha \mu} J^{\beta \nu} (\partial_{\nu} Q_{\mu} - \partial_{\mu} Q_{\nu}) \nonumber\\ &\quad = \varrho^{\alpha\beta} - J^{\alpha \mu} J^{\beta \nu} (\partial_{\nu}Q_{\mu} - \partial_{\mu}Q_{\nu}) - ( \Theta^{\gamma \beta} (\partial_{\gamma}v^{\alpha}) - \Theta^{\alpha \gamma}(\partial_{\gamma}v^{\beta}) )/2 \nonumber\\ &\quad = J^{\alpha \mu} J^{\beta \nu} ((\partial_{\nu} v^{\lambda}) R_{\lambda \mu} - (\partial_{\mu}v^{\lambda}) R_{\lambda \nu}) + J^{\alpha \mu} J^{\gamma \nu} (\partial_{\gamma} v^{\beta}) R_{\mu \nu} - J^{\gamma \mu}J^{\beta \nu} (\partial_{\gamma}v^{\alpha}) R_{\mu \nu} \nonumber\\ &\quad = J^{\alpha \mu} J^{\beta \nu} (\partial_{\nu}v^{\lambda}) R_{\lambda \mu} - J^{\alpha \mu} J^{\beta \nu} (\partial_{\mu}v^{\lambda}) R_{\lambda \nu} + J^{\alpha \mu} J^{\gamma \nu} (\partial_{\gamma}v^{\beta}) R_{\mu \nu} - J^{\gamma \mu} J^{\beta \nu} (\partial_{\gamma}v^{\alpha})R_{\mu \nu} \nonumber\\ &\quad = J^{\alpha \mu} J^{\beta \lambda} (\partial_{\lambda}v^{\nu}) R_{\mu \nu} - J^{\alpha \lambda} J^{\beta \nu}(\partial_{\lambda} v^{\mu}) R_{\mu \nu} + J^{\alpha \mu} J^{\gamma \nu} (\partial_{\gamma}v^{\beta}) R_{\mu \nu} - J^{\gamma \mu}J^{\beta \nu}(\partial_{\gamma}v^{\alpha}) R_{\mu \nu} \nonumber\\ &\quad = ( J^{\alpha \mu} J^{\beta \lambda} J^{\nu \gamma} - J^{\alpha \lambda} J^{\beta \nu} J^{\mu \gamma} + J^{\alpha \mu}J^{\gamma \nu}J^{\beta \lambda} - J^{\gamma \mu}J^{\beta \nu}J^{\alpha \lambda} ) (\partial_{\gamma \lambda}^2\overline{H}) R_{\mu \nu} \nonumber\\ &\quad = ( J^{\alpha \mu} J^{\beta \lambda} J^{\nu \gamma} - J^{\alpha \lambda} J^{\beta \nu} J^{\mu \gamma} - J^{\alpha \mu} J^{\gamma \nu} J^{\lambda \beta} + J^{\mu \gamma} J^{\beta \nu} J^{\alpha \lambda} ) (\partial_{\gamma \lambda}^2\overline{H}) R_{\mu \nu} \nonumber\\ &\quad = 0, \end{align}
\begin{align} &U ^{\alpha\beta} - J^{\alpha \mu} J^{\beta \nu} (\partial_{\nu} Q_{\mu} - \partial_{\mu} Q_{\nu}) \nonumber\\ &\quad = \varrho^{\alpha\beta} - J^{\alpha \mu} J^{\beta \nu} (\partial_{\nu}Q_{\mu} - \partial_{\mu}Q_{\nu}) - ( \Theta^{\gamma \beta} (\partial_{\gamma}v^{\alpha}) - \Theta^{\alpha \gamma}(\partial_{\gamma}v^{\beta}) )/2 \nonumber\\ &\quad = J^{\alpha \mu} J^{\beta \nu} ((\partial_{\nu} v^{\lambda}) R_{\lambda \mu} - (\partial_{\mu}v^{\lambda}) R_{\lambda \nu}) + J^{\alpha \mu} J^{\gamma \nu} (\partial_{\gamma} v^{\beta}) R_{\mu \nu} - J^{\gamma \mu}J^{\beta \nu} (\partial_{\gamma}v^{\alpha}) R_{\mu \nu} \nonumber\\ &\quad = J^{\alpha \mu} J^{\beta \nu} (\partial_{\nu}v^{\lambda}) R_{\lambda \mu} - J^{\alpha \mu} J^{\beta \nu} (\partial_{\mu}v^{\lambda}) R_{\lambda \nu} + J^{\alpha \mu} J^{\gamma \nu} (\partial_{\gamma}v^{\beta}) R_{\mu \nu} - J^{\gamma \mu} J^{\beta \nu} (\partial_{\gamma}v^{\alpha})R_{\mu \nu} \nonumber\\ &\quad = J^{\alpha \mu} J^{\beta \lambda} (\partial_{\lambda}v^{\nu}) R_{\mu \nu} - J^{\alpha \lambda} J^{\beta \nu}(\partial_{\lambda} v^{\mu}) R_{\mu \nu} + J^{\alpha \mu} J^{\gamma \nu} (\partial_{\gamma}v^{\beta}) R_{\mu \nu} - J^{\gamma \mu}J^{\beta \nu}(\partial_{\gamma}v^{\alpha}) R_{\mu \nu} \nonumber\\ &\quad = ( J^{\alpha \mu} J^{\beta \lambda} J^{\nu \gamma} - J^{\alpha \lambda} J^{\beta \nu} J^{\mu \gamma} + J^{\alpha \mu}J^{\gamma \nu}J^{\beta \lambda} - J^{\gamma \mu}J^{\beta \nu}J^{\alpha \lambda} ) (\partial_{\gamma \lambda}^2\overline{H}) R_{\mu \nu} \nonumber\\ &\quad = ( J^{\alpha \mu} J^{\beta \lambda} J^{\nu \gamma} - J^{\alpha \lambda} J^{\beta \nu} J^{\mu \gamma} - J^{\alpha \mu} J^{\gamma \nu} J^{\lambda \beta} + J^{\mu \gamma} J^{\beta \nu} J^{\alpha \lambda} ) (\partial_{\gamma \lambda}^2\overline{H}) R_{\mu \nu} \nonumber\\ &\quad = 0, \end{align}
where we used (3.8) for ![]() $v^\alpha$ and the anti-symmetry of
$v^\alpha$ and the anti-symmetry of ![]() $J^{\alpha \beta }$. Therefore,
$J^{\alpha \beta }$. Therefore,
and accordingly,
 \begin{align} \partial_{\alpha}U^{\alpha\beta} & = (J^{\alpha \mu}J^{\beta \nu} - J^{\alpha \nu}J^{\beta \mu})\partial_{\nu \alpha}^2 Q_{\mu} = J^{\alpha \mu} J^{\beta \nu} \partial_{\nu \alpha}^2 Q_{\mu} \nonumber\\ & = J^{\nu \mu} J^{\beta \alpha} \partial_{\nu \alpha}^2 Q_{\mu} = J^{\beta \alpha} \partial_{\alpha} (J^{\nu \mu} \partial_{\nu} Q_{\mu}) ={-} J^{\alpha\beta} \partial_{\alpha} (J^{\mu \nu} \partial_{\mu}Q_{\nu}) \equiv J^{\alpha\beta} \partial_{\alpha}\varPhi. \end{align}
\begin{align} \partial_{\alpha}U^{\alpha\beta} & = (J^{\alpha \mu}J^{\beta \nu} - J^{\alpha \nu}J^{\beta \mu})\partial_{\nu \alpha}^2 Q_{\mu} = J^{\alpha \mu} J^{\beta \nu} \partial_{\nu \alpha}^2 Q_{\mu} \nonumber\\ & = J^{\nu \mu} J^{\beta \alpha} \partial_{\nu \alpha}^2 Q_{\mu} = J^{\beta \alpha} \partial_{\alpha} (J^{\nu \mu} \partial_{\nu} Q_{\mu}) ={-} J^{\alpha\beta} \partial_{\alpha} (J^{\mu \nu} \partial_{\mu}Q_{\nu}) \equiv J^{\alpha\beta} \partial_{\alpha}\varPhi. \end{align}
Here, ![]() $\smash {\varPhi \doteq -J^{\mu \nu }\partial _{\mu }Q_{\nu }}$, which is equivalent to (5.24). From (B29) and the fact that
$\smash {\varPhi \doteq -J^{\mu \nu }\partial _{\mu }Q_{\nu }}$, which is equivalent to (5.24). From (B29) and the fact that ![]() $\smash {U^{\alpha \beta }\partial _{\alpha \beta } = 0}$ due to the anti-symmetry of
$\smash {U^{\alpha \beta }\partial _{\alpha \beta } = 0}$ due to the anti-symmetry of ![]() $\smash {U^{\alpha \beta }}$, one has
$\smash {U^{\alpha \beta }}$, one has
B.7 Proof of (6.30)
The correlation function
can be readily expressed as
 \begin{align*} \mathfrak{C}_{ss'} = \bigg(\delta_{ss'}\!\sum_{\sigma_s = \sigma'_{s'}} + \sum_{\sigma_s \ne \sigma'_{s'}}\bigg)\, \langle &\delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma_s}(t + \tau/2))\delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma_s}(t + \tau/2))\\ & \times \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma'_{s'}}(t - \tau/2))\delta({\boldsymbol{p}}' - \overline{{\boldsymbol{p}}}_{\sigma'_{s'}}(t - \tau/2)) \rangle - \mathfrak{C}_{\overline{\mathfrak{f}}}. \end{align*}
\begin{align*} \mathfrak{C}_{ss'} = \bigg(\delta_{ss'}\!\sum_{\sigma_s = \sigma'_{s'}} + \sum_{\sigma_s \ne \sigma'_{s'}}\bigg)\, \langle &\delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma_s}(t + \tau/2))\delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma_s}(t + \tau/2))\\ & \times \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma'_{s'}}(t - \tau/2))\delta({\boldsymbol{p}}' - \overline{{\boldsymbol{p}}}_{\sigma'_{s'}}(t - \tau/2)) \rangle - \mathfrak{C}_{\overline{\mathfrak{f}}}. \end{align*}
Here, ![]() $\smash {\left\langle {\ldots }\right\rangle}$ is another (in addition to overbar) notation for averaging used in this appendix, the dependence of
$\smash {\left\langle {\ldots }\right\rangle}$ is another (in addition to overbar) notation for averaging used in this appendix, the dependence of ![]() $\smash {\overline {\mathfrak {f}}_s}$ on
$\smash {\overline {\mathfrak {f}}_s}$ on ![]() $\smash {(t, {\boldsymbol {x}})}$ is neglected and ‘
$\smash {(t, {\boldsymbol {x}})}$ is neglected and ‘![]() $\smash {\sigma _s \ne \sigma '_{s'}}$’ denotes that excluded are the terms that have
$\smash {\sigma _s \ne \sigma '_{s'}}$’ denotes that excluded are the terms that have ![]() $\smash {s' = s}$ and
$\smash {s' = s}$ and ![]() $\smash {\sigma _s = \sigma '_{s'}}$ simultaneously. Aside from this, the summations over
$\smash {\sigma _s = \sigma '_{s'}}$ simultaneously. Aside from this, the summations over ![]() $\smash {\sigma _s}$ are taken over all
$\smash {\sigma _s}$ are taken over all ![]() $\smash {N_s \gg 1}$ particles of type
$\smash {N_s \gg 1}$ particles of type ![]() $\smash {s}$, and the summations over
$\smash {s}$, and the summations over ![]() $\smash {\sigma _{s'}}$ are taken over all
$\smash {\sigma _{s'}}$ are taken over all ![]() $\smash {N_{s'} \gg 1}$ particles of type
$\smash {N_{s'} \gg 1}$ particles of type ![]() $\smash {s'}$. Also,
$\smash {s'}$. Also,
To the leading order, pair correlations can be neglected. Then,
 \begin{align} \sum_{\sigma_s \ne \sigma'_{s'}} \left\langle{\ldots}\right\rangle & = \sum_{\sigma_s \ne \sigma'_{s'}} \underbrace{\left\langle{\delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma_s}(t + \tau/2))\delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma_s}(t + \tau/2))}\right\rangle}_{\overline{\mathfrak{f}}_s(t + \tau/2, {\boldsymbol{x}} + {\boldsymbol{s}}/2, {\boldsymbol{p}})/N_s} \nonumber\\ &\hphantom{\sum_{\sigma_s \ne \sigma'_{s'}} }\times \underbrace{\left\langle{\delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma'_{s'}}(t - \tau/2))\delta({\boldsymbol{p}}' - \overline{{\boldsymbol{p}}}_{\sigma'_{s'}}(t - \tau/2))}\right\rangle}_{\overline{\mathfrak{f}}_{s'}(t - \tau/2, {\boldsymbol{x}} - {\boldsymbol{s}}/2, {\boldsymbol{p}}')/N_{s'}} \nonumber\\ &= \frac{\mathfrak{C}_{\overline{\mathfrak{f}}}}{N_s N_{s'}}\sum_{\sigma_s, \sigma'_{s'}} (1 - \delta_{ss'}\delta_{\sigma_s\sigma'_{s'}}) = (1 - N_s^{{-}1} \delta_{ss'}) \mathfrak{C}_{\overline{\mathfrak{f}}} \approx \mathfrak{C}_{\overline{\mathfrak{f}}}. \end{align}
\begin{align} \sum_{\sigma_s \ne \sigma'_{s'}} \left\langle{\ldots}\right\rangle & = \sum_{\sigma_s \ne \sigma'_{s'}} \underbrace{\left\langle{\delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma_s}(t + \tau/2))\delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma_s}(t + \tau/2))}\right\rangle}_{\overline{\mathfrak{f}}_s(t + \tau/2, {\boldsymbol{x}} + {\boldsymbol{s}}/2, {\boldsymbol{p}})/N_s} \nonumber\\ &\hphantom{\sum_{\sigma_s \ne \sigma'_{s'}} }\times \underbrace{\left\langle{\delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma'_{s'}}(t - \tau/2))\delta({\boldsymbol{p}}' - \overline{{\boldsymbol{p}}}_{\sigma'_{s'}}(t - \tau/2))}\right\rangle}_{\overline{\mathfrak{f}}_{s'}(t - \tau/2, {\boldsymbol{x}} - {\boldsymbol{s}}/2, {\boldsymbol{p}}')/N_{s'}} \nonumber\\ &= \frac{\mathfrak{C}_{\overline{\mathfrak{f}}}}{N_s N_{s'}}\sum_{\sigma_s, \sigma'_{s'}} (1 - \delta_{ss'}\delta_{\sigma_s\sigma'_{s'}}) = (1 - N_s^{{-}1} \delta_{ss'}) \mathfrak{C}_{\overline{\mathfrak{f}}} \approx \mathfrak{C}_{\overline{\mathfrak{f}}}. \end{align}
Let us also use ![]() $\smash {\overline {{\boldsymbol {p}}}_{\sigma _s}(t + \tau /2) \approx \overline {{\boldsymbol {p}}}_{\sigma _s}(t)}$. Then,
$\smash {\overline {{\boldsymbol {p}}}_{\sigma _s}(t + \tau /2) \approx \overline {{\boldsymbol {p}}}_{\sigma _s}(t)}$. Then,
 \begin{align} \mathfrak{C}_{ss'} \approx \delta_{ss'}\delta({\boldsymbol{p}} - {\boldsymbol{p}}') \sum_{\sigma=1}^{N_s} \langle & \delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2))\nonumber\\ & \times \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) \rangle. \end{align}
\begin{align} \mathfrak{C}_{ss'} \approx \delta_{ss'}\delta({\boldsymbol{p}} - {\boldsymbol{p}}') \sum_{\sigma=1}^{N_s} \langle & \delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2))\nonumber\\ & \times \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) \rangle. \end{align}Next, notice that
 \begin{align} &\left\langle{ \delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2)) \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ & = \left\langle{ \delta({\boldsymbol{s}} + \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2) - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2)) \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ & = \left\langle{ \delta({\boldsymbol{s}} + \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2) - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2)) \delta({\boldsymbol{x}} - (\overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2) + \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2))/2) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ &\approx \left\langle{ \delta({\boldsymbol{s}} - {\boldsymbol{v}}_s(t, \overline{{\boldsymbol{x}}}_\sigma, \overline{{\boldsymbol{p}}}_\sigma) \tau) \delta({\boldsymbol{x}} - \overline{{\boldsymbol{x}}}_{\sigma}(t)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ &\approx \delta({\boldsymbol{s}} - {\boldsymbol{v}}_s(t, {\boldsymbol{x}}, {\boldsymbol{p}})\tau) \left\langle{ \delta({\boldsymbol{x}} - \overline{{\boldsymbol{x}}}_{\sigma}(t)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ & = \delta({\boldsymbol{s}} - {\boldsymbol{v}}_s(t, {\boldsymbol{x}}, {\boldsymbol{p}})\tau) \overline{\mathfrak{f}}_{s}(t, {\boldsymbol{x}}, {\boldsymbol{p}})/N_s. \end{align}
\begin{align} &\left\langle{ \delta({\boldsymbol{x}} + {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2)) \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ & = \left\langle{ \delta({\boldsymbol{s}} + \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2) - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2)) \delta({\boldsymbol{x}} - {\boldsymbol{s}}/2 - \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ & = \left\langle{ \delta({\boldsymbol{s}} + \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2) - \overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2)) \delta({\boldsymbol{x}} - (\overline{{\boldsymbol{x}}}_{\sigma}(t + \tau/2) + \overline{{\boldsymbol{x}}}_{\sigma}(t - \tau/2))/2) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ &\approx \left\langle{ \delta({\boldsymbol{s}} - {\boldsymbol{v}}_s(t, \overline{{\boldsymbol{x}}}_\sigma, \overline{{\boldsymbol{p}}}_\sigma) \tau) \delta({\boldsymbol{x}} - \overline{{\boldsymbol{x}}}_{\sigma}(t)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ &\approx \delta({\boldsymbol{s}} - {\boldsymbol{v}}_s(t, {\boldsymbol{x}}, {\boldsymbol{p}})\tau) \left\langle{ \delta({\boldsymbol{x}} - \overline{{\boldsymbol{x}}}_{\sigma}(t)) \delta({\boldsymbol{p}} - \overline{{\boldsymbol{p}}}_{\sigma}(t)) }\right\rangle \nonumber\\ & = \delta({\boldsymbol{s}} - {\boldsymbol{v}}_s(t, {\boldsymbol{x}}, {\boldsymbol{p}})\tau) \overline{\mathfrak{f}}_{s}(t, {\boldsymbol{x}}, {\boldsymbol{p}})/N_s. \end{align}Hence,
where we used ![]() $\smash {\overline {\mathfrak {f}}_{s} \approx F_s}$. Therefore,
$\smash {\overline {\mathfrak {f}}_{s} \approx F_s}$. Therefore,
 \begin{align} \mathfrak{G}_{ss'}(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') & =\int \frac{\mathrm{d}\tau}{2{\rm \pi}}\frac{\mathrm{d}{\boldsymbol{s}}}{(2{\rm \pi})^n}\,\mathrm{e}^{\mathrm{i}\omega\tau - \mathrm{i}{\boldsymbol{k}}\cdot{\boldsymbol{s}}}\, \mathfrak{C}_{ss'}(t, {\boldsymbol{x}}, \tau, {\boldsymbol{s}}; {\boldsymbol{p}}, {\boldsymbol{p}}')\nonumber\\ & \approx \frac{1}{(2{\rm \pi})^n}\,\delta_{ss'}\delta({\boldsymbol{p}} - {\boldsymbol{p}}') F_{s}(t, {\boldsymbol{x}}, {\boldsymbol{p}}). \end{align}
\begin{align} \mathfrak{G}_{ss'}(t, {\boldsymbol{x}}, \omega, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') & =\int \frac{\mathrm{d}\tau}{2{\rm \pi}}\frac{\mathrm{d}{\boldsymbol{s}}}{(2{\rm \pi})^n}\,\mathrm{e}^{\mathrm{i}\omega\tau - \mathrm{i}{\boldsymbol{k}}\cdot{\boldsymbol{s}}}\, \mathfrak{C}_{ss'}(t, {\boldsymbol{x}}, \tau, {\boldsymbol{s}}; {\boldsymbol{p}}, {\boldsymbol{p}}')\nonumber\\ & \approx \frac{1}{(2{\rm \pi})^n}\,\delta_{ss'}\delta({\boldsymbol{p}} - {\boldsymbol{p}}') F_{s}(t, {\boldsymbol{x}}, {\boldsymbol{p}}). \end{align}B.8 Proof of (9.80)
Using the symmetry ![]() $\smash {{\mathsf {U}}^{\alpha \beta \gamma \delta } = {\mathsf {U}}^{\beta \alpha \gamma \delta } = {\mathsf {U}}^{\beta \alpha \delta \gamma }}$, one readily obtains from (6.47) that
$\smash {{\mathsf {U}}^{\alpha \beta \gamma \delta } = {\mathsf {U}}^{\beta \alpha \gamma \delta } = {\mathsf {U}}^{\beta \alpha \delta \gamma }}$, one readily obtains from (6.47) that
where ![]() $\smash {\varpi \doteq k_\rho p^\rho = P^0({\boldsymbol {k}} \cdot {\boldsymbol {v}} - \omega )}$ and the prime in
$\smash {\varpi \doteq k_\rho p^\rho = P^0({\boldsymbol {k}} \cdot {\boldsymbol {v}} - \omega )}$ and the prime in ![]() $\smash {\partial '}$ denotes that
$\smash {\partial '}$ denotes that ![]() $\smash {p_0}$ is considered as a function of
$\smash {p_0}$ is considered as a function of ![]() $\smash {{\boldsymbol {p}}}$ at differentiation. One can also write this as follows:
$\smash {{\boldsymbol {p}}}$ at differentiation. One can also write this as follows:
As shown in Garg & Dodin (Reference Garg and Dodin2020, Appendix B), the following equality is satisfied:
Also notice that
 \begin{align} \frac{\partial'}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) & = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) + \frac{\partial P_0}{\partial {\boldsymbol{p}}} \cdot\frac{\partial}{\partial p_0} \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) \nonumber\\ & = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}\, \frac{\partial}{\partial p_0} \left(\frac{\mathfrak{E}}{\varpi}\right), \end{align}
\begin{align} \frac{\partial'}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) & = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) + \frac{\partial P_0}{\partial {\boldsymbol{p}}} \cdot\frac{\partial}{\partial p_0} \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) \nonumber\\ & = \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}\, \frac{\partial}{\partial p_0} \left(\frac{\mathfrak{E}}{\varpi}\right), \end{align}
where we used Hamilton's equation ![]() $\smash {\partial _{{\boldsymbol {p}}} P_0 = -\partial _{{\boldsymbol {p}}} H = -{\boldsymbol {v}}}$. Therefore,
$\smash {\partial _{{\boldsymbol {p}}} P_0 = -\partial _{{\boldsymbol {p}}} H = -{\boldsymbol {v}}}$. Therefore,
The first and the last terms can be merged; then, one obtains
 \begin{align} \mathcal{J} & ={-} \frac{1}{P^0} \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) + \frac{{\boldsymbol{k}} \cdot {\boldsymbol{v}}}{P^0}\frac{\partial}{\partial p_0} \left(\frac{\mathfrak{E}}{\varpi}\right) - \frac{\varpi}{(P^0)^2}\frac{\partial}{\partial p_0}\left(\frac{\mathfrak{E}}{\varpi}\right) \nonumber\\ & ={-} \frac{1}{P^0} \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) + \frac{\omega}{P^0}\frac{\partial}{\partial p_0}\left(\frac{\mathfrak{E}}{\varpi}\right) \nonumber\\ & ={-} \frac{1}{P^0} \frac{\partial}{\partial p_\lambda} \left(\frac{k_\lambda\mathfrak{E}}{\varpi}\right). \end{align}
\begin{align} \mathcal{J} & ={-} \frac{1}{P^0} \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) + \frac{{\boldsymbol{k}} \cdot {\boldsymbol{v}}}{P^0}\frac{\partial}{\partial p_0} \left(\frac{\mathfrak{E}}{\varpi}\right) - \frac{\varpi}{(P^0)^2}\frac{\partial}{\partial p_0}\left(\frac{\mathfrak{E}}{\varpi}\right) \nonumber\\ & ={-} \frac{1}{P^0} \frac{\partial}{\partial {\boldsymbol{p}}} \cdot \left(\frac{{\boldsymbol{k}}\mathfrak{E}}{\varpi}\right) + \frac{\omega}{P^0}\frac{\partial}{\partial p_0}\left(\frac{\mathfrak{E}}{\varpi}\right) \nonumber\\ & ={-} \frac{1}{P^0} \frac{\partial}{\partial p_\lambda} \left(\frac{k_\lambda\mathfrak{E}}{\varpi}\right). \end{align}Appendix C. Properties of the collision operator
Here, we prove the properties of the collision operator discussed in § 6.8. To shorten the calculations, we introduce two auxiliary functions,
 \begin{align} \displaystyle \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \doteq &\,{\rm \pi}\,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) \mathcal{Q}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}'),\nonumber\\ \displaystyle \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') &\doteq \frac{\partial F_s({\boldsymbol{p}})}{\partial p_j}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial p_j'}, \end{align}
\begin{align} \displaystyle \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \doteq &\,{\rm \pi}\,\delta({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s - {\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) \mathcal{Q}_{ss'}({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s, {\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}'),\nonumber\\ \displaystyle \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') &\doteq \frac{\partial F_s({\boldsymbol{p}})}{\partial p_j}\,F_{s'}({\boldsymbol{p}}') - F_s({\boldsymbol{p}})\,\frac{\partial F_{s'}({\boldsymbol{p}}')}{\partial p_j'}, \end{align}which have the following properties:
C.1 Momentum conservation
Momentum conservation is proven as follows. Using integration by parts, one obtains
 \begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l\mathcal{C}_s\nonumber\\ & = \sum_{s,s'} \int \mathrm{d}{\boldsymbol{p}}\,p_l\, \frac{\partial}{\partial p_i} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,k_i k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & ={-}\sum_{s,s'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\,k_l k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
\begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l\mathcal{C}_s\nonumber\\ & = \sum_{s,s'} \int \mathrm{d}{\boldsymbol{p}}\,p_l\, \frac{\partial}{\partial p_i} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,k_i k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & ={-}\sum_{s,s'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\,k_l k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
Now we swap the dummy variables ![]() $\smash {s \leftrightarrow s'}$ and
$\smash {s \leftrightarrow s'}$ and ![]() $\smash {{\boldsymbol {p}} \leftrightarrow {\boldsymbol {p}}'}$ and then apply (C2):
$\smash {{\boldsymbol {p}} \leftrightarrow {\boldsymbol {p}}'}$ and then apply (C2):
 \begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l\mathcal{C}_s\nonumber\\ & ={-}\sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,k_l k_j\, \mathcal{Z}_{s's}({\boldsymbol{k}}; {\boldsymbol{p}}', {\boldsymbol{p}}) \mathcal{F}_{s's}({\boldsymbol{p}}', {\boldsymbol{p}}) \nonumber\\ & = \sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,k_l k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
\begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l\mathcal{C}_s\nonumber\\ & ={-}\sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,k_l k_j\, \mathcal{Z}_{s's}({\boldsymbol{k}}; {\boldsymbol{p}}', {\boldsymbol{p}}) \mathcal{F}_{s's}({\boldsymbol{p}}', {\boldsymbol{p}}) \nonumber\\ & = \sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,k_l k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
The expression on the right-hand side of (C4) is minus that in (C3). Hence, both are zero, which proves that ![]() $\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,p_l\mathcal {C}_s = 0}$.
$\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,p_l\mathcal {C}_s = 0}$.
C.2 Energy conservation
Energy conservation is proven similarly, using that ![]() $\smash {v_s^i = \partial \mathcal {H}_s/\partial p_i}$ and the fact that
$\smash {v_s^i = \partial \mathcal {H}_s/\partial p_i}$ and the fact that ![]() $\smash {{\boldsymbol {k}} \cdot {\boldsymbol {v}}_s}$ and
$\smash {{\boldsymbol {k}} \cdot {\boldsymbol {v}}_s}$ and ![]() $\smash {{\boldsymbol {k}} \cdot {\boldsymbol {v}}'_{s'}}$ are interchangeable due to the presence of
$\smash {{\boldsymbol {k}} \cdot {\boldsymbol {v}}'_{s'}}$ are interchangeable due to the presence of ![]() $\smash {\delta ({\boldsymbol {k}} \cdot {\boldsymbol {v}}_s - {\boldsymbol {k}} \cdot {\boldsymbol {v}}'_{s'})}$ in
$\smash {\delta ({\boldsymbol {k}} \cdot {\boldsymbol {v}}_s - {\boldsymbol {k}} \cdot {\boldsymbol {v}}'_{s'})}$ in ![]() $\smash {\mathcal {Z}_{ss'}}$:
$\smash {\mathcal {Z}_{ss'}}$:
 \begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\mathcal{C}_s\nonumber\\ & = \sum_{s,s'} \int \mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\, \frac{\partial}{\partial p_i} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,k_i k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & ={-}\sum_{s,s'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & ={-}\sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) k_j\, \mathcal{Z}_{s's}({\boldsymbol{k}}; {\boldsymbol{p}}', {\boldsymbol{p}}) \mathcal{F}_{s's}({\boldsymbol{p}}', {\boldsymbol{p}}) \nonumber\\ & = \sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
\begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\mathcal{C}_s\nonumber\\ & = \sum_{s,s'} \int \mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\, \frac{\partial}{\partial p_i} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,k_i k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & ={-}\sum_{s,s'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & ={-}\sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}'_{s'}) k_j\, \mathcal{Z}_{s's}({\boldsymbol{k}}; {\boldsymbol{p}}', {\boldsymbol{p}}) \mathcal{F}_{s's}({\boldsymbol{p}}', {\boldsymbol{p}}) \nonumber\\ & = \sum_{s',s} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,\mathrm{d}{\boldsymbol{p}}\,({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s) k_j\, \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
Like in the previous case, the third and the fifth lines are minus each other, whence ![]() $\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,\mathcal {H}_s\mathcal {C}_s = 0}$.
$\smash {\sum _s \int \mathrm {d}{\boldsymbol {p}}\,\mathcal {H}_s\mathcal {C}_s = 0}$.
C.3  ${H}$-theorem
${H}$-theorem
From (6.72) and (6.73), one has
where we used particle conservation, ![]() $\smash {\int \mathrm {d}{\boldsymbol {p}}\,\mathcal {C}_s = 0}$. Then,
$\smash {\int \mathrm {d}{\boldsymbol {p}}\,\mathcal {C}_s = 0}$. Then,
 \begin{align} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} & ={-} \sum_{ss'} \int \mathrm{d}{\boldsymbol{p}}\,\ln F_s({\boldsymbol{p}})\,\frac{\partial}{\partial p_i} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,k_i k_j \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & = \sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\, \mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, k_i k_j\, \frac{\partial \ln F_s({\boldsymbol{p}})}{\partial p_i}\,\mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
\begin{align} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} & ={-} \sum_{ss'} \int \mathrm{d}{\boldsymbol{p}}\,\ln F_s({\boldsymbol{p}})\,\frac{\partial}{\partial p_i} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}'\,k_i k_j \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ & = \sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\, \mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, k_i k_j\, \frac{\partial \ln F_s({\boldsymbol{p}})}{\partial p_i}\,\mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{align}
Let us swap the dummy variables ![]() $\smash {s \leftrightarrow s'}$ and
$\smash {s \leftrightarrow s'}$ and ![]() $\smash {{\boldsymbol {p}} \leftrightarrow {\boldsymbol {p}}'}$ and then apply (C2) to obtain
$\smash {{\boldsymbol {p}} \leftrightarrow {\boldsymbol {p}}'}$ and then apply (C2) to obtain
 \begin{equation} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} ={-}\sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\int\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, k_i k_j\, \frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial p_i'}\,\mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{equation}
\begin{equation} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} ={-}\sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\int\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, k_i k_j\, \frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial p_i'}\,\mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}'). \end{equation}Upon comparing (C8) with (C7), one can put the result in a symmetrized form
 \begin{align} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} = \frac{1}{2}\sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, k_i k_j & \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ &\times \left(\frac{\partial \ln F_s({\boldsymbol{p}})}{\partial p_i} - \frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial p_i'}\right). \end{align}
\begin{align} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} = \frac{1}{2}\sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\,\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, k_i k_j & \mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') \nonumber\\ &\times \left(\frac{\partial \ln F_s({\boldsymbol{p}})}{\partial p_i} - \frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial p_i'}\right). \end{align}But notice that
 \begin{equation} \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') = \left( \frac{\partial \ln F_s({\boldsymbol{p}})}{\partial p_j} - \frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial p_j'} \right) F_s({\boldsymbol{p}})F_{s'}({\boldsymbol{p}}'). \end{equation}
\begin{equation} \mathcal{F}_{ss'}({\boldsymbol{p}}, {\boldsymbol{p}}') = \left( \frac{\partial \ln F_s({\boldsymbol{p}})}{\partial p_j} - \frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial p_j'} \right) F_s({\boldsymbol{p}})F_{s'}({\boldsymbol{p}}'). \end{equation}Thus,
 \begin{align} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} = \frac{1}{2}\sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\, \mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, &\mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') F_s({\boldsymbol{p}})F_{s'}({\boldsymbol{p}}') \nonumber\\ &\times \left({\boldsymbol{k}}\cdot \frac{\partial \ln F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}} - {\boldsymbol{k}}\cdot\frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right)^2 \geqslant 0. \end{align}
\begin{align} \left(\frac{\mathrm{d}\sigma}{\mathrm{d} t}\right)_{\text{coll}} = \frac{1}{2}\sum_{ss'} \int \frac{\mathrm{d}{\boldsymbol{k}}}{(2{\rm \pi})^n}\, \mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{p}}'\, &\mathcal{Z}_{ss'}({\boldsymbol{k}}; {\boldsymbol{p}}, {\boldsymbol{p}}') F_s({\boldsymbol{p}})F_{s'}({\boldsymbol{p}}') \nonumber\\ &\times \left({\boldsymbol{k}}\cdot \frac{\partial \ln F_s({\boldsymbol{p}})}{\partial {\boldsymbol{p}}} - {\boldsymbol{k}}\cdot\frac{\partial \ln F_{s'}({\boldsymbol{p}}')}{\partial {\boldsymbol{p}}'} \right)^2 \geqslant 0. \end{align}Appendix D. Conservation laws for on-shell waves
Here, we prove the momentum-conservation theorem (7.87) and the energy-conservation theorem (7.89) for QL interactions of plasmas with on-shell waves.
D.1 Momentum conservation
Let us multiply (7.83) by ![]() $k_l$ and integrate over
$k_l$ and integrate over ![]() ${\boldsymbol {k}}$. Then, one obtains
${\boldsymbol {k}}$. Then, one obtains
 \begin{align} 0&= \int \mathrm{d}{\boldsymbol{k}}\,k_l\,\frac{\partial J}{\partial t} + \int \mathrm{d}{\boldsymbol{k}}\,k_l\,\frac{\partial(v_{\text{g}}^i J)}{\partial x^i} - \int \mathrm{d}{\boldsymbol{k}}\,k_l\frac{\partial}{\partial k_i}\left(\frac{\partial w}{\partial x^i}\,J\right) - 2\int \mathrm{d}{\boldsymbol{k}}\,k_l\gamma J \nonumber\\ &= \frac{\partial}{\partial t} \int \mathrm{d}{\boldsymbol{k}}\,k_l J + \frac{\partial}{\partial x^i} \int\mathrm{d}{\boldsymbol{k}}\,k_l v_{\text{g}}^i J + \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial x^l}\,J - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J. \end{align}
\begin{align} 0&= \int \mathrm{d}{\boldsymbol{k}}\,k_l\,\frac{\partial J}{\partial t} + \int \mathrm{d}{\boldsymbol{k}}\,k_l\,\frac{\partial(v_{\text{g}}^i J)}{\partial x^i} - \int \mathrm{d}{\boldsymbol{k}}\,k_l\frac{\partial}{\partial k_i}\left(\frac{\partial w}{\partial x^i}\,J\right) - 2\int \mathrm{d}{\boldsymbol{k}}\,k_l\gamma J \nonumber\\ &= \frac{\partial}{\partial t} \int \mathrm{d}{\boldsymbol{k}}\,k_l J + \frac{\partial}{\partial x^i} \int\mathrm{d}{\boldsymbol{k}}\,k_l v_{\text{g}}^i J + \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial x^l}\,J - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J. \end{align}
Similarly, multiplying (7.84) by ![]() $\smash {\mathcal {H}_s}$ and integrating over
$\smash {\mathcal {H}_s}$ and integrating over ![]() $\smash {{\boldsymbol {p}}}$ yields
$\smash {{\boldsymbol {p}}}$ yields
 \begin{align} 0&= \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial F_s}{\partial t} + \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial (v_s^i F_s)}{\partial x^i} - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial}{\partial p_i} \left(\frac{\partial \mathcal{H}_s}{\partial x^i} \,F_s\right) \nonumber\\ &\quad - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial}{\partial p_i} \left({\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j}\right) - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,p_l F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, p_l v_s^i F_s + \frac{\partial}{\partial x^l}\int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s F_s + \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial x^l} \,F_s \nonumber\\ &\quad - \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial x^l} + \int\mathrm{d}{\boldsymbol{p}}\,{\mathsf{D}}_{s,lj}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\mathcal{C}_s. \end{align}
\begin{align} 0&= \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial F_s}{\partial t} + \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial (v_s^i F_s)}{\partial x^i} - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial}{\partial p_i} \left(\frac{\partial \mathcal{H}_s}{\partial x^i} \,F_s\right) \nonumber\\ &\quad - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial}{\partial p_i} \left({\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j}\right) - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,p_l F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, p_l v_s^i F_s + \frac{\partial}{\partial x^l}\int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s F_s + \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial x^l} \,F_s \nonumber\\ &\quad - \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial x^l} + \int\mathrm{d}{\boldsymbol{p}}\,{\mathsf{D}}_{s,lj}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,p_l\,\mathcal{C}_s. \end{align}Let us sum up (D2) over species and also add it with (D1). The contribution of the collision integral disappears due to (6.71), so one obtains
 \begin{align} 0 &= \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,p_l F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l J \right) + \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, p_l v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l v_{\text{g}}^i J \right)\nonumber\\ &\quad + \sum_s\frac{\partial}{\partial x^l}\int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s F_s + \sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial x^l}\,F_s\nonumber\\ &\quad + \sum_s\int\mathrm{d}{\boldsymbol{p}}\,{\mathsf{D}}_{s,lj}\,\frac{\partial F_s}{\partial p_j} - 2\int \mathrm{d}{\boldsymbol{k}}\,k_l \gamma J\nonumber\\ &\quad - \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial x^l} + \int \mathrm{d}{\boldsymbol{k}}\,J\,\frac{\partial w}{\partial x^l}. \end{align}
\begin{align} 0 &= \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,p_l F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l J \right) + \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, p_l v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,k_l v_{\text{g}}^i J \right)\nonumber\\ &\quad + \sum_s\frac{\partial}{\partial x^l}\int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s F_s + \sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial x^l}\,F_s\nonumber\\ &\quad + \sum_s\int\mathrm{d}{\boldsymbol{p}}\,{\mathsf{D}}_{s,lj}\,\frac{\partial F_s}{\partial p_j} - 2\int \mathrm{d}{\boldsymbol{k}}\,k_l \gamma J\nonumber\\ &\quad - \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial x^l} + \int \mathrm{d}{\boldsymbol{k}}\,J\,\frac{\partial w}{\partial x^l}. \end{align}Next, notice that
 \begin{align} 2 \int\mathrm{d}{\boldsymbol{k}}\,k_l \gamma J & = 2 {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{k}}\, k_l k_j\,\frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda}\,J \delta(w - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,\frac{\partial F_s}{\partial p_j}\nonumber\\ &= \sum_s \int\mathrm{d}{\boldsymbol{p}}\,{\mathsf{D}}_{s,l j}\,\frac{\partial F_s}{\partial p_j}. \end{align}
\begin{align} 2 \int\mathrm{d}{\boldsymbol{k}}\,k_l \gamma J & = 2 {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{k}}\, k_l k_j\,\frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda}\,J \delta(w - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,\frac{\partial F_s}{\partial p_j}\nonumber\\ &= \sum_s \int\mathrm{d}{\boldsymbol{p}}\,{\mathsf{D}}_{s,l j}\,\frac{\partial F_s}{\partial p_j}. \end{align}
Also, assuming that ![]() $\smash {{\boldsymbol {\varXi }}_0}$,
$\smash {{\boldsymbol {\varXi }}_0}$, ![]() $\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and
$\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and ![]() $\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of
$\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of ![]() $\smash {{\boldsymbol {x}}}$ and using (7.80), one gets
$\smash {{\boldsymbol {x}}}$ and using (7.80), one gets
 \begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\varDelta_s\frac{\partial F_s}{\partial x^l} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial x^l} \bigg( \frac{\partial}{\partial p_i} {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\frac{k_i}{2(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)}\, |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2 (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\, \delta(\omega - w({\boldsymbol{k}}))\nonumber\\ & \hphantom{= \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial x^l} \bigg(} + \frac{1}{2} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}}) (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\bigg)\nonumber\\ & ={-} \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\, \delta(\omega - w({\boldsymbol{k}}))\, \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, \frac{\partial^2 F_s}{\partial x^l\partial p_i} \nonumber\\ &\hphantom{\,=\,} + \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\, \frac{\partial}{\partial x^l}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}} F_s)\nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial}{\partial x^l} {\unicode{x2A0F}}\mathrm{d}{\boldsymbol{p}}\,\left( \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \frac{\partial F_s}{\partial p_i} - {\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}}F_s \right) \nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial ({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\varXi}}{\boldsymbol{\eta}})}{\partial x^l} \nonumber\\ & ={-} \sum_s \int \mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\,\frac{\partial \varLambda(w({\boldsymbol{k}}), {\boldsymbol{k}})}{\partial x^l} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{k}}\, J\,\frac{\partial w}{\partial x^l}, \end{align}
\begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\varDelta_s\frac{\partial F_s}{\partial x^l} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial x^l} \bigg( \frac{\partial}{\partial p_i} {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\frac{k_i}{2(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)}\, |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2 (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\, \delta(\omega - w({\boldsymbol{k}}))\nonumber\\ & \hphantom{= \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial x^l} \bigg(} + \frac{1}{2} \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}}) (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\bigg)\nonumber\\ & ={-} \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\, \delta(\omega - w({\boldsymbol{k}}))\, \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, \frac{\partial^2 F_s}{\partial x^l\partial p_i} \nonumber\\ &\hphantom{\,=\,} + \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\, \frac{\partial}{\partial x^l}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}} F_s)\nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial}{\partial x^l} {\unicode{x2A0F}}\mathrm{d}{\boldsymbol{p}}\,\left( \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \frac{\partial F_s}{\partial p_i} - {\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}}F_s \right) \nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial ({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\varXi}}{\boldsymbol{\eta}})}{\partial x^l} \nonumber\\ & ={-} \sum_s \int \mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\,\frac{\partial \varLambda(w({\boldsymbol{k}}), {\boldsymbol{k}})}{\partial x^l} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{k}}\, J\,\frac{\partial w}{\partial x^l}, \end{align}where we also used (7.75b). Substituting (D4) and (D5) into (D3) leads to (7.87).
D.2 Energy conservation
Let us multiply (7.83) by ![]() $w$ and integrate over
$w$ and integrate over ![]() ${\boldsymbol {k}}$. Then, one obtains
${\boldsymbol {k}}$. Then, one obtains
 \begin{align} 0&= \int \mathrm{d}{\boldsymbol{k}}\,w\,\frac{\partial J}{\partial t} + \int \mathrm{d}{\boldsymbol{k}}\,w\,\frac{\partial(v_{\text{g}}^i J)}{\partial x^i} - \int \mathrm{d}{\boldsymbol{k}}\,w\,\frac{\partial}{\partial k_i}\left(\frac{\partial w}{\partial x^i}J\right) - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J\nonumber\\ &= \frac{\partial}{\partial t} \int \mathrm{d}{\boldsymbol{k}}\,w J - \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial t}\,J + \frac{\partial}{\partial x^i} \int\mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J - \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial x^i}\, v_{\text{g}}^i J \nonumber\\ &\quad + \int \mathrm{d}{\boldsymbol{k}}\,v_{\text{g}}^i\,\frac{\partial w}{\partial x^i}\,J - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J\nonumber\\ &= \frac{\partial}{\partial t} \int \mathrm{d}{\boldsymbol{k}}\,w J + \frac{\partial}{\partial x^i}\int \mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J - \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial t}\,J - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J. \end{align}
\begin{align} 0&= \int \mathrm{d}{\boldsymbol{k}}\,w\,\frac{\partial J}{\partial t} + \int \mathrm{d}{\boldsymbol{k}}\,w\,\frac{\partial(v_{\text{g}}^i J)}{\partial x^i} - \int \mathrm{d}{\boldsymbol{k}}\,w\,\frac{\partial}{\partial k_i}\left(\frac{\partial w}{\partial x^i}J\right) - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J\nonumber\\ &= \frac{\partial}{\partial t} \int \mathrm{d}{\boldsymbol{k}}\,w J - \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial t}\,J + \frac{\partial}{\partial x^i} \int\mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J - \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial x^i}\, v_{\text{g}}^i J \nonumber\\ &\quad + \int \mathrm{d}{\boldsymbol{k}}\,v_{\text{g}}^i\,\frac{\partial w}{\partial x^i}\,J - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J\nonumber\\ &= \frac{\partial}{\partial t} \int \mathrm{d}{\boldsymbol{k}}\,w J + \frac{\partial}{\partial x^i}\int \mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J - \int \mathrm{d}{\boldsymbol{k}}\,\frac{\partial w}{\partial t}\,J - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J. \end{align}
Similarly, multiplying (7.84) by ![]() $\smash {\mathcal {H}_s}$ and integrating over
$\smash {\mathcal {H}_s}$ and integrating over ![]() $\smash {{\boldsymbol {p}}}$ yields
$\smash {{\boldsymbol {p}}}$ yields
 \begin{align} 0&= \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial F_s}{\partial t} + \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial (v_s^i F_s)}{\partial x^i} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial}{\partial p_i} \left(\frac{\partial \mathcal{H}_s}{\partial x^i} \,F_s\right) \nonumber\\ &\quad - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial}{\partial p_i} \left({\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j}\right) - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial \mathcal{H}_s}{\partial t}\,F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, \mathcal{H}_s v_s^i F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial \mathcal{H}_s }{\partial x^i}\,v_s^i F_s \nonumber\\ &\quad + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i\,\frac{\partial \mathcal{H}_s}{\partial x^i} \,F_s + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, \mathcal{H}_s v_s^i F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial \varDelta_s}{\partial t}\,F_s \nonumber\\ &\quad + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, H_{0s} v_s^i F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s v_s^i F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s \nonumber\\ &\quad + \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial t} + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s. \end{align}
\begin{align} 0&= \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial F_s}{\partial t} + \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial (v_s^i F_s)}{\partial x^i} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial}{\partial p_i} \left(\frac{\partial \mathcal{H}_s}{\partial x^i} \,F_s\right) \nonumber\\ &\quad - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\frac{\partial}{\partial p_i} \left({\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j}\right) - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial \mathcal{H}_s}{\partial t}\,F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, \mathcal{H}_s v_s^i F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial \mathcal{H}_s }{\partial x^i}\,v_s^i F_s \nonumber\\ &\quad + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i\,\frac{\partial \mathcal{H}_s}{\partial x^i} \,F_s + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, \mathcal{H}_s v_s^i F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial \varDelta_s}{\partial t}\,F_s \nonumber\\ &\quad + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s \nonumber\\ &= \frac{\partial}{\partial t} \int\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, H_{0s} v_s^i F_s + \frac{\partial}{\partial x^i}\int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s v_s^i F_s - \int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s \nonumber\\ &\quad + \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial t} + \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - \int\mathrm{d}{\boldsymbol{p}}\,\mathcal{H}_s\,\mathcal{C}_s. \end{align}Let us sum up (D7) over species and also add it with (D6). The contribution of the collision integral disappears due to (6.71), so one obtains
 \begin{align} 0 &= \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \int \mathrm{d}{\boldsymbol{k}}\,w J \right) + \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, H_{0s} v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J \right)\nonumber\\ &\quad + \frac{\partial}{\partial x^i}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s v_s^i F_s - \sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s \nonumber\\ &\quad + \sum_s \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J \nonumber\\ &\quad + \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial t} - \int \mathrm{d}{\boldsymbol{k}}\,J\,\frac{\partial w}{\partial t}. \end{align}
\begin{align} 0 &= \frac{\partial}{\partial t} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \int \mathrm{d}{\boldsymbol{k}}\,w J \right) + \frac{\partial}{\partial x^i} \left( \sum_s \int\mathrm{d}{\boldsymbol{p}}\, H_{0s} v_s^i F_s + \int \mathrm{d}{\boldsymbol{k}}\,w v_{\text{g}}^i J \right)\nonumber\\ &\quad + \frac{\partial}{\partial x^i}\sum_s \int\mathrm{d}{\boldsymbol{p}}\, \varDelta_s v_s^i F_s - \sum_s\int\mathrm{d}{\boldsymbol{p}}\,\frac{\partial H_{0s}}{\partial t}\,F_s \nonumber\\ &\quad + \sum_s \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,ij}\,\frac{\partial F_s}{\partial p_j} - 2\int \mathrm{d}{\boldsymbol{k}}\,w \gamma J \nonumber\\ &\quad + \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\varDelta_s\,\frac{\partial F_s}{\partial t} - \int \mathrm{d}{\boldsymbol{k}}\,J\,\frac{\partial w}{\partial t}. \end{align}Next, notice that
 \begin{align} 2 \int\mathrm{d}{\boldsymbol{k}}\,w \gamma J & = 2 {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{k}}\, w k_j\,\frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda}\,J \delta(w - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,\frac{\partial F_s}{\partial p_j}\nonumber\\ &= \sum_s \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,i j}\,\frac{\partial F_s}{\partial p_j}. \end{align}
\begin{align} 2 \int\mathrm{d}{\boldsymbol{k}}\,w \gamma J & = 2 {\rm \pi}\sum_s \int\mathrm{d}{\boldsymbol{p}}\,\mathrm{d}{\boldsymbol{k}}\, w k_j\,\frac{|{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\partial_{\omega}\varLambda}\,J \delta(w - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)\,\frac{\partial F_s}{\partial p_j}\nonumber\\ &= \sum_s \int\mathrm{d}{\boldsymbol{p}}\,v_s^i {\mathsf{D}}_{s,i j}\,\frac{\partial F_s}{\partial p_j}. \end{align}
Also, assuming that ![]() $\smash {{\boldsymbol {\varXi }}_0}$,
$\smash {{\boldsymbol {\varXi }}_0}$, ![]() $\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and
$\smash {|{\boldsymbol {\alpha }}_s^{{\dagger}} {\boldsymbol {\eta }}|^2}$ and ![]() $\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of
$\smash {{\boldsymbol {\eta }}^{{\dagger}} {\boldsymbol {\wp }}_s{\boldsymbol {\eta }}}$ are independent of ![]() $\smash {t}$ and using (7.80), one gets
$\smash {t}$ and using (7.80), one gets
 \begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\varDelta_s\frac{\partial F_s}{\partial t} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial t} \,\bigg( \frac{\partial}{\partial p_i} {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\frac{k_i}{2(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)}\, |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2 (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\, \delta(\omega - w({\boldsymbol{k}})) \nonumber\\ & \hphantom{= \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial t} \bigg(} + \frac{1}{2}\int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}}) (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}})) \bigg) \nonumber\\ & ={-} \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\, \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\frac{\partial^2 F_s}{\partial t\partial p_i} \nonumber\\ & \hphantom{\,=\,} + \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\, \frac{\partial}{\partial t}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}} F_s) \nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial}{\partial t} {\unicode{x2A0F}}\mathrm{d}{\boldsymbol{p}}\left( \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \frac{\partial F_s}{\partial p_i} - {\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}} F_s \right)\nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial ({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\varXi}}{\boldsymbol{\eta}})}{\partial t} \nonumber\\ &={-} \sum_s \int \mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\,\frac{\partial \varLambda(w({\boldsymbol{k}}), {\boldsymbol{k}})}{\partial t} \nonumber\\ &= \sum_s \int \mathrm{d}{\boldsymbol{k}}\, J\,\frac{\partial w}{\partial t}, \end{align}
\begin{align} & \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\varDelta_s\frac{\partial F_s}{\partial t} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial t} \,\bigg( \frac{\partial}{\partial p_i} {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\frac{k_i}{2(\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)}\, |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2 (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\, \delta(\omega - w({\boldsymbol{k}})) \nonumber\\ & \hphantom{= \sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{\partial F_s}{\partial t} \bigg(} + \frac{1}{2}\int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}}) (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}})) \bigg) \nonumber\\ & ={-} \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\, \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\frac{\partial^2 F_s}{\partial t\partial p_i} \nonumber\\ & \hphantom{\,=\,} + \frac{1}{2}\sum_s {\unicode{x2A0F}} \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\mathrm{d}{\boldsymbol{p}}\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}}))\,\delta(\omega - w({\boldsymbol{k}}))\, \frac{\partial}{\partial t}\,({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}} F_s) \nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial}{\partial t} {\unicode{x2A0F}}\mathrm{d}{\boldsymbol{p}}\left( \frac{k_i |{\boldsymbol{\alpha}}_s^{{\dagger}} {\boldsymbol{\eta}}|^2}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s} \frac{\partial F_s}{\partial p_i} - {\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\wp}}_s{\boldsymbol{\eta}} F_s \right)\nonumber\\ & ={-} \sum_s \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\, \delta(\omega - w({\boldsymbol{k}}))\,\frac{\partial ({\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\varXi}}{\boldsymbol{\eta}})}{\partial t} \nonumber\\ &={-} \sum_s \int \mathrm{d}{\boldsymbol{k}}\, h({\boldsymbol{k}})\,\frac{\partial \varLambda(w({\boldsymbol{k}}), {\boldsymbol{k}})}{\partial t} \nonumber\\ &= \sum_s \int \mathrm{d}{\boldsymbol{k}}\, J\,\frac{\partial w}{\partial t}, \end{align}where we also used (7.75a). Substituting (D9) and (D10) into (D8) leads to (7.89).
Appendix E. Uniqueness of the entropy-preserving distribution
Here, we prove that the Boltzmann–Gibbs distribution is the only distribution for which the entropy density ![]() $\smash {\sigma }$ is conserved. According to (C11),
$\smash {\sigma }$ is conserved. According to (C11), ![]() $\smash {\sigma }$ is conserved when
$\smash {\sigma }$ is conserved when
(for all ![]() $\smash {{\boldsymbol {p}}}$,
$\smash {{\boldsymbol {p}}}$, ![]() $\smash {{\boldsymbol {p}}'}$ and
$\smash {{\boldsymbol {p}}'}$ and ![]() $\smash {{\boldsymbol {k}}}$, as well as all
$\smash {{\boldsymbol {k}}}$, as well as all ![]() $\smash {s}$ and
$\smash {s}$ and ![]() $\smash {s'}$), where
$\smash {s'}$), where
Let us decompose the vector ![]() $\smash {{\boldsymbol {G}}_{ss'}({\boldsymbol {p}}, {\boldsymbol {p}}')}$ into components parallel and perpendicular to the vector
$\smash {{\boldsymbol {G}}_{ss'}({\boldsymbol {p}}, {\boldsymbol {p}}')}$ into components parallel and perpendicular to the vector ![]() $\smash {{\boldsymbol {v}}_s - {\boldsymbol {v}}'_{s'}}$:
$\smash {{\boldsymbol {v}}_s - {\boldsymbol {v}}'_{s'}}$:
where ![]() $\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'})}$ is a scalar function. (Because the velocities are functions of the momenta, one can as well consider
$\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'})}$ is a scalar function. (Because the velocities are functions of the momenta, one can as well consider ![]() $\smash {\lambda _{ss'}}$ as a function of
$\smash {\lambda _{ss'}}$ as a function of ![]() $\smash {{\boldsymbol {p}}}$ and
$\smash {{\boldsymbol {p}}}$ and ![]() $\smash {{\boldsymbol {p}}'}$.) Due to the presence of the delta function in (E1), the contribution of the first term to (E1) is zero, so (E1) can be written as
$\smash {{\boldsymbol {p}}'}$.) Due to the presence of the delta function in (E1), the contribution of the first term to (E1) is zero, so (E1) can be written as
By considering this formula for ![]() $\smash {{\boldsymbol {k}}}$ parallel to
$\smash {{\boldsymbol {k}}}$ parallel to ![]() $\smash {{\boldsymbol {G}}_{ss'}^\perp ({\boldsymbol {p}}, {\boldsymbol {p}}')}$ (and thus perpendicular to
$\smash {{\boldsymbol {G}}_{ss'}^\perp ({\boldsymbol {p}}, {\boldsymbol {p}}')}$ (and thus perpendicular to ![]() $\smash {{\boldsymbol {v}}_s - {\boldsymbol {v}}'_{s'}}$), one finds that
$\smash {{\boldsymbol {v}}_s - {\boldsymbol {v}}'_{s'}}$), one finds that ![]() $\smash {{\boldsymbol {G}}_{ss'}^\perp ({\boldsymbol {p}}, {\boldsymbol {p}}') = 0}$. Combined with (E2) and (E3), this yields
$\smash {{\boldsymbol {G}}_{ss'}^\perp ({\boldsymbol {p}}, {\boldsymbol {p}}') = 0}$. Combined with (E2) and (E3), this yields
Also, by swapping ![]() $\smash {{\boldsymbol {p}} \leftrightarrow {\boldsymbol {p}}'}$ and
$\smash {{\boldsymbol {p}} \leftrightarrow {\boldsymbol {p}}'}$ and ![]() $\smash {s \leftrightarrow s'}$, one finds that
$\smash {s \leftrightarrow s'}$, one finds that
Equation (E5) yields, in particular, thatFootnote 46
where we have assumed some coordinate axes in the momentum and velocity space labelled ![]() $\smash {(1, 2, 3, \ldots )}$. Then,
$\smash {(1, 2, 3, \ldots )}$. Then,
where the derivative with respect to ![]() $\smash {v_{s,1}}$ is taken at fixed
$\smash {v_{s,1}}$ is taken at fixed ![]() $\smash {v_{s, i \ne 1}}$ and at fixed
$\smash {v_{s, i \ne 1}}$ and at fixed ![]() $\smash {{\boldsymbol {v}}'_{s'}}$. Due to (E5),
$\smash {{\boldsymbol {v}}'_{s'}}$. Due to (E5), ![]() $\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'})}$ is continuous for all
$\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'})}$ is continuous for all ![]() $\smash {F_s}$ and
$\smash {F_s}$ and ![]() $\smash {F_{s'}}$. (Here, we consider only physical distributions, which are always differentiable.) Then, (E8) leads to
$\smash {F_{s'}}$. (Here, we consider only physical distributions, which are always differentiable.) Then, (E8) leads to
By differentiating this with respect to ![]() $\smash {v'_{s',2}}$, one obtains
$\smash {v'_{s',2}}$, one obtains
whence (E8a) yields
By repeating this argument for other axes and for ![]() $\smash {{\boldsymbol {v}}'}$ instead of
$\smash {{\boldsymbol {v}}'}$ instead of ![]() $\smash {{\boldsymbol {v}}}$, one can also extend (E11) to
$\smash {{\boldsymbol {v}}}$, one can also extend (E11) to
Hence, ![]() $\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'})}$ is actually independent of the velocities; i.e.
$\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'})}$ is actually independent of the velocities; i.e. ![]() $\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'}) = \lambda _{ss'}}$. Using this along with (E6), one also finds that
$\smash {\lambda _{ss'}({\boldsymbol {v}}_s, {\boldsymbol {v}}'_{s'}) = \lambda _{ss'}}$. Using this along with (E6), one also finds that
Let us rewrite (E5) as follows:
Here, the left-hand side is independent of ![]() $\smash {{\boldsymbol {p}}'}$ and the right-hand side is independent of
$\smash {{\boldsymbol {p}}'}$ and the right-hand side is independent of ![]() $\smash {{\boldsymbol {p}}}$, so both must be equal to some vector
$\smash {{\boldsymbol {p}}}$, so both must be equal to some vector
that is independent of both ![]() $\smash {{\boldsymbol {p}}}$ and
$\smash {{\boldsymbol {p}}}$ and ![]() $\smash {{\boldsymbol {p}}'}$. Because
$\smash {{\boldsymbol {p}}'}$. Because ![]() $\smash {{\boldsymbol {v}}_s = \partial _{{\boldsymbol {p}}}\mathcal {H}_s}$, this is equivalent to
$\smash {{\boldsymbol {v}}_s = \partial _{{\boldsymbol {p}}}\mathcal {H}_s}$, this is equivalent to
(and similarly for ![]() $\smash {{\boldsymbol {p}}'}$), where the integration constant
$\smash {{\boldsymbol {p}}'}$), where the integration constant ![]() $\smash {\eta _{ss'}}$ is independent of both
$\smash {\eta _{ss'}}$ is independent of both ![]() $\smash {{\boldsymbol {p}}}$ and
$\smash {{\boldsymbol {p}}}$ and ![]() $\smash {{\boldsymbol {p}}'}$. This is supposed to hold for any
$\smash {{\boldsymbol {p}}'}$. This is supposed to hold for any ![]() $\smash {s'}$, so one can also write
$\smash {s'}$, so one can also write
where ![]() $\smash {s''}$ is any other species index. Subtracting equations (E16) from each other gives
$\smash {s''}$ is any other species index. Subtracting equations (E16) from each other gives
By differentiating this with respect to ![]() $\smash {{\boldsymbol {p}}}$, one finds
$\smash {{\boldsymbol {p}}}$, one finds
By differentiating this further with respect to ![]() $\smash {{\boldsymbol {v}}_s}$, one obtains
$\smash {{\boldsymbol {v}}_s}$, one obtains ![]() $\smash {\lambda _{ss'} = \lambda _{ss''}}$. Then, (E18) yields
$\smash {\lambda _{ss'} = \lambda _{ss''}}$. Then, (E18) yields ![]() $\smash {{\boldsymbol {\mu }}_{ss'} = {\boldsymbol {\mu }}_{ss''}}$, and (E17) yields
$\smash {{\boldsymbol {\mu }}_{ss'} = {\boldsymbol {\mu }}_{ss''}}$, and (E17) yields ![]() $\smash {\eta _{ss'} = \eta _{ss''}}$. In other words, the functions
$\smash {\eta _{ss'} = \eta _{ss''}}$. In other words, the functions ![]() $\smash {\lambda _{ss'}}$,
$\smash {\lambda _{ss'}}$, ![]() $\smash {{\boldsymbol {\mu }}_{ss'}}$ and
$\smash {{\boldsymbol {\mu }}_{ss'}}$ and ![]() $\smash {\eta _{ss'}}$ are independent of their second index and thus can as well be written as
$\smash {\eta _{ss'}}$ are independent of their second index and thus can as well be written as
But then, (E13) and (E15) also yield ![]() $\smash {\lambda _s = \lambda _{s'} \equiv \lambda }$ and
$\smash {\lambda _s = \lambda _{s'} \equiv \lambda }$ and ![]() $\smash {{\boldsymbol {\mu }}_s = {\boldsymbol {\mu }}_{s'} \equiv {\boldsymbol {\mu }}}$. Therefore, (E16) can be written as
$\smash {{\boldsymbol {\mu }}_s = {\boldsymbol {\mu }}_{s'} \equiv {\boldsymbol {\mu }}}$. Therefore, (E16) can be written as
which is the Boltzmann–Gibbs distribution (§ 8.1). This proves that a plasma that conserves its entropy density necessarily has the Boltzmann–Gibbs distribution.
Appendix F. Total momentum and energy
Here, we show that the total momentum and energy in the OC–wave representation equals the total momentum and energy in the particle–field representation.
F.1 Non-relativistic electrostatic interactions
F.1.1 Momentum
Assuming the notation ![]() $\smash {\mathcal {P}_l \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,p_l \overline {f}_s}$ and using (9.17) for
$\smash {\mathcal {P}_l \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,p_l \overline {f}_s}$ and using (9.17) for ![]() $\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC momentum density as follows:
$\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC momentum density as follows:
 \begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l F_s & = \mathcal{P}_l + \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial}{\partial p_i}\left(\Theta_{s,ij}\,\frac{\partial \overline{f}_s}{\partial p_j}\right) \nonumber\\ & \approx \mathcal{P}_l - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,\Theta_{s,lj}\,\frac{\partial F_s}{\partial p_j} \nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\left.\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{k_l}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}}\cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}\nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\, k_l h({\boldsymbol{k}})\left.\frac{\partial}{\partial \vartheta}\left(\frac{k^2(\epsilon_{{\parallel}\text{H}}(w({\boldsymbol{k}}) + \vartheta, {\boldsymbol{k}})-1)}{4{\rm \pi}}\right) \right|_{\vartheta=0} \nonumber\\ & = \mathcal{P}_l - \int \mathrm{d}{\boldsymbol{k}}\,k_l J, \end{align}
\begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l F_s & = \mathcal{P}_l + \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l\,\frac{\partial}{\partial p_i}\left(\Theta_{s,ij}\,\frac{\partial \overline{f}_s}{\partial p_j}\right) \nonumber\\ & \approx \mathcal{P}_l - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,\Theta_{s,lj}\,\frac{\partial F_s}{\partial p_j} \nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\left.\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{k_l}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}}\cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}\nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\, k_l h({\boldsymbol{k}})\left.\frac{\partial}{\partial \vartheta}\left(\frac{k^2(\epsilon_{{\parallel}\text{H}}(w({\boldsymbol{k}}) + \vartheta, {\boldsymbol{k}})-1)}{4{\rm \pi}}\right) \right|_{\vartheta=0} \nonumber\\ & = \mathcal{P}_l - \int \mathrm{d}{\boldsymbol{k}}\,k_l J, \end{align}F.1.2 Energy
Assuming the notation ![]() $\smash {\mathcal {K} \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,H_{0s} \overline {f}_s}$ and using (9.17) for
$\smash {\mathcal {K} \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,H_{0s} \overline {f}_s}$ and using (9.17) for ![]() $\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC energy density as follows:
$\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC energy density as follows:
 \begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s & = \mathcal{K} + \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{p^2}{2m_s}\,\frac{\partial}{\partial p_i}\left(\Theta_{s,ij}\,\frac{\partial \overline{f}_s}{\partial p_j}\right) \nonumber\\ & \approx \mathcal{K} - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,v_s^i\Theta_{s,ij}\,\frac{\partial F_s}{\partial p_j} \nonumber\\ & = \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}} \left. \frac{{\boldsymbol{k}}\cdot{{\boldsymbol{v}}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}}\cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}. \end{align}
\begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s & = \mathcal{K} + \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,\frac{p^2}{2m_s}\,\frac{\partial}{\partial p_i}\left(\Theta_{s,ij}\,\frac{\partial \overline{f}_s}{\partial p_j}\right) \nonumber\\ & \approx \mathcal{K} - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,v_s^i\Theta_{s,ij}\,\frac{\partial F_s}{\partial p_j} \nonumber\\ & = \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}} \left. \frac{{\boldsymbol{k}}\cdot{{\boldsymbol{v}}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}}\cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}. \end{align}Notice that
 \begin{align} \frac{\partial}{\partial \vartheta}\frac{{\boldsymbol{k}}\cdot{{\boldsymbol{v}}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} & = \frac{\partial}{\partial \vartheta}\left({-}1 + \frac{w({\boldsymbol{k}}) + \vartheta}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\right) \nonumber\\ & = \frac{1}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} + w({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta} \frac{1}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}. \end{align}
\begin{align} \frac{\partial}{\partial \vartheta}\frac{{\boldsymbol{k}}\cdot{{\boldsymbol{v}}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} & = \frac{\partial}{\partial \vartheta}\left({-}1 + \frac{w({\boldsymbol{k}}) + \vartheta}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\right) \nonumber\\ & = \frac{1}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta} + w({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta} \frac{1}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}. \end{align}Then,
 \begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s &= \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,w({\boldsymbol{k}}) h({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta} \sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}} \left. \frac{{\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, \cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}\nonumber\\ &\quad -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}}) \sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, \cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}}\nonumber\\ &= \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,w({\boldsymbol{k}}) h({\boldsymbol{k}}) \left.\frac{\partial}{\partial \vartheta}\left(\frac{k^2(\epsilon_{{\parallel}\text{H}}(w({\boldsymbol{k}}) + \vartheta, {\boldsymbol{k}})-1)}{4{\rm \pi}}\right) \right|_{\vartheta=0} \nonumber\\ &\quad -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\, \frac{k^2(\epsilon_{{\parallel}\text{H}}(w({\boldsymbol{k}}), {\boldsymbol{k}})-1)}{4{\rm \pi}}. \end{align}
\begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s &= \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,w({\boldsymbol{k}}) h({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta} \sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}} \left. \frac{{\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, \cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}\nonumber\\ &\quad -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}}) \sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{k}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, \cdot\frac{\partial F_s}{\partial {\boldsymbol{p}}}\nonumber\\ &= \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,w({\boldsymbol{k}}) h({\boldsymbol{k}}) \left.\frac{\partial}{\partial \vartheta}\left(\frac{k^2(\epsilon_{{\parallel}\text{H}}(w({\boldsymbol{k}}) + \vartheta, {\boldsymbol{k}})-1)}{4{\rm \pi}}\right) \right|_{\vartheta=0} \nonumber\\ &\quad -\int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\, \frac{k^2(\epsilon_{{\parallel}\text{H}}(w({\boldsymbol{k}}), {\boldsymbol{k}})-1)}{4{\rm \pi}}. \end{align}Using (9.14) and (9.16), one obtains that the sum of the OC and wave energy is given by
 \begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \int \mathrm{d}{\boldsymbol{k}}\,w J & = \mathcal{K} + \int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\,\frac{k^2}{4{\rm \pi}} \nonumber\\ & = \mathcal{K} + \sum_\sigma\frac{\overline{k}_\sigma^2 |{\breve{\varphi}}_\sigma|^2}{16{\rm \pi}} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{p}}\left(\frac{p^2}{2m_s} + e_s\overline{\varphi}_s\right)\overline{f}_s + \frac{1}{8{\rm \pi}}\,\overline{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}, \end{align}
\begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s + \int \mathrm{d}{\boldsymbol{k}}\,w J & = \mathcal{K} + \int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\,\frac{k^2}{4{\rm \pi}} \nonumber\\ & = \mathcal{K} + \sum_\sigma\frac{\overline{k}_\sigma^2 |{\breve{\varphi}}_\sigma|^2}{16{\rm \pi}} \nonumber\\ & = \sum_s \int \mathrm{d}{\boldsymbol{p}}\left(\frac{p^2}{2m_s} + e_s\overline{\varphi}_s\right)\overline{f}_s + \frac{1}{8{\rm \pi}}\,\overline{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}, \end{align}where we also substituted (7.64).
F.2 Relativistic electromagnetic interactions
F.2.1 Momentum
Let us assume the notation ![]() $\smash {{\boldsymbol {\mathcal {P}}} \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,{\boldsymbol {p}} \overline {f}_s}$ and
$\smash {{\boldsymbol {\mathcal {P}}} \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,{\boldsymbol {p}} \overline {f}_s}$ and
 \begin{equation} {\boldsymbol{\chi}}(\omega, {\boldsymbol{k}}) \doteq \sum_s \frac{4{\rm \pi} e_s^2}{\omega^2}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\,{\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial{\boldsymbol{p}}} = {\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}) - {\boldsymbol{1}} + \frac{{\boldsymbol{\mathfrak{w}}}_p}{\omega^2}. \end{equation}
\begin{equation} {\boldsymbol{\chi}}(\omega, {\boldsymbol{k}}) \doteq \sum_s \frac{4{\rm \pi} e_s^2}{\omega^2}{\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{\omega - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\,{\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial{\boldsymbol{p}}} = {\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}) - {\boldsymbol{1}} + \frac{{\boldsymbol{\mathfrak{w}}}_p}{\omega^2}. \end{equation}
Then, using (9.52) for ![]() $\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC momentum density as follows:
$\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC momentum density as follows:
 \begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l F_s & \approx \mathcal{P}_l - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,\Theta_{s,lj}\,\frac{\partial F_s}{\partial p_j} \nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\,k_l h({\boldsymbol{k}})\left.\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{1}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}})}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\,{\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial p_j} \right|_{\vartheta=0}\nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\, \frac{k_l h({\boldsymbol{k}})}{4{\rm \pi} w^2({\boldsymbol{k}})} \left.{\boldsymbol{\eta}}^{{\dagger}}\frac{\partial}{\partial \omega}\left( \omega^2{\boldsymbol{\chi}}(\omega, {\boldsymbol{k}}) \right){\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})}\nonumber\\ & = \mathcal{P}_l + \int \mathrm{d}{\boldsymbol{k}}\,\frac{k_l h({\boldsymbol{k}})}{2{\rm \pi} w({\boldsymbol{k}})} -\int \mathrm{d}{\boldsymbol{k}}\, \frac{k_l h({\boldsymbol{k}})}{4{\rm \pi} w^2({\boldsymbol{k}})} \left.{\boldsymbol{\eta}}^{{\dagger}}\frac{\partial}{\partial \omega}\left( \omega^2{\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}) \right){\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})} \nonumber\\ & = \mathcal{P}_l + \int \mathrm{d}{\boldsymbol{k}}\,\frac{k_l}{4{\rm \pi} w({\boldsymbol{k}})}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) - \int \mathrm{d}{\boldsymbol{k}}\,k_l J, \end{align}
\begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,p_l F_s & \approx \mathcal{P}_l - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,\Theta_{s,lj}\,\frac{\partial F_s}{\partial p_j} \nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\,k_l h({\boldsymbol{k}})\left.\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{1}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}})}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\,{\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial p_j} \right|_{\vartheta=0}\nonumber\\ & = \mathcal{P}_l -\int \mathrm{d}{\boldsymbol{k}}\, \frac{k_l h({\boldsymbol{k}})}{4{\rm \pi} w^2({\boldsymbol{k}})} \left.{\boldsymbol{\eta}}^{{\dagger}}\frac{\partial}{\partial \omega}\left( \omega^2{\boldsymbol{\chi}}(\omega, {\boldsymbol{k}}) \right){\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})}\nonumber\\ & = \mathcal{P}_l + \int \mathrm{d}{\boldsymbol{k}}\,\frac{k_l h({\boldsymbol{k}})}{2{\rm \pi} w({\boldsymbol{k}})} -\int \mathrm{d}{\boldsymbol{k}}\, \frac{k_l h({\boldsymbol{k}})}{4{\rm \pi} w^2({\boldsymbol{k}})} \left.{\boldsymbol{\eta}}^{{\dagger}}\frac{\partial}{\partial \omega}\left( \omega^2{\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}) \right){\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})} \nonumber\\ & = \mathcal{P}_l + \int \mathrm{d}{\boldsymbol{k}}\,\frac{k_l}{4{\rm \pi} w({\boldsymbol{k}})}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) - \int \mathrm{d}{\boldsymbol{k}}\,k_l J, \end{align}where we substituted (9.51) and used (7.23). Next, let us rewrite (9.54) as
where the last equality is due to Gauss's law. This gives
Then, using (2.53) and also (7.63) for ![]() $\smash {{{\boldsymbol {\mathsf {U}}}}}$, one obtains
$\smash {{{\boldsymbol {\mathsf {U}}}}}$, one obtains
 \begin{align} \mathcal{P}_l - \mathcal{P}^{(\text{kin})}_l & \approx{-}\frac{\mathrm{i}}{4 {\rm \pi}}\, \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\omega^{{-}1} {\mathsf{U}}_l{}^j(\omega, {\boldsymbol{k}})(\mathrm{i} k_j)^* \nonumber\\ & \approx{-} \int \mathrm{d}{\boldsymbol{k}}\,\frac{{\boldsymbol{k}} \cdot {\boldsymbol{\eta}}^*}{4{\rm \pi} w({\boldsymbol{k}})}\,\eta_l (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})), \end{align}
\begin{align} \mathcal{P}_l - \mathcal{P}^{(\text{kin})}_l & \approx{-}\frac{\mathrm{i}}{4 {\rm \pi}}\, \int \mathrm{d}\omega\,\mathrm{d}{\boldsymbol{k}}\,\omega^{{-}1} {\mathsf{U}}_l{}^j(\omega, {\boldsymbol{k}})(\mathrm{i} k_j)^* \nonumber\\ & \approx{-} \int \mathrm{d}{\boldsymbol{k}}\,\frac{{\boldsymbol{k}} \cdot {\boldsymbol{\eta}}^*}{4{\rm \pi} w({\boldsymbol{k}})}\,\eta_l (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})), \end{align}and thus (F7) can be written as follows:
 \begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,{\boldsymbol{p}} F_s & + \int \mathrm{d}{\boldsymbol{k}}\,{\boldsymbol{k}} J \approx {\boldsymbol{\mathcal{P}}} + \int \mathrm{d}{\boldsymbol{k}}\,\frac{{\boldsymbol{k}}}{4{\rm \pi} w({\boldsymbol{k}})}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \nonumber\\ & \approx {\boldsymbol{\mathcal{P}}}^{(\text{kin})} + \int \mathrm{d}{\boldsymbol{k}}\,\frac{1}{4{\rm \pi} w({\boldsymbol{k}})}\, ({\boldsymbol{k}} - {\boldsymbol{\eta}} ({\boldsymbol{k}} \cdot {\boldsymbol{\eta}}^*))\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \nonumber\\ & = {\boldsymbol{\mathcal{P}}}^{(\text{kin})} + \operatorname{re} \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{2{\rm \pi} w({\boldsymbol{k}})}\, {\boldsymbol{\eta}}^* \times ({\boldsymbol{k}} \times {\boldsymbol{\eta}}), \end{align}
\begin{align} \sum_s \int \mathrm{d}{\boldsymbol{p}}\,{\boldsymbol{p}} F_s & + \int \mathrm{d}{\boldsymbol{k}}\,{\boldsymbol{k}} J \approx {\boldsymbol{\mathcal{P}}} + \int \mathrm{d}{\boldsymbol{k}}\,\frac{{\boldsymbol{k}}}{4{\rm \pi} w({\boldsymbol{k}})}\,(h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \nonumber\\ & \approx {\boldsymbol{\mathcal{P}}}^{(\text{kin})} + \int \mathrm{d}{\boldsymbol{k}}\,\frac{1}{4{\rm \pi} w({\boldsymbol{k}})}\, ({\boldsymbol{k}} - {\boldsymbol{\eta}} ({\boldsymbol{k}} \cdot {\boldsymbol{\eta}}^*))\, (h({\boldsymbol{k}}) + h(-{\boldsymbol{k}})) \nonumber\\ & = {\boldsymbol{\mathcal{P}}}^{(\text{kin})} + \operatorname{re} \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{2{\rm \pi} w({\boldsymbol{k}})}\, {\boldsymbol{\eta}}^* \times ({\boldsymbol{k}} \times {\boldsymbol{\eta}}), \end{align}
where we used (7.7) and (7.23) again. For an eikonal wave (9.57), which has ![]() $\smash {h({\boldsymbol {k}}) = \delta ({\boldsymbol {k}} - \overline {{\boldsymbol {k}}})|{\breve {{\boldsymbol {E}}}}|^2/4}$ (§ 7.4.1), this gives
$\smash {h({\boldsymbol {k}}) = \delta ({\boldsymbol {k}} - \overline {{\boldsymbol {k}}})|{\breve {{\boldsymbol {E}}}}|^2/4}$ (§ 7.4.1), this gives
 \begin{equation} \operatorname{re} \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{2{\rm \pi} w({\boldsymbol{k}})}\, {\boldsymbol{\eta}}^* \times ({\boldsymbol{k}} \times {\boldsymbol{\eta}}) = \frac{1}{8{\rm \pi} c} \,\operatorname{re} \left(\smash{{\breve{{\boldsymbol{E}}}}}^* \times \left(\frac{c\overline{{\boldsymbol{k}}}}{\overline{\omega}} \times {\breve{{\boldsymbol{E}}}}\right)\right) = \frac{\overline{\widetilde{{\boldsymbol{E}}} \times \widetilde{{\boldsymbol{B}}}}}{4{\rm \pi} c}. \end{equation}
\begin{equation} \operatorname{re} \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{2{\rm \pi} w({\boldsymbol{k}})}\, {\boldsymbol{\eta}}^* \times ({\boldsymbol{k}} \times {\boldsymbol{\eta}}) = \frac{1}{8{\rm \pi} c} \,\operatorname{re} \left(\smash{{\breve{{\boldsymbol{E}}}}}^* \times \left(\frac{c\overline{{\boldsymbol{k}}}}{\overline{\omega}} \times {\breve{{\boldsymbol{E}}}}\right)\right) = \frac{\overline{\widetilde{{\boldsymbol{E}}} \times \widetilde{{\boldsymbol{B}}}}}{4{\rm \pi} c}. \end{equation}In case of a broadband spectrum, the same equality applies as well, because contributions of the individual eikonal waves to both left-hand side and the right-hand side are additive. (Alternatively, one can invoke (2.53) again.) This leads to (9.53).
F.2.2 Energy
Assuming the notation ![]() $\smash {\mathcal {K} \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,H_{0s} \overline {f}_s}$ and using (9.52) for
$\smash {\mathcal {K} \doteq \sum _s \int \mathrm {d}{\boldsymbol {p}}\,H_{0s} \overline {f}_s}$ and using (9.52) for ![]() $\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC energy density as follows:
$\smash {{\boldsymbol {\Theta }}_s}$, one can represent the OC energy density as follows:
 \begin{align*} \sum_s \int &\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s \approx \mathcal{K} - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,v_s^i\Theta_{s,ij}\,\frac{\partial F_s}{\partial p_j}\\ & \approx \mathcal{K} - \int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}} \left. \frac{({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}})}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}. \end{align*}
\begin{align*} \sum_s \int &\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s \approx \mathcal{K} - \frac{1}{2}\sum_s \int \mathrm{d}{\boldsymbol{p}}\,v_s^i\Theta_{s,ij}\,\frac{\partial F_s}{\partial p_j}\\ & \approx \mathcal{K} - \int \mathrm{d}{\boldsymbol{k}}\,h({\boldsymbol{k}})\,\frac{\partial}{\partial \vartheta}\sum_s e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}} \left. \frac{({\boldsymbol{k}} \cdot {\boldsymbol{v}}_s)}{w^2({\boldsymbol{k}})} \frac{({\boldsymbol{\eta}}^{{\dagger}} {\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}} {\boldsymbol{\eta}})}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}} \right|_{\vartheta=0}. \end{align*}
Using (F3) and (F6) for ![]() $\smash {{\boldsymbol {\chi }}}$, one further obtains
$\smash {{\boldsymbol {\chi }}}$, one further obtains
 \begin{align*} \sum_s \int &\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s \\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w({\boldsymbol{k}})} \left. {\boldsymbol{\eta}}^{{\dagger}}\,\frac{\partial}{\partial \vartheta}\bigg( \sum_s 4{\rm \pi} e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}} \bigg){\boldsymbol{\eta}} \right|_{\vartheta=0} \\ & -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\, {\boldsymbol{\eta}}^{{\dagger}}\,\bigg( \sum_s \frac{4{\rm \pi} e_s^2}{w^2({\boldsymbol{k}})} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, {\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}} \bigg){\boldsymbol{\eta}}\\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w({\boldsymbol{k}})} \left. {\boldsymbol{\eta}}^{{\dagger}} \frac{\partial(\omega^2{\boldsymbol{\chi}}(\omega, {\boldsymbol{k}}))}{\partial\omega} {\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\,{\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\chi}}{\boldsymbol{\eta}} \\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w({\boldsymbol{k}})} \left. {\boldsymbol{\eta}}^{{\dagger}} \frac{\partial(\omega^2{\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}))}{\partial\omega} {\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})} + \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{2{\rm \pi}}\\ &- \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\,{\boldsymbol{\eta}}^{{\dagger}}\left( {\boldsymbol{\epsilon}}(w({\boldsymbol{k}}), {\boldsymbol{k}}) - {\boldsymbol{1}} + \frac{{\boldsymbol{\mathfrak{w}}}_p}{w^2({\boldsymbol{k}})} \right){\boldsymbol{\eta}}\\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,w J + \int \mathrm{d}{\boldsymbol{k}}\,\frac{3h({\boldsymbol{k}})}{4{\rm \pi}} - \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\,{\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\epsilon}}(w({\boldsymbol{k}}), {\boldsymbol{k}}){\boldsymbol{\eta}} \\ & - \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w^2({\boldsymbol{k}})}\,{\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\mathfrak{w}}}_p{\boldsymbol{\eta}}. \end{align*}
\begin{align*} \sum_s \int &\mathrm{d}{\boldsymbol{p}}\,H_{0s} F_s \\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w({\boldsymbol{k}})} \left. {\boldsymbol{\eta}}^{{\dagger}}\,\frac{\partial}{\partial \vartheta}\bigg( \sum_s 4{\rm \pi} e_s^2 {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s + \vartheta}\, {\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}} \bigg){\boldsymbol{\eta}} \right|_{\vartheta=0} \\ & -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\, {\boldsymbol{\eta}}^{{\dagger}}\,\bigg( \sum_s \frac{4{\rm \pi} e_s^2}{w^2({\boldsymbol{k}})} {\unicode{x2A0F}} \mathrm{d}{\boldsymbol{p}}\, \frac{{\boldsymbol{v}}_s {\boldsymbol{v}}_s^{{\dagger}}}{w({\boldsymbol{k}}) - {\boldsymbol{k}} \cdot {\boldsymbol{v}}_s}\, {\boldsymbol{k}} \cdot \frac{\partial F_s}{\partial {\boldsymbol{p}}} \bigg){\boldsymbol{\eta}}\\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w({\boldsymbol{k}})} \left. {\boldsymbol{\eta}}^{{\dagger}} \frac{\partial(\omega^2{\boldsymbol{\chi}}(\omega, {\boldsymbol{k}}))}{\partial\omega} {\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\,{\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\chi}}{\boldsymbol{\eta}} \\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w({\boldsymbol{k}})} \left. {\boldsymbol{\eta}}^{{\dagger}} \frac{\partial(\omega^2{\boldsymbol{\epsilon}}(\omega, {\boldsymbol{k}}))}{\partial\omega} {\boldsymbol{\eta}} \right|_{\omega = w({\boldsymbol{k}})} + \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{2{\rm \pi}}\\ &- \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\,{\boldsymbol{\eta}}^{{\dagger}}\left( {\boldsymbol{\epsilon}}(w({\boldsymbol{k}}), {\boldsymbol{k}}) - {\boldsymbol{1}} + \frac{{\boldsymbol{\mathfrak{w}}}_p}{w^2({\boldsymbol{k}})} \right){\boldsymbol{\eta}}\\ =\,& \mathcal{K} -\int \mathrm{d}{\boldsymbol{k}}\,w J + \int \mathrm{d}{\boldsymbol{k}}\,\frac{3h({\boldsymbol{k}})}{4{\rm \pi}} - \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi}}\,{\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\epsilon}}(w({\boldsymbol{k}}), {\boldsymbol{k}}){\boldsymbol{\eta}} \\ & - \int \mathrm{d}{\boldsymbol{k}}\,\frac{h({\boldsymbol{k}})}{4{\rm \pi} w^2({\boldsymbol{k}})}\,{\boldsymbol{\eta}}^{{\dagger}}{\boldsymbol{\mathfrak{w}}}_p{\boldsymbol{\eta}}. \end{align*}Using (9.50) and proceeding as in § F.2.1, one can also cast this as follows:
Now, notice that
 \begin{align} \mathcal{K} & = \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\overline{H_{0s}({\boldsymbol{p}})f_s^{(\text{kin})}({\boldsymbol{p}} - e_s\widetilde{{\boldsymbol{A}}}/c)} \nonumber\\ & = \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\overline{H_{0s}({\boldsymbol{p}} + e_s\widetilde{{\boldsymbol{A}}}/c)f_s^{(\text{kin})}({\boldsymbol{p}})} \nonumber\\ & \approx \mathcal{K}^{(\text{kin})} + \overline{(\widetilde{{\boldsymbol{A}}}/c) \cdot \sum_s e_s \textstyle \int\mathrm{d}{\boldsymbol{p}}\,{\boldsymbol{v}}_s f_s^{(\text{kin})}} + \sum_s \frac{e_s^2}{2c^2} \int\mathrm{d}{\boldsymbol{p}}\,\overline{(\widetilde{{\boldsymbol{A}}} {\boldsymbol{\mu}}_s^{{-}1} \widetilde{{\boldsymbol{A}}})\,f_s^{(\text{kin})}} \nonumber\\ & \approx \mathcal{K}^{(\text{kin})} + \frac{1}{c}\,\overline{\widetilde{{\boldsymbol{A}}} \cdot \widetilde{{\boldsymbol{j}}}} + \frac{1}{8{\rm \pi} c^2}\, \overline{\smash{\widetilde{{\boldsymbol{A}}}}^{{\dagger}}{\boldsymbol{\mathfrak{w}}}_p\widetilde{{\boldsymbol{A}}}}, \end{align}
\begin{align} \mathcal{K} & = \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\overline{H_{0s}({\boldsymbol{p}})f_s^{(\text{kin})}({\boldsymbol{p}} - e_s\widetilde{{\boldsymbol{A}}}/c)} \nonumber\\ & = \sum_s \int\mathrm{d}{\boldsymbol{p}}\,\overline{H_{0s}({\boldsymbol{p}} + e_s\widetilde{{\boldsymbol{A}}}/c)f_s^{(\text{kin})}({\boldsymbol{p}})} \nonumber\\ & \approx \mathcal{K}^{(\text{kin})} + \overline{(\widetilde{{\boldsymbol{A}}}/c) \cdot \sum_s e_s \textstyle \int\mathrm{d}{\boldsymbol{p}}\,{\boldsymbol{v}}_s f_s^{(\text{kin})}} + \sum_s \frac{e_s^2}{2c^2} \int\mathrm{d}{\boldsymbol{p}}\,\overline{(\widetilde{{\boldsymbol{A}}} {\boldsymbol{\mu}}_s^{{-}1} \widetilde{{\boldsymbol{A}}})\,f_s^{(\text{kin})}} \nonumber\\ & \approx \mathcal{K}^{(\text{kin})} + \frac{1}{c}\,\overline{\widetilde{{\boldsymbol{A}}} \cdot \widetilde{{\boldsymbol{j}}}} + \frac{1}{8{\rm \pi} c^2}\, \overline{\smash{\widetilde{{\boldsymbol{A}}}}^{{\dagger}}{\boldsymbol{\mathfrak{w}}}_p\widetilde{{\boldsymbol{A}}}}, \end{align}
where ![]() $\smash {\widetilde {{\boldsymbol {j}}}}$ is the oscillating-current density. From Ampere's law,
$\smash {\widetilde {{\boldsymbol {j}}}}$ is the oscillating-current density. From Ampere's law,
 \begin{align} \frac{1}{c}\,\overline{\widetilde{{\boldsymbol{A}}} \cdot \widetilde{{\boldsymbol{j}}}} & = \overline{\frac{(-\mathrm{i} \widehat{\omega}^{{-}1}\widetilde{{\boldsymbol{E}}})^{{\dagger}}}{4{\rm \pi}} \big(\mathrm{i} c \widehat{\boldsymbol{k}} \times \widetilde{{\boldsymbol{B}}} + \mathrm{i} \widehat{\omega}\widetilde{{\boldsymbol{E}}}\big)} \nonumber\\ & \approx{-}\overline{\frac{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}{4{\rm \pi}}} -\overline{\frac{\widetilde{{\boldsymbol{E}}}}{4{\rm \pi}} \cdot\bigg(\frac{c \widehat{\boldsymbol{k}}}{\widehat{\omega}} \times \widetilde{{\boldsymbol{B}}}\bigg)} \nonumber\\ & \approx{-}\overline{\frac{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}{4{\rm \pi}}} -\overline{\bigg(\widetilde{{\boldsymbol{E}}} \times \frac{c \widehat{\boldsymbol{k}}}{\widehat{\omega}}\bigg) \cdot \frac{\widetilde{{\boldsymbol{B}}}}{4{\rm \pi}}} \nonumber\\ & \approx \frac{1}{4{\rm \pi}}\,\big(\overline{\smash{\widetilde{{\boldsymbol{B}}}}^{{\dagger}} \widetilde{{\boldsymbol{B}}}} - \overline{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}\big). \end{align}
\begin{align} \frac{1}{c}\,\overline{\widetilde{{\boldsymbol{A}}} \cdot \widetilde{{\boldsymbol{j}}}} & = \overline{\frac{(-\mathrm{i} \widehat{\omega}^{{-}1}\widetilde{{\boldsymbol{E}}})^{{\dagger}}}{4{\rm \pi}} \big(\mathrm{i} c \widehat{\boldsymbol{k}} \times \widetilde{{\boldsymbol{B}}} + \mathrm{i} \widehat{\omega}\widetilde{{\boldsymbol{E}}}\big)} \nonumber\\ & \approx{-}\overline{\frac{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}{4{\rm \pi}}} -\overline{\frac{\widetilde{{\boldsymbol{E}}}}{4{\rm \pi}} \cdot\bigg(\frac{c \widehat{\boldsymbol{k}}}{\widehat{\omega}} \times \widetilde{{\boldsymbol{B}}}\bigg)} \nonumber\\ & \approx{-}\overline{\frac{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}{4{\rm \pi}}} -\overline{\bigg(\widetilde{{\boldsymbol{E}}} \times \frac{c \widehat{\boldsymbol{k}}}{\widehat{\omega}}\bigg) \cdot \frac{\widetilde{{\boldsymbol{B}}}}{4{\rm \pi}}} \nonumber\\ & \approx \frac{1}{4{\rm \pi}}\,\big(\overline{\smash{\widetilde{{\boldsymbol{B}}}}^{{\dagger}} \widetilde{{\boldsymbol{B}}}} - \overline{\smash{\widetilde{{\boldsymbol{E}}}}^{{\dagger}} \widetilde{{\boldsymbol{E}}}}\big). \end{align}Appendix G. Selected notation
This paper uses the following notation (also see § 2 for the index convention):