Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-06-01T10:08:35.146Z Has data issue: false hasContentIssue false
  • English
  • Français

DOES 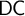$\mathsf {DC}$ IMPLY 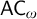${\mathsf {AC}}_\omega $, UNIFORMLY?

Part of: Set theory

Published online by Cambridge University Press:  06 May 2024

ALESSANDRO ANDRETTA Open the ORCID record for ALESSANDRO ANDRETTA [Opens in a new window]  and
LORENZO NOTARO Open the ORCID record for LORENZO NOTARO [Opens in a new window]
ALESSANDRO ANDRETTA
Affiliation:
DIPARTIMENTO DI MATEMATICA “G. PEANO” UNIVERSITÀ DEGLI STUDI DI TORINO VIA CARLO ALBERTO 10 10123 TORINO, ITALY E-mail: alessandro.andretta@unito.it
LORENZO NOTARO*
Affiliation:
DIPARTIMENTO DI MATEMATICA “G. PEANO” UNIVERSITÀ DEGLI STUDI DI TORINO VIA CARLO ALBERTO 10 10123 TORINO, ITALY E-mail: alessandro.andretta@unito.it
*
E-mail: lorenzo.notaro@unito.it
Get access Rights & Permissions [Opens in a new window]

Abstract

The axiom of dependent choice (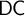$\mathsf {DC}$) and the axiom of countable choice (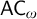${\mathsf {AC}}_\omega $) are two weak forms of the axiom of choice that can be stated for a specific set: 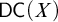$\mathsf {DC} ( X )$ asserts that any total binary relation on X has an infinite chain, while 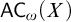${\mathsf {AC}}_\omega ( X )$ asserts that any countable collection of nonempty subsets of X has a choice function. It is well-known that 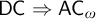$\mathsf {DC} \Rightarrow {\mathsf {AC}}_\omega $. We study for which sets and under which hypotheses 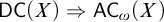$\mathsf {DC} ( X ) \Rightarrow {\mathsf {AC}}_\omega ( X )$, and then we show it is consistent with $\mathsf {ZF}$ that there is a set 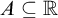$A \subseteq \mathbb {R}$ for which 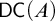$\mathsf {DC} ( A )$ holds, but 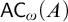${\mathsf {AC}}_\omega ( A )$ fails.

Keywords

symmetric extensioniterated symmetric extensionaxiom of choicedependent choicecountable choice

MSC classification

Primary: 03E25: Axiom of choice and related propositions
Secondary: 03E35: Consistency and independence results 03E40: Other aspects of forcing and Boolean-valued models
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andretta, A. and Ros, L. M., Souslin quasi-orders and bi-embeddability of uncountable structures . Memoirs of the American Mathematical Society , vol. 277 (2022), no. 1365, pp. vii+189.CrossRefGoogle Scholar
Jech, T., The Axiom of Choice , Studies in Logic and the Foundations of Mathematics, 75, North-Holland, Amsterdam, 1973.Google Scholar
Jech, T., Set Theory , Springer Monographs in Mathematics, Springer, Berlin, 2003, The third millennium edition, revised and expanded.Google Scholar
Kanamori, A., The Higher Infinite , second ed., Springer Monographs in Mathematics, Springer, Berlin, 2003, Large cardinals in set theory from their beginnings.Google Scholar
Karagila, A., Iterating symmetric extensions . Journal of Symbolic Logic , vol. 84 (2019), no. 1, pp. 123–159.CrossRefGoogle Scholar
Karagila, A., Iterated failures of choice, preprint, 2021, arXiv:1911.09285.Google Scholar
Miller, A. W., Long Borel hierarchies . Mathematical Logic Quarterly , vol. 54 (2008), no. 3, pp. 307–322.CrossRefGoogle Scholar
Miller, A. W., A Dedekind finite Borel set . Archive for Mathematical Logic , vol. 50 (2011), nos. 1–2, pp. 1–17.CrossRefGoogle Scholar
Monro, G. P., The cardinal equation $2m=m$ . Colloquium Mathematicum , vol. 29 (1974), pp. 1–5.CrossRefGoogle Scholar
Sageev, G., An independence result concerning the axiom of choice . Annals of Mathematical Logic , vol. 8 (1975), pp. 1–184.CrossRefGoogle Scholar
Semadeni, Z., Banach Spaces of Continuous Functions. Vol. I , Monografie Matematyczne [Mathematical Monographs], Tom 55, PWN—Polish Scientific Publishers, Warsaw, 1971.Google Scholar