Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-15T13:46:17.370Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly 2-dimensional theories

Published online by Cambridge University Press:  12 March 2014

Akito Tsuboi
Akito Tsuboi*
Affiliation:
Institute of Mathematics, University of Tsukuba, Ibaraki, 305., Japan
Get access Rights & Permissions [Opens in a new window]

Extract

In [8], we have shown the equivalence of almost strong minimality and strong unidimensionality. More precisely, we proved:

Theorem [8]. Let T be a countable stable theory. Then the following two conditions are equivalent:

(i) T is almost strongly minimal;

(ii) T can be extended to a theory such that any two nonalgebraic types are not almost orthogonal.

In the present paper, we define the notion of strong 2-dimensionality (of T). We show that if T is strongly 2-dimensional then T is ω-stable and its model has a simple structure. Roughly speaking, in a model of a strongly 2-dimensional theory, one of the following holds: (a) every element is in acl 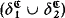(δi is strongly minimal), or (b) every element is in acl 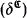(δ is strongly regular). Shelah's definition of 2-dimensionality does not imply even superstability. (See Exercise 5.5 in [6, Chapter V, §5].) We show also that condition (a) above implies strong 2-dimensionality of T. However condition (b) does not imply strong 2-dimensionality in general.

Our notations and conventions are standard. T is always countable and stable. We work in 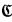. A,B,… are used to denote small subsets of 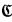. 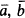, … are used to denote finite sequences of elements in 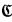. δ, φ,… are used to denote formulas (with parameters), p, q, … are used to denote types (with parameters). The fact that p is a nonforking (forking) extension of q is denoted by p ⊃nfq(p ⊃fq). If p is stationary, p∣A denotes the type in S(A) which is parallel to p. 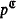(or 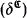) denotes the set of realizations of p (or δ). The Morley rank of p is denoted by RM(p).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 3 , September 1988 , pp. 931 - 936
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J. T. and Lachlan, A. H., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 487–493.Google Scholar
[2]Hrushovski, E. U., Countable stable unidimensional theories are superstable (to appear).Google Scholar
[3]Hrushovski, E. U., Contributions to stable model theory, Ph. D. thesis, University of California, Berkeley, California, 1986.Google Scholar
[4]Kikyo, H., A note on strongly ω-dimensional theories (to appear).Google Scholar
[5]Pillay, A., An introduction to stability theory, Oxford University Press, London, 1983.Google Scholar
[6]Poizat, B., Paires de structures stables, this Journal, vol. 48 (1983), pp. 239–249.Google Scholar
[7]Shelah, S., Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1978.Google Scholar
[8]Tsuboi, A., Categoricity and non-orthogonality of types, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 33 (1987), pp. 335–338.CrossRefGoogle Scholar