Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-01T04:51:45.278Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXPLICIT MEAN-VALUE ESTIMATE FOR THE PRIME NUMBER THEOREM IN INTERVALS

Published online by Cambridge University Press:  19 September 2023

MICHAELA CULLY-HUGILL  and
ADRIAN W. DUDEK
MICHAELA CULLY-HUGILL*
Affiliation:
School of Science, UNSW Canberra, Canberra ACT 2612, Australia
ADRIAN W. DUDEK
Affiliation:
School of Mathematics and Physics, University of Queensland, St Lucia, QLD 4072, Australia e-mail: a.dudek@uq.edu.au
*
e-mail: m.cully-hugill@adfa.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper gives an explicit version of Selberg’s mean-value estimate for the prime number theorem in intervals, assuming the Riemann hypothesis [25]. Two applications are given to short-interval results for primes and for Goldbach numbers. Under the Riemann hypothesis, we show there exists a prime in 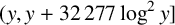$(y,y+32\,277\log ^2 y]$ for at least half the 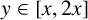$y\in [x,2x]$ for all 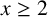$x\geq 2$, and at least one Goldbach number in 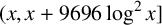$(x,x+9696 \log ^2 x]$ for all 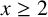$x\geq 2$.

Type
Research Article
Information
Journal of the Australian Mathematical Society , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Michael Coons

References

Brent, R. P., Platt, D. J. and Trudgian, T. S., ‘Accurate estimation of sums over zeros of the Riemann zeta-function’, Math. Comp. 90(332) (2021), 2923–2935.CrossRefGoogle Scholar
Carneiro, E., Chandee, V., Chirre, A. and Milinovich, M. B., ‘On Montgomery’s pair correlation conjecture: a tale of three integrals’, J. reine angew. Math. 786 (2022), 205–243.CrossRefGoogle Scholar
Cramér, H., ‘On the order of magnitude of the difference between consecutive prime numbers’, Acta Arith. 2(1) (1936), 23–46.CrossRefGoogle Scholar
Davenport, H., Multiplicative Number Theory, 2nd edn, Graduate Texts in Mathematics, 74 (Springer-Verlag, New York, 1980).CrossRefGoogle Scholar
Delange, H., ‘Une remarque sur la dérivée logarithmique de la fonction zêta de Riemann’, Colloq. Math. 53(2) (1987), 333–335.CrossRefGoogle Scholar
Dudek, A. W., ‘An explicit result for primes between cubes’, Funct. Approx. Comment. Math. 55(2) (2016), 177–197.CrossRefGoogle Scholar
Farmer, D. W., ‘Mean values of ${\zeta}^{\prime}/ \zeta$ and the Gaussian unitary ensemble hypothesis’, Int. Math. Res. Not. IMRN 1995(2) (1995), 71–82.CrossRefGoogle Scholar
Goldston, D. A., ‘Linnik’s theorem on Goldbach numbers in short intervals’, Glasg. Math. J. 32(3) (1990), 285–297.CrossRefGoogle Scholar
Goldston, D. A., Gonek, S. M. and Montgomery, H. L., ‘Mean values of the logarithmic derivative of the Riemann zeta-function with applications to primes in short intervals’, J. reine angew. Math. 537 (2001), 105–126.Google Scholar
Goldston, D. A., Pintz, J. and Yıldırım, C. Y., ‘Positive proportion of small gaps between consecutive primes’, Publ. Math. Debrecen 79(3–4) (2011), 433–444.CrossRefGoogle Scholar
Goldston, D. A. and Suriajaya, A. I., ‘On an average Goldbach representation formula of Fujii’, Nagoya Math. J. 250 (2023), 511–532.CrossRefGoogle Scholar
Granville, A., ‘Harald Cramér and the distribution of prime numbers’, Scand. Actuar. J. 1995(1) (1995), 12–28; Harald Cramér Symposium (Stockholm, 1993).CrossRefGoogle Scholar
Jia, C., ‘Almost all short intervals containing prime numbers’, Acta Arith. 76(1) (1996), 21–84.CrossRefGoogle Scholar
Karatsuba, A. A. and Korolëv, M. A., ‘The argument of the Riemann zeta function’, Uspekhi Mat. Nauk 60(3) (2005), 41–96.Google Scholar
Kátai, I., ‘A comment on a paper of J. V. Linnik’, Magyar Tud. Akad. Mat. Fiz. Oszt. Közl. 17 (1967), 99–100.Google Scholar
Languasco, A., ‘Some results on Goldbach’s problem’, Number Theory 53(4) (1995), 325–337; Number Theory, II (Rome, 1995).Google Scholar
Languasco, A., ‘A singular series average and Goldbach numbers in short intervals’, Acta Arith. 83(2) (1998), 171–179; doi:10.4064/aa-83-2-171-179.CrossRefGoogle Scholar
Languasco, A. and Perelli, A., ‘On Linnik’s theorem on Goldbach numbers in short intervals and related problems’, Ann. Inst. Fourier (Grenoble) 44(2) (1994), 307–322.CrossRefGoogle Scholar
Linnik, Y. V., ‘Some conditional theorems concerning the binary Goldbach problem’, Izvestiya Akad. Nauk SSSR. Ser. Mat. 16 (1952), 503–520.Google Scholar
Montgomery, H. L., ‘The pair correlation of zeros of the zeta function’, in: Analytic Number Theory St. Louis, MO, 27–30 March 1972, Proceedings of Symposia in Pure Mathematics, 24 (ed. H. G. Diamond) (American Mathematical Society, Providence, RI, 1973), 181–193.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., ‘The exceptional set in Goldbach’s problem’, Acta Arith. 27 (1975), 353–370.CrossRefGoogle Scholar
Oliveira e Silva, T., Herzog, S. and Pardi, S., ‘Empirical verification of the even Goldbach conjecture and computation of prime gaps up to $4\cdot 1{0}^{18}$ ’, Math. Comp. 83(288) (2014), 2033–2060.CrossRefGoogle Scholar
Pintz, J., ‘Cramér vs. Cramér. On Cramér’s probabilistic model for primes’, Funct. Approx. Comment. Math. 37(part 2) (2007), 361–376.CrossRefGoogle Scholar
Saffari, B. and Vaughan, R. C., ‘On the fractional parts of $x/ n$ and related sequences. II’, Ann. Inst. Fourier (Grenoble) 27(2) (1977), 1–30.CrossRefGoogle Scholar
Selberg, A., ‘On the normal density of primes in small intervals, and the difference between consecutive primes’, Arch. Math. Naturvid 47(6) (1943), 87–105.Google Scholar
Simonič, A., ‘On explicit estimates for $S(t)$ , ${S}_1(t)$ , and $\zeta \left(1/ 2+\mathrm{it}\right)$ under the Riemann Hypothesis’, J. Number Theory 231 (2022), 464–491.CrossRefGoogle Scholar
Simonič, A., ‘Estimates for L-functions in the critical strip under GRH with effective applications’, Mediterr. J. Math. 20 (2023), 87.CrossRefGoogle Scholar
Wiener, N., The Fourier Integral and Certain of its Applications (Cambridge University Press, Cambridge, 1988).CrossRefGoogle Scholar
Wolke, D., ‘On the explicit formula of Riemann–von Mangoldt, II’, J. Lond. Math. Soc. (2) 2(3) (1983), 406–416.CrossRefGoogle Scholar
Zaccagnini, A., ‘Primes in almost all short intervals’, Acta Arith. 84(3) (1998), 225–244.CrossRefGoogle Scholar
Zaccagnini, A., ‘The Selberg integral and a new pair-correlation function for the zeros of the Riemann zeta-function’, Riv. Math. Univ. Parma (N.S.) 7(1) (2016), 133–151.Google Scholar