Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-02T10:43:56.042Z Has data issue: false hasContentIssue false
  • English
  • Français

QUASI-ISOMETRIC EMBEDDINGS INAPPROXIMABLE BY ANOSOV REPRESENTATIONS

Part of: Other groups of matrices Lie groups

Published online by Cambridge University Press:  14 March 2022

Konstantinos Tsouvalas Open the ORCID record for Konstantinos Tsouvalas [Opens in a new window]
Konstantinos Tsouvalas*
Affiliation:
CNRS and Laboratoire Alexander Grothendieck, Institut des Hautes Études Scientifiques, Universite Paris-Saclay, 35 route de Chartres, 91440 Bures-sur-Yvette, France
*
tsouvkon@ihes.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct examples of quasi-isometric embeddings of word hyperbolic groups into 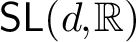$\mathsf {SL}(d,\mathbb {R})$ for 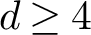$d \geq 4$ which are not limits of Anosov representations into 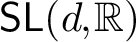$\mathsf {SL}(d,\mathbb {R})$. As a consequence, we conclude that an analogue of the density theorem for 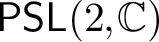$\mathsf {PSL}(2,\mathbb {C})$ does not hold for 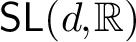$\mathsf {SL}(d,\mathbb {R})$ when 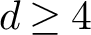$d \geq 4$.

Keywords

hyperbolic groupsAnosov representationsquasi-isometric embeddings

MSC classification

Primary: 22E40: Discrete subgroups of Lie groups
Secondary: 20H10: Fuchsian groups and their generalizations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 5 , September 2023 , pp. 2497 - 2514
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benoist, Y., Automorphismes des cônes convexes, Invent. Math. 141(1) (2000), 149–193.CrossRefGoogle Scholar
Benoist, Y., Convexes divisibles III, Ann. Sci. Éc. Norm. Supér. (4) 38(5) (2005), 793–832.CrossRefGoogle Scholar
Bestvina, M. and Feighn, M., A combination theorem for negatively curved groups, J. Differential Geom. 35(1) (1992), 85–101.CrossRefGoogle Scholar
Bochi, J., Potrie, R. and Sambarino, A., Anosov representations and dominated splittings, J. Eur. Math. Soc. (JEMS) 21(11) (2019), 3343–3414.CrossRefGoogle Scholar
Brock, J. and Bromberg, K., On the density of geometrically finite hyperbolic 3-manifolds, Acta Math. 192(1) (2004), 33–93.CrossRefGoogle Scholar
Brock, J., Canary, R. and Minsky, Y., The classification of Kleinian surface groups II: The ending lamination conjecture, Ann. Math. 176(1) (2012), 1–149.CrossRefGoogle Scholar
Canary, R. D., Epstein, D. B. A. and Green, P., Notes on notes of Thurston, in Analytical and Geometric Aspects of Hyperbolic Spaces, pp. 3–92 (Cambridge University Press, Cambridge, 1987).Google Scholar
Canary, R., Minsky, Y. and Taylor, E., Spectral theory, Hausdorff dimension and the topology of hyperbolic 3-manifolds, J. Geom. Anal. 9(1) (1999), 17–40.CrossRefGoogle Scholar
Choi, S. and Goldman, W., Convex projective structures on closed surfaces are closed, Proc. Amer. Math. Soc. 118(2) (1993), 657–661.CrossRefGoogle Scholar
Dalbo, F. and Kim, I., A criterion of conjugacy for Zariski dense subgroups, C. R. Math. Acad. Sci. Paris 330(1) (2000), 647–650.CrossRefGoogle Scholar
Guéritaud, F., Guichard, O., Kassel, F. and Wienhard, A., Anosov representations and proper actions, Geom. Topol. 21(1) (2017), 485–584.CrossRefGoogle Scholar
Guichard, O., Déformation de sous-groupes discrets de groupes de rang un, PhD thesis, Université Paris 7, 2004.Google Scholar
Guichard, O. and Wienhard, A., Anosov representations: Domains of discontinuity and applications, Invent. Math. 190(2) (2012), 357–438.CrossRefGoogle Scholar
Johnson, D. and Millson, J., Deformation spaces associated to compact hyperbolic manifolds, in Discrete Groups in Geometry and Analysis, Progress in Mathematics, 67, pp. 48–106 (Birkhäuser, Boston, MA, 1987).CrossRefGoogle Scholar
Kapovich, M., Leeb, B. and Porti, J., A Morse Lemma for quasigeodesics in symmetric spaces and Euclidean buildings, Geom. Topol. 22(7) (2018), 3827–3923.CrossRefGoogle Scholar
Kassel, F., Deformations of proper actions on homogeneous spaces, Math. Ann. 352(2) (2012), 599–632.CrossRefGoogle Scholar
Labourie, F., Anosov flows, surface groups and curves in projective space, Invent. Math. 165(1) (2006), 51–114.CrossRefGoogle Scholar
Long, D. and Reid, A., Subgroup seperability and virtual retractions of groups, Topology 47(3) (2008), 137–159.CrossRefGoogle Scholar
Morgan, J., On Thurston’s uniformization theorem for three-dimensional manifolds, in The Smith Conjecture, Pure and Applied Mathematics, 112, pp. 37–125 (Academic Press, Cambridge, MA, 1984).Google Scholar
Namazi, H. and Souto, J., Non-realizability and ending laminations: proof of the density conjecture, Acta Math. 209(2) (2012), 323–395.CrossRefGoogle Scholar
Ohshika, K., Realising end invariants by limits of minimally parabolic, geometrically finite groups, Geom. Topol. 15(2) (2011), 827–890.CrossRefGoogle Scholar
Serre, J. P., Trees and amalgams, in Trees, pp. 1-68 (Springer, Berlin, Heidelberg, 1980).Google Scholar
Thurston, W., Geometry and topology of 3-manifolds, Notes from Princeton University, Princeton, 1978.Google Scholar