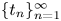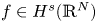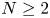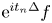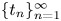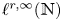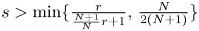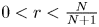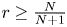1. Introduction
The solution of the Schrödinger equation

can be formally written as
where $\hat {f}(\xi )=\int _{\mathbb {R}^{N}}e^{-ix\cdot \xi }f(x)\,{\rm d}x$![]() . $e^{it\Delta }f$
. $e^{it\Delta }f$![]() is referred to as the Schrödinger mean of $f$
is referred to as the Schrödinger mean of $f$![]() at time $t$
at time $t$![]() . The problem of almost everywhere convergence as $t\rightarrow 0$
. The problem of almost everywhere convergence as $t\rightarrow 0$![]() has been studied extensively, under the assumption that $f$
has been studied extensively, under the assumption that $f$![]() belongs to the Sobolev space $H^{s}(\mathbb {R}^{N})$
belongs to the Sobolev space $H^{s}(\mathbb {R}^{N})$![]() . The a.e. convergence result holds for $s\ge 1/4$
. The a.e. convergence result holds for $s\ge 1/4$![]() when $N=1$
when $N=1$![]() by Carleson [Reference Carleson3], and for $s > \frac {N}{2(N+1)}$
by Carleson [Reference Carleson3], and for $s > \frac {N}{2(N+1)}$![]() when $N \ge 2$
when $N \ge 2$![]() by Du-Guth-Li [Reference Du, Guth and Li8] and Du-Zhang [Reference Du and Zhang9]. These results are sharp (except for the endpoints when $N\ge 2$
by Du-Guth-Li [Reference Du, Guth and Li8] and Du-Zhang [Reference Du and Zhang9]. These results are sharp (except for the endpoints when $N\ge 2$![]() ) according to Dahlberg–Kenig [Reference Dahlberg and Kenig6] and Bourgain [Reference Bourgain2]. It is worth mentioning that a different counterexample was raised by Lucà-Rogers [Reference Lucà and Rogers12] for $N \ge 2$
) according to Dahlberg–Kenig [Reference Dahlberg and Kenig6] and Bourgain [Reference Bourgain2]. It is worth mentioning that a different counterexample was raised by Lucà-Rogers [Reference Lucà and Rogers12] for $N \ge 2$![]() .
.
In this paper, we consider a related problem: to investigate the almost everywhere convergence properties of $e^{it_{n}\Delta }f$![]() , where $t_{n}$
, where $t_{n}$![]() belongs to some decreasing sequence $\{t_{n}\}_{n=1}^{\infty }$
belongs to some decreasing sequence $\{t_{n}\}_{n=1}^{\infty }$![]() converging to zero. One may expect that less regularity on $f$
converging to zero. One may expect that less regularity on $f$![]() is enough to ensure a.e. convergence along some special sequences $\{t_{n}\}_{n=1}^{\infty }$
is enough to ensure a.e. convergence along some special sequences $\{t_{n}\}_{n=1}^{\infty }$![]() , such as $t_{n} = 2^{-n},\, n \in \mathbb {N}$
, such as $t_{n} = 2^{-n},\, n \in \mathbb {N}$![]() . However, this is not always true for general discrete sequence $\{t_{n}\}_{n=1}^{\infty }$
. However, this is not always true for general discrete sequence $\{t_{n}\}_{n=1}^{\infty }$![]() . For example, when $N=1$
. For example, when $N=1$![]() and $t_{n}=1/n$
and $t_{n}=1/n$![]() , $n=1,\,2,\,\cdots$
, $n=1,\,2,\,\cdots$![]() , Carleson [Reference Carleson3] proved that the a.e. convergence result holds for $s >1/4$
, Carleson [Reference Carleson3] proved that the a.e. convergence result holds for $s >1/4$![]() but fails for $s < \frac {1}{8}$
but fails for $s < \frac {1}{8}$![]() . Indeed, it actually fails for $s < 1/4$
. Indeed, it actually fails for $s < 1/4$![]() by the counterexample in Dahlberg–Kenig [Reference Dahlberg and Kenig6]; a detailed explanation can be found in Section 3 of Lee–Rogers [Reference Lee and Rogers11]. Recently, this kind of problem was further considered by Dimou–Seeger [Reference Dimou and Seeger7] when $N=1$
by the counterexample in Dahlberg–Kenig [Reference Dahlberg and Kenig6]; a detailed explanation can be found in Section 3 of Lee–Rogers [Reference Lee and Rogers11]. Recently, this kind of problem was further considered by Dimou–Seeger [Reference Dimou and Seeger7] when $N=1$![]() , Sjölin [Reference Sjölin14] and Sjölin–Strömberg [Reference Sjölin and Strömberg15] in general dimensions. In particular, under the assumption that $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r,\infty }(\mathbb {N})$
, Sjölin [Reference Sjölin14] and Sjölin–Strömberg [Reference Sjölin and Strömberg15] in general dimensions. In particular, under the assumption that $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r,\infty }(\mathbb {N})$![]() , $0< r<\infty$
, $0< r<\infty$![]() , i.e.,
, i.e.,
it has been shown in [Reference Dimou and Seeger7] that $e^{it_{n}\Delta }f$![]() converges almost everywhere to $f$
converges almost everywhere to $f$![]() if $s \ge \min \{ \frac {r}{2r+1},\, \frac {1}{4} \}$
if $s \ge \min \{ \frac {r}{2r+1},\, \frac {1}{4} \}$![]() ; moreover in [Reference Dimou and Seeger7], this condition is also shown to be necessary under the additional assumption that $t_{n}-t_{n+1}$
; moreover in [Reference Dimou and Seeger7], this condition is also shown to be necessary under the additional assumption that $t_{n}-t_{n+1}$![]() is decreasing. By Theorem 1 in [Reference Sjölin14], the a.e. convergence results hold if $s > \min \{r,\, \frac {N}{2(N+1)}\}$
is decreasing. By Theorem 1 in [Reference Sjölin14], the a.e. convergence results hold if $s > \min \{r,\, \frac {N}{2(N+1)}\}$![]() for general dimension $N$
for general dimension $N$![]() . Theorem 3 and Corollary 6 in [Reference Sjölin and Strömberg15] imply that $s > \min \{\frac {r}{r+1},\, \frac {N}{2(N+)}\}$
. Theorem 3 and Corollary 6 in [Reference Sjölin and Strömberg15] imply that $s > \min \{\frac {r}{r+1},\, \frac {N}{2(N+)}\}$![]() suffices for a.e. convergence. In this paper, we obtain essentially sharp results in all dimensions.
suffices for a.e. convergence. In this paper, we obtain essentially sharp results in all dimensions.
1.1. Outline of this paper
We first state the main results on a.e. convergence for sequences of Schrödinger means, which are sharp (up to endpoints). Then, we obtain some generalizations to the fractional Schrödinger means $e^{it\Delta ^{\frac {a}{2}}}f$![]() ($1 < a < \infty$
($1 < a < \infty$![]() ) and nonelliptic Schrödinger means $e^{it_{n}L}f$
) and nonelliptic Schrödinger means $e^{it_{n}L}f$![]() , where
, where
and
Conventions: Throughout this article, we shall use the notation $A\gg B$![]() , which means if there is a sufficiently large constant $G$
, which means if there is a sufficiently large constant $G$![]() , which does not depend on the relevant parameters arising in the context in which the quantities $A$
, which does not depend on the relevant parameters arising in the context in which the quantities $A$![]() and $B$
and $B$![]() appear, such that $A\geq GB$
appear, such that $A\geq GB$![]() . We write $A\sim B$
. We write $A\sim B$![]() , and mean that $A$
, and mean that $A$![]() and $B$
and $B$![]() are comparable. By $A\lesssim B$
are comparable. By $A\lesssim B$![]() we mean that $A \le CB$
we mean that $A \le CB$![]() for some constant $C$
for some constant $C$![]() independent of the parameters related to $A$
independent of the parameters related to $A$![]() and $B$
and $B$![]() .
.
1.2. Almost everywhere convergence for sequences of Schrödinger means
Theorem 1.1 Let $N \ge 2$![]() and $r\in (0,\,\infty )$
and $r\in (0,\,\infty )$![]() . For any decreasing sequence $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r,\infty }(\mathbb {N})$
. For any decreasing sequence $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r,\infty }(\mathbb {N})$![]() converging to zero and $\{t_{n}\}_{n=1}^{\infty } \subset (0,\,1)$
converging to zero and $\{t_{n}\}_{n=1}^{\infty } \subset (0,\,1)$![]() , we have
, we have
whenever $f\in H^s(\mathbb {R}^N)$![]() and $s> s_{0}=\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$
and $s> s_{0}=\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$![]() .
.
By standard arguments, it is sufficient to show a corresponding maximal estimate in $\mathbb {R}^{N}$![]() .
.
Theorem 1.2 Under the assumptions of theorem 1.1, we have

whenever $f\in H^s(\mathbb {R}^N)$![]() and $s> s_{0}=\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$
and $s> s_{0}=\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$![]() , where the constant $C$
, where the constant $C$![]() does not depend on $f$
does not depend on $f$![]() .
.
By translation invariance in the $x$![]() -direction, $B(0,\,1)$
-direction, $B(0,\,1)$![]() in theorem 1.2 can be replaced by any ball of radius $1$
in theorem 1.2 can be replaced by any ball of radius $1$![]() in $\mathbb {R}^{N}$
in $\mathbb {R}^{N}$![]() , which implies theorem 1.1. The a.e. convergence result is almost sharp by the Nikisin–Stein maximal principle and the fact that theorem 1.2 is sharp up to the endpoints.
, which implies theorem 1.1. The a.e. convergence result is almost sharp by the Nikisin–Stein maximal principle and the fact that theorem 1.2 is sharp up to the endpoints.
Theorem 1.3 For each $r \in (0,\,\infty )$![]() , there exists a sequence $\{t_n\}_{n=1}^{\infty }$
, there exists a sequence $\{t_n\}_{n=1}^{\infty }$![]() which belongs to ${\ell }^{r,\infty }(\mathbb {N})$
which belongs to ${\ell }^{r,\infty }(\mathbb {N})$![]() , for which the maximal estimate (1.7) fails if $s< s_{0}=\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$
, for which the maximal estimate (1.7) fails if $s< s_{0}=\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$![]() .
.
Remark 1.4 One expects that the sparser the time sequences become, the lower the regularity of almost everywhere convergence requires. Theorems 1.2 and 1.3 reveal a perhaps surprising phenomenon, namely if $0< r<\frac {N}{N+1}$![]() , there is a gain over the almost everywhere convergence result from [Reference Bourgain2, Reference Du, Guth and Li8, Reference Du and Zhang9, Reference Lucà and Rogers12] when time tends continuously to zero, but not when $r\geq \frac {N}{N+1}$
, there is a gain over the almost everywhere convergence result from [Reference Bourgain2, Reference Du, Guth and Li8, Reference Du and Zhang9, Reference Lucà and Rogers12] when time tends continuously to zero, but not when $r\geq \frac {N}{N+1}$![]() . In fact this phenomenon already appeared in the one-dimensional case [Reference Dimou and Seeger7].
. In fact this phenomenon already appeared in the one-dimensional case [Reference Dimou and Seeger7].
Our counterexample is presented in § 3. The construction is inspired by the work [Reference Lucà and Rogers12], which is an alternative proof for Bourgain's counterexample that showed the necessary condition for $\lim _{t\rightarrow 0}e^{it\Delta }f(x)=f(x)$![]() , a.e. $x\in \mathbb {R}^N$
, a.e. $x\in \mathbb {R}^N$![]() .
.
Next, we briefly explain how to prove theorem 1.2. Notice that when $\frac {r}{\frac {N+1}{N}r+1} \ge \frac {N}{2(N+1)}$![]() , theorem 1.2 follows from the celebrated results by [Reference Du, Guth and Li8] ($N=2$
, theorem 1.2 follows from the celebrated results by [Reference Du, Guth and Li8] ($N=2$![]() ), and [Reference Du and Zhang9] ($N \ge 3$
), and [Reference Du and Zhang9] ($N \ge 3$![]() ). Therefore, we only need to consider the case when $\frac {r}{\frac {N+1}{N}r+1} < \frac {N}{2(N+1)}$
). Therefore, we only need to consider the case when $\frac {r}{\frac {N+1}{N}r+1} < \frac {N}{2(N+1)}$![]() , so we always assume that $0< r < \frac {N}{N+1}$
, so we always assume that $0< r < \frac {N}{N+1}$![]() in what follows.
in what follows.
By Littlewood–Paley decomposition and standard arguments, we just concentrate on the case when ${\rm supp}\hat {f} \subset \{\xi : |\xi | \sim 2^{k}\}$![]() , $k \gg 1$
, $k \gg 1$![]() . We consider the maximal functions
. We consider the maximal functions
and
We deal with the first term by the assumption that the decreasing sequence $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r,\infty }(\mathbb {N})$![]() and Plancherel's theorem. For the second term, since $k< \frac {2k}{\frac {N+1}{N}r+1}< 2k$
and Plancherel's theorem. For the second term, since $k< \frac {2k}{\frac {N+1}{N}r+1}< 2k$![]() , the proof can be completed by the following theorem.
, the proof can be completed by the following theorem.
Theorem 1.5 Let $j \in \mathbb {R}$![]() with $k < j < 2k$
with $k < j < 2k$![]() . For any $\epsilon >0$
. For any $\epsilon >0$![]() , there exists a constant $C_{\epsilon } >0$
, there exists a constant $C_{\epsilon } >0$![]() such that
such that

for all $f$![]() with supp $\hat {f} \subset \{\xi : |\xi | \sim 2^{k}\}$
with supp $\hat {f} \subset \{\xi : |\xi | \sim 2^{k}\}$![]() . The constant $C_{\epsilon }$
. The constant $C_{\epsilon }$![]() does not depend on $f$
does not depend on $f$![]() , $j$
, $j$![]() and $k$
and $k$![]() .
.
In the case $N=1$![]() , a similar result was proved in [Reference Dimou and Seeger7] by the $TT^{*}$
, a similar result was proved in [Reference Dimou and Seeger7] by the $TT^{*}$![]() argument and stationary phase method. But their method seems not to work well in the higher dimensional case. In order to prove theorem 1.5, we first observe that (1.8) holds true if the spatial variable is restricted to a ball of radius $2^{k-j}$
argument and stationary phase method. But their method seems not to work well in the higher dimensional case. In order to prove theorem 1.5, we first observe that (1.8) holds true if the spatial variable is restricted to a ball of radius $2^{k-j}$![]() . Due to references [Reference Du, Guth and Li8, Reference Du and Zhang9], for any function $g$
. Due to references [Reference Du, Guth and Li8, Reference Du and Zhang9], for any function $g$![]() with supp $\hat {g} \subset \{\xi : |\xi | \sim 2^{2k-j}\}$
with supp $\hat {g} \subset \{\xi : |\xi | \sim 2^{2k-j}\}$![]() , there holds
, there holds

By scaling, we have

whenever supp $\hat {g} \subset \{\xi : |\xi | \sim 2^{k}\}$![]() . Then, we obtain the following lemma by translation invariance in the $x$
. Then, we obtain the following lemma by translation invariance in the $x$![]() -direction.
-direction.
Lemma 1.6 When $k < j < 2k$![]() , for any $\epsilon >0$
, for any $\epsilon >0$![]() and $x_{0} \in \mathbb {R}^{N}$
and $x_{0} \in \mathbb {R}^{N}$![]() , there exists a constant $C_{\epsilon } >0$
, there exists a constant $C_{\epsilon } >0$![]() such that
such that

whenever supp $\hat {f} \subset \{\xi : |\xi | \sim 2^{k}\}$![]() . The constant $C_{\epsilon }$
. The constant $C_{\epsilon }$![]() does not depend on $x_{0}$
does not depend on $x_{0}$![]() and $f$
and $f$![]() .
.
Then we can obtain theorem 1.5 with the help of lemma 1.6, wave packets decomposition and an orthogonality argument. See § 2 for details. Moreover, we give the following remark on theorem 1.5.
Remark 1.7 We notice that theorem 1.5 is almost sharp when $j=k$![]() and $j=2k$
and $j=2k$![]() . Indeed, when $j = 2k$
. Indeed, when $j = 2k$![]() , Sobolev's embedding implies
, Sobolev's embedding implies

By taking $\hat {f}$![]() as the characteristic function on the set $\{\xi : |\xi | \sim 2^{k}\}$
as the characteristic function on the set $\{\xi : |\xi | \sim 2^{k}\}$![]() , it can be observed that the uniform estimate (1.11) is optimal. When $j = k$
, it can be observed that the uniform estimate (1.11) is optimal. When $j = k$![]() , it follows from [Reference Du, Guth and Li8, Reference Du and Zhang9] that
, it follows from [Reference Du, Guth and Li8, Reference Du and Zhang9] that

The above inequality (1.12) is sharp up to the endpoints according to the counterexample in [Reference Bourgain2] or [Reference Lucà and Rogers12]. However, the presence of $2^{\epsilon k}$![]() on the right-hand side of inequality (1.8) leads us to lose the endpoint results in theorem 1.2.
on the right-hand side of inequality (1.8) leads us to lose the endpoint results in theorem 1.2.
1.3. Related generalizations
The method we adopted to prove theorem 1.2 can be generalized to the fractional case and the nonelliptic case. Then, the corresponding a.e. convergence results follow. We omit most of details of the proof because they are very similar with that of theorem 1.2. Moreover, the sharpness of the result for the nonelliptic case will be proved in § 4.
Firstly, for the fractional case, we have the following maximal estimate. When $a =2$![]() , it coincides with theorem 1.2.
, it coincides with theorem 1.2.
Theorem 1.8 Under the conditions of theorem 1.2, for $1 < a < \infty$![]() , we have
, we have

whenever $f\in H^s(\mathbb {R}^N)$![]() and $s> s_{0}=\min \{\frac {a}{2} \cdot \frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$
and $s> s_{0}=\min \{\frac {a}{2} \cdot \frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\}$![]() , where the constant $C$
, where the constant $C$![]() does not depend on $f$
does not depend on $f$![]() .
.
We now consider maximal estimates for the nonelliptic Schrödinger means, as defined in (1.5). The following result is sharp up to the endpoints, as will be shown in § 4 below.
Theorem 1.9 Under the conditions of theorem 1.2, we have

whenever $f\in H^s(\mathbb {R}^N)$![]() and $s >s_{0} = \min \{\frac {r}{r+1},\, \frac {1}{2}\}$
and $s >s_{0} = \min \{\frac {r}{r+1},\, \frac {1}{2}\}$![]() , where the constant $C$
, where the constant $C$![]() does not depend on $f$
does not depend on $f$![]() .
.
The proof of theorem 1.9 depends heavily on the following theorem.
Theorem 1.10 If supp $\hat {f} \subset \{\xi : |\xi | \sim \lambda \}$![]() , $\lambda \ge 1$
, $\lambda \ge 1$![]() , then for any interval $I$
, then for any interval $I$![]() with $\lambda ^{-2} \le |I| \le \lambda ^{-1},$
with $\lambda ^{-2} \le |I| \le \lambda ^{-1},$![]() we have
we have

where the constant $C$![]() does not depend on $f$
does not depend on $f$![]() .
.
Theorem 1.10 follows directly from Sobolev's embedding. Specially, theorem 1.10 is sharp when $|I|= \lambda ^{-1}$![]() according to the counterexample in Rogers–Vargas–Vega [Reference Rogers, Vargas and Vega13]. When $|I|= \lambda ^{-2}$
according to the counterexample in Rogers–Vargas–Vega [Reference Rogers, Vargas and Vega13]. When $|I|= \lambda ^{-2}$![]() , the sharpness can be proved by taking $\tilde {f}$
, the sharpness can be proved by taking $\tilde {f}$![]() as the characteristic function over the annulus $\{\xi : |\xi | \sim \lambda \}$
as the characteristic function over the annulus $\{\xi : |\xi | \sim \lambda \}$![]() . We point out that the sharpness of theorem 1.10 enables us to apply the similar decomposition as Proposition 2.3 in [Reference Dimou and Seeger7] to get a stronger result than theorem 1.9 when $r \in (0,\,1)$
. We point out that the sharpness of theorem 1.10 enables us to apply the similar decomposition as Proposition 2.3 in [Reference Dimou and Seeger7] to get a stronger result than theorem 1.9 when $r \in (0,\,1)$![]() .
.
Theorem 1.11 If $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r(s),\infty }(\mathbb {N})$![]() , $r(s)= \frac {s}{1-s}$
, $r(s)= \frac {s}{1-s}$![]() . Then for any $0< s <\frac {1}{2}$
. Then for any $0< s <\frac {1}{2}$![]() , we have
, we have

whenever $f\in H^s(\mathbb {R}^N)$![]() , where the constant $C$
, where the constant $C$![]() does not depend on $f$
does not depend on $f$![]() .
.
Remark 1.12 In table 1, we synthesize our theorems and all results to our best knowledge, and list all almost sharp requirements of regularity on a.e. convergence for different Schrödinger-type operators. We also notice that some results in the table 1 come from theorems 1.1, 1.8, 1.9 and 1.11 in this paper. For the remaining results, readers can refer to the relevant results of the nonelliptic Schrödinger operators in [Reference Rogers, Vargas and Vega13]; the conclusions about the fractional Schrödinger operators when $t$![]() continuously tends to $0$
continuously tends to $0$![]() can be found in [Reference Cho and Ko4] ($a > 1$
can be found in [Reference Cho and Ko4] ($a > 1$![]() ) and [Reference Walther16] ($0 < a <1$
) and [Reference Walther16] ($0 < a <1$![]() ); other results were introduced at the beginning of the introduction and will not be repeated here.
); other results were introduced at the beginning of the introduction and will not be repeated here.
Table 1. A summary of a.e. convergence for some Schrödinger operators.

Remark 1.13 Shortly after our paper was posted on arXiv.org in July 2022, Cho, Ko, Koh and Lee posted a paper with partially overlapping results, which has now been published in [Reference Cho, Ko, Koh and Lee5].
2. Proof of theorems 1.2 and 1.5
Proof of theorem 1.2 Let $s_{1}=\frac {r}{\frac {N+1}{N}r+1} + \epsilon$![]() for some constant $\epsilon >0$
for some constant $\epsilon >0$![]() . We decompose $f$
. We decompose $f$![]() as $f=\sum _{k=0}^{\infty }{f_{k}},$
as $f=\sum _{k=0}^{\infty }{f_{k}},$![]() where ${\rm supp} \hat {f_{0}} \subset B(0,\,1)$
where ${\rm supp} \hat {f_{0}} \subset B(0,\,1)$![]() , ${\rm supp} \hat {f_{k}} \subset \{\xi : |\xi | \sim 2^{k}\},\, k \ge 1$
, ${\rm supp} \hat {f_{k}} \subset \{\xi : |\xi | \sim 2^{k}\},\, k \ge 1$![]() . Then, we have
. Then, we have

For $k \lesssim 1$![]() and arbitrary $x \in B(0,\,1)$
and arbitrary $x \in B(0,\,1)$![]() , $|e^{it_{n}\Delta }f_{k}(x)| \lesssim \|f_{k}\|_{L^{2}(\mathbb {R}^{N})}$
, $|e^{it_{n}\Delta }f_{k}(x)| \lesssim \|f_{k}\|_{L^{2}(\mathbb {R}^{N})}$![]() , it is obvious that
, it is obvious that

For each $k \gg 1$![]() , we decompose $\{t_{n}\}_{n=1}^{\infty }$
, we decompose $\{t_{n}\}_{n=1}^{\infty }$![]() as
as
and
Then, we have

We first estimate $I$![]() . Since $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r,\infty }(\mathbb {N})$
. Since $\{t_{n}\}_{n=1}^{\infty } \in {\ell }^{r,\infty }(\mathbb {N})$![]() , we have
, we have
which implies that

For $II$![]() , since
, since
By previous discussion, we have $k<\frac {2k}{\frac {N+1}{N}r+1}<2k.$![]() Then it follows from theorem 1.5 that,
Then it follows from theorem 1.5 that,
Inequalities (2.3), (2.5), and (2.6) yield for $k \gg 1$![]() ,
,

Combining inequalities (2.1), (2.2), and (2.7), inequality (1.7) holds true for $s_1$![]() . Because $\epsilon > 0$
. Because $\epsilon > 0$![]() , we have finished the proof of theorem 1.2. It remains to prove theorem 1.5.
, we have finished the proof of theorem 1.2. It remains to prove theorem 1.5.
Proof of theorem 1.5 We use a wave packets decomposition and an orthogonality argument to prove theorem 1.5.
$\bullet$![]() Wave packets decomposition.
Wave packets decomposition.
We first decompose $e^{it\Delta }f$![]() on $B(0,\,1) \times (0,\,2^{-j})$
on $B(0,\,1) \times (0,\,2^{-j})$![]() in a standard way. For this goal, we decompose the annulus $\{\xi : |\xi | \sim 2^{k}\}$
in a standard way. For this goal, we decompose the annulus $\{\xi : |\xi | \sim 2^{k}\}$![]() into almost disjoint $2^{j-k}$
into almost disjoint $2^{j-k}$![]() -cubes $\theta$
-cubes $\theta$![]() with sides parallel to the coordinate axes in $\mathbb {R}^{N}$
with sides parallel to the coordinate axes in $\mathbb {R}^{N}$![]() . Let $2^{k-j}$
. Let $2^{k-j}$![]() -cube $\nu$
-cube $\nu$![]() be dual to $\theta$
be dual to $\theta$![]() and cover $\mathbb {R}^{N}$
and cover $\mathbb {R}^{N}$![]() by almost disjoint cubes $\nu$
by almost disjoint cubes $\nu$![]() . Denote the centre of $\theta$
. Denote the centre of $\theta$![]() by $c(\theta )$
by $c(\theta )$![]() and the centre of $\nu$
and the centre of $\nu$![]() by $c(\nu )$
by $c(\nu )$![]() . We notice that if $\nu \neq \nu ^{\prime }$
. We notice that if $\nu \neq \nu ^{\prime }$![]() , then $|c(\nu ) - c(\nu ^{\prime })| \ge 2^{k-j}$
, then $|c(\nu ) - c(\nu ^{\prime })| \ge 2^{k-j}$![]() .
.
Let $\varphi$![]() be a Schwartz function defined on $\mathbb {R}^{N}$
be a Schwartz function defined on $\mathbb {R}^{N}$![]() whose fourier transform is non-negative and supported in a small neighbourhood of the origin, and identically equal to $1$
whose fourier transform is non-negative and supported in a small neighbourhood of the origin, and identically equal to $1$![]() in another smaller ball centred at the origin. Let $\widehat {\varphi _{\theta }}(\xi ) = 2^{-\frac {(j-k)N}{2}} \hat {\varphi }(\frac {\xi - c(\theta )}{2^{j-k}})$
in another smaller ball centred at the origin. Let $\widehat {\varphi _{\theta }}(\xi ) = 2^{-\frac {(j-k)N}{2}} \hat {\varphi }(\frac {\xi - c(\theta )}{2^{j-k}})$![]() and $\widehat {\varphi _{\theta, \nu }}(\xi )= e^{-ic(\nu ) \cdot \xi } \widehat {\varphi _{\theta }}(\xi )$
and $\widehat {\varphi _{\theta, \nu }}(\xi )= e^{-ic(\nu ) \cdot \xi } \widehat {\varphi _{\theta }}(\xi )$![]() . Then $f$
. Then $f$![]() can be decomposed by
can be decomposed by
and
When $t \in (0,\,2^{-j})$![]() , integration by parts implies
, integration by parts implies

Here, $M$![]() can be sufficiently large. Therefore, $e^{it\Delta } \varphi _{\theta,\nu }(x)$
can be sufficiently large. Therefore, $e^{it\Delta } \varphi _{\theta,\nu }(x)$![]() is essentially supported in a tube
is essentially supported in a tube
where $\delta =\epsilon ^3$![]() . The direction of $T_{\theta, \nu }$
. The direction of $T_{\theta, \nu }$![]() is parallel to the vector $(-2c(\theta ),\, 1)$
is parallel to the vector $(-2c(\theta ),\, 1)$![]() , and the angle between $(-2c(\theta ),\, 1)$
, and the angle between $(-2c(\theta ),\, 1)$![]() and the $x$
and the $x$![]() -plane is approximately $2^{-k}$
-plane is approximately $2^{-k}$![]() .
.
$\bullet$![]() Orthogonality argument.
Orthogonality argument.
We decompose $B(0,\,1)$![]() by $B(0,\,1) = \cup _{\nu ^{\prime }} B(c( \nu ^{\prime }),\, 2^{k-j})$
by $B(0,\,1) = \cup _{\nu ^{\prime }} B(c( \nu ^{\prime }),\, 2^{k-j})$![]() with $|c(\nu ^{\prime })| \lesssim 1$
with $|c(\nu ^{\prime })| \lesssim 1$![]() . Then
. Then

We will consider two cases: (i) $j < k+\frac {\epsilon k}{N}$![]() and (ii) $j \geq k+\frac {\epsilon k}{N}$
and (ii) $j \geq k+\frac {\epsilon k}{N}$![]() , respectively. In case (i), let $j=k+\epsilon _0k$
, respectively. In case (i), let $j=k+\epsilon _0k$![]() , $0<\epsilon _0<\frac {\epsilon }{N}$
, $0<\epsilon _0<\frac {\epsilon }{N}$![]() , by lemma 1.6,
, by lemma 1.6,

We use an orthogonality argument in the proof of case (ii). Fix $c(\nu ^{\prime })$![]() , we divide $f$
, we divide $f$![]() into two terms
into two terms
and
For $f_{1}$![]() , by lemma 1.6 and the $L^{2}$
, by lemma 1.6 and the $L^{2}$![]() -orthogonality, we have
-orthogonality, we have

We will complete the proof by showing that the contribution from $|e^{it\Delta }f_{2}|$![]() is negligible when $(x,\,t)$
is negligible when $(x,\,t)$![]() belongs to $B(c(\nu ^{\prime }),\, 2^{k-j}) \times (0,\,2^{-j})$
belongs to $B(c(\nu ^{\prime }),\, 2^{k-j}) \times (0,\,2^{-j})$![]() .
.
Indeed, by the Cauchy–Schwarz inequality and the $L^{2}$![]() -orthogonality, there holds
-orthogonality, there holds

For each $\theta$![]() , $|x- c(\nu ) + 2t c(\theta )| \ge |c(\nu ) -c(\nu ^{\prime })|/2$
, $|x- c(\nu ) + 2t c(\theta )| \ge |c(\nu ) -c(\nu ^{\prime })|/2$![]() , then we have
, then we have

Notice that the number of $\theta$![]() 's is dominated by $2^{Nk}$
's is dominated by $2^{Nk}$![]() . So by choosing $M$
. So by choosing $M$![]() sufficiently large, for each $(x,\,t) \in B(c(\nu ^{\prime }),\, 2^{k-j}) \times (0,\,2^{-j})$
sufficiently large, for each $(x,\,t) \in B(c(\nu ^{\prime }),\, 2^{k-j}) \times (0,\,2^{-j})$![]() , we have
, we have
Then, the proof is finished since

3. A counterexample: theorem 1.3
We notice that the counterexample for $r=\frac {N}{N+1}$![]() can be also applied to the case when $r > \frac {N}{N+1}$
can be also applied to the case when $r > \frac {N}{N+1}$![]() , since ${\ell }^{N/(N+1),\infty }(\mathbb {N}) \subset {\ell }^{r,\infty }(\mathbb {N})$
, since ${\ell }^{N/(N+1),\infty }(\mathbb {N}) \subset {\ell }^{r,\infty }(\mathbb {N})$![]() and $\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\} = \frac {N}{2(N+1)}$
and $\min \{\frac {r}{\frac {N+1}{N}r+1},\, \frac {N}{2(N+1)}\} = \frac {N}{2(N+1)}$![]() when $r > \frac {N}{N+1}$
when $r > \frac {N}{N+1}$![]() . Therefore, next we always assume $r \in (0,\, \frac {N}{N+1}]$
. Therefore, next we always assume $r \in (0,\, \frac {N}{N+1}]$![]() .
.
Fix $r \in (0,\, \frac {N}{N+1}]$![]() , we first construct a sequence which belongs to ${\ell }^{r,\infty }(\mathbb {N})$
, we first construct a sequence which belongs to ${\ell }^{r,\infty }(\mathbb {N})$![]() . Put $\beta = \frac {2}{\frac {N+1}{N}r+1}$
. Put $\beta = \frac {2}{\frac {N+1}{N}r+1}$![]() . Let $R_{1}=2$
. Let $R_{1}=2$![]() and for each positive integer $n$
and for each positive integer $n$![]() , $R_{n+1}^{-\beta } \le \frac {1}{2} R_{n}^{-\beta (r+1)}$
, $R_{n+1}^{-\beta } \le \frac {1}{2} R_{n}^{-\beta (r+1)}$![]() . Denote the intervals $I_{n}=[R_{n}^{-\beta (r+1)},\, R_{n}^{-\beta })$
. Denote the intervals $I_{n}=[R_{n}^{-\beta (r+1)},\, R_{n}^{-\beta })$![]() , $n \in \mathbb {N}^+$
, $n \in \mathbb {N}^+$![]() . On each $I_{n}$
. On each $I_{n}$![]() , we get an equidistributed subsequence $t_{n_{j}},\, j =1,\, 2,\,...,\, j_{n}$
, we get an equidistributed subsequence $t_{n_{j}},\, j =1,\, 2,\,...,\, j_{n}$![]() such that
such that
and $t_{n_{j}} - t_{n_{j+1}} = R_{n}^{-\beta (r+1)}$![]() . We claim that the sequence $t_{n_{j}},\, j=1,\,2,\,...,\,j_{n},\, n=1,\,2,\,...$
. We claim that the sequence $t_{n_{j}},\, j=1,\,2,\,...,\,j_{n},\, n=1,\,2,\,...$![]() belongs to ${\ell }^{r,\infty }(\mathbb {N})$
belongs to ${\ell }^{r,\infty }(\mathbb {N})$![]() .
.
Indeed, according to Lemma 3.2 from [Reference Dimou and Seeger7], it suffices to show that
Notice that we only need to consider $0 < b <1$![]() because $t_{n_{j}} \in (0,\,1)$
because $t_{n_{j}} \in (0,\,1)$![]() for each $n$
for each $n$![]() and $j$
and $j$![]() . Assume that $(b,\, 2b] \cap I_{n} \neq \emptyset$
. Assume that $(b,\, 2b] \cap I_{n} \neq \emptyset$![]() for some $n$
for some $n$![]() , then we have $b < R_{n}^{-\beta }$
, then we have $b < R_{n}^{-\beta }$![]() , $2b \ge R_{n}^{-\beta (r+1)}.$
, $2b \ge R_{n}^{-\beta (r+1)}.$![]() Therefore,
Therefore,
This yields $(b,\, 2b] \cap I_{n^{\prime }} = \emptyset$![]() for any $n^{\prime } \neq n$
for any $n^{\prime } \neq n$![]() , hence
, hence
Then (3.1) follows by the arbitrariness of $b$![]() .
.
Our counterexample comes from the following lemma.
Lemma 3.1 Let $R \gg 1$![]() and $I=[R^{-\beta (r+1)},\, R^{-\beta })$
and $I=[R^{-\beta (r+1)},\, R^{-\beta })$![]() . Assume that the sequence $\{ t_{j} : 1 \le j \le j_{0}\} = R^{-\beta (r+1)}\mathbb {Z} \cap I$
. Assume that the sequence $\{ t_{j} : 1 \le j \le j_{0}\} = R^{-\beta (r+1)}\mathbb {Z} \cap I$![]() and $t_{j} - t_{j+1} = R^{-\beta (r+1)}$
and $t_{j} - t_{j+1} = R^{-\beta (r+1)}$![]() for each $1 \le j \le j_{0}-1$
for each $1 \le j \le j_{0}-1$![]() . Then there exists a function $f$
. Then there exists a function $f$![]() with supp $\hat {f} \subset B(0,\,2R)$
with supp $\hat {f} \subset B(0,\,2R)$![]() such that
such that

and
Here, $\epsilon$![]() is any positive number.
is any positive number.
We use lemma 3.1 to show the counterexample here and prove the lemma a moment later. Assume that the maximal estimate

holds for some $s >0$![]() and each $f \in H^{s}(\mathbb {R}^{N})$
and each $f \in H^{s}(\mathbb {R}^{N})$![]() , then for each $n \in \mathbb {N}^+$
, then for each $n \in \mathbb {N}^+$![]() , we have
, we have

whenever $f \in H^{s}(\mathbb {R}^{N})$![]() . Lemma 3.1 and inequality (3.5) yield
. Lemma 3.1 and inequality (3.5) yield
Then, we have $s \ge \frac {r}{\frac {N+1}{N}r +1}$![]() , since $R_{n}$
, since $R_{n}$![]() can be sufficiently large and $\epsilon$
can be sufficiently large and $\epsilon$![]() is arbitrarily small. Finally, we obtain a sequence $\frac {t_{n_{j}}}{2\pi },\, j=1,\,2,\,...,\,j_{n},\, n=1,\,2,\,... \in {\ell }^{r,\infty }(\mathbb {N})$
is arbitrarily small. Finally, we obtain a sequence $\frac {t_{n_{j}}}{2\pi },\, j=1,\,2,\,...,\,j_{n},\, n=1,\,2,\,... \in {\ell }^{r,\infty }(\mathbb {N})$![]() such that the maximal estimate (3.4) holds only if $s \ge \frac {r}{\frac {N+1}{N}r +1}$
such that the maximal estimate (3.4) holds only if $s \ge \frac {r}{\frac {N+1}{N}r +1}$![]() .
.
In the rest of this section, we prove lemma 3.1. Setting

then we define $\hat {f_{1}}(\xi _{1}) = \hat {h}(\xi _{1} + \pi R)$![]() , $\hat {f_{2}}(\bar {\xi }) = \hat {g} (\bar {\xi } + \pi R\theta )$
, $\hat {f_{2}}(\bar {\xi }) = \hat {g} (\bar {\xi } + \pi R\theta )$![]() , where $\hat {h} = \chi _{\Omega _{1} }$
, where $\hat {h} = \chi _{\Omega _{1} }$![]() , $\hat {g} = \chi _{\Omega _{2}}$
, $\hat {g} = \chi _{\Omega _{2}}$![]() , and some $\theta \in \mathbb {S}^{N-2}$
, and some $\theta \in \mathbb {S}^{N-2}$![]() (when $N=2$
(when $N=2$![]() , $\theta \in (0,\,1)$
, $\theta \in (0,\,1)$![]() ) which will be determined later. Define $f$
) which will be determined later. Define $f$![]() by $\hat {f} = \hat {f_{1}}\hat {f_{2}}$
by $\hat {f} = \hat {f_{1}}\hat {f_{2}}$![]() , it is easy to check that $f$
, it is easy to check that $f$![]() satisfies (3.3). We are left to prove that inequality (3.2) holds for such $f$
satisfies (3.3). We are left to prove that inequality (3.2) holds for such $f$![]() . Notice that
. Notice that
We first consider $|e^{i\frac {t_{j}}{2\pi }\Delta }f_{1}(x_{1})|$![]() . A change of variables implies
. A change of variables implies
It is easy to check that $|e^{i\frac {t_{j}}{2\pi }\Delta }h(x_{1})| \gtrsim |\Omega _{1}|$![]() for each $j$
for each $j$![]() whenever $|x_{1}| \le R^{-\frac {\beta }{2}}$
whenever $|x_{1}| \le R^{-\frac {\beta }{2}}$![]() . Note that for each $x_{1} \in (0,\, R^{1-\beta })$
. Note that for each $x_{1} \in (0,\, R^{1-\beta })$![]() , there exists at least one $t_{j}$
, there exists at least one $t_{j}$![]() such that $|x_{1}- Rt_{j}| \le R^{1-\beta (r+1)} \le R^{-\frac {\beta }{2}}$
such that $|x_{1}- Rt_{j}| \le R^{1-\beta (r+1)} \le R^{-\frac {\beta }{2}}$![]() since $\{t_j\}_{j=1}^{j_0}\subset [R^{-\beta (r+1)},\,R^{-\beta })$
since $\{t_j\}_{j=1}^{j_0}\subset [R^{-\beta (r+1)},\,R^{-\beta })$![]() and $t_j-t_{j+1}=R^{-\beta (r+1)}$
and $t_j-t_{j+1}=R^{-\beta (r+1)}$![]() . Hence, we have
. Hence, we have
whenever $x_{1} \in (0,\, \frac {1}{2}R^{1-\beta })$![]() and $Rt_{j} \in (x_{1},\, x_{1} + R^{-\frac {\beta }{2}})$
and $Rt_{j} \in (x_{1},\, x_{1} + R^{-\frac {\beta }{2}})$![]() .
.
For $|e^{i\frac {t_{j}}{2\pi }\Delta }f_{2}(\bar {x})|$![]() , we have
, we have
According to Barceló–Bennett–Carbery–Ruiz–Vilela [Reference Barceló, Bennett, Carbery, Ruiz and Vilela1], for each $j$![]() and $\bar {x} \in U_{0}$
and $\bar {x} \in U_{0}$![]() ,
,
here
We sketch the main idea of the proof of inequality (3.9) for the reader's convenience. Indeed, for each $\bar {\xi } \in \Omega _{2}$![]() , we write $\bar {\xi } = 2 \pi R^{\frac {(r+1)\beta }{2}}l + \bar {\eta }$
, we write $\bar {\xi } = 2 \pi R^{\frac {(r+1)\beta }{2}}l + \bar {\eta }$![]() , $l \in \mathbb {Z}^{N-1}$
, $l \in \mathbb {Z}^{N-1}$![]() , $2\pi |l| \le R^{1-\frac {(r+1)\beta }{2}-\epsilon }$
, $2\pi |l| \le R^{1-\frac {(r+1)\beta }{2}-\epsilon }$![]() , $\bar {\eta } \in B(0,\, \frac {1}{1000})$
, $\bar {\eta } \in B(0,\, \frac {1}{1000})$![]() . Then for any $\bar {x}_{m}= R^{-\frac {(r+1)\beta }{2}}m$
. Then for any $\bar {x}_{m}= R^{-\frac {(r+1)\beta }{2}}m$![]() , $m \in \mathbb {Z}^{N-1}$
, $m \in \mathbb {Z}^{N-1}$![]() , $|m| \le 2 R^{\frac {(r+1)\beta }{2}}$
, $|m| \le 2 R^{\frac {(r+1)\beta }{2}}$![]() , $t_{j} = R^{-(r+1)\beta }(j_0+1-j)$
, $t_{j} = R^{-(r+1)\beta }(j_0+1-j)$![]() , $1 \le j \le j_{0}$
, $1 \le j \le j_{0}$![]() , we have
, we have

Noting that $|\bar {x}_{m}| \le 2$![]() , $|t_{j}| \le R^{-\beta }$
, $|t_{j}| \le R^{-\beta }$![]() and $|\bar {\eta }| \le \frac {1}{1000}$
and $|\bar {\eta }| \le \frac {1}{1000}$![]() imply
imply
then, we have
Moreover, for each $\bar {x} \in U_{0}$![]() , there exits an $\bar {x}_{m}$
, there exits an $\bar {x}_{m}$![]() such that $|\bar {x} - \bar {x}_{m}| \le \frac {1}{1000} R^{-1 + \epsilon }$
such that $|\bar {x} - \bar {x}_{m}| \le \frac {1}{1000} R^{-1 + \epsilon }$![]() , by the mean value theorem and the fact that $|\bar {\xi }| \le 2R^{1-\epsilon }$
, by the mean value theorem and the fact that $|\bar {\xi }| \le 2R^{1-\epsilon }$![]() ,
,
Finally, we arrive at inequality (3.9) by the triangle inequality.
Therefore, we have
Set $U_{x_{1}} = \bigcup _{j: Rt_{j} \in R^{1-(r+1)\beta }\mathbb {Z} \cap (x_{1},\, x_{1} + R^{-\beta /2}) } U_{0} + Rt_{j} \theta$![]() . Then inequalities (3.8) and (3.10) imply that for each $x_{1} \in (0,\, \frac {1}{2}R^{1-\beta })$
. Then inequalities (3.8) and (3.10) imply that for each $x_{1} \in (0,\, \frac {1}{2}R^{1-\beta })$![]() and $\bar {x} \in U_{x_{1}}$
and $\bar {x} \in U_{x_{1}}$![]() , there holds
, there holds
Next, we need to select a $\theta \in \mathbb {S}^{N-2}$![]() , such that $|U_{x_{1}}| \gtrsim 1$
, such that $|U_{x_{1}}| \gtrsim 1$![]() for each $x_{1} \in (0,\, \frac {1}{2} R^{1-\beta })$
for each $x_{1} \in (0,\, \frac {1}{2} R^{1-\beta })$![]() , which follows if we can prove that there exists a $\theta \in \mathbb {S}^{N-2}$
, which follows if we can prove that there exists a $\theta \in \mathbb {S}^{N-2}$![]() such that $B(0,\,1/2)\subset U_{x_1}$
such that $B(0,\,1/2)\subset U_{x_1}$![]() for all $x_{1} \in (0,\, \frac {1}{2} R^{1-\beta })$
for all $x_{1} \in (0,\, \frac {1}{2} R^{1-\beta })$![]() . So it remains to prove the claim that there exists a $\theta \in \mathbb {S}^{N-2}$
. So it remains to prove the claim that there exists a $\theta \in \mathbb {S}^{N-2}$![]() such that
such that

is $\frac {1}{1000}R^{-1 + \epsilon }$![]() dense in the ball $B(0,\, 1/2)$
dense in the ball $B(0,\, 1/2)$![]() . In order to apply Lemma 2.1 from Lucà–Rogers [Reference Lucà and Rogers12] to get this claim, we first rescale by $R^{\frac {\beta (r+1)}{2}}$
. In order to apply Lemma 2.1 from Lucà–Rogers [Reference Lucà and Rogers12] to get this claim, we first rescale by $R^{\frac {\beta (r+1)}{2}}$![]() , and replace $R^{1+\frac {\beta (r+1)}{2}}t_{j}$
, and replace $R^{1+\frac {\beta (r+1)}{2}}t_{j}$![]() by $s_{j}$
by $s_{j}$![]() , replace $R^{\frac {\beta r}{2}}$
, replace $R^{\frac {\beta r}{2}}$![]() by $R^{\prime }$
by $R^{\prime }$![]() , recall that $\beta = \frac {2}{\frac {N+1}{N}r+1}$
, recall that $\beta = \frac {2}{\frac {N+1}{N}r+1}$![]() , then we are reduced to show
, then we are reduced to show

is $\frac {1}{1000}(R^{\prime })^{-\frac {1}{N} + \frac {(\frac {N+1}{N}r+1)\epsilon }{ r}}$![]() dense in the ball $B(0,\, \frac {1}{2} (R^{\prime })^{(r+1)/r})$
dense in the ball $B(0,\, \frac {1}{2} (R^{\prime })^{(r+1)/r})$![]() , which is equivalent to prove that for any $y\in B(0,\,\frac {1}{2}(R')^{(r+1)/r})$
, which is equivalent to prove that for any $y\in B(0,\,\frac {1}{2}(R')^{(r+1)/r})$![]() , there exist
, there exist

such that
for a fixed $\theta \in \mathbb {S}^{N-2}$![]() , which is independent of $y$
, which is independent of $y$![]() and $x_1$
and $x_1$![]() . This is implied by the following Lemma 3.2 from Lucà–Rogers [Reference Lucà and Rogers12], but we prefer to omit the proof of (3.12), because a similar but more detailed proof can be found in Corollary 2.2 of [Reference Lucà and Rogers12].
. This is implied by the following Lemma 3.2 from Lucà–Rogers [Reference Lucà and Rogers12], but we prefer to omit the proof of (3.12), because a similar but more detailed proof can be found in Corollary 2.2 of [Reference Lucà and Rogers12].
Lemma 3.2 [Reference Lucà and Rogers12, Lemma 2.1]
Let $d\geq 2$![]() , $0<\epsilon,\,\delta <1$
, $0<\epsilon,\,\delta <1$![]() and $\kappa >\frac {1}{d+1}$
and $\kappa >\frac {1}{d+1}$![]() . Then, if $\delta <\kappa$
. Then, if $\delta <\kappa$![]() and $R>1$
and $R>1$![]() is sufficiently large, there is $\theta \in \mathbb {S}^{d-1}$
is sufficiently large, there is $\theta \in \mathbb {S}^{d-1}$![]() for which, given any $[y]\in \mathbb {T}^d$
for which, given any $[y]\in \mathbb {T}^d$![]() and $a\in \mathbb {R}$
and $a\in \mathbb {R}$![]() , there is a $t_y\in R^{\delta }\mathbb {Z} \cap (a,\,a+R)$
, there is a $t_y\in R^{\delta }\mathbb {Z} \cap (a,\,a+R)$![]() such that
such that
where ‘$[\cdot ]$![]() ’ means taking the quotient $\mathbb {R}^d/\mathbb {Z}^d=\mathbb {T}^d$
’ means taking the quotient $\mathbb {R}^d/\mathbb {Z}^d=\mathbb {T}^d$![]() . Moreover, this remains true with $d=1$
. Moreover, this remains true with $d=1$![]() , for some $\theta \in (0,\,1)$
, for some $\theta \in (0,\,1)$![]() .
.
Finally, it follows from (3.7) and (3.11) that

which implies inequality (3.2).
4. A counterexample for theorem 1.9
For convenience, we first set $N=2$![]() . By changing of variables, the nonelliptic Schrödinger operator can be written as
. By changing of variables, the nonelliptic Schrödinger operator can be written as
For each $r \in (0,\,1]$![]() , we will show that there exists $\{t_{n}\}_{n=1}^{\infty } \in \ell ^{r, \infty }(\mathbb {N})$
, we will show that there exists $\{t_{n}\}_{n=1}^{\infty } \in \ell ^{r, \infty }(\mathbb {N})$![]() , such that the maximal estimate
, such that the maximal estimate

holds for all $f \in H^{s}(\mathbb {R}^{2})$![]() only if $s \ge \frac {r}{r+1}$
only if $s \ge \frac {r}{r+1}$![]() .
.
Indeed, we may choose $t_{n}=1/n^{\frac {1}{r} + \epsilon }$![]() , it is clear that $\{t_{n}\}_{n=1}^{\infty } \in \ell ^{r, \infty }(\mathbb {N})$
, it is clear that $\{t_{n}\}_{n=1}^{\infty } \in \ell ^{r, \infty }(\mathbb {N})$![]() but never belongs to $\ell ^{r-\epsilon, \infty }(\mathbb {N})$
but never belongs to $\ell ^{r-\epsilon, \infty }(\mathbb {N})$![]() for any small $\epsilon >0$
for any small $\epsilon >0$![]() . Moreover, $t_{n} -t_{n+1}$
. Moreover, $t_{n} -t_{n+1}$![]() is decreasing. According to Lemma 3.2 in [Reference Dimou and Seeger7], we can select $\{b_{j}\}_{j=1}^{\infty }$
is decreasing. According to Lemma 3.2 in [Reference Dimou and Seeger7], we can select $\{b_{j}\}_{j=1}^{\infty }$![]() and $\{M_{j}\}_{j=1}^{\infty }$
and $\{M_{j}\}_{j=1}^{\infty }$![]() satisfying $\lim _{j \rightarrow \infty }b_{j} = 0,\, \:\ \lim _{j \rightarrow \infty }M_{j} = \infty,\,$
satisfying $\lim _{j \rightarrow \infty }b_{j} = 0,\, \:\ \lim _{j \rightarrow \infty }M_{j} = \infty,\,$![]() and
and
such that
By the similar argument as Proposition 3.3 in [Reference Dimou and Seeger7], when $t_{n} \le b_{j}$![]() , we have
, we have
For fixed $j$![]() , choose $\lambda _{j}=\frac {1}{1000} M_{j}^{\frac {1}{2}}b_{j}^{-\frac {r-\epsilon +1}{2}}$
, choose $\lambda _{j}=\frac {1}{1000} M_{j}^{\frac {1}{2}}b_{j}^{-\frac {r-\epsilon +1}{2}}$![]() and $\widehat {f_{j}}(\xi _{1},\,\xi _{2}) =\frac {1}{\lambda _{j}} \chi _{[0,\lambda _{j}]\times [{-\lambda _{j}-1,\,-\lambda _{j}}]} (\xi _{1},\,\xi _{2}).$
and $\widehat {f_{j}}(\xi _{1},\,\xi _{2}) =\frac {1}{\lambda _{j}} \chi _{[0,\lambda _{j}]\times [{-\lambda _{j}-1,\,-\lambda _{j}}]} (\xi _{1},\,\xi _{2}).$![]() Therefore,
Therefore,
Let $U_{j}=(0,\,\frac {\lambda _{j}b_{j}}{2}) \times (-\frac {1}{1000},\, \frac {1}{1000}).$![]() Notice that $U_{j} \subset B(0,\,1)$
Notice that $U_{j} \subset B(0,\,1)$![]() due to inequality (4.3). Next, we will show that for each $x \in U_{j}$
due to inequality (4.3). Next, we will show that for each $x \in U_{j}$![]() ,
,
After changing variables, we have for each $n \in \mathbb {N}$![]() ,
,
For each $x \in U_{j}$![]() , there exists a unique $n(x,\,j)$
, there exists a unique $n(x,\,j)$![]() such that
such that
It is obvious that $t_{n(x,j)+1} \le \frac {b_{j}}{2}$![]() , then $t_{n(x,j)} \le b_{j}$
, then $t_{n(x,j)} \le b_{j}$![]() due to inequality (4.4) and the assumption that $t_{n} -t_{n+1}$
due to inequality (4.4) and the assumption that $t_{n} -t_{n+1}$![]() is decreasing. Then it follows from inequality (4.5) that
is decreasing. Then it follows from inequality (4.5) that
Also, $| x_{2}\eta _{2}| \le \frac {1}{1000},$![]() and by inequality (4.3), we have $|\lambda _{j}t_{n(x,j)}\eta _{1}\eta _{2}| \le \lambda _{j}b_{j} \le \frac {1}{1000}.$
and by inequality (4.3), we have $|\lambda _{j}t_{n(x,j)}\eta _{1}\eta _{2}| \le \lambda _{j}b_{j} \le \frac {1}{1000}.$![]() Therefore, if we take $n=n(x,\,j)$
Therefore, if we take $n=n(x,\,j)$![]() in (4.8), then the phase function will be sufficiently small such that $|e^{it_{n(x,j)}\square }f_{j}(x)| > \frac {1}{2(2\pi )^{2}}$
in (4.8), then the phase function will be sufficiently small such that $|e^{it_{n(x,j)}\square }f_{j}(x)| > \frac {1}{2(2\pi )^{2}}$![]() for each $x \in U_{j}$
for each $x \in U_{j}$![]() , which implies inequality (4.7). Then, it follows from inequalities (4.6) and (4.7) that
, which implies inequality (4.7). Then, it follows from inequalities (4.6) and (4.7) that

This implies that the maximal estimate (4.2) can not hold when $s \le \frac {r-\epsilon }{r-\epsilon +1}$![]() , hence when $s < \frac {r}{r+1}$
, hence when $s < \frac {r}{r+1}$![]() by the arbitrariness of $\epsilon$
by the arbitrariness of $\epsilon$![]() .
.
Remark 4.1 The original idea we adopted to construct the above counterexample comes from [Reference Rogers, Vargas and Vega13]. The same idea remains valid in general dimensions. For example, in $\mathbb {R}^{3}$![]() , by changing variables, we can write
, by changing variables, we can write
In order to prove the necessary condition, we only need to take
and
Data
Our manuscript has no associated data.
Acknowledgements
We would like to express our gratitude to the referees for his/her insightful and helpful suggestions and comments.
This work is supported by the National Natural Science Foundation of China (No.12271435; No.12271501; No.12071052).
Competing interest
None.