What is a causal effect?
The goal of much observational research is to establish causal effects and quantify their magnitude in the context of risk factors and their impact on health and social outcomes. To establish whether a specific exposure has a causal effect on an outcome of interest we need to know what would happen if a person were exposed, and what would happen if they were not exposed. If these outcomes differ, then we can conclude that the exposure is causally related to the outcome. However, individual causal effects cannot be identified with confidence in observational data because we can only observe the outcome that occurred for a certain individual under one possible value of the exposure (Hernan, Reference Hernan2004). In a statistical model using observational data, we can only compare the risk of the outcome in those exposed, to the risk of the outcome in those unexposed (two subsets of the population determined by an individuals’ actual exposure value); however, inferring causation implies a comparison of the risk of the outcome if all individuals were exposed and if all were unexposed (the same population under two different exposure values) (Hernán & Robins, Reference Hernán and Robins2020). Inferring population causal effects from observed associations between variables can therefore be viewed as a missing data problem, where several untestable assumptions need to be made regarding bias due to confounding, selection and measurement (Edwards, Cole, & Westreich, Reference Edwards, Cole and Westreich2015).
The findings of observational research can therefore be inconsistent, or consistent but unlikely to reflect true cause and effect relationships. For example, observational studies have shown that those who drink no alcohol show worse outcomes on a range of measures than those who drink a small amount (Corrao, Rubbiati, Bagnardi, Zambon, & Poikolainen, Reference Corrao, Rubbiati, Bagnardi, Zambon and Poikolainen2000; Howard, Arnsten, & Gourevitch, Reference Howard, Arnsten and Gourevitch2004; Koppes, Dekker, Hendriks, Bouter, & Heine, Reference Koppes, Dekker, Hendriks, Bouter and Heine2005; Reynolds et al., Reference Reynolds, Lewis, Nolen, Kinney, Sathya and He2003; Ruitenberg et al., Reference Ruitenberg, van Swieten, Witteman, Mehta, van Duijn, Hofman and Breteler2002). This pattern of findings could be due to confounding (e.g. by socio-economic status), selection bias (e.g. healthier or more resilient drinkers may be more likely to take part in research), reverse causality (e.g. some of those who abstain from alcohol do so because of pre-existing ill-health which leads them to stop drinking) (Chikritzhs, Naimi, & Stockwell, Reference Chikritzhs, Naimi and Stockwell2017; Liang & Chikritzhs, Reference Liang and Chikritzhs2013; Naimi et al., Reference Naimi, Stockwell, Zhao, Xuan, Dangardt, Saitz and Chikritzhs2017), or a combination of all of these. However, the difficulty in establishing generalizable causal claims is not simply restricted to observational studies. No single study or method, no matter the degree of excellence, can provide a definite answer to a causal question.
Approaches to causal inference may be broadly divided into two kinds – those that use statistical adjustment to control confounding and arrive at a causal estimate, and those that use design-based methods to do so. The former approaches rely on the assumption that there is no remaining unmeasured confounding and no measurement error after the application of statistical methods, while the latter does not. Effective statistical adjustment for confounding requires knowing what to measure – and measuring it accurately – whereas many design-based approaches [for example, randomized controlled trials (RCTs)] do not have that requirement. Approaches that rely on statistical adjustment are likely to have similar (or at least related) sources of bias, whereas those that rely on design-based methods are more likely to have different sources of bias. Although the distinction between statistical and design-based approaches is not absolute (all approaches require the application of statistical methods, for example), it nevertheless provides a framework for triangulation. That is, ‘The practice of strengthening causal inferences by integrating results from several different approaches, where each approach has different (and assumed to be largely unrelated) key sources of potential bias’ (Munafo & Davey Smith, Reference Munafo and Davey Smith2018). No single approach can provide a definitive answer to a causal question, but the thoughtful application of multiple approaches (e.g. statistical and design based), each with their own strengths and weaknesses, and in particular sources and directions of bias, can provide a stronger basis for causal inference.
Although the concept of triangulation is not new, the specific, explicit application of this framework in the mental health literature is relatively limited and recent. Here we describe threats to causal inference, focusing on different sources of potential bias, and review methods that use statistical adjustment and design to control confounding and support the causal inference. We conclude with a review of how these different approaches, within and between statistical and design-based methods, can be integrated within a triangulation framework. We illustrate this with examples of studies that explicitly use a triangulation framework, drawn from the relevant mental health literature.
Statistical approaches to causal inference
Three types of bias can arise in observational data: (i) confounding bias (which includes reverse causality), (ii) selection bias (inappropriate selection of participants through stratifying, adjusting or selecting) and (iii) measurement bias (poor measurement of variables in analysis). A glossary of italic terms is shown in Box 1.
Box 1. Glossary of terms

These biases can all result from opening, or failing to close, a backdoor pathway between the exposure and outcome. Confounding bias is addressed by identifying and adjusting for variables that can block a backdoor pathway between the exposure and outcome, or alternatively, identifying a population in which the confounder does not operate. Selection bias is addressed by not conditioning on colliders (or a consequence of a collider), and therefore opening a backdoor pathway, or removing potential bias when conditioning cannot be prevented. Measurement bias is addressed by careful assessment of variables in analysis and, where possible, collecting repeated measures or using multiple sources of data. In Box 2 we outline each of these biases in more detail using causal diagrams – accessible introductions to causal diagrams are available elsewhere (Elwert & Winship, Reference Elwert and Winship2014; Greenland, Pearl, & Robins, Reference Greenland, Pearl and Robins1999; Rohrer, Reference Rohrer2018) – together with examples from the mental health literature.
Box 2. Threats to causal inference.

Various statistical approaches exist that aim to minimize biases in observational data and can increase confidence to a certain degree. This section focuses on a few key approaches that are either frequently used or particularly relevant for research questions in mental health epidemiology. In Box 3 we discuss the importance of mechanisms, and the use of counterfactual mediation in the mental health literature.
Box 3. Mechanisms


Figure 1. Causal diagrams representing confounding, selection bias and measurement bias
Note: in the causal diagrams above, we assume that: (i) all observed and unobserved common causes in the process under investigation are displayed, (ii) there is no chance variation (i.e. we are working with the entire population), and (iii) the absence of an arrow represents no causal effect between variables. Additionally, to demonstrate selection bias, we also show diagrams with non-causal paths, where associations have been induced by conditioning on a common effect (or collider). Explanations of how biases due to confounding, selection and measurement can be described using potential outcomes are available elsewhere (Edwards et al., Reference Edwards, Cole and Westreich2015; Hernan, Reference Hernan2004)
In Table 1, we outline the assumptions and limitations for the main statistical approaches highlighted in this review and provide examples of each using mental health research.
Table 1. Assumptions and limitations of statistical and design-based approaches to causal inference

MAR, missing at random; MCAR, missing completely at random; MNAR, missing not at random; SEM, structural equation modelling; RCT, randomized controlled trial; MR, Mendelian randomization.
Confounding and reverse causality
The most common approach to address confounding bias is to include any confounders in a regression model for the effect of the exposure on the outcome. Alternative methods to address either time-invariant confounding (e.g. propensity scores) or time-varying confounding (e.g. marginal structural models) are increasingly being used in the field of mental health (Bray, Dziak, Patrick, & Lanza, Reference Bray, Dziak, Patrick and Lanza2019; Howe, Cole, Mehta, & Kirk, Reference Howe, Cole, Mehta and Kirk2012; Itani et al., Reference Itani, Rai, Jones, Taylor, Thomas, Martin and Taylor2019; Li, Evans, & Hser, Reference Li, Evans and Hser2010; Slade et al., Reference Slade, Stuart, Salkever, Karakus, Green and Ialongo2008; Taylor et al., Reference Taylor, Itani, Thomas, Rai, Jones, Windmeijer and Taylor2020). However, these approaches all rely on all potential confounders being measured and no confounders being measured with error. These are typically unrealistic assumptions when using observational data, resulting in the likelihood of residual confounding (Phillips & Smith, Reference Phillips and Smith1992). Ohlsson and Kendler provide a more in-depth review of the use of these methods in psychiatric epidemiology (Ohlsson & Kendler, Reference Ohlsson and Kendler2020).
Another approach to address confounding is fixed-effects regression; for a more recent extension to this method, see (Curran, Howard, Bainter, Lane, & McGinley, Reference Curran, Howard, Bainter, Lane and McGinley2014). Fixed-effects regression models use repeated measures of an exposure and an outcome to account for the possibility of an association between the exposure and the unexplained variability in the outcome (representing unmeasured confounding) (Judge, Griffiths, Hill, & Lee, Reference Judge, Griffiths, Hill and Lee1980). These models adjusted for all time-invariant confounders, including unobserved confounders, and can incorporate observed time-varying confounders. This method has been described in detail elsewhere – see (Fergusson & Horwood, Reference Fergusson and Horwood2000; Fergusson, Swain-Campbell, & Horwood, Reference Fergusson, Swain-Campbell and Horwood2002) – and fixed-effects regression models have been used to address various mental health questions, including the relationship between alcohol use and crime (Fergusson & Horwood, Reference Fergusson and Horwood2000), cigarette smoking and depression (Boden, Fergusson, & Horwood, Reference Boden, Fergusson and Horwood2010), and cultural engagement and depression (Fancourt & Steptoe, Reference Fancourt and Steptoe2019).
Selection bias
One of the most common types of selection bias present in observational data is from selective non-response and attrition. Conventional approaches to address this potential bias (and loss of power) include multiple imputation, full information maximum likelihood estimation, inverse probability weighting, and covariate adjustment. Comprehensive descriptions of these methods are available (Enders, Reference Enders2011; Seaman & White, Reference Seaman and White2013; Sterne et al., Reference Sterne, White, Carlin, Spratt, Royston, Kenward and Carpenter2009; White, Royston, & Wood, Reference White, Royston and Wood2011). In general, these approaches assume that data are missing at random (MAR); however, missing data relating to mental health are likely to be missing not at random (MNAR). In other words, the probability of Z being missing still depends on unobserved values of Z even after allowing for dependence on observed values of Z and other observed variables. Introductory texts on missing data mechanisms are available (Graham, Reference Graham2009; Schafer & Graham, Reference Schafer and Graham2002). An exception to this is using complete case analysis, with covariate adjustment which can be unbiased when data are MNAR as long as the chance of being a complete case does not depend on the outcome after adjusting for covariates (Hughes, Heron, Sterne, & Tilling, Reference Hughes, Heron, Sterne and Tilling2019). Additionally, extensions to standard multiple imputation exist that allow for MNAR mechanisms using sensitivity parameters (Leacy, Floyd, Yates, & White, Reference Leacy, Floyd, Yates and White2017; Tompsett, Leacy, Moreno-Betancur, Heron, & White, Reference Tompsett, Leacy, Moreno-Betancur, Heron and White2018).
Further approaches to address potential MNAR mechanisms include linkage to external data (Cornish, Macleod, Carpenter, & Tilling, Reference Cornish, Macleod, Carpenter and Tilling2017; Cornish, Tilling, Boyd, Macleod, & Van Staa, Reference Cornish, Tilling, Boyd, Macleod and Van Staa2015), MNAR analysis models for longitudinal data (Enders, Reference Enders2011; Muthen, Asparouhov, Hunter, & Leuchter, Reference Muthen, Asparouhov, Hunter and Leuchter2011) and sensitivity analyses (Leacy et al., Reference Leacy, Floyd, Yates and White2017; Moreno-Betancur & Chavance, Reference Moreno-Betancur and Chavance2016). Linkage to routinely collected health data is starting to be used in the context of mental health (Christensen, Ekholm, Gray, Glumer, & Juel, Reference Christensen, Ekholm, Gray, Glumer and Juel2015; Cornish et al., Reference Cornish, Tilling, Boyd, Macleod and Van Staa2015; Gorman et al., Reference Gorman, Leyland, McCartney, White, Katikireddi, Rutherford and Gray2014; Gray et al., Reference Gray, McCartney, White, Katikireddi, Rutherford, Gorman and Leyland2013; Mars et al., Reference Mars, Cornish, Heron, Boyd, Crane, Hawton and Gunnell2016) to examine the extent of biases from selective non-response by providing data on those that did and did not respond to assessments within population cohorts or health surveys. In addition to using linked data to detect potential non-response bias, it can also be used as a proxy for the missing study outcome in multiple imputation or deriving weights to adjust for potential bias and make the assumption of MAR more plausible (Cornish et al., Reference Cornish, Tilling, Boyd, Macleod and Van Staa2015, Reference Cornish, Macleod, Carpenter and Tilling2017; Gorman et al., Reference Gorman, Leyland, McCartney, Katikireddi, Rutherford, Graham and Gray2017; Gray et al., Reference Gray, McCartney, White, Katikireddi, Rutherford, Gorman and Leyland2013).
Measurement bias
Conventional approaches to address measurement error include using latent variables. Here, when we use the term measurement error, we are specifically referring to variability in a measure that is not due to the construct that we are interested in. Using a latent variable holds several advantages over using an observed measure that represents a sum of the relevant items, for example, allowing each item to contribute differently to the underlying construct (via factor loadings) and reducing measurement error (Muthen & Asparouhov, Reference Muthen and Asparouhov2015). However, if the source of measurement error is shared across all the indicators (for example, when using multiple self-report questions), the measurement error may not be removed from the construct of interest. Various extensions to latent variable methods have been developed to specifically address measurement bias from using self-report questionnaires. For example, using items assessed with multiple methods, each with different sources of bias (such as self-report and objective measures), means that variability due to bias shared across particular items can be removed from the latent variable representing the construct of interest. For an example using cigarette smoking see Palmer and colleagues (Palmer, Graham, Taylor, & Tatterson, Reference Palmer, Graham, Taylor and Tatterson2002). Alternative approaches to address measurement error in a covariate exist, but will not be discussed further here, including regression calibration (Hardin, Schmiediche, & Carroll, Reference Hardin, Schmiediche and Carroll2003; Rosner, Spiegelman, & Willett, Reference Rosner, Spiegelman and Willett1990) and the simulation extrapolation method (Cook & Stefanski, Reference Cook and Stefanski1994; Hardin et al., Reference Hardin, Schmiediche and Carroll2003; Stefanski & Cook, Reference Stefanski and Cook1995).
Conclusions
Various advanced statistical approaches exist that bring certain advantages in terms of addressing biases present in observational data. These approaches are easily accessible and are starting to be used in the field of mental health. Most commonly, these approaches are applied in isolation, or sequentially to account for a combination of bias due to confounding, selection and measurement. However, other methods also exist that use models to simultaneously address all three types of bias – van Smeden and colleagues (van Smeden, Penning de Vries, Nab, & Groenwold, Reference van Smeden, Penning de Vries, Nab and Groenwold2020) provide a review on these types of biases. The first step in causal inference with observational data is to identify and measure the important confounders and include them correctly in the statistical model. This process can be facilitated using causal diagrams (Box 2). However, even when studies have measured potential confounders extensively, there could still be some bias from residual confounding because of measurement error. In practice, these statistical approaches cannot always completely remove key sources of bias; therefore, using design-based approaches to improve causal inference (outlined below) is also important.
Design-based approaches to causal inference
A fundamentally different approach to causal inference is to use design-based approaches, rather than statistical approaches that attempt to minimize or remove sources of bias (e.g. by adjustment for potential confounders). Here it is the design of the study that addresses the problem of potential bias – either by ensuring it is not present (under certain assumptions), or by comparing results across methods with different sources and direction of potential bias (Richmond, Al-Amin, Davey Smith, & Relton, Reference Richmond, Al-Amin, Davey Smith and Relton2014). This final point will be returned to when we discuss triangulation of results. In Table 1, we outline the assumptions and limitations of each design-based approach, and provide specific examples drawn from the mental health literature. For further examples of the use of natural experiments in psychiatric epidemiology see the review by Ohlsson and Kendler (Ohlsson & Kendler, Reference Ohlsson and Kendler2020).
Randomized controlled trials
The RCT is typically regarded as the most robust basis for causal inference and represents the most common approach that uses study design to support the causal inference. Nevertheless, RCTs rest on the critical assumption that the groups are similar except with respect to the intervention. If this assumption is met, the exposed and unexposed groups are considered exchangeable, which is equivalent to observing the outcome that would occur if a person were exposed, and what would occur if they were not exposed. An RCT is also still prone to potential bias, such as lack of concealment of the random allocation, failure to maintain randomization, and differential loss to follow-up between groups. These sources of bias are typically addressed through the application of robust randomization and other study procedures. Further limitations include that RCTs are not always feasible, and often recruit highly selected samples (e.g. for safety considerations, or to ensure high levels of compliance), so the generalizability of results from RCTs can be an important limitation.
Natural experiments
Where RCTs are not practical or ethical, natural experiments can provide an alternative. These compare populations before and after a ‘natural’ exposure, leading to ‘quasi-random’ exposure (e.g. using regression discontinuity analysis). The key assumption is that the populations compared are comparable (e.g. with respect to the underlying confounding structure) except for the naturally occurring exposure. Potential sources of bias include differences in characteristics that may confound any observed association or misclassification of the exposure that relates to the naturally occurring exposure. This approach also relies on the occurrence of appropriate natural experiments that manipulate the exposure of interest (e.g. policy changes that mandate longer compulsory schooling, resulting in an increase in years of education from one cohort to another) (Davies, Dickson, Davey Smith, van den Berg, & Windmeijer, Reference Davies, Dickson, Davey Smith, van den Berg and Windmeijer2018a).
Instrumental variables
In the absence of an appropriate natural experiment, an alternative is to identify an instrumental variable that can be used as a proxy for the exposure of interest. An instrumental variable is a variable that is robustly associated with an exposure of interest but is not a confounder of the exposure and outcome. For example, the tendency of physicians to prefer prescribing one medication over another (e.g. nicotine replacement therapy v. varenicline for smoking cessation) has been used as an instrument in pharmacoepidemiological studies (Itani et al., Reference Itani, Rai, Jones, Taylor, Thomas, Martin and Taylor2019; Taylor et al., Reference Taylor, Itani, Thomas, Rai, Jones, Windmeijer and Taylor2020). The key assumption is that the instrument is not associated with the outcome other than that via its association with the exposure (the exclusion restriction assumption). Other assumptions include the relevance assumption (that the instrument has a causal effect on the exposure), and the exchangeability assumption (that the instrument is not associated with potential confounders of the exposure–outcome relationship). Potential sources of bias include the instrument not truly being associated with the exposure, or the exclusion restriction criterion being violated. If the association of the instrument with the exposure is weak this may lead to so-called weak instrument bias (Davies, Holmes, & Davey Smith, Reference Davies, Holmes and Davey Smith2018b), which may, for example, amplify biases due to violations of other assumptions (Labrecque & Swanson, Reference Labrecque and Swanson2018). This can be a particular problem in genetically informed approaches such as Mendelian randomization (MR) (see below), where genetic variants typically only predict a small proportion of variance in the exposure of interest. A key challenge with this approach is testing the assumption that the instrument is not associated with the outcome via other pathways, which may not always be possible. More detailed descriptions of the instrumental variable approach, including the underlying assumptions and potential pitfalls, are available elsewhere (Labrecque & Swanson, Reference Labrecque and Swanson2018; Lousdal, Reference Lousdal2018).
Different confounding structures
If it is not possible to use design-based approaches that (in principle) are protected from confounding, an alternative is to use multiple samples with different confounding structures. For example, multiple control groups within a case−control design, where bias for the control groups is in different directions, can be used under the assumption that if the sources of bias in the different groups are indeed different, this would produce different associations, whereas a causal effect would produce the same observed association. A related approach is the use of cross-context comparisons, where results across multiple populations with different confounding structures are compared, again on the assumption that the bias introduced by confounding will be different across contexts so that congruent results are more likely to reflect causal effects. For example, Sellers and colleagues (Sellers et al., Reference Sellers, Warne, Rice, Langley, Maughan, Pickles and Collishaw2020) compared the association between maternal smoking in pregnancy and offspring birthweight, cognition and hyperactivity in two national UK cohorts born in 1958 and 2000/2001 with different confounding structures.
Positive and negative controls
The use of positive and negative controls – common in fields such as preclinical experimental research – can be applied to both exposures and outcomes in observational epidemiology. This allows us to test whether an exposure or outcome is behaving as we would expect (a positive control), and as we would not expect (a negative control). A positive control exposure is one that is known to be causally related to the outcome and can be used to ensure the population sampled generates credible associations that would be expected (i.e. is not unduly biased), and vice versa for a positive control outcome. A negative control exposure is one that is not plausibly causally related to the outcome, and again vice versa for a negative control outcome. For example, smoking is associated with suicide, which is plausibly causal but is also equally strongly associated with homicide, which is not. The latter casts doubt on a causal interpretation of the former (Davey Smith, Phillips, & Neaton, Reference Davey Smith, Phillips and Neaton1992). Brand and colleagues (Brand et al., Reference Brand, Gaillard, West, McEachan, Wright, Voerman and Lawlor2019) used paternal smoking during pregnancy as a negative control exposure to investigate whether the association between maternal smoking during pregnancy and foetal growth is likely be causal, on the assumption that any biological effects of paternal smoking on foetal growth will be negligible, but that confounding structures will be similar to maternal smoking. Overall, negative controls provide a powerful means by which the assumptions underlying a particular approach (e.g. that confounding has been adequately dealt with) can be tested, although in some cases identifying an appropriate negative control can be challenging (e.g. where exposure may have diverse effects on a range of outcomes). Lipsitch and colleagues (Lipsitch, Tchetgen Tchetgen, & Cohen, Reference Lipsitch, Tchetgen Tchetgen and Cohen2010) described their use as a means whereby we can ‘detect both suspected and unsuspected sources of spurious causal inference’. In particular, negative controls can be used in conjunction with most of the methodologies we discuss here – for example, negative controls can be used to test some of the assumptions of an instrumental variable or genetically informed approaches. For example, there is evidence that genetic variants associated with smoking may also be associated with outcomes at age 7, prior to exposure to smoking, which provides reasons to be cautious when using these variants as proxies for smoking initiation in MR (see below) (Khouja, Wootton, Taylor, Davey Smith, & Munafo, Reference Khouja, Wootton, Taylor, Davey Smith and Munafo2020). Madley-Dowd and colleagues (Madley-Dowd, Rai, Zammit, & Heron, Reference Madley-Dowd, Rai, Zammit and Heron2020b) provide an accessible introduction to the prenatal negative control design and the importance of considering assortative mating, explained using causal diagrams, whereas Lipsitch and colleagues (Lipsitch et al., Reference Lipsitch, Tchetgen Tchetgen and Cohen2010) provide a more general review of the use of negative controls in epidemiology.
Discordant siblings
Family-based study designs can provide a degree of control over family-level confounding. For example, two siblings born to a mother who smoked during one pregnancy, but not the other, provide information on the intrauterine effects of tobacco exposure while controlling for observed and unobserved familial confounding (both genetic and environmental), including shared confounders and 50% of genetic confounding. This approach assumes that any misclassification of the exposure or the outcome is similar across siblings, and there is little or no individual-level confounding, an assumption that is often not met (e.g. in the plausible scenario where a mother is both older and less likely to be smoking for the second pregnancy). An extension of this approach is the use of identical twins within a discordant-sibling design, which controls for 100% of genetic confounding (Keyes, Davey Smith, & Susser, Reference Keyes, Davey Smith and Susser2013). An advantage of this approach is that does not require the direct measurement of genotype, but it depends on the availability of suitable samples. This can mean that the sample size may be limited. Pingault and colleagues (Pingault et al., Reference Pingault, O'Reilly, Schoeler, Ploubidis, Rijsdijk and Dudbridge2018) describe a range of genetically informed approaches in more detail, including family-based designs such as the use of sibling and twin designs.
Genetically informed approaches
MR is a now a widely used genetically informed design-based method for causal inference, which is often implemented through an instrumental variable analysis (Richmond & Davey Smith, Reference Richmond and Davey Smith2020). MR is generally implemented through the use of genetic variants as proxies for the exposure of interest (Davey Smith & Ebrahim, Reference Davey Smith and Ebrahim2003; Davies et al., Reference Davies, Holmes and Davey Smith2018b). For example, Harrison and colleagues (Harrison, Munafo, Davey Smith, & Wootton, Reference Harrison, Munafo, Davey Smith and Wootton2020) used genetic variants associated with a range of smoking behaviours as proxies to examine the effects of smoking on suicidal ideation and suicide attempts. Violation of the exclusion restriction criterion due to horizontal (or biological) pleiotropy is the main likely source of bias, and for this reason, a number of extensions to the foundational method have been developed that are robust to horizontal pleiotropy (Hekselman & Yeger-Lotem, Reference Hekselman and Yeger-Lotem2020; Hemani, Bowden, & Davey Smith, Reference Hemani, Bowden and Davey Smith2018). Population stratification is another potential source of bias, which may require focusing on an ethnically homogeneous population, or adjusting for genetic principal components that reflect different population sub-groups. Weak instrument bias (see above) is also a common problem in MR (although often underappreciated), given that genetic variants often only account for a small proportion of variance in the exposure of interest. Diemer and colleagues (Diemer, Labrecque, Neumann, Tiemeier, & Swanson, Reference Diemer, Labrecque, Neumann, Tiemeier and Swanson2020) describe the reporting of methodological limitations of MR studies in the context of prenatal exposure research and find that weak instrument bias is reported less often as a potential limitation than pleiotropy or population stratification. MR approaches can be extended to include comparisons across context, the use of positive and negative controls, and the use of family-based designs (including discordant siblings). More detailed reviews of a range of genetically informed approaches, including MR, are available elsewhere (Davies et al., Reference Davies, Howe, Brumpton, Havdahl, Evans and Davey Smith2019; Pingault et al., Reference Pingault, O'Reilly, Schoeler, Ploubidis, Rijsdijk and Dudbridge2018).
Conclusions
A variety of design-based approaches to causal inference exist that should be considered complementary to statistical approaches. In particular, several of these approaches (e.g. analyses across groups with different confounding structures, and the use of positive and negative controls) can be implemented using the range of statistical methods described above. These are again increasingly being used in the field of mental health. However, despite their strengths, it is unlikely that any single method (whether statistical or design-based) can provide a definite answer to a causal question.
Triangulation and causal inference
One reason to include design-based approaches is that these may be less likely to suffer from similar sources and directions of bias compared with statistical approaches, particularly when these are conducted within the same data set (Lawlor, Tilling, & Davey Smith, Reference Lawlor, Tilling and Davey Smith2016). Ideally, we would identify different sources of evidence that we could apply to a research question and understand the likely sources and directions of bias operating within each so that we could ensure that these are different. This means that triangulation should be a prospective approach, rather than simply selecting sources of evidence that support a particular conclusion post hoc.
A range of examples of studies that explicitly use triangulation to support stronger causal inference in the context of substance use and mental health is presented in Table 2. Although this is not an exhaustive list of studies that have used triangulation in mental health research, we identified several studies by searching (i) for studies that cited a review on triangulation in aetiological epidemiology from 2017 (Lawlor et al., Reference Lawlor, Tilling and Davey Smith2016), (ii) two databases (PubMed and Web of Science) in March 2020 using the search terms ‘triangulat*’ and ‘mental health’ for papers published since 2017 and (iii) the reference list of another recent review on triangulation of evidence in genetically informed designs (Munafo, Higgins, & Davey Smith, Reference Munafo, Higgins and Davey Smith2020). For a description of two additional studies in psychiatric epidemiology that have used a triangulation framework see the review by Ohlsson and Kendler (Ohlsson & Kendler, Reference Ohlsson and Kendler2020). These studies use a range of statistical and design-based approaches. For example, Caramaschi and colleagues (Caramaschi et al., Reference Caramaschi, Taylor, Richmond, Havdahl, Golding, Relton and Rai2018) explore the impact of maternal smoking during pregnancy on offspring autism spectrum disorder (ASD), using paternal smoking during pregnancy as a negative control, and MR using genetic variants associated with heaviness of smoking as a proxy for the exposure, together with conventional regression-based analyses. The evidence was not consistent with a causal effect for maternal smoking in pregnancy on ASD.
Table 2. Studies using triangulation to address a research question in mental health epidemiology
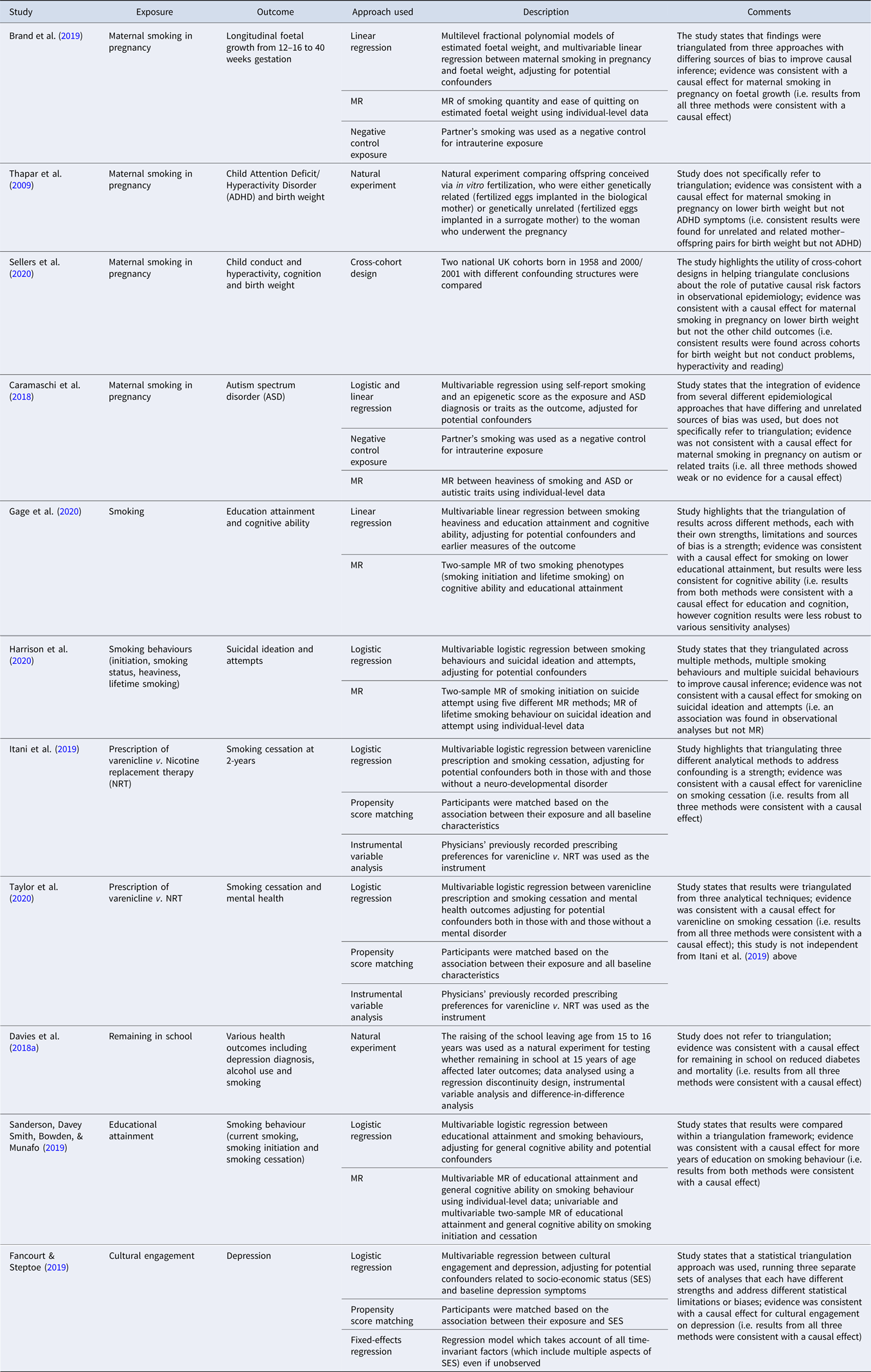
The limitations of observational data for causal inference are well known. However, the thoughtful application of multiple statistical and design-based approaches, each with their own strengths and weaknesses, and in particular sources and directions of bias, can support stronger causal inference through the triangulation of evidence provided by these. Triangulation can be within broad methods (e.g. propensity score matching and fixed-effects regression within regression-based statistical approaches, or different pleiotropy-robust MR methods), but is most powerful when it draws on fundamentally different methods, as this is most likely to ensure that sources of bias are different, and operating in different directions. It will be strongest when applied prospectively. This could in principle include the pre-registration of a triangulation strategy. This will encourage new research that does not simply have the same strengths and limitations as prior studies, but instead intentionally has a different configuration of strengths and limitations, and different sources (and, ideally, direction) of potential bias. It is also worth noting that triangulation is currently largely a qualitative exercise, although methods are being developed to support the quantitative synthesis of estimates provided by different methods.
Although triangulation is beginning to be applied in the context of mental health, our review of recent studies that explicitly make reference to triangulation revealed relatively few that did so. Of course, others will have included multiple approaches without describing the approach as one of triangulation, but it is in part this explicit (and ideally prospective) recognition of the need to understand potential sources of bias associated with these different methods that is a key. Our hope is that this approach will become more widely adopted – resulting in weightier outputs that provide more robust answers to key questions. This will have other implications – for example, larger teams of researchers contributing distinct elements to studies will become more common, and these contributions will need to be recognized in ways that conventional authorship does not fully capture. Triangulation can therefore be considered part of wider efforts to improve the transparency and robustness of scientific research, and the wider scientific infrastructure and system of incentives. Ultimately, we must always be cautious when attempting to infer causality from observational data. However, there are clear examples where causality was confirmed, even before the underlying mechanisms were well understood (e.g. smoking and lung cancer). In many respects, these conclusions might be considered the result of the accumulation of evidence from multiple sources – a triangulation of a kind. However, in our view, the adoption of a prospective and explicit triangulation framework offers the potential to accelerate progress to the point where we feel more confident in our causal inferences.
Acknowledgements
MRM is a member of the MRC Integrative Epidemiology Unit at the University of Bristol (MC_UU_00011/7). This research was funded in whole, or in part, by the Wellcome Trust [209138/Z/17/Z]. For the purpose of Open Access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission.






