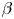1. Introduction
Until recently, our understanding of Alfvén waves (AWs) at scales much larger than plasma-kinetic scales has been largely agnostic of the rate of Coulomb collisions. Indeed, linear shear AWs and nonlinear torsional AWs do not change the form of the velocity distribution function of the particles, but rather define the moving frame in which any changes to it are to be measured (e.g. Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). As a result, it has been predicted that many defining characteristics of Alfvénic turbulence, such as its spectral indices or spatial anisotropies, are at most subtly affected by a lack of collisions. In introducing the concept of AW interruption however, Squire, Quataert & Schekochihin (Reference Squire, Quataert and Schekochihin2016) and Squire, Schekochihin & Quataert (Reference Squire, Schekochihin and Quataert2017b) established that shear AWs in collisionless, high-![]() $\beta$ plasmas are susceptible to non-equilibrium effects that place constraints on their ability to propagate freely, complicating the Alfvénic dynamics in new and novel ways.Footnote 1 This is just one example of how even small deviations from local thermodynamic equilibrium (LTE), made possible by low collisionality, can have large dynamical consequences for the evolution of high-
$\beta$ plasmas are susceptible to non-equilibrium effects that place constraints on their ability to propagate freely, complicating the Alfvénic dynamics in new and novel ways.Footnote 1 This is just one example of how even small deviations from local thermodynamic equilibrium (LTE), made possible by low collisionality, can have large dynamical consequences for the evolution of high-![]() $\beta$ systems. As a result, there has been increased interest in revisiting many problems in collisionless, high-
$\beta$ systems. As a result, there has been increased interest in revisiting many problems in collisionless, high-![]() $\beta$ plasmas that are fundamentally connected to Alfvénic dynamics, such as turbulence (Bott et al. Reference Bott, Arzamasskiy, Kunz, Quataert and Squire2021; Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023; Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023), the fluctuation dynamo (Santos-Lima et al. Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014; Rincon, Schekochihin & Cowley Reference Rincon, Schekochihin and Cowley2015; St-Onge & Kunz Reference St-Onge and Kunz2018; St-Onge et al. Reference St-Onge, Kunz, Squire and Schekochihin2020; Sironi, Comisso & Golant Reference Sironi, Comisso and Golant2023; Zhou et al. Reference Zhou, Zhdankin, Kunz, Loureiro and Uzdensky2024) and magnetic reconnection (Cassak et al. Reference Cassak, Baylor, Fermo, Beidler, Shay, Swisdak, Drake and Karimabadi2015; Alt & Kunz Reference Alt and Kunz2019; Winarto & Kunz Reference Winarto and Kunz2022; Egedal et al. Reference Egedal, Gurram, Greess, Daughton and Lê2023).
$\beta$ plasmas that are fundamentally connected to Alfvénic dynamics, such as turbulence (Bott et al. Reference Bott, Arzamasskiy, Kunz, Quataert and Squire2021; Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023; Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023), the fluctuation dynamo (Santos-Lima et al. Reference Santos-Lima, de Gouveia Dal Pino, Kowal, Falceta-Gonçalves, Lazarian and Nakwacki2014; Rincon, Schekochihin & Cowley Reference Rincon, Schekochihin and Cowley2015; St-Onge & Kunz Reference St-Onge and Kunz2018; St-Onge et al. Reference St-Onge, Kunz, Squire and Schekochihin2020; Sironi, Comisso & Golant Reference Sironi, Comisso and Golant2023; Zhou et al. Reference Zhou, Zhdankin, Kunz, Loureiro and Uzdensky2024) and magnetic reconnection (Cassak et al. Reference Cassak, Baylor, Fermo, Beidler, Shay, Swisdak, Drake and Karimabadi2015; Alt & Kunz Reference Alt and Kunz2019; Winarto & Kunz Reference Winarto and Kunz2022; Egedal et al. Reference Egedal, Gurram, Greess, Daughton and Lê2023).
In well-magnetized and collisionless plasmas, the importance of these non-equilibrium effects can be parametrized by the product ![]() $\beta \varDelta$, where
$\beta \varDelta$, where ![]() $\varDelta \doteq p_\perp /p_\parallel -1$ is the normalized difference between thermal pressures across (
$\varDelta \doteq p_\perp /p_\parallel -1$ is the normalized difference between thermal pressures across (![]() $\perp$) and along (
$\perp$) and along (![]() $\parallel$) the local magnetic-field direction. Aside from determining whether a plasma is unstable to various pressure-anisotropy-driven microinstabilities, the quantity
$\parallel$) the local magnetic-field direction. Aside from determining whether a plasma is unstable to various pressure-anisotropy-driven microinstabilities, the quantity ![]() $\beta \varDelta$ also quantifies the competition between the plasma's pressure anisotropy and the magnetic tension, with the characteristic propagation speed of magnetic disturbances being the effective Alfvén speed
$\beta \varDelta$ also quantifies the competition between the plasma's pressure anisotropy and the magnetic tension, with the characteristic propagation speed of magnetic disturbances being the effective Alfvén speed ![]() $v_{{\rm A},{\rm eff}} \doteq v_{{\rm A}}\sqrt {1+\beta \varDelta /2}$. When
$v_{{\rm A},{\rm eff}} \doteq v_{{\rm A}}\sqrt {1+\beta \varDelta /2}$. When ![]() $\beta \varDelta \sim \pm 1$, the restoring tension force can be significantly enhanced or even entirely eliminated, rendering Alfvénic fluctuations impotent. If
$\beta \varDelta \sim \pm 1$, the restoring tension force can be significantly enhanced or even entirely eliminated, rendering Alfvénic fluctuations impotent. If ![]() $\beta \gtrsim 10$, then such circumstances are rather easy to achieve by even small deviations from LTE.
$\beta \gtrsim 10$, then such circumstances are rather easy to achieve by even small deviations from LTE.
The collisionless high-![]() $\beta$ plasmas in which these effects appear are in fact pervasive throughout the universe. Indeed, from radiatively inefficient accretion flows onto supermassive black holes, to the hot and dilute intracluster medium of galaxy clusters, to certain regions of the solar wind at and beyond the Earth's orbit, it is often the case that Coulomb collisions are rare and magnetic fields, while strong enough to magnetize particles, are energetically weak (Kunz et al. Reference Kunz, Squire, Balbus, Bale, Chen, Churazov, Cowley, Forest, Gammie and Quataert2019). Further, turbulence is a ubiquitous phenomenon within these systems, and it plays a crucial role in processes like plasma heating (e.g. Sharma et al. Reference Sharma, Quataert, Hammett and Stone2007; Kunz et al. Reference Kunz, Abel, Klein and Schekochihin2018; Kawazura, Barnes & Schekochihin Reference Kawazura, Barnes and Schekochihin2019; Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023) and angular-momentum transport (e.g. Sharma et al. Reference Sharma, Hammett, Quataert and Stone2006; Kunz, Stone & Quataert Reference Kunz, Stone and Quataert2016; Bacchini et al. Reference Bacchini, Arzamasskiy, Zhdankin, Werner, Begelman and Uzdensky2022; Sandoval et al. Reference Sandoval, Riquelme, Spitkovsky and Bacchini2023). To describe these processes within high-
$\beta$ plasmas in which these effects appear are in fact pervasive throughout the universe. Indeed, from radiatively inefficient accretion flows onto supermassive black holes, to the hot and dilute intracluster medium of galaxy clusters, to certain regions of the solar wind at and beyond the Earth's orbit, it is often the case that Coulomb collisions are rare and magnetic fields, while strong enough to magnetize particles, are energetically weak (Kunz et al. Reference Kunz, Squire, Balbus, Bale, Chen, Churazov, Cowley, Forest, Gammie and Quataert2019). Further, turbulence is a ubiquitous phenomenon within these systems, and it plays a crucial role in processes like plasma heating (e.g. Sharma et al. Reference Sharma, Quataert, Hammett and Stone2007; Kunz et al. Reference Kunz, Abel, Klein and Schekochihin2018; Kawazura, Barnes & Schekochihin Reference Kawazura, Barnes and Schekochihin2019; Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023) and angular-momentum transport (e.g. Sharma et al. Reference Sharma, Hammett, Quataert and Stone2006; Kunz, Stone & Quataert Reference Kunz, Stone and Quataert2016; Bacchini et al. Reference Bacchini, Arzamasskiy, Zhdankin, Werner, Begelman and Uzdensky2022; Sandoval et al. Reference Sandoval, Riquelme, Spitkovsky and Bacchini2023). To describe these processes within high-![]() $\beta$ astrophysical environments accurately, some refinement of our understanding of their turbulent fluctuations is necessary. Therefore, with a focus on the role of
$\beta$ astrophysical environments accurately, some refinement of our understanding of their turbulent fluctuations is necessary. Therefore, with a focus on the role of ![]() $\beta \varDelta$, this work revisits the following three tenets of Alfvénic turbulence that are known to hold in magnetohydrodynamics (MHD) and even
$\beta \varDelta$, this work revisits the following three tenets of Alfvénic turbulence that are known to hold in magnetohydrodynamics (MHD) and even ![]() $\beta \sim 1$ collisionless gyrokinetics: (i) that co-propagating AWs do not interact with one another; (ii) that weak interactions between AWs do not modify their field-aligned wavenumbers; and (iii) that compressive fluctuations in the inertial range are only passively mixed by the Alfvénic cascade.Footnote 2
$\beta \sim 1$ collisionless gyrokinetics: (i) that co-propagating AWs do not interact with one another; (ii) that weak interactions between AWs do not modify their field-aligned wavenumbers; and (iii) that compressive fluctuations in the inertial range are only passively mixed by the Alfvénic cascade.Footnote 2
The assertion that co-propagating AWs do not interact with each other in Alfvénic turbulence (point (i)) is a simple result of ![]() $v_{\rm A}$ being relatively insensitive to nonlinearities in
$v_{\rm A}$ being relatively insensitive to nonlinearities in ![]() $\beta \sim 1$ plasmas. This effect arises naturally from the MHD equations and governs wave interactions across both weak and strong turbulence. Specific to weak AW interactions however (point (ii)), one can effectively apply energy and momentum conservation to pairs of interacting waves since they remain correlated for many linear times. Those constraints, combined with the fact that all Alfvénic fluctuations propagate at
$\beta \sim 1$ plasmas. This effect arises naturally from the MHD equations and governs wave interactions across both weak and strong turbulence. Specific to weak AW interactions however (point (ii)), one can effectively apply energy and momentum conservation to pairs of interacting waves since they remain correlated for many linear times. Those constraints, combined with the fact that all Alfvénic fluctuations propagate at ![]() $v_{\rm A}$, prevent the generation of a cascade in
$v_{\rm A}$, prevent the generation of a cascade in ![]() $k_\|$. Lastly, for point (iii), inertial-range compressive fluctuations being passively mixed by AWs results from the lack of overlap between the linearized eigenvectors of acoustic and Alfvénic fluctuations in
$k_\|$. Lastly, for point (iii), inertial-range compressive fluctuations being passively mixed by AWs results from the lack of overlap between the linearized eigenvectors of acoustic and Alfvénic fluctuations in ![]() $\beta \sim 1$ plasmas when
$\beta \sim 1$ plasmas when ![]() $k_\perp \gg k_\|$. None of the perturbed quantities of the acoustic waves enter to linear order in the propagation of AWs. However, among other things, AWs distort the direction of the magnetic field along which acoustic waves linearly perturb the thermal pressure. As such, they are sensitive to the presence of Alfvénic fluctuations. Yet, all of these phenomena may be expected to change in collisionless high-
$k_\perp \gg k_\|$. None of the perturbed quantities of the acoustic waves enter to linear order in the propagation of AWs. However, among other things, AWs distort the direction of the magnetic field along which acoustic waves linearly perturb the thermal pressure. As such, they are sensitive to the presence of Alfvénic fluctuations. Yet, all of these phenomena may be expected to change in collisionless high-![]() $\beta$ plasmas.
$\beta$ plasmas.
To understand the need for revisiting these wave interactions, consider the example of AW interruption (Squire et al. Reference Squire, Quataert and Schekochihin2016, Reference Squire, Schekochihin and Quataert2017b). In the interruption process, a transverse perturbation (![]() $\delta B_\perp$) to the magnetic field begins to oscillate at the Alfvén frequency and initially decreases in amplitude. As a result, the field strength
$\delta B_\perp$) to the magnetic field begins to oscillate at the Alfvén frequency and initially decreases in amplitude. As a result, the field strength ![]() $|B|\sim B_0 + \delta B_\perp ^2/2B_0$ decreases nonlinearly. Conservation of the double adiabats
$|B|\sim B_0 + \delta B_\perp ^2/2B_0$ decreases nonlinearly. Conservation of the double adiabats ![]() $p_\perp /\rho B$ and
$p_\perp /\rho B$ and ![]() $p_\parallel B^2/\rho ^3$ then dictates that negative pressure anisotropy
$p_\parallel B^2/\rho ^3$ then dictates that negative pressure anisotropy ![]() $\varDelta <0$ is produced. If the amplitude is large enough (
$\varDelta <0$ is produced. If the amplitude is large enough (![]() $\delta B_\perp /B_0 \gtrsim 2\beta ^{-1/2}$), a pressure anisotropy of
$\delta B_\perp /B_0 \gtrsim 2\beta ^{-1/2}$), a pressure anisotropy of ![]() $\varDelta \sim -2\beta ^{-1}$ can be produced by the changing
$\varDelta \sim -2\beta ^{-1}$ can be produced by the changing ![]() $|B|$, although limited to
$|B|$, although limited to ![]() $\varDelta = -2\beta ^{-1}$ by the Alfvénic firehose instability threshold. However, the rate of anisotropy production is Alfvénic, while
$\varDelta = -2\beta ^{-1}$ by the Alfvénic firehose instability threshold. However, the rate of anisotropy production is Alfvénic, while ![]() $p_{\perp /\|}$ are diffused by heat fluxes operating on sonic time scales (
$p_{\perp /\|}$ are diffused by heat fluxes operating on sonic time scales (![]() $\tau _{\rm sonic} \propto L /c_{\rm s} \ll L/v_{\rm A}$, where
$\tau _{\rm sonic} \propto L /c_{\rm s} \ll L/v_{\rm A}$, where ![]() $c_{\rm s} \equiv \sqrt {(2p_\perp /3+p_\|/3)/\rho }$ is the sound speed). The anisotropy is then smoothed out by the heat fluxes and fills the domain with a nearly constant
$c_{\rm s} \equiv \sqrt {(2p_\perp /3+p_\|/3)/\rho }$ is the sound speed). The anisotropy is then smoothed out by the heat fluxes and fills the domain with a nearly constant ![]() $\varDelta = -2\beta ^{-1}$. At this point, the magnetic tension that supports the AW is nullified and the fluctuation ceases propagation, hence the term ‘interruption’.Footnote 3 If an AW is capable of experiencing a dramatic change in its propagation due to its own nonlinearly generated anisotropy, then one would expect that it would similarly respond to the anisotropy generated by other fluctuations within a turbulent system. It is for this reason that we revisit wave–wave interactions within high-
$\varDelta = -2\beta ^{-1}$. At this point, the magnetic tension that supports the AW is nullified and the fluctuation ceases propagation, hence the term ‘interruption’.Footnote 3 If an AW is capable of experiencing a dramatic change in its propagation due to its own nonlinearly generated anisotropy, then one would expect that it would similarly respond to the anisotropy generated by other fluctuations within a turbulent system. It is for this reason that we revisit wave–wave interactions within high-![]() $\beta$ collisionless plasmas.
$\beta$ collisionless plasmas.
In this paper, we focus on the dynamical and thermodynamical interactions between two waves: either ion acoustic waves (IAWs) and AWs, or two co-propagating AWs. In § 2, we outline expectations for these interactions based off of analytical theory performed within the CGL-MHD framework with the help of simplified Landau-fluid heat fluxes (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956; Snyder, Hammett & Dorland Reference Snyder, Hammett and Dorland1997). Following this, in § 3, we test these predictions using a finite-volume Riemann-based code that numerically solves the CGL-MHD equations using the Landau-fluid heat fluxes. Finally, § 4 lays out the implications our results have for both weak and strong turbulence, and details some of the barriers that remain to establish a complete theory of Alfvénic turbulence in high-![]() $\beta$ collisionless plasmas.
$\beta$ collisionless plasmas.
2. Theory
The degrees of freedom associated with wave–wave interactions in a collisionless plasma are numerous, and so to focus our investigation, we make several simplifying assumptions. First, we take the electrons to be much colder than the ions, so that we may set their temperature ![]() $T_{\rm e} = 0$. Certain high-
$T_{\rm e} = 0$. Certain high-![]() $\beta$ astrophysical plasmas are thought to produce these circumstances, such as radiatively inefficient accretion flows onto supermassive black holes (e.g. Quataert Reference Quataert2003). However, the results we present are easily generalizeable to non-zero electron temperature (see § 4). Second, our focus is on the dynamics that occurs on wavelengths much larger than the ion Larmor radius and at frequencies much smaller than the ion gyrofrequency. Accordingly, we employ a fluid model that accounts for the adiabatic production of pressure anisotropy, its spatial redistribution by field-aligned heat fluxes and its dynamical feedback on the plasma through the action of an anisotropic pressure, all while neglecting finite-Larmor-radius effects. These ‘CGL-MHD’ equations (Chew et al. Reference Chew, Goldberger and Low1956) are
$\beta$ astrophysical plasmas are thought to produce these circumstances, such as radiatively inefficient accretion flows onto supermassive black holes (e.g. Quataert Reference Quataert2003). However, the results we present are easily generalizeable to non-zero electron temperature (see § 4). Second, our focus is on the dynamics that occurs on wavelengths much larger than the ion Larmor radius and at frequencies much smaller than the ion gyrofrequency. Accordingly, we employ a fluid model that accounts for the adiabatic production of pressure anisotropy, its spatial redistribution by field-aligned heat fluxes and its dynamical feedback on the plasma through the action of an anisotropic pressure, all while neglecting finite-Larmor-radius effects. These ‘CGL-MHD’ equations (Chew et al. Reference Chew, Goldberger and Low1956) are
Our notation is standard: ![]() $\rho$ is the mass density,
$\rho$ is the mass density, ![]() $\boldsymbol {u}$ is the bulk fluid velocity,
$\boldsymbol {u}$ is the bulk fluid velocity, ![]() $\boldsymbol {B}$ is the magnetic field, and
$\boldsymbol {B}$ is the magnetic field, and ![]() $p_\perp$ and
$p_\perp$ and ![]() $p_\parallel$ are the components of the pressure tensor oriented perpendicular and parallel to the local magnetic-field direction
$p_\parallel$ are the components of the pressure tensor oriented perpendicular and parallel to the local magnetic-field direction ![]() $\hat {\boldsymbol {b}}=\boldsymbol {B}/B$. Note that (2.1a) and (2.1c) may be used in (2.1d) and (2.1e) to obtain
$\hat {\boldsymbol {b}}=\boldsymbol {B}/B$. Note that (2.1a) and (2.1c) may be used in (2.1d) and (2.1e) to obtain
where ![]() ${\rm d}/{\rm d} t\doteq \partial /\partial t + \boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla }$ is the comoving time derivative. These equations express conservation of the first and second adiabatic invariants in the frame of the flow but for the conservative redistribution of
${\rm d}/{\rm d} t\doteq \partial /\partial t + \boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla }$ is the comoving time derivative. These equations express conservation of the first and second adiabatic invariants in the frame of the flow but for the conservative redistribution of ![]() $p_\perp$ and
$p_\perp$ and ![]() $p_\parallel$ by the field-aligned conductive flows of perpendicular and parallel heat,
$p_\parallel$ by the field-aligned conductive flows of perpendicular and parallel heat, ![]() $q_\perp$ and
$q_\perp$ and ![]() $q_\parallel$, respectively. Our third assumption is that these heat fluxes are given by the ‘
$q_\parallel$, respectively. Our third assumption is that these heat fluxes are given by the ‘![]() $3+1$ model’ of Snyder et al. (Reference Snyder, Hammett and Dorland1997), which is tailored to capture the linear collisionless damping rates of small-amplitude fluctuations:
$3+1$ model’ of Snyder et al. (Reference Snyder, Hammett and Dorland1997), which is tailored to capture the linear collisionless damping rates of small-amplitude fluctuations:
 \begin{gather} q_{{\perp}}={-}\frac{2 c_{{\rm s}\|}^2}{\sqrt{2 {\rm \pi}} c_{{\rm s} \|}\left|k_{\|}\right|}\left[\rho \boldsymbol{\nabla}_{\|} \left(\frac{p_{{\perp}}}{\rho}\right)-p_{{\perp}}\left(1-\frac{p_{{\perp}}}{p_{\|}}\right) \frac{\boldsymbol{\nabla}_{\|} B}{B}\right], \end{gather}
\begin{gather} q_{{\perp}}={-}\frac{2 c_{{\rm s}\|}^2}{\sqrt{2 {\rm \pi}} c_{{\rm s} \|}\left|k_{\|}\right|}\left[\rho \boldsymbol{\nabla}_{\|} \left(\frac{p_{{\perp}}}{\rho}\right)-p_{{\perp}}\left(1-\frac{p_{{\perp}}}{p_{\|}}\right) \frac{\boldsymbol{\nabla}_{\|} B}{B}\right], \end{gather} \begin{gather}q_{\|}={-}\frac{8 c_{{\rm s}\|}^2}{\sqrt{8 {\rm \pi}} c_{{\rm s} \|}\left|k_{\|}\right|} \rho \boldsymbol{\nabla}_{\|}\left(\frac{p_{\|}}{\rho}\right), \end{gather}
\begin{gather}q_{\|}={-}\frac{8 c_{{\rm s}\|}^2}{\sqrt{8 {\rm \pi}} c_{{\rm s} \|}\left|k_{\|}\right|} \rho \boldsymbol{\nabla}_{\|}\left(\frac{p_{\|}}{\rho}\right), \end{gather}
where ![]() $c_{{\rm s},\|}=\sqrt {p_\|/\rho }$ is the parallel sound speed. The parameter
$c_{{\rm s},\|}=\sqrt {p_\|/\rho }$ is the parallel sound speed. The parameter ![]() $|k_\parallel |$ is a characteristic field-aligned wavenumber for the fluctuations in
$|k_\parallel |$ is a characteristic field-aligned wavenumber for the fluctuations in ![]() $B$,
$B$, ![]() $p_{\perp /\|}$, and
$p_{\perp /\|}$, and ![]() $\rho$ (e.g. Sharma et al. Reference Sharma, Hammett, Quataert and Stone2006); it is a simplification of the magnitude of the magnetic-field-aligned gradient operator, which would otherwise be very costly to calculate exactly because it is defined with respect to the local magnetic field and involves global operations. Because these heat fluxes describe linear collisionless damping, inherent in their use is the assumption that any perturbations produced by the waves studied here are sufficiently small with respect to the background plasma that nonlinear effects, such as saturation of the collisionless damping, can be ignored. Accordingly, while their analytical simplicity is invaluable in closing the CGL-MHD system, we discuss in § 2.3 some circumstances in which these heat fluxes become inaccurate.
$\rho$ (e.g. Sharma et al. Reference Sharma, Hammett, Quataert and Stone2006); it is a simplification of the magnitude of the magnetic-field-aligned gradient operator, which would otherwise be very costly to calculate exactly because it is defined with respect to the local magnetic field and involves global operations. Because these heat fluxes describe linear collisionless damping, inherent in their use is the assumption that any perturbations produced by the waves studied here are sufficiently small with respect to the background plasma that nonlinear effects, such as saturation of the collisionless damping, can be ignored. Accordingly, while their analytical simplicity is invaluable in closing the CGL-MHD system, we discuss in § 2.3 some circumstances in which these heat fluxes become inaccurate.
2.1. Formulation of the problem
Armed with (2.1), we now constrain the waves whose interactions are the focus of this paper. First, we consider only waves that propagate parallel to the background magnetic field ![]() $\boldsymbol {B}_0$, such that
$\boldsymbol {B}_0$, such that ![]() $k_\perp =0$. This choice removes the nonlinear Alfvénic interaction that normally drives a cascade to small scales, meaning that any interaction seen is solely a consequence of the effects of pressure anisotropy discussed in this work. Admittedly, many problems of interest involve fluctuations that possess
$k_\perp =0$. This choice removes the nonlinear Alfvénic interaction that normally drives a cascade to small scales, meaning that any interaction seen is solely a consequence of the effects of pressure anisotropy discussed in this work. Admittedly, many problems of interest involve fluctuations that possess ![]() $k_\perp /k_\parallel$ of order unity or even much greater, such as critically balanced Alfvénic turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995). However, as we demonstrate in § 2.2, one of the most important aspects of these wave interactions concerns the time scales associated with each interacting wave. Because AWs and IAWs possess frequencies that are independent of
$k_\perp /k_\parallel$ of order unity or even much greater, such as critically balanced Alfvénic turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995). However, as we demonstrate in § 2.2, one of the most important aspects of these wave interactions concerns the time scales associated with each interacting wave. Because AWs and IAWs possess frequencies that are independent of ![]() $k_\perp$, this facet of their interaction is captured regardless of
$k_\perp$, this facet of their interaction is captured regardless of ![]() $k_\perp$ (further discussion of the
$k_\perp$ (further discussion of the ![]() $k_\perp =0$ assumption can be found within § 4). Second, we assume that no constant background pressure anisotropy
$k_\perp =0$ assumption can be found within § 4). Second, we assume that no constant background pressure anisotropy ![]() $\varDelta _0$ is present in the plasma. A non-zero background pressure anisotropy may be included with little effect to the results (so long as the plasma remains stable) by replacing the Alfvén speed
$\varDelta _0$ is present in the plasma. A non-zero background pressure anisotropy may be included with little effect to the results (so long as the plasma remains stable) by replacing the Alfvén speed ![]() $v_{\rm A}\doteq B_0/\sqrt {4{\rm \pi} \rho _0}$, where
$v_{\rm A}\doteq B_0/\sqrt {4{\rm \pi} \rho _0}$, where ![]() $\rho _0$ is the (assumed uniform) background density, with an effective Alfvén speed
$\rho _0$ is the (assumed uniform) background density, with an effective Alfvén speed ![]() $v_{{\rm A},{\rm eff}}\doteq v_{\rm A}\sqrt {1+\beta \varDelta _0/2}$.
$v_{{\rm A},{\rm eff}}\doteq v_{\rm A}\sqrt {1+\beta \varDelta _0/2}$.
Our chief interest in this paper is how an AW responds to the fluctuating pressure anisotropy that results from other waves – a channel of communication that is customarily ignored in studies of plasma turbulence. Therefore, to distil this physics from (2.1), we pursue an asymptotic ordering of the wave perturbations that isolates the Alfvénic response to an externally generated pressure anisotropy ![]() $\varDelta =\varDelta (t,\boldsymbol {r})$. First, the AWs subject to
$\varDelta =\varDelta (t,\boldsymbol {r})$. First, the AWs subject to ![]() $\varDelta$ are taken to be small enough in amplitude that their own nonlinearities can be ignored on the time scales of interest here, viz.
$\varDelta$ are taken to be small enough in amplitude that their own nonlinearities can be ignored on the time scales of interest here, viz. ![]() ${\delta \boldsymbol {B}_\perp /B_0\sim \boldsymbol {u}_\perp /v_{\rm A}\ll 1}$. With
${\delta \boldsymbol {B}_\perp /B_0\sim \boldsymbol {u}_\perp /v_{\rm A}\ll 1}$. With ![]() $k_\perp = 0$, the vectors
$k_\perp = 0$, the vectors ![]() $\delta \boldsymbol {B}_\perp$ and
$\delta \boldsymbol {B}_\perp$ and ![]() $\boldsymbol {u}_\perp$ can be oriented along any perpendicular coordinate without loss of generality, and so henceforth we refer only to
$\boldsymbol {u}_\perp$ can be oriented along any perpendicular coordinate without loss of generality, and so henceforth we refer only to ![]() $\delta B_\perp$ and
$\delta B_\perp$ and ![]() $u_\perp$. Second, we take
$u_\perp$. Second, we take ![]() $\varDelta$ to be large enough that its effect on the Alfvénic dynamics cannot be neglected, i.e.
$\varDelta$ to be large enough that its effect on the Alfvénic dynamics cannot be neglected, i.e. ![]() $|\beta \varDelta | \sim 1$. This ordering allows the stress associated with the pressure anisotropy,
$|\beta \varDelta | \sim 1$. This ordering allows the stress associated with the pressure anisotropy, ![]() $(p_\perp -p_\parallel )\hat {\boldsymbol {b}}\hat {\boldsymbol {b}}$, to be comparable to the Maxwell stress,
$(p_\perp -p_\parallel )\hat {\boldsymbol {b}}\hat {\boldsymbol {b}}$, to be comparable to the Maxwell stress, ![]() $\boldsymbol {BB}/4{\rm \pi}$. Lastly, we allow for compressive fluctuations in the parallel velocity (
$\boldsymbol {BB}/4{\rm \pi}$. Lastly, we allow for compressive fluctuations in the parallel velocity (![]() $u_\|$) and density (
$u_\|$) and density (![]() $\delta \rho$). Because
$\delta \rho$). Because ![]() $k_\perp = 0$ implies
$k_\perp = 0$ implies ![]() $\delta B_\parallel =0$, these fluctuations are purely acoustic, propagating at a speed
$\delta B_\parallel =0$, these fluctuations are purely acoustic, propagating at a speed ![]() ${\sim }c_{\rm s}$ that is much faster than
${\sim }c_{\rm s}$ that is much faster than ![]() $v_{\rm A}$. These assertions combined, the resulting maximal ordering is given by
$v_{\rm A}$. These assertions combined, the resulting maximal ordering is given by
To complete the ordering, we also make assumptions regarding the time evolution of these quantities. In particular, we assume that the time derivatives of ![]() $\delta B_\perp$ and
$\delta B_\perp$ and ![]() $u_\perp$ are Alfvénic (
$u_\perp$ are Alfvénic (![]() $\partial _t \sim k_\parallel v_{\rm A}$), while all other (compressive) quantities evolve on sonic time scales (
$\partial _t \sim k_\parallel v_{\rm A}$), while all other (compressive) quantities evolve on sonic time scales (![]() $\partial _t \sim k_\parallel c_{\rm s}$).
$\partial _t \sim k_\parallel c_{\rm s}$).
Without yet discussing the production/evolution of ![]() $\varDelta$ (to be addressed in §§ 2.2 and 2.3), we may then derive the evolution equations for our ordered Alfvénic fluctuations. Applying (2.4) to the components of (2.1b) and (2.1c) that are perpendicular to the guide field, and retaining only the leading-order terms in
$\varDelta$ (to be addressed in §§ 2.2 and 2.3), we may then derive the evolution equations for our ordered Alfvénic fluctuations. Applying (2.4) to the components of (2.1b) and (2.1c) that are perpendicular to the guide field, and retaining only the leading-order terms in ![]() $\epsilon$, we find that
$\epsilon$, we find that
The transparency of these equations can be improved somewhat by rewriting them in terms of Elsässer variables ![]() $z^\pm = u_\perp \pm \delta B_\perp /\sqrt {4{\rm \pi} \rho _0}$ (Elsässer Reference Elsässer1950):
$z^\pm = u_\perp \pm \delta B_\perp /\sqrt {4{\rm \pi} \rho _0}$ (Elsässer Reference Elsässer1950):
The left-hand side of these Elsässer equations describe forward (![]() $-$) and backward (
$-$) and backward (![]() $+$) propagating AWs. The right-hand side provides the nonlinear interaction with another fluctuation that perturbs the pressure anisotropically. This anisotropy can arise from linear acoustic modes, or even other large-amplitude AWs that generate
$+$) propagating AWs. The right-hand side provides the nonlinear interaction with another fluctuation that perturbs the pressure anisotropically. This anisotropy can arise from linear acoustic modes, or even other large-amplitude AWs that generate ![]() $\varDelta$ nonlinearly. We analyse both of these situations in §§ 2.2 and 2.3.
$\varDelta$ nonlinearly. We analyse both of these situations in §§ 2.2 and 2.3.
2.2. Interaction between ion-acoustic and Alfvén waves
In this section, we describe the interaction between monochromatic IAWs and AWs in an otherwise uniform plasma with density ![]() $\rho _0$ and pressure
$\rho _0$ and pressure ![]() $p_0 = \beta B_0^2/8{\rm \pi}$. This demands an understanding of the evolution of the
$p_0 = \beta B_0^2/8{\rm \pi}$. This demands an understanding of the evolution of the ![]() $\varDelta$ that appears on the right-hand side of (2.6). In our high-
$\varDelta$ that appears on the right-hand side of (2.6). In our high-![]() $\beta$ ordering (2.4), the IAW fluctuations are energetically dominant over the Alfvénic fluctuations and, given their compressive nature, are chiefly responsible for the pressure perturbations
$\beta$ ordering (2.4), the IAW fluctuations are energetically dominant over the Alfvénic fluctuations and, given their compressive nature, are chiefly responsible for the pressure perturbations ![]() $\delta p_\|$ and
$\delta p_\|$ and ![]() $\delta p_\perp$. This can be seen by applying (2.4) to the compressive components of (2.1), recalling that the time derivatives of compressive quantities are ordered as
$\delta p_\perp$. This can be seen by applying (2.4) to the compressive components of (2.1), recalling that the time derivatives of compressive quantities are ordered as ![]() $\partial _t \sim k c_{\rm s}$, and retaining only leading-order terms:
$\partial _t \sim k c_{\rm s}$, and retaining only leading-order terms:
These equations describing ion-acoustic fluctuations are entirely linear, with no feedback from the Alfvénic fluctuations. Therefore, we may simply prescribe the pressure anisotropy in (2.6) being due to ion-acoustic fluctuations as
where ![]() $\omega _{\rm C} \approx (\pm 1.47 + 0.46\mathrm {i})k_{\rm C} c_{\rm s}$ is the (complex) linear frequency of a damped ion-acoustic wave.Footnote 4 Substituting this anisotropy (with
$\omega _{\rm C} \approx (\pm 1.47 + 0.46\mathrm {i})k_{\rm C} c_{\rm s}$ is the (complex) linear frequency of a damped ion-acoustic wave.Footnote 4 Substituting this anisotropy (with ![]() $+\omega _{\rm C}$ to start) into the Elsässer equation (2.6) and Fourier transforming into
$+\omega _{\rm C}$ to start) into the Elsässer equation (2.6) and Fourier transforming into ![]() $k$-space yields the following evolution equation for AWs at each wavenumber:
$k$-space yields the following evolution equation for AWs at each wavenumber:
The right-hand side of (2.9) shows that both forward- and backward-propagating AWs are generated at different wavenumbers when an AW is subject to the pressure anisotropy of an acoustic wave. Although this interaction term is not precisely proportional to the level of imbalance ![]() $|z^+(k)|^2-|z^-(k)|^2$, no change to either
$|z^+(k)|^2-|z^-(k)|^2$, no change to either ![]() $z^+$ or
$z^+$ or ![]() $z^-$ will result if their initial amplitudes are exactly equal.
$z^-$ will result if their initial amplitudes are exactly equal.
Assuming only an initial ![]() $z^-$, which makes the acoustic and Alfvén waves counter-propagating, the dynamics at the initial Alfvén mode's wavenumber
$z^-$, which makes the acoustic and Alfvén waves counter-propagating, the dynamics at the initial Alfvén mode's wavenumber ![]() $k_{\rm A}$ is simply
$k_{\rm A}$ is simply
The leading-order wave–wave interaction can be found at ![]() $k_{\rm A}+k_{\rm C}$ by evaluating (2.9) given (2.10):
$k_{\rm A}+k_{\rm C}$ by evaluating (2.9) given (2.10):
 \begin{gather} \left.\begin{aligned} z^+(k_{\rm A}+k_{\rm C}) \approx z_0\frac{\beta\varDelta_0}{4} \left( \frac{\omega_{\rm A}+k_{\rm C}v_{\rm A}}{2\omega_{\rm A} \,{-}\, \omega _{\rm C}+k_{\rm C}v_{\rm A}} \right) \left[\exp({{\rm i}(\omega _{\rm C}\,{-}\,\omega_{\rm A})t}) \,{-}\, \exp({{\rm i} (k_{\rm A} +k_{\rm C})v_{\rm A} t})\right], \\ z^-(k_{\rm A}+k_{\rm C}) \approx z_0\frac{\beta\varDelta_0}{4} \left( \frac{\omega_{\rm A}+k_{\rm C}v_{\rm A}}{\omega _{\rm C} + k_{\rm C}v_{\rm A}} \right) \left[\exp({{\rm i}(\omega _{\rm C}-\omega_{\rm A})t}) \,{-}\, \exp({-{\rm i} (k_{\rm A} +k_{\rm C})v_{\rm A} t})\right] , \end{aligned}\!\right\} \end{gather}
\begin{gather} \left.\begin{aligned} z^+(k_{\rm A}+k_{\rm C}) \approx z_0\frac{\beta\varDelta_0}{4} \left( \frac{\omega_{\rm A}+k_{\rm C}v_{\rm A}}{2\omega_{\rm A} \,{-}\, \omega _{\rm C}+k_{\rm C}v_{\rm A}} \right) \left[\exp({{\rm i}(\omega _{\rm C}\,{-}\,\omega_{\rm A})t}) \,{-}\, \exp({{\rm i} (k_{\rm A} +k_{\rm C})v_{\rm A} t})\right], \\ z^-(k_{\rm A}+k_{\rm C}) \approx z_0\frac{\beta\varDelta_0}{4} \left( \frac{\omega_{\rm A}+k_{\rm C}v_{\rm A}}{\omega _{\rm C} + k_{\rm C}v_{\rm A}} \right) \left[\exp({{\rm i}(\omega _{\rm C}-\omega_{\rm A})t}) \,{-}\, \exp({-{\rm i} (k_{\rm A} +k_{\rm C})v_{\rm A} t})\right] , \end{aligned}\!\right\} \end{gather}
where we have defined ![]() $\omega _{\rm A} \doteq k_{\rm A}v_{\rm A}$. Note that the choice
$\omega _{\rm A} \doteq k_{\rm A}v_{\rm A}$. Note that the choice ![]() $k_{\rm C} \sim k_{\rm A}$ implies
$k_{\rm C} \sim k_{\rm A}$ implies ![]() $|\omega _{\rm C}| \gg \omega _{\rm A}$, and thus a weak interaction in high-
$|\omega _{\rm C}| \gg \omega _{\rm A}$, and thus a weak interaction in high-![]() $\beta$ plasmas. To obtain a stronger interaction, we focus on the amplitude of the reflected wave packet (for
$\beta$ plasmas. To obtain a stronger interaction, we focus on the amplitude of the reflected wave packet (for ![]() $\mathrm {Re}(\omega _{\rm C})>0$) and maximize the absolute value of the
$\mathrm {Re}(\omega _{\rm C})>0$) and maximize the absolute value of the ![]() $z^+$ coefficient. Doing so indicates that the strongest interaction occurs when
$z^+$ coefficient. Doing so indicates that the strongest interaction occurs when
where the subscripts ‘![]() ${\rm r}$’ and ‘
${\rm r}$’ and ‘![]() ${\rm i}$’ denote the real and imaginary parts of
${\rm i}$’ denote the real and imaginary parts of ![]() $\omega _{\rm C}$. With
$\omega _{\rm C}$. With ![]() ${\beta \gg 1}$, (2.12) makes the absolute value of the
${\beta \gg 1}$, (2.12) makes the absolute value of the ![]() $z^-$ coefficient
$z^-$ coefficient ![]() ${\approx }0.3z_0\beta \varDelta _0$. For
${\approx }0.3z_0\beta \varDelta _0$. For ![]() $\beta \varDelta _0 \sim 1$, this is always an
$\beta \varDelta _0 \sim 1$, this is always an ![]() $\mathcal {O}(1)$ interaction, decreasing linearly with the amplitude of the acoustic mode. Perhaps unsurprisingly, the strongest interaction occurs when the frequencies are nearly matched, although this also means that there is effectively no change in wavenumber of the Alfvénic fluctuations, since
$\mathcal {O}(1)$ interaction, decreasing linearly with the amplitude of the acoustic mode. Perhaps unsurprisingly, the strongest interaction occurs when the frequencies are nearly matched, although this also means that there is effectively no change in wavenumber of the Alfvénic fluctuations, since ![]() $k_{\rm A}+k_{\rm C} \approx k_{\rm A} (1 + 2/\sqrt {\beta }) \sim k_{\rm A}$. In this sense, the strongest IAW–AW interaction resembles the frequency-matching condition of the parametric decay instability (Sagdeev & Galeev Reference Sagdeev and Galeev1969). Additionally, while the maximum
$k_{\rm A}+k_{\rm C} \approx k_{\rm A} (1 + 2/\sqrt {\beta }) \sim k_{\rm A}$. In this sense, the strongest IAW–AW interaction resembles the frequency-matching condition of the parametric decay instability (Sagdeev & Galeev Reference Sagdeev and Galeev1969). Additionally, while the maximum ![]() $z^+$ coefficient occurs for
$z^+$ coefficient occurs for ![]() $\omega _{{\rm C}, {\rm r}}>0$, the situation with
$\omega _{{\rm C}, {\rm r}}>0$, the situation with ![]() $k_{\rm C} \sim k_{\rm A}/\sqrt {\beta }$ still yields an
$k_{\rm C} \sim k_{\rm A}/\sqrt {\beta }$ still yields an ![]() $\mathcal {O}(1)$ reflection if
$\mathcal {O}(1)$ reflection if ![]() $\omega _{{\rm C}, {\rm r}} <0$ (i.e. if the waves are co-propagating).
$\omega _{{\rm C}, {\rm r}} <0$ (i.e. if the waves are co-propagating).
To apply these conclusions to physical systems, we must also consider the case where ![]() $\varDelta$ is purely real. This demands that the Fourier expansion of
$\varDelta$ is purely real. This demands that the Fourier expansion of ![]() $\varDelta$ contains both
$\varDelta$ contains both ![]() $+\textrm {i} k_{\rm C}$ and
$+\textrm {i} k_{\rm C}$ and ![]() $-\textrm {i} k_{\rm C}$ exponentials, which in turn create source terms on the right-hand side of (2.9) from both
$-\textrm {i} k_{\rm C}$ exponentials, which in turn create source terms on the right-hand side of (2.9) from both ![]() $k-k_{\rm C}$ and
$k-k_{\rm C}$ and ![]() $k+k_{\rm C}$. While this complicates the problem somewhat, (2.11) can still be used to obtain an order-of-magnitude estimate for the solution. The reason for this stems from the fact that the acoustic mode collisionlessly damps on the same time scale as it propagates. By the time an Alfvénic fluctuation at
$k+k_{\rm C}$. While this complicates the problem somewhat, (2.11) can still be used to obtain an order-of-magnitude estimate for the solution. The reason for this stems from the fact that the acoustic mode collisionlessly damps on the same time scale as it propagates. By the time an Alfvénic fluctuation at ![]() $k_{\rm A}+k_{\rm C}$ grows because of the interaction to a similar amplitude as that of the original wave at
$k_{\rm A}+k_{\rm C}$ grows because of the interaction to a similar amplitude as that of the original wave at ![]() $k_{\rm A}$,
$k_{\rm A}$, ![]() $\varDelta$ has largely vanished. The subsequent interaction of the
$\varDelta$ has largely vanished. The subsequent interaction of the ![]() $k_{\rm A}+k_{\rm C}$ AW with the now nearly depleted
$k_{\rm A}+k_{\rm C}$ AW with the now nearly depleted ![]() $\varDelta$ to generate a
$\varDelta$ to generate a ![]() $k_{\rm A}+2k_{\rm C}$ mode will be considerably weaker. As a result, the amplitude of the
$k_{\rm A}+2k_{\rm C}$ mode will be considerably weaker. As a result, the amplitude of the ![]() $k_{\rm A}+2k_{\rm C}$ fluctuation is likely to be small, and may not provide significant feedback to the evolution of the mode at
$k_{\rm A}+2k_{\rm C}$ fluctuation is likely to be small, and may not provide significant feedback to the evolution of the mode at ![]() $k_{\rm A}+k_{\rm C}$. This prediction is tested using numerical simulations in § 3.
$k_{\rm A}+k_{\rm C}$. This prediction is tested using numerical simulations in § 3.
The conservation of certain quantities by this interaction may also be of interest. In particular, it may appear jarring that there is a nonlinear mechanism in (2.6) by which new Alfvénic fluctuations can be generated, but no corresponding sink present in (2.7). This would seem to imply that energy is not conserved if ![]() $|z^\pm |^2$ increase but nothing happens to the acoustic fluctuations. In this case, the apparent mismatch stems from the fact that, if
$|z^\pm |^2$ increase but nothing happens to the acoustic fluctuations. In this case, the apparent mismatch stems from the fact that, if ![]() $u_\parallel /c_{\rm s} \sim u_\perp /v_{\rm A}$, then there is considerably more (
$u_\parallel /c_{\rm s} \sim u_\perp /v_{\rm A}$, then there is considerably more (![]() ${\sim } \beta \times$) energy present in the acoustic fluctuations than in the Alfvénic ones. As a result, any energy given up by the acoustic fluctuations is higher order to themselves, but leading order to an AW with comparable amplitude. This can be demonstrated by going to third order in the compressive equations and re-establishing conservation of energy, a calculation presented in detail in Appendix A.Footnote 5 Why energy goes to the Alfvénic from the acoustic fluctuations is not as obvious. The reason becomes apparent, however, when considering the same interaction without damping of the acoustic wave. With
${\sim } \beta \times$) energy present in the acoustic fluctuations than in the Alfvénic ones. As a result, any energy given up by the acoustic fluctuations is higher order to themselves, but leading order to an AW with comparable amplitude. This can be demonstrated by going to third order in the compressive equations and re-establishing conservation of energy, a calculation presented in detail in Appendix A.Footnote 5 Why energy goes to the Alfvénic from the acoustic fluctuations is not as obvious. The reason becomes apparent, however, when considering the same interaction without damping of the acoustic wave. With ![]() $\omega _{{\rm C},{\rm i}}=0$ in (2.11), the leading-order Alfvénic response would then have a purely periodic amplitude at each
$\omega _{{\rm C},{\rm i}}=0$ in (2.11), the leading-order Alfvénic response would then have a purely periodic amplitude at each ![]() $k$. Essentially, the effects of a fluctuation with
$k$. Essentially, the effects of a fluctuation with ![]() $\varDelta >0$ would be nearly wiped out by the subsequent equivalent negative anisotropy. Only the root mean square amplitude of the newly generated fluctuations would grow, and on a time scale much slower than the AW propagation. Instead, if the anisotropy decays, then the positive anisotropy generated during the first half of the acoustic period would be larger than the negative anisotropy generated during the second half-period, meaning that the difference in the nonlinear effects accumulates. Once the acoustic wave is decayed away, each
$\varDelta >0$ would be nearly wiped out by the subsequent equivalent negative anisotropy. Only the root mean square amplitude of the newly generated fluctuations would grow, and on a time scale much slower than the AW propagation. Instead, if the anisotropy decays, then the positive anisotropy generated during the first half of the acoustic period would be larger than the negative anisotropy generated during the second half-period, meaning that the difference in the nonlinear effects accumulates. Once the acoustic wave is decayed away, each ![]() $k$ of the Alfvénic spectrum is left with only a steady-state amplitude and energy.
$k$ of the Alfvénic spectrum is left with only a steady-state amplitude and energy.
2.3. Interaction between two AWs
The other source of pressure anisotropy we consider for (2.6) is another, larger-amplitude AW. In particular, we are interested in the ability of nonlinear AWs to generate pressure anisotropy, thereby modifying their own ![]() $v_{{\rm A},\textrm {eff}}$ in a manner that is dependent upon their amplitudes (similarly to the interruption process described in § 1; Squire et al. Reference Squire, Quataert and Schekochihin2016). We therefore choose to study the interaction between two co-propagating AW packets, which are initially isolated such that their self-modified
$v_{{\rm A},\textrm {eff}}$ in a manner that is dependent upon their amplitudes (similarly to the interruption process described in § 1; Squire et al. Reference Squire, Quataert and Schekochihin2016). We therefore choose to study the interaction between two co-propagating AW packets, which are initially isolated such that their self-modified ![]() $v_{{\rm A},\textrm {eff}}$ do not affect the other wavepacket. In this set-up, one of the wave packets will be large enough in amplitude such that it generates a pressure anisotropy
$v_{{\rm A},\textrm {eff}}$ do not affect the other wavepacket. In this set-up, one of the wave packets will be large enough in amplitude such that it generates a pressure anisotropy ![]() $\varDelta \sim \beta ^{-1}$, thereby fulfilling the role of the IAW in § 2.2. This will be called the ‘primary’ wave packet (with relevant quantities denoted by the subscript ‘p’). We first calculate the pressure anisotropy generated by this primary wave packet and demonstrate that its
$\varDelta \sim \beta ^{-1}$, thereby fulfilling the role of the IAW in § 2.2. This will be called the ‘primary’ wave packet (with relevant quantities denoted by the subscript ‘p’). We first calculate the pressure anisotropy generated by this primary wave packet and demonstrate that its ![]() $v_{{\rm A},\textrm {eff}}$ is increased as a result. Given sufficient time then, the two initially separated wave packets will be able to interact if the trailing wave packet is of larger amplitude. To study the subsequent interaction, we consider the leading (‘secondary’) wave packet to satisfy the Alfvénic components of (2.4), thereby allowing us to employ (2.6) in solving for its nonlinear deformation, while ignoring the back reaction on the primary AW packet.
$v_{{\rm A},\textrm {eff}}$ is increased as a result. Given sufficient time then, the two initially separated wave packets will be able to interact if the trailing wave packet is of larger amplitude. To study the subsequent interaction, we consider the leading (‘secondary’) wave packet to satisfy the Alfvénic components of (2.4), thereby allowing us to employ (2.6) in solving for its nonlinear deformation, while ignoring the back reaction on the primary AW packet.
The mechanism for producing pressure anisotropy differs considerably between IAWs and shear-Alfvén waves. While pressure anisotropy is produced at linear order for the former, the latter change neither the magnetic-field strength nor the plasma density to linear order in the fluctuation amplitude, and so by adiabatic invariance have no associated linear pressure anisotropy. Indeed, (2.2) without the heat fluxes giveFootnote 6
The magnetic-field strength changes only at second order in the fluctuation amplitude, according to ![]() $B = \sqrt {B_0^2 +\delta B_{\perp,{\rm p}}^2}$ (while
$B = \sqrt {B_0^2 +\delta B_{\perp,{\rm p}}^2}$ (while ![]() $\delta \rho = 0$). From this, it is clear that
$\delta \rho = 0$). From this, it is clear that ![]() $\delta B^2_{\perp,{\rm p}}/B^2_0$ must be
$\delta B^2_{\perp,{\rm p}}/B^2_0$ must be ![]() ${\gtrsim }1/\beta$ for the stress associated with the induced pressure anisotropy to be comparable to the Maxwell stress (the usual restoring force in an AW; Squire et al. Reference Squire, Quataert and Schekochihin2016). In AW packets of this amplitude, the addition of a competitive pressure-anisotropic stress dictates that their initial perturbation will be unable to propagate rigidly at
${\gtrsim }1/\beta$ for the stress associated with the induced pressure anisotropy to be comparable to the Maxwell stress (the usual restoring force in an AW; Squire et al. Reference Squire, Quataert and Schekochihin2016). In AW packets of this amplitude, the addition of a competitive pressure-anisotropic stress dictates that their initial perturbation will be unable to propagate rigidly at ![]() $v_{\rm A}$ as is the case when
$v_{\rm A}$ as is the case when ![]() $\varDelta =0$. Instead, a strictly positive (owing to
$\varDelta =0$. Instead, a strictly positive (owing to ![]() $\delta B_{\perp, {\rm p}}^2 >0$) nonlinear pressure anisotropy will be generated by the oscillating
$\delta B_{\perp, {\rm p}}^2 >0$) nonlinear pressure anisotropy will be generated by the oscillating ![]() $\delta B_{\perp, {\rm p}}$ with a dominant wavenumber of
$\delta B_{\perp, {\rm p}}$ with a dominant wavenumber of ![]() $k=2k_{\rm A}$. This cannot, however, last in the presence of the heat fluxes (2.4). The pressure anisotropy
$k=2k_{\rm A}$. This cannot, however, last in the presence of the heat fluxes (2.4). The pressure anisotropy ![]() $\varDelta _{\rm p}$ is generated by the AW packet as it propagates at a rate of
$\varDelta _{\rm p}$ is generated by the AW packet as it propagates at a rate of ![]() $\sim kv_{\rm A}$, while it is diffused by the heat fluxes at a much faster rate of
$\sim kv_{\rm A}$, while it is diffused by the heat fluxes at a much faster rate of ![]() $\sim kc_{\rm s}$. As a result,
$\sim kc_{\rm s}$. As a result, ![]() $\varDelta _{\rm p}$ is smeared out across the wave packet as it propagates, inheriting the spatial structure of the wave packet envelope rather than the mode itself. The end result is that shear AW packets initialized with an amplitude
$\varDelta _{\rm p}$ is smeared out across the wave packet as it propagates, inheriting the spatial structure of the wave packet envelope rather than the mode itself. The end result is that shear AW packets initialized with an amplitude ![]() $\delta B_\perp /B_0 \gtrsim \beta ^{-1/2}$ generate smooth, envelope-scale, positive pressure anisotropies. Accordingly,
$\delta B_\perp /B_0 \gtrsim \beta ^{-1/2}$ generate smooth, envelope-scale, positive pressure anisotropies. Accordingly, ![]() $v_{{\rm A},\textrm {eff}}>v_{\rm A}$ and such packets propagate faster than those with small (linear) amplitudes.Footnote 7
$v_{{\rm A},\textrm {eff}}>v_{\rm A}$ and such packets propagate faster than those with small (linear) amplitudes.Footnote 7
With a ![]() $\varDelta _{\rm p}$ profile resembling the envelope of the parent AW packet (rather than the oscillating wave within the envelope), there will be a peak in the magnitude of
$\varDelta _{\rm p}$ profile resembling the envelope of the parent AW packet (rather than the oscillating wave within the envelope), there will be a peak in the magnitude of ![]() $\varDelta _{\rm p}$ at the centre of the packet, where
$\varDelta _{\rm p}$ at the centre of the packet, where ![]() $\delta B_{\perp, {\rm p}}^2$ is the largest. Through
$\delta B_{\perp, {\rm p}}^2$ is the largest. Through ![]() $v_{{\rm A},\textrm {eff}} = v_{\rm A}\sqrt {1+\beta \varDelta _{\rm p}(x)/2}$, this region of the packet will travel faster than the regions with lower
$v_{{\rm A},\textrm {eff}} = v_{\rm A}\sqrt {1+\beta \varDelta _{\rm p}(x)/2}$, this region of the packet will travel faster than the regions with lower ![]() $\delta B_{\perp, {\rm p}}^2$ that occur at the trailing edge of the envelope. In time, an isolated AW packet should therefore steepen to form a shock-like wavefront, which propagates at an enhanced
$\delta B_{\perp, {\rm p}}^2$ that occur at the trailing edge of the envelope. In time, an isolated AW packet should therefore steepen to form a shock-like wavefront, which propagates at an enhanced ![]() $v_{{\rm A},\textrm {eff}}$ from the background.Footnote 8 It is this shocked, more rapidly propagating wave packet that can interact with smaller amplitude AW packets in front of it. In a collisionless plasma, however, the heat fluxes driven by a shock-like gradient in the pressure cannot be accurately described by (2.3). This complicates our effort to solve (2.1d) and (2.1e) for the
$v_{{\rm A},\textrm {eff}}$ from the background.Footnote 8 It is this shocked, more rapidly propagating wave packet that can interact with smaller amplitude AW packets in front of it. In a collisionless plasma, however, the heat fluxes driven by a shock-like gradient in the pressure cannot be accurately described by (2.3). This complicates our effort to solve (2.1d) and (2.1e) for the ![]() $\varDelta _{\rm p}$ of the steepened packet. In this case, two alternative descriptions of
$\varDelta _{\rm p}$ of the steepened packet. In this case, two alternative descriptions of ![]() $\boldsymbol {q}_{\perp /\|}$ are likely to be more accurate. For one, the heat fluxes may simply be that of free streaming particles. Unless reflected by the mirror force, plasma particles would transit the shock front and change their perpendicular temperature adiabatically according to
$\boldsymbol {q}_{\perp /\|}$ are likely to be more accurate. For one, the heat fluxes may simply be that of free streaming particles. Unless reflected by the mirror force, plasma particles would transit the shock front and change their perpendicular temperature adiabatically according to ![]() $\delta T_{\perp,{\rm p}}/T_0 \approx \delta B_{\perp,{\rm p}}^2/2B_0^2$. Another possibility, which is likely for near-interruption AW packets in particular, is that the distribution of particle velocities resulting from an adiabatic response to
$\delta T_{\perp,{\rm p}}/T_0 \approx \delta B_{\perp,{\rm p}}^2/2B_0^2$. Another possibility, which is likely for near-interruption AW packets in particular, is that the distribution of particle velocities resulting from an adiabatic response to ![]() $\delta B_{\perp,{\rm p}}$ would be unstable to kinetic microinstabilities. Larmor-scale magnetic fluctuations generated by the ion-acoustic or whistler heat-flux instabilities (Komarov et al. Reference Komarov, Schekochihin, Churazov and Spitkovsky2018; Roberg-Clark et al. Reference Roberg-Clark, Drake, Swisdak and Reynolds2018) could scatter particles in pitch angle, giving the heat fluxes a similar functional form as (2.3), but with a different effective diffusion rate. We choose to continue our analysis under this assumption of diffusive heat fluxes, both because it may apply in particular to near-interruption AW packets, and for the fact that our ‘
$\delta B_{\perp,{\rm p}}$ would be unstable to kinetic microinstabilities. Larmor-scale magnetic fluctuations generated by the ion-acoustic or whistler heat-flux instabilities (Komarov et al. Reference Komarov, Schekochihin, Churazov and Spitkovsky2018; Roberg-Clark et al. Reference Roberg-Clark, Drake, Swisdak and Reynolds2018) could scatter particles in pitch angle, giving the heat fluxes a similar functional form as (2.3), but with a different effective diffusion rate. We choose to continue our analysis under this assumption of diffusive heat fluxes, both because it may apply in particular to near-interruption AW packets, and for the fact that our ‘![]() $3+1$’ Landau-fluid heat fluxes (2.3) are also diffusive, allowing us to verify the results numerically for arbitrary diffusion coefficients by modifying
$3+1$’ Landau-fluid heat fluxes (2.3) are also diffusive, allowing us to verify the results numerically for arbitrary diffusion coefficients by modifying ![]() $|k_\||$ (Appendix B). In this case, given that particle motions are thermal, the upstream plasma with its higher temperature is able to pass through the shock front and diffuse downstream, at a rate controlled by the diffusion coefficient. This leads to the development of a pressure anisotropy precursor, which stretches in front of the shock as it propagates. For a finite diffusion coefficient, this precursor decays away steadily as one moves further downstream of the shock. We derive this precursor analytically in Appendix B for a general diffusion coefficient
$|k_\||$ (Appendix B). In this case, given that particle motions are thermal, the upstream plasma with its higher temperature is able to pass through the shock front and diffuse downstream, at a rate controlled by the diffusion coefficient. This leads to the development of a pressure anisotropy precursor, which stretches in front of the shock as it propagates. For a finite diffusion coefficient, this precursor decays away steadily as one moves further downstream of the shock. We derive this precursor analytically in Appendix B for a general diffusion coefficient ![]() $\kappa$, finding that the functional form of the pressure anisotropy is a decaying exponential in a frame moving with the shock.
$\kappa$, finding that the functional form of the pressure anisotropy is a decaying exponential in a frame moving with the shock.
What remains to be discussed is how the ![]() $\varDelta _{\rm p}$ precursor of a large AW packet affects smaller-amplitude AW packets that cannot outrun its increased propagation speed,
$\varDelta _{\rm p}$ precursor of a large AW packet affects smaller-amplitude AW packets that cannot outrun its increased propagation speed, ![]() $v_{{\rm A},\textrm {eff}}>v_{\rm A}$. As the tail of a secondary wave packet begins to feel the
$v_{{\rm A},\textrm {eff}}>v_{\rm A}$. As the tail of a secondary wave packet begins to feel the ![]() $\varDelta _{\rm p}$ of the larger-amplitude primary packet approaching from behind it, there will be a larger
$\varDelta _{\rm p}$ of the larger-amplitude primary packet approaching from behind it, there will be a larger ![]() $v_{{\rm A},\textrm {eff}}$ at the back of the secondary wave packet than at the front. This will cause the secondary packet to compress, shortening its parallel wavelength. Unlike the IAW–AW interaction however, no backward propagating AW packet will be created. To see why, consider the evolution equation (2.6) for
$v_{{\rm A},\textrm {eff}}$ at the back of the secondary wave packet than at the front. This will cause the secondary packet to compress, shortening its parallel wavelength. Unlike the IAW–AW interaction however, no backward propagating AW packet will be created. To see why, consider the evolution equation (2.6) for ![]() $z^+$ assuming only an initial
$z^+$ assuming only an initial ![]() $z^-$:
$z^-$:
The final term on the right-hand side represents a possible source or sink, depending on its sign. However, for ![]() $\partial _x \varDelta _{\rm p} <0$, the first term on the right-hand side damps
$\partial _x \varDelta _{\rm p} <0$, the first term on the right-hand side damps ![]() $z^+$ exponentially along the wave characteristics. Given that the
$z^+$ exponentially along the wave characteristics. Given that the ![]() $\varDelta$-precursor of a large-amplitude
$\varDelta$-precursor of a large-amplitude ![]() $z^-$ packet is monotonically decreasing in
$z^-$ packet is monotonically decreasing in ![]() $x$,
$x$, ![]() $z^+$ fluctuations are always damped in this interaction. This simplifies the equation for
$z^+$ fluctuations are always damped in this interaction. This simplifies the equation for ![]() $z^-$, which can be written in terms of its energy density
$z^-$, which can be written in terms of its energy density ![]() $\mathcal {E}^-(x) \doteq |z^-|^2$ by assuming
$\mathcal {E}^-(x) \doteq |z^-|^2$ by assuming ![]() $z^+=0$:
$z^+=0$:
Solving (2.15) using the method of characteristics yields
 \begin{equation} \mathcal{E}^-(x,t) = \mathcal{E}_0^-(x_0(t,x)) \exp \left\{{-}v_{\rm A}\frac{\beta}{2}\int\limits_0^t\,\mathrm{d}t'\left.\frac{\partial \varDelta _{\rm p}}{\partial x}\right|_{x(t',x_0)}\right\}, \end{equation}
\begin{equation} \mathcal{E}^-(x,t) = \mathcal{E}_0^-(x_0(t,x)) \exp \left\{{-}v_{\rm A}\frac{\beta}{2}\int\limits_0^t\,\mathrm{d}t'\left.\frac{\partial \varDelta _{\rm p}}{\partial x}\right|_{x(t',x_0)}\right\}, \end{equation}
where ![]() $x(t,x_0)$ is the trajectory of the
$x(t,x_0)$ is the trajectory of the ![]() $x_0$ characteristic determined by the solution of
$x_0$ characteristic determined by the solution of
and ![]() $x_0(t,x)$ is the foot of the characteristic obtained by inverting
$x_0(t,x)$ is the foot of the characteristic obtained by inverting ![]() $x(t,x_0)$. Equation (2.16) states that the tail of the smaller-amplitude AW packet will steepen according to
$x(t,x_0)$. Equation (2.16) states that the tail of the smaller-amplitude AW packet will steepen according to ![]() ${d}_tx$, while growing exponentially along characteristics (and more rapidly so for steeper
${d}_tx$, while growing exponentially along characteristics (and more rapidly so for steeper ![]() $\varDelta _{\rm p}$). Motivated by the derivation of the
$\varDelta _{\rm p}$). Motivated by the derivation of the ![]() $\varDelta _{\rm p}$ precursor for diffusive heat fluxes in Appendix B, we consider an exponentially decaying anisotropy
$\varDelta _{\rm p}$ precursor for diffusive heat fluxes in Appendix B, we consider an exponentially decaying anisotropy
which propagates rigidly at ![]() $v_{{\rm A},\textrm {eff}} = v_{\rm A}\sqrt {1+\beta \varDelta _{{\rm p}, 0}/2}$. Figure 1(a) shows the characteristics that such an anisotropy would generate if
$v_{{\rm A},\textrm {eff}} = v_{\rm A}\sqrt {1+\beta \varDelta _{{\rm p}, 0}/2}$. Figure 1(a) shows the characteristics that such an anisotropy would generate if ![]() $\varDelta _{{\rm p},0} = \beta ^{-1}$ and
$\varDelta _{{\rm p},0} = \beta ^{-1}$ and ![]() $l=0.1L$, where
$l=0.1L$, where ![]() $L$ is a characteristic domain length. The compression of characteristics indicates that the trailing end of the secondary mode develops a shorter wavelength over time. Figure 1(b) exhibits the gain in energy experienced by a Gaussian wave packet that is subjected to this
$L$ is a characteristic domain length. The compression of characteristics indicates that the trailing end of the secondary mode develops a shorter wavelength over time. Figure 1(b) exhibits the gain in energy experienced by a Gaussian wave packet that is subjected to this ![]() $\varDelta _{\rm p}(x)$ after
$\varDelta _{\rm p}(x)$ after ![]() $t=L/v_{\rm A}$, for different values of the decay length
$t=L/v_{\rm A}$, for different values of the decay length ![]() $l_{\varDelta }/L$. As
$l_{\varDelta }/L$. As ![]() $l_{\varDelta }/L$ becomes smaller, the gain in energy of the mode begins to increase. In general, this trend of increasing energy gain will continue, but here the gain curve drops when
$l_{\varDelta }/L$ becomes smaller, the gain in energy of the mode begins to increase. In general, this trend of increasing energy gain will continue, but here the gain curve drops when ![]() $l_{\varDelta }/L$ becomes small enough that the packets becomes too well separated to feel the effect of
$l_{\varDelta }/L$ becomes small enough that the packets becomes too well separated to feel the effect of ![]() $\varDelta$ within a time
$\varDelta$ within a time ![]() $t=L/v_{\rm A}$ (for verification of this, we show the gain curve for two identical secondary packets initially separated from the primary by
$t=L/v_{\rm A}$ (for verification of this, we show the gain curve for two identical secondary packets initially separated from the primary by ![]() $\delta x = 0.4L$ and
$\delta x = 0.4L$ and ![]() $\delta x = 0.8L$). Without the interference of other waves in this duo, the secondary packet compression will likely continue until the anisotropy of the primary wave damps away, or the wavelength of the secondary packet reaches dissipation scales. In a scenario where the large-amplitude wave interacts with many smaller-amplitude fluctuations, the compression (and therefore energization) of the smaller modes should be considered in the damping of the larger-amplitude mode, likely enhancing the rate of decay.Footnote 9
$\delta x = 0.8L$). Without the interference of other waves in this duo, the secondary packet compression will likely continue until the anisotropy of the primary wave damps away, or the wavelength of the secondary packet reaches dissipation scales. In a scenario where the large-amplitude wave interacts with many smaller-amplitude fluctuations, the compression (and therefore energization) of the smaller modes should be considered in the damping of the larger-amplitude mode, likely enhancing the rate of decay.Footnote 9

Figure 1. (a) Characteristic curves for an AW subjected to an exponentially decaying pressure anisotropy (2.18) with characteristic decay length ![]() $l_\varDelta =0.1L$ and phase speed
$l_\varDelta =0.1L$ and phase speed ![]() $v_{{\rm A},\textrm {eff}}=\sqrt {2}v_{\rm A}$. Characteristics originating near the left of the domain begin to converge by the time they reach the right side of the domain, indicating
$v_{{\rm A},\textrm {eff}}=\sqrt {2}v_{\rm A}$. Characteristics originating near the left of the domain begin to converge by the time they reach the right side of the domain, indicating ![]() $\varDelta$-induced AW steepening. (b) Energy gain by the secondary AW packet after one Alfvén-crossing time for different
$\varDelta$-induced AW steepening. (b) Energy gain by the secondary AW packet after one Alfvén-crossing time for different ![]() $l_\varDelta$, demonstrating that a steeper
$l_\varDelta$, demonstrating that a steeper ![]() $\varDelta$ profile leads to more rapid gain in energy by the secondary packet.
$\varDelta$ profile leads to more rapid gain in energy by the secondary packet.
We do not describe in any detail the interaction between primary and secondary anti-propagating AWs; however, there is a notable asymmetry in the ![]() $\varDelta$-mediated interactions between co- and anti-propagating AWs. Anti-propagating interactions are considerably weaker, both because of the much shorter interaction time caused by the larger difference in propagation velocity, and because of the difficulty of establishing any sort of frequency matching with an exponential pressure anisotropy. With co-propagating AW packets, the primary packet modifies
$\varDelta$-mediated interactions between co- and anti-propagating AWs. Anti-propagating interactions are considerably weaker, both because of the much shorter interaction time caused by the larger difference in propagation velocity, and because of the difficulty of establishing any sort of frequency matching with an exponential pressure anisotropy. With co-propagating AW packets, the primary packet modifies ![]() $v_{{\rm A},\textrm {eff}}$ nonlinearly, thus the difference in velocities between packets is proportional to
$v_{{\rm A},\textrm {eff}}$ nonlinearly, thus the difference in velocities between packets is proportional to ![]() $\delta B_\perp ^2/B_0^2$; in the anti-propagating case, the difference in velocities is
$\delta B_\perp ^2/B_0^2$; in the anti-propagating case, the difference in velocities is ![]() ${\approx }2v_{\rm A}$. Furthermore, due to the monotonically decreasing
${\approx }2v_{\rm A}$. Furthermore, due to the monotonically decreasing ![]() $v_{{\rm A},\textrm {eff}}$ associated with the
$v_{{\rm A},\textrm {eff}}$ associated with the ![]() $\varDelta$-precursor of the primary packet, the primary packet carries the co-propagating secondary packet with it and the two can interact until microphysical effects interfere. Alternatively, for an anti-propagating interaction, if one were to calculate the
$\varDelta$-precursor of the primary packet, the primary packet carries the co-propagating secondary packet with it and the two can interact until microphysical effects interfere. Alternatively, for an anti-propagating interaction, if one were to calculate the ![]() $k$-space dependence of the primary packet's
$k$-space dependence of the primary packet's ![]() $\varDelta$, then the corresponding version of (2.9) could be solved, but instead with numerous
$\varDelta$, then the corresponding version of (2.9) could be solved, but instead with numerous ![]() $k_{\rm C}$ because
$k_{\rm C}$ because ![]() $\varDelta$ would not be monochromatic. That said, unlike in the IAW–AW interactions, the fact that
$\varDelta$ would not be monochromatic. That said, unlike in the IAW–AW interactions, the fact that ![]() $\varDelta$ is not monochromatic makes it difficult to achieve any semblance of frequency matching, and thus the interaction cannot similarly be tuned to maximize its strength.
$\varDelta$ is not monochromatic makes it difficult to achieve any semblance of frequency matching, and thus the interaction cannot similarly be tuned to maximize its strength.
3. Numerical simulations
To test the predictions made in § 2, we perform fluid simulations of each wave–wave interaction within the CGL-MHD framework (2.1). Our numerical approach uses a new Riemann solver implemented in a version of the finite-volume simulation code Athena++ (Stone et al. Reference Stone, Gardiner, Teuben, Hawley and Simon2008) that evolves ![]() $p_\perp$ and
$p_\perp$ and ![]() $p_\parallel$ using CGL equations that are closed with Landau-fluid heat fluxes (2.3) (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023). Unless otherwise stated, the field-aligned wavenumber
$p_\parallel$ using CGL equations that are closed with Landau-fluid heat fluxes (2.3) (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023). Unless otherwise stated, the field-aligned wavenumber ![]() $|k_\parallel |$ in the Landau-fluid heat fluxes is set equal to the initial dominant wavenumber of the primary pressure-anisotropy-generating fluctuation, viz. the IAW in the acoustic–Alfvén interaction and the larger-amplitude AW in the Alfvén–Alfvén interaction. All simulations are performed with
$|k_\parallel |$ in the Landau-fluid heat fluxes is set equal to the initial dominant wavenumber of the primary pressure-anisotropy-generating fluctuation, viz. the IAW in the acoustic–Alfvén interaction and the larger-amplitude AW in the Alfvén–Alfvén interaction. All simulations are performed with ![]() $\beta =400$, with only linear perturbations being initialized for the fluid moments of each wave:
$\beta =400$, with only linear perturbations being initialized for the fluid moments of each wave: ![]() $u_\perp$ and
$u_\perp$ and ![]() $\delta B_\perp$ for AWs; and
$\delta B_\perp$ for AWs; and ![]() $u_\parallel$,
$u_\parallel$, ![]() $\delta \rho$ and
$\delta \rho$ and ![]() $\delta p_{\perp /\parallel }$ for acoustic waves. The interaction of acoustic and Alfvénic fluctuations is studied primarily using monochromatic plane waves, while Alfvén–Alfvén interactions are studied using wave packets to demonstrate how a larger-amplitude AW packet can ‘catch up’ with an initially separated, smaller-amplitude AW packet. An acoustic–Alfvén interaction simulation was also performed using wave packets to visually depict the generation of a reflected AW as well as the non-locality of the interaction with respect to wavenumber. All monochromatic plane-wave simulations use periodic boundary conditions, while all simulations involving wave packets make use of outflow boundary conditions (where the derivatives of all fluid fields are set to zero at the boundaries).Footnote 10 The only spatial coordinate is
$\delta p_{\perp /\parallel }$ for acoustic waves. The interaction of acoustic and Alfvénic fluctuations is studied primarily using monochromatic plane waves, while Alfvén–Alfvén interactions are studied using wave packets to demonstrate how a larger-amplitude AW packet can ‘catch up’ with an initially separated, smaller-amplitude AW packet. An acoustic–Alfvén interaction simulation was also performed using wave packets to visually depict the generation of a reflected AW as well as the non-locality of the interaction with respect to wavenumber. All monochromatic plane-wave simulations use periodic boundary conditions, while all simulations involving wave packets make use of outflow boundary conditions (where the derivatives of all fluid fields are set to zero at the boundaries).Footnote 10 The only spatial coordinate is ![]() $x \in [0,1]$, aligned with the background magnetic field and measured in dimensionless Alfvénic units (where
$x \in [0,1]$, aligned with the background magnetic field and measured in dimensionless Alfvénic units (where ![]() $v_{\rm A} = B_0/\sqrt {4{\rm \pi} \rho _0}=1$) such that the Alfvén crossing time of a domain of length
$v_{\rm A} = B_0/\sqrt {4{\rm \pi} \rho _0}=1$) such that the Alfvén crossing time of a domain of length ![]() $L=1$ is
$L=1$ is ![]() $L/v_{\rm A}=1$. AW packets are initialized according to
$L/v_{\rm A}=1$. AW packets are initialized according to ![]() $\delta B_\perp = \alpha B_0 \psi (x)\cos (kx)$ and
$\delta B_\perp = \alpha B_0 \psi (x)\cos (kx)$ and ![]() $u_\perp = \pm \alpha v_{\rm A} \psi (x)\cos (kx)$, with amplitude
$u_\perp = \pm \alpha v_{\rm A} \psi (x)\cos (kx)$, with amplitude ![]() $\alpha$ and Gaussian envelopes
$\alpha$ and Gaussian envelopes ![]() $\psi (x)$ having standard deviations of approximately
$\psi (x)$ having standard deviations of approximately ![]() $2{\rm \pi} /k$. For the AW–AW interaction, the primary packet amplitude is
$2{\rm \pi} /k$. For the AW–AW interaction, the primary packet amplitude is ![]() $\alpha = 4/\sqrt {\beta }$, while the secondary packet amplitude is
$\alpha = 4/\sqrt {\beta }$, while the secondary packet amplitude is ![]() $\alpha = 1/\beta$. In the IAW–AW interaction, the acoustic wave is initialized with amplitude
$\alpha = 1/\beta$. In the IAW–AW interaction, the acoustic wave is initialized with amplitude ![]() $\delta u_\parallel /v_\textrm {th} = 2/3\beta$, and the Alfvén wave is initialized with
$\delta u_\parallel /v_\textrm {th} = 2/3\beta$, and the Alfvén wave is initialized with ![]() $\delta B_\perp /B_0 = \delta u_\perp /v_{\rm A} = 1/2\beta$. Because strong IAW–AW interactions at high
$\delta B_\perp /B_0 = \delta u_\perp /v_{\rm A} = 1/2\beta$. Because strong IAW–AW interactions at high ![]() $\beta$ are very non-local in
$\beta$ are very non-local in ![]() $k$ space, AW fluctuations with wavelengths of as little as one-hundredth of the domain length need to be resolved. Similarly, for an AW packet to remain well separated from the outflow boundaries but still propagate for several linear times, the wave packet envelope and its dominant wavelength must be much smaller than the domain length. To capture these high-
$k$ space, AW fluctuations with wavelengths of as little as one-hundredth of the domain length need to be resolved. Similarly, for an AW packet to remain well separated from the outflow boundaries but still propagate for several linear times, the wave packet envelope and its dominant wavelength must be much smaller than the domain length. To capture these high-![]() $k$ fluctuations adequately, a resolution of 9216 cells is used for the AW–AW interactions and up to 12 288 cells for the IAW–AW interactions. Importantly, the amplitudes of all fluctuations are chosen such that their associated pressure anisotropies are within the bounds of the firehose and mirror instabilities,
$k$ fluctuations adequately, a resolution of 9216 cells is used for the AW–AW interactions and up to 12 288 cells for the IAW–AW interactions. Importantly, the amplitudes of all fluctuations are chosen such that their associated pressure anisotropies are within the bounds of the firehose and mirror instabilities, ![]() $-2 \lesssim \beta \varDelta \lesssim 1$ (Rudakov & Sagdeev Reference Rudakov and Sagdeev1958; Southwood & Kivelson Reference Southwood and Kivelson1993).
$-2 \lesssim \beta \varDelta \lesssim 1$ (Rudakov & Sagdeev Reference Rudakov and Sagdeev1958; Southwood & Kivelson Reference Southwood and Kivelson1993).
3.1. Interaction between ion-acoustic and Alfvén waves
To illustrate the problem being studied, we begin with a simple example of co-propagating, quasi-monochromatic acoustic- and Alfvén-wave packets. We set the dominant wavenumber of the acoustic wave to ![]() $k_{\rm C} = k_{\rm A}/\sqrt {\beta }$, such that the modes are nearly matched in their linear frequencies. Figure 2 shows the evolution of these two packets from the initial set-up until the point when the IAW has passed out of the domain, leaving behind only the modified AW packet(s). The top panel, showing the initial conditions, demonstrates that the initial pressure anisotropy associated with the IAW (black) dips as low as
$k_{\rm C} = k_{\rm A}/\sqrt {\beta }$, such that the modes are nearly matched in their linear frequencies. Figure 2 shows the evolution of these two packets from the initial set-up until the point when the IAW has passed out of the domain, leaving behind only the modified AW packet(s). The top panel, showing the initial conditions, demonstrates that the initial pressure anisotropy associated with the IAW (black) dips as low as ![]() $\beta \varDelta \approx -2$, and does not overlap with the AW to any significant degree. As the acoustic wave propagates, it decays rapidly at a rate of
$\beta \varDelta \approx -2$, and does not overlap with the AW to any significant degree. As the acoustic wave propagates, it decays rapidly at a rate of ![]() ${\simeq }0.31\omega _{\rm C}$. Therefore, by the time it overlaps with the AW, the amplitude of its driven pressure anisotropy has decayed significantly (middle panel). Nonetheless, the modification of the local
${\simeq }0.31\omega _{\rm C}$. Therefore, by the time it overlaps with the AW, the amplitude of its driven pressure anisotropy has decayed significantly (middle panel). Nonetheless, the modification of the local ![]() $v_{{\rm A},\textrm {eff}}$ can be seen in the tail of the AW as giving rise to a new, smaller-amplitude fluctuation. By the time the IAW has decayed away and propagated out of the simulation domain, two changes have occurred to the initial wave packet. Most obvious is that, as predicted by (2.11), a smaller-amplitude, backward-propagating AW packet of roughly equal wavelength to the parent AW packet has been generated. This process therefore appears to mimic some features of the parametric decay instability of AWs. It distinguishes itself from parametric decay, however, by the more subtle increase in the amplitude of the initial forward-propagating AW packet. Instead of reflecting a portion of the initial wave packet and decreasing its amplitude, the IAW spawns these modifications to the AW packet by giving up an infinitesimal (with respect to itself, not the AW) portion of its own energy. In the end, the degree of Alfvénic imbalance, normalized by the total energy of the AW fluctuations, decreases by roughly
$v_{{\rm A},\textrm {eff}}$ can be seen in the tail of the AW as giving rise to a new, smaller-amplitude fluctuation. By the time the IAW has decayed away and propagated out of the simulation domain, two changes have occurred to the initial wave packet. Most obvious is that, as predicted by (2.11), a smaller-amplitude, backward-propagating AW packet of roughly equal wavelength to the parent AW packet has been generated. This process therefore appears to mimic some features of the parametric decay instability of AWs. It distinguishes itself from parametric decay, however, by the more subtle increase in the amplitude of the initial forward-propagating AW packet. Instead of reflecting a portion of the initial wave packet and decreasing its amplitude, the IAW spawns these modifications to the AW packet by giving up an infinitesimal (with respect to itself, not the AW) portion of its own energy. In the end, the degree of Alfvénic imbalance, normalized by the total energy of the AW fluctuations, decreases by roughly ![]() $5\,\%$.
$5\,\%$.

Figure 2. Landau-fluid CGL-MHD simulation of the interaction between the pressure anisotropy driven by an IAW packet (black) and an AW packet (orange) with matched frequencies. The IAW packet collisionlessly damps rapidly from the initial conditions (top frame), before nonlinearly deforming the short-wavelength AW packet (middle). After the IAW has decayed and propagated rightwards out of the domain, a backward-propagating AW packet has developed, with no apparent change to the wavenumber of the parent AW.
The interaction between the wave packets in figure 2 is expected to peak when the frequencies of the IAW and AW are roughly matched. However, the exact amplitude of the reflected fluctuation will depend on the minutia of the initial conditions, such as the packets’ initial separation and the widths of their envelopes. We therefore move to the periodic plane-wave set-up used to derive (2.9), so that we can assess the accuracy of (2.11) with fewer variable factors. In doing so, we choose to initialize a standing IAW with zero initial pressure anisotropy (otherwise the intensity of the interaction would be hidden by an immediate Alfvénic response to the non-zero anisotropy at ![]() $t=0$). This is accomplished by perturbing
$t=0$). This is accomplished by perturbing ![]() $u_\parallel (x,t=0) = \alpha v_\textrm {th}\sin (k_{\rm C}x)$ alone, with an amplitude
$u_\parallel (x,t=0) = \alpha v_\textrm {th}\sin (k_{\rm C}x)$ alone, with an amplitude ![]() $\alpha =2/3\beta$ such that the corresponding ‘forced’ anisotropy in (2.6) would be given by
$\alpha =2/3\beta$ such that the corresponding ‘forced’ anisotropy in (2.6) would be given by ![]() $\varDelta (x) = \beta ^{-1}\sin (\omega _{{\rm C,r}}t)\cos (k_{\rm C}x) \exp (-\omega _{{\rm C,i}}t)$. We simulate the interaction for a range of
$\varDelta (x) = \beta ^{-1}\sin (\omega _{{\rm C,r}}t)\cos (k_{\rm C}x) \exp (-\omega _{{\rm C,i}}t)$. We simulate the interaction for a range of ![]() $k_{\rm A}/k_{\rm C}$, all for an elapsed time of
$k_{\rm A}/k_{\rm C}$, all for an elapsed time of ![]() $t_{f}= 2{\rm \pi} \omega _{\rm A}^{-1}$. The energy
$t_{f}= 2{\rm \pi} \omega _{\rm A}^{-1}$. The energy ![]() $\mathcal {E}^-=|z^-|^2$ contained within all
$\mathcal {E}^-=|z^-|^2$ contained within all ![]() $z^-$ fluctuations at the end of each simulation is plotted versus
$z^-$ fluctuations at the end of each simulation is plotted versus ![]() $k_{\rm A}/k_{\rm C}$ in figure 3, compared with an analytic estimate based off of (2.11). The analytic estimate is simply obtained by accounting only for the initial AW within the source term on the right-hand side of (2.9). Separating the expression for the pressure anisotropy generated by the standing wave into its complex exponential parts, the approximation is given by
$k_{\rm A}/k_{\rm C}$ in figure 3, compared with an analytic estimate based off of (2.11). The analytic estimate is simply obtained by accounting only for the initial AW within the source term on the right-hand side of (2.9). Separating the expression for the pressure anisotropy generated by the standing wave into its complex exponential parts, the approximation is given by
 \begin{align} \mathcal{E}^-(t) &\approx \tfrac{1}{8}\left[ \left|z^-(k_{\rm A}+k_{\rm C}, \omega_{{\rm C,r}}) - z^-(k_{\rm A}+k_{\rm C}, - \omega_{{\rm C,r}})\right|^2 \right.\nonumber\\ &\quad \left.+ \left|z^-(k_{\rm A}-k_{\rm C}, \omega_{{\rm C,r}}) - z^-(k_{\rm A}-k_{\rm C}, -\omega_{{\rm C,r}})\right|^2 \right], \end{align}
\begin{align} \mathcal{E}^-(t) &\approx \tfrac{1}{8}\left[ \left|z^-(k_{\rm A}+k_{\rm C}, \omega_{{\rm C,r}}) - z^-(k_{\rm A}+k_{\rm C}, - \omega_{{\rm C,r}})\right|^2 \right.\nonumber\\ &\quad \left.+ \left|z^-(k_{\rm A}-k_{\rm C}, \omega_{{\rm C,r}}) - z^-(k_{\rm A}-k_{\rm C}, -\omega_{{\rm C,r}})\right|^2 \right], \end{align}
where the ![]() $\pm \omega _{\rm C}$ in parentheses indicates the direction of IAW propagation used when evaluating
$\pm \omega _{\rm C}$ in parentheses indicates the direction of IAW propagation used when evaluating ![]() $z(k_{\rm A}+k_{\rm C})$. As expected, both the prediction and the analytic estimate peak in interaction strength when
$z(k_{\rm A}+k_{\rm C})$. As expected, both the prediction and the analytic estimate peak in interaction strength when ![]() $k_{\rm A}/k_{\rm C} \sim \sqrt {\beta }/2\sim 10$ and agree rather well. The reason for this agreement can be found within figure 4(a), which shows the energy spectra of the forward- and backward-propagating Alfvénic fluctuations at
$k_{\rm A}/k_{\rm C} \sim \sqrt {\beta }/2\sim 10$ and agree rather well. The reason for this agreement can be found within figure 4(a), which shows the energy spectra of the forward- and backward-propagating Alfvénic fluctuations at ![]() $t=2{\rm \pi} (5\omega _{\rm A})^{-1}$ and
$t=2{\rm \pi} (5\omega _{\rm A})^{-1}$ and ![]() $t=2{\rm \pi} (\omega _{\rm A})^{-1}$. In figure 4(a), the slow, diffusive
$t=2{\rm \pi} (\omega _{\rm A})^{-1}$. In figure 4(a), the slow, diffusive ![]() $k$-space nature of the IAW–AW interaction can be seen. With the initial AW represented by the peak in
$k$-space nature of the IAW–AW interaction can be seen. With the initial AW represented by the peak in ![]() $\mathcal {E}^-(k)$, each Fourier component of the energy is several orders of magnitude smaller than the initial
$\mathcal {E}^-(k)$, each Fourier component of the energy is several orders of magnitude smaller than the initial ![]() $k_{\rm A}$, with the sole exception being
$k_{\rm A}$, with the sole exception being ![]() $k_{\rm A} \pm k_{\rm C}$ (denoted by two vertical dotted lines). Furthermore, the difference between
$k_{\rm A} \pm k_{\rm C}$ (denoted by two vertical dotted lines). Furthermore, the difference between ![]() $\mathcal {E}(k_{\rm A}\pm k_{\rm C})$ at
$\mathcal {E}(k_{\rm A}\pm k_{\rm C})$ at ![]() $t=2{\rm \pi} (5 \omega _{\rm A})^{-1}$ and
$t=2{\rm \pi} (5 \omega _{\rm A})^{-1}$ and ![]() $t=2{\rm \pi} (\omega _{\rm A})^{-1}$ is much smaller than that for the higher/smaller
$t=2{\rm \pi} (\omega _{\rm A})^{-1}$ is much smaller than that for the higher/smaller ![]() $k$. Indeed, it is possible to show that when energy cascades in both directions and
$k$. Indeed, it is possible to show that when energy cascades in both directions and ![]() $k_{\rm C}/k_{\rm A}$ is infinitesimal, (2.9) exhibits diffusive-like behaviour in
$k_{\rm C}/k_{\rm A}$ is infinitesimal, (2.9) exhibits diffusive-like behaviour in ![]() $k$-space, with a diffusion rate that is proportional to
$k$-space, with a diffusion rate that is proportional to ![]() $k_{\rm C}^2$. Therefore, our estimate (3.1) is supported by this observation of
$k_{\rm C}^2$. Therefore, our estimate (3.1) is supported by this observation of ![]() $k_{\rm A}\pm k_{\rm C}$ being the dominant newly generated wavenumbers within a single Alfvén time. The
$k_{\rm A}\pm k_{\rm C}$ being the dominant newly generated wavenumbers within a single Alfvén time. The ![]() $\mathcal {E}^\pm$ additionally evolve nearly identically, demonstrated by the relatively small change in cross-helicity with respect to the total energy shown in figure 4(b). This is expected, given that the form of (2.9) suggests this interaction relates to the degree of imbalance at each wavenumber and appears to effectively damp it over time.
$\mathcal {E}^\pm$ additionally evolve nearly identically, demonstrated by the relatively small change in cross-helicity with respect to the total energy shown in figure 4(b). This is expected, given that the form of (2.9) suggests this interaction relates to the degree of imbalance at each wavenumber and appears to effectively damp it over time.

Figure 3. Energy contained within backward-propagating AWs after one Alfvén time of interaction between a forward-propagating monochromatic AW and a standing monochromatic IAW, determined numerically as a function of the ratio of the Alfvén and acoustic wavenumbers using Landau-fluid simulations (red pluses). An approximate analytical solution for the energy (3.1) is shown as the solid line. Overall good agreement between theory and simulation is found, demonstrating strong interaction when the wave frequencies are approximately matched.

Figure 4. (a) Energy spectrum of forward- and backward-propagating Alfvénic fluctuations during interaction with a standing IAW. (b) Total change in wave energy (orange) and imbalance (black), normalized to the initial Alfvénic fluctuation energy ![]() $\mathcal {E}_0$, versus time. In panel (a), the IAW–AW interaction primarily generates new AW fluctuations at
$\mathcal {E}_0$, versus time. In panel (a), the IAW–AW interaction primarily generates new AW fluctuations at ![]() $k_{\rm A}\pm k_{\rm C}$, exhibited by the steepness of the spectra outside of the interval
$k_{\rm A}\pm k_{\rm C}$, exhibited by the steepness of the spectra outside of the interval ![]() $k \in [k_{\rm A}-k_{\rm C}, k_{\rm A}+k_{\rm C}]$. This explains the accuracy of (3.1), as fluctuations at
$k \in [k_{\rm A}-k_{\rm C}, k_{\rm A}+k_{\rm C}]$. This explains the accuracy of (3.1), as fluctuations at ![]() $k_{\rm A} \pm 2k_{\rm C}$ are too weak to affect the solution dramatically. In panel (b), the change in energy imbalance is several orders of magnitude smaller than the increase in total energy of the Alfvénic fluctuations, demonstrating that the IAW–AW interaction decreases imbalance with respect to overall AW energy.
$k_{\rm A} \pm 2k_{\rm C}$ are too weak to affect the solution dramatically. In panel (b), the change in energy imbalance is several orders of magnitude smaller than the increase in total energy of the Alfvénic fluctuations, demonstrating that the IAW–AW interaction decreases imbalance with respect to overall AW energy.
3.2. Interaction between two AWs
The interaction of co-propagating AWs relies upon the differing propagation speeds that result when different amplitudes generate different local pressure anisotropies. Accordingly, all simulations presented in this section will be of initially isolated wave packets with outflow boundary conditions. Both wave packets are initialized with a dominant wavenumber of ![]() $k_{\rm A} = 80{\rm \pi}$, with amplitudes of
$k_{\rm A} = 80{\rm \pi}$, with amplitudes of ![]() $\delta B_z/B_0 = -\delta u_z/v_{\rm A} = 4/\sqrt {\beta }$ and
$\delta B_z/B_0 = -\delta u_z/v_{\rm A} = 4/\sqrt {\beta }$ and ![]() $\delta B_y/B_0 = -\delta u_y/v_{\rm A} = \beta ^{-1}$ for the large-amplitude and small-amplitude waves, respectively. The magnetic perturbations have been assigned to different directions only for the purpose of visualizing them separately; this choice is not necessary for the interaction itself. The standard deviations of the Gaussian wave envelopes are
$\delta B_y/B_0 = -\delta u_y/v_{\rm A} = \beta ^{-1}$ for the large-amplitude and small-amplitude waves, respectively. The magnetic perturbations have been assigned to different directions only for the purpose of visualizing them separately; this choice is not necessary for the interaction itself. The standard deviations of the Gaussian wave envelopes are ![]() $2{\rm \pi} /k_{\rm A}$ for both packets, the centres of which are initially separated by a distance of
$2{\rm \pi} /k_{\rm A}$ for both packets, the centres of which are initially separated by a distance of ![]() $\Delta x = 0.11$.
$\Delta x = 0.11$.
Before examining the interaction between these two wave packets, we first verify our predictions about the evolution of the primary wave packet. Figure 5(a) displays the primary AW packet after it has steepened to form a shock. As reported by Squire et al. (Reference Squire, Quataert and Schekochihin2016), the waveform (orange) has become square-like to minimize the change in ![]() $\delta B_{\perp, {\rm p}}^2$. Due to the rapid action of the heat fluxes, the pressure anisotropy (black) has assumed a shape similar to that of the wave envelope, with an additional precursor that extends in front of the magnetic perturbation. A negative dip in
$\delta B_{\perp, {\rm p}}^2$. Due to the rapid action of the heat fluxes, the pressure anisotropy (black) has assumed a shape similar to that of the wave envelope, with an additional precursor that extends in front of the magnetic perturbation. A negative dip in ![]() $\beta \varDelta$ is present behind the tail of the wave packet, although it does not propagate with the packet; it actually results from the magnetic perturbation departing from its initial location, causing a net decrease in
$\beta \varDelta$ is present behind the tail of the wave packet, although it does not propagate with the packet; it actually results from the magnetic perturbation departing from its initial location, causing a net decrease in ![]() $|B|$ at the location where it was initialized. This localized dip is akin to the negative anisotropy generated during the more conventional interruption process of a monochromatic AW (Squire et al. Reference Squire, Kunz, Quataert and Schekochihin2017a), as we did not initialize the wave packet with the pressure anisotropy that it generates shortly thereafter. Interruption does not occur here because the
$|B|$ at the location where it was initialized. This localized dip is akin to the negative anisotropy generated during the more conventional interruption process of a monochromatic AW (Squire et al. Reference Squire, Kunz, Quataert and Schekochihin2017a), as we did not initialize the wave packet with the pressure anisotropy that it generates shortly thereafter. Interruption does not occur here because the ![]() $\beta \varDelta$ dip is not sufficiently negative to nullify the magnetic tension. Figure 5(b) demonstrates the relationship between the perpendicular temperature and the perturbation to the magnetic-field strength. After an initial adjustment into the near-steady-state shocked AW packet,
$\beta \varDelta$ dip is not sufficiently negative to nullify the magnetic tension. Figure 5(b) demonstrates the relationship between the perpendicular temperature and the perturbation to the magnetic-field strength. After an initial adjustment into the near-steady-state shocked AW packet, ![]() $\delta T_\perp$ closely follows the peak value of
$\delta T_\perp$ closely follows the peak value of ![]() $\delta |B| = \delta B_{\perp,{\rm p}}^2$ at the shock front. This supports our prediction made in Appendix B that the maximum value of the pressure anisotropy can be calculated via conservation of the double adiabats.
$\delta |B| = \delta B_{\perp,{\rm p}}^2$ at the shock front. This supports our prediction made in Appendix B that the maximum value of the pressure anisotropy can be calculated via conservation of the double adiabats.

Figure 5. (a) Magnetic field and pressure anisotropy profiles of the steepened AW packet, and (b) relationship between the perpendicular pressure and the magnetic perturbation amplitude at the front of the shock. The steepened wave packet is led by a shock in the magnetic-field profile, with a smoothed pressure anisotropy profile and ![]() $\varDelta$ precursor modifying the local Alfvén speed. The dip in
$\varDelta$ precursor modifying the local Alfvén speed. The dip in ![]() $\varDelta$ behind the wave packet results from the initial conditions of the AW not including
$\varDelta$ behind the wave packet results from the initial conditions of the AW not including ![]() $\varDelta$, hence the magnetic-field strength decreases in this region as the packet propagates away. As this packet propagates, the approximate conservation of the
$\varDelta$, hence the magnetic-field strength decreases in this region as the packet propagates away. As this packet propagates, the approximate conservation of the ![]() $T_\perp /B$ adiabat sets the amplitude of the decaying anisotropy, and thus
$T_\perp /B$ adiabat sets the amplitude of the decaying anisotropy, and thus ![]() $v_{{\rm A},\textrm {eff}}$, at the shock front.
$v_{{\rm A},\textrm {eff}}$, at the shock front.
In § 2.3, we predicted that the pressure-anisotropy-enhanced propagation speed of large-amplitude (primary) AW packets would allow them to ‘catch up’ to and then distort smaller-amplitude (secondary) AW packets. Evidence of this physics can be found in figure 6, which shows how the pressure anisotropy generated by the primary (black) interacts with the magnetic-field perturbation of the secondary (orange).

Figure 6. Time slices of a Landau-fluid simulation of the the AW–AW packet interaction. The pressure anisotropy of the primary packet is evolved alongside the magnetic perturbation of the secondary packet. The packets are initially separated (top), yet over time, the enhanced effective speed allow the primary packet to approach the secondary from behind (middle). By the end of the simulation, the effective wavenumber of the secondary packet has more than doubled from the steepening induced by the primary packet's ![]() $\varDelta$ precursor.
$\varDelta$ precursor.
In the top panel, shortly after the magnetic disturbance of the large-amplitude mode begins to propagate, there is a short-wavelength ![]() $\varDelta$. This pressure anisotropy is smoothed out rapidly by the action of heat fluxes, however, and leads to a smoothly increasing positive anisotropy perturbation whose front propagates at a slightly enhanced
$\varDelta$. This pressure anisotropy is smoothed out rapidly by the action of heat fluxes, however, and leads to a smoothly increasing positive anisotropy perturbation whose front propagates at a slightly enhanced ![]() $v_{{\rm A},\textrm {eff}}>v_{\rm A}$. The middle panel at
$v_{{\rm A},\textrm {eff}}>v_{\rm A}$. The middle panel at ![]() $k_{\rm A} v_{\rm A}t=9.9$ illustrates the moment that this front catches up to the tail end of the smaller-amplitude AW; the overlap between the two fluctuations causes this tail to propagate slightly faster, thereby compressing the waveform of the secondary. As this process continues into the final frame, the small-amplitude wave packet has had its width reduced by roughly half, and its amplitude increased due to the growth of
$k_{\rm A} v_{\rm A}t=9.9$ illustrates the moment that this front catches up to the tail end of the smaller-amplitude AW; the overlap between the two fluctuations causes this tail to propagate slightly faster, thereby compressing the waveform of the secondary. As this process continues into the final frame, the small-amplitude wave packet has had its width reduced by roughly half, and its amplitude increased due to the growth of ![]() $\mathcal {E}^-(x)$ (see (2.16)). Because the difference in Alfvén speeds between these two packets is relatively small, the cumulative deformation occurs slowly with respect to the Alfvén time of one of the packets, making this a weak interaction even though it leads to such a dramatic change in the structure of the wave packet envelope. This compression is expected to continue until the anisotropy of the large-amplitude packet has nonlinearly damped to be sufficiently small, or it is deformed by interaction with other wave packets.
$\mathcal {E}^-(x)$ (see (2.16)). Because the difference in Alfvén speeds between these two packets is relatively small, the cumulative deformation occurs slowly with respect to the Alfvén time of one of the packets, making this a weak interaction even though it leads to such a dramatic change in the structure of the wave packet envelope. This compression is expected to continue until the anisotropy of the large-amplitude packet has nonlinearly damped to be sufficiently small, or it is deformed by interaction with other wave packets.
4. Discussion: applications in turbulence
The analysis presented in §§ 2 and 3 suggests that modern theories of turbulence in high-![]() $\beta$ collisionless plasmas must account for fundamentally different wave–wave interactions. In weak MHD turbulence, energy and momentum conservation dictate that AWs are unable to modify their
$\beta$ collisionless plasmas must account for fundamentally different wave–wave interactions. In weak MHD turbulence, energy and momentum conservation dictate that AWs are unable to modify their ![]() $k_\|$ through interaction (Montgomery & Turner Reference Montgomery and Turner1981; Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000). Yet, we have just demonstrated a weak interaction of two AWs with differing amplitudes where the parallel wavelength does in fact change significantly. In a similar vein, the compressive cascade of MHD turbulence relies on the fact that slow modes possess a linear time scale that never exceeds the Alfvénic time scale of the turbulence that mixes them. Further, these slow modes have no effect on the Alfvénic cascade and effectively decouple from it below the forcing scale (Lithwick & Goldreich Reference Lithwick and Goldreich2001; Cho & Lazarian Reference Cho and Lazarian2003; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Nazarenko & Schekochihin Reference Nazarenko and Schekochihin2011; Howes & Nielson Reference Howes and Nielson2013). However, when slow modes are replaced by collisionless IAWs, these roles nearly reverse, with acoustic modes propagating too fast to be mixed effectively by the AWs, and in some cases, even demonstrating an ability to reflect Alfvénic fluctuations.
$k_\|$ through interaction (Montgomery & Turner Reference Montgomery and Turner1981; Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000). Yet, we have just demonstrated a weak interaction of two AWs with differing amplitudes where the parallel wavelength does in fact change significantly. In a similar vein, the compressive cascade of MHD turbulence relies on the fact that slow modes possess a linear time scale that never exceeds the Alfvénic time scale of the turbulence that mixes them. Further, these slow modes have no effect on the Alfvénic cascade and effectively decouple from it below the forcing scale (Lithwick & Goldreich Reference Lithwick and Goldreich2001; Cho & Lazarian Reference Cho and Lazarian2003; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Nazarenko & Schekochihin Reference Nazarenko and Schekochihin2011; Howes & Nielson Reference Howes and Nielson2013). However, when slow modes are replaced by collisionless IAWs, these roles nearly reverse, with acoustic modes propagating too fast to be mixed effectively by the AWs, and in some cases, even demonstrating an ability to reflect Alfvénic fluctuations.
Still, certain aspects of these waves that may be important in a turbulence setting are not considered in this study. In particular, because we focused solely on wave amplitudes for which the induced pressure anisotropies satisfy ![]() $|\varDelta |\lesssim 1/\beta$, we do not consider the effects of the firehose or mirror instabilities. Previous work has shown that AWs, IAWs, and other compressive fluctuations evolve quite differently if their self-generated pressure anisotropies are large enough in magnitude to excite these Larmor-scale instabilities (Squire et al. Reference Squire, Kunz, Quataert and Schekochihin2017a; Kunz et al. Reference Kunz, Squire, Schekochihin and Quataert2020; Majeski, Kunz & Squire Reference Majeski, Kunz and Squire2023). As demonstrated from first principles by Arzamasskiy et al. (Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023), the anomalous scattering that results from these instabilities is likely to influence the entire turbulent cascade, yielding yet another source of non-local energy transfer.
$|\varDelta |\lesssim 1/\beta$, we do not consider the effects of the firehose or mirror instabilities. Previous work has shown that AWs, IAWs, and other compressive fluctuations evolve quite differently if their self-generated pressure anisotropies are large enough in magnitude to excite these Larmor-scale instabilities (Squire et al. Reference Squire, Kunz, Quataert and Schekochihin2017a; Kunz et al. Reference Kunz, Squire, Schekochihin and Quataert2020; Majeski, Kunz & Squire Reference Majeski, Kunz and Squire2023). As demonstrated from first principles by Arzamasskiy et al. (Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023), the anomalous scattering that results from these instabilities is likely to influence the entire turbulent cascade, yielding yet another source of non-local energy transfer.
As mentioned in § 2, this study was performed assuming cold electrons. However, generalizing to electrons with finite temperature is quite straightforward, as long as the electrons remain barotropic. With an electron pressure tensor that satisfies ![]() $\boldsymbol{\mathsf{p}}_{{\rm e}} = p_{{\rm e}} \boldsymbol{\mathsf{I}} = (\rho T_{\rm e} /m_{\rm i})\boldsymbol{\mathsf{I}}$, no additional pressure anisotropy is produced by either wave, and so AW propagation is entirely unaffected. The only modification is to the ratio of the real and complex parts of the IAW frequency
$\boldsymbol{\mathsf{p}}_{{\rm e}} = p_{{\rm e}} \boldsymbol{\mathsf{I}} = (\rho T_{\rm e} /m_{\rm i})\boldsymbol{\mathsf{I}}$, no additional pressure anisotropy is produced by either wave, and so AW propagation is entirely unaffected. The only modification is to the ratio of the real and complex parts of the IAW frequency ![]() $\omega _{{\rm C,i}}/\omega _{{\rm C,r}}$, which, unless the electrons partake in Landau damping of the acoustic mode, decreases with increasing
$\omega _{{\rm C,i}}/\omega _{{\rm C,r}}$, which, unless the electrons partake in Landau damping of the acoustic mode, decreases with increasing ![]() $T_{\rm e}$. This would bolster the effectiveness of the IAW–AW interaction by extending the lifetime of the pressure anisotropy and allowing the interaction to occur over more than one linear time of the frequency-matched modes.
$T_{\rm e}$. This would bolster the effectiveness of the IAW–AW interaction by extending the lifetime of the pressure anisotropy and allowing the interaction to occur over more than one linear time of the frequency-matched modes.
In § 2.1, we noted the lack of ![]() $k_\perp$ as a key difference between these pressure-anisotropy-induced interactions and those found within standard Alfvénic turbulence. The nature of the pressure-anisotropic stress we highlight is significantly different from the Reynolds and Maxwell stresses, which dominate energy transfer in Alfvénic turbulence (Grete et al. Reference Grete, O'Shea, Beckwith, Schmidt and Christlieb2017). Most importantly,
$k_\perp$ as a key difference between these pressure-anisotropy-induced interactions and those found within standard Alfvénic turbulence. The nature of the pressure-anisotropic stress we highlight is significantly different from the Reynolds and Maxwell stresses, which dominate energy transfer in Alfvénic turbulence (Grete et al. Reference Grete, O'Shea, Beckwith, Schmidt and Christlieb2017). Most importantly, ![]() $\beta \varDelta$, being a scalar, will always affect
$\beta \varDelta$, being a scalar, will always affect ![]() $v_{{\rm A},\textrm {eff}}$ regardless of the ratio
$v_{{\rm A},\textrm {eff}}$ regardless of the ratio ![]() $k_\perp /k_\|$, doing so through the same nonlinearity that we retain in (2.6). Therefore, the effects of IAWs or AWs with
$k_\perp /k_\|$, doing so through the same nonlinearity that we retain in (2.6). Therefore, the effects of IAWs or AWs with ![]() $\beta \varDelta \sim 1$ are expected to remain leading order when
$\beta \varDelta \sim 1$ are expected to remain leading order when ![]() $k_\perp \neq 0$. Furthermore, the linear time scales of IAWs and AWs are independent of
$k_\perp \neq 0$. Furthermore, the linear time scales of IAWs and AWs are independent of ![]() $k_\perp$, thus the frequency-matching criterion of their interaction, and its spectral non-locality, are unlikely to change.
$k_\perp$, thus the frequency-matching criterion of their interaction, and its spectral non-locality, are unlikely to change.
Given the further complications of microinstabilities and other high-![]() $\beta$ effects such as magneto-immutability (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023), formulating an analytical model for turbulence in this parameter regime remains a challenging task. The intention of this work is primarily to hint at the physics underlying changes in the observed behaviour of collisionless turbulence at
$\beta$ effects such as magneto-immutability (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023), formulating an analytical model for turbulence in this parameter regime remains a challenging task. The intention of this work is primarily to hint at the physics underlying changes in the observed behaviour of collisionless turbulence at ![]() $\beta \gg 1$, such as non-local energy transfer due to the pressure-anisotropic stress (Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023). To that end, we may still speculate upon some of the more qualitative consequences of the wave–wave interactions described herein. One of the most effective tools for describing strong turbulence is an appropriately reduced set of equations. For example, reduced MHD incorporates the concept of critical balance directly by ordering the linear frequency comparable to the nonlinear frequency,
$\beta \gg 1$, such as non-local energy transfer due to the pressure-anisotropic stress (Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023). To that end, we may still speculate upon some of the more qualitative consequences of the wave–wave interactions described herein. One of the most effective tools for describing strong turbulence is an appropriately reduced set of equations. For example, reduced MHD incorporates the concept of critical balance directly by ordering the linear frequency comparable to the nonlinear frequency, ![]() $\tau _\textrm {lin}^{-1} \doteq k_\parallel v_{\rm A} \sim \tau _\textrm {nl}^{-1} \approx k_\perp u_\perp$ (Goldreich & Sridhar Reference Goldreich and Sridhar1995; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Reinstating non-zero
$\tau _\textrm {lin}^{-1} \doteq k_\parallel v_{\rm A} \sim \tau _\textrm {nl}^{-1} \approx k_\perp u_\perp$ (Goldreich & Sridhar Reference Goldreich and Sridhar1995; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Reinstating non-zero ![]() $k_\perp$ then, we can consider the reduced Alfvénic Elsässer equations that result from our 1-D high-
$k_\perp$ then, we can consider the reduced Alfvénic Elsässer equations that result from our 1-D high-![]() $\beta$ ordering (2.4), modified to include
$\beta$ ordering (2.4), modified to include ![]() $k_\|/k_\perp \sim \delta B_\parallel /B_0 \sim \epsilon$:
$k_\|/k_\perp \sim \delta B_\parallel /B_0 \sim \epsilon$:
 \begin{align} &\frac{\partial \boldsymbol{z}^\pm_\perp}{\partial t} \mp v_{\rm A} \boldsymbol{\nabla}_\parallel \boldsymbol{z}^\pm_\perp{+} \boldsymbol{z}^\mp_\perp \boldsymbol{\cdot}\boldsymbol{\nabla}_\perp \boldsymbol{z}^\pm_\perp{+} \boldsymbol{\nabla}_\perp P_{\rm total} \nonumber\\ &\quad = v_{\rm A}\frac{\beta}{4}\boldsymbol{\nabla}_\parallel\left[(\boldsymbol{z}_\perp^+{-}\boldsymbol{z}_\perp^-)\varDelta\right] + \frac{\beta}{4}(\boldsymbol{z}_\perp^+{-}\boldsymbol{z}_\perp^-)\boldsymbol{\cdot}{\boldsymbol{\nabla}}_\perp\left[(\boldsymbol{z}_\perp^+{-}\boldsymbol{z}_\perp^-)\varDelta\right], \end{align}
\begin{align} &\frac{\partial \boldsymbol{z}^\pm_\perp}{\partial t} \mp v_{\rm A} \boldsymbol{\nabla}_\parallel \boldsymbol{z}^\pm_\perp{+} \boldsymbol{z}^\mp_\perp \boldsymbol{\cdot}\boldsymbol{\nabla}_\perp \boldsymbol{z}^\pm_\perp{+} \boldsymbol{\nabla}_\perp P_{\rm total} \nonumber\\ &\quad = v_{\rm A}\frac{\beta}{4}\boldsymbol{\nabla}_\parallel\left[(\boldsymbol{z}_\perp^+{-}\boldsymbol{z}_\perp^-)\varDelta\right] + \frac{\beta}{4}(\boldsymbol{z}_\perp^+{-}\boldsymbol{z}_\perp^-)\boldsymbol{\cdot}{\boldsymbol{\nabla}}_\perp\left[(\boldsymbol{z}_\perp^+{-}\boldsymbol{z}_\perp^-)\varDelta\right], \end{align}
where ![]() $P_\textrm {total}$ represents the combined perpendicular and magnetic pressures. Contained within the right-hand side of (4.1) are the various new effects discussed throughout this work that are absent in a collisional MHD model, or even a
$P_\textrm {total}$ represents the combined perpendicular and magnetic pressures. Contained within the right-hand side of (4.1) are the various new effects discussed throughout this work that are absent in a collisional MHD model, or even a ![]() $\beta \sim \mathcal {O}(1)$ gyrokinetic model. The first term on the right-hand side incorporates the ability of AWs to travel at different
$\beta \sim \mathcal {O}(1)$ gyrokinetic model. The first term on the right-hand side incorporates the ability of AWs to travel at different ![]() $v_{{\rm A},\textrm {eff}}$, while both terms describe the deformation in
$v_{{\rm A},\textrm {eff}}$, while both terms describe the deformation in ![]() $\boldsymbol {z}^\pm$ that results from wave–wave interactions. Equation (4.1) does not distinguish between the source of
$\boldsymbol {z}^\pm$ that results from wave–wave interactions. Equation (4.1) does not distinguish between the source of ![]() $\beta \varDelta$; be it generated by AWs with
$\beta \varDelta$; be it generated by AWs with ![]() $\delta B_\perp /B_0 \sim \beta ^{-1/2}$ or IAWs with
$\delta B_\perp /B_0 \sim \beta ^{-1/2}$ or IAWs with ![]() $\delta \rho /\rho \sim \beta ^{-1}$, the Alfvénic cascade will be modified. In each case, however, the description of the source of fluctuations can be more difficult. For example, IAWs act non-locally to affect Alfvénic fluctuations in
$\delta \rho /\rho \sim \beta ^{-1}$, the Alfvénic cascade will be modified. In each case, however, the description of the source of fluctuations can be more difficult. For example, IAWs act non-locally to affect Alfvénic fluctuations in ![]() $k$-space, but the reverse may not be true for Alfvénic mixing of acoustic waves. In that case, there is not necessarily a single acoustic Elsässer equation that can be written at each scale, because multiple
$k$-space, but the reverse may not be true for Alfvénic mixing of acoustic waves. In that case, there is not necessarily a single acoustic Elsässer equation that can be written at each scale, because multiple ![]() $\boldsymbol {k}_\perp$ and
$\boldsymbol {k}_\perp$ and ![]() $k_\parallel$ are inherent to the problem. Furthermore, in a collisionless turbulent cascade,
$k_\parallel$ are inherent to the problem. Furthermore, in a collisionless turbulent cascade, ![]() $\beta \varDelta$ cannot remain
$\beta \varDelta$ cannot remain ![]() $\mathcal {O}(1)$ at every wavenumber throughout the inertial range. As all of the other quantities cascade,
$\mathcal {O}(1)$ at every wavenumber throughout the inertial range. As all of the other quantities cascade, ![]() $\beta$ will remain constant, so it is likely that interactions mediated by
$\beta$ will remain constant, so it is likely that interactions mediated by ![]() $\varDelta$ are a leading-order effect only in a specific portion of the inertial range where
$\varDelta$ are a leading-order effect only in a specific portion of the inertial range where ![]() $\beta \varDelta \sim 1$. One subtle conclusion of the above reduced equations is that pressure balance in these plasmas should be struck primarily between
$\beta \varDelta \sim 1$. One subtle conclusion of the above reduced equations is that pressure balance in these plasmas should be struck primarily between ![]() $B^2$ and the perpendicular pressure
$B^2$ and the perpendicular pressure ![]() $p_\perp$, rather than the isotropic pressure (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023). The leading order of (4.1) implies that
$p_\perp$, rather than the isotropic pressure (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023). The leading order of (4.1) implies that ![]() $\delta p_\perp /p_0 \sim \beta ^{-1}\delta B_\parallel /B_0 \sim \epsilon ^2$. In essence, the anisotropy generated should be dominated by the parallel pressure perturbation. This was found empirically in simulations of incompressibly driven turbulence using the same CGL-MHD Athena++ code employed here (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023), as well as in the hybrid-kinetic simulations of Arzamasskiy et al. (Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023).
$\delta p_\perp /p_0 \sim \beta ^{-1}\delta B_\parallel /B_0 \sim \epsilon ^2$. In essence, the anisotropy generated should be dominated by the parallel pressure perturbation. This was found empirically in simulations of incompressibly driven turbulence using the same CGL-MHD Athena++ code employed here (Squire et al. Reference Squire, Kunz, Arzamasskiy, Johnston, Quataert and Schekochihin2023), as well as in the hybrid-kinetic simulations of Arzamasskiy et al. (Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023).
Additional effects may be uncovered by studying the weak turbulence resulting from these wave–wave interactions. Isolated wave packets are not typically considered within strong turbulence; however, the long deformation times associated with weak turbulence allows waves to remain correlated over many local Alfvén-crossing times (Iroshnikov Reference Iroshnikov1964; Kraichnan Reference Kraichnan1968). This also expands upon the range of scales over which ![]() $\beta \varDelta$ exerts an influence by not requiring that the interaction remain strong. One effect that may be impactful to weak turbulence is the ability of AWs to modify each others’
$\beta \varDelta$ exerts an influence by not requiring that the interaction remain strong. One effect that may be impactful to weak turbulence is the ability of AWs to modify each others’ ![]() $k_\parallel$. Current understandings of weak AW interactions involve resonance conditions describing three-wave interactions (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000):
$k_\parallel$. Current understandings of weak AW interactions involve resonance conditions describing three-wave interactions (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000):
which demand that ![]() $k_{\parallel 2}=0$ and
$k_{\parallel 2}=0$ and ![]() $k_{\parallel 1} = k_{\parallel 3}$. However, these resonance conditions assume that
$k_{\parallel 1} = k_{\parallel 3}$. However, these resonance conditions assume that ![]() $v_{\rm A}(k_\parallel ) = v_{\rm A}$, which is subject to modification if
$v_{\rm A}(k_\parallel ) = v_{\rm A}$, which is subject to modification if ![]() $v_{{\rm A},\textrm {eff}}$ is a function of the fluctuation amplitude, and hence the scale
$v_{{\rm A},\textrm {eff}}$ is a function of the fluctuation amplitude, and hence the scale ![]() $k_\parallel$ of concern. In fact, for
$k_\parallel$ of concern. In fact, for ![]() $\beta \varDelta \ll 1$, the frequency resonance condition would become
$\beta \varDelta \ll 1$, the frequency resonance condition would become
Unlike in weak MHD Alfvénic turbulence, a ![]() $k_{\parallel 2} = 0$ mode is no longer a solution of the above condition by virtue of
$k_{\parallel 2} = 0$ mode is no longer a solution of the above condition by virtue of ![]() $\varDelta (k_{\parallel 2})$ increasing with decreasing
$\varDelta (k_{\parallel 2})$ increasing with decreasing ![]() $k_{\parallel 2}$ (assuming a cascade to higher wavenumbers for
$k_{\parallel 2}$ (assuming a cascade to higher wavenumbers for ![]() $\varDelta$). This holds regardless of the additional fact that co-propagating interactions can occur, which have been shown to change
$\varDelta$). This holds regardless of the additional fact that co-propagating interactions can occur, which have been shown to change ![]() $k_\parallel$ as well. Together, these effects may be capable of modifying the onset of critical balance, changing the transition scale between weak and strong turbulence. Well-crafted simulations of Alfvénic and compressive turbulence in both collisionless and weakly collisional high-
$k_\parallel$ as well. Together, these effects may be capable of modifying the onset of critical balance, changing the transition scale between weak and strong turbulence. Well-crafted simulations of Alfvénic and compressive turbulence in both collisionless and weakly collisional high-![]() $\beta$ plasmas are the clear next step.
$\beta$ plasmas are the clear next step.
Acknowledgements
The authors thank Jonathan Squire, Alexander Schekochihin, Eliot Quataert and the participants of the 14th Plasma Kinetics Working Meeting at the Wolfgang Pauli Institute in Vienna for useful discussions, as well as the two anonymous reviewers for comments that helped sharpen the presentation.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Funding
S.M. and M.W.K. were supported in part by NSF CAREER Award No. 1944972. High-performance computing resources were provided by the PICSciE-OIT TIGRESS High Performance Computing Center and Visualization Laboratory at Princeton University.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Energy conservation in IAW–AW interactions
Without going to higher order in ![]() $\epsilon$ when deriving an equation for the evolution of the ion acoustic wave, the solution (2.11) describing the interaction of AWs with ion acoustic waves does not conserve the total energy. The reasoning for this is that, while the effect of the acoustic wave's pressure anisotropy on the AW is leading order in
$\epsilon$ when deriving an equation for the evolution of the ion acoustic wave, the solution (2.11) describing the interaction of AWs with ion acoustic waves does not conserve the total energy. The reasoning for this is that, while the effect of the acoustic wave's pressure anisotropy on the AW is leading order in ![]() $\epsilon$, the back reaction of the AW on the acoustic wave occurs at
$\epsilon$, the back reaction of the AW on the acoustic wave occurs at ![]() $\mathcal {O}(\epsilon ^2)$. As assurance for the concerned reader, however, we demonstrate here that by going to at least third order in the compressive dynamical equations, energy conservation can be re-established. Additionally, this result aids in confirming that the frequency matching condition
$\mathcal {O}(\epsilon ^2)$. As assurance for the concerned reader, however, we demonstrate here that by going to at least third order in the compressive dynamical equations, energy conservation can be re-established. Additionally, this result aids in confirming that the frequency matching condition ![]() $k_{\rm A} \sim \sqrt {\beta }k_{\rm C}$ does not violate the assumptions used to obtain the ordered equations (2.6) and (2.7). To achieve this task, we begin by writing down the total energy of the background plus perturbations, which we normalize using
$k_{\rm A} \sim \sqrt {\beta }k_{\rm C}$ does not violate the assumptions used to obtain the ordered equations (2.6) and (2.7). To achieve this task, we begin by writing down the total energy of the background plus perturbations, which we normalize using ![]() $\rho _0 v_{\textrm {th},{\rm i}}^2 = 2p_0$ to make the orders of each contribution more apparent. Following this, we evaluate the time derivative of the total energy using the evolution equations (2.1), with the proper adjustments made for our assumptions about the problem geometry. Once this has been done, we examine the orders of the remaining terms to demonstrate that energy conservation is re-established by including all terms of order
$\rho _0 v_{\textrm {th},{\rm i}}^2 = 2p_0$ to make the orders of each contribution more apparent. Following this, we evaluate the time derivative of the total energy using the evolution equations (2.1), with the proper adjustments made for our assumptions about the problem geometry. Once this has been done, we examine the orders of the remaining terms to demonstrate that energy conservation is re-established by including all terms of order ![]() $\epsilon ^3$ or higher.
$\epsilon ^3$ or higher.
The total energy normalized to ![]() $\rho _0 v_{\textrm {th},{\rm i}}^2$ is given by
$\rho _0 v_{\textrm {th},{\rm i}}^2$ is given by
 \begin{equation} \frac{E}{\rho_0 v_{{\rm th},{\rm i}}^2} = \int \mathrm{d}x \left\{ \frac{1}{\beta}\frac{\rho}{\rho_0} \left( \frac{u_\perp}{v_{\rm A}} \right)^2 +\frac{1}{\beta}\left(1+\frac{\delta B_\perp^2}{B_0^2} \right) + \frac{\rho}{\rho_0} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}}\right)^2 + \frac{p_\perp}{p_0}+ \frac{1}{2}\frac{p_\parallel}{p_0} \right\}. \end{equation}
\begin{equation} \frac{E}{\rho_0 v_{{\rm th},{\rm i}}^2} = \int \mathrm{d}x \left\{ \frac{1}{\beta}\frac{\rho}{\rho_0} \left( \frac{u_\perp}{v_{\rm A}} \right)^2 +\frac{1}{\beta}\left(1+\frac{\delta B_\perp^2}{B_0^2} \right) + \frac{\rho}{\rho_0} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}}\right)^2 + \frac{p_\perp}{p_0}+ \frac{1}{2}\frac{p_\parallel}{p_0} \right\}. \end{equation}
Already, it is clear from (A1) that, according to the ordering (2.4), the Alfvénic contributions to the energy (terms involving ![]() $u_\perp$ and
$u_\perp$ and ![]() $\delta B_\perp$) are at most of order
$\delta B_\perp$) are at most of order ![]() $\epsilon ^3$, while the compressive contributions (the last three terms) are up to linear in
$\epsilon ^3$, while the compressive contributions (the last three terms) are up to linear in ![]() $\epsilon$. Taking the time derivative of (A1), the rate of change of the total energy is given by
$\epsilon$. Taking the time derivative of (A1), the rate of change of the total energy is given by
 \begin{align} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t}&= \int \mathrm{d}x \left\{ \frac{1}{\beta} \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left(\frac{u_\perp}{v_{\rm A}} \right)^2 + \frac{1}{\beta} \left( \frac{\rho}{\rho_0} \right) \frac{\partial }{\partial t} \left( \frac{u_\perp}{v_{\rm A}} \right)^2 + \frac{1}{\beta} \frac{\partial }{\partial t} \left(\frac{\delta B_\perp}{B_0} \right)^2 \right.\nonumber\\ &\quad \left. + \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 + \left( \frac{\rho}{\rho_0} \right) \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 + \frac{\partial }{\partial t}\frac{\delta p_\perp}{p_0} +\frac{1}{2}\frac{\partial }{\partial t}\frac{\delta p_\parallel}{p_0} \right\}. \end{align}
\begin{align} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t}&= \int \mathrm{d}x \left\{ \frac{1}{\beta} \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left(\frac{u_\perp}{v_{\rm A}} \right)^2 + \frac{1}{\beta} \left( \frac{\rho}{\rho_0} \right) \frac{\partial }{\partial t} \left( \frac{u_\perp}{v_{\rm A}} \right)^2 + \frac{1}{\beta} \frac{\partial }{\partial t} \left(\frac{\delta B_\perp}{B_0} \right)^2 \right.\nonumber\\ &\quad \left. + \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 + \left( \frac{\rho}{\rho_0} \right) \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 + \frac{\partial }{\partial t}\frac{\delta p_\perp}{p_0} +\frac{1}{2}\frac{\partial }{\partial t}\frac{\delta p_\parallel}{p_0} \right\}. \end{align}We examine these terms in turn with the aim of establishing the lowest order at which they appear.
First, we focus on those terms relating directly to the energy carried by the Alfvénic fluctuations, i.e. the top line of (A2). Denote the characteristic Alfvénic and compressive wavenumbers by ![]() $k_{\rm A}$ and
$k_{\rm A}$ and ![]() $k_{\rm C}$, respectively. The first term is of order
$k_{\rm C}$, respectively. The first term is of order ![]() $k_{\rm C} c_{\rm s} \epsilon ^4$ (due to the continuity equation's compressive nature in
$k_{\rm C} c_{\rm s} \epsilon ^4$ (due to the continuity equation's compressive nature in ![]() $\partial _t$), while the second and third terms are of order
$\partial _t$), while the second and third terms are of order ![]() $k_{\rm A} v_{\rm A} \epsilon ^3$. For all circumstances studied in this paper then (including frequency-matched fluctuations), the leading order of the second and third terms will dominate and be the main mechanism by which the Alfvénic fluctuations extract energy from the compressive ones. Therefore, neglecting the first term and inserting (2.5) for
$k_{\rm A} v_{\rm A} \epsilon ^3$. For all circumstances studied in this paper then (including frequency-matched fluctuations), the leading order of the second and third terms will dominate and be the main mechanism by which the Alfvénic fluctuations extract energy from the compressive ones. Therefore, neglecting the first term and inserting (2.5) for ![]() $\partial _t u_\perp$ and
$\partial _t u_\perp$ and ![]() $\partial _t \delta B_\perp$, the energy rate of change simplifies to
$\partial _t \delta B_\perp$, the energy rate of change simplifies to
 \begin{align} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t} & \approx \int \mathrm{d}x \left\{ u_\perp \frac{\partial }{\partial x}\left(\frac{\delta B_\perp}{B_0} \frac{\varDelta p}{p_0} \right) + \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 \right.\nonumber\\ &\quad \left.\vphantom{\left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2}+ \left( \frac{2\rho}{\rho_0} \right) \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right) + \frac{\partial }{\partial t}\frac{\delta p_\perp}{p_0} + \frac{1}{2}\frac{\partial }{\partial t}\frac{\delta p_\parallel}{p_0} \right\}. \end{align}
\begin{align} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t} & \approx \int \mathrm{d}x \left\{ u_\perp \frac{\partial }{\partial x}\left(\frac{\delta B_\perp}{B_0} \frac{\varDelta p}{p_0} \right) + \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 \right.\nonumber\\ &\quad \left.\vphantom{\left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2}+ \left( \frac{2\rho}{\rho_0} \right) \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right) + \frac{\partial }{\partial t}\frac{\delta p_\perp}{p_0} + \frac{1}{2}\frac{\partial }{\partial t}\frac{\delta p_\parallel}{p_0} \right\}. \end{align}
For ![]() $\omega _{\rm A} \approx \omega _{\rm C}$, the remaining Alfvénic term on the first line of (A3) is of the exact same order as the kinetic energy terms on the bottom line, while, for
$\omega _{\rm A} \approx \omega _{\rm C}$, the remaining Alfvénic term on the first line of (A3) is of the exact same order as the kinetic energy terms on the bottom line, while, for ![]() $k_{\rm A} \approx k_{\rm C}$, it is one half-order in
$k_{\rm A} \approx k_{\rm C}$, it is one half-order in ![]() $\epsilon$ smaller. To satisfy energy conservation, we must then include all compressive terms that are up to, but not including, those of order
$\epsilon$ smaller. To satisfy energy conservation, we must then include all compressive terms that are up to, but not including, those of order ![]() $\epsilon ^4$.
$\epsilon ^4$.
Before embarking on the compressive terms, however, we note that the heat fluxes need not be included in (2.1e) and (2.1d) for the proof of energy conservation between Alfvén and acoustic waves. Their effect is to diffuse wave energy into the background, and not to facilitate communication between the Alfvénic and compressive fluctuations. We therefore proceed by evolving the pressure perturbations according to the double adiabats (2.13), which can be combined in the following manner:
 \begin{align} \frac{\partial p_\perp}{\partial t} + \frac{1}{2} \frac{\partial p_\parallel}{\partial t} &= \frac{1}{2}\frac{\Delta p}{B^2}\frac{\partial B^2}{\partial t} + \frac{3p_\parallel}{2\rho}\frac{\partial \rho}{\partial t} - \frac{u_\parallel}{2}\frac{\partial p_\parallel}{\partial x} + \frac{3u_\parallel}{2} \left( \frac{p_\parallel}{\rho}\right) \frac{\partial \rho}{\partial x}\nonumber\\ &\quad + \frac{p_\perp}{\rho} \frac{\partial \rho}{\partial t} - u_\parallel\rho\frac{\partial }{\partial x}\left(\frac{p_\perp}{\rho}\right) + u_\parallel \left(\frac{p_\perp}{B}\right) \frac{\partial B}{\partial x} - u_\parallel\left(\frac{p_\parallel}{B}\right) \frac{\partial B}{\partial x} . \end{align}
\begin{align} \frac{\partial p_\perp}{\partial t} + \frac{1}{2} \frac{\partial p_\parallel}{\partial t} &= \frac{1}{2}\frac{\Delta p}{B^2}\frac{\partial B^2}{\partial t} + \frac{3p_\parallel}{2\rho}\frac{\partial \rho}{\partial t} - \frac{u_\parallel}{2}\frac{\partial p_\parallel}{\partial x} + \frac{3u_\parallel}{2} \left( \frac{p_\parallel}{\rho}\right) \frac{\partial \rho}{\partial x}\nonumber\\ &\quad + \frac{p_\perp}{\rho} \frac{\partial \rho}{\partial t} - u_\parallel\rho\frac{\partial }{\partial x}\left(\frac{p_\perp}{\rho}\right) + u_\parallel \left(\frac{p_\perp}{B}\right) \frac{\partial B}{\partial x} - u_\parallel\left(\frac{p_\parallel}{B}\right) \frac{\partial B}{\partial x} . \end{align}
Noting that ![]() $\delta B \propto \delta B_\perp ^2$, which makes
$\delta B \propto \delta B_\perp ^2$, which makes ![]() $B^{-1}\partial _xB$ second order in
$B^{-1}\partial _xB$ second order in ![]() $\epsilon$, the final two terms cancel up to and including
$\epsilon$, the final two terms cancel up to and including ![]() $\mathcal {O}(\epsilon ^3)$. We also use the fact that (A4) will be integrated over space to swap the remaining
$\mathcal {O}(\epsilon ^3)$. We also use the fact that (A4) will be integrated over space to swap the remaining ![]() $x$-derivative on the bottom line from
$x$-derivative on the bottom line from ![]() $p_\perp /\rho$ to
$p_\perp /\rho$ to ![]() $u_\parallel \rho$, picking up a sign change. Using the continuity equation to cancel the first two terms on the second line, no more of the second line remains. Normalization and integration of the first term on the right-hand side of (A4) then gives
$u_\parallel \rho$, picking up a sign change. Using the continuity equation to cancel the first two terms on the second line, no more of the second line remains. Normalization and integration of the first term on the right-hand side of (A4) then gives
where (2.5a) has been used to substitute for ![]() $\partial _t \delta B_\perp$. This term will cancel the first term on the right-hand side of (A3), leaving us with the following expression for the energy rate of change:
$\partial _t \delta B_\perp$. This term will cancel the first term on the right-hand side of (A3), leaving us with the following expression for the energy rate of change:
 \begin{align} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t} & \approx \int \mathrm{d}x \left\{\vphantom{\left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2} \frac{3p_\parallel}{2p_0}\left(\frac{1}{\rho} \frac{\partial \rho}{\partial t}\right) - \frac{u_\parallel}{2p_0}\frac{\partial p_\parallel}{\partial x} + \frac{3u_\parallel}{2\rho} \left( \frac{p_\parallel}{p_0}\right) \frac{\partial \rho}{\partial x} \right.\nonumber\\ &\quad \left. + \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 + \left( \frac{2\rho}{\rho_0} \right) \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right) \right\} + \mathcal{O}(\epsilon^4). \end{align}
\begin{align} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t} & \approx \int \mathrm{d}x \left\{\vphantom{\left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2} \frac{3p_\parallel}{2p_0}\left(\frac{1}{\rho} \frac{\partial \rho}{\partial t}\right) - \frac{u_\parallel}{2p_0}\frac{\partial p_\parallel}{\partial x} + \frac{3u_\parallel}{2\rho} \left( \frac{p_\parallel}{p_0}\right) \frac{\partial \rho}{\partial x} \right.\nonumber\\ &\quad \left. + \frac{\partial }{\partial t} \left(\frac{\delta \rho}{\rho_0}\right) \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 + \left( \frac{2\rho}{\rho_0} \right) \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right) \right\} + \mathcal{O}(\epsilon^4). \end{align}
At this point, it is may become obvious that, with all of the remaining terms being compressive in nature, they must cancel because the nonlinear interaction of a wave with itself generally conserves energy in the absence of dissipative effects like heat fluxes or collisions. Regardless, to solidify the argument, we will continue and demonstrate that there are no other Alfvénic feedback terms that appear at orders greater than ![]() $\epsilon ^4$. Using the continuity equation to simplify the top line of (A6) yields
$\epsilon ^4$. Using the continuity equation to simplify the top line of (A6) yields
which, after once again employing continuity, reduces (A6) to
 \begin{equation} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t} \approx \int \mathrm{d}x \left\{\frac{u_\parallel}{p_0}\frac{\partial p_\parallel}{\partial x} + \frac{2\rho}{\rho_0} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 \frac{\partial u_\parallel}{\partial x} + \left(\frac{2\rho}{\rho_0} \right) \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right) \right\} + \mathcal{O}(\epsilon^4). \end{equation}
\begin{equation} \frac{1}{\rho_0 v_{{\rm th},{\rm i}}^2}\frac{\mathrm{d} E}{\mathrm{d}t} \approx \int \mathrm{d}x \left\{\frac{u_\parallel}{p_0}\frac{\partial p_\parallel}{\partial x} + \frac{2\rho}{\rho_0} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right)^2 \frac{\partial u_\parallel}{\partial x} + \left(\frac{2\rho}{\rho_0} \right) \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \frac{\partial }{\partial t} \left( \frac{u_\parallel}{v_{{\rm th},{\rm i}}} \right) \right\} + \mathcal{O}(\epsilon^4). \end{equation}The fully nonlinear parallel momentum in this case is given by
Multiplying (A9) by ![]() $u_\parallel /\rho _0 v_{\textrm {th},{\rm i}}^2 = u_\parallel /2p_0$, the last two terms on its right-hand side become of order
$u_\parallel /\rho _0 v_{\textrm {th},{\rm i}}^2 = u_\parallel /2p_0$, the last two terms on its right-hand side become of order ![]() $\mathcal {O}(\epsilon ^4)$, while the first two cancel the remaining terms in (A8). As a result, we have shown that, up to and including
$\mathcal {O}(\epsilon ^4)$, while the first two cancel the remaining terms in (A8). As a result, we have shown that, up to and including ![]() $\mathcal {O}(\epsilon ^3)$ terms, total energy is conserved by the interaction of Alfvén and ion-acoustic waves according to the ordering (2.4). This finding tells us that, even when the frequencies of the two modes are matched and
$\mathcal {O}(\epsilon ^3)$ terms, total energy is conserved by the interaction of Alfvén and ion-acoustic waves according to the ordering (2.4). This finding tells us that, even when the frequencies of the two modes are matched and ![]() $k_{\rm A} \sim \sqrt {\beta }k_{\rm C}$, the leading order for the dynamical equations describing each wave remains unchanged. Naturally, no terms neglected in deriving (2.5) are enhanced with respect to the leading order by letting
$k_{\rm A} \sim \sqrt {\beta }k_{\rm C}$, the leading order for the dynamical equations describing each wave remains unchanged. Naturally, no terms neglected in deriving (2.5) are enhanced with respect to the leading order by letting ![]() $k_{\rm A}$ increase by
$k_{\rm A}$ increase by ![]() $\epsilon ^{-1/2}$. At the same time, Alfvénic feedback effects on the compressive fluctuations were of order
$\epsilon ^{-1/2}$. At the same time, Alfvénic feedback effects on the compressive fluctuations were of order ![]() $\epsilon ^3$, meaning the leading order compressive equations (2.7) remain the same until
$\epsilon ^3$, meaning the leading order compressive equations (2.7) remain the same until ![]() $\omega _{\rm A} \sim \beta ^{2}\omega _{\rm C}$. Nonlinear steepening will remain far more important in the frequency-matched regime of strong interaction, thus for (small) acoustic fluctuations of amplitude
$\omega _{\rm A} \sim \beta ^{2}\omega _{\rm C}$. Nonlinear steepening will remain far more important in the frequency-matched regime of strong interaction, thus for (small) acoustic fluctuations of amplitude ![]() ${\sim }\beta ^{-1}$, the assumption of linearity is quite robust.
${\sim }\beta ^{-1}$, the assumption of linearity is quite robust.
Appendix B. The  $\varDelta$ profile of a Landau-fluid AW packet
$\varDelta$ profile of a Landau-fluid AW packet
This appendix provides a derivation of the pressure anisotropy generated by an isolated, parallel-propagating, large-amplitude (![]() $\delta B_\perp /B_0 \sim \beta ^{-1/2}$) AW packet, specifically for the diffusive heat fluxes of a Landau-fluid-type model. As discussed in § 2.3, we predict that AWs of this type will steepen to form shocks in the profile of their
$\delta B_\perp /B_0 \sim \beta ^{-1/2}$) AW packet, specifically for the diffusive heat fluxes of a Landau-fluid-type model. As discussed in § 2.3, we predict that AWs of this type will steepen to form shocks in the profile of their ![]() $\delta B_\perp$ and
$\delta B_\perp$ and ![]() $u_\perp$ perturbations. These shocks will propagate at a speed near
$u_\perp$ perturbations. These shocks will propagate at a speed near ![]() $v_{\rm A}$, which is much slower than the thermal speed of the plasma, allowing the change in pressure anisotropy generated by
$v_{\rm A}$, which is much slower than the thermal speed of the plasma, allowing the change in pressure anisotropy generated by ![]() $\delta B_\perp$ to diffuse upstream ahead of the shock. Here we derive the functional form of
$\delta B_\perp$ to diffuse upstream ahead of the shock. Here we derive the functional form of ![]() $\varDelta (x)$ as it propagates with the shock.
$\varDelta (x)$ as it propagates with the shock.
The first step is to introduce another ordering that describes this large-amplitude AW near the interruption limit and which is distinct from (2.4). The need for a new ordering originates from the fact that in the AW–AW interaction, the primary AW cannot be derived from the ordering (2.4) as (2.4) relies on linear perturbations to produce the pressure anisotropy. As stated in § 2.3, the primary AW induces pressure anisotropy nonlinearly. Therefore, to produce ![]() $\varDelta \sim \beta ^{-1}$, it must have
$\varDelta \sim \beta ^{-1}$, it must have ![]() $\delta B_\perp /B_0$ larger than that of the secondary packet, which obeys the Alfvénic components of (2.4). Our new ordering must then capture the fact that AWs perturb the pressure and other compressive fields nonlinearly, while being consistent with the high-
$\delta B_\perp /B_0$ larger than that of the secondary packet, which obeys the Alfvénic components of (2.4). Our new ordering must then capture the fact that AWs perturb the pressure and other compressive fields nonlinearly, while being consistent with the high-![]() $\beta$ and
$\beta$ and ![]() $\beta \varDelta \sim 1$ assumptions of (2.4) (such that the resultant
$\beta \varDelta \sim 1$ assumptions of (2.4) (such that the resultant ![]() $\varDelta (x)$ may be used in (2.6)):
$\varDelta (x)$ may be used in (2.6)):
Here, ![]() $\sigma$ is a new expansion parameter satisfying
$\sigma$ is a new expansion parameter satisfying ![]() $\sigma \gg \epsilon$. The estimates of
$\sigma \gg \epsilon$. The estimates of ![]() $\partial _t$ for compressive and Alfvénic fields are the same as those used with (2.4) (
$\partial _t$ for compressive and Alfvénic fields are the same as those used with (2.4) (![]() ${\sim }k c_{\rm s}$ and
${\sim }k c_{\rm s}$ and ![]() ${\sim }kv_{\rm A}$, respectively). Note that as an ordering, this is unaffected by the Alfvénic dynamics following
${\sim }kv_{\rm A}$, respectively). Note that as an ordering, this is unaffected by the Alfvénic dynamics following ![]() $v_{{\rm A},\textrm {eff}}$ rather than
$v_{{\rm A},\textrm {eff}}$ rather than ![]() $v_{\rm A}$, as the pressure anisotropy is strictly positive and thus will never approach the firehose limit where
$v_{\rm A}$, as the pressure anisotropy is strictly positive and thus will never approach the firehose limit where ![]() $v_{{\rm A},\textrm {eff}} \ll v_{\rm A}$.
$v_{{\rm A},\textrm {eff}} \ll v_{\rm A}$.
The next step is to use (B1) to obtain an estimate for the size of the parallel pressure perturbation ![]() $\delta p_\parallel$, and show that it is much smaller than the perpendicular pressure perturbation
$\delta p_\parallel$, and show that it is much smaller than the perpendicular pressure perturbation ![]() $\delta p_\perp$. We apply (B1) to the parallel momentum equation evaluated downstream of the shock (where the gradient in
$\delta p_\perp$. We apply (B1) to the parallel momentum equation evaluated downstream of the shock (where the gradient in ![]() $\delta B_\perp$ is non-existent), finding that the leading-order equation is simply linear:
$\delta B_\perp$ is non-existent), finding that the leading-order equation is simply linear:
This approximate equation implies that ![]() $\delta p_\parallel \sim \sigma ^2 \rho _0 v_{\rm A}c_{\rm s}$, or
$\delta p_\parallel \sim \sigma ^2 \rho _0 v_{\rm A}c_{\rm s}$, or ![]() $\delta p_\parallel /p_0 \sim \sigma ^3$. Comparatively, no such restraint is placed on
$\delta p_\parallel /p_0 \sim \sigma ^3$. Comparatively, no such restraint is placed on ![]() $\delta p_\perp$ by the perpendicular momentum equation, so the pressure anisotropy must be dominated by
$\delta p_\perp$ by the perpendicular momentum equation, so the pressure anisotropy must be dominated by ![]() $\delta p_\perp$. The equation for
$\delta p_\perp$. The equation for ![]() $\delta p_\perp$ is in this case more easily formulated in terms of the perpendicular temperature
$\delta p_\perp$ is in this case more easily formulated in terms of the perpendicular temperature ![]() $\delta T_\perp$, which according to (B1) and (2.1d) evaluated downstream from the shock satisfies
$\delta T_\perp$, which according to (B1) and (2.1d) evaluated downstream from the shock satisfies
where ![]() $\kappa$ is a diffusion coefficient (equal to
$\kappa$ is a diffusion coefficient (equal to ![]() $\rho _0v_\textrm {th}/\sqrt {{\rm \pi} }|k_\||$ in the ‘
$\rho _0v_\textrm {th}/\sqrt {{\rm \pi} }|k_\||$ in the ‘![]() $3+1$’ Landau-fluid model; Snyder et al. Reference Snyder, Hammett and Dorland1997). Given that
$3+1$’ Landau-fluid model; Snyder et al. Reference Snyder, Hammett and Dorland1997). Given that ![]() $\kappa$ operates on thermal time scales, the diffusion of
$\kappa$ operates on thermal time scales, the diffusion of ![]() $\delta T_\perp$, and thus
$\delta T_\perp$, and thus ![]() $\Delta p$, downstream is effectively instantaneous as the AW packet propagates. In the frame of the shock then,
$\Delta p$, downstream is effectively instantaneous as the AW packet propagates. In the frame of the shock then, ![]() $\delta T_\perp$ attains a steady-state profile, meaning that it can be represented as
$\delta T_\perp$ attains a steady-state profile, meaning that it can be represented as ![]() $\delta T_\perp (x-v_{{\rm A},\max }t)$ (where
$\delta T_\perp (x-v_{{\rm A},\max }t)$ (where ![]() $v_{{\rm A},\max }$ is a constant equal to the peak value of
$v_{{\rm A},\max }$ is a constant equal to the peak value of ![]() $v_{{\rm A},\textrm {eff}}$ evaluated at the shock front). Accordingly, the relation (B3) becomes
$v_{{\rm A},\textrm {eff}}$ evaluated at the shock front). Accordingly, the relation (B3) becomes
This gives the functional form of ![]() $\delta T_\perp$ leading up to the shock front (where
$\delta T_\perp$ leading up to the shock front (where ![]() $\delta T_{\perp, \max }$ is determined), and motivates our choice of exponentially decaying pressure anisotropy as a source for (2.6) used in § 2.3. To test the accuracy of this estimate of the decay length of
$\delta T_{\perp, \max }$ is determined), and motivates our choice of exponentially decaying pressure anisotropy as a source for (2.6) used in § 2.3. To test the accuracy of this estimate of the decay length of ![]() $\delta T_\perp$, a series of Landau-fluid simulations were performed with varying choices of
$\delta T_\perp$, a series of Landau-fluid simulations were performed with varying choices of ![]() $\beta$ and for
$\beta$ and for ![]() $|k_\||$ in (2.3), shown in figure 7. The set-up of the wave packet in these runs is the same as that of the primary packet described in § 3.2. The decay length of
$|k_\||$ in (2.3), shown in figure 7. The set-up of the wave packet in these runs is the same as that of the primary packet described in § 3.2. The decay length of ![]() $\delta T_\perp$ is found in these simulations by waiting until the wave packet steepens to form a shock, then fitting an exponentially decaying function to the region directly in front of the peak of the magnetic-field perturbation. Compared with the theoretical estimate using the ‘
$\delta T_\perp$ is found in these simulations by waiting until the wave packet steepens to form a shock, then fitting an exponentially decaying function to the region directly in front of the peak of the magnetic-field perturbation. Compared with the theoretical estimate using the ‘![]() $3+1$’ heat fluxes, strong agreement is found.
$3+1$’ heat fluxes, strong agreement is found.

Figure 7. Comparison of the analytically predicted and simulated decay lengths of the pressure anisotropy precursor of a steepened AW packet, for ![]() $\boldsymbol {q}_{\perp /\|}$ given by the ‘
$\boldsymbol {q}_{\perp /\|}$ given by the ‘![]() $3+1$’ heat fluxes (2.3). The calculated decay length
$3+1$’ heat fluxes (2.3). The calculated decay length ![]() $\lambda _{{\rm T},\perp }$ is normalized by the dominant wavelength of the AW packet
$\lambda _{{\rm T},\perp }$ is normalized by the dominant wavelength of the AW packet ![]() $\lambda _{{\rm A}}$. On the left, the decay length is varied with respect to the Landau wavenumber
$\lambda _{{\rm A}}$. On the left, the decay length is varied with respect to the Landau wavenumber ![]() $|k_\||$, while on the right, it is varied with respect to
$|k_\||$, while on the right, it is varied with respect to ![]() $\beta$.
$\beta$.
The actual magnitude of ![]() $\delta T_{\perp, \max }$ is determined by acknowledging that
$\delta T_{\perp, \max }$ is determined by acknowledging that ![]() $\partial _x \delta B_\perp ^2$ is large in the region of the shock, and including its associated term at leading order in the equation left of the arrow in (B4) provides
$\partial _x \delta B_\perp ^2$ is large in the region of the shock, and including its associated term at leading order in the equation left of the arrow in (B4) provides
Integrating this equation from the shock front to the distant downstream region where ![]() $\partial _x \delta T_\perp \approx 0$, we obtain the simple result that
$\partial _x \delta T_\perp \approx 0$, we obtain the simple result that ![]() $\delta T_{\perp, \max }/T_0 \approx (1/2)\delta B_{\perp, \max }^2/B_0^2$. Knowing that
$\delta T_{\perp, \max }/T_0 \approx (1/2)\delta B_{\perp, \max }^2/B_0^2$. Knowing that ![]() $\delta p_\parallel$ may be neglected, the same steps can be applied to (2.1e) to obtain a diffusion equation for
$\delta p_\parallel$ may be neglected, the same steps can be applied to (2.1e) to obtain a diffusion equation for ![]() $\delta \rho$, which is found to decay on a length scale of
$\delta \rho$, which is found to decay on a length scale of ![]() $(3/2)\kappa /v_{{\rm A},\max }$ instead of
$(3/2)\kappa /v_{{\rm A},\max }$ instead of ![]() $\kappa /v_{{\rm A},\max }$. Similarly,
$\kappa /v_{{\rm A},\max }$. Similarly, ![]() $\delta \rho _{\max }$ is determined to be
$\delta \rho _{\max }$ is determined to be ![]() $\delta \rho _{\max }\approx (1/3)\delta B_{\perp, \max }^2/B_0^2$. Combined, these yield the final result that
$\delta \rho _{\max }\approx (1/3)\delta B_{\perp, \max }^2/B_0^2$. Combined, these yield the final result that ![]() $\varDelta _{\max } \approx \delta p_{\perp, \max }/p_0 \approx (5/6)\delta B_{\perp, \max }^2/B_0^2$, and
$\varDelta _{\max } \approx \delta p_{\perp, \max }/p_0 \approx (5/6)\delta B_{\perp, \max }^2/B_0^2$, and ![]() $v_{{\rm A},\max } = v_{\rm A}\sqrt {1+\beta \varDelta _{\max }/2}$.
$v_{{\rm A},\max } = v_{\rm A}\sqrt {1+\beta \varDelta _{\max }/2}$.