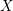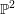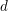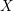1 Introduction
A fundamental problem in algebraic geometry is the study of the dimension of linear systems on projective varieties, and many tools have been developed by researchers to this end (e.g. the different versions of the Riemann–Roch theorem). It is usually the case that there is an expected dimension (or codimension), given by naively counting constants; understanding the special linear systems, that is, those whose actual dimensions are greater than the expected ones, is a subtle problem of substantial interest.
For example, consider the complete linear system
![]() ${\mathcal{L}}_{j}$
of plane curves of degree
${\mathcal{L}}_{j}$
of plane curves of degree
![]() $j$
; its (projective) dimension is
$j$
; its (projective) dimension is
![]() $\binom{j+2}{2}-1$
. For
$\binom{j+2}{2}-1$
. For
![]() $j\geqslant m$
, the requirement that the curves all have multiplicity at least
$j\geqslant m$
, the requirement that the curves all have multiplicity at least
![]() $m$
at a fixed point
$m$
at a fixed point
![]() $P$
imposes
$P$
imposes
![]() $\binom{m+1}{2}$
linear conditions, and the linear subsystem of all such curves indeed has codimension
$\binom{m+1}{2}$
linear conditions, and the linear subsystem of all such curves indeed has codimension
![]() $\binom{m+1}{2}$
in
$\binom{m+1}{2}$
in
![]() ${\mathcal{L}}_{j}$
, so the actual and expected codimensions coincide. We will refer to this as the linear subsystem of curves passing through a fat point of multiplicity
${\mathcal{L}}_{j}$
, so the actual and expected codimensions coincide. We will refer to this as the linear subsystem of curves passing through a fat point of multiplicity
![]() $m$
supported at
$m$
supported at
![]() $P$
. It is a very well-studied (but still open) problem to compute the dimension of the linear subsystem of
$P$
. It is a very well-studied (but still open) problem to compute the dimension of the linear subsystem of
![]() ${\mathcal{L}}_{j}$
of curves of degree
${\mathcal{L}}_{j}$
of curves of degree
![]() $j$
passing through a general set of
$j$
passing through a general set of
![]() $r$
fat points
$r$
fat points
![]() $P_{1},\ldots ,P_{r}$
with multiplicities
$P_{1},\ldots ,P_{r}$
with multiplicities
![]() $m_{1},\ldots ,m_{r}$
. The still open SHGH conjecture gives a putative solution to this problem; we will recall this conjecture in more detail below. When
$m_{1},\ldots ,m_{r}$
. The still open SHGH conjecture gives a putative solution to this problem; we will recall this conjecture in more detail below. When
![]() $m_{1}=\cdots =m_{r}=2$
, results of Alexander and Hirschowitz not only confirm the SHGH conjecture for those cases, but also solve the corresponding problem for double points in projective spaces of dimension greater than 2; however, little is known for fat points with arbitrary multiplicity in higher dimensions.
$m_{1}=\cdots =m_{r}=2$
, results of Alexander and Hirschowitz not only confirm the SHGH conjecture for those cases, but also solve the corresponding problem for double points in projective spaces of dimension greater than 2; however, little is known for fat points with arbitrary multiplicity in higher dimensions.
Motivated by results in this paper described below, we propose a refinement of the above problem. That is, rather than beginning with
![]() ${\mathcal{L}}_{j}$
, we propose to begin with the linear system
${\mathcal{L}}_{j}$
, we propose to begin with the linear system
![]() ${\mathcal{V}}={\mathcal{L}}_{Z,j}$
of all plane curves of degree
${\mathcal{V}}={\mathcal{L}}_{Z,j}$
of all plane curves of degree
![]() $j$
containing a fixed, reduced zero-dimensional scheme
$j$
containing a fixed, reduced zero-dimensional scheme
![]() $Z$
. We then impose the passage through a general set
$Z$
. We then impose the passage through a general set
![]() $X$
of fat points and ask for the dimension of the resulting linear subsystem. The expected dimension depends only on the dimension of the homogeneous component
$X$
of fat points and ask for the dimension of the resulting linear subsystem. The expected dimension depends only on the dimension of the homogeneous component
![]() $[I_{Z}]_{j}$
of degree
$[I_{Z}]_{j}$
of degree
![]() $j$
of the ideal of
$j$
of the ideal of
![]() $Z$
and the number of points of
$Z$
and the number of points of
![]() $X$
, counted with multiplicity: each point of multiplicity
$X$
, counted with multiplicity: each point of multiplicity
![]() $m$
is expected to impose
$m$
is expected to impose
![]() $\binom{m+1}{2}$
independent conditions, as long as the expected dimension of the linear system is non-negative.
$\binom{m+1}{2}$
independent conditions, as long as the expected dimension of the linear system is non-negative.
The problem in this generality is currently inaccessible; the case where
![]() $X$
is an arbitrary finite general set of fat points and
$X$
is an arbitrary finite general set of fat points and
![]() $Z=\varnothing$
, for example, has only a conjectural solution, given by the still open SHGH conjecture. So for this paper we begin a study of this problem by focusing on the first non-trivial case at the other extreme, namely,
$Z=\varnothing$
, for example, has only a conjectural solution, given by the still open SHGH conjecture. So for this paper we begin a study of this problem by focusing on the first non-trivial case at the other extreme, namely,
![]() $X$
a single fat point of multiplicity
$X$
a single fat point of multiplicity
![]() $j-1$
and
$j-1$
and
![]() $Z$
an arbitrary finite reduced set of points. It is surprising (as the example of [Reference Di Gennaro, Ilardi and VallèsDIV14] in the next paragraph shows) that already in this case it is no longer true that the expected dimension is necessarily achieved, as it was when we began with
$Z$
an arbitrary finite reduced set of points. It is surprising (as the example of [Reference Di Gennaro, Ilardi and VallèsDIV14] in the next paragraph shows) that already in this case it is no longer true that the expected dimension is necessarily achieved, as it was when we began with
![]() ${\mathcal{V}}={\mathcal{L}}_{j}$
(i.e. when
${\mathcal{V}}={\mathcal{L}}_{j}$
(i.e. when
![]() $X$
is one fat point and
$X$
is one fat point and
![]() $Z=\varnothing$
). Since
$Z=\varnothing$
). Since
![]() $Z$
is not assumed to be a general set of points, the problem obtains a new and central aspect, namely to understand how the geometry of
$Z$
is not assumed to be a general set of points, the problem obtains a new and central aspect, namely to understand how the geometry of
![]() $Z$
can affect the desired dimension. In this paper we carefully analyze this surprising behavior. Furthermore, we show that our results have interesting connections to the study of line arrangements. In particular, they give new perspectives on Terao’s freeness conjecture, including a generalization to non-free arrangements.
$Z$
can affect the desired dimension. In this paper we carefully analyze this surprising behavior. Furthermore, we show that our results have interesting connections to the study of line arrangements. In particular, they give new perspectives on Terao’s freeness conjecture, including a generalization to non-free arrangements.
One of our inspirations for this work was an example by Di Gennaro et al. in [Reference Di Gennaro, Ilardi and VallèsDIV14]. They observe that the set of nine points in
![]() $\mathbb{P}^{2}$
dual to the so-called
$\mathbb{P}^{2}$
dual to the so-called
![]() $B_{3}$
arrangement has an unusual geometric property [Reference Di Gennaro, Ilardi and VallèsDIV14, Proposition 7.3]: for every point
$B_{3}$
arrangement has an unusual geometric property [Reference Di Gennaro, Ilardi and VallèsDIV14, Proposition 7.3]: for every point
![]() $P$
of the plane, there is a curve of degree
$P$
of the plane, there is a curve of degree
![]() $4$
passing through these nine points and vanishing to order
$4$
passing through these nine points and vanishing to order
![]() $3$
at
$3$
at
![]() $P$
. This is surprising because a naive dimension count suggests that the linear system of curves of degree 4 containing the nine points and
$P$
. This is surprising because a naive dimension count suggests that the linear system of curves of degree 4 containing the nine points and
![]() $3P$
should be empty except for a special locus of points
$3P$
should be empty except for a special locus of points
![]() $P$
, but in fact it is non-empty for a general point
$P$
, but in fact it is non-empty for a general point
![]() $P$
.
$P$
.
This led us to study finite sets of points
![]() $Z$
in the plane for which, for some integer
$Z$
in the plane for which, for some integer
![]() $j$
, the dimension of the linear system of plane curves of degree
$j$
, the dimension of the linear system of plane curves of degree
![]() $j+1$
that pass through the points of
$j+1$
that pass through the points of
![]() $Z$
and have multiplicity
$Z$
and have multiplicity
![]() $j$
at a general point
$j$
at a general point
![]() $P$
is unexpectedly large. In this case, we say that
$P$
is unexpectedly large. In this case, we say that
![]() $Z$
admits (or has) an unexpected curve of degree
$Z$
admits (or has) an unexpected curve of degree
![]() $j+1$
(see Definition 2.1). We establish a numerical criterion for the occurrence of unexpected curves. It involves two invariants. The first, which arose in the work of Faenzi and Vallès [Reference Faenzi and VallèsFV14], we call the multiplicity index
$j+1$
(see Definition 2.1). We establish a numerical criterion for the occurrence of unexpected curves. It involves two invariants. The first, which arose in the work of Faenzi and Vallès [Reference Faenzi and VallèsFV14], we call the multiplicity index
![]() $m_{Z}$
of
$m_{Z}$
of
![]() $Z$
. It is the least integer
$Z$
. It is the least integer
![]() $j$
such that the linear system of degree
$j$
such that the linear system of degree
![]() $j+1$
forms vanishing at
$j+1$
forms vanishing at
![]() $Z+jP$
(the scheme defined by the ideal
$Z+jP$
(the scheme defined by the ideal
![]() $I_{P}^{j}\cap I_{Z}$
) is not empty (see Definition 3.1). The second invariant, which is new, is
$I_{P}^{j}\cap I_{Z}$
) is not empty (see Definition 3.1). The second invariant, which is new, is
![]() $t_{Z}:=\min \{j\geqslant 0\;:\;h^{0}({\mathcal{I}}_{Z}(j+1))-\binom{j+1}{2}>0\}$
(see Definition 2.5). It depends only on the Hilbert function of
$t_{Z}:=\min \{j\geqslant 0\;:\;h^{0}({\mathcal{I}}_{Z}(j+1))-\binom{j+1}{2}>0\}$
(see Definition 2.5). It depends only on the Hilbert function of
![]() $Z$
.
$Z$
.
It turns out that a set
![]() $Z$
of points can have unexpected curves of various degrees. To understand this range of degrees we introduce another new invariant,
$Z$
of points can have unexpected curves of various degrees. To understand this range of degrees we introduce another new invariant,
![]() $u_{Z}$
, called the speciality index of
$u_{Z}$
, called the speciality index of
![]() $Z$
, as the least integer
$Z$
, as the least integer
![]() $j$
such that the scheme
$j$
such that the scheme
![]() $Z+jP$
, where
$Z+jP$
, where
![]() $P$
is a general point, imposes independent conditions on forms of degree
$P$
is a general point, imposes independent conditions on forms of degree
![]() $j+1$
(see Definition 3.1). Our first main result (see Theorem 3.9) is as follows.
$j+1$
(see Definition 3.1). Our first main result (see Theorem 3.9) is as follows.
Theorem 1.1.
![]() $Z$
admits an unexpected curve if and only if
$Z$
admits an unexpected curve if and only if
![]() $m_{Z}<t_{Z}$
. Furthermore, in this case
$m_{Z}<t_{Z}$
. Furthermore, in this case
![]() $Z$
has an unexpected curve of degree
$Z$
has an unexpected curve of degree
![]() $j$
if and only if
$j$
if and only if
![]() $m_{Z}<j\leqslant u_{Z}$
.
$m_{Z}<j\leqslant u_{Z}$
.
In particular, the existence of an unexpected curve forces
![]() $m_{Z}<u_{Z}$
. The converse is almost but not quite true. Example 7.3 gives a counterexample to the converse. It has
$m_{Z}<u_{Z}$
. The converse is almost but not quite true. Example 7.3 gives a counterexample to the converse. It has
![]() $m_{Z}<u_{Z}$
and admits no unexpected curve. However,
$m_{Z}<u_{Z}$
and admits no unexpected curve. However,
![]() $Z$
has a subset of at least
$Z$
has a subset of at least
![]() $m_{Z}+2$
collinear points. This led us to the following more geometric version of Theorem 1.1 (see Corollary 5.7).
$m_{Z}+2$
collinear points. This led us to the following more geometric version of Theorem 1.1 (see Corollary 5.7).
Theorem 1.2. Let
![]() $Z\subset \mathbb{P}^{2}$
be a finite set of points. Then
$Z\subset \mathbb{P}^{2}$
be a finite set of points. Then
![]() $Z$
admits an unexpected curve if and only if
$Z$
admits an unexpected curve if and only if
![]() $2m_{Z}+2<|Z|$
but no subset of
$2m_{Z}+2<|Z|$
but no subset of
![]() $m_{Z}+2$
(or more) of the points is collinear. In this case,
$m_{Z}+2$
(or more) of the points is collinear. In this case,
![]() $Z$
has an unexpected curve of degree
$Z$
has an unexpected curve of degree
![]() $j$
if and only if
$j$
if and only if
![]() $m_{Z}<j\leqslant |Z|-m_{Z}-2$
.
$m_{Z}<j\leqslant |Z|-m_{Z}-2$
.
As we will show (see Lemma 3.5(c)),
![]() $2m_{Z}+2<|Z|$
is equivalent to
$2m_{Z}+2<|Z|$
is equivalent to
![]() $m_{Z}<u_{Z}$
. Thus
$m_{Z}<u_{Z}$
. Thus
![]() $m_{Z}<u_{Z}$
together with there being no large collinear subsets of
$m_{Z}<u_{Z}$
together with there being no large collinear subsets of
![]() $Z$
implies the occurrence of unexpected curves.
$Z$
implies the occurrence of unexpected curves.
We also show that unexpected curves have a very particular structure. If
![]() $Z$
has any unexpected curve, then the unexpected curve of degree
$Z$
has any unexpected curve, then the unexpected curve of degree
![]() $m_{Z}+1$
is uniquely determined by
$m_{Z}+1$
is uniquely determined by
![]() $Z$
and the general point
$Z$
and the general point
![]() $P$
. Denote it by
$P$
. Denote it by
![]() $C_{P}(Z)$
. Any other unexpected curve of
$C_{P}(Z)$
. Any other unexpected curve of
![]() $Z$
associated to
$Z$
associated to
![]() $P$
contains
$P$
contains
![]() $C_{P}(Z)$
(see Proposition 5.2). Moreover, the curve
$C_{P}(Z)$
(see Proposition 5.2). Moreover, the curve
![]() $C_{P}(Z)$
either is irreducible or is the union of a reduced irreducible curve unexpected with respect to a proper subset
$C_{P}(Z)$
either is irreducible or is the union of a reduced irreducible curve unexpected with respect to a proper subset
![]() $Z^{\prime }\neq \emptyset$
of
$Z^{\prime }\neq \emptyset$
of
![]() $Z$
and the
$Z$
and the
![]() $|Z\setminus Z^{\prime }|$
lines through
$|Z\setminus Z^{\prime }|$
lines through
![]() $P$
and a point of
$P$
and a point of
![]() $Z\setminus Z^{\prime }$
(see Theorem 5.9). The curve
$Z\setminus Z^{\prime }$
(see Theorem 5.9). The curve
![]() $C_{P}(Z^{\prime })$
is rational, and we give a parametrization of it (see Proposition 5.10).
$C_{P}(Z^{\prime })$
is rational, and we give a parametrization of it (see Proposition 5.10).
One conclusion that can be drawn from the aforementioned results is that understanding unexpected curves reduces to understanding irreducible ones, since whenever
![]() $Z$
gives an unexpected curve, then
$Z$
gives an unexpected curve, then
![]() $Z$
uniquely determines a subset
$Z$
uniquely determines a subset
![]() $Z^{\prime }$
which gives an irreducible unexpected curve, and
$Z^{\prime }$
which gives an irreducible unexpected curve, and
![]() $Z$
arises from
$Z$
arises from
![]() $Z^{\prime }$
in a prescribed way (see Remark 5.16).
$Z^{\prime }$
in a prescribed way (see Remark 5.16).
By Theorem 1.1, checking for the existence of unexpected curves requires computing
![]() $m_{Z}$
and
$m_{Z}$
and
![]() $t_{Z}$
. Since
$t_{Z}$
. Since
![]() $t_{Z}$
depends only on the fixed reduced scheme
$t_{Z}$
depends only on the fixed reduced scheme
![]() $Z$
, it is typically easy to compute. In contrast,
$Z$
, it is typically easy to compute. In contrast,
![]() $m_{Z}$
is much harder to compute rigorously (although one can get experimental evidence for its value using randomly selected points
$m_{Z}$
is much harder to compute rigorously (although one can get experimental evidence for its value using randomly selected points
![]() $P$
). Work of Faenzi and Vallès [Reference Faenzi and VallèsFV14] relates
$P$
). Work of Faenzi and Vallès [Reference Faenzi and VallèsFV14] relates
![]() $m_{Z}$
to properties of the arrangement of lines
$m_{Z}$
to properties of the arrangement of lines
![]() ${\mathcal{A}}_{Z}$
dual to the points of
${\mathcal{A}}_{Z}$
dual to the points of
![]() $Z$
.
$Z$
.
Recall that associated to any line arrangement
![]() ${\mathcal{A}}_{Z}$
is a locally free sheaf
${\mathcal{A}}_{Z}$
is a locally free sheaf
![]() ${\mathcal{D}}_{Z}$
of rank
${\mathcal{D}}_{Z}$
of rank
![]() $2$
, called the derivation bundle. Restricted to a general line
$2$
, called the derivation bundle. Restricted to a general line
![]() $L$
, it splits as
$L$
, it splits as
![]() ${\mathcal{O}}_{L}(-a_{Z})\oplus {\mathcal{O}}_{L}(-b_{Z})$
with
${\mathcal{O}}_{L}(-a_{Z})\oplus {\mathcal{O}}_{L}(-b_{Z})$
with
![]() $a_{Z}+b_{Z}=|Z|-1$
. The pair
$a_{Z}+b_{Z}=|Z|-1$
. The pair
![]() $(a_{Z},b_{Z})$
, where
$(a_{Z},b_{Z})$
, where
![]() $a_{Z}\leqslant b_{Z}$
, is called the splitting type of
$a_{Z}\leqslant b_{Z}$
, is called the splitting type of
![]() ${\mathcal{D}}_{Z}$
or
${\mathcal{D}}_{Z}$
or
![]() ${\mathcal{A}}_{Z}$
. Theorem 4.3 in [Reference Faenzi and VallèsFV14] shows that the number
${\mathcal{A}}_{Z}$
. Theorem 4.3 in [Reference Faenzi and VallèsFV14] shows that the number
![]() $a_{Z}$
is equal to the multiplicity index
$a_{Z}$
is equal to the multiplicity index
![]() $m_{Z}$
. We observe that
$m_{Z}$
. We observe that
![]() $b_{Z}=u_{Z}+1$
(see Lemma 3.5). This allows us to translate our results about finite sets of points into statements on line arrangements. In the other direction, we use methods for studying line arrangements to determine multiplicity indices of sets of points. For example, we determine the multiplicity index and the speciality index of a set of points in linearly general position and conclude that such a set does not admit any unexpected curves (see Corollary 6.8). We also show that the set of points dual to a Fermat configuration of
$b_{Z}=u_{Z}+1$
(see Lemma 3.5). This allows us to translate our results about finite sets of points into statements on line arrangements. In the other direction, we use methods for studying line arrangements to determine multiplicity indices of sets of points. For example, we determine the multiplicity index and the speciality index of a set of points in linearly general position and conclude that such a set does not admit any unexpected curves (see Corollary 6.8). We also show that the set of points dual to a Fermat configuration of
![]() $3t\geqslant 15$
lines admits unexpected curves of degrees
$3t\geqslant 15$
lines admits unexpected curves of degrees
![]() $t+2,\ldots ,2t-3$
, and that the unexpected curve of degree
$t+2,\ldots ,2t-3$
, and that the unexpected curve of degree
![]() $t+2$
is irreducible (see Proposition 6.12). Furthermore, we exhibit a family of free line arrangements, defined over the rational numbers, with the property that any of the dual sets of points admits a unique unexpected curve which is in fact irreducible (see Proposition 6.15). This relies on new stability criteria for derivation bundles (see Lemma 6.5).
$t+2$
is irreducible (see Proposition 6.12). Furthermore, we exhibit a family of free line arrangements, defined over the rational numbers, with the property that any of the dual sets of points admits a unique unexpected curve which is in fact irreducible (see Proposition 6.15). This relies on new stability criteria for derivation bundles (see Lemma 6.5).
Another way that [Reference Di Gennaro, Ilardi and VallèsDIV14] inspired our work relates to a fundamental open problem in the study of hyperplane arrangements, namely, Terao’s conjecture, which is open even for line arrangements. A line arrangement
![]() ${\mathcal{A}}={\mathcal{A}}(f)$
is said to be free if the Jacobian ideal of
${\mathcal{A}}={\mathcal{A}}(f)$
is said to be free if the Jacobian ideal of
![]() $f$
is saturated, where
$f$
is saturated, where
![]() $f$
is the product of linear forms defining the lines in
$f$
is the product of linear forms defining the lines in
![]() ${\mathcal{A}}$
. Terao conjectured that freeness is a combinatorial property, that is, it depends only on the incidence lattice of the lines in
${\mathcal{A}}$
. Terao conjectured that freeness is a combinatorial property, that is, it depends only on the incidence lattice of the lines in
![]() ${\mathcal{A}}$
. In [Reference Di Gennaro, Ilardi and VallèsDIV14], the authors give an equivalent version of Terao’s conjecture in terms of Lefschetz properties. In trying to understand their proof we realized that some of the results used in [Reference Di Gennaro, Ilardi and VallèsDIV14] to derive the claimed equivalence are not quite true as stated. We use our results on points to clarify and to adjust the needed results. For example, in Theorem 7.5 we show that the existence of an unexpected curve is equivalent to the failure of a certain Lefschetz property. We also establish that Terao’s conjecture is equivalent to a Lefschetz-like condition (see Proposition 7.13). This allows us to show that the (adjusted) Lefschetz condition given in [Reference Di Gennaro, Ilardi and VallèsDIV14] implies Terao’s conjecture (see Corollary 7.14). We do not know if this condition is also necessary. We observe that the condition suggests that, for a set of points, having maximal multiplicity index is a combinatorial property. If that is true, then Terao’s conjecture for line arrangements is a consequence (see Corollary 7.16).
${\mathcal{A}}$
. In [Reference Di Gennaro, Ilardi and VallèsDIV14], the authors give an equivalent version of Terao’s conjecture in terms of Lefschetz properties. In trying to understand their proof we realized that some of the results used in [Reference Di Gennaro, Ilardi and VallèsDIV14] to derive the claimed equivalence are not quite true as stated. We use our results on points to clarify and to adjust the needed results. For example, in Theorem 7.5 we show that the existence of an unexpected curve is equivalent to the failure of a certain Lefschetz property. We also establish that Terao’s conjecture is equivalent to a Lefschetz-like condition (see Proposition 7.13). This allows us to show that the (adjusted) Lefschetz condition given in [Reference Di Gennaro, Ilardi and VallèsDIV14] implies Terao’s conjecture (see Corollary 7.14). We do not know if this condition is also necessary. We observe that the condition suggests that, for a set of points, having maximal multiplicity index is a combinatorial property. If that is true, then Terao’s conjecture for line arrangements is a consequence (see Corollary 7.16).
We end the introduction with the more detailed discussion of the SHGH conjecture which we promised above in the context of the larger problem which frames the work we are doing here. Let
![]() $V=[R]_{j}$
be the vector space of degree
$V=[R]_{j}$
be the vector space of degree
![]() $j$
forms in three variables, let
$j$
forms in three variables, let
![]() ${\mathcal{L}}_{j}$
be its projectivization, and let
${\mathcal{L}}_{j}$
be its projectivization, and let
![]() $X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
be a fat point scheme supported on a set of
$X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
be a fat point scheme supported on a set of
![]() $r$
points
$r$
points
![]() $P_{1},\ldots ,P_{r}$
. Thus
$P_{1},\ldots ,P_{r}$
. Thus
![]() $X$
is defined by
$X$
is defined by
We say that
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V$
(or on
$V$
(or on
![]() ${\mathcal{L}}_{j}$
) if
${\mathcal{L}}_{j}$
) if
If the points
![]() $P_{i}$
are general, it is a well-known and difficult open problem to classify all
$P_{i}$
are general, it is a well-known and difficult open problem to classify all
![]() $m_{i}$
and
$m_{i}$
and
![]() $j$
such that the subscheme
$j$
such that the subscheme
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V$
, but a conjectural answer is given by the SHGH conjecture [Reference SegreSeg61, Reference HarbourneHar86, Reference GimiglianoGim87, Reference HirschowitzHir89]. Segre’s version of the conjecture, which ostensibly gives only a necessary criterion, is as follows.
$V$
, but a conjectural answer is given by the SHGH conjecture [Reference SegreSeg61, Reference HarbourneHar86, Reference GimiglianoGim87, Reference HirschowitzHir89]. Segre’s version of the conjecture, which ostensibly gives only a necessary criterion, is as follows.
Conjecture 1.3 (SHGH conjecture).
For
![]() $X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
with general points
$X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
with general points
![]() $P_{i}$
,
$P_{i}$
,
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V$
only if
$V$
only if
![]() $[I_{X}]_{j}\neq 0$
but the base locus of
$[I_{X}]_{j}\neq 0$
but the base locus of
![]() $[I_{X}]_{j}$
contains a multiple of a rational curve of a prescribed kind.
$[I_{X}]_{j}$
contains a multiple of a rational curve of a prescribed kind.
In fact, the SHGH conjecture as stated above is equivalent to versions [Reference HarbourneHar86, Reference GimiglianoGim87, Reference HirschowitzHir89] that not only provide an explicit and complete list of all
![]() $(m_{1},\ldots ,m_{r})$
and
$(m_{1},\ldots ,m_{r})$
and
![]() $j$
for which
$j$
for which
![]() $[I_{X}]_{j}$
conjecturally fails to impose independent conditions on
$[I_{X}]_{j}$
conjecturally fails to impose independent conditions on
![]() $V$
but which also conjecturally determine the extent to which the conditions fail to be independent. Although we will not discuss the details here, we note that it took 40 years [Reference Ciliberto and MirandaCM01] to recognize that the partial characterization as given in Conjecture 1.3 above actually provides a full quantitative conjectural solution.
$V$
but which also conjecturally determine the extent to which the conditions fail to be independent. Although we will not discuss the details here, we note that it took 40 years [Reference Ciliberto and MirandaCM01] to recognize that the partial characterization as given in Conjecture 1.3 above actually provides a full quantitative conjectural solution.
Similarly, our focus here will be on identifying failures of independence in a generalized context, with a long-term goal of obtaining a more complete characterization. The generalized context is that we consider the case where
![]() $V$
is a subspace of
$V$
is a subspace of
![]() $R_{j}$
, in particular,
$R_{j}$
, in particular,
![]() $V=[I_{Z}]_{j}$
, where
$V=[I_{Z}]_{j}$
, where
![]() $Z$
is a fat point subscheme. Then the overall problem becomes the following.
$Z$
is a fat point subscheme. Then the overall problem becomes the following.
Problem 1.4. Characterize and then classify all triples
![]() $(Z,X,j)$
where
$(Z,X,j)$
where
![]() $Z=c_{1}Q_{1}+\cdots +c_{s}Q_{s}$
for distinct points
$Z=c_{1}Q_{1}+\cdots +c_{s}Q_{s}$
for distinct points
![]() $Q_{i}$
, and
$Q_{i}$
, and
![]() $X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
for general points
$X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
for general points
![]() $P_{i}$
, such that
$P_{i}$
, such that
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V=[I_{Z}]_{j}$
.
$V=[I_{Z}]_{j}$
.
If
![]() $Z$
is the empty set, then
$Z$
is the empty set, then
![]() $V=[R]_{j}$
, so this is addressed by the SHGH conjecture. If
$V=[R]_{j}$
, so this is addressed by the SHGH conjecture. If
![]() $Z$
is reduced,
$Z$
is reduced,
![]() $r=1$
and
$r=1$
and
![]() $j=m_{1}+1$
, this becomes the problem of deciding the existence of an unexpected curve of degree
$j=m_{1}+1$
, this becomes the problem of deciding the existence of an unexpected curve of degree
![]() $j$
.
$j$
.
Our results give criteria for when a general fat point
![]() $mP$
fails to impose the expected number of conditions on
$mP$
fails to impose the expected number of conditions on
![]() $[I_{Z}]_{m+1}$
for a reduced point scheme
$[I_{Z}]_{m+1}$
for a reduced point scheme
![]() $Z$
. Similarly to the SHGH conjecture, they show the particular role of rational curves (see Remark 5.21).
$Z$
. Similarly to the SHGH conjecture, they show the particular role of rational curves (see Remark 5.21).
It would be interesting to understand exactly for which sets
![]() $Z$
such failures occur. Furthermore, our results strongly suggest that finding answers to Problem 1.4 in other cases is worth investigating.
$Z$
such failures occur. Furthermore, our results strongly suggest that finding answers to Problem 1.4 in other cases is worth investigating.
Our paper is organized as follows. In § 2 we introduce unexpected curves and the invariant
![]() $t_{Z}$
, and we establish properties of this invariant. Section 3 is entirely geared towards establishing our criteria for the existence of unexpected curves. A key ingredient of the argument is shown in § 4. The structure of unexpected curves is described in § 5. In § 6 we use line arrangements to show that points in linearly general position do not admit unexpected curves and to exhibit configurations of points that do have unexpected curves. The relation of the Lefschetz properties to the existence of unexpected curves and to Terao’s freeness conjecture is described in § 7.
$t_{Z}$
, and we establish properties of this invariant. Section 3 is entirely geared towards establishing our criteria for the existence of unexpected curves. A key ingredient of the argument is shown in § 4. The structure of unexpected curves is described in § 5. In § 6 we use line arrangements to show that points in linearly general position do not admit unexpected curves and to exhibit configurations of points that do have unexpected curves. The relation of the Lefschetz properties to the existence of unexpected curves and to Terao’s freeness conjecture is described in § 7.
2 Unexpected curves and the invariant
 $t_{Z}$
$t_{Z}$
In this section we formally define the notion of an unexpected curve. Our main results on when such curves exist will require understanding a certain invariant, which we denote by
![]() $t_{Z}$
. Here we also derive the elementary geometric properties of this invariant.
$t_{Z}$
. Here we also derive the elementary geometric properties of this invariant.
Let
![]() $K$
be an arbitrary infinite field (when necessary we will add assumptions) and let
$K$
be an arbitrary infinite field (when necessary we will add assumptions) and let
![]() $Z=P_{1}+\cdots +P_{d}$
be a reduced subscheme of
$Z=P_{1}+\cdots +P_{d}$
be a reduced subscheme of
![]() $\mathbb{P}_{K}^{2}$
consisting of
$\mathbb{P}_{K}^{2}$
consisting of
![]() $d>0$
distinct points
$d>0$
distinct points
![]() $P_{i}$
, with homogeneous ideal
$P_{i}$
, with homogeneous ideal
![]() $I_{Z}\subset K[\mathbb{P}^{2}]=K[x,y,z]=R$
. (In particular,
$I_{Z}\subset K[\mathbb{P}^{2}]=K[x,y,z]=R$
. (In particular,
![]() $Z$
will always be non-empty.) For a general point
$Z$
will always be non-empty.) For a general point
![]() $P$
we denote by
$P$
we denote by
![]() $X=Z+jP$
the scheme defined by the ideal
$X=Z+jP$
the scheme defined by the ideal
![]() $I_{X}=I_{P}^{j}\cap I_{Z}$
. Throughout this paper, ‘dimension’ refers to the vector space dimension over
$I_{X}=I_{P}^{j}\cap I_{Z}$
. Throughout this paper, ‘dimension’ refers to the vector space dimension over
![]() $K$
. For any
$K$
. For any
![]() $j$
and a fixed
$j$
and a fixed
![]() $Z$
, by semicontinuity there is a Zariski open subset of points
$Z$
, by semicontinuity there is a Zariski open subset of points
![]() $P$
on which the dimension of
$P$
on which the dimension of
![]() $\dim [I_{Z+jP}]_{j+1}$
takes its minimum value. Thus it makes sense to talk about the number of conditions imposed on
$\dim [I_{Z+jP}]_{j+1}$
takes its minimum value. Thus it makes sense to talk about the number of conditions imposed on
![]() $[I_{Z}]_{j+1}$
by a general fat point
$[I_{Z}]_{j+1}$
by a general fat point
![]() $jP$
.
$jP$
.
In each degree
![]() $t$
, note that
$t$
, note that
![]() $\dim _{K}[I_{X}]_{t}\geqslant \dim _{K}[I_{Z}]_{t}-\binom{j+1}{2}$
; that is, the forms in
$\dim _{K}[I_{X}]_{t}\geqslant \dim _{K}[I_{Z}]_{t}-\binom{j+1}{2}$
; that is, the forms in
![]() $[I_{X}]_{t}$
are obtained from those of
$[I_{X}]_{t}$
are obtained from those of
![]() $[I_{Z}]_{t}$
by imposing at most
$[I_{Z}]_{t}$
by imposing at most
![]() $\binom{j+1}{2}$
linear conditions coming from
$\binom{j+1}{2}$
linear conditions coming from
![]() $jP$
. Typically, if
$jP$
. Typically, if
![]() $\dim _{K}[I_{X}]_{t}>\dim _{K}[I_{Z}]_{t}-\binom{j+1}{2}$
(i.e. if
$\dim _{K}[I_{X}]_{t}>\dim _{K}[I_{Z}]_{t}-\binom{j+1}{2}$
(i.e. if
![]() $jP$
imposes fewer than
$jP$
imposes fewer than
![]() $\binom{j+1}{2}$
conditions on
$\binom{j+1}{2}$
conditions on
![]() $[I_{Z}]_{t}$
) for a general point
$[I_{Z}]_{t}$
) for a general point
![]() $P$
, it is because
$P$
, it is because
![]() $\dim _{K}[I_{Z}]_{t}<\binom{j+1}{2}$
and
$\dim _{K}[I_{Z}]_{t}<\binom{j+1}{2}$
and
![]() $\dim _{K}[I_{X}]_{t}=0$
. For special choices of
$\dim _{K}[I_{X}]_{t}=0$
. For special choices of
![]() $Z$
, however, it can happen that
$Z$
, however, it can happen that
![]() $jP$
imposes fewer than
$jP$
imposes fewer than
![]() $\binom{j+1}{2}$
conditions even though
$\binom{j+1}{2}$
conditions even though
![]() $P$
is general and
$P$
is general and
![]() $\dim _{K}[I_{X}]_{t}>0$
. We are interested in exploring this situation when the degree
$\dim _{K}[I_{X}]_{t}>0$
. We are interested in exploring this situation when the degree
![]() $t$
is
$t$
is
![]() $j+1$
. This motivates the following definition, where we denote the sheafification of a homogeneous ideal
$j+1$
. This motivates the following definition, where we denote the sheafification of a homogeneous ideal
![]() $I$
by
$I$
by
![]() ${\mathcal{I}}$
. Also, given a sheaf
${\mathcal{I}}$
. Also, given a sheaf
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() $\mathbb{P}^{2}$
, we will usually write
$\mathbb{P}^{2}$
, we will usually write
![]() $h^{0}(\mathbb{P}^{2},{\mathcal{F}})$
simply as
$h^{0}(\mathbb{P}^{2},{\mathcal{F}})$
simply as
![]() $h^{0}({\mathcal{F}})$
. Thus, for example,
$h^{0}({\mathcal{F}})$
. Thus, for example,
![]() ${\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j}={\mathcal{I}}_{X}={\mathcal{I}}_{Z+jP}$
,
${\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j}={\mathcal{I}}_{X}={\mathcal{I}}_{Z+jP}$
,
![]() $h^{0}(\mathbb{P}^{2},{\mathcal{I}}_{Z}(t))=h^{0}({\mathcal{I}}_{Z}(t))=\dim _{K}[I_{Z}]_{t}$
and
$h^{0}(\mathbb{P}^{2},{\mathcal{I}}_{Z}(t))=h^{0}({\mathcal{I}}_{Z}(t))=\dim _{K}[I_{Z}]_{t}$
and
![]() $h^{0}(\mathbb{P}^{2},({\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j})(t))=h^{0}({\mathcal{I}}_{Z+jP}(t))=h^{0}({\mathcal{I}}_{X}(t))=\dim _{K}[I_{X}]_{t}=\dim _{K}[I_{Z+jP}]_{t}$
. From now on we will suppress the subscript
$h^{0}(\mathbb{P}^{2},({\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j})(t))=h^{0}({\mathcal{I}}_{Z+jP}(t))=h^{0}({\mathcal{I}}_{X}(t))=\dim _{K}[I_{X}]_{t}=\dim _{K}[I_{Z+jP}]_{t}$
. From now on we will suppress the subscript
![]() $K$
in the dimension notation.
$K$
in the dimension notation.
Definition 2.1. We say that a reduced finite set of points
![]() $Z\subset \mathbb{P}^{2}$
admits an unexpected curve of degree
$Z\subset \mathbb{P}^{2}$
admits an unexpected curve of degree
![]() $j+1$
if there is an integer
$j+1$
if there is an integer
![]() $j>0$
such that, for a general point
$j>0$
such that, for a general point
![]() $P$
,
$P$
,
![]() $jP$
fails to impose the expected number of conditions on the linear system of curves of degree
$jP$
fails to impose the expected number of conditions on the linear system of curves of degree
![]() $j+1$
containing
$j+1$
containing
![]() $Z$
. That is,
$Z$
. That is,
![]() $Z$
admits an unexpected curve of degree
$Z$
admits an unexpected curve of degree
![]() $j+1$
if
$j+1$
if
Remark 2.2. While it certainly can be of interest to ask when different kinds of non-reduced schemes admit ‘unexpected curves’ of this sort, in this paper we are concerned only with the case where
![]() $Z$
is reduced, of degree at least
$Z$
is reduced, of degree at least
![]() $2$
(i.e.
$2$
(i.e.
![]() $|Z|\geqslant 2$
).
$|Z|\geqslant 2$
).
Remark 2.3. If
![]() $0\leqslant j\leqslant 1$
and
$0\leqslant j\leqslant 1$
and
![]() $P$
is general, then
$P$
is general, then
![]() $h^{0}(({\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j})(j+1))>0$
implies
$h^{0}(({\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j})(j+1))>0$
implies
![]() $h^{0}(({\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j})(j+1))=h^{0}({\mathcal{I}}_{Z}(j+1))-\binom{j+1}{2}\geqslant 0$
. Thus unexpected curves must have degree at least 3.
$h^{0}(({\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{P}^{j})(j+1))=h^{0}({\mathcal{I}}_{Z}(j+1))-\binom{j+1}{2}\geqslant 0$
. Thus unexpected curves must have degree at least 3.
Example 2.4. By Remark 2.3, the least degree for which an unexpected curve can occur is 3. We now reprise an example of Serre (see [Reference HartshorneHar77, Exercise III.10.7]) to show that unexpected curves of degree 3 can occur. Although the occurrence of unexpected curves is not purely a characteristic
![]() $p>0$
phenomenon (later we will give examples in characteristic 0), it is only in characteristic 2 that an unexpected curve of degree 3 can occur (see [Reference AkessehAke17, Reference Farnik, Galuppi, Sodomaco and TrokFGST18]). So for this example assume
$p>0$
phenomenon (later we will give examples in characteristic 0), it is only in characteristic 2 that an unexpected curve of degree 3 can occur (see [Reference AkessehAke17, Reference Farnik, Galuppi, Sodomaco and TrokFGST18]). So for this example assume
![]() $K$
has characteristic 2 and take
$K$
has characteristic 2 and take
![]() $Z$
to be the seven points whose homogeneous coordinates
$Z$
to be the seven points whose homogeneous coordinates
![]() $[a:b:c]$
consist of just zeros and ones. We now show that (2.1) holds with
$[a:b:c]$
consist of just zeros and ones. We now show that (2.1) holds with
![]() $j+1=3$
and with the right-hand side of (2.1) being 0. Note that the seven points are the points of the Fano plane and that any line through two of them goes through a third. There are only seven such lines, and they are projectively dual to the seven points. Let
$j+1=3$
and with the right-hand side of (2.1) being 0. Note that the seven points are the points of the Fano plane and that any line through two of them goes through a third. There are only seven such lines, and they are projectively dual to the seven points. Let
![]() $P=[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D6FE}]\in \mathbb{P}^{2}$
be a general point. One can check that
$P=[\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D6FE}]\in \mathbb{P}^{2}$
be a general point. One can check that
![]() $Z$
imposes independent conditions on cubics (in fact,
$Z$
imposes independent conditions on cubics (in fact,
![]() $I_{Z}=(yz(y+z),xz(x+z),xy(x+y))$
). Since
$I_{Z}=(yz(y+z),xz(x+z),xy(x+y))$
). Since
![]() $Z+2P$
imposes 10 conditions, one would expect that there would not be a cubic containing
$Z+2P$
imposes 10 conditions, one would expect that there would not be a cubic containing
![]() $Z$
having a double point at
$Z$
having a double point at
![]() $P$
. But the conditions are not independent: one can easily check that
$P$
. But the conditions are not independent: one can easily check that
![]() $F=\unicode[STIX]{x1D6FC}^{2}yz(y+z)+\unicode[STIX]{x1D6FD}^{2}xz(x+z)+\unicode[STIX]{x1D6FE}^{2}xy(x+y)$
defines a curve
$F=\unicode[STIX]{x1D6FC}^{2}yz(y+z)+\unicode[STIX]{x1D6FD}^{2}xz(x+z)+\unicode[STIX]{x1D6FE}^{2}xy(x+y)$
defines a curve
![]() $C$
(reduced and irreducible in fact) which is singular at
$C$
(reduced and irreducible in fact) which is singular at
![]() $P$
and hence
$P$
and hence
![]() $C$
is an unexpected curve of degree 3 for
$C$
is an unexpected curve of degree 3 for
![]() $Z$
.
$Z$
.
Note for
![]() $j\geqslant 0$
that it is always true that
$j\geqslant 0$
that it is always true that
 $$\begin{eqnarray}\displaystyle \dim [I_{Z+jP}]_{j+1} & {\geqslant} & \displaystyle \dim [I_{Z}]_{j+1}-\binom{j+1}{2}\nonumber\\ \displaystyle & = & \displaystyle \binom{j+3}{2}-h_{Z}(j+1)-\binom{j+1}{2}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \binom{j+3}{2}-|Z|-\binom{j+1}{2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim [I_{Z+jP}]_{j+1} & {\geqslant} & \displaystyle \dim [I_{Z}]_{j+1}-\binom{j+1}{2}\nonumber\\ \displaystyle & = & \displaystyle \binom{j+3}{2}-h_{Z}(j+1)-\binom{j+1}{2}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \binom{j+3}{2}-|Z|-\binom{j+1}{2}\end{eqnarray}$$
and
where
![]() $h_{Z}(j)=\dim [R/I_{Z}]_{j}=\binom{j+2}{2}-\dim [I_{Z}]_{j}$
is the Hilbert function of
$h_{Z}(j)=\dim [R/I_{Z}]_{j}=\binom{j+2}{2}-\dim [I_{Z}]_{j}$
is the Hilbert function of
![]() $Z$
.
$Z$
.
The definition of an unexpected curve already suggests the importance of the following invariant.
Definition 2.5. We define
![]() $t_{Z}$
to be the least
$t_{Z}$
to be the least
![]() $j$
such that
$j$
such that
![]() $\dim [I_{Z}]_{j+1}>\binom{j+1}{2}$
.
$\dim [I_{Z}]_{j+1}>\binom{j+1}{2}$
.
Remark 2.6. One sees immediately that
![]() $t_{Z}$
depends only on the Hilbert function of
$t_{Z}$
depends only on the Hilbert function of
![]() $Z$
. However, the existence of an unexpected curve does not depend only on the Hilbert function, as one can see from easy examples.
$Z$
. However, the existence of an unexpected curve does not depend only on the Hilbert function, as one can see from easy examples.
Lemma 2.7.
(a)
 $0\leqslant t_{Z}\leqslant \lfloor (|Z|-1)/2\rfloor$
.
$0\leqslant t_{Z}\leqslant \lfloor (|Z|-1)/2\rfloor$
.(b)
 $t_{Z}=\lfloor (|Z|-1)/2\rfloor$
if and only if
$t_{Z}=\lfloor (|Z|-1)/2\rfloor$
if and only if
 $\left\{\begin{array}{@{}ll@{}}h_{Z}(t_{Z})=|Z| & if|Z|isodd,\\ h_{Z}(t_{Z})\geqslant |Z|-1 & if|Z|iseven.\end{array}\right.$
$\left\{\begin{array}{@{}ll@{}}h_{Z}(t_{Z})=|Z| & if|Z|isodd,\\ h_{Z}(t_{Z})\geqslant |Z|-1 & if|Z|iseven.\end{array}\right.$
Proof. The fact that
![]() $0\leqslant t_{Z}$
follows from the definition. From (2.3) we have
$0\leqslant t_{Z}$
follows from the definition. From (2.3) we have
with equality if and only if
![]() $h_{Z}(j+1)=|Z|$
. Thus
$h_{Z}(j+1)=|Z|$
. Thus
 $$\begin{eqnarray}\displaystyle t_{Z} & = & \displaystyle \min \{j\mid 2j+3-h_{Z}(j+1)>0\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \min \{j\mid 2j+3-|Z|>0\}\nonumber\\ \displaystyle & = & \displaystyle \min \biggl\{j\mid j\geqslant \frac{|Z|-2}{2}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\lfloor\frac{|Z|-1}{2}\biggr\rfloor.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle t_{Z} & = & \displaystyle \min \{j\mid 2j+3-h_{Z}(j+1)>0\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \min \{j\mid 2j+3-|Z|>0\}\nonumber\\ \displaystyle & = & \displaystyle \min \biggl\{j\mid j\geqslant \frac{|Z|-2}{2}\biggr\}\nonumber\\ \displaystyle & = & \displaystyle \biggl\lfloor\frac{|Z|-1}{2}\biggr\rfloor.\nonumber\end{eqnarray}$$
For (b), suppose first that
![]() $t_{Z}=\lfloor (|Z|-1)/2\rfloor$
. Since
$t_{Z}=\lfloor (|Z|-1)/2\rfloor$
. Since
![]() $2(t_{Z}-1)+3-h_{Z}(t_{Z})\leqslant 0$
, we have
$2(t_{Z}-1)+3-h_{Z}(t_{Z})\leqslant 0$
, we have
Recalling that
![]() $h_{Z}(j)\leqslant |Z|$
for all
$h_{Z}(j)\leqslant |Z|$
for all
![]() $j$
, this gives:
$j$
, this gives:
– if
 $|Z|$
is odd and
$|Z|$
is odd and
 $t_{Z}=\lfloor (|Z|-1)/2\rfloor thenh_{Z}(t_{Z})=|Z|$
;
$t_{Z}=\lfloor (|Z|-1)/2\rfloor thenh_{Z}(t_{Z})=|Z|$
;– if
 $|Z|$
is even and
$|Z|$
is even and
 $t_{Z}=\lfloor (|Z|-1)/2\rfloor thenh_{Z}(t_{Z})\geqslant |Z|-1$
.
$t_{Z}=\lfloor (|Z|-1)/2\rfloor thenh_{Z}(t_{Z})\geqslant |Z|-1$
.
For the converse, assume that the parity condition holds. In both cases,
![]() $h_{Z}(t_{Z}+1)=|Z|$
since
$h_{Z}(t_{Z}+1)=|Z|$
since
![]() $h_{Z}$
is strictly increasing until it reaches the value
$h_{Z}$
is strictly increasing until it reaches the value
![]() $|Z|$
. So the only inequality in the calculation in (a) is an equality, and we are done.◻
$|Z|$
. So the only inequality in the calculation in (a) is an equality, and we are done.◻
Remark 2.8. If
![]() $|Z|$
is even, both
$|Z|$
is even, both
![]() $h_{Z}(t_{Z})=|Z|$
and
$h_{Z}(t_{Z})=|Z|$
and
![]() $h_{Z}(t_{Z})=|Z|-1$
are possible. For example, take
$h_{Z}(t_{Z})=|Z|-1$
are possible. For example, take
![]() $|Z|=6$
and choose
$|Z|=6$
and choose
![]() $Z$
to be a set of six general points versus a set of six points on a smooth conic. In both cases
$Z$
to be a set of six general points versus a set of six points on a smooth conic. In both cases
![]() $t_{Z}=2$
, but
$t_{Z}=2$
, but
![]() $h_{Z}(t_{Z})=|Z|$
for six general points, while
$h_{Z}(t_{Z})=|Z|$
for six general points, while
![]() $h_{Z}(t_{Z})=|Z|-1$
for six points on the conic.
$h_{Z}(t_{Z})=|Z|-1$
for six points on the conic.
Example 2.9. Here we evaluate
![]() $t_{Z}$
exactly when
$t_{Z}$
exactly when
![]() $Z$
lies on a curve of low degree.
$Z$
lies on a curve of low degree.
(i) The definition immediately gives that
 $t_{Z}=0$
if and only if the points of
$t_{Z}=0$
if and only if the points of
 $Z$
are collinear, so in this case
$Z$
are collinear, so in this case
 $t_{Z}$
is as small as possible.
$t_{Z}$
is as small as possible.(ii) If
 $Z$
lies on an irreducible conic, then it is not hard to check that
$Z$
lies on an irreducible conic, then it is not hard to check that
 $t_{Z}=\lfloor (|Z|-1)/2\rfloor$
, so in this case
$t_{Z}=\lfloor (|Z|-1)/2\rfloor$
, so in this case
 $t_{Z}$
is as large as possible.
$t_{Z}$
is as large as possible.
Proposition 2.10. Let
![]() $Z\subset \mathbb{P}^{2}$
be a reduced scheme consisting of a finite set of points. Then the following conditions are equivalent:
$Z\subset \mathbb{P}^{2}$
be a reduced scheme consisting of a finite set of points. Then the following conditions are equivalent:
(a)
 $h_{Z}(t_{Z})<|Z|$
;
$h_{Z}(t_{Z})<|Z|$
;(b)
(i) the scheme
 $Z$
is a complete intersection cut out by two curves meeting transversely, of degree
$Z$
is a complete intersection cut out by two curves meeting transversely, of degree
 $2$
and
$2$
and
 $t_{Z}+1$
respectively, with
$t_{Z}+1$
respectively, with
 $t_{Z}>0$
; or
$t_{Z}>0$
; or(ii) there is a line that contains precisely
 $|Z|-t_{Z}\geqslant t_{Z}+2$
points of
$|Z|-t_{Z}\geqslant t_{Z}+2$
points of
 $Z$
.
$Z$
.
Furthermore, in case (b)(i) we have
![]() $t_{Z}=(|Z|-2)/2$
, while for case (b)(ii) we have
$t_{Z}=(|Z|-2)/2$
, while for case (b)(ii) we have
![]() $t_{Z}\leqslant (|Z|-2)/2$
.
$t_{Z}\leqslant (|Z|-2)/2$
.
Proof. To simplify notation, put
![]() $t=t_{Z}$
. We use
$t=t_{Z}$
. We use
![]() $\unicode[STIX]{x1D6E5}h_{Z}$
to denote the first difference of the Hilbert function of
$\unicode[STIX]{x1D6E5}h_{Z}$
to denote the first difference of the Hilbert function of
![]() $Z$
; that is,
$Z$
; that is,
![]() $\unicode[STIX]{x1D6E5}h_{Z}(j)=h_{Z}(j)-h_{Z}(j-1)$
.
$\unicode[STIX]{x1D6E5}h_{Z}(j)=h_{Z}(j)-h_{Z}(j-1)$
.
First assume
![]() $t=0$
. By Example 2.9, the points of
$t=0$
. By Example 2.9, the points of
![]() $Z$
are collinear, so (a) holds if and only if
$Z$
are collinear, so (a) holds if and only if
![]() $|Z|>1$
, and (b) holds if and only if
$|Z|>1$
, and (b) holds if and only if
![]() $|Z|\geqslant 2$
, so (a) and (b) are equivalent, and clearly
$|Z|\geqslant 2$
, so (a) and (b) are equivalent, and clearly
![]() $0=t\leqslant (|Z|-2)/2$
for
$0=t\leqslant (|Z|-2)/2$
for
![]() $|Z|>1$
. Thus it is now enough to consider the case where
$|Z|>1$
. Thus it is now enough to consider the case where
![]() $t\geqslant 1$
, that is, where
$t\geqslant 1$
, that is, where
![]() $Z$
is not collinear.
$Z$
is not collinear.
Assume (a) holds. By the definition of
![]() $t_{Z}$
, Equation (2.3) and the fact that
$t_{Z}$
, Equation (2.3) and the fact that
![]() $h_{Z}$
is strictly increasing until it stabilizes at the value
$h_{Z}$
is strictly increasing until it stabilizes at the value
![]() $|Z|$
, this forces
$|Z|$
, this forces
and thus
![]() $h_{Z}(t+1)=2t+2=1+h_{Z}(t)$
. In particular,
$h_{Z}(t+1)=2t+2=1+h_{Z}(t)$
. In particular,
![]() $\unicode[STIX]{x1D6E5}h_{Z}(t+1)=1$
. By standard results (see, for example, [Reference Davis, Geramita and MarosciaDGM84, Proposition 3.9]), this implies that the values of
$\unicode[STIX]{x1D6E5}h_{Z}(t+1)=1$
. By standard results (see, for example, [Reference Davis, Geramita and MarosciaDGM84, Proposition 3.9]), this implies that the values of
![]() $\unicode[STIX]{x1D6E5}h_{Z}$
are as follows (where
$\unicode[STIX]{x1D6E5}h_{Z}$
are as follows (where
![]() $s$
is the regularity of
$s$
is the regularity of
![]() $I_{Z}$
):
$I_{Z}$
):
Thus,
![]() $h_{Z}(t+1)=2t+2$
implies
$h_{Z}(t+1)=2t+2$
implies
Using
![]() $h_{Z}(t+1)=2t+2\leqslant |Z|$
, we conclude that
$h_{Z}(t+1)=2t+2\leqslant |Z|$
, we conclude that
![]() $s=|Z|-t\geqslant t+2$
.
$s=|Z|-t\geqslant t+2$
.
Now we consider two cases.
Case 1. Assume
![]() $Z$
does not lie on a conic, that is,
$Z$
does not lie on a conic, that is,
![]() $\unicode[STIX]{x1D6E5}h_{Z}(2)=3$
. Hence
$\unicode[STIX]{x1D6E5}h_{Z}(2)=3$
. Hence
forces
![]() $\unicode[STIX]{x1D6E5}h_{Z}(t)=1$
, and thus
$\unicode[STIX]{x1D6E5}h_{Z}(t)=1$
, and thus
![]() $\unicode[STIX]{x1D6E5}h_{Z}(s-2)=\unicode[STIX]{x1D6E5}h_{Z}(s-1)=1>\unicode[STIX]{x1D6E5}h_{Z}(s)$
. By [Reference DavisDav86, (2.3)] (or by applying results of [Reference Bigatti, Geramita and MiglioreBGM94]), it follows that
$\unicode[STIX]{x1D6E5}h_{Z}(s-2)=\unicode[STIX]{x1D6E5}h_{Z}(s-1)=1>\unicode[STIX]{x1D6E5}h_{Z}(s)$
. By [Reference DavisDav86, (2.3)] (or by applying results of [Reference Bigatti, Geramita and MiglioreBGM94]), it follows that
![]() $[I_{Z}]_{s-1}$
has a linear form
$[I_{Z}]_{s-1}$
has a linear form
![]() $\ell$
as a common divisor. Since
$\ell$
as a common divisor. Since
![]() $I_{Z}$
has a minimal set of homogeneous generators all of whose degrees are at most
$I_{Z}$
has a minimal set of homogeneous generators all of whose degrees are at most
![]() $s$
, there must be a generator
$s$
, there must be a generator
![]() $f$
of degree
$f$
of degree
![]() $s$
and by [Reference CampanellaCam86, Theorem 2.1] there is only one generator of degree
$s$
and by [Reference CampanellaCam86, Theorem 2.1] there is only one generator of degree
![]() $s$
in a minimal set of homogeneous generators. Moreover, since
$s$
in a minimal set of homogeneous generators. Moreover, since
![]() $Z$
is reduced, the curves defined by
$Z$
is reduced, the curves defined by
![]() $f$
and
$f$
and
![]() $\ell$
must intersect transversely. Thus the ideal
$\ell$
must intersect transversely. Thus the ideal
![]() $(\ell ,f)$
defines a subset of
$(\ell ,f)$
defines a subset of
![]() $s$
collinear points of
$s$
collinear points of
![]() $Z$
and clearly
$Z$
and clearly
![]() $\ell$
vanishes at no point of
$\ell$
vanishes at no point of
![]() $Z$
other than these
$Z$
other than these
![]() $s$
. Therefore, condition (ii) is satisfied.
$s$
. Therefore, condition (ii) is satisfied.
Case 2. Assume
![]() $Z$
is contained in a conic, defined, say, by a homogeneous form
$Z$
is contained in a conic, defined, say, by a homogeneous form
![]() $q$
. Again taking into account
$q$
. Again taking into account
![]() $h_{Z}(t+1)=2t+2$
, we get
$h_{Z}(t+1)=2t+2$
, we get
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}h_{Z}(j)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }j=0\text{ or }t+1\leqslant j<s,\\ 2\quad & \text{if }1\leqslant j\leqslant t,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}h_{Z}(j)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }j=0\text{ or }t+1\leqslant j<s,\\ 2\quad & \text{if }1\leqslant j\leqslant t,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
If
![]() $t=1$
, then
$t=1$
, then
![]() $\unicode[STIX]{x1D6E5}h_{Z}=(1,2,1,\ldots ,1)$
. Thus
$\unicode[STIX]{x1D6E5}h_{Z}=(1,2,1,\ldots ,1)$
. Thus
![]() $Z$
is either four general points (i.e. a complete intersection) or
$Z$
is either four general points (i.e. a complete intersection) or
![]() $Z$
consists of three or more collinear points and one point off the line; in both cases it is easy to check that the assertions hold. Now assume that
$Z$
consists of three or more collinear points and one point off the line; in both cases it is easy to check that the assertions hold. Now assume that
![]() $t>1$
. It follows that
$t>1$
. It follows that
![]() $q$
is a common factor for
$q$
is a common factor for
![]() $[I_{Z}]_{j}$
for
$[I_{Z}]_{j}$
for
![]() $j\leqslant t$
, but not for
$j\leqslant t$
, but not for
![]() $j=t+1$
, so any minimal set of homogeneous generators for
$j=t+1$
, so any minimal set of homogeneous generators for
![]() $I_{Z}$
must contain
$I_{Z}$
must contain
![]() $q$
and a generator
$q$
and a generator
![]() $g$
of degree
$g$
of degree
![]() $t+1$
. If
$t+1$
. If
![]() $q$
and
$q$
and
![]() $g$
are coprime, then
$g$
are coprime, then
![]() $|Z|\leqslant \deg (q)\deg (g)=2t+2$
. Since
$|Z|\leqslant \deg (q)\deg (g)=2t+2$
. Since
![]() $|Z|=t+s$
and
$|Z|=t+s$
and
![]() $s\geqslant t+2$
, this means
$s\geqslant t+2$
, this means
![]() $s=t+2$
and
$s=t+2$
and
![]() $|Z|=2t+2$
, so
$|Z|=2t+2$
, so
![]() $Z$
is a complete intersection as claimed in (i). Otherwise,
$Z$
is a complete intersection as claimed in (i). Otherwise,
![]() $q$
and
$q$
and
![]() $g$
have a linear common factor
$g$
have a linear common factor
![]() $\ell$
and
$\ell$
and
![]() $I_{Z}$
has another minimal generator
$I_{Z}$
has another minimal generator
![]() $f$
of degree
$f$
of degree
![]() $s$
. As in Case 1 we conclude that the line defined by
$s$
. As in Case 1 we conclude that the line defined by
![]() $\ell$
contains precisely
$\ell$
contains precisely
![]() $s$
points of
$s$
points of
![]() $Z$
, and so condition (ii) is met.
$Z$
, and so condition (ii) is met.
Conversely, assume one of the conditions in (b) is true. Thus,
![]() $|Z|-t\geqslant t+2$
(and hence
$|Z|-t\geqslant t+2$
(and hence
![]() $t\leqslant (|Z|-2)/2$
), by hypothesis for part (ii) and using the fact that
$t\leqslant (|Z|-2)/2$
), by hypothesis for part (ii) and using the fact that
![]() $Z$
is a transverse complete intersection of a conic with a curve of degree
$Z$
is a transverse complete intersection of a conic with a curve of degree
![]() $t+1$
for part (i). Again, we consider two cases.
$t+1$
for part (i). Again, we consider two cases.
If (i) is true, then
![]() $h_{Z}(t)=2t+1<2t+2=|Z|$
, as desired. Moreover, here we have
$h_{Z}(t)=2t+1<2t+2=|Z|$
, as desired. Moreover, here we have
![]() $t=(|Z|-2)/2$
.
$t=(|Z|-2)/2$
.
Finally, assume (ii) is true, let
![]() $Y\subset Z$
be a subset of
$Y\subset Z$
be a subset of
![]() $|Z|-t$
collinear points and let
$|Z|-t$
collinear points and let
![]() $U$
be the complement of
$U$
be the complement of
![]() $Y$
in
$Y$
in
![]() $Z$
. Then
$Z$
. Then
![]() $t=|U|$
and
$t=|U|$
and
![]() $U$
is reduced, so
$U$
is reduced, so
![]() $U$
imposes independent conditions on forms of degree
$U$
imposes independent conditions on forms of degree
![]() $t-1$
; that is,
$t-1$
; that is,
![]() $h_{U}(t-1)=t$
and thus
$h_{U}(t-1)=t$
and thus
![]() $\dim [I_{U}]_{t-1}=\binom{t+1}{2}-t$
. But the linear form
$\dim [I_{U}]_{t-1}=\binom{t+1}{2}-t$
. But the linear form
![]() $\ell$
vanishing on
$\ell$
vanishing on
![]() $Y$
is, by Bezout’s theorem, a common divisor of
$Y$
is, by Bezout’s theorem, a common divisor of
![]() $[I_{Z}]_{t}$
, so
$[I_{Z}]_{t}$
, so
![]() $\dim [I_{Z}]_{t}=\dim [I_{U}]_{t-1}$
, and we have
$\dim [I_{Z}]_{t}=\dim [I_{U}]_{t-1}$
, and we have
![]() $h_{Z}(t)=2t+1<2t+2\leqslant |Z|$
.◻
$h_{Z}(t)=2t+1<2t+2\leqslant |Z|$
.◻
As a consequence we show that adding a point to
![]() $Z$
will change the invariant
$Z$
will change the invariant
![]() $t_{Z}$
by at most
$t_{Z}$
by at most
![]() $1$
.
$1$
.
Corollary 2.11. Let
![]() $Z\subset \mathbb{P}^{2}$
be a finite reduced scheme. If
$Z\subset \mathbb{P}^{2}$
be a finite reduced scheme. If
![]() $Q\notin Z$
is any other point of
$Q\notin Z$
is any other point of
![]() $\mathbb{P}^{2}$
, then
$\mathbb{P}^{2}$
, then
Proof. By definition, we clearly have
![]() $t_{Z}\leqslant t_{Z+Q}$
. It remains to show the second inequality. Suppose
$t_{Z}\leqslant t_{Z+Q}$
. It remains to show the second inequality. Suppose
![]() $t_{Z+Q}\geqslant t_{Z}+2$
. Then the definition gives
$t_{Z+Q}\geqslant t_{Z}+2$
. Then the definition gives
![]() $h_{Z}(t_{Z}+1)\leqslant 2t_{Z}+2$
and
$h_{Z}(t_{Z}+1)\leqslant 2t_{Z}+2$
and
![]() $h_{Z+Q}(t_{Z}+1)\geqslant 2t_{Z}+3$
. Since the Hilbert functions of
$h_{Z+Q}(t_{Z}+1)\geqslant 2t_{Z}+3$
. Since the Hilbert functions of
![]() $Z$
and
$Z$
and
![]() $Z+Q$
differ at most by
$Z+Q$
differ at most by
![]() $1$
in each degree, we conclude that
$1$
in each degree, we conclude that
and, in particular,
![]() $h_{Z}(t_{Z}+1)=2t_{Z}+2$
. Considering degree
$h_{Z}(t_{Z}+1)=2t_{Z}+2$
. Considering degree
![]() $t_{Z}+2\leqslant t_{Z+Q}$
, we get
$t_{Z}+2\leqslant t_{Z+Q}$
, we get
![]() $h_{Z+Q}(t_{Z}+2)\geqslant 2t_{Z}+5$
, which implies
$h_{Z+Q}(t_{Z}+2)\geqslant 2t_{Z}+5$
, which implies
It follows that
![]() $h_{Z}(t_{Z})<|Z|$
and
$h_{Z}(t_{Z})<|Z|$
and
![]() $t_{Z}\leqslant (|Z|-4)/2$
. Hence, Proposition 2.10 shows that
$t_{Z}\leqslant (|Z|-4)/2$
. Hence, Proposition 2.10 shows that
![]() $|Z|-t_{Z}$
of the points in
$|Z|-t_{Z}$
of the points in
![]() $Z$
are collinear. Denote by
$Z$
are collinear. Denote by
![]() $Y$
this subset of
$Y$
this subset of
![]() $Z$
, and so
$Z$
, and so
![]() $|Y|=|Z|-t_{Z}\geqslant t_{Z}+4$
. Now, using that the points in
$|Y|=|Z|-t_{Z}\geqslant t_{Z}+4$
. Now, using that the points in
![]() $Y$
are collinear, we obtain
$Y$
are collinear, we obtain
contradicting our estimate above that
![]() $h_{Z+Q}(t_{Z}+2)\geqslant 2t_{Z}+5$
.◻
$h_{Z+Q}(t_{Z}+2)\geqslant 2t_{Z}+5$
.◻
3 Line arrangements and a criterion for unexpected curves
The following are the additional invariants that we will need.
Definition 3.1. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
.
$\mathbb{P}^{2}$
.
(a) [Reference Faenzi and VallèsFV14, Definition 4.1] Given a point
 $P\notin Z$
, we call the multiplicity index of
$P\notin Z$
, we call the multiplicity index of $$\begin{eqnarray}m_{Z,P}=\min \{j\geqslant 0\mid \dim [I_{Z+jP}]_{j+1}>0\}\end{eqnarray}$$
$$\begin{eqnarray}m_{Z,P}=\min \{j\geqslant 0\mid \dim [I_{Z+jP}]_{j+1}>0\}\end{eqnarray}$$
 $Z$
with respect to
$Z$
with respect to
 $P$
. We define the multiplicity index,
$P$
. We define the multiplicity index,
 $m_{Z}$
, to be for a general point
$m_{Z}$
, to be for a general point $$\begin{eqnarray}m_{Z}=\min \{j\in \mathbb{Z}\mid \dim [I_{Z+jP}]_{j+1}>0\}\end{eqnarray}$$
$$\begin{eqnarray}m_{Z}=\min \{j\in \mathbb{Z}\mid \dim [I_{Z+jP}]_{j+1}>0\}\end{eqnarray}$$
 $P$
.
$P$
.(b) Let
 $P\in \mathbb{P}^{2}$
be a general point. We define the speciality index,
$P\in \mathbb{P}^{2}$
be a general point. We define the speciality index,
 $u_{Z}$
, to be the least
$u_{Z}$
, to be the least
 $j$
such that
$j$
such that
 $Z+jP$
imposes independent conditions on plane curves of degree
$Z+jP$
imposes independent conditions on plane curves of degree
 $j+1$
, that is, the least
$j+1$
, that is, the least
 $j$
such that
$j$
such that  $$\begin{eqnarray}\dim [I_{Z+jP}]_{j+1}=\binom{j+3}{2}-\binom{j+1}{2}-|Z|.\end{eqnarray}$$
$$\begin{eqnarray}\dim [I_{Z+jP}]_{j+1}=\binom{j+3}{2}-\binom{j+1}{2}-|Z|.\end{eqnarray}$$
Remark 3.2.
(i) We note that
 $m_{Z,P}$
exists for each point
$m_{Z,P}$
exists for each point
 $P\notin Z$
, since it is easy to see that
$P\notin Z$
, since it is easy to see that
 $\dim [I_{Z+jP}]_{j+1}>0$
holds for all
$\dim [I_{Z+jP}]_{j+1}>0$
holds for all
 $j\geqslant |Z|$
(pick
$j\geqslant |Z|$
(pick
 $j$
lines through
$j$
lines through
 $P$
which also go through the
$P$
which also go through the
 $|Z|$
points of
$|Z|$
points of
 $Z$
), and hence
$Z$
), and hence
 $m_{Z,P}\leqslant |Z|$
, so also
$m_{Z,P}\leqslant |Z|$
, so also
 $m_{Z}\leqslant |Z|$
. We also note that
$m_{Z}\leqslant |Z|$
. We also note that
 $\dim [I_{Z+jP}]_{j+1}$
is a non-decreasing function of
$\dim [I_{Z+jP}]_{j+1}$
is a non-decreasing function of
 $j$
, since we have an injection
$j$
, since we have an injection
 $[I_{Z}\cap I_{P}^{j}]_{j+1}\rightarrow [I_{Z}\cap I_{P}^{j+1}]_{j+2}$
given by multiplication by any linear form
$[I_{Z}\cap I_{P}^{j}]_{j+1}\rightarrow [I_{Z}\cap I_{P}^{j+1}]_{j+2}$
given by multiplication by any linear form
 $\ell$
vanishing at
$\ell$
vanishing at
 $P$
. Thus if
$P$
. Thus if
 $\dim [I_{Z+jP}]_{j+1}=0$
then
$\dim [I_{Z+jP}]_{j+1}=0$
then
 $m_{Z,P}>j$
, hence
$m_{Z,P}>j$
, hence
 $m_{Z}>j$
by semicontinuity.
$m_{Z}>j$
by semicontinuity.(ii) Observe that
 $u_{Z}$
can equivalently be defined as
$u_{Z}$
can equivalently be defined as  $$\begin{eqnarray}u_{Z}=\min \{j\mid h^{1}(\mathbb{P}^{2},{\mathcal{I}}_{Z+jP}(j+1))=0\}.\end{eqnarray}$$
$$\begin{eqnarray}u_{Z}=\min \{j\mid h^{1}(\mathbb{P}^{2},{\mathcal{I}}_{Z+jP}(j+1))=0\}.\end{eqnarray}$$
(iii) We also note that
 $u_{Z}$
exists, and in fact
$u_{Z}$
exists, and in fact
 $u_{Z}\leqslant |Z|-2$
. Indeed, if
$u_{Z}\leqslant |Z|-2$
. Indeed, if
 $Z$
is a set of
$Z$
is a set of
 $d$
points in
$d$
points in
 $\mathbb{P}^{2}$
, and
$\mathbb{P}^{2}$
, and
 $P\in \mathbb{P}^{2}$
is a point that is not on any line through two of the points of
$P\in \mathbb{P}^{2}$
is a point that is not on any line through two of the points of
 $Z$
, then we will show that
$Z$
, then we will show that
 $h^{1}(\mathbb{P}^{2},{\mathcal{I}}_{Z+(d-2)P}(d-1))=0$
.
$h^{1}(\mathbb{P}^{2},{\mathcal{I}}_{Z+(d-2)P}(d-1))=0$
.To see this, we have to show that
 $Z+(d-2)P$
imposes
$Z+(d-2)P$
imposes
 $d+\binom{d-1}{2}$
conditions on the linear system of plane curves of degree
$d+\binom{d-1}{2}$
conditions on the linear system of plane curves of degree
 $d-1$
. Clearly
$d-1$
. Clearly
 $(d-2)P$
imposes
$(d-2)P$
imposes
 $\binom{d-1}{2}$
conditions (since the regularity of
$\binom{d-1}{2}$
conditions (since the regularity of
 $(d-2)P$
is
$(d-2)P$
is
 $d-1$
), so we want to show that the points of
$d-1$
), so we want to show that the points of
 $Z$
impose
$Z$
impose
 $d$
independent conditions on the linear system,
$d$
independent conditions on the linear system,
 ${\mathcal{L}}$
, of plane curves of degree
${\mathcal{L}}$
, of plane curves of degree
 $d-1$
vanishing to order
$d-1$
vanishing to order
 $d-2$
at
$d-2$
at
 $P$
. It is enough to show that, given any point
$P$
. It is enough to show that, given any point
 $Q$
of
$Q$
of
 $Z$
, there is a curve of degree
$Z$
, there is a curve of degree
 $d-1$
vanishing to order
$d-1$
vanishing to order
 $d-2$
at the general point
$d-2$
at the general point
 $P$
and vanishing at each point of
$P$
and vanishing at each point of
 $Z\backslash \{Q\}$
, but not vanishing at
$Z\backslash \{Q\}$
, but not vanishing at
 $Q$
. This can be done (for instance) with a suitable union of
$Q$
. This can be done (for instance) with a suitable union of
 $d-1$
lines, each joining
$d-1$
lines, each joining
 $P$
and a point of
$P$
and a point of
 $Z\backslash \{Q\}$
.
$Z\backslash \{Q\}$
.
Next we bring in an important tool derived from a result of Faenzi and Vallès. We continue with the assumption that
![]() $Z=P_{1}+\cdots +P_{d}$
is a reduced subscheme of
$Z=P_{1}+\cdots +P_{d}$
is a reduced subscheme of
![]() $\mathbb{P}^{2}$
consisting of distinct points
$\mathbb{P}^{2}$
consisting of distinct points
![]() $P_{i}$
. Let
$P_{i}$
. Let
![]() $\ell _{i}$
be the corresponding linear form dual to
$\ell _{i}$
be the corresponding linear form dual to
![]() $P_{i}$
and
$P_{i}$
and
![]() $L_{i}$
the line defined by
$L_{i}$
the line defined by
![]() $\ell _{i}$
, and define
$\ell _{i}$
, and define
![]() $f$
to be the product
$f$
to be the product
![]() $f=\ell _{1}\cdots \ell _{d}$
(so
$f=\ell _{1}\cdots \ell _{d}$
(so
![]() $f$
is square-free). We denote by
$f$
is square-free). We denote by
![]() ${\mathcal{A}}(f)$
, or simply
${\mathcal{A}}(f)$
, or simply
![]() ${\mathcal{A}}$
, the line arrangement in
${\mathcal{A}}$
, the line arrangement in
![]() $\mathbb{P}^{2}$
defined by
$\mathbb{P}^{2}$
defined by
![]() $f$
. In most cases we will not need to use different sets of variables for
$f$
. In most cases we will not need to use different sets of variables for
![]() $Z$
and for
$Z$
and for
![]() $f$
.
$f$
.
Note that if
![]() $\text{char}(K)$
does not divide
$\text{char}(K)$
does not divide
![]() $d=\deg (f)$
, then
$d=\deg (f)$
, then
![]() $xf_{x}+yf_{y}+zf_{z}=df$
is a non-zero scalar multiple of
$xf_{x}+yf_{y}+zf_{z}=df$
is a non-zero scalar multiple of
![]() $f$
. In the case where
$f$
. In the case where
![]() $\text{char}(K)$
does divide
$\text{char}(K)$
does divide
![]() $\deg (f)$
, Euler’s theorem gives
$\deg (f)$
, Euler’s theorem gives
![]() $xf_{x}+yf_{y}+zf_{z}=0$
, a syzygy of degree
$xf_{x}+yf_{y}+zf_{z}=0$
, a syzygy of degree
![]() $1$
on
$1$
on
![]() $f_{x},f_{y},f_{z}$
. In this case it is not necessarily true that
$f_{x},f_{y},f_{z}$
. In this case it is not necessarily true that
![]() $f$
is in the ideal
$f$
is in the ideal
![]() $\operatorname{Jac}(f)=(f_{x},f_{y},f_{z})$
generated by its first partial derivatives, although it can happen. For instance, let
$\operatorname{Jac}(f)=(f_{x},f_{y},f_{z})$
generated by its first partial derivatives, although it can happen. For instance, let
Then
![]() $F$
is in
$F$
is in
![]() $\operatorname{Jac}(F)=(y^{2}z,x^{2}z,x^{2}y+xy^{2})$
since
$\operatorname{Jac}(F)=(y^{2}z,x^{2}z,x^{2}y+xy^{2})$
since
![]() $F$
is
$F$
is
![]() $z$
times
$z$
times
![]() $(x^{2}y+xy^{2})$
. In fact, whenever there is only one factor with a
$(x^{2}y+xy^{2})$
. In fact, whenever there is only one factor with a
![]() $z$
in it, and that factor is
$z$
in it, and that factor is
![]() $z$
, we get this. In this situation it follows that
$z$
, we get this. In this situation it follows that
![]() $Z$
consists of all but one of the points on a line. (We do not know if this, up to change of variables, is the only situation in which this behavior can happen.)
$Z$
consists of all but one of the points on a line. (We do not know if this, up to change of variables, is the only situation in which this behavior can happen.)
Let
![]() $J^{\prime }=\operatorname{Jac}(f)=(f_{x},f_{y},f_{z})$
. Let
$J^{\prime }=\operatorname{Jac}(f)=(f_{x},f_{y},f_{z})$
. Let
![]() $J=(J^{\prime },f)$
. If
$J=(J^{\prime },f)$
. If
![]() $\text{char}(K)$
divides
$\text{char}(K)$
divides
![]() $d$
, we have seen that it may or may not happen that
$d$
, we have seen that it may or may not happen that
![]() $J=J^{\prime }$
, and in any case
$J=J^{\prime }$
, and in any case
![]() $J^{\prime }$
has a syzygy of degree 1 coming from the Euler relation that does not occur when
$J^{\prime }$
has a syzygy of degree 1 coming from the Euler relation that does not occur when
![]() $\text{char}(K)$
does not divide
$\text{char}(K)$
does not divide
![]() $d$
. Nevertheless, it turns out that the issue of whether or not
$d$
. Nevertheless, it turns out that the issue of whether or not
![]() $\text{char}(K)$
divides
$\text{char}(K)$
divides
![]() $d$
is less crucial than these considerations might lead one to expect, and in fact until § 5 we will make no assumption on the characteristic. The justification of this omission, and the role of the characteristic, seems to be known at least to the experts, but since we are not aware of a detailed reference in the literature, we include it as an Appendix.
$d$
is less crucial than these considerations might lead one to expect, and in fact until § 5 we will make no assumption on the characteristic. The justification of this omission, and the role of the characteristic, seems to be known at least to the experts, but since we are not aware of a detailed reference in the literature, we include it as an Appendix.
Define the submodule
![]() $D(Z)\subset R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)\cong R^{3}$
to be the
$D(Z)\subset R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)\cong R^{3}$
to be the
![]() $K$
-linear derivations
$K$
-linear derivations
![]() $\unicode[STIX]{x1D6FF}$
such that
$\unicode[STIX]{x1D6FF}$
such that
![]() $\unicode[STIX]{x1D6FF}(f)\in Rf$
. In particular,
$\unicode[STIX]{x1D6FF}(f)\in Rf$
. In particular,
![]() $D(Z)$
contains the Euler derivation
$D(Z)$
contains the Euler derivation
![]() $\unicode[STIX]{x1D6FF}_{E}=x(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)+y(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)+z(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)$
, and
$\unicode[STIX]{x1D6FF}_{E}=x(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)+y(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)+z(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)$
, and
![]() $\unicode[STIX]{x1D6FF}_{E}$
generates a submodule
$\unicode[STIX]{x1D6FF}_{E}$
generates a submodule
![]() $R\unicode[STIX]{x1D6FF}_{E}\cong R(-1)$
. We can now define the quotient
$R\unicode[STIX]{x1D6FF}_{E}\cong R(-1)$
. We can now define the quotient
![]() $D_{0}(Z)=D(Z)/R\unicode[STIX]{x1D6FF}_{E}$
. Let
$D_{0}(Z)=D(Z)/R\unicode[STIX]{x1D6FF}_{E}$
. Let
![]() ${\mathcal{D}}_{Z}$
be the sheafification of
${\mathcal{D}}_{Z}$
be the sheafification of
![]() $D_{0}(Z)$
, which we call the derivation bundle of
$D_{0}(Z)$
, which we call the derivation bundle of
![]() $Z$
.
$Z$
.
The following facts are shown in the Appendix and will be used freely throughout this paper.
–
 ${\mathcal{D}}_{Z}$
is locally free of rank 2.
${\mathcal{D}}_{Z}$
is locally free of rank 2.– When
 $\text{char}(K)$
does not divide
$\text{char}(K)$
does not divide
 $d$
,
$d$
,
 ${\mathcal{D}}_{Z}$
is isomorphic to the syzygy bundle (suitably twisted) of
${\mathcal{D}}_{Z}$
is isomorphic to the syzygy bundle (suitably twisted) of
 $J^{\prime }$
.
$J^{\prime }$
.– In any case
 $D(Z)$
is isomorphic to the syzygy module of
$D(Z)$
is isomorphic to the syzygy module of
 $J$
.
$J$
.– The restriction of
 ${\mathcal{D}}_{Z}$
to a general line splits as a direct sum
${\mathcal{D}}_{Z}$
to a general line splits as a direct sum
 ${\mathcal{O}}_{\mathbb{P}^{1}}(-a_{Z})\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(-b_{Z})$
for positive integers
${\mathcal{O}}_{\mathbb{P}^{1}}(-a_{Z})\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(-b_{Z})$
for positive integers
 $a_{Z},b_{Z}$
satisfying
$a_{Z},b_{Z}$
satisfying
 $a_{Z}+b_{Z}=|Z|-1=d-1$
. We call the ordered pair
$a_{Z}+b_{Z}=|Z|-1=d-1$
. We call the ordered pair
 $(a_{Z},b_{Z})$
, with
$(a_{Z},b_{Z})$
, with
 $a_{Z}\leqslant b_{Z}$
, the splitting type of
$a_{Z}\leqslant b_{Z}$
, the splitting type of
 $Z$
.
$Z$
.
Lemma 3.3. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
and let
$\mathbb{P}^{2}$
and let
![]() $P$
be a general point. Then one has, for each integer
$P$
be a general point. Then one has, for each integer
![]() $j$
,
$j$
,
Proof. Let
![]() $q:Y\rightarrow \mathbb{P}^{2}$
be the blow up of
$q:Y\rightarrow \mathbb{P}^{2}$
be the blow up of
![]() $\mathbb{P}^{2}$
at the point
$\mathbb{P}^{2}$
at the point
![]() $P$
. Let
$P$
. Let
![]() $H$
be the pullback of a line and
$H$
be the pullback of a line and
![]() $E=q^{-1}(P)$
the exceptional curve coming from
$E=q^{-1}(P)$
the exceptional curve coming from
![]() $P$
. The proper transforms of the lines through
$P$
. The proper transforms of the lines through
![]() $P$
give the linear system
$P$
give the linear system
![]() $|H-E|$
, which gives a morphism
$|H-E|$
, which gives a morphism
![]() $p:Y\rightarrow L=\mathbb{P}^{1}$
with fibers the elements of
$p:Y\rightarrow L=\mathbb{P}^{1}$
with fibers the elements of
![]() $|H-E|$
, making
$|H-E|$
, making
![]() $Y$
a
$Y$
a
![]() $\mathbb{P}^{1}$
-bundle over
$\mathbb{P}^{1}$
-bundle over
![]() $L$
. (In fact,
$L$
. (In fact,
![]() $Y$
is just the Hirzebruch surface
$Y$
is just the Hirzebruch surface
![]() $H_{1}$
.)
$H_{1}$
.)
Let
![]() ${\mathcal{I}}_{Z}$
be the sheaf of ideals of
${\mathcal{I}}_{Z}$
be the sheaf of ideals of
![]() $Z$
on
$Z$
on
![]() $\mathbb{P}^{2}$
. Since
$\mathbb{P}^{2}$
. Since
![]() $P$
is general (and hence the
$P$
is general (and hence the
![]() $t_{Z,y}$
appearing in [Reference Faenzi and VallèsFV14, Theorem 4.3] is 0), we have the isomorphism
$t_{Z,y}$
appearing in [Reference Faenzi and VallèsFV14, Theorem 4.3] is 0), we have the isomorphism
![]() $p_{\ast }(q^{\ast }({\mathcal{I}}_{Z}(1)))\cong {\mathcal{O}}_{L}(-a_{Z})\oplus {\mathcal{O}}_{L}(-b_{Z})$
from [Reference Faenzi and VallèsFV14, Theorem 4.3]. Since
$p_{\ast }(q^{\ast }({\mathcal{I}}_{Z}(1)))\cong {\mathcal{O}}_{L}(-a_{Z})\oplus {\mathcal{O}}_{L}(-b_{Z})$
from [Reference Faenzi and VallèsFV14, Theorem 4.3]. Since
![]() $P\not \in Z$
,
$P\not \in Z$
,
![]() $q$
is an isomorphism on an open set containing
$q$
is an isomorphism on an open set containing
![]() $Z$
, so we can regard
$Z$
, so we can regard
![]() $Z$
as being on
$Z$
as being on
![]() $\mathbb{P}^{2}$
or on
$\mathbb{P}^{2}$
or on
![]() $Y$
, hence there is a natural identification of
$Y$
, hence there is a natural identification of
![]() ${\mathcal{I}}_{Z}$
with
${\mathcal{I}}_{Z}$
with
![]() $q^{\ast }({\mathcal{I}}_{Z})$
. Under this identification we can regard
$q^{\ast }({\mathcal{I}}_{Z})$
. Under this identification we can regard
![]() $q^{\ast }({\mathcal{I}}_{Z}(1))$
as being the sheaf
$q^{\ast }({\mathcal{I}}_{Z}(1))$
as being the sheaf
![]() ${\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}(H)$
. Thus we have
${\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}(H)$
. Thus we have
![]() $p_{\ast }({\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}(H))\cong {\mathcal{O}}_{L}(-a_{Z})\oplus {\mathcal{O}}_{L}(-b_{Z})$
. Now tensor through by
$p_{\ast }({\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}(H))\cong {\mathcal{O}}_{L}(-a_{Z})\oplus {\mathcal{O}}_{L}(-b_{Z})$
. Now tensor through by
![]() ${\mathcal{O}}_{L}(j)$
to get
${\mathcal{O}}_{L}(j)$
to get
Since
![]() $p_{\ast }$
preserves global sections, taking global sections gives
$p_{\ast }$
preserves global sections, taking global sections gives
 $$\begin{eqnarray}\displaystyle [I_{Z+jP}]_{j+1} & \cong & \displaystyle \unicode[STIX]{x1D6E4}(\mathbb{P}^{2},{\mathcal{I}}_{Z+jP}\otimes {\mathcal{O}}_{\mathbb{P}^{2}}((j+1)H))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(\mathbb{P}^{2},{\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{jP}\otimes {\mathcal{O}}_{\mathbb{P}^{2}}((j+1)H))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(Y,{\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}((j+1)H-jE))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(L,p_{\ast }({\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}((j+1)H-jE)))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(L,{\mathcal{O}}_{L}(j-a_{Z})\oplus {\mathcal{O}}_{L}(j-b_{Z}))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(L,{\mathcal{O}}_{L}(j-a_{Z}))\oplus \unicode[STIX]{x1D6E4}(L,{\mathcal{O}}_{L}(j-b_{Z})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [I_{Z+jP}]_{j+1} & \cong & \displaystyle \unicode[STIX]{x1D6E4}(\mathbb{P}^{2},{\mathcal{I}}_{Z+jP}\otimes {\mathcal{O}}_{\mathbb{P}^{2}}((j+1)H))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(\mathbb{P}^{2},{\mathcal{I}}_{Z}\otimes {\mathcal{I}}_{jP}\otimes {\mathcal{O}}_{\mathbb{P}^{2}}((j+1)H))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(Y,{\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}((j+1)H-jE))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(L,p_{\ast }({\mathcal{I}}_{Z}\otimes {\mathcal{O}}_{Y}((j+1)H-jE)))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(L,{\mathcal{O}}_{L}(j-a_{Z})\oplus {\mathcal{O}}_{L}(j-b_{Z}))\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}(L,{\mathcal{O}}_{L}(j-a_{Z}))\oplus \unicode[STIX]{x1D6E4}(L,{\mathcal{O}}_{L}(j-b_{Z})).\nonumber\end{eqnarray}$$
The result now follows by taking dimensions. ◻
Remark 3.4.
(i) From Lemma 3.3 it follows immediately that
 $\dim [I_{Z+a_{Z}P}]_{a_{Z}+1}$
is equal to either 1 or 2, and the latter holds if and only if
$\dim [I_{Z+a_{Z}P}]_{a_{Z}+1}$
is equal to either 1 or 2, and the latter holds if and only if
 $a_{Z}=b_{Z}$
.
$a_{Z}=b_{Z}$
.(ii) It also follows immediately from Lemma 3.3 and the fact that
 $a_{Z}+b_{Z}+1=|Z|$
that if
$a_{Z}+b_{Z}+1=|Z|$
that if
 $Z$
is a set of points with splitting type
$Z$
is a set of points with splitting type
 $(a_{Z},b_{Z})$
and
$(a_{Z},b_{Z})$
and
 $Q$
is a general point then
$Q$
is a general point then
 $Z\cup Q$
has splitting type
$Z\cup Q$
has splitting type
 $(a_{Z}+1,b_{Z})$
(noting that if
$(a_{Z}+1,b_{Z})$
(noting that if
 $a_{Z}=b_{Z}$
then this should be written
$a_{Z}=b_{Z}$
then this should be written
 $(a_{Z},b_{Z}+1)$
to preserve the proper inequality).
$(a_{Z},b_{Z}+1)$
to preserve the proper inequality).
We record some immediate consequences of these observations.
Lemma 3.5. Let
![]() $Z$
be a reduced set of points in
$Z$
be a reduced set of points in
![]() $\mathbb{P}^{2}$
.
$\mathbb{P}^{2}$
.
(a)
 $m_{Z}=a_{Z}$
.
$m_{Z}=a_{Z}$
.(b)
 $m_{Z}=0$
if and only if the points of
$m_{Z}=0$
if and only if the points of
 $Z$
lie on a line.
$Z$
lie on a line.(c)
 $u_{Z}=b_{Z}-1$
(hence
$u_{Z}=b_{Z}-1$
(hence
 $m_{Z}-1\leqslant u_{Z}=|Z|-m_{Z}-2$
).
$m_{Z}-1\leqslant u_{Z}=|Z|-m_{Z}-2$
).(d)
 $m_{Z}\leqslant t_{Z}\leqslant \lfloor (|Z|-1)/2\rfloor$
.
$m_{Z}\leqslant t_{Z}\leqslant \lfloor (|Z|-1)/2\rfloor$
.(e) If
 $m_{Z}<t_{Z}$
, then
$m_{Z}<t_{Z}$
, then
 $t_{Z}\leqslant u_{Z}$
.
$t_{Z}\leqslant u_{Z}$
.
Proof. Part (a) follows immediately from Lemma 3.3, while (b) follows from the definition of
![]() $m_{Z}$
. For (c), note that for any
$m_{Z}$
. For (c), note that for any
![]() $j$
,
$j$
,
the latter since
![]() $a_{Z}+b_{Z}=|Z|-1$
. Because
$a_{Z}+b_{Z}=|Z|-1$
. Because
![]() $a_{Z}\leqslant b_{Z}$
, the result follows from the definition of
$a_{Z}\leqslant b_{Z}$
, the result follows from the definition of
![]() $u_{Z}$
, Lemma 3.3 and
$u_{Z}$
, Lemma 3.3 and
![]() $a_{Z}+b_{Z}=|Z|-1$
. Part (d) comes from Lemma 2.7 and the definitions.
$a_{Z}+b_{Z}=|Z|-1$
. Part (d) comes from Lemma 2.7 and the definitions.
For (e), assume that
![]() $m_{Z}=a_{Z}<t_{Z}$
. It is enough to prove that
$m_{Z}=a_{Z}<t_{Z}$
. It is enough to prove that
![]() $a_{Z}\leqslant j<t_{Z}$
implies
$a_{Z}\leqslant j<t_{Z}$
implies
![]() $j<u_{Z}$
. But
$j<u_{Z}$
. But
![]() $a_{Z}\leqslant j<t_{Z}$
implies that
$a_{Z}\leqslant j<t_{Z}$
implies that
![]() $Z+jP$
does not impose independent conditions on forms of degree
$Z+jP$
does not impose independent conditions on forms of degree
![]() $j+1$
, so
$j+1$
, so
![]() $j<u_{Z}$
and we are done.◻
$j<u_{Z}$
and we are done.◻
Lemma 3.6. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
and let
$\mathbb{P}^{2}$
and let
![]() $h_{Z}$
be its Hilbert function. If
$h_{Z}$
be its Hilbert function. If
![]() $h_{Z}(t_{Z})=|Z|$
and
$h_{Z}(t_{Z})=|Z|$
and
![]() $m_{Z}<u_{Z}$
, then
$m_{Z}<u_{Z}$
, then
![]() $m_{Z}<t_{Z}$
.
$m_{Z}<t_{Z}$
.
Proof. From Lemma 3.5 we have
![]() $a_{Z}\leqslant t_{Z}$
and
$a_{Z}\leqslant t_{Z}$
and
![]() $u_{Z}=b_{Z}-1$
. Since
$u_{Z}=b_{Z}-1$
. Since
![]() $a_{Z}<b_{Z}-1$
, applying Lemma 3.3 and (3.1) with
$a_{Z}<b_{Z}-1$
, applying Lemma 3.3 and (3.1) with
![]() $j=a_{Z}$
, we get
$j=a_{Z}$
, we get
Now suppose that
![]() $a_{Z}=t_{Z}$
. Since
$a_{Z}=t_{Z}$
. Since
![]() $h_{Z}(t_{Z})=|Z|$
, the points of
$h_{Z}(t_{Z})=|Z|$
, the points of
![]() $Z$
impose independent conditions on curves of degree
$Z$
impose independent conditions on curves of degree
![]() $t_{Z}=a_{Z}$
and hence also on curves of degree
$t_{Z}=a_{Z}$
and hence also on curves of degree
![]() $a_{Z}+1$
,
$a_{Z}+1$
,
![]() $\binom{a_{Z}+3}{2}-|Z|-\binom{a_{Z}+1}{2}=\dim [I_{Z}]_{a_{Z}+1}-\binom{a_{Z}+1}{2}>0$
(by definition of
$\binom{a_{Z}+3}{2}-|Z|-\binom{a_{Z}+1}{2}=\dim [I_{Z}]_{a_{Z}+1}-\binom{a_{Z}+1}{2}>0$
(by definition of
![]() $t_{Z}$
). Combining with the previous inequality, we obtain
$t_{Z}$
). Combining with the previous inequality, we obtain
which is impossible since the middle expression is an integer. Thus
![]() $m_{Z}=a_{Z}<t_{Z}$
.◻
$m_{Z}=a_{Z}<t_{Z}$
.◻
The definition of unexpected curves implies already that if
![]() $Z$
admits an unexpected curve of degree
$Z$
admits an unexpected curve of degree
![]() $j+1$
then
$j+1$
then
![]() $Z+jP$
fails to impose independent conditions on plane curves of degree
$Z+jP$
fails to impose independent conditions on plane curves of degree
![]() $j+1$
. We will see that the converse is false. The following result is critical for our main theorems, but the proof is rather involved, so we put off addressing it until the next section where we prove a stronger result of which Theorem 3.7 is an immediate consequence.
$j+1$
. We will see that the converse is false. The following result is critical for our main theorems, but the proof is rather involved, so we put off addressing it until the next section where we prove a stronger result of which Theorem 3.7 is an immediate consequence.
Theorem 3.7. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
. If
$\mathbb{P}^{2}$
. If
![]() $h_{Z}(t_{Z})<|Z|$
, then
$h_{Z}(t_{Z})<|Z|$
, then
![]() $Z$
admits no unexpected curves.
$Z$
admits no unexpected curves.
Proof. See Theorem 4.3. ◻
Remark 3.8. Definition 2.1 leaves open the possibility that the points of
![]() $Z$
themselves do not impose independent conditions on curves of some degree
$Z$
themselves do not impose independent conditions on curves of some degree
![]() $j+1$
, and moreover the addition of the general fat point
$j+1$
, and moreover the addition of the general fat point
![]() $jP$
fails to impose the expected number of conditions on the linear system defined by
$jP$
fails to impose the expected number of conditions on the linear system defined by
![]() $[I_{Z}]_{j+1}$
(i.e. there is still an unexpected curve). Theorem 3.7 gives the surprising result that this is impossible.
$[I_{Z}]_{j+1}$
(i.e. there is still an unexpected curve). Theorem 3.7 gives the surprising result that this is impossible.
The following result restates Theorem 1.1.
Theorem 3.9. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
. Then
$\mathbb{P}^{2}$
. Then
![]() $Z$
admits an unexpected curve if and only if
$Z$
admits an unexpected curve if and only if
![]() $m_{Z}<t_{Z}$
. Furthermore, in this case
$m_{Z}<t_{Z}$
. Furthermore, in this case
![]() $Z$
has an unexpected curve of degree
$Z$
has an unexpected curve of degree
![]() $j+1$
if and only if
$j+1$
if and only if
![]() $m_{Z}\leqslant j<u_{Z}$
.
$m_{Z}\leqslant j<u_{Z}$
.
Proof. Assume
![]() $Z$
admits an unexpected curve. Then, for a general point
$Z$
admits an unexpected curve. Then, for a general point
![]() $P$
, there is an
$P$
, there is an
![]() $m\geqslant a_{Z}=m_{Z}$
such that
$m\geqslant a_{Z}=m_{Z}$
such that
By Theorem 3.7 we have
![]() $h_{Z}(t_{Z})=|Z|$
. We now claim that
$h_{Z}(t_{Z})=|Z|$
. We now claim that
![]() $m_{Z}<u_{Z}$
. Indeed, if it were true that
$m_{Z}<u_{Z}$
. Indeed, if it were true that
![]() $u_{Z}\leqslant m_{Z}\leqslant m$
then
$u_{Z}\leqslant m_{Z}\leqslant m$
then
 $$\begin{eqnarray}\begin{array}{@{}rclll@{}}\displaystyle \max \biggl\{0,\dim [I_{Z}]_{m+1}-\binom{m+1}{2}\!\biggr\} & {\geqslant} & \displaystyle \binom{m+3}{2}-\binom{m+1}{2}-|Z| & & (by(2.2))\\ & = & \displaystyle \dim [I_{Z+mP}]_{m+1} & & \displaystyle (sincem\geqslant u_{Z})\\ & {>} & \displaystyle \max \biggl\{0,\dim [I_{Z}]_{m+1}-\binom{m+1}{2}\!\biggr\} & & (bychoiceofm).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rclll@{}}\displaystyle \max \biggl\{0,\dim [I_{Z}]_{m+1}-\binom{m+1}{2}\!\biggr\} & {\geqslant} & \displaystyle \binom{m+3}{2}-\binom{m+1}{2}-|Z| & & (by(2.2))\\ & = & \displaystyle \dim [I_{Z+mP}]_{m+1} & & \displaystyle (sincem\geqslant u_{Z})\\ & {>} & \displaystyle \max \biggl\{0,\dim [I_{Z}]_{m+1}-\binom{m+1}{2}\!\biggr\} & & (bychoiceofm).\end{array}\end{eqnarray}$$
Lemma 3.6 now implies
![]() $m_{Z}<t_{Z}$
.
$m_{Z}<t_{Z}$
.
Conversely, if
![]() $m_{Z}<t_{Z}$
, then
$m_{Z}<t_{Z}$
, then
and so
![]() $Z$
admits an unexpected curve of degree
$Z$
admits an unexpected curve of degree
![]() $m_{Z}+1$
.
$m_{Z}+1$
.
For the rest, assume
![]() $m_{Z}<t_{Z}$
and
$m_{Z}<t_{Z}$
and
![]() $h_{Z}(t_{Z})=|Z|$
. Then
$h_{Z}(t_{Z})=|Z|$
. Then
![]() $t_{Z}\leqslant u_{Z}$
by Lemma 3.5(e). If
$t_{Z}\leqslant u_{Z}$
by Lemma 3.5(e). If
![]() $m_{Z}\leqslant j<t_{Z}$
, we have
$m_{Z}\leqslant j<t_{Z}$
, we have
![]() $\dim [I_{Z+jP}]_{j+1}>0=\max \{0,\dim [I_{Z}]_{j+1}-\binom{j+1}{2}\!\}$
, and so there are unexpected curves for each such
$\dim [I_{Z+jP}]_{j+1}>0=\max \{0,\dim [I_{Z}]_{j+1}-\binom{j+1}{2}\!\}$
, and so there are unexpected curves for each such
![]() $j$
.
$j$
.
Now assume that
![]() $t_{Z}\leqslant j<u_{Z}=b_{Z}-1$
(Lemma 3.5(c)). Since
$t_{Z}\leqslant j<u_{Z}=b_{Z}-1$
(Lemma 3.5(c)). Since
![]() $h_{Z}(t_{Z})=|Z|$
, we know that
$h_{Z}(t_{Z})=|Z|$
, we know that
![]() $Z$
imposes independent conditions on curves of degree
$Z$
imposes independent conditions on curves of degree
![]() $j$
. Then using Lemma 3.3, we have
$j$
. Then using Lemma 3.3, we have
 $$\begin{eqnarray}\displaystyle \dim [I_{Z+jP}]_{j+1} & = & \displaystyle j-m_{Z}+1\nonumber\\ \displaystyle & {>} & \displaystyle (j+1-a_{Z})+(j-b_{Z}+1)\nonumber\\ \displaystyle & = & \displaystyle \binom{j+3}{2}-|Z|-\binom{j+1}{2}\nonumber\\ \displaystyle & = & \displaystyle \dim [I_{Z}]_{j+1}-\binom{j+1}{2}\nonumber\\ \displaystyle & = & \displaystyle \max \biggl\{0,\dim [I_{Z}]_{j+1}-\binom{j+1}{2}\!\biggr\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim [I_{Z+jP}]_{j+1} & = & \displaystyle j-m_{Z}+1\nonumber\\ \displaystyle & {>} & \displaystyle (j+1-a_{Z})+(j-b_{Z}+1)\nonumber\\ \displaystyle & = & \displaystyle \binom{j+3}{2}-|Z|-\binom{j+1}{2}\nonumber\\ \displaystyle & = & \displaystyle \dim [I_{Z}]_{j+1}-\binom{j+1}{2}\nonumber\\ \displaystyle & = & \displaystyle \max \biggl\{0,\dim [I_{Z}]_{j+1}-\binom{j+1}{2}\!\biggr\},\nonumber\end{eqnarray}$$
hence there are unexpected curves for each such
![]() $j$
.
$j$
.
Finally, if
![]() $j\geqslant u_{Z}$
, we have
$j\geqslant u_{Z}$
, we have
so there are no unexpected curves of any such degree
![]() $j+1$
.◻
$j+1$
.◻
Later we show that unexpected curves of degree greater than
![]() $m_{Z}+1$
are always reducible (see Corollary 5.5).
$m_{Z}+1$
are always reducible (see Corollary 5.5).
An alternative characterization of the occurrence of unexpected curves is given by the following theorem.
Theorem 3.10. Let
![]() $Z\subset \mathbb{P}^{2}$
be a finite set of points whose dual is a line arrangement with splitting type
$Z\subset \mathbb{P}^{2}$
be a finite set of points whose dual is a line arrangement with splitting type
![]() $(a_{Z},b_{Z})$
. Let
$(a_{Z},b_{Z})$
. Let
![]() $P$
be a general point. Then the subscheme
$P$
be a general point. Then the subscheme
![]() $X=mP$
fails to impose the expected number of conditions on
$X=mP$
fails to impose the expected number of conditions on
![]() $V=[I_{Z}]_{m+1}$
if and only if
$V=[I_{Z}]_{m+1}$
if and only if
(i)
 $a_{Z}\leqslant m<b_{Z}-1$
; and
$a_{Z}\leqslant m<b_{Z}-1$
; and(ii)
 $h_{Z}(t_{Z})=|Z|$
.
$h_{Z}(t_{Z})=|Z|$
.
Proof. Assume
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V=[I_{Z}]_{m+1}$
; that is,
$V=[I_{Z}]_{m+1}$
; that is,
![]() $Z$
has an unexpected curve of degree
$Z$
has an unexpected curve of degree
![]() $m+1$
. Then
$m+1$
. Then
![]() $a_{Z}\leqslant m<u_{Z}$
by Theorem 3.9 and
$a_{Z}\leqslant m<u_{Z}$
by Theorem 3.9 and
![]() $h_{Z}(t_{Z})=|Z|$
by Theorem 3.7.
$h_{Z}(t_{Z})=|Z|$
by Theorem 3.7.
Conversely, if
![]() $a_{Z}<u_{Z}$
and
$a_{Z}<u_{Z}$
and
![]() $h_{Z}(t_{Z})=|Z|$
, then
$h_{Z}(t_{Z})=|Z|$
, then
![]() $a_{Z}<t_{Z}$
by Lemma 3.6, and hence by Theorem 3.9 there are unexpected curves of degree
$a_{Z}<t_{Z}$
by Lemma 3.6, and hence by Theorem 3.9 there are unexpected curves of degree
![]() $m+1$
for each
$m+1$
for each
![]() $m$
in the range
$m$
in the range
![]() $a_{Z}\leqslant m<u_{Z}$
.◻
$a_{Z}\leqslant m<u_{Z}$
.◻
Remark 3.11. By Proposition 2.10, condition (ii) of the previous theorem imposes a very weak restriction.
4 Proof of Theorem 3.7
Lemma 4.1. For each integer
![]() $j\geqslant 0$
, we have
$j\geqslant 0$
, we have
Proof. This follows from the exact sequence
Lemma 4.2. Let
![]() $Z\subset \mathbb{P}^{2}$
be a reduced scheme consisting of a finite set of points. Then, for each general point
$Z\subset \mathbb{P}^{2}$
be a reduced scheme consisting of a finite set of points. Then, for each general point
![]() $P\in \mathbb{P}^{2}$
,
$P\in \mathbb{P}^{2}$
,
In this case we have, furthermore,
and
![]() $h^{1}({\mathcal{I}}_{Z}(j-1))=h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
for
$h^{1}({\mathcal{I}}_{Z}(j-1))=h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
for
![]() $j\geqslant |Z|$
.
$j\geqslant |Z|$
.
Proof. If
![]() $f\in [I_{Z+jP}]_{j}$
then any line joining
$f\in [I_{Z+jP}]_{j}$
then any line joining
![]() $P$
to a point of
$P$
to a point of
![]() $Z$
is a component of
$Z$
is a component of
![]() $f$
, since the restriction of
$f$
, since the restriction of
![]() $f$
to a line is either zero or has at most
$f$
to a line is either zero or has at most
![]() $j$
roots up to multiplicity. If
$j$
roots up to multiplicity. If
![]() $P$
is general, any such line contains no other points of
$P$
is general, any such line contains no other points of
![]() $Z$
. Hence
$Z$
. Hence
![]() $\dim [I_{Z+jP}]_{j}=0$
if
$\dim [I_{Z+jP}]_{j}=0$
if
![]() $j<|Z|$
and
$j<|Z|$
and
![]() $\dim [I_{Z+|Z|\cdot P}]_{|Z|}=1$
. In particular, by adding suitable lines through
$\dim [I_{Z+|Z|\cdot P}]_{|Z|}=1$
. In particular, by adding suitable lines through
![]() $P$
we obtain the first assertion.
$P$
we obtain the first assertion.
Now,
![]() $1=\dim [I_{Z+|Z|\cdot P}]_{|Z|}\geqslant \dim [I_{Z}]_{|Z|}-\binom{|Z|+1}{2}\geqslant \binom{|Z|+2}{2}-|Z|-\binom{|Z|+1}{2}=1$
, hence
$1=\dim [I_{Z+|Z|\cdot P}]_{|Z|}\geqslant \dim [I_{Z}]_{|Z|}-\binom{|Z|+1}{2}\geqslant \binom{|Z|+2}{2}-|Z|-\binom{|Z|+1}{2}=1$
, hence
![]() $Z+|Z|\cdot P$
(and thus
$Z+|Z|\cdot P$
(and thus
![]() $Z$
) imposes independent conditions on forms of degree
$Z$
) imposes independent conditions on forms of degree
![]() $|Z|$
. This means
$|Z|$
. This means
![]() $h^{1}({\mathcal{I}}_{Z}(j))=0$
for
$h^{1}({\mathcal{I}}_{Z}(j))=0$
for
![]() $j=|Z|$
(and hence for
$j=|Z|$
(and hence for
![]() $j\geqslant |Z|$
), and it means
$j\geqslant |Z|$
), and it means
![]() $h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
for
$h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
for
![]() $j=|Z|$
. Replacing
$j=|Z|$
. Replacing
![]() $Z$
by
$Z$
by
![]() $Z+Q$
for any point
$Z+Q$
for any point
![]() $Q\notin Z$
, we now get
$Q\notin Z$
, we now get
![]() $h^{1}({\mathcal{I}}_{Z+Q+jP}(j))=0$
for
$h^{1}({\mathcal{I}}_{Z+Q+jP}(j))=0$
for
![]() $j=|Z+Q|=|Z|+1$
and hence
$j=|Z+Q|=|Z|+1$
and hence
![]() $Z+Q+jP$
imposes independent conditions on forms of degree
$Z+Q+jP$
imposes independent conditions on forms of degree
![]() $j=|Z|+1$
, and therefore
$j=|Z|+1$
, and therefore
![]() $Z+jP$
also imposes independent conditions on forms of degree
$Z+jP$
also imposes independent conditions on forms of degree
![]() $j=|Z|+1$
. Continuing in this way, we see that for any
$j=|Z|+1$
. Continuing in this way, we see that for any
![]() $j\geqslant |Z|$
,
$j\geqslant |Z|$
,
![]() $Z+jP$
imposes independent conditions on forms of degree
$Z+jP$
imposes independent conditions on forms of degree
![]() $j$
; hence for such
$j$
; hence for such
![]() $j$
we have
$j$
we have
![]() $h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
. Thus
$h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
. Thus
![]() $\dim [I_{Z+jP}]_{j}=\binom{j+2}{2}-|Z|-\binom{j+1}{2}=j+1-|Z|$
as asserted. Since
$\dim [I_{Z+jP}]_{j}=\binom{j+2}{2}-|Z|-\binom{j+1}{2}=j+1-|Z|$
as asserted. Since
![]() $h^{1}({\mathcal{I}}_{Z}(j))=0$
for
$h^{1}({\mathcal{I}}_{Z}(j))=0$
for
![]() $j\geqslant |Z|$
, we also have
$j\geqslant |Z|$
, we also have
![]() $\dim [I_{Z}]_{j}=\binom{j+2}{2}-|Z|$
, so
$\dim [I_{Z}]_{j}=\binom{j+2}{2}-|Z|$
, so
![]() $\dim [I_{Z+jP}]_{j}$
can in addition be written as
$\dim [I_{Z+jP}]_{j}$
can in addition be written as
![]() $\dim [I_{Z}]_{j}-\binom{j+1}{2}$
.
$\dim [I_{Z}]_{j}-\binom{j+1}{2}$
.
Since we have already shown that
![]() $h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
for
$h^{1}({\mathcal{I}}_{Z+jP}(j))=0$
for
![]() $j\geqslant |Z|$
, it remains only to prove that
$j\geqslant |Z|$
, it remains only to prove that
![]() $h^{1}({\mathcal{I}}_{Z}(j-1))=0$
for
$h^{1}({\mathcal{I}}_{Z}(j-1))=0$
for
![]() $j\geqslant |Z|$
. But this is true for any finite set of points, so we are done.◻
$j\geqslant |Z|$
. But this is true for any finite set of points, so we are done.◻
Theorem 4.3. Let
![]() $Z\subset \mathbb{P}^{2}$
be a reduced scheme consisting of a finite set of points such that
$Z\subset \mathbb{P}^{2}$
be a reduced scheme consisting of a finite set of points such that
![]() $h_{Z}(t_{Z})<|Z|$
and let
$h_{Z}(t_{Z})<|Z|$
and let
![]() $P\in \mathbb{P}^{2}$
be a general point. Then
$P\in \mathbb{P}^{2}$
be a general point. Then
and
![]() $\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
. Furthermore,
$\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
. Furthermore,
for all
![]() $j\geqslant m_{Z}$
(hence
$j\geqslant m_{Z}$
(hence
![]() $Z$
admits no unexpected curves).
$Z$
admits no unexpected curves).
Proof. If
![]() $t_{Z}=0$
, then the points of
$t_{Z}=0$
, then the points of
![]() $Z$
are collinear, in which case it is not hard to check that the claims hold. So we may assume
$Z$
are collinear, in which case it is not hard to check that the claims hold. So we may assume
![]() $t_{Z}>0$
. By Proposition 2.10 we have to consider two cases.
$t_{Z}>0$
. By Proposition 2.10 we have to consider two cases.
Case 1. Assume
![]() $Z$
is defined by an ideal
$Z$
is defined by an ideal
![]() $I_{Z}=(q,g)$
, where
$I_{Z}=(q,g)$
, where
![]() $q,g\in R$
are forms of degree
$q,g\in R$
are forms of degree
![]() $2$
and
$2$
and
![]() $t_{Z}+1$
, respectively. We have (from the proof of Proposition 2.10)
$t_{Z}+1$
, respectively. We have (from the proof of Proposition 2.10)
Then for
![]() $j+1<t_{Z}+1$
, we get
$j+1<t_{Z}+1$
, we get
which implies
![]() $m_{Z}=t_{Z}$
by Lemma 3.5(d). Since
$m_{Z}=t_{Z}$
by Lemma 3.5(d). Since
![]() $a_{Z}+b_{Z}=|Z|-1=2t_{Z}+1$
, we also obtain
$a_{Z}+b_{Z}=|Z|-1=2t_{Z}+1$
, we also obtain
![]() $b_{Z}=u_{Z}+1=t_{Z}+1$
. Then Lemma 3.3 gives
$b_{Z}=u_{Z}+1=t_{Z}+1$
. Then Lemma 3.3 gives
![]() $\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
as desired. And since
$\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
as desired. And since
![]() $|Z|=2t_{Z}+2$
, we have
$|Z|=2t_{Z}+2$
, we have
![]() $t_{Z}<(|Z|-1)/2$
.
$t_{Z}<(|Z|-1)/2$
.
To show
![]() $\dim [I_{Z+jP}]_{j+1}=\dim [I_{Z}]_{j+1}-\binom{j+1}{2}$
for
$\dim [I_{Z+jP}]_{j+1}=\dim [I_{Z}]_{j+1}-\binom{j+1}{2}$
for
![]() $j\geqslant m_{Z}$
, first note that we have
$j\geqslant m_{Z}$
, first note that we have
 $$\begin{eqnarray}\displaystyle 1 & = & \displaystyle \dim [I_{Z+m_{Z}P}]_{m_{Z}+1}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim [I_{Z}]_{m_{Z}+1}-\binom{m_{Z}+1}{2}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \binom{t_{Z}+3}{2}-(2t_{Z}+2)-\binom{t_{Z}+1}{2}\nonumber\\ \displaystyle & = & \displaystyle 1,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1 & = & \displaystyle \dim [I_{Z+m_{Z}P}]_{m_{Z}+1}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \dim [I_{Z}]_{m_{Z}+1}-\binom{m_{Z}+1}{2}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \binom{t_{Z}+3}{2}-(2t_{Z}+2)-\binom{t_{Z}+1}{2}\nonumber\\ \displaystyle & = & \displaystyle 1,\nonumber\end{eqnarray}$$
hence
![]() $Z+m_{Z}P$
imposes independent conditions on forms of degree
$Z+m_{Z}P$
imposes independent conditions on forms of degree
![]() $m_{Z}+1$
. This also means that the points of
$m_{Z}+1$
. This also means that the points of
![]() $Z$
impose independent conditions on
$Z$
impose independent conditions on
![]() $[I_{P}^{m_{Z}}]_{m_{Z}+1}$
. By adding lines through
$[I_{P}^{m_{Z}}]_{m_{Z}+1}$
. By adding lines through
![]() $P$
, it is then clear that the points of
$P$
, it is then clear that the points of
![]() $Z$
also impose independent conditions on
$Z$
also impose independent conditions on
![]() $[I_{P}^{m_{Z}+k}]_{m_{Z}+1+k}$
, which implies
$[I_{P}^{m_{Z}+k}]_{m_{Z}+1+k}$
, which implies
![]() $\dim [I_{Z+jP}]_{j+1}=\dim [I_{Z}]_{j+1}-\binom{j+1}{2}$
for all
$\dim [I_{Z+jP}]_{j+1}=\dim [I_{Z}]_{j+1}-\binom{j+1}{2}$
for all
![]() $j\geqslant m_{Z}$
as desired.
$j\geqslant m_{Z}$
as desired.
Case 2. Assume a line defined by a linear form
![]() $\ell \in R$
contains precisely
$\ell \in R$
contains precisely
![]() $|Z|-t_{Z}\geqslant t_{Z}+2$
points of
$|Z|-t_{Z}\geqslant t_{Z}+2$
points of
![]() $Z$
(and hence
$Z$
(and hence
![]() $t_{Z}<(|Z|-1)/2$
) and let
$t_{Z}<(|Z|-1)/2$
) and let
![]() $Y$
be the set of these points. Let
$Y$
be the set of these points. Let
![]() $U\subset Z$
be the subset of the other
$U\subset Z$
be the subset of the other
![]() $t_{Z}$
points. Then
$t_{Z}$
points. Then
![]() $I_{Y}=(\ell ,f)$
for some form
$I_{Y}=(\ell ,f)$
for some form
![]() $f$
, where
$f$
, where
![]() $\deg f\geqslant t_{Z}+2$
. Thus, for each integer
$\deg f\geqslant t_{Z}+2$
. Thus, for each integer
![]() $j$
and any general point
$j$
and any general point
![]() $P\in \mathbb{P}^{2}$
, we get
$P\in \mathbb{P}^{2}$
, we get
Since
![]() $\deg f\geqslant t_{Z}+2$
, it follows for
$\deg f\geqslant t_{Z}+2$
, it follows for
![]() $j+1\leqslant t_{Z}+1$
that
$j+1\leqslant t_{Z}+1$
that
because
![]() $\ell$
does not vanish at
$\ell$
does not vanish at
![]() $P$
or at any of the points in
$P$
or at any of the points in
![]() $U$
. Since
$U$
. Since
![]() $|U|=t_{Z}$
, Lemma 4.2 gives
$|U|=t_{Z}$
, Lemma 4.2 gives
![]() $\dim [I_{U+jP}]_{j}\leqslant 1$
for
$\dim [I_{U+jP}]_{j}\leqslant 1$
for
![]() $j\leqslant t_{Z}$
, with equality exactly when
$j\leqslant t_{Z}$
, with equality exactly when
![]() $j=t_{Z}$
. Thus
$j=t_{Z}$
. Thus
![]() $m_{Z}=t_{Z}$
and
$m_{Z}=t_{Z}$
and
![]() $\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
.
$\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
.
Now assume
![]() $j\geqslant m_{Z}=t_{Z}$
. Using Equation (2.4), we have
$j\geqslant m_{Z}=t_{Z}$
. Using Equation (2.4), we have
Hence
Then
 $$\begin{eqnarray}\displaystyle \displaystyle \dim [I_{Z}]_{j+1}-\binom{j+1}{2} & = & \displaystyle \displaystyle \max \{2j+3-(m_{Z}+j+2),2j+3-|Z|\}\nonumber\\ \displaystyle & = & \displaystyle \max \{j+1-m_{Z},(j+1-m_{Z})+(j+1-b_{Z})\}\nonumber\\ \displaystyle & = & \displaystyle \dim [I_{Z+jP}]_{j+1},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \dim [I_{Z}]_{j+1}-\binom{j+1}{2} & = & \displaystyle \displaystyle \max \{2j+3-(m_{Z}+j+2),2j+3-|Z|\}\nonumber\\ \displaystyle & = & \displaystyle \max \{j+1-m_{Z},(j+1-m_{Z})+(j+1-b_{Z})\}\nonumber\\ \displaystyle & = & \displaystyle \dim [I_{Z+jP}]_{j+1},\nonumber\end{eqnarray}$$
the latter thanks to Lemma 3.3. ◻
5 The structure of unexpected curves and relation to syzygies
We now give a rather detailed description of unexpected curves of a finite set of points
![]() $Z\subset \mathbb{P}^{2}$
. It turns out that any such curve has exactly one irreducible component of degree greater than
$Z\subset \mathbb{P}^{2}$
. It turns out that any such curve has exactly one irreducible component of degree greater than
![]() $1$
, and that this irreducible curve is rational and is an unexpected curve of a subset of
$1$
, and that this irreducible curve is rational and is an unexpected curve of a subset of
![]() $Z$
(which can be equal to
$Z$
(which can be equal to
![]() $Z$
).
$Z$
).
We begin with a description of curves whose existence is guaranteed by the definition of the multiplicity index
![]() $m_{Z}$
. When
$m_{Z}$
. When
![]() $P$
is a general point and
$P$
is a general point and
![]() $\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
we will for later use denote the unique curve defined by
$\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
we will for later use denote the unique curve defined by
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
by
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
by
![]() $C_{P}(Z)$
. Thus when
$C_{P}(Z)$
. Thus when
![]() $\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
, by the next result there is an open set of points
$\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
, by the next result there is an open set of points
![]() $P$
such that for each
$P$
such that for each
![]() $P$
there is a subset
$P$
there is a subset
![]() $Z_{P}^{\prime \prime }$
of
$Z_{P}^{\prime \prime }$
of
![]() $Z$
such that
$Z$
such that
![]() $C_{P}(Z)$
is the union of the
$C_{P}(Z)$
is the union of the
![]() $|Z_{P}^{\prime \prime }|$
lines through
$|Z_{P}^{\prime \prime }|$
lines through
![]() $P$
and each point of
$P$
and each point of
![]() $Z_{P}^{\prime \prime }$
, together with an irreducible curve
$Z_{P}^{\prime \prime }$
, together with an irreducible curve
![]() $C_{P}(Z_{P}^{\prime })$
of degree
$C_{P}(Z_{P}^{\prime })$
of degree
![]() $m_{Z}+1-|Z_{P}^{\prime \prime }|$
containing
$m_{Z}+1-|Z_{P}^{\prime \prime }|$
containing
![]() $Z_{P}^{\prime }$
, where
$Z_{P}^{\prime }$
, where
![]() $Z_{P}^{\prime }=Z\setminus Z_{P}^{\prime \prime }$
. Therefore, by semicontinuity applied to
$Z_{P}^{\prime }=Z\setminus Z_{P}^{\prime \prime }$
. Therefore, by semicontinuity applied to
![]() $\dim [I_{Y+(m_{Z}-|Y|)P}]_{m_{Z}+1-|Y|}$
for the various subsets
$\dim [I_{Y+(m_{Z}-|Y|)P}]_{m_{Z}+1-|Y|}$
for the various subsets
![]() $Y$
of
$Y$
of
![]() $Z$
, there is a single subset
$Z$
, there is a single subset
![]() $Z^{\prime \prime }$
of
$Z^{\prime \prime }$
of
![]() $Z$
such that for a non-empty open set of points
$Z$
such that for a non-empty open set of points
![]() $P$
we have
$P$
we have
![]() $Z_{P}^{\prime \prime }=Z^{\prime \prime }$
. That is, when
$Z_{P}^{\prime \prime }=Z^{\prime \prime }$
. That is, when
![]() $\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
, it makes sense to talk about the components of
$\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
, it makes sense to talk about the components of
![]() $C_{P}(Z)$
for a general point
$C_{P}(Z)$
for a general point
![]() $P$
.
$P$
.
Lemma 5.1. Let
![]() $Z$
be a finite set of points of
$Z$
be a finite set of points of
![]() $\mathbb{P}^{2}$
, and let
$\mathbb{P}^{2}$
, and let
![]() $P\in \mathbb{P}^{2}$
be a general point. If
$P\in \mathbb{P}^{2}$
be a general point. If
![]() $C$
is a curve of degree
$C$
is a curve of degree
![]() $m_{Z}+1$
containing
$m_{Z}+1$
containing
![]() $Z$
, with multiplicity
$Z$
, with multiplicity
![]() $m_{Z}$
at a general point
$m_{Z}$
at a general point
![]() $P$
, then it is reduced and either irreducible or a union of lines through
$P$
, then it is reduced and either irreducible or a union of lines through
![]() $P$
and an irreducible curve
$P$
and an irreducible curve
![]() $C^{\prime }$
whose multiplicity at
$C^{\prime }$
whose multiplicity at
![]() $P$
is
$P$
is
![]() $-1+\deg C^{\prime }$
. The curve
$-1+\deg C^{\prime }$
. The curve
![]() $C^{\prime }$
is rational and smooth away from
$C^{\prime }$
is rational and smooth away from
![]() $P$
.
$P$
.
Furthermore, the set
![]() $Z^{\prime }=Z\cap C^{\prime }$
has multiplicity index
$Z^{\prime }=Z\cap C^{\prime }$
has multiplicity index
![]() $m_{Z^{\prime }}=m_{Z}-|Z^{\prime \prime }|$
, where
$m_{Z^{\prime }}=m_{Z}-|Z^{\prime \prime }|$
, where
![]() $Z^{\prime \prime }=Z-Z^{\prime }$
, and each of the components of
$Z^{\prime \prime }=Z-Z^{\prime }$
, and each of the components of
![]() $C$
other than
$C$
other than
![]() $C^{\prime }$
passes through exactly one of the points of
$C^{\prime }$
passes through exactly one of the points of
![]() $Z^{\prime \prime }$
. In particular,
$Z^{\prime \prime }$
. In particular,
![]() $\deg C^{\prime }=\deg C-|Z^{\prime \prime }|=m_{Z^{\prime }}+1$
.
$\deg C^{\prime }=\deg C-|Z^{\prime \prime }|=m_{Z^{\prime }}+1$
.
Proof. Note that the multiplicity of an irreducible curve at a point is at most the degree of the curve and that the multiplicity is equal to the degree if and only if the curve is a line. Since the degree of
![]() $C$
at
$C$
at
![]() $P$
is precisely one more than its multiplicity at
$P$
is precisely one more than its multiplicity at
![]() $P$
, it follows that
$P$
, it follows that
![]() $C$
has a unique irreducible component
$C$
has a unique irreducible component
![]() $C^{\prime }$
whose multiplicity at
$C^{\prime }$
whose multiplicity at
![]() $P$
is
$P$
is
![]() $-1+\deg C^{\prime }$
and that this component has multiplicity
$-1+\deg C^{\prime }$
and that this component has multiplicity
![]() $1$
. Thus,
$1$
. Thus,
![]() $f=f^{\prime }\cdot \ell _{1}\cdots \ell _{k}$
, where
$f=f^{\prime }\cdot \ell _{1}\cdots \ell _{k}$
, where
![]() $f$
and
$f$
and
![]() $f^{\prime }$
define the curves
$f^{\prime }$
define the curves
![]() $C$
and
$C$
and
![]() $C^{\prime }$
, respectively,
$C^{\prime }$
, respectively,
![]() $k\geqslant 0$
, and each
$k\geqslant 0$
, and each
![]() $\ell _{i}$
is a linear form in
$\ell _{i}$
is a linear form in
![]() $I_{P}$
, so
$I_{P}$
, so
![]() $\deg (C^{\prime })=\deg (C)-k=m_{Z}+1-k$
. The genus formula implies that
$\deg (C^{\prime })=\deg (C)-k=m_{Z}+1-k$
. The genus formula implies that
![]() $C^{\prime }$
is rational and smooth at all points other than
$C^{\prime }$
is rational and smooth at all points other than
![]() $P$
.
$P$
.
Put
![]() $Z^{\prime }=Z\cap C^{\prime }$
. Since
$Z^{\prime }=Z\cap C^{\prime }$
. Since
![]() $P$
is general, each of the
$P$
is general, each of the
![]() $k$
components of
$k$
components of
![]() $C$
other than
$C$
other than
![]() $C^{\prime }$
passes through at most one point of
$C^{\prime }$
passes through at most one point of
![]() $Z$
. The union of these lines must contain
$Z$
. The union of these lines must contain
![]() $Z^{\prime \prime }=Z-Z^{\prime }$
, and so
$Z^{\prime \prime }=Z-Z^{\prime }$
, and so
![]() $|Z^{\prime \prime }|\leqslant k$
.
$|Z^{\prime \prime }|\leqslant k$
.
We have seen that
![]() $f^{\prime }$
is in
$f^{\prime }$
is in
![]() $[I_{Z^{\prime }+(m_{Z}-k)P}]_{m_{Z}-k+1}$
, which implies
$[I_{Z^{\prime }+(m_{Z}-k)P}]_{m_{Z}-k+1}$
, which implies
![]() $m_{Z^{\prime }}\leqslant m_{Z}-k$
. Hence, the estimate
$m_{Z^{\prime }}\leqslant m_{Z}-k$
. Hence, the estimate
![]() $m_{Z^{\prime }}=m_{Z-Z^{\prime \prime }}\geqslant m_{Z}-|Z^{\prime \prime }|$
gives
$m_{Z^{\prime }}=m_{Z-Z^{\prime \prime }}\geqslant m_{Z}-|Z^{\prime \prime }|$
gives
![]() $k\leqslant |Z^{\prime \prime }|$
. Therefore, we obtain
$k\leqslant |Z^{\prime \prime }|$
. Therefore, we obtain
![]() $|Z^{\prime \prime }|=k$
, so
$|Z^{\prime \prime }|=k$
, so
![]() $m_{Z^{\prime }}=m_{Z}-k=m_{Z}-|Z^{\prime \prime }|$
and
$m_{Z^{\prime }}=m_{Z}-k=m_{Z}-|Z^{\prime \prime }|$
and
![]() $\deg (C^{\prime })=\deg (C)-k=\deg (C)-|Z^{\prime \prime }|=m_{Z}+1-|Z^{\prime \prime }|=m_{Z^{\prime }}+1$
. It also follows that each of the
$\deg (C^{\prime })=\deg (C)-k=\deg (C)-|Z^{\prime \prime }|=m_{Z}+1-|Z^{\prime \prime }|=m_{Z^{\prime }}+1$
. It also follows that each of the
![]() $k$
lines defined by some
$k$
lines defined by some
![]() $\ell _{i}$
passes through one of the
$\ell _{i}$
passes through one of the
![]() $k$
points of
$k$
points of
![]() $Z^{\prime \prime }$
, and no two lines pass through the same point of
$Z^{\prime \prime }$
, and no two lines pass through the same point of
![]() $Z^{\prime \prime }$
. Thus, the curve
$Z^{\prime \prime }$
. Thus, the curve
![]() $C$
is reduced.◻
$C$
is reduced.◻
We now slightly improve Lemma 3.3. Recall by Lemma 3.5 that
![]() $u_{Z}+1\geqslant m_{Z}$
.
$u_{Z}+1\geqslant m_{Z}$
.
Proposition 5.2. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
. If
$\mathbb{P}^{2}$
. If
![]() $P$
is a general point, then there is a plane curve
$P$
is a general point, then there is a plane curve
![]() $C$
defined by a form
$C$
defined by a form
![]() $f$
of degree
$f$
of degree
![]() $m_{Z}+1$
that vanishes on
$m_{Z}+1$
that vanishes on
![]() $Z$
and to order
$Z$
and to order
![]() $m_{Z}$
on
$m_{Z}$
on
![]() $P$
, and a plane curve
$P$
, and a plane curve
![]() $D$
defined by a form
$D$
defined by a form
![]() $g$
of degree
$g$
of degree
![]() $u_{Z}+2$
that vanishes on
$u_{Z}+2$
that vanishes on
![]() $Z$
and to order
$Z$
and to order
![]() $u_{Z}+1$
on
$u_{Z}+1$
on
![]() $P$
, such that
$P$
, such that
![]() $C\cap D$
is a zero-dimensional subscheme, and, for all integers
$C\cap D$
is a zero-dimensional subscheme, and, for all integers
![]() $j\geqslant 0$
, there is an isomorphism of
$j\geqslant 0$
, there is an isomorphism of
![]() $K$
-vector spaces
$K$
-vector spaces
Proof. The existence of a curve
![]() $C$
with the desired properties is guaranteed by the definition of the multiplicity index
$C$
with the desired properties is guaranteed by the definition of the multiplicity index
![]() $m_{Z}$
. Suppose
$m_{Z}$
. Suppose
![]() $C$
is defined by a form
$C$
is defined by a form
![]() $f$
. Then
$f$
. Then
![]() $f\cdot [I_{(j-m_{Z})P}]_{j-m_{Z}}\subset [I_{Z+jP}]_{j+1}$
, and, comparing dimensions by using Lemma 3.3, we see that
$f\cdot [I_{(j-m_{Z})P}]_{j-m_{Z}}\subset [I_{Z+jP}]_{j+1}$
, and, comparing dimensions by using Lemma 3.3, we see that
Since, by definition,
![]() $[I_{Z+jP}]_{j+1}=0$
if
$[I_{Z+jP}]_{j+1}=0$
if
![]() $j<m_{Z}$
, this proves our claim if
$j<m_{Z}$
, this proves our claim if
![]() $j\leqslant u_{Z}$
. If
$j\leqslant u_{Z}$
. If
![]() $j=u_{Z}+1$
, then Lemma 3.3 gives that there is a form
$j=u_{Z}+1$
, then Lemma 3.3 gives that there is a form
![]() $g$
of degree
$g$
of degree
![]() $u_{Z}+2$
such that
$u_{Z}+2$
such that
We will now show that
![]() $f$
and
$f$
and
![]() $g$
are relatively prime. Using the notation of Lemma 5.1, write
$g$
are relatively prime. Using the notation of Lemma 5.1, write
![]() $f=f^{\prime }\cdot \ell _{1}\cdots \ell _{k}$
, where
$f=f^{\prime }\cdot \ell _{1}\cdots \ell _{k}$
, where
![]() $f^{\prime }$
defines the irreducible curve
$f^{\prime }$
defines the irreducible curve
![]() $C^{\prime }$
and each
$C^{\prime }$
and each
![]() $\ell _{i}$
defines a line though
$\ell _{i}$
defines a line though
![]() $P$
and one of the
$P$
and one of the
![]() $k$
points of
$k$
points of
![]() $Z^{\prime \prime }=Z-Z^{\prime }$
. Assume first that
$Z^{\prime \prime }=Z-Z^{\prime }$
. Assume first that
![]() $f^{\prime }$
divides
$f^{\prime }$
divides
![]() $g$
. Then the curve defined by
$g$
. Then the curve defined by
![]() $g/f^{\prime }$
has multiplicity
$g/f^{\prime }$
has multiplicity
![]() $u_{Z}+1-(m_{Z}-k)=\deg g/f^{\prime }$
. Thus,
$u_{Z}+1-(m_{Z}-k)=\deg g/f^{\prime }$
. Thus,
![]() $g/f^{\prime }$
is a product of linear forms of
$g/f^{\prime }$
is a product of linear forms of
![]() $I_{P}$
that must vanish on
$I_{P}$
that must vanish on
![]() $Z^{\prime \prime }$
. Hence,
$Z^{\prime \prime }$
. Hence,
![]() $\ell _{1}\cdots \ell _{k}$
divides
$\ell _{1}\cdots \ell _{k}$
divides
![]() $g/f^{\prime }$
, which implies
$g/f^{\prime }$
, which implies
![]() $g\in f\cdot [I_{(u_{Z}+1-m_{Z})P}]_{u_{Z}+1-m_{Z}}$
, in contradiction to the choice of
$g\in f\cdot [I_{(u_{Z}+1-m_{Z})P}]_{u_{Z}+1-m_{Z}}$
, in contradiction to the choice of
![]() $g$
.
$g$
.
Assume next that
![]() $k\geqslant 1$
and that one of the linear forms
$k\geqslant 1$
and that one of the linear forms
![]() $\ell _{i}$
divides
$\ell _{i}$
divides
![]() $g$
. Let
$g$
. Let
![]() $P_{i}\in Z^{\prime \prime }$
be the point of
$P_{i}\in Z^{\prime \prime }$
be the point of
![]() $Z$
on which
$Z$
on which
![]() $\ell _{i}$
vanishes. By Lemma 5.1, we know that
$\ell _{i}$
vanishes. By Lemma 5.1, we know that
![]() $m_{Z^{\prime }}=m_{Z-Z^{\prime \prime }}=m_{Z}-|Z^{\prime \prime }|$
. This gives
$m_{Z^{\prime }}=m_{Z-Z^{\prime \prime }}=m_{Z}-|Z^{\prime \prime }|$
. This gives
![]() $m_{Z-P_{i}}=m_{Z}-1$
, and thus
$m_{Z-P_{i}}=m_{Z}-1$
, and thus
![]() $u_{Z-P_{i}}=u_{Z}$
. It follows that
$u_{Z-P_{i}}=u_{Z}$
. It follows that
![]() $f/\ell _{i}\in [I_{Z-P_{i}+m_{Z-P_{i}}P}]_{m_{Z-P_{i}}+1}$
and
$f/\ell _{i}\in [I_{Z-P_{i}+m_{Z-P_{i}}P}]_{m_{Z-P_{i}}+1}$
and
![]() $g/\ell _{i}\in [I_{Z-P_{i}+u_{Z-P_{i}}P}]_{u_{Z-P_{i}}+1}$
. Applying the part of the statement we have already shown to
$g/\ell _{i}\in [I_{Z-P_{i}+u_{Z-P_{i}}P}]_{u_{Z-P_{i}}+1}$
. Applying the part of the statement we have already shown to
![]() $Z-P_{i}$
, we conclude that
$Z-P_{i}$
, we conclude that
![]() $g/\ell _{i}\in f/\ell _{i}\cdot [I_{(u_{Z-P_{i}}-m_{Z-P_{i}})P}]_{u_{Z-P_{i}}-m_{Z-P_{i}}}=f/\ell _{i}\cdot [I_{(u_{Z}-m_{Z}+1)P}]_{u_{Z}-m_{Z}+1}$
, which is again in contradiction to the choice of
$g/\ell _{i}\in f/\ell _{i}\cdot [I_{(u_{Z-P_{i}}-m_{Z-P_{i}})P}]_{u_{Z-P_{i}}-m_{Z-P_{i}}}=f/\ell _{i}\cdot [I_{(u_{Z}-m_{Z}+1)P}]_{u_{Z}-m_{Z}+1}$
, which is again in contradiction to the choice of
![]() $g$
.
$g$
.
Thus, we have shown that
![]() $f$
and
$f$
and
![]() $g$
form a regular sequence. We claim that
$g$
form a regular sequence. We claim that
This is clear if
![]() $j\leqslant |Z|$
because the degrees of the syzygies of the ideal
$j\leqslant |Z|$
because the degrees of the syzygies of the ideal
![]() $(f,g)$
are at least
$(f,g)$
are at least
![]() $m_{Z}+1+u_{Z}+2=|Z|+1$
. Assume now that the claim is false for some
$m_{Z}+1+u_{Z}+2=|Z|+1$
. Assume now that the claim is false for some
![]() $j\geqslant |Z|+1$
. That is, there are forms
$j\geqslant |Z|+1$
. That is, there are forms
![]() $h_{1},h_{2}$
of suitable degrees such that
$h_{1},h_{2}$
of suitable degrees such that
![]() $fh_{1}=gh_{2}$
, where
$fh_{1}=gh_{2}$
, where
![]() $h_{2}$
is a product of
$h_{2}$
is a product of
![]() $j-u_{Z}-2\geqslant m_{Z}+1$
linear forms in
$j-u_{Z}-2\geqslant m_{Z}+1$
linear forms in
![]() $I_{P}$
. Since
$I_{P}$
. Since
![]() $f$
and
$f$
and
![]() $g$
are coprime, it follows that
$g$
are coprime, it follows that
![]() $f$
is a product of
$f$
is a product of
![]() $m_{Z}+1$
linear forms in
$m_{Z}+1$
linear forms in
![]() $I_{P}$
. By the generality of
$I_{P}$
. By the generality of
![]() $P$
, each of these linear forms vanishes on at most one point of
$P$
, each of these linear forms vanishes on at most one point of
![]() $Z$
. However, by definition
$Z$
. However, by definition
![]() $f$
vanishes at each point of
$f$
vanishes at each point of
![]() $Z$
, which implies
$Z$
, which implies
![]() $m_{Z}+1\geqslant |Z|=m_{Z}+u_{Z}+2$
. This is a contradiction because
$m_{Z}+1\geqslant |Z|=m_{Z}+u_{Z}+2$
. This is a contradiction because
![]() $u_{Z}\geqslant 0$
(as
$u_{Z}\geqslant 0$
(as
![]() $|Z|\geqslant 2$
). Thus, the above claim is shown. It gives that the sum
$|Z|\geqslant 2$
). Thus, the above claim is shown. It gives that the sum
is a direct sum. Since both sides have the same dimension we get equality, as desired. ◻
As a first consequence, we see that if
![]() $u_{Z}=m_{Z}-1$
then there is an irreducible curve of degree
$u_{Z}=m_{Z}-1$
then there is an irreducible curve of degree
![]() $m_{Z}+1$
that vanishes on
$m_{Z}+1$
that vanishes on
![]() $Z$
and at a general point
$Z$
and at a general point
![]() $P$
to order
$P$
to order
![]() $m_{Z}$
.
$m_{Z}$
.
Corollary 5.3. If
![]() $Z$
satisfies
$Z$
satisfies
![]() $u_{Z}=m_{Z}-1$
(i.e.
$u_{Z}=m_{Z}-1$
(i.e.
![]() $a_{Z}=b_{Z}$
), then there is an irreducible curve of degree
$a_{Z}=b_{Z}$
), then there is an irreducible curve of degree
![]() $m_{Z}+1$
that vanishes on
$m_{Z}+1$
that vanishes on
![]() $Z$
and at a general point
$Z$
and at a general point
![]() $P$
to order
$P$
to order
![]() $m_{Z}$
.
$m_{Z}$
.
Proof. By Proposition 5.2, the vector space
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
contains two polynomials,
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
contains two polynomials,
![]() $F$
and
$F$
and
![]() $G$
, that form a regular sequence. By Lemma 5.1, any
$G$
, that form a regular sequence. By Lemma 5.1, any
![]() $K$
-linear combination of
$K$
-linear combination of
![]() $F$
and
$F$
and
![]() $G$
which is not irreducible has a linear factor. Suppose there are two such linear combinations, for example
$G$
which is not irreducible has a linear factor. Suppose there are two such linear combinations, for example
![]() $aF+G$
and
$aF+G$
and
![]() $bF+G$
for distinct scalars
$bF+G$
for distinct scalars
![]() $a$
and
$a$
and
![]() $b$
, which have a common linear factor
$b$
, which have a common linear factor
![]() $L$
. We have
$L$
. We have
![]() $aF+G=LH_{1}$
and
$aF+G=LH_{1}$
and
![]() $bF+G=LH_{2}$
for some forms
$bF+G=LH_{2}$
for some forms
![]() $H_{1}$
and
$H_{1}$
and
![]() $H_{2}$
, so
$H_{2}$
, so
![]() $(a-b)F=L(H_{1}-H_{2})$
. Then
$(a-b)F=L(H_{1}-H_{2})$
. Then
![]() $L$
is a factor of
$L$
is a factor of
![]() $F$
, so from the equation
$F$
, so from the equation
![]() $aF+G=LH_{1}$
we also have that
$aF+G=LH_{1}$
we also have that
![]() $L$
is a factor of
$L$
is a factor of
![]() $G$
, and hence of every curve in the linear system. This contradicts the fact that
$G$
, and hence of every curve in the linear system. This contradicts the fact that
![]() $F$
and
$F$
and
![]() $G$
are a regular sequence.
$G$
are a regular sequence.
By Lemma 5.1 there are only finitely many possible linear factors, each of which corresponds to a point of
![]() $Z$
, so we can conclude that at most
$Z$
, so we can conclude that at most
![]() $|Z|$
curves in the pencil defined by
$|Z|$
curves in the pencil defined by
![]() $F$
and
$F$
and
![]() $G$
are reducible. Since
$G$
are reducible. Since
![]() $K$
is infinite, the general element must be irreducible.◻
$K$
is infinite, the general element must be irreducible.◻
Example 5.4. We give an example of Corollary 5.3, which shows that not all of the curves
![]() $C$
of Lemma 5.1 need be irreducible. Let
$C$
of Lemma 5.1 need be irreducible. Let
![]() $P$
be a general point of
$P$
be a general point of
![]() $\mathbb{P}^{2}$
. Let
$\mathbb{P}^{2}$
. Let
![]() $D$
be an irreducible plane quartic with a triple point
$D$
be an irreducible plane quartic with a triple point
![]() $P^{\prime }$
. Let
$P^{\prime }$
. Let
![]() $B$
be a smooth cubic through
$B$
be a smooth cubic through
![]() $P^{\prime }$
meeting
$P^{\prime }$
meeting
![]() $D$
transversely at nine points away from
$D$
transversely at nine points away from
![]() $P^{\prime }$
. Let
$P^{\prime }$
. Let
![]() $Z$
be any subset of seven of those nine points. By Bezout’s theorem, there is no cubic through
$Z$
be any subset of seven of those nine points. By Bezout’s theorem, there is no cubic through
![]() $Z$
singular at
$Z$
singular at
![]() $P^{\prime }$
, hence
$P^{\prime }$
, hence
![]() $\dim [I_{Z+2P^{\prime }}]_{3}=0$
. Now by semicontinuity we have
$\dim [I_{Z+2P^{\prime }}]_{3}=0$
. Now by semicontinuity we have
![]() $\dim [I_{Z+2P}]_{3}=0$
. A dimension count shows that
$\dim [I_{Z+2P}]_{3}=0$
. A dimension count shows that
![]() $\dim [I_{Z+3P}]_{4}>0$
, hence
$\dim [I_{Z+3P}]_{4}>0$
, hence
![]() $m_{Z}=3$
. Thus
$m_{Z}=3$
. Thus
![]() $u_{Z}=|Z|-m_{Z}-2=2$
, so by Corollary 5.3,
$u_{Z}=|Z|-m_{Z}-2=2$
, so by Corollary 5.3,
![]() $[I_{Z+3P}]_{4}$
contains an irreducible form. For each
$[I_{Z+3P}]_{4}$
contains an irreducible form. For each
![]() $P$
, pick such an irreducible form and let
$P$
, pick such an irreducible form and let
![]() $D_{P}$
be the curve it defines. Let
$D_{P}$
be the curve it defines. Let
![]() $Y$
be any subset of six points of
$Y$
be any subset of six points of
![]() $Z$
. Since the splitting type of
$Z$
. Since the splitting type of
![]() $Z$
is
$Z$
is
![]() $(3,3)$
, the splitting type of
$(3,3)$
, the splitting type of
![]() $Y$
is
$Y$
is
![]() $(2,3)$
. Thus there is a cubic through
$(2,3)$
. Thus there is a cubic through
![]() $Y$
singular at
$Y$
singular at
![]() $P$
. Let
$P$
. Let
![]() $B_{P}$
be any such cubic. Then
$B_{P}$
be any such cubic. Then
![]() $B_{P}$
cannot contain
$B_{P}$
cannot contain
![]() $Z$
since then
$Z$
since then
![]() $B_{P}$
and
$B_{P}$
and
![]() $D_{P}$
would contain a common component. However, if
$D_{P}$
would contain a common component. However, if
![]() $L$
is the line through
$L$
is the line through
![]() $P$
and the point of
$P$
and the point of
![]() $Z$
not on
$Z$
not on
![]() $B_{P}$
, then
$B_{P}$
, then
![]() $B_{P}+L$
is a quartic through
$B_{P}+L$
is a quartic through
![]() $Z$
with a triple point at
$Z$
with a triple point at
![]() $P$
, so we see that not every form in
$P$
, so we see that not every form in
![]() $[I_{Z+3P}]_{4}$
is irreducible. Thus if
$[I_{Z+3P}]_{4}$
is irreducible. Thus if
![]() $C$
is a curve defined by a form in
$C$
is a curve defined by a form in
![]() $[I_{Z+3P}]_{4}$
, then either
$[I_{Z+3P}]_{4}$
, then either
![]() $C$
is irreducible or
$C$
is irreducible or
![]() $C$
is reducible, and both cases occur. By Lemma 5.1, if
$C$
is reducible, and both cases occur. By Lemma 5.1, if
![]() $C$
is irreducible, then
$C$
is irreducible, then
![]() $C=C^{\prime }$
, and if
$C=C^{\prime }$
, and if
![]() $C$
is reducible, then
$C$
is reducible, then
![]() $C$
has one linear component containing
$C$
has one linear component containing
![]() $P$
and a point of
$P$
and a point of
![]() $Z$
and
$Z$
and
![]() $C^{\prime }$
is an irreducible cubic singular at
$C^{\prime }$
is an irreducible cubic singular at
![]() $P$
and containing the other six points of
$P$
and containing the other six points of
![]() $Z$
. A priori,
$Z$
. A priori,
![]() $C$
could have two linear components, each containing
$C$
could have two linear components, each containing
![]() $P$
and a point of
$P$
and a point of
![]() $Z$
, with
$Z$
, with
![]() $C^{\prime }$
being an irreducible conic through
$C^{\prime }$
being an irreducible conic through
![]() $P$
and containing the other five points of
$P$
and containing the other five points of
![]() $Z$
, or
$Z$
, or
![]() $C$
could have three linear components, each containing
$C$
could have three linear components, each containing
![]() $P$
and a point of
$P$
and a point of
![]() $Z$
, with
$Z$
, with
![]() $C^{\prime }$
being a line that does not contain
$C^{\prime }$
being a line that does not contain
![]() $P$
but does contain the other four points of
$P$
but does contain the other four points of
![]() $Z$
. Neither can occur here, though: if there were an irreducible conic through five points, that conic is the only conic through those five points, so it cannot contain a general point
$Z$
. Neither can occur here, though: if there were an irreducible conic through five points, that conic is the only conic through those five points, so it cannot contain a general point
![]() $P$
, and if there a line through four points of
$P$
, and if there a line through four points of
![]() $Z$
, then that line would have to be a component of
$Z$
, then that line would have to be a component of
![]() $B$
.
$B$
.
Recall from Theorem 3.9 that
![]() $Z$
admits unexpected curves if and only if
$Z$
admits unexpected curves if and only if
![]() $Z$
has an unexpected curve of degree
$Z$
has an unexpected curve of degree
![]() $m_{Z}+1$
, the least degree possible, and that if
$m_{Z}+1$
, the least degree possible, and that if
![]() $Z$
has any unexpected curves then the degrees
$Z$
has any unexpected curves then the degrees
![]() $t$
in which they occur are exactly
$t$
in which they occur are exactly
![]() $m_{Z}+1\leqslant t\leqslant u_{Z}$
. By the following result, understanding unexpected curves for
$m_{Z}+1\leqslant t\leqslant u_{Z}$
. By the following result, understanding unexpected curves for
![]() $Z$
reduces to understanding them in degree
$Z$
reduces to understanding them in degree
![]() $m_{Z}+1$
.
$m_{Z}+1$
.
Corollary 5.5. Let
![]() $Z$
be a finite set of points with an unexpected curve. Then
$Z$
be a finite set of points with an unexpected curve. Then
![]() $Z$
has a unique unexpected curve
$Z$
has a unique unexpected curve
![]() $C$
in degree
$C$
in degree
![]() $m_{Z}+1$
, and for each
$m_{Z}+1$
, and for each
![]() $m_{Z}+1<t\leqslant u_{Z}$
, the unexpected curves of degree
$m_{Z}+1<t\leqslant u_{Z}$
, the unexpected curves of degree
![]() $t$
are precisely the curves
$t$
are precisely the curves
![]() $C+L_{1}+\cdots +L_{r}$
, where
$C+L_{1}+\cdots +L_{r}$
, where
![]() $r=t-m_{Z}-1$
and each
$r=t-m_{Z}-1$
and each
![]() $L_{i}$
is an arbitrary line through the point
$L_{i}$
is an arbitrary line through the point
![]() $P$
(i.e. the general point at which
$P$
(i.e. the general point at which
![]() $C$
is singular).
$C$
is singular).
Proof. This is an immediate consequence of Proposition 5.2 and the fact for
![]() $j\geqslant m_{Z}$
that the non-zero forms in
$j\geqslant m_{Z}$
that the non-zero forms in
![]() $[I_{(j-m_{Z})P}]_{j-m_{Z}}$
are precisely the products of
$[I_{(j-m_{Z})P}]_{j-m_{Z}}$
are precisely the products of
![]() $j-m_{Z}$
linear forms vanishing at
$j-m_{Z}$
linear forms vanishing at
![]() $P$
(the
$P$
(the
![]() $j$
in Proposition 5.2 corresponds to
$j$
in Proposition 5.2 corresponds to
![]() $t-1$
here).◻
$t-1$
here).◻
We begin our quest to understand unexpected curves by, more generally, considering the case where there is a unique curve
![]() $C_{P}(Z)$
containing
$C_{P}(Z)$
containing
![]() $Z$
with multiplicity
$Z$
with multiplicity
![]() $m_{Z}$
at a general point
$m_{Z}$
at a general point
![]() $P$
. By Proposition 5.2 this is precisely the case where
$P$
. By Proposition 5.2 this is precisely the case where
![]() $m_{Z}\leqslant u_{Z}$
(i.e. where
$m_{Z}\leqslant u_{Z}$
(i.e. where
![]() $2m_{Z}+2\leqslant |Z|$
, since
$2m_{Z}+2\leqslant |Z|$
, since
![]() $u_{Z}=|Z|-m_{Z}-2$
). Even when unexpected, the curve
$u_{Z}=|Z|-m_{Z}-2$
). Even when unexpected, the curve
![]() $C_{P}(Z)$
sometimes is and sometimes is not irreducible (see Example 6.1 and Propositions 6.12, 6.15). The following result clarifies the connection between irreducibility and being unexpected.
$C_{P}(Z)$
sometimes is and sometimes is not irreducible (see Example 6.1 and Propositions 6.12, 6.15). The following result clarifies the connection between irreducibility and being unexpected.
Corollary 5.6. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
with
$\mathbb{P}^{2}$
with
![]() $m_{Z}\leqslant u_{Z}$
, let
$m_{Z}\leqslant u_{Z}$
, let
![]() $P\in \mathbb{P}^{2}$
be a general point, let
$P\in \mathbb{P}^{2}$
be a general point, let
![]() $C=C_{P}(Z)$
be the unique curve containing
$C=C_{P}(Z)$
be the unique curve containing
![]() $Z$
with multiplicity
$Z$
with multiplicity
![]() $m_{Z}$
at
$m_{Z}$
at
![]() $P$
and let
$P$
and let
![]() $t+1$
be the number of components of
$t+1$
be the number of components of
![]() $C$
.
$C$
.
(a) The component
 $C^{\prime }$
of
$C^{\prime }$
of
 $C$
given in Lemma 5.1 is the unique curve containing
$C$
given in Lemma 5.1 is the unique curve containing
 $Z^{\prime }$
with multiplicity
$Z^{\prime }$
with multiplicity
 $m_{Z^{\prime }}$
at
$m_{Z^{\prime }}$
at
 $P$
, where
$P$
, where
 $Z^{\prime }\subset Z$
is the subset given in the lemma; that is,
$Z^{\prime }\subset Z$
is the subset given in the lemma; that is,
 $C^{\prime }=C_{P}(Z^{\prime })$
, and we have
$C^{\prime }=C_{P}(Z^{\prime })$
, and we have
 $m_{Z^{\prime }}+t\leqslant u_{Z^{\prime }}$
.
$m_{Z^{\prime }}+t\leqslant u_{Z^{\prime }}$
.(b)
 $C$
is unexpected for
$C$
is unexpected for
 $Z$
if and only if
$Z$
if and only if
 $1\leqslant m_{Z^{\prime }}$
and
$1\leqslant m_{Z^{\prime }}$
and
 $m_{Z}<u_{Z}$
. (In particular, if
$m_{Z}<u_{Z}$
. (In particular, if
 $C$
is irreducible, then
$C$
is irreducible, then
 $C$
is unexpected for
$C$
is unexpected for
 $Z$
if and only if
$Z$
if and only if
 $1\leqslant m_{Z}<u_{Z}$
.)
$1\leqslant m_{Z}<u_{Z}$
.)(c) If
 $C$
is not irreducible, then
$C$
is not irreducible, then
 $C^{\prime }$
is unexpected for
$C^{\prime }$
is unexpected for
 $Z^{\prime }$
if and only if
$Z^{\prime }$
if and only if
 $1\leqslant m_{Z^{\prime }}$
.
$1\leqslant m_{Z^{\prime }}$
.
Proof. (a) Since
![]() $C^{\prime }$
is a component of
$C^{\prime }$
is a component of
![]() $C$
and is defined by an element of
$C$
and is defined by an element of
![]() $[I_{Z^{\prime }+m_{Z^{\prime }}P}]_{m_{Z^{\prime }}+1}$
, we see
$[I_{Z^{\prime }+m_{Z^{\prime }}P}]_{m_{Z^{\prime }}+1}$
, we see
![]() $\dim [I_{Z^{\prime }+m_{Z^{\prime }}P}]_{m_{Z^{\prime }}+1}=1$
, so
$\dim [I_{Z^{\prime }+m_{Z^{\prime }}P}]_{m_{Z^{\prime }}+1}=1$
, so
![]() $C^{\prime }=C_{P}(Z^{\prime })$
. Moreover,
$C^{\prime }=C_{P}(Z^{\prime })$
. Moreover,
![]() $m_{Z^{\prime }}+t=m_{Z}$
and
$m_{Z^{\prime }}+t=m_{Z}$
and
![]() $m_{Z}+u_{Z}+2=|Z|=|Z^{\prime }|+t=m_{Z^{\prime }}+u_{Z^{\prime }}+2+t$
, so
$m_{Z}+u_{Z}+2=|Z|=|Z^{\prime }|+t=m_{Z^{\prime }}+u_{Z^{\prime }}+2+t$
, so
![]() $u_{Z^{\prime }}=u_{Z}$
. Thus we have
$u_{Z^{\prime }}=u_{Z}$
. Thus we have
![]() $m_{Z^{\prime }}+t=m_{Z}\leqslant u_{Z}=u_{Z^{\prime }}$
.
$m_{Z^{\prime }}+t=m_{Z}\leqslant u_{Z}=u_{Z^{\prime }}$
.
(b) We first show unexpectedness. If
![]() $h_{Z}(t_{Z})=|Z|$
then by Theorem 3.10 we obtain that
$h_{Z}(t_{Z})=|Z|$
then by Theorem 3.10 we obtain that
![]() $Z$
has an unexpected curve if
$Z$
has an unexpected curve if
![]() $m_{Z}<u_{Z}$
. (We did not explicitly need to use
$m_{Z}<u_{Z}$
. (We did not explicitly need to use
![]() $1\leqslant m_{Z^{\prime }}$
yet.) Thus, it remains to rule out that
$1\leqslant m_{Z^{\prime }}$
yet.) Thus, it remains to rule out that
![]() $h_{Z}(t_{Z})<|Z|$
. Indeed, if
$h_{Z}(t_{Z})<|Z|$
. Indeed, if
![]() $h_{Z}(t_{Z})<|Z|$
, then Theorem 4.3 gives
$h_{Z}(t_{Z})<|Z|$
, then Theorem 4.3 gives
![]() $m_{Z}=t_{Z}$
. By Proposition 2.10, there are two cases.
$m_{Z}=t_{Z}$
. By Proposition 2.10, there are two cases.
– In case (b)(i) we have that
 $Z$
is the complete intersection of a conic and a curve of degree
$Z$
is the complete intersection of a conic and a curve of degree
 $t_{Z}+1$
, so
$t_{Z}+1$
, so
 $|Z|=2t_{Z}+2=2m_{Z}+2$
. But then
$|Z|=2t_{Z}+2=2m_{Z}+2$
. But then
 $u_{Z}+1=|Z|-m_{Z}-1=2m_{Z}+2-m_{Z}-1=m_{Z}+1$
, contradicting our hypothesis. (We still did not explicitly need to use
$u_{Z}+1=|Z|-m_{Z}-1=2m_{Z}+2-m_{Z}-1=m_{Z}+1$
, contradicting our hypothesis. (We still did not explicitly need to use
 $1\leqslant m_{Z^{\prime }}$
.)
$1\leqslant m_{Z^{\prime }}$
.)– In case (b)(ii), there is a line through
 $|Z|-t_{Z}\geqslant t_{Z}+2$
of the points, that is, through
$|Z|-t_{Z}\geqslant t_{Z}+2$
of the points, that is, through
 $|Z|-m_{Z}\geqslant m_{Z}+2$
of the points. Thus this line is a component of any curve of degree
$|Z|-m_{Z}\geqslant m_{Z}+2$
of the points. Thus this line is a component of any curve of degree
 $m_{Z}+1$
containing
$m_{Z}+1$
containing
 $Z+m_{Z}P$
, but does not itself contain
$Z+m_{Z}P$
, but does not itself contain
 $P$
; that is, this line is
$P$
; that is, this line is
 $C^{\prime }$
, hence
$C^{\prime }$
, hence
 $m_{Z^{\prime }}=0$
, contrary to assumption.
$m_{Z^{\prime }}=0$
, contrary to assumption.
Conversely,
![]() $0<m_{Z}$
by Remark 2.3, and
$0<m_{Z}$
by Remark 2.3, and
![]() $m_{Z}<u_{Z}$
by Theorem 3.9.
$m_{Z}<u_{Z}$
by Theorem 3.9.
(c) We have
![]() $m_{Z^{\prime }}<u_{Z^{\prime }}$
by (a) and
$m_{Z^{\prime }}<u_{Z^{\prime }}$
by (a) and
![]() $C^{\prime }$
is irreducible, so
$C^{\prime }$
is irreducible, so
![]() $C^{\prime }$
is unexpected for
$C^{\prime }$
is unexpected for
![]() $Z^{\prime }$
by (b) if
$Z^{\prime }$
by (b) if
![]() $1\leqslant m_{Z^{\prime }}$
. Conversely, if
$1\leqslant m_{Z^{\prime }}$
. Conversely, if
![]() $C^{\prime }$
is unexpected for
$C^{\prime }$
is unexpected for
![]() $Z^{\prime }$
, then
$Z^{\prime }$
, then
![]() $1\leqslant m_{Z^{\prime }}$
by Remark 2.3.◻
$1\leqslant m_{Z^{\prime }}$
by Remark 2.3.◻
We can now prove Theorem 1.2.
Corollary 5.7. Let
![]() $Z\subset \mathbb{P}^{2}$
be a finite set of points. Then
$Z\subset \mathbb{P}^{2}$
be a finite set of points. Then
![]() $Z$
admits an unexpected curve if and only if
$Z$
admits an unexpected curve if and only if
![]() $2m_{Z}+2<|Z|$
but no subset of
$2m_{Z}+2<|Z|$
but no subset of
![]() $m_{Z}+2$
(or more) of the points is collinear. In this case,
$m_{Z}+2$
(or more) of the points is collinear. In this case,
![]() $Z$
has an unexpected curve of degree
$Z$
has an unexpected curve of degree
![]() $j$
if and only if
$j$
if and only if
![]() $m_{Z}<j\leqslant |Z|-m_{Z}-2$
.
$m_{Z}<j\leqslant |Z|-m_{Z}-2$
.
Proof. For convenience we set
![]() $d=|Z|$
, the number of points. Since
$d=|Z|$
, the number of points. Since
![]() $d-m_{Z}-2=u_{Z}$
by Lemma 3.5(c), the range of degrees in which unexpected curves can occur is due to Theorem 3.9. Now assume
$d-m_{Z}-2=u_{Z}$
by Lemma 3.5(c), the range of degrees in which unexpected curves can occur is due to Theorem 3.9. Now assume
![]() $Z$
admits an unexpected curve. Then it has one (call it
$Z$
admits an unexpected curve. Then it has one (call it
![]() $C$
) of degree
$C$
) of degree
![]() $m_{Z}+1$
, so by Corollary 5.6(b),
$m_{Z}+1$
, so by Corollary 5.6(b),
![]() $m_{Z}<u_{Z}$
and hence
$m_{Z}<u_{Z}$
and hence
![]() $2m_{Z}+2<d$
. However, if there were a subset of
$2m_{Z}+2<d$
. However, if there were a subset of
![]() $m_{Z}+2$
(or more) points of
$m_{Z}+2$
(or more) points of
![]() $Z$
on a line
$Z$
on a line
![]() $L$
, let
$L$
, let
![]() $Z^{\prime }$
be the points of
$Z^{\prime }$
be the points of
![]() $Z$
on
$Z$
on
![]() $L$
and let
$L$
and let
![]() $Z^{\prime \prime }$
be the rest. By Bezout’s theorem,
$Z^{\prime \prime }$
be the rest. By Bezout’s theorem,
![]() $L$
is a component of
$L$
is a component of
![]() $C_{P}(Z)$
not through
$C_{P}(Z)$
not through
![]() $P$
, so
$P$
, so
![]() $L=C_{P}(Z^{\prime })$
by Lemma 5.1. Then clearly
$L=C_{P}(Z^{\prime })$
by Lemma 5.1. Then clearly
![]() $m_{Z^{\prime }}=0$
, and
$m_{Z^{\prime }}=0$
, and
![]() $t_{Z^{\prime }}=0$
by Example 2.9, so again by Lemma 5.1 we obtain
$t_{Z^{\prime }}=0$
by Example 2.9, so again by Lemma 5.1 we obtain
![]() $|Z^{\prime \prime }|=m_{Z}$
. Furthermore,
$|Z^{\prime \prime }|=m_{Z}$
. Furthermore,
![]() $m_{Z}\leqslant t_{Z}\leqslant t_{Z^{\prime }}+|Z^{\prime \prime }|=m_{Z}$
by Corollary 2.11. Thus
$m_{Z}\leqslant t_{Z}\leqslant t_{Z^{\prime }}+|Z^{\prime \prime }|=m_{Z}$
by Corollary 2.11. Thus
![]() $m_{Z}=t_{Z}$
so
$m_{Z}=t_{Z}$
so
![]() $Z$
cannot admit an unexpected curve, by Theorem 1.1, contrary to hypothesis.
$Z$
cannot admit an unexpected curve, by Theorem 1.1, contrary to hypothesis.
Conversely, assume
![]() $2m_{Z}+2<d$
but no subset of
$2m_{Z}+2<d$
but no subset of
![]() $m_{Z}+2$
(or more) of the points is collinear. Then
$m_{Z}+2$
(or more) of the points is collinear. Then
![]() $m_{Z}<u_{Z}$
, hence
$m_{Z}<u_{Z}$
, hence
![]() $\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
by Proposition 5.2, so we can speak of
$\dim [I_{Z+m_{Z}P}]_{m_{Z}+1}=1$
by Proposition 5.2, so we can speak of
![]() $C_{P}(Z)$
. If we now show that
$C_{P}(Z)$
. If we now show that
![]() $m_{Z^{\prime }}\geqslant 1$
, then
$m_{Z^{\prime }}\geqslant 1$
, then
![]() $C_{P}(Z)$
is unexpected by Corollary 5.6 and we will be done. If
$C_{P}(Z)$
is unexpected by Corollary 5.6 and we will be done. If
![]() $m_{Z^{\prime }}=0$
, then
$m_{Z^{\prime }}=0$
, then
![]() $C_{P}(Z)$
consists of the line
$C_{P}(Z)$
consists of the line
![]() $C_{P}(Z^{\prime })$
through
$C_{P}(Z^{\prime })$
through
![]() $s\leqslant m_{Z}+1$
points of
$s\leqslant m_{Z}+1$
points of
![]() $Z$
, plus
$Z$
, plus
![]() $m_{Z}$
additional lines, one each for the remaining
$m_{Z}$
additional lines, one each for the remaining
![]() $d-s\geqslant d-m_{Z}-1>2m_{Z}+2-m_{Z}-1=m_{Z}+1$
. Thus
$d-s\geqslant d-m_{Z}-1>2m_{Z}+2-m_{Z}-1=m_{Z}+1$
. Thus
![]() $m_{Z}\geqslant d-s>m_{Z}+1$
, which contradicts
$m_{Z}\geqslant d-s>m_{Z}+1$
, which contradicts
![]() $m_{Z^{\prime }}=0$
.◻
$m_{Z^{\prime }}=0$
.◻
Remark 5.8. The hypothesis
![]() $2m_{Z}+2<|Z|$
of Corollary 5.7 is equivalent to
$2m_{Z}+2<|Z|$
of Corollary 5.7 is equivalent to
![]() $(m_{Z}+1)^{2}-m_{Z}^{2}-|Z|<-1$
. If we let
$(m_{Z}+1)^{2}-m_{Z}^{2}-|Z|<-1$
. If we let
![]() $X\rightarrow \mathbb{P}^{2}$
be the blow up of the points of
$X\rightarrow \mathbb{P}^{2}$
be the blow up of the points of
![]() $Z$
and a general point
$Z$
and a general point
![]() $P$
, then
$P$
, then
![]() $C^{2}=(m_{Z}+1)^{2}-m_{Z}^{2}-|Z|$
, where
$C^{2}=(m_{Z}+1)^{2}-m_{Z}^{2}-|Z|$
, where
![]() $C$
is the proper transform of the curve defined by an element of
$C$
is the proper transform of the curve defined by an element of
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
. Thus, for example, if
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
. Thus, for example, if
![]() $C$
is reduced and irreducible with
$C$
is reduced and irreducible with
![]() $m_{Z}>0$
, then
$m_{Z}>0$
, then
![]() $Z$
admits an unexpected curve if and only if
$Z$
admits an unexpected curve if and only if
![]() $C^{2}<-1$
. More generally, if
$C^{2}<-1$
. More generally, if
![]() $C$
has fewer than
$C$
has fewer than
![]() $m_{Z}+1$
components, then
$m_{Z}+1$
components, then
![]() $Z$
admits an unexpected curve if and only if
$Z$
admits an unexpected curve if and only if
![]() $C^{2}<-1$
.
$C^{2}<-1$
.
We summarize part of our results from Lemma 5.1 and Corollary 5.6 as follows.
Theorem 5.9. Let
![]() $Z$
be a reduced zero-dimensional subscheme of
$Z$
be a reduced zero-dimensional subscheme of
![]() $\mathbb{P}^{2}$
that admits an unexpected curve and let
$\mathbb{P}^{2}$
that admits an unexpected curve and let
![]() $P\in \mathbb{P}^{2}$
be a general point. Then there is a unique unexpected curve of degree
$P\in \mathbb{P}^{2}$
be a general point. Then there is a unique unexpected curve of degree
![]() $m_{Z}+1$
, namely
$m_{Z}+1$
, namely
![]() $C_{P}(Z)$
, and there is a unique subset
$C_{P}(Z)$
, and there is a unique subset
![]() $Z^{\prime }\subset Z$
such that
$Z^{\prime }\subset Z$
such that
![]() $C_{P}(Z)$
is the union of
$C_{P}(Z)$
is the union of
![]() $C_{P}(Z^{\prime })$
and
$C_{P}(Z^{\prime })$
and
![]() $|Z\setminus Z^{\prime }|$
lines, where
$|Z\setminus Z^{\prime }|$
lines, where
![]() $C_{P}(Z^{\prime })$
is irreducible and is the unique unexpected curve of
$C_{P}(Z^{\prime })$
is irreducible and is the unique unexpected curve of
![]() $Z^{\prime }$
of degree
$Z^{\prime }$
of degree
![]() $m_{Z^{\prime }}+1$
. Furthermore,
$m_{Z^{\prime }}+1$
. Furthermore,
![]() $C_{P}(Z^{\prime })$
is rational and smooth away from
$C_{P}(Z^{\prime })$
is rational and smooth away from
![]() $P$
.
$P$
.
Since by Remark 2.3 the degree of any unexpected curve is at least three, it follows in combination with Theorem 5.9 that every unexpected curve of a finite set
![]() $Z\subset \mathbb{P}^{2}$
has exactly one irreducible component of degree greater than
$Z\subset \mathbb{P}^{2}$
has exactly one irreducible component of degree greater than
![]() $1$
. This component is a rational curve that is an unexpected curve of the unique subset
$1$
. This component is a rational curve that is an unexpected curve of the unique subset
![]() $Z^{\prime }\subset Z$
such that
$Z^{\prime }\subset Z$
such that
![]() $m_{Z^{\prime }}=m_{Z}-(|Z|-|Z^{\prime }|)$
. There is a very natural parametrization of this curve, which works more generally for the curve
$m_{Z^{\prime }}=m_{Z}-(|Z|-|Z^{\prime }|)$
. There is a very natural parametrization of this curve, which works more generally for the curve
![]() $C_{P}(Z)$
when
$C_{P}(Z)$
when
![]() $m_{Z}\leqslant u_{Z}$
.
$m_{Z}\leqslant u_{Z}$
.
So let
![]() $Z$
be a reduced scheme of
$Z$
be a reduced scheme of
![]() $d$
points
$d$
points
![]() $P_{i}\in \mathbb{P}^{2}$
with
$P_{i}\in \mathbb{P}^{2}$
with
![]() $m_{Z}\leqslant u_{Z}$
. For each point
$m_{Z}\leqslant u_{Z}$
. For each point
![]() $P_{i}$
we have the dual line
$P_{i}$
we have the dual line
![]() $L_{i}\subset (\mathbb{P}^{2})^{\vee }$
defined by linear form
$L_{i}\subset (\mathbb{P}^{2})^{\vee }$
defined by linear form
![]() $\ell _{i}\in R=K[x,y,z]$
. Set
$\ell _{i}\in R=K[x,y,z]$
. Set
![]() $f=\ell _{1}\cdots \ell _{d}$
, and let
$f=\ell _{1}\cdots \ell _{d}$
, and let
![]() $\ell =\ell _{P}\in R$
be a general linear form, defining a line
$\ell =\ell _{P}\in R$
be a general linear form, defining a line
![]() $L\subset (\mathbb{P}^{2})^{\vee }$
that is dual to a general point
$L\subset (\mathbb{P}^{2})^{\vee }$
that is dual to a general point
![]() $P\in \mathbb{P}^{2}$
.
$P\in \mathbb{P}^{2}$
.
Proposition 5.10. Assume that the characteristic of
![]() $K$
does not divide
$K$
does not divide
![]() $|Z|$
, that
$|Z|$
, that
![]() $K$
is algebraically closed, and that
$K$
is algebraically closed, and that
![]() $Z$
satisfies
$Z$
satisfies
![]() $m_{Z}\leqslant u_{Z}$
. Consider a syzygy
$m_{Z}\leqslant u_{Z}$
. Consider a syzygy
of least degree of
![]() $\operatorname{Jac}(f)+(\ell )=(f_{x},f_{y},f_{z},\ell )$
, and a rational map
$\operatorname{Jac}(f)+(\ell )=(f_{x},f_{y},f_{z},\ell )$
, and a rational map
where
![]() $t_{0}=ys_{2}-zs_{1}$
,
$t_{0}=ys_{2}-zs_{1}$
,
![]() $t_{1}=-(xs_{2}-zs_{0})$
, and
$t_{1}=-(xs_{2}-zs_{0})$
, and
![]() $t_{2}=xs_{1}-ys_{0}$
. Then the image of the restriction of
$t_{2}=xs_{1}-ys_{0}$
. Then the image of the restriction of
![]() $\unicode[STIX]{x1D719}$
to the line
$\unicode[STIX]{x1D719}$
to the line
![]() $L$
defined by
$L$
defined by
![]() $\ell$
is the irreducible curve
$\ell$
is the irreducible curve
![]() $C_{P}(Z^{\prime })$
determined by the subset
$C_{P}(Z^{\prime })$
determined by the subset
![]() $Z^{\prime }\subset Z$
specified in Theorem 5.9.
$Z^{\prime }\subset Z$
specified in Theorem 5.9.
Proof. The assumption on the characteristic guarantees that the derivation bundle
![]() ${\mathcal{D}}_{Z}$
is isomorphic to the syzygy bundle of
${\mathcal{D}}_{Z}$
is isomorphic to the syzygy bundle of
![]() $\operatorname{Jac}(f)$
(cf. Lemma A.1), and thus each form
$\operatorname{Jac}(f)$
(cf. Lemma A.1), and thus each form
![]() $s_{i}$
has degree
$s_{i}$
has degree
![]() $m_{Z}=a_{Z}$
.
$m_{Z}=a_{Z}$
.
For a polynomial
![]() $g\in R$
, denote by
$g\in R$
, denote by
![]() $\bar{g}$
its restriction to
$\bar{g}$
its restriction to
![]() $L$
. It is a polynomial in two variables, and thus a product of linear forms since
$L$
. It is a polynomial in two variables, and thus a product of linear forms since
![]() $K$
is algebraically closed. The fact that
$K$
is algebraically closed. The fact that
![]() $\deg s_{i}=a_{Z}$
implies (by definition of
$\deg s_{i}=a_{Z}$
implies (by definition of
![]() $a_{Z}$
) that
$a_{Z}$
) that
![]() $\bar{\unicode[STIX]{x1D70E}}=(\bar{s}_{0},\bar{s}_{1},\bar{s}_{2})$
is a syzygy of minimal degree of the restriction of
$\bar{\unicode[STIX]{x1D70E}}=(\bar{s}_{0},\bar{s}_{1},\bar{s}_{2})$
is a syzygy of minimal degree of the restriction of
![]() $\operatorname{Jac}(f)$
. It follows that the ideal generated by
$\operatorname{Jac}(f)$
. It follows that the ideal generated by
![]() $\bar{s}_{0},\bar{s}_{1}$
and
$\bar{s}_{0},\bar{s}_{1}$
and
![]() $\bar{s}_{2}$
has codimension
$\bar{s}_{2}$
has codimension
![]() $2$
, that is, that these polynomials do not have a common factor. Hence, the rational map
$2$
, that is, that these polynomials do not have a common factor. Hence, the rational map
induces a morphism
![]() $\bar{\unicode[STIX]{x1D70E}}:L\rightarrow (\mathbb{P}^{2})^{\vee }$
.
$\bar{\unicode[STIX]{x1D70E}}:L\rightarrow (\mathbb{P}^{2})^{\vee }$
.
For each
![]() $i$
,
$i$
,
![]() $1\leqslant i\leqslant d$
, let
$1\leqslant i\leqslant d$
, let
![]() $Q_{i}$
be the point of intersection of
$Q_{i}$
be the point of intersection of
![]() $L$
with
$L$
with
![]() $L_{i}$
. Since
$L_{i}$
. Since
![]() $L$
is general, the
$L$
is general, the
![]() $Q_{i}$
are distinct. Note that the line
$Q_{i}$
are distinct. Note that the line
![]() $L_{Q_{i}}$
dual to
$L_{Q_{i}}$
dual to
![]() $Q_{i}$
contains
$Q_{i}$
contains
![]() $P$
and
$P$
and
![]() $P_{i}$
.
$P_{i}$
.
Put
![]() $t=(t_{0},t_{1},t_{2})$
and let
$t=(t_{0},t_{1},t_{2})$
and let
![]() $p$
be a point of
$p$
be a point of
![]() $L$
. Abusing notation, regard
$L$
. Abusing notation, regard
![]() $t$
and
$t$
and
![]() $p$
as vectors in
$p$
as vectors in
![]() $K^{3}$
; then
$K^{3}$
; then
![]() $t(p)=p\times \unicode[STIX]{x1D70E}(p)$
with
$t(p)=p\times \unicode[STIX]{x1D70E}(p)$
with
![]() $\unicode[STIX]{x1D70E}(p)\neq 0$
. Hence,
$\unicode[STIX]{x1D70E}(p)\neq 0$
. Hence,
![]() $t(p)=0$
(i.e.
$t(p)=0$
(i.e.
![]() $\unicode[STIX]{x1D719}(p)$
is undefined) if and only if
$\unicode[STIX]{x1D719}(p)$
is undefined) if and only if
![]() $\unicode[STIX]{x1D70E}(p)=p$
as points of
$\unicode[STIX]{x1D70E}(p)=p$
as points of
![]() $\mathbb{P}^{2}$
. Assume that this is the case. Then since
$\mathbb{P}^{2}$
. Assume that this is the case. Then since
![]() $\unicode[STIX]{x1D70E}$
is a syzygy modulo
$\unicode[STIX]{x1D70E}$
is a syzygy modulo
![]() $\ell$
, we have
$\ell$
, we have
![]() $0=\unicode[STIX]{x1D70E}(p)\cdot \unicode[STIX]{x1D6FB}f(p)=p\cdot \unicode[STIX]{x1D6FB}f(p)=d\cdot f(p)$
, where
$0=\unicode[STIX]{x1D70E}(p)\cdot \unicode[STIX]{x1D6FB}f(p)=p\cdot \unicode[STIX]{x1D6FB}f(p)=d\cdot f(p)$
, where
![]() $d=|Z|$
. This proves the following:
$d=|Z|$
. This proves the following:
If
![]() $p\in L$
and
$p\in L$
and
![]() $\unicode[STIX]{x1D719}(p)$
is undefined then
$\unicode[STIX]{x1D719}(p)$
is undefined then
![]() $p=L_{i}\cap L=Q_{i}$
for some
$p=L_{i}\cap L=Q_{i}$
for some
![]() $i$
.
$i$
.
Notice that it does not follow that
![]() $\unicode[STIX]{x1D719}(Q_{i})$
is undefined for all
$\unicode[STIX]{x1D719}(Q_{i})$
is undefined for all
![]() $i$
. For future reference, let
$i$
. For future reference, let
![]() $Y^{\prime \prime }=\{Q_{1},\ldots ,Q_{n}\}$
be the set of points on
$Y^{\prime \prime }=\{Q_{1},\ldots ,Q_{n}\}$
be the set of points on
![]() $L$
at which the map
$L$
at which the map
![]() $\unicode[STIX]{x1D719}$
is not defined, and let
$\unicode[STIX]{x1D719}$
is not defined, and let
![]() $Z^{\prime \prime }=\{P_{1},\ldots ,P_{n}\}$
be the corresponding subset of
$Z^{\prime \prime }=\{P_{1},\ldots ,P_{n}\}$
be the corresponding subset of
![]() $Z$
. Furthermore, set
$Z$
. Furthermore, set
![]() $Z^{\prime }=Z-Z^{\prime \prime }$
, and let
$Z^{\prime }=Z-Z^{\prime \prime }$
, and let
![]() $Y^{\prime }$
be comprised of the corresponding points
$Y^{\prime }$
be comprised of the corresponding points
![]() $Q_{i}=L\cap L_{i}$
with
$Q_{i}=L\cap L_{i}$
with
![]() $P_{i}\in Z^{\prime }$
.
$P_{i}\in Z^{\prime }$
.
It follows that
![]() $h=\bar{\ell _{1}}\cdots \bar{\ell _{n}}$
is a greatest common divisor of
$h=\bar{\ell _{1}}\cdots \bar{\ell _{n}}$
is a greatest common divisor of
![]() $\bar{t_{0}}$
,
$\bar{t_{0}}$
,
![]() $\bar{t_{1}}$
, and
$\bar{t_{1}}$
, and
![]() $\bar{t_{2}}$
and that the map
$\bar{t_{2}}$
and that the map
![]() $\unicode[STIX]{x1D719}^{\prime }:L\rightarrow \mathbb{P}^{2}$
defined by
$\unicode[STIX]{x1D719}^{\prime }:L\rightarrow \mathbb{P}^{2}$
defined by
![]() $(\bar{t_{0}}/h:\bar{t_{1}}/h:\bar{t_{2}}/h)$
is a morphism. Let
$(\bar{t_{0}}/h:\bar{t_{1}}/h:\bar{t_{2}}/h)$
is a morphism. Let
![]() $\unicode[STIX]{x1D6FF}=\deg (\unicode[STIX]{x1D719}^{\prime })$
be the degree of the mapping (i.e. the degree of the inverse image of
$\unicode[STIX]{x1D6FF}=\deg (\unicode[STIX]{x1D719}^{\prime })$
be the degree of the mapping (i.e. the degree of the inverse image of
![]() $\unicode[STIX]{x1D719}^{\prime }(p)$
for a general
$\unicode[STIX]{x1D719}^{\prime }(p)$
for a general
![]() $p\in L$
). Then
$p\in L$
). Then
![]() $\unicode[STIX]{x1D719}^{\prime }(L)$
is an irreducible curve
$\unicode[STIX]{x1D719}^{\prime }(L)$
is an irreducible curve
![]() $C^{\prime }$
of degree
$C^{\prime }$
of degree
![]() $(m_{Z}+1-n)/\unicode[STIX]{x1D6FF}$
that is equal to the Zariski closure of
$(m_{Z}+1-n)/\unicode[STIX]{x1D6FF}$
that is equal to the Zariski closure of
![]() $\unicode[STIX]{x1D719}(L)$
.
$\unicode[STIX]{x1D719}(L)$
.
Next we show that
![]() $\unicode[STIX]{x1D70E}(Q_{i})$
is on the line
$\unicode[STIX]{x1D70E}(Q_{i})$
is on the line
![]() $L_{i}$
for each
$L_{i}$
for each
![]() $Q_{i}\in Y=Y^{\prime }+Y^{\prime \prime }$
. Indeed, since
$Q_{i}\in Y=Y^{\prime }+Y^{\prime \prime }$
. Indeed, since
![]() $Q_{i}$
is on
$Q_{i}$
is on
![]() $L$
, the above syzygy gives
$L$
, the above syzygy gives
![]() $\unicode[STIX]{x1D70E}(Q_{i})\cdot \unicode[STIX]{x1D6FB}f(Q_{i})=0$
. Now write
$\unicode[STIX]{x1D70E}(Q_{i})\cdot \unicode[STIX]{x1D6FB}f(Q_{i})=0$
. Now write
![]() $f=\ell _{i}g$
. Since
$f=\ell _{i}g$
. Since
![]() $\unicode[STIX]{x1D6FB}\ell _{i}=P_{i}$
, the Leibniz rule gives
$\unicode[STIX]{x1D6FB}\ell _{i}=P_{i}$
, the Leibniz rule gives
![]() $\unicode[STIX]{x1D6FB}f=gP_{i}+\ell _{i}\unicode[STIX]{x1D6FB}g$
. As
$\unicode[STIX]{x1D6FB}f=gP_{i}+\ell _{i}\unicode[STIX]{x1D6FB}g$
. As
![]() $Q_{i}$
is on
$Q_{i}$
is on
![]() $L_{i}$
, we get
$L_{i}$
, we get
![]() $\unicode[STIX]{x1D6FB}f(Q_{i})=g(Q_{i})P_{i}$
. Since
$\unicode[STIX]{x1D6FB}f(Q_{i})=g(Q_{i})P_{i}$
. Since
![]() $g(Q_{i})\neq 0$
, from
$g(Q_{i})\neq 0$
, from
![]() $0=\unicode[STIX]{x1D70E}(Q_{i})\cdot \unicode[STIX]{x1D6FB}f(Q_{i})=g(Q_{i})\unicode[STIX]{x1D70E}(Q_{i})\cdot P_{i}$
we conclude
$0=\unicode[STIX]{x1D70E}(Q_{i})\cdot \unicode[STIX]{x1D6FB}f(Q_{i})=g(Q_{i})\unicode[STIX]{x1D70E}(Q_{i})\cdot P_{i}$
we conclude
![]() $\unicode[STIX]{x1D70E}(Q_{i})\cdot P_{i}=0$
, hence
$\unicode[STIX]{x1D70E}(Q_{i})\cdot P_{i}=0$
, hence
![]() $\unicode[STIX]{x1D70E}(Q_{i})\in L_{i}$
, as desired.
$\unicode[STIX]{x1D70E}(Q_{i})\in L_{i}$
, as desired.
Notice that if
![]() $Q\in L\backslash Y^{\prime \prime }$
(so
$Q\in L\backslash Y^{\prime \prime }$
(so
![]() $\unicode[STIX]{x1D70E}(Q)\neq Q$
) then
$\unicode[STIX]{x1D70E}(Q)\neq Q$
) then
![]() $(t_{0},t_{1},t_{2})$
are the coordinates of the point dual to the line through the points
$(t_{0},t_{1},t_{2})$
are the coordinates of the point dual to the line through the points
![]() $Q$
and
$Q$
and
![]() $\unicode[STIX]{x1D70E}(Q)$
. Hence
$\unicode[STIX]{x1D70E}(Q)$
. Hence
![]() $\unicode[STIX]{x1D719}^{\prime }$
is a morphism that maps a point
$\unicode[STIX]{x1D719}^{\prime }$
is a morphism that maps a point
![]() $Q\in L\backslash Y^{\prime \prime }$
to the point that is dual to the line through the points
$Q\in L\backslash Y^{\prime \prime }$
to the point that is dual to the line through the points
![]() $Q$
and
$Q$
and
![]() $\unicode[STIX]{x1D70E}(Q)$
. In particular, if
$\unicode[STIX]{x1D70E}(Q)$
. In particular, if
![]() $Q_{i}\in Y^{\prime }$
, then
$Q_{i}\in Y^{\prime }$
, then
![]() $L_{i}$
is the line through
$L_{i}$
is the line through
![]() $Q_{i}$
and
$Q_{i}$
and
![]() $\unicode[STIX]{x1D70E}(Q_{i})$
, and hence
$\unicode[STIX]{x1D70E}(Q_{i})$
, and hence
![]() $\unicode[STIX]{x1D719}^{\prime }(Q_{i})=P_{i}$
. Thus, we see that the curve
$\unicode[STIX]{x1D719}^{\prime }(Q_{i})=P_{i}$
. Thus, we see that the curve
![]() $C^{\prime }$
contains
$C^{\prime }$
contains
![]() $Z^{\prime }$
.
$Z^{\prime }$
.
Now we compute the multiplicity of
![]() $C^{\prime }$
at
$C^{\prime }$
at
![]() $P$
. We have seen that for
$P$
. We have seen that for
![]() $p\in L$
,
$p\in L$
,
![]() $\unicode[STIX]{x1D719}(p)$
is undefined if and only if
$\unicode[STIX]{x1D719}(p)$
is undefined if and only if
![]() $\bar{\unicode[STIX]{x1D70E}}(p)=p$
, and there are
$\bar{\unicode[STIX]{x1D70E}}(p)=p$
, and there are
![]() $n$
such points, namely the set
$n$
such points, namely the set
![]() $Y^{\prime \prime }$
. We have also seen that for
$Y^{\prime \prime }$
. We have also seen that for
![]() $p\in L\backslash Y^{\prime \prime }$
,
$p\in L\backslash Y^{\prime \prime }$
,
![]() $\unicode[STIX]{x1D719}^{\prime }$
maps
$\unicode[STIX]{x1D719}^{\prime }$
maps
![]() $p$
to the point dual to the line through
$p$
to the point dual to the line through
![]() $p$
and
$p$
and
![]() $\bar{\unicode[STIX]{x1D70E}}(p)$
. Thus the points of
$\bar{\unicode[STIX]{x1D70E}}(p)$
. Thus the points of
![]() $L$
mapping to
$L$
mapping to
![]() $P$
include all points of
$P$
include all points of
![]() $(L\cap \unicode[STIX]{x1D70E}(L))\backslash Y^{\prime \prime }$
. Since each
$(L\cap \unicode[STIX]{x1D70E}(L))\backslash Y^{\prime \prime }$
. Since each
![]() $s_{i}$
has degree
$s_{i}$
has degree
![]() $m_{Z}$
,
$m_{Z}$
,
![]() $D=\unicode[STIX]{x1D70E}(L)\cap L$
is a divisor of degree
$D=\unicode[STIX]{x1D70E}(L)\cap L$
is a divisor of degree
![]() $m_{Z}$
. Therefore, the multiplicity of
$m_{Z}$
. Therefore, the multiplicity of
![]() $C^{\prime }$
at
$C^{\prime }$
at
![]() $P$
is at least
$P$
is at least
![]() $(m_{Z}-n)/\unicode[STIX]{x1D6FF}$
. Let
$(m_{Z}-n)/\unicode[STIX]{x1D6FF}$
. Let
![]() $\unicode[STIX]{x1D716}+(m_{Z}-n)/\unicode[STIX]{x1D6FF}$
be the multiplicity of
$\unicode[STIX]{x1D716}+(m_{Z}-n)/\unicode[STIX]{x1D6FF}$
be the multiplicity of
![]() $C^{\prime }$
at
$C^{\prime }$
at
![]() $P$
. Thus
$P$
. Thus
![]() $\unicode[STIX]{x1D716}+(m_{Z}-n)/\unicode[STIX]{x1D6FF}<\deg (C^{\prime })=(m_{Z}-n+1)/\unicode[STIX]{x1D6FF}$
, so
$\unicode[STIX]{x1D716}+(m_{Z}-n)/\unicode[STIX]{x1D6FF}<\deg (C^{\prime })=(m_{Z}-n+1)/\unicode[STIX]{x1D6FF}$
, so
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}+m_{Z}-n\leqslant m_{Z}-n+1$
. Since
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}+m_{Z}-n\leqslant m_{Z}-n+1$
. Since
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}$
is a non-negative integer, we must have
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}$
is a non-negative integer, we must have
![]() $\unicode[STIX]{x1D716}=0$
, hence
$\unicode[STIX]{x1D716}=0$
, hence
![]() $(m_{Z}-n)/\unicode[STIX]{x1D6FF}$
and
$(m_{Z}-n)/\unicode[STIX]{x1D6FF}$
and
![]() $(m_{Z}-n+1)/\unicode[STIX]{x1D6FF}$
are integers so
$(m_{Z}-n+1)/\unicode[STIX]{x1D6FF}$
are integers so
![]() $\unicode[STIX]{x1D6FF}=1$
. Thus
$\unicode[STIX]{x1D6FF}=1$
. Thus
![]() $\deg (C^{\prime })=m_{Z}-n+1$
and
$\deg (C^{\prime })=m_{Z}-n+1$
and
![]() $C^{\prime }$
has multiplicity
$C^{\prime }$
has multiplicity
![]() $m_{Z}-n$
at
$m_{Z}-n$
at
![]() $P$
.
$P$
.
We now have that
![]() $C^{\prime }\cup (\bigcup _{j=1}^{n}L_{Q_{i_{j}}})$
has degree
$C^{\prime }\cup (\bigcup _{j=1}^{n}L_{Q_{i_{j}}})$
has degree
![]() $m_{Z}+1$
, contains
$m_{Z}+1$
, contains
![]() $Z$
and has
$Z$
and has
![]() $P$
as a point of multiplicity
$P$
as a point of multiplicity
![]() $m_{Z}$
. Thus,
$m_{Z}$
. Thus,
![]() $C^{\prime }\cup (\bigcup _{j=1}^{n}L_{Q_{i_{j}}})$
is the unique curve
$C^{\prime }\cup (\bigcup _{j=1}^{n}L_{Q_{i_{j}}})$
is the unique curve
![]() $C_{P}(Z)$
with these properties, and
$C_{P}(Z)$
with these properties, and
![]() $C^{\prime }=C_{P}(Z^{\prime })$
by Corollary 5.6.◻
$C^{\prime }=C_{P}(Z^{\prime })$
by Corollary 5.6.◻
In the proof of the result above, if none of the
![]() $\bar{\ell _{i}}$
is a common factor for
$\bar{\ell _{i}}$
is a common factor for
![]() $\bar{t_{0}},\bar{t_{1}}$
and
$\bar{t_{0}},\bar{t_{1}}$
and
![]() $\bar{t_{2}}$
, then
$\bar{t_{2}}$
, then
![]() $n=0$
so
$n=0$
so
![]() $\deg (C_{P}(Z^{\prime }))=m_{Z}+1=\deg (C_{P}(Z))$
, hence
$\deg (C_{P}(Z^{\prime }))=m_{Z}+1=\deg (C_{P}(Z))$
, hence
![]() $C_{P}(Z^{\prime })=C_{P}(Z)$
is irreducible. If, in the above result,
$C_{P}(Z^{\prime })=C_{P}(Z)$
is irreducible. If, in the above result,
![]() $\unicode[STIX]{x1D70E}$
is a global syzygy (i.e.
$\unicode[STIX]{x1D70E}$
is a global syzygy (i.e.
![]() $s_{3}=0$
), then
$s_{3}=0$
), then
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\ell$
become independent of each other, and a minor modification of the argument above then gives us the following criterion for irreducibility. The advantage here is not having to work modulo a general linear form
$\ell$
become independent of each other, and a minor modification of the argument above then gives us the following criterion for irreducibility. The advantage here is not having to work modulo a general linear form
![]() $\ell$
, which can be a computational convenience when testing irreducibility explicitly.
$\ell$
, which can be a computational convenience when testing irreducibility explicitly.
Proposition 5.11. Assume that the characteristic of
![]() $K$
does not divide
$K$
does not divide
![]() $|Z|$
, that
$|Z|$
, that
![]() $K$
is algebraically closed, and that
$K$
is algebraically closed, and that
![]() $Z$
satisfies
$Z$
satisfies
![]() $m_{Z}\leqslant u_{Z}$
. Suppose further that
$m_{Z}\leqslant u_{Z}$
. Suppose further that
![]() $\operatorname{Jac}(f)$
has a syzygy
$\operatorname{Jac}(f)$
has a syzygy
![]() $s_{0}f_{x}+s_{1}f_{y}+s_{2}f_{z}=0$
, where each
$s_{0}f_{x}+s_{1}f_{y}+s_{2}f_{z}=0$
, where each
![]() $s_{i}$
has degree
$s_{i}$
has degree
![]() $m_{Z}$
. If none of the forms
$m_{Z}$
. If none of the forms
![]() $\ell _{i}$
is a common divisor of
$\ell _{i}$
is a common divisor of
![]() $t_{0}=ys_{2}-zs_{1}$
,
$t_{0}=ys_{2}-zs_{1}$
,
![]() $t_{1}=-(xs_{2}-zs_{0})$
, and
$t_{1}=-(xs_{2}-zs_{0})$
, and
![]() $t_{2}=xs_{1}-ys_{0}$
, then the curve
$t_{2}=xs_{1}-ys_{0}$
, then the curve
![]() $C_{P}(Z)$
is irreducible.
$C_{P}(Z)$
is irreducible.
Remark 5.12. Given the parametrization
![]() $\unicode[STIX]{x1D719}$
in Proposition 5.10, keeping in mind that
$\unicode[STIX]{x1D719}$
in Proposition 5.10, keeping in mind that
![]() $\bar{\unicode[STIX]{x1D70E}}\cdot \overline{\unicode[STIX]{x1D6FB}f}=0$
, we can recover
$\bar{\unicode[STIX]{x1D70E}}\cdot \overline{\unicode[STIX]{x1D6FB}f}=0$
, we can recover
![]() $\bar{\unicode[STIX]{x1D70E}}$
using facts about triple vector products. Working formally, the first component of
$\bar{\unicode[STIX]{x1D70E}}$
using facts about triple vector products. Working formally, the first component of
![]() $(p\times \unicode[STIX]{x1D70E}(p))\times \unicode[STIX]{x1D6FB}f$
is
$(p\times \unicode[STIX]{x1D70E}(p))\times \unicode[STIX]{x1D6FB}f$
is
But
![]() $x(f_{y}s_{1}+f_{z}s_{2})=-xf_{x}s_{0}$
modulo
$x(f_{y}s_{1}+f_{z}s_{2})=-xf_{x}s_{0}$
modulo
![]() $\ell$
, so the first component modulo
$\ell$
, so the first component modulo
![]() $\ell$
is
$\ell$
is
![]() $-s_{0}(xf_{x}+yf_{y}+zf_{z})=-\text{deg}(f)fs_{0}$
. In the same way the second and third components are
$-s_{0}(xf_{x}+yf_{y}+zf_{z})=-\text{deg}(f)fs_{0}$
. In the same way the second and third components are
![]() $-\text{deg}(f)fs_{1}$
and
$-\text{deg}(f)fs_{1}$
and
![]() $-\text{deg}(f)fs_{2}$
. Thus, for all
$-\text{deg}(f)fs_{2}$
. Thus, for all
![]() $p\in L$
, we have
$p\in L$
, we have
that is,
![]() $\unicode[STIX]{x1D719}^{\prime }\times \overline{\unicode[STIX]{x1D6FB}f}=-\text{deg}(f)(\bar{f}/h)\bar{\unicode[STIX]{x1D70E}}$
, where
$\unicode[STIX]{x1D719}^{\prime }\times \overline{\unicode[STIX]{x1D6FB}f}=-\text{deg}(f)(\bar{f}/h)\bar{\unicode[STIX]{x1D70E}}$
, where
![]() $h$
is a greatest common divisor of
$h$
is a greatest common divisor of
![]() $\bar{t_{0}}$
,
$\bar{t_{0}}$
,
![]() $\bar{t_{1}}$
, and
$\bar{t_{1}}$
, and
![]() $\bar{t_{2}}$
.
$\bar{t_{2}}$
.
Similarly, in Proposition 5.11 we have
![]() $\unicode[STIX]{x1D719}\times \unicode[STIX]{x1D6FB}f=-\text{deg}(f)(f/h)\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D719}\times \unicode[STIX]{x1D6FB}f=-\text{deg}(f)(f/h)\unicode[STIX]{x1D70E}$
.
We now consider the change in the multiplicity index if one adds a point to a given set of points.
Lemma 5.13. Let
![]() $P_{1},\ldots ,P_{s},Q$
be distinct points of
$P_{1},\ldots ,P_{s},Q$
be distinct points of
![]() $\mathbb{P}^{2}$
and let
$\mathbb{P}^{2}$
and let
![]() $Z=P_{1}+\cdots +P_{s}$
. Then
$Z=P_{1}+\cdots +P_{s}$
. Then
![]() $m_{Z+Q}=m_{Z}$
if either
$m_{Z+Q}=m_{Z}$
if either
![]() $u_{Z}=m_{Z}-1$
or
$u_{Z}=m_{Z}-1$
or
![]() $Q\in \bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
. Otherwise
$Q\in \bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
. Otherwise
![]() $m_{Z+Q}=m_{Z}+1$
.
$m_{Z+Q}=m_{Z}+1$
.
Proof. Note that
![]() $\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}>1$
if and only if
$\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}>1$
if and only if
![]() $u_{Z}=m_{Z}-1$
. For each integer
$u_{Z}=m_{Z}-1$
. For each integer
![]() $j\geqslant 0$
, one has
$j\geqslant 0$
, one has
![]() $I_{Z+Q}\cap I_{P}^{j}\subset I_{Z}\cap I_{P}^{j}$
, hence
$I_{Z+Q}\cap I_{P}^{j}\subset I_{Z}\cap I_{P}^{j}$
, hence
![]() $m_{Z+Q,P}\geqslant m_{Z}$
. If
$m_{Z+Q,P}\geqslant m_{Z}$
. If
![]() $Q$
lies on
$Q$
lies on
![]() $C_{P}$
for all
$C_{P}$
for all
![]() $P$
then
$P$
then
![]() $\dim [I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}=\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}\geqslant 1$
, so
$\dim [I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}=\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}\geqslant 1$
, so
![]() $m_{Z+Q,P}=m_{Z}$
. If
$m_{Z+Q,P}=m_{Z}$
. If
![]() $\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}>1$
, then, since
$\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}>1$
, then, since
![]() $\dim _{K}[I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}$
drops by at most 1, we have
$\dim _{K}[I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}$
drops by at most 1, we have
![]() $\dim [I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}\geqslant 1$
, and again
$\dim [I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}\geqslant 1$
, and again
![]() $m_{Z+Q,P}=m_{Z}$
. If
$m_{Z+Q,P}=m_{Z}$
. If
![]() $Q$
does not lie on
$Q$
does not lie on
![]() $C_{P}$
for some (hence for general)
$C_{P}$
for some (hence for general)
![]() $P$
then the dimension drops by exactly
$P$
then the dimension drops by exactly
![]() $1$
, so if also
$1$
, so if also
![]() $\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}=1$
we get
$\dim _{K}[I_{Z}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}=1$
we get
![]() $\dim [I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}=0$
, hence
$\dim [I_{Z+Q}\cap I_{P}^{m_{Z}}]_{m_{Z}+1}=0$
, hence
![]() $m_{Z+Q,P}\geqslant m_{Z}+1$
. But let
$m_{Z+Q,P}\geqslant m_{Z}+1$
. But let
![]() $f\neq 0$
be a form of degree
$f\neq 0$
be a form of degree
![]() $m_{Z}+1$
in
$m_{Z}+1$
in
![]() $I_{Z}\cap I_{P}^{m_{Z}}$
. Let
$I_{Z}\cap I_{P}^{m_{Z}}$
. Let
![]() $\ell$
be a linear form that defines the line through
$\ell$
be a linear form that defines the line through
![]() $P$
and
$P$
and
![]() $Q$
. Then
$Q$
. Then
![]() $\ell f\neq 0$
is in
$\ell f\neq 0$
is in
![]() $[I_{Z+Q}\cap I_{P}^{m_{Z}+1}]_{m_{Z}+2}$
, which shows
$[I_{Z+Q}\cap I_{P}^{m_{Z}+1}]_{m_{Z}+2}$
, which shows
![]() $m_{Z+Q,P}\leqslant m_{Z}+1$
.◻
$m_{Z+Q,P}\leqslant m_{Z}+1$
.◻
See Example 6.1 for an illustration of how
![]() $Q$
can lie on all the curves
$Q$
can lie on all the curves
![]() $C_{P}(Z)$
.
$C_{P}(Z)$
.
Thus, given
![]() $m_{Z}$
, there are only two possible values of
$m_{Z}$
, there are only two possible values of
![]() $m_{Z+Q}$
. When the number of points of
$m_{Z+Q}$
. When the number of points of
![]() $Z$
is odd and
$Z$
is odd and
![]() $m_{Z}$
is as large as possible, we can say which of these values occurs for an arbitrary point
$m_{Z}$
is as large as possible, we can say which of these values occurs for an arbitrary point
![]() $Q$
.
$Q$
.
Corollary 5.14. Let
![]() $Z$
be a finite reduced subscheme of
$Z$
be a finite reduced subscheme of
![]() $\mathbb{P}^{2}$
. If
$\mathbb{P}^{2}$
. If
![]() $m_{Z}=(|Z|-1)/2$
, then
$m_{Z}=(|Z|-1)/2$
, then
![]() $m_{Z+Q}=m_{Z}$
for any point
$m_{Z+Q}=m_{Z}$
for any point
![]() $Q$
not in
$Q$
not in
![]() $Z$
.
$Z$
.
Proof. If
![]() $m_{Z}=(|Z|-1)/2$
, then
$m_{Z}=(|Z|-1)/2$
, then
![]() $|Z|=2m_{Z}+1$
, so
$|Z|=2m_{Z}+1$
, so
![]() $u_{Z}=|Z|-2-m_{Z}=m_{Z}-1$
. Now the result follows by Lemma 5.13.◻
$u_{Z}=|Z|-2-m_{Z}=m_{Z}-1$
. Now the result follows by Lemma 5.13.◻
If
![]() $m_{Z}<(|Z|-1)/2$
and
$m_{Z}<(|Z|-1)/2$
and
![]() $Q$
is a general point, we now find the value of
$Q$
is a general point, we now find the value of
![]() $m_{Z+Q}$
.
$m_{Z+Q}$
.
Corollary 5.15. Let
![]() $Z$
be a finite reduced subscheme of
$Z$
be a finite reduced subscheme of
![]() $\mathbb{P}^{2}$
and let
$\mathbb{P}^{2}$
and let
![]() $Q$
be a general point. If
$Q$
be a general point. If
![]() $m_{Z}<(|Z|-1)/2$
, then
$m_{Z}<(|Z|-1)/2$
, then
![]() $m_{Z+Q}=m_{Z}+1$
.
$m_{Z+Q}=m_{Z}+1$
.
Proof. If
![]() $m_{Z}<(|Z|-1)/2$
, then
$m_{Z}<(|Z|-1)/2$
, then
![]() $|Z|>2m_{Z}+1$
, so
$|Z|>2m_{Z}+1$
, so
![]() $u_{Z}=|Z|-2-m_{Z}>m_{Z}-1$
. Moreover,
$u_{Z}=|Z|-2-m_{Z}>m_{Z}-1$
. Moreover,
![]() $\bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
is a finite set. Hence the result follows from Lemma 5.13.◻
$\bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
is a finite set. Hence the result follows from Lemma 5.13.◻
Remark 5.16. We can describe more precisely how unexpected curves arise. Assume a reduced point scheme
![]() $Z$
has an unexpected curve
$Z$
has an unexpected curve
![]() $C$
of some degree
$C$
of some degree
![]() $t$
. By Theorem 3.9 and Proposition 5.2,
$t$
. By Theorem 3.9 and Proposition 5.2,
![]() $m_{Z}<t\leqslant u_{Z}$
and
$m_{Z}<t\leqslant u_{Z}$
and
![]() $C$
is the union of
$C$
is the union of
![]() $C_{P}(Z)$
with
$C_{P}(Z)$
with
![]() $t-m_{Z}-1$
lines though
$t-m_{Z}-1$
lines though
![]() $P$
(indeed, the linear system of curves corresponding to
$P$
(indeed, the linear system of curves corresponding to
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
is the union of
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
is the union of
![]() $C_{P}(Z)$
with all choices of
$C_{P}(Z)$
with all choices of
![]() $t-m_{Z}-1$
lines though
$t-m_{Z}-1$
lines though
![]() $P$
, and so they are all unexpected). Moreover, by Lemma 5.1 and Corollary 5.6, there is a unique subset
$P$
, and so they are all unexpected). Moreover, by Lemma 5.1 and Corollary 5.6, there is a unique subset
![]() $Z^{\prime }\subseteq Z$
such that
$Z^{\prime }\subseteq Z$
such that
![]() $C_{P}(Z^{\prime })$
is irreducible and unexpected for
$C_{P}(Z^{\prime })$
is irreducible and unexpected for
![]() $Z^{\prime }$
; it has degree
$Z^{\prime }$
; it has degree
![]() $m_{Z^{\prime }}+1=m_{Z}+1-(|Z|-|Z^{\prime }|)$
and we have that
$m_{Z^{\prime }}+1=m_{Z}+1-(|Z|-|Z^{\prime }|)$
and we have that
![]() $C_{P}(Z)$
is the union of
$C_{P}(Z)$
is the union of
![]() $C_{P}(Z^{\prime })$
with the lines through
$C_{P}(Z^{\prime })$
with the lines through
![]() $P$
and the
$P$
and the
![]() $|Z|-|Z^{\prime }|$
points of
$|Z|-|Z^{\prime }|$
points of
![]() $Z$
not in
$Z$
not in
![]() $Z^{\prime }$
.
$Z^{\prime }$
.
Thus every
![]() $Z$
with an unexpected curve
$Z$
with an unexpected curve
![]() $C$
comes from a
$C$
comes from a
![]() $Z^{\prime }$
with an irreducible unexpected curve, and
$Z^{\prime }$
with an irreducible unexpected curve, and
![]() $Z=Z^{\prime }+Q_{1}+\cdots +Q_{r}$
for some set of
$Z=Z^{\prime }+Q_{1}+\cdots +Q_{r}$
for some set of
![]() $r$
distinct points
$r$
distinct points
![]() $Q_{i}$
not in
$Q_{i}$
not in
![]() $Z^{\prime }$
. Since
$Z^{\prime }$
. Since
![]() $m_{Z}<u_{Z}$
,
$m_{Z}<u_{Z}$
,
![]() $m_{Z^{\prime }}+r=m_{Z}$
and
$m_{Z^{\prime }}+r=m_{Z}$
and
![]() $m_{Z}+u_{Z}+2=|Z|=|Z^{\prime }|+r=m_{Z^{\prime }}+u_{Z^{\prime }}+2+r$
, we see that
$m_{Z}+u_{Z}+2=|Z|=|Z^{\prime }|+r=m_{Z^{\prime }}+u_{Z^{\prime }}+2+r$
, we see that
![]() $m_{Z^{\prime }}+r=m_{Z}<u_{Z}=u_{Z^{\prime }}$
, so
$m_{Z^{\prime }}+r=m_{Z}<u_{Z}=u_{Z^{\prime }}$
, so
![]() $r\leqslant u_{Z^{\prime }}-(m_{Z^{\prime }}+1)$
.
$r\leqslant u_{Z^{\prime }}-(m_{Z^{\prime }}+1)$
.
In fact, if
![]() $Z$
has an unexpected curve, then
$Z$
has an unexpected curve, then
![]() $Z+Q_{1}+\cdots +Q_{i}$
also has an unexpected curve for any distinct points
$Z+Q_{1}+\cdots +Q_{i}$
also has an unexpected curve for any distinct points
![]() $Q_{i}$
not in
$Q_{i}$
not in
![]() $Z$
, for any
$Z$
, for any
![]() $0\leqslant i\leqslant u_{Z}-(m_{Z}+1)$
. To see this, assume
$0\leqslant i\leqslant u_{Z}-(m_{Z}+1)$
. To see this, assume
![]() $u_{Z}>m_{Z}+1$
and let
$u_{Z}>m_{Z}+1$
and let
![]() $Y=Z+Q$
for any point
$Y=Z+Q$
for any point
![]() $Q\not \in Z$
. By induction it is enough to show
$Q\not \in Z$
. By induction it is enough to show
![]() $Y$
has an unexpected curve and that
$Y$
has an unexpected curve and that
![]() $u_{Y}-m_{Y}\geqslant u_{Z}-m_{Z}-1$
. But
$u_{Y}-m_{Y}\geqslant u_{Z}-m_{Z}-1$
. But
![]() $m_{Z}\leqslant m_{Y}\leqslant m_{Z}+1$
by Lemma 5.13, so
$m_{Z}\leqslant m_{Y}\leqslant m_{Z}+1$
by Lemma 5.13, so
![]() $u_{Y}\geqslant u_{Z}$
(since
$u_{Y}\geqslant u_{Z}$
(since
![]() $m_{Z}+u_{Z}+2=|Z|$
and
$m_{Z}+u_{Z}+2=|Z|$
and
![]() $m_{Y}+u_{Y}+2=|Y|=|Z|+1$
), hence
$m_{Y}+u_{Y}+2=|Y|=|Z|+1$
), hence
![]() $u_{Y}-m_{Y}\geqslant u_{Z}-m_{Z}-1$
.
$u_{Y}-m_{Y}\geqslant u_{Z}-m_{Z}-1$
.
Assume that
![]() $Y$
does not have an unexpected curve. Then Theorem 3.9 gives
$Y$
does not have an unexpected curve. Then Theorem 3.9 gives
![]() $m_{Y}\geqslant t_{Y}$
, and Corollary 5.7 shows that at least
$m_{Y}\geqslant t_{Y}$
, and Corollary 5.7 shows that at least
![]() $m_{Y}+2$
points of
$m_{Y}+2$
points of
![]() $Y$
are on a line
$Y$
are on a line
![]() $L$
. Hence
$L$
. Hence
![]() $L$
contains at least
$L$
contains at least
![]() $m_{Y}+1$
points of
$m_{Y}+1$
points of
![]() $Z$
. If
$Z$
. If
![]() $m_{Y}>m_{Z}$
, then at least
$m_{Y}>m_{Z}$
, then at least
![]() $m_{Z}+2$
points of
$m_{Z}+2$
points of
![]() $Z$
are collinear, which contradicts the assumption that
$Z$
are collinear, which contradicts the assumption that
![]() $Z$
has an unexpected curve, using again Corollary 5.7. We conclude that
$Z$
has an unexpected curve, using again Corollary 5.7. We conclude that
![]() $m_{Y}=m_{Z}$
. Now Theorem 3.9 and Corollary 2.11 yield
$m_{Y}=m_{Z}$
. Now Theorem 3.9 and Corollary 2.11 yield
![]() $m_{Y}=m_{Z}<t_{Z}\leqslant t_{Y}$
, in contradiction to
$m_{Y}=m_{Z}<t_{Z}\leqslant t_{Y}$
, in contradiction to
![]() $m_{Y}\geqslant t_{Y}$
. Hence,
$m_{Y}\geqslant t_{Y}$
. Hence,
![]() $Y$
has an unexpected curve, as claimed.
$Y$
has an unexpected curve, as claimed.
We will observe on more than one occasion below that it is of interest to know when
![]() $Z$
admits an irreducible unexpected curve of minimal degree
$Z$
admits an irreducible unexpected curve of minimal degree
![]() $m_{Z}+1$
. This motivates the next result.
$m_{Z}+1$
. This motivates the next result.
Corollary 5.17. Assume that
![]() $Z$
is a finite set of points in
$Z$
is a finite set of points in
![]() $\mathbb{P}^{2}$
and let
$\mathbb{P}^{2}$
and let
![]() $P\in \mathbb{P}^{2}$
be a general point. Then every non-zero form in
$P\in \mathbb{P}^{2}$
be a general point. Then every non-zero form in
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
is irreducible if and only if
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
is irreducible if and only if
![]() $m_{Z-Q}=m_{Z}$
for each point
$m_{Z-Q}=m_{Z}$
for each point
![]() $Q\in Z$
.
$Q\in Z$
.
Proof. Assume
![]() $m_{Z-Q}=m_{Z}$
for all
$m_{Z-Q}=m_{Z}$
for all
![]() $Q\in Z$
. Let
$Q\in Z$
. Let
![]() $C$
be a curve of degree
$C$
be a curve of degree
![]() $m_{Z}+1$
containing
$m_{Z}+1$
containing
![]() $Z$
and having multiplicity
$Z$
and having multiplicity
![]() $m_{Z}$
at the general point
$m_{Z}$
at the general point
![]() $P$
. By Lemma 5.1, if
$P$
. By Lemma 5.1, if
![]() $C$
is not irreducible then there is at least one component of
$C$
is not irreducible then there is at least one component of
![]() $C$
consisting of a line joining
$C$
consisting of a line joining
![]() $P$
and a point
$P$
and a point
![]() $Q\in Z$
. Removing this point and this line shows that
$Q\in Z$
. Removing this point and this line shows that
![]() $m_{Z-Q}<m_{Z}$
, giving a contradiction.
$m_{Z-Q}<m_{Z}$
, giving a contradiction.
Now assume
![]() $m_{Z-Q}\neq m_{Z}$
for some
$m_{Z-Q}\neq m_{Z}$
for some
![]() $Q$
(hence
$Q$
(hence
![]() $m_{Z-Q}=m_{Z}-1$
by Lemma 5.13), let
$m_{Z-Q}=m_{Z}-1$
by Lemma 5.13), let
![]() $0\neq F\in [I_{Z-Q+(m_{Z}-1)P}]_{m_{Z}}$
and let
$0\neq F\in [I_{Z-Q+(m_{Z}-1)P}]_{m_{Z}}$
and let
![]() $\ell$
be the linear form defining the line joining
$\ell$
be the linear form defining the line joining
![]() $Q$
to
$Q$
to
![]() $P$
. Then
$P$
. Then
![]() $\ell F\in [I_{Z+m_{Z}P}]_{m_{Z}+1}$
is not irreducible.◻
$\ell F\in [I_{Z+m_{Z}P}]_{m_{Z}+1}$
is not irreducible.◻
We now give a different criterion from the dual point of view (compared to Lemma 5.13) concerning when the addition of a point increases the multiplicity index
![]() $m_{Z}$
(recall this is equal to
$m_{Z}$
(recall this is equal to
![]() $a_{Z}$
) and when it does not. Let
$a_{Z}$
) and when it does not. Let
![]() $Z$
be a reduced scheme of points, and let
$Z$
be a reduced scheme of points, and let
![]() $Y=Z+Q$
for some
$Y=Z+Q$
for some
![]() $Q=(a:b:c)$
not in
$Q=(a:b:c)$
not in
![]() $Z$
. Note the line dual to
$Z$
. Note the line dual to
![]() $Q$
is defined by
$Q$
is defined by
![]() $\ell _{Q}=ax+by+cz$
. Let
$\ell _{Q}=ax+by+cz$
. Let
![]() $g$
be the product of the linear forms dual to the points of
$g$
be the product of the linear forms dual to the points of
![]() $Z$
, and so
$Z$
, and so
![]() $f=\ell _{Q}g$
is the product of the linear forms dual to the points of
$f=\ell _{Q}g$
is the product of the linear forms dual to the points of
![]() $Y$
. Let
$Y$
. Let
![]() $\ell$
be the general linear form dual to a general point
$\ell$
be the general linear form dual to a general point
![]() $P\in \mathbb{P}^{2}$
. Denote the image of a polynomial
$P\in \mathbb{P}^{2}$
. Denote the image of a polynomial
![]() $h\in R$
in
$h\in R$
in
![]() $\overline{R}=R/\ell R$
by
$\overline{R}=R/\ell R$
by
![]() $\overline{h}$
.
$\overline{h}$
.
Proposition 5.18. Assume that
![]() $m_{Z}\leqslant u_{Z}$
, that the characteristic of
$m_{Z}\leqslant u_{Z}$
, that the characteristic of
![]() $K$
does not divide
$K$
does not divide
![]() $|Z|$
or
$|Z|$
or
![]() $|Y|$
, and that
$|Y|$
, and that
![]() $K$
is algebraically closed. Then one has the following results.
$K$
is algebraically closed. Then one has the following results.
(a) For a general linear form
 $\ell$
, consider a syzygy of least degree
$\ell$
, consider a syzygy of least degree
 $rg_{x}+sg_{y}+tg_{z}+u\ell =0$
of
$rg_{x}+sg_{y}+tg_{z}+u\ell =0$
of
 $\operatorname{Jac}(g)+(\ell )$
, and so
$\operatorname{Jac}(g)+(\ell )$
, and so
 $r,s,t\in [R]_{m_{Z}}$
. Then
$r,s,t\in [R]_{m_{Z}}$
. Then
 $\overline{\ell }_{Q}$
divides
$\overline{\ell }_{Q}$
divides
 $\overline{ar+bs+ct}$
in
$\overline{ar+bs+ct}$
in
 $\overline{R}$
if and only if
$\overline{R}$
if and only if
 $m_{Y}=m_{Z}$
.
$m_{Y}=m_{Z}$
.(b) Assume
 $\operatorname{Jac}(g)$
has a syzygy
$\operatorname{Jac}(g)$
has a syzygy
 $rg_{x}+sg_{y}+tg_{z}=0$
with
$rg_{x}+sg_{y}+tg_{z}=0$
with
 $r,s,t\in [R]_{m_{Z}}$
(this will certainly be the case if the line arrangement dual to
$r,s,t\in [R]_{m_{Z}}$
(this will certainly be the case if the line arrangement dual to
 $Z$
is free). Then
$Z$
is free). Then
 $m_{Y}=m_{Z}$
if and only if
$m_{Y}=m_{Z}$
if and only if
 $\ell _{Q}$
divides
$\ell _{Q}$
divides
 $ar+bs+ct$
.
$ar+bs+ct$
.
Proof. By Euler’s theorem we have
![]() $xf_{x}+yf_{y}+zf_{z}=(d+1)f$
, where
$xf_{x}+yf_{y}+zf_{z}=(d+1)f$
, where
![]() $d=|Z|$
. Abusing notation, regard
$d=|Z|$
. Abusing notation, regard
![]() $Q=(a,b,c)$
as a vector in
$Q=(a,b,c)$
as a vector in
![]() $K^{3}$
. As observed above, the Leibniz rule gives
$K^{3}$
. As observed above, the Leibniz rule gives
![]() $\unicode[STIX]{x1D6FB}f=gQ+\ell _{Q}\unicode[STIX]{x1D6FB}g$
.
$\unicode[STIX]{x1D6FB}f=gQ+\ell _{Q}\unicode[STIX]{x1D6FB}g$
.
We first prove (a). Consider the dot product
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \biggl[\ell _{Q}(r,s,t)-\frac{1}{d+1}(Q\cdot (r,s,t))(x,y,z)\biggr]\cdot \unicode[STIX]{x1D6FB}f\nonumber\\ \displaystyle & & \displaystyle \quad =\ell _{Q}(r,s,t)\cdot [gQ+\ell _{Q}\unicode[STIX]{x1D6FB}g]-(Q\cdot (r,s,t))f\nonumber\\ \displaystyle & & \displaystyle \quad =\ell _{Q}g(Q\cdot (r,s,t))+\ell _{Q}^{2}(\unicode[STIX]{x1D6FB}g\cdot (r,s,t))-(Q\cdot (r,s,t))f\nonumber\\ \displaystyle & & \displaystyle \quad =-\ell _{Q}^{2}u\ell .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \biggl[\ell _{Q}(r,s,t)-\frac{1}{d+1}(Q\cdot (r,s,t))(x,y,z)\biggr]\cdot \unicode[STIX]{x1D6FB}f\nonumber\\ \displaystyle & & \displaystyle \quad =\ell _{Q}(r,s,t)\cdot [gQ+\ell _{Q}\unicode[STIX]{x1D6FB}g]-(Q\cdot (r,s,t))f\nonumber\\ \displaystyle & & \displaystyle \quad =\ell _{Q}g(Q\cdot (r,s,t))+\ell _{Q}^{2}(\unicode[STIX]{x1D6FB}g\cdot (r,s,t))-(Q\cdot (r,s,t))f\nonumber\\ \displaystyle & & \displaystyle \quad =-\ell _{Q}^{2}u\ell .\nonumber\end{eqnarray}$$
This equation represents a syzygy of
![]() $\operatorname{Jac}(f)+(\ell )$
. If
$\operatorname{Jac}(f)+(\ell )$
. If
![]() $\ell _{Q}$
divides
$\ell _{Q}$
divides
![]() $ar+bs+ct=Q\cdot (r,s,t)$
modulo
$ar+bs+ct=Q\cdot (r,s,t)$
modulo
![]() $\ell$
, then canceling
$\ell$
, then canceling
![]() $\ell _{Q}$
gives a syzygy, where the coefficients of the partial derivatives of
$\ell _{Q}$
gives a syzygy, where the coefficients of the partial derivatives of
![]() $f$
have degree
$f$
have degree
![]() $m_{Z}$
. Hence we conclude
$m_{Z}$
. Hence we conclude
![]() $m_{Y}=m_{Z}$
.
$m_{Y}=m_{Z}$
.
Conversely, assume
![]() $m_{Y}=m_{Z}$
. Thus, there is a syzygy
$m_{Y}=m_{Z}$
. Thus, there is a syzygy
![]() $mf_{z}+nf_{y}+of_{z}+p\ell =0$
with
$mf_{z}+nf_{y}+of_{z}+p\ell =0$
with
![]() $m,n,o\in [R]_{m_{Z}}$
. The assumption
$m,n,o\in [R]_{m_{Z}}$
. The assumption
![]() $m_{Z}\leqslant u_{Z}$
implies that
$m_{Z}\leqslant u_{Z}$
implies that
![]() $C_{P}(Z)=C_{P}(Y)$
. Proposition 5.10 gives a parametrization of its irreducible component
$C_{P}(Z)=C_{P}(Y)$
. Proposition 5.10 gives a parametrization of its irreducible component
![]() $C_{P}(Z^{\prime })=C_{P}(Y^{\prime })$
. It is obtained from the cross product of
$C_{P}(Z^{\prime })=C_{P}(Y^{\prime })$
. It is obtained from the cross product of
![]() $(r,s,t)$
and
$(r,s,t)$
and
![]() $(x,y,z)$
and of
$(x,y,z)$
and of
![]() $(m,n,o)$
and
$(m,n,o)$
and
![]() $(x,y,z)$
, respectively. It follows that there is a form
$(x,y,z)$
, respectively. It follows that there is a form
![]() $h\in R$
such that
$h\in R$
such that
Taking the dot product with
![]() $\overline{\unicode[STIX]{x1D6FB}f}=\overline{\ell }_{Q}\overline{\unicode[STIX]{x1D6FB}g}+\overline{g}\,\overline{Q}$
, we obtain in
$\overline{\unicode[STIX]{x1D6FB}f}=\overline{\ell }_{Q}\overline{\unicode[STIX]{x1D6FB}g}+\overline{g}\,\overline{Q}$
, we obtain in
![]() $\overline{R}$
,
$\overline{R}$
,
Since
![]() $\overline{f}=\overline{\ell }_{Q}\overline{g}$
, we conclude that
$\overline{f}=\overline{\ell }_{Q}\overline{g}$
, we conclude that
![]() $\overline{\ell }_{Q}$
divides
$\overline{\ell }_{Q}$
divides
![]() $\overline{(r,s,t)\cdot Q}$
, as claimed.
$\overline{(r,s,t)\cdot Q}$
, as claimed.
We now prove (b). By assumption,
![]() $ar+bs+ct$
and
$ar+bs+ct$
and
![]() $\ell _{Q}$
are independent of
$\ell _{Q}$
are independent of
![]() $\ell$
. Hence, part (a) gives the desired conclusion.◻
$\ell$
. Hence, part (a) gives the desired conclusion.◻
Remark 5.19. Let
![]() $Z$
be a finite set of points such that
$Z$
be a finite set of points such that
![]() $m_{Z}\leqslant u_{Z}$
. Let
$m_{Z}\leqslant u_{Z}$
. Let
![]() $g$
be the product of the linear forms dual to the points of
$g$
be the product of the linear forms dual to the points of
![]() $Z$
, and assume there exists a syzygy
$Z$
, and assume there exists a syzygy
![]() $rg_{x}+sg_{y}+tg_{z}=0$
of degree
$rg_{x}+sg_{y}+tg_{z}=0$
of degree
![]() $m_{Z}$
. Then Proposition 5.18 gives a way to compute
$m_{Z}$
. Then Proposition 5.18 gives a way to compute
![]() $\bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
. One just finds the locus of all
$\bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
. One just finds the locus of all
![]() $(a,b,c)$
such that
$(a,b,c)$
such that
![]() $ax+by+cz$
divides
$ax+by+cz$
divides
![]() $ar+bs+ct$
. For example, to find all such
$ar+bs+ct$
. For example, to find all such
![]() $(a,b,c)$
with
$(a,b,c)$
with
![]() $a\neq 0$
, just plug
$a\neq 0$
, just plug
![]() $-(by+cz)/a$
in for
$-(by+cz)/a$
in for
![]() $x$
in
$x$
in
![]() $ar+bs+ct$
and regard the result as a polynomial with coefficients in
$ar+bs+ct$
and regard the result as a polynomial with coefficients in
![]() $K(b/a,c/a)$
. The locus is given by the vanishing of these coefficients.
$K(b/a,c/a)$
. The locus is given by the vanishing of these coefficients.
We conclude this section by relating our results to a more explicit version of the SHGH conjecture.
Conjecture 5.20 (SHGH conjecture).
For
![]() $X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
with general points
$X=m_{1}P_{1}+\cdots +m_{r}P_{r}$
with general points
![]() $P_{i}$
,
$P_{i}$
,
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V=[R]_{t}$
if and only if
$V=[R]_{t}$
if and only if
![]() $[I_{X}]_{t}\neq 0$
and every element of
$[I_{X}]_{t}\neq 0$
and every element of
![]() $[I_{X}]_{t}$
is divisible by
$[I_{X}]_{t}$
is divisible by
![]() $G^{n}$
for some
$G^{n}$
for some
![]() $n>0$
where
$n>0$
where
![]() $G$
is irreducible and defines a rational curve
$G$
is irreducible and defines a rational curve
![]() $E$
such that
$E$
such that
![]() $d^{2}-\sum _{i}e_{i}^{2}-3d+\sum _{j}e_{j}=-2$
and
$d^{2}-\sum _{i}e_{i}^{2}-3d+\sum _{j}e_{j}=-2$
and
![]() $d^{2}-\sum _{i}e_{i}^{2}=-1$
, where
$d^{2}-\sum _{i}e_{i}^{2}=-1$
, where
![]() $d=\deg (E)$
and
$d=\deg (E)$
and
![]() $e_{i}=\operatorname{mult}_{P_{i}}(E)$
.
$e_{i}=\operatorname{mult}_{P_{i}}(E)$
.
Remark 5.21. In all cases of which we are aware, if
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V=[I_{Z}]_{t}$
, then every element of
$V=[I_{Z}]_{t}$
, then every element of
![]() $[I_{X}]_{t}$
is divisible by
$[I_{X}]_{t}$
is divisible by
![]() $G$
, where
$G$
, where
![]() $G$
is irreducible and defines a rational curve
$G$
is irreducible and defines a rational curve
![]() $E$
such that
$E$
such that
![]() $d^{2}-\sum _{i}e_{i}^{2}-\sum _{j}f_{j}^{2}-3d+\sum _{i}e_{i}+\sum _{j}f_{j}=-2$
and
$d^{2}-\sum _{i}e_{i}^{2}-\sum _{j}f_{j}^{2}-3d+\sum _{i}e_{i}+\sum _{j}f_{j}=-2$
and
![]() $(nd)^{2}-\sum _{i}(ne_{i})^{2}-\sum _{j}(nf_{j})^{2}<-1$
, where
$(nd)^{2}-\sum _{i}(ne_{i})^{2}-\sum _{j}(nf_{j})^{2}<-1$
, where
![]() $f_{j}=\operatorname{mult}_{Q_{j}}(E)$
.
$f_{j}=\operatorname{mult}_{Q_{j}}(E)$
.
Moreover, we prove that if
![]() $X=mP\neq 0$
and
$X=mP\neq 0$
and
![]() $Z=Q_{1}+\cdots +Q_{s}$
, then
$Z=Q_{1}+\cdots +Q_{s}$
, then
![]() $X$
fails to impose the expected number of conditions on
$X$
fails to impose the expected number of conditions on
![]() $V=[I_{Z}]_{m+1}$
if and only if
$V=[I_{Z}]_{m+1}$
if and only if
![]() $V\neq 0$
and
$V\neq 0$
and
![]() $[I_{X+Z}]_{m+1}$
is divisible by
$[I_{X+Z}]_{m+1}$
is divisible by
![]() $G^{n}$
for some
$G^{n}$
for some
![]() $n>0$
where
$n>0$
where
![]() $G$
is irreducible and defines a rational curve
$G$
is irreducible and defines a rational curve
![]() $E$
where
$E$
where
![]() $e_{1}=d-1$
and
$e_{1}=d-1$
and
![]() $0\leqslant f_{j}\leqslant 1$
for all
$0\leqslant f_{j}\leqslant 1$
for all
![]() $j$
(and hence
$j$
(and hence
![]() $d^{2}-e_{1}^{2}-\sum _{j}f_{j}^{2}-3d+e_{1}+\sum _{j}f_{j}=-2$
) and
$d^{2}-e_{1}^{2}-\sum _{j}f_{j}^{2}-3d+e_{1}+\sum _{j}f_{j}=-2$
) and
![]() $(m+1)d-me_{1}-\sum _{j}f_{j}<-1$
.
$(m+1)d-me_{1}-\sum _{j}f_{j}<-1$
.
6 Examples
In this section we use the theory of line arrangements to present examples that illustrate some of the ideas in the preceding sections, including the role of the characteristic. We also establish new stability results and show that points in linearly general position do not have unexpected curves. These examples make it clear that sets of points that admit unexpected curves are special, but nevertheless they occur surprisingly often.
We first exhibit a line arrangement that is not free and is dual to a set of points that has a unique unexpected curve, which is reducible.
Example 6.1. For this example we assume our ground field has characteristic 0. Consider the line configuration given by the lines defined by the following 19 linear forms:
![]() $x$
,
$x$
,
![]() $y$
,
$y$
,
![]() $z$
,
$z$
,
![]() $x+y$
,
$x+y$
,
![]() $x-y$
,
$x-y$
,
![]() $2x+y$
,
$2x+y$
,
![]() $2x-y$
,
$2x-y$
,
![]() $x+z$
,
$x+z$
,
![]() $x-z$
,
$x-z$
,
![]() $y+z$
,
$y+z$
,
![]() $y-z$
,
$y-z$
,
![]() $x+2z$
,
$x+2z$
,
![]() $x-2z$
,
$x-2z$
,
![]() $y+2z$
,
$y+2z$
,
![]() $y-2z$
,
$y-2z$
,
![]() $x-y+z$
,
$x-y+z$
,
![]() $x-y-z$
,
$x-y-z$
,
![]() $x-y+2z$
,
$x-y+2z$
,
![]() $x-y-2z$
, shown in Figure 1. Let
$x-y-2z$
, shown in Figure 1. Let
![]() $Z$
be the corresponding reduced scheme consisting of the 19 points dual to the lines, sketched in Figure 2.
$Z$
be the corresponding reduced scheme consisting of the 19 points dual to the lines, sketched in Figure 2.

Figure 1. A configuration of 19 lines (the line at infinity,
![]() $z=0$
, is not shown).
$z=0$
, is not shown).

Figure 2. A sketch of the points dual to the lines of the line configuration given in Figure 1.
It is not hard to verify that the first difference of the Hilbert function of
![]() $Z$
is
$Z$
is
![]() $\unicode[STIX]{x1D6E5}h_{Z}=(1,2,3,4,4,4,1)$
, from which we find that
$\unicode[STIX]{x1D6E5}h_{Z}=(1,2,3,4,4,4,1)$
, from which we find that
![]() $t_{Z}=9$
. Picking a random point
$t_{Z}=9$
. Picking a random point
![]() $P$
, Macaulay2 [Reference Grayson and StillmanGS] finds that
$P$
, Macaulay2 [Reference Grayson and StillmanGS] finds that
![]() $[I_{Z+7P}]_{8}=0$
. By upper semicontinuity, this means
$[I_{Z+7P}]_{8}=0$
. By upper semicontinuity, this means
![]() $m_{Z}>7$
. Thus we have
$m_{Z}>7$
. Thus we have
![]() $8\leqslant m_{Z}\leqslant t_{Z}=9$
. We claim that in fact
$8\leqslant m_{Z}\leqslant t_{Z}=9$
. We claim that in fact
![]() $m_{Z}=8$
, that is, that the splitting type is
$m_{Z}=8$
, that is, that the splitting type is
![]() $(8,10)$
.
$(8,10)$
.
For a general linear form
![]() $\ell$
, set
$\ell$
, set
![]() $\bar{R}=R/\ell R$
and
$\bar{R}=R/\ell R$
and
![]() $\bar{J}=(J+(\ell ))/(\ell )$
, where
$\bar{J}=(J+(\ell ))/(\ell )$
, where
![]() $J\subset R$
is the Jacobian ideal. Consider the graded exact sequence induced by multiplication by
$J\subset R$
is the Jacobian ideal. Consider the graded exact sequence induced by multiplication by
![]() $\ell$
:
$\ell$
:
Using a computer algebra system, one gets
![]() $\dim _{K}[R/J]_{25}=243$
and
$\dim _{K}[R/J]_{25}=243$
and
![]() $\dim _{K}[R/J]_{26}=244$
. Hence, the above exact sequence, considered in degree 26, gives
$\dim _{K}[R/J]_{26}=244$
. Hence, the above exact sequence, considered in degree 26, gives
![]() $[\bar{R}/\bar{J}]_{26}\neq 0$
. The minimal free resolution of
$[\bar{R}/\bar{J}]_{26}\neq 0$
. The minimal free resolution of
![]() $\bar{R}/\bar{J}$
over
$\bar{R}/\bar{J}$
over
![]() $\bar{R}$
has the form
$\bar{R}$
has the form
where
![]() $\mathbb{F}$
is a free
$\mathbb{F}$
is a free
![]() $\bar{R}$
-module. From the resolution we can see that
$\bar{R}$
-module. From the resolution we can see that
![]() $\mathbb{F}$
has rank
$\mathbb{F}$
has rank
![]() $2$
, say
$2$
, say
![]() $\mathbb{F}=\bar{R}(-c)\oplus \bar{R}(-d)$
. Again from the resolution we see that
$\mathbb{F}=\bar{R}(-c)\oplus \bar{R}(-d)$
. Again from the resolution we see that
![]() $c+d=3(18)=54$
. Looking in degree 26, the components of the second and third free modules in this resolution both have dimension 27. Since
$c+d=3(18)=54$
. Looking in degree 26, the components of the second and third free modules in this resolution both have dimension 27. Since
![]() $[\bar{R}/\bar{J}]_{26}\neq 0$
, we obtain
$[\bar{R}/\bar{J}]_{26}\neq 0$
, we obtain
![]() $[\mathbb{F}]_{26}\neq 0$
.
$[\mathbb{F}]_{26}\neq 0$
.
We saw above that the splitting type is either balanced
![]() $(9,9)$
(if
$(9,9)$
(if
![]() $m_{Z}=9$
) or differs by two
$m_{Z}=9$
) or differs by two
![]() $(8,10)$
(if
$(8,10)$
(if
![]() $m_{Z}=8$
). If it were balanced then we would have
$m_{Z}=8$
). If it were balanced then we would have
![]() $\mathbb{F}=\bar{R}(-27)\oplus \bar{R}(-27)$
(since
$\mathbb{F}=\bar{R}(-27)\oplus \bar{R}(-27)$
(since
![]() $c+d=54$
), which contradicts
$c+d=54$
), which contradicts
![]() $[\mathbb{F}]_{26}\neq 0$
. Thus
$[\mathbb{F}]_{26}\neq 0$
. Thus
![]() $\mathbb{F}=\bar{R}(-26)\oplus \bar{R}(-28)$
. It follows that the splitting type is
$\mathbb{F}=\bar{R}(-26)\oplus \bar{R}(-28)$
. It follows that the splitting type is
![]() $(26-18,28-18)=(8,10)$
as claimed. Thus there is an unexpected curve only in degree 9. One can verify using Corollary 5.17 and a computer algebra program that the unexpected curve is not irreducible, and indeed has two components, one of which is a line. Indeed, using [CoCoA], we have seen that the linear component is the line joining the general point
$(26-18,28-18)=(8,10)$
as claimed. Thus there is an unexpected curve only in degree 9. One can verify using Corollary 5.17 and a computer algebra program that the unexpected curve is not irreducible, and indeed has two components, one of which is a line. Indeed, using [CoCoA], we have seen that the linear component is the line joining the general point
![]() $P$
to the point
$P$
to the point
![]() $[2,1,0]$
.
$[2,1,0]$
.
Example 6.2. It is interesting to note (based on computer experiments) that the arrangement of Example 6.1 is not free, but that if we either (i) remove
![]() $2x+y$
alone or (ii) replace
$2x+y$
alone or (ii) replace
![]() $2x+y$
by
$2x+y$
by
![]() $2y-x$
or (iii) add
$2y-x$
or (iii) add
![]() $(2y-x)$
to the configuration of 19 lines, these new configurations are free with splitting type
$(2y-x)$
to the configuration of 19 lines, these new configurations are free with splitting type
![]() $(7,10)$
,
$(7,10)$
,
![]() $(7,11)$
or
$(7,11)$
or
![]() $(8,11)$
, respectively.
$(8,11)$
, respectively.
In fact, we can make the following observations about Figure 3.
– The arrangement of 18 solid lines is free and irreducible but not complete (‘irreducible’ meaning
 $C_{P}(Z)$
is irreducible for a general point
$C_{P}(Z)$
is irreducible for a general point
 $P$
, where
$P$
, where
 $Z$
is the point scheme dual to the 18 lines, and ‘not complete’ meaning there is a point
$Z$
is the point scheme dual to the 18 lines, and ‘not complete’ meaning there is a point
 $Q$
not in
$Q$
not in
 $Z$
such that
$Z$
such that
 $m_{Z+Q}=m_{Z}$
).
$m_{Z+Q}=m_{Z}$
).– The arrangement of 18 solid lines plus the short-dashed line is free, irreducible and complete (i.e. if
 $Z$
is the point scheme dual to the 19 lines, then
$Z$
is the point scheme dual to the 19 lines, then
 $m_{Z+Q}=m_{Z}+1$
for all points
$m_{Z+Q}=m_{Z}+1$
for all points
 $Q$
not in
$Q$
not in
 $Z$
).
$Z$
).– The arrangement of 18 solid lines plus the long-dashed line is not free, not irreducible and not complete.
– The arrangement of all 20 lines is free and complete, but not irreducible.
These observations suggest the following question. Is the line arrangement
![]() ${\mathcal{L}}_{Z}$
for
${\mathcal{L}}_{Z}$
for
![]() $Z$
always free if
$Z$
always free if
![]() ${\mathcal{L}}_{Z}$
is irreducible or complete? Or the converse?
${\mathcal{L}}_{Z}$
is irreducible or complete? Or the converse?

Figure 3. A configuration of 20 lines (the line at infinity is not shown).
On the dual side, taking
![]() $Z$
from Example 6.1, if we set
$Z$
from Example 6.1, if we set
![]() $Z_{1}=Z\backslash \{[2,1,0]\}$
,
$Z_{1}=Z\backslash \{[2,1,0]\}$
,
![]() $Z_{2}=Z_{1}\cup \{[-1,2,0]\}$
and
$Z_{2}=Z_{1}\cup \{[-1,2,0]\}$
and
![]() $Z_{3}=Z\cup \{[-1,2,0]\}$
, we obtain
$Z_{3}=Z\cup \{[-1,2,0]\}$
, we obtain
![]() $m_{Z_{1}}=m_{Z_{2}}=7$
and
$m_{Z_{1}}=m_{Z_{2}}=7$
and
![]() $m_{Z}=m_{Z_{3}}=8$
. Checking the Hilbert functions, one can show that these sets all have unexpected curves (
$m_{Z}=m_{Z_{3}}=8$
. Checking the Hilbert functions, one can show that these sets all have unexpected curves (
![]() $t_{Z_{1}}=8,t_{Z}=t_{Z_{2}}=t_{Z_{3}}=9$
) and, using the results of § 5, one can verify that the unexpected curve for
$t_{Z_{1}}=8,t_{Z}=t_{Z_{2}}=t_{Z_{3}}=9$
) and, using the results of § 5, one can verify that the unexpected curve for
![]() $Z_{1}$
is irreducible and coincides with the unexpected curve for
$Z_{1}$
is irreducible and coincides with the unexpected curve for
![]() $Z_{2}$
, while the unexpected curve for
$Z_{2}$
, while the unexpected curve for
![]() $Z_{3}$
coincides with that for
$Z_{3}$
coincides with that for
![]() $Z$
and is not irreducible. As the general point
$Z$
and is not irreducible. As the general point
![]() $P$
varies, all unexpected curves for
$P$
varies, all unexpected curves for
![]() $Z_{1}$
also contain
$Z_{1}$
also contain
![]() $[-1,2,0]$
.
$[-1,2,0]$
.
In order to derive our next results we need the concept of a stable vector bundle. Since we need the Grauert and Mülich theorem, we will assume now that
![]() $K$
has characteristic
$K$
has characteristic
![]() $0$
and is algebraically closed. Recall that for a reflexive sheaf
$0$
and is algebraically closed. Recall that for a reflexive sheaf
![]() ${\mathcal{F}}$
of rank
${\mathcal{F}}$
of rank
![]() $2$
over
$2$
over
![]() $\mathbb{P}^{n}$
, there is a uniquely determined integer
$\mathbb{P}^{n}$
, there is a uniquely determined integer
![]() $k$
such that the first Chern class satisfies
$k$
such that the first Chern class satisfies
![]() $c_{1}({\mathcal{F}}(k))\in \{0,1\}$
(see [Reference Okonek, Schneider and SpindlerOSS80, page 165]). We set
$c_{1}({\mathcal{F}}(k))\in \{0,1\}$
(see [Reference Okonek, Schneider and SpindlerOSS80, page 165]). We set
![]() ${\mathcal{F}}_{\text{norm}}={\mathcal{F}}(k)$
. Recall also that stable vector bundles of rank
${\mathcal{F}}_{\text{norm}}={\mathcal{F}}(k)$
. Recall also that stable vector bundles of rank
![]() $2$
can be characterized cohomologically.
$2$
can be characterized cohomologically.
Lemma 6.3 [Reference HartshorneHar80, Lemma 3.1].
A reflexive sheaf
![]() ${\mathcal{F}}$
of rank
${\mathcal{F}}$
of rank
![]() $2$
over
$2$
over
![]() $\mathbb{P}^{n}$
is stable if and only if
$\mathbb{P}^{n}$
is stable if and only if
![]() $H^{0}({\mathcal{F}}_{\text{norm}})=0$
. If
$H^{0}({\mathcal{F}}_{\text{norm}})=0$
. If
![]() $c_{1}({\mathcal{F}})$
is even, then
$c_{1}({\mathcal{F}})$
is even, then
![]() ${\mathcal{F}}$
is semistable if and only if
${\mathcal{F}}$
is semistable if and only if
![]() $H^{0}({\mathcal{F}}_{\text{norm}}(-1))=0$
. If
$H^{0}({\mathcal{F}}_{\text{norm}}(-1))=0$
. If
![]() $c_{1}({\mathcal{F}})$
is odd then semistability and stability coincide.
$c_{1}({\mathcal{F}})$
is odd then semistability and stability coincide.
Stability is related to the existence of unexpected curves, as we now see.
Proposition 6.4. Let
![]() ${\mathcal{A}}$
be a line arrangement with splitting type
${\mathcal{A}}$
be a line arrangement with splitting type
![]() $(a_{Z},b_{Z})$
, dual to a set of points
$(a_{Z},b_{Z})$
, dual to a set of points
![]() $Z$
. If
$Z$
. If
![]() $Z$
admits an unexpected curve, then
$Z$
admits an unexpected curve, then
![]() $b_{Z}\geqslant a_{Z}+2$
. In particular, the derivation bundle of
$b_{Z}\geqslant a_{Z}+2$
. In particular, the derivation bundle of
![]() ${\mathcal{A}}$
is not semistable.
${\mathcal{A}}$
is not semistable.
Proof. We have seen in Theorem 1.1 that if
![]() $Z$
has an unexpected curve then
$Z$
has an unexpected curve then
![]() $b_{Z}-a_{Z}\geqslant 2$
. If the derivation bundle of
$b_{Z}-a_{Z}\geqslant 2$
. If the derivation bundle of
![]() ${\mathcal{A}}$
were semistable, then the Grauert and Mülich theorem [Reference Grauert and MülichGM75] gives
${\mathcal{A}}$
were semistable, then the Grauert and Mülich theorem [Reference Grauert and MülichGM75] gives
![]() $b_{Z}-a_{Z}\leqslant 1$
, hence the result.◻
$b_{Z}-a_{Z}\leqslant 1$
, hence the result.◻
Let
![]() ${\mathcal{A}}={\mathcal{A}}(f)$
be a line arrangement in
${\mathcal{A}}={\mathcal{A}}(f)$
be a line arrangement in
![]() $\mathbb{P}^{2}$
. Let
$\mathbb{P}^{2}$
. Let
![]() $L$
be one of the components of
$L$
be one of the components of
![]() ${\mathcal{A}}$
defined by a linear form
${\mathcal{A}}$
defined by a linear form
![]() $\ell$
. Let
$\ell$
. Let
![]() $g=f/\ell$
. Then
$g=f/\ell$
. Then
![]() $\bar{g}$
, the restriction of
$\bar{g}$
, the restriction of
![]() $g$
to
$g$
to
![]() $L$
, is a polynomial of the same degree as
$L$
, is a polynomial of the same degree as
![]() $g$
, though it is not necessarily reduced. If
$g$
, though it is not necessarily reduced. If
![]() $\bar{g}^{\prime }$
is the radical of
$\bar{g}^{\prime }$
is the radical of
![]() $\bar{g}$
, then
$\bar{g}$
, then
![]() $\bar{g}^{\prime }$
defines a hyperplane arrangement of
$\bar{g}^{\prime }$
defines a hyperplane arrangement of
![]() $L=\mathbb{P}^{1}$
, called the restriction, which we denote by
$L=\mathbb{P}^{1}$
, called the restriction, which we denote by
![]() ${\mathcal{A}}^{\prime \prime }$
. Moreover, the arrangement defined by
${\mathcal{A}}^{\prime \prime }$
. Moreover, the arrangement defined by
![]() $g$
is often denoted by
$g$
is often denoted by
![]() ${\mathcal{A}}^{\prime }$
, and one refers to
${\mathcal{A}}^{\prime }$
, and one refers to
![]() $({\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime })$
as a triple of hyperplane arrangements. Thus if
$({\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime })$
as a triple of hyperplane arrangements. Thus if
![]() ${\mathcal{A}}$
is a line arrangement then
${\mathcal{A}}$
is a line arrangement then
![]() ${\mathcal{A}}^{\prime }$
is obtained from
${\mathcal{A}}^{\prime }$
is obtained from
![]() ${\mathcal{A}}$
by removing a line
${\mathcal{A}}$
by removing a line
![]() $L$
, and
$L$
, and
![]() ${\mathcal{A}}^{\prime \prime }$
is the restriction of
${\mathcal{A}}^{\prime \prime }$
is the restriction of
![]() ${\mathcal{A}}^{\prime }$
to
${\mathcal{A}}^{\prime }$
to
![]() $L$
. The splitting type associated to
$L$
. The splitting type associated to
![]() ${\mathcal{A}}$
is sometimes referred to as the exponents of
${\mathcal{A}}$
is sometimes referred to as the exponents of
![]() ${\mathcal{A}}$
. Notice that the arrangement
${\mathcal{A}}$
. Notice that the arrangement
![]() ${\mathcal{A}}^{\prime \prime }\subset \mathbb{P}^{1}$
is free, and the exponent of
${\mathcal{A}}^{\prime \prime }\subset \mathbb{P}^{1}$
is free, and the exponent of
![]() ${\mathcal{A}}^{\prime \prime }$
refers to the integer
${\mathcal{A}}^{\prime \prime }$
refers to the integer
![]() $|{\mathcal{A}}^{\prime \prime }|-1$
.
$|{\mathcal{A}}^{\prime \prime }|-1$
.
The following result is useful for establishing stability.
Lemma 6.5. Let
![]() ${\mathcal{A}}$
be
${\mathcal{A}}$
be
![]() $({\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime })$
a triple of line arrangements, where
$({\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime })$
a triple of line arrangements, where
![]() ${\mathcal{A}}$
consists of
${\mathcal{A}}$
consists of
![]() $d$
lines. Let
$d$
lines. Let
![]() ${\mathcal{D}}$
and
${\mathcal{D}}$
and
![]() ${\mathcal{D}}^{\prime }$
be the derivation bundles of
${\mathcal{D}}^{\prime }$
be the derivation bundles of
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() ${\mathcal{A}}^{\prime }$
, respectively. Then one has the following results.
${\mathcal{A}}^{\prime }$
, respectively. Then one has the following results.
(a) [Reference SchenckSch03, Theorem 4.5(a)] If
 $d$
is odd, then
$d$
is odd, then
 ${\mathcal{D}}$
is stable if
${\mathcal{D}}$
is stable if
 ${\mathcal{D}}^{\prime }$
is stable and
${\mathcal{D}}^{\prime }$
is stable and
 $|{\mathcal{A}}^{\prime \prime }|>(d+1)/2$
.
$|{\mathcal{A}}^{\prime \prime }|>(d+1)/2$
.(b) If
 $d$
is odd, then
$d$
is odd, then
 ${\mathcal{D}}$
is semistable if
${\mathcal{D}}$
is semistable if
 ${\mathcal{D}}^{\prime }$
is stable.
${\mathcal{D}}^{\prime }$
is stable.(c) [Reference SchenckSch03, Theorem 4.5(c)] If
 $d$
is even, then
$d$
is even, then
 ${\mathcal{D}}$
is stable if
${\mathcal{D}}$
is stable if
 ${\mathcal{D}}^{\prime }$
is semistable and
${\mathcal{D}}^{\prime }$
is semistable and
 $|{\mathcal{A}}^{\prime \prime }|>d/2$
.
$|{\mathcal{A}}^{\prime \prime }|>d/2$
.(d) If
 $d$
is even, then
$d$
is even, then
 ${\mathcal{D}}$
is stable if
${\mathcal{D}}$
is stable if
 ${\mathcal{D}}^{\prime }$
is stable.
${\mathcal{D}}^{\prime }$
is stable.
Proof. According to [Reference SchenckSch03, Theorem 3.2], there is an exact sequence
This implies parts (a) and (c). Using that for any vector bundle
![]() ${\mathcal{E}}$
of rank
${\mathcal{E}}$
of rank
![]() $2$
on
$2$
on
![]() $\mathbb{P}^{2}$
one has
$\mathbb{P}^{2}$
one has
![]() ${\mathcal{E}}^{\vee }\cong {\mathcal{E}}(c_{1}({\mathcal{E}}))$
, dualizing gives the exact sequence (see also [Reference Faenzi and VallèsFV14, Proposition 5.1])
${\mathcal{E}}^{\vee }\cong {\mathcal{E}}(c_{1}({\mathcal{E}}))$
, dualizing gives the exact sequence (see also [Reference Faenzi and VallèsFV14, Proposition 5.1])
Applying Lemma 6.3, parts (b) and (d) follow. ◻
Remark 6.6. Lemma 6.5(b) improves [Reference SchenckSch03, Theorem 4.5(b)] by eliminating any assumption on
![]() ${\mathcal{A}}^{\prime \prime }$
. Note that in this case stability and semistability of
${\mathcal{A}}^{\prime \prime }$
. Note that in this case stability and semistability of
![]() ${\mathcal{D}}^{\prime }$
are equivalent by Lemma 6.3.
${\mathcal{D}}^{\prime }$
are equivalent by Lemma 6.3.
As a first consequence, we get information on sufficiently general line arrangements. The following result is, in a sense, known since it follows from Proposition 2.10, Theorem 3.5 and Theorem 3.11 in [Reference Dolgachev and KapranovDK93], which is much more general. A. Dimca has also informed us that it follows (with a little work) from results in [Reference Abe and DimcaAD18] and [Reference Dimca and SticlaruDS15]. However, for the convenience of the reader we give the following simpler proof in our setting.
Proposition 6.7. Let
![]() ${\mathcal{A}}_{d}$
be a configuration of
${\mathcal{A}}_{d}$
be a configuration of
![]() $d$
lines in
$d$
lines in
![]() $\mathbb{P}^{2}$
such that no three lines of
$\mathbb{P}^{2}$
such that no three lines of
![]() ${\mathcal{A}}_{d}$
meet in a point. Then the splitting type for
${\mathcal{A}}_{d}$
meet in a point. Then the splitting type for
![]() ${\mathcal{A}}_{d}$
is
${\mathcal{A}}_{d}$
is
Moreover,
![]() ${\mathcal{A}}_{d}$
is free if and only if
${\mathcal{A}}_{d}$
is free if and only if
![]() $d\leqslant 3$
.
$d\leqslant 3$
.
Proof. Let
![]() $J_{d}$
be the Jacobian ideal of
$J_{d}$
be the Jacobian ideal of
![]() ${\mathcal{A}}_{d}$
and let
${\mathcal{A}}_{d}$
and let
![]() $\bar{J}_{d}$
be its saturation. By assumption, the lines in
$\bar{J}_{d}$
be its saturation. By assumption, the lines in
![]() ${\mathcal{A}}_{d}$
form a star configuration. Thus, by [Reference Geramita, Harbourne and MiglioreGHM13] we know that the minimal free resolution of
${\mathcal{A}}_{d}$
form a star configuration. Thus, by [Reference Geramita, Harbourne and MiglioreGHM13] we know that the minimal free resolution of
![]() $\bar{J}_{d}$
is
$\bar{J}_{d}$
is
In particular,
![]() $J_{d}$
is saturated if and only if
$J_{d}$
is saturated if and only if
![]() $d\leqslant 3$
, so
$d\leqslant 3$
, so
![]() ${\mathcal{A}}_{d}$
is free if and only if
${\mathcal{A}}_{d}$
is free if and only if
![]() $d\leqslant 3$
.
$d\leqslant 3$
.
Let us establish some notation. This minimal free resolution for
![]() $J_{d}$
truncates to a short exact sequence
$J_{d}$
truncates to a short exact sequence
Let
![]() ${\mathcal{E}}_{d}$
be the sheafification of the reflexive module
${\mathcal{E}}_{d}$
be the sheafification of the reflexive module
![]() $E_{d}$
. Then
$E_{d}$
. Then
![]() ${\mathcal{D}}_{d}={\mathcal{E}}_{d}(d-1)$
is the derivation bundle of
${\mathcal{D}}_{d}={\mathcal{E}}_{d}(d-1)$
is the derivation bundle of
![]() ${\mathcal{A}}_{d}$
. Note also that
${\mathcal{A}}_{d}$
. Note also that
![]() $({\mathcal{D}}_{d})_{\text{norm}}={\mathcal{E}}_{d}((3d-3)/2)$
when
$({\mathcal{D}}_{d})_{\text{norm}}={\mathcal{E}}_{d}((3d-3)/2)$
when
![]() $d$
is odd, and
$d$
is odd, and
![]() $({\mathcal{D}}_{d})_{\text{norm}}={\mathcal{E}}_{d}((3d-4)/2)$
if
$({\mathcal{D}}_{d})_{\text{norm}}={\mathcal{E}}_{d}((3d-4)/2)$
if
![]() $d$
is even.
$d$
is even.
First, consider
![]() $d=3$
. Then
$d=3$
. Then
![]() ${\mathcal{A}}_{d}$
is free and we have the minimal free resolution
${\mathcal{A}}_{d}$
is free and we have the minimal free resolution
Thus
![]() ${\mathcal{E}}_{3}={\mathcal{O}}_{\mathbb{P}^{2}}(-3)^{2}$
,
${\mathcal{E}}_{3}={\mathcal{O}}_{\mathbb{P}^{2}}(-3)^{2}$
,
![]() ${\mathcal{D}}_{3}={\mathcal{O}}_{\mathbb{P}^{2}}(-1)^{2}$
and
${\mathcal{D}}_{3}={\mathcal{O}}_{\mathbb{P}^{2}}(-1)^{2}$
and
![]() $({\mathcal{D}}_{3})_{\text{norm}}={\mathcal{O}}_{\mathbb{P}^{2}}^{2}$
. By Lemma 6.3,
$({\mathcal{D}}_{3})_{\text{norm}}={\mathcal{O}}_{\mathbb{P}^{2}}^{2}$
. By Lemma 6.3,
![]() ${\mathcal{D}}_{3}$
is semistable. Clearly the splitting type for
${\mathcal{D}}_{3}$
is semistable. Clearly the splitting type for
![]() ${\mathcal{A}}_{3}$
is
${\mathcal{A}}_{3}$
is
![]() $(1,1)$
as claimed.
$(1,1)$
as claimed.
Now assume that
![]() $d=4$
. It follows from Lemma 6.5 that
$d=4$
. It follows from Lemma 6.5 that
![]() ${\mathcal{D}}_{4}$
is stable, so the splitting type is as claimed thanks to the Grauert–Mülich theorem [Reference Grauert and MülichGM75].
${\mathcal{D}}_{4}$
is stable, so the splitting type is as claimed thanks to the Grauert–Mülich theorem [Reference Grauert and MülichGM75].
Using Lemma 6.5, we obtain by induction that
![]() ${\mathcal{D}}_{d}$
is stable for all
${\mathcal{D}}_{d}$
is stable for all
![]() $d\geqslant 4$
. Hence by the Grauert–Mülich theorem, the splitting type of
$d\geqslant 4$
. Hence by the Grauert–Mülich theorem, the splitting type of
![]() ${\mathcal{D}}_{d}$
is as claimed.◻
${\mathcal{D}}_{d}$
is as claimed.◻
This has the following consequence for the dual set of points. Recall that a set of points in
![]() $\mathbb{P}^{2}$
is said to be in linearly general position if no three of its points are on a line. Note that this is very different from assuming that
$\mathbb{P}^{2}$
is said to be in linearly general position if no three of its points are on a line. Note that this is very different from assuming that
![]() $Z$
is a general set of points.
$Z$
is a general set of points.
Corollary 6.8. Let
![]() $Z$
be a set of points in
$Z$
be a set of points in
![]() $\mathbb{P}^{2}$
in linear general position. Then
$\mathbb{P}^{2}$
in linear general position. Then
![]() $m_{Z}=\lfloor (|Z|-1)/2\rfloor$
,
$m_{Z}=\lfloor (|Z|-1)/2\rfloor$
,
![]() $u_{Z}=\lceil (|Z|-1)/2\rceil -1$
, and
$u_{Z}=\lceil (|Z|-1)/2\rceil -1$
, and
![]() $Z$
does not admit an unexpected curve. Furthermore, for a general point
$Z$
does not admit an unexpected curve. Furthermore, for a general point
![]() $P$
,
$P$
,
and
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
contains an irreducible form.
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
contains an irreducible form.
Proof. Notice that a set of points is in linearly general position if and only if the set of dual lines has the property that no three of them meet in a point. Hence, Proposition 6.7 gives the asserted values of
![]() $m_{Z}$
and
$m_{Z}$
and
![]() $u_{Z}$
. Combined with Theorem 1.1, we get that
$u_{Z}$
. Combined with Theorem 1.1, we get that
![]() $Z$
does not admit an unexpected curve. It remains to show the irreducibility statement.
$Z$
does not admit an unexpected curve. It remains to show the irreducibility statement.
First, assume
![]() $Z$
is even. Then we have seen that, for each point
$Z$
is even. Then we have seen that, for each point
![]() $Q\in Z$
, one has
$Q\in Z$
, one has
![]() $m_{Z}=(|Z|-2)/2=m_{Z-Q}$
. Hence, the unique curve determined by
$m_{Z}=(|Z|-2)/2=m_{Z-Q}$
. Hence, the unique curve determined by
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
is irreducible by Corollary 5.17.
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
is irreducible by Corollary 5.17.
Second, assume
![]() $Z$
is odd. Then
$Z$
is odd. Then
![]() $u_{Z}=m_{Z}-1$
and Corollary 5.3 gives the claim.◻
$u_{Z}=m_{Z}-1$
and Corollary 5.3 gives the claim.◻
Remark 6.9.
(i) Corollary 6.8 is a statement about a set of points. It would be interesting to have a more direct proof and to decide if the conclusion is also true if the base field has positive characteristic.
(ii) The assumption that no three lines of
 ${\mathcal{A}}_{d}$
meet in a point (or the dual version, that the points are in linearly general position) allows for a clean result. Nevertheless, the proof requires much less. If the line arrangement can be built up from a set of lines with semistable syzygy bundle such that each line added meets the existing
${\mathcal{A}}_{d}$
meet in a point (or the dual version, that the points are in linearly general position) allows for a clean result. Nevertheless, the proof requires much less. If the line arrangement can be built up from a set of lines with semistable syzygy bundle such that each line added meets the existing
 $e$
lines (say) in more than
$e$
lines (say) in more than
 $\lfloor (e+1)/2\rfloor$
points then the same conclusion holds, thanks to Lemma 6.5.
$\lfloor (e+1)/2\rfloor$
points then the same conclusion holds, thanks to Lemma 6.5.
There are some further theoretical tools for determining splitting types, which we consider now.
Remark 6.10. A line arrangement
![]() ${\mathcal{A}}$
in
${\mathcal{A}}$
in
![]() $\mathbb{P}^{2}$
is supersolvable if it has a so-called modular point, that is, a point
$\mathbb{P}^{2}$
is supersolvable if it has a so-called modular point, that is, a point
![]() $P$
with the property that if
$P$
with the property that if
![]() $\ell _{1},\ell _{2}\in {\mathcal{A}}$
and if
$\ell _{1},\ell _{2}\in {\mathcal{A}}$
and if
![]() $Q$
is the intersection of
$Q$
is the intersection of
![]() $\ell _{1}$
and
$\ell _{1}$
and
![]() $\ell _{2}$
then the line joining
$\ell _{2}$
then the line joining
![]() $P$
and
$P$
and
![]() $Q$
is a line of
$Q$
is a line of
![]() ${\mathcal{A}}$
. (See [Reference Di Marca, Malara and OnetoDMO18] for examples of supersolvable line arrangements giving rise to unexpected curves.) A standard fact is that if
${\mathcal{A}}$
. (See [Reference Di Marca, Malara and OnetoDMO18] for examples of supersolvable line arrangements giving rise to unexpected curves.) A standard fact is that if
![]() ${\mathcal{A}}$
is a supersolvable line arrangement consisting of
${\mathcal{A}}$
is a supersolvable line arrangement consisting of
![]() $d$
lines,
$d$
lines,
![]() $m$
of which pass through the modular point
$m$
of which pass through the modular point
![]() $P$
, then
$P$
, then
![]() ${\mathcal{A}}$
is free, and the splitting type is
${\mathcal{A}}$
is free, and the splitting type is
![]() $(m-1,d-m)$
. We are grateful to Ş. Tohǎneanu for pointing out that the computation of the splitting type is a simple application of the addition–deletion theorem (Theorem 6.11 below) using induction on
$(m-1,d-m)$
. We are grateful to Ş. Tohǎneanu for pointing out that the computation of the splitting type is a simple application of the addition–deletion theorem (Theorem 6.11 below) using induction on
![]() $d$
, with the base case being that all lines pass through a single point.
$d$
, with the base case being that all lines pass through a single point.
Theorem 6.11 (Addition–deletion theorem; see, for example, [Reference Orlik and TeraoOT92, Theorem 4.51]).
Let
![]() $({\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime })$
be a triple of line arrangements. Then any two of the following imply the third:
$({\mathcal{A}}^{\prime },{\mathcal{A}},{\mathcal{A}}^{\prime \prime })$
be a triple of line arrangements. Then any two of the following imply the third:
 ${\mathcal{A}}$
is free with exponents
${\mathcal{A}}$
is free with exponents
 $(a+1,b)$
(respectively,
$(a+1,b)$
(respectively,
 $(a,b+1)$
);
$(a,b+1)$
); ${\mathcal{A}}^{\prime }$
is free with exponents
${\mathcal{A}}^{\prime }$
is free with exponents
 $(a,b)$
;
$(a,b)$
; ${\mathcal{A}}^{\prime \prime }$
is free with exponent
${\mathcal{A}}^{\prime \prime }$
is free with exponent
 $(b)$
or
$(b)$
or
 $(a)$
(i.e.
$(a)$
(i.e.
 ${\mathcal{A}}^{\prime }$
meets
${\mathcal{A}}^{\prime }$
meets
 $\ell$
in
$\ell$
in
 $b+1$
(respectively,
$b+1$
(respectively,
 $a+1$
) points, ignoring multiplicity).
$a+1$
) points, ignoring multiplicity).
We use this result to study so-called Fermat arrangements of lines [Reference UrzúaUrz08]. We note that these are also sometimes known as monomial arrangements (see [Reference Suciu, Cogolludo-Augustín and HironakaSuc11, Example 10.6] and [Reference Orlik and TeraoOT92, p. 247]). These arrangements consist of
![]() $3t$
lines (
$3t$
lines (
![]() $t\geqslant 1$
) that are defined by the linear factors of
$t\geqslant 1$
) that are defined by the linear factors of
![]() $f=(x^{t}-y^{t})(x^{t}-z^{t})(y^{t}-z^{t})$
. If
$f=(x^{t}-y^{t})(x^{t}-z^{t})(y^{t}-z^{t})$
. If
![]() $t>3$
or
$t>3$
or
![]() $t=2$
, there are
$t=2$
, there are
![]() $t^{2}$
points where exactly three lines cross and three points where exactly
$t^{2}$
points where exactly three lines cross and three points where exactly
![]() $t$
lines cross, and no other crossing points. When
$t$
lines cross, and no other crossing points. When
![]() $t=3$
, there are 12 points where exactly three lines cross and no other crossing points. When
$t=3$
, there are 12 points where exactly three lines cross and no other crossing points. When
![]() $t=1$
there is only one crossing point, and three lines cross there. The set of points
$t=1$
there is only one crossing point, and three lines cross there. The set of points
![]() $Z_{t}$
dual to the lines is defined by the ideal
$Z_{t}$
dual to the lines is defined by the ideal
![]() $(x^{t}+y^{t}+z^{t},xyz)$
(i.e. the intersection of the Fermat
$(x^{t}+y^{t}+z^{t},xyz)$
(i.e. the intersection of the Fermat
![]() $t$
-ic with the coordinate axes) when
$t$
-ic with the coordinate axes) when
![]() $t$
is odd, and by
$t$
is odd, and by
![]() $(x^{t}-y^{t},z)\cap (x^{t}-z^{t},y)\cap (y^{t}-z^{t},x)$
when
$(x^{t}-y^{t},z)\cap (x^{t}-z^{t},y)\cap (y^{t}-z^{t},x)$
when
![]() $t$
is even. Although the freeness is known (and the splitting types too, in terms of degrees of generators of certain rings of invariants) [Reference Orlik and TeraoOT92, Theorem 6.60 and p. 247], for the reader’s convenience, we include a short proof here as part of the next result.
$t$
is even. Although the freeness is known (and the splitting types too, in terms of degrees of generators of certain rings of invariants) [Reference Orlik and TeraoOT92, Theorem 6.60 and p. 247], for the reader’s convenience, we include a short proof here as part of the next result.
Proposition 6.12. Suppose that the base field
![]() $K$
contains a primitive
$K$
contains a primitive
![]() $t$
th root of unity. If
$t$
th root of unity. If
![]() $t>2$
, then the Fermat line configuration is free, with splitting type
$t>2$
, then the Fermat line configuration is free, with splitting type
![]() $(t+1,2t-2)$
. If
$(t+1,2t-2)$
. If
![]() $t\geqslant 5$
, the dual set of points
$t\geqslant 5$
, the dual set of points
![]() $Z=Z_{t}$
admits unexpected curves of degrees
$Z=Z_{t}$
admits unexpected curves of degrees
![]() $t+2,\ldots ,2t-3$
and we have
$t+2,\ldots ,2t-3$
and we have
![]() $m_{Z}=t+1$
,
$m_{Z}=t+1$
,
![]() $u_{Z}=2t-3$
and, for
$u_{Z}=2t-3$
and, for
![]() $t\geqslant 5$
,
$t\geqslant 5$
,
![]() $t+1<t_{Z}\leqslant (3t-1)/2$
. The unexpected curve of degree
$t+1<t_{Z}\leqslant (3t-1)/2$
. The unexpected curve of degree
![]() $t+2$
is unique and irreducible.
$t+2$
is unique and irreducible.
Proof. We first prove freeness. We will start with a slightly larger line arrangement, and produce the Fermat arrangement by removing two lines. The configuration of lines defined by the factors of
![]() $g=xy(x^{t}-y^{t})(x^{t}-z^{t})(y^{t}-z^{t})$
is supersolvable since every point of intersection of two of the lines is on one of the lines through the point defined by
$g=xy(x^{t}-y^{t})(x^{t}-z^{t})(y^{t}-z^{t})$
is supersolvable since every point of intersection of two of the lines is on one of the lines through the point defined by
![]() $x=0$
and
$x=0$
and
![]() $y=0$
. Thus the line arrangement
$y=0$
. Thus the line arrangement
![]() ${\mathcal{A}}(g)$
is free (see Remark 6.10).
${\mathcal{A}}(g)$
is free (see Remark 6.10).
Now we determine its splitting type,
![]() $(a,b)$
, where
$(a,b)$
, where
![]() $a\leqslant b$
. Observe that there are
$a\leqslant b$
. Observe that there are
![]() $d=3t+2$
lines in
$d=3t+2$
lines in
![]() ${\mathcal{A}}={\mathcal{A}}(g)$
, and the modular point lies on
${\mathcal{A}}={\mathcal{A}}(g)$
, and the modular point lies on
![]() $m=t+2$
lines. Hence by Remark 6.10, the splitting type of
$m=t+2$
lines. Hence by Remark 6.10, the splitting type of
![]() ${\mathcal{A}}$
is
${\mathcal{A}}$
is
![]() $(t+1,2t)$
.
$(t+1,2t)$
.
Next we successively remove the lines defined by
![]() $x$
and
$x$
and
![]() $y$
from
$y$
from
![]() ${\mathcal{A}}$
. First let
${\mathcal{A}}$
. First let
![]() ${\mathcal{A}}^{\prime }={\mathcal{A}}(g/x)$
and let
${\mathcal{A}}^{\prime }={\mathcal{A}}(g/x)$
and let
![]() $A^{\prime \prime }$
be the arrangement obtained by restricting
$A^{\prime \prime }$
be the arrangement obtained by restricting
![]() ${\mathcal{A}}^{\prime }$
to
${\mathcal{A}}^{\prime }$
to
![]() $x=0$
. Clearly
$x=0$
. Clearly
![]() ${\mathcal{A}}^{\prime \prime }$
is free with type
${\mathcal{A}}^{\prime \prime }$
is free with type
![]() $t+1$
, so by the addition–deletion theorem (Theorem 6.11)
$t+1$
, so by the addition–deletion theorem (Theorem 6.11)
![]() ${\mathcal{A}}^{\prime }$
is an arrangement which is free of type
${\mathcal{A}}^{\prime }$
is an arrangement which is free of type
![]() $(t+1,2t-1)$
. Now delete
$(t+1,2t-1)$
. Now delete
![]() $y$
from
$y$
from
![]() ${\mathcal{A}}^{\prime }$
and apply the addition–deletion theorem again to see that
${\mathcal{A}}^{\prime }$
and apply the addition–deletion theorem again to see that
![]() $(x^{t}-y^{t})(x^{t}-z^{t})(y^{t}-z^{t})$
gives a free arrangement of type
$(x^{t}-y^{t})(x^{t}-z^{t})(y^{t}-z^{t})$
gives a free arrangement of type
![]() $(t+1,2t-2)$
.
$(t+1,2t-2)$
.
Thus for the dual set of points
![]() $Z$
we have that
$Z$
we have that
![]() $m_{Z}=t+1$
and
$m_{Z}=t+1$
and
![]() $u_{Z}=2t-3$
. By [Reference HarbourneHar97, Theorem III.1(a)], the
$u_{Z}=2t-3$
. By [Reference HarbourneHar97, Theorem III.1(a)], the
![]() $3t$
points of
$3t$
points of
![]() $Z$
impose independent conditions on forms of degree
$Z$
impose independent conditions on forms of degree
![]() $t+1$
or more, so
$t+1$
or more, so
![]() $h^{0}({\mathcal{I}}_{Z}(j+1))=\binom{j+3}{2}-3t$
for
$h^{0}({\mathcal{I}}_{Z}(j+1))=\binom{j+3}{2}-3t$
for
![]() $j+1\geqslant t+1$
. Thus, taking
$j+1\geqslant t+1$
. Thus, taking
![]() $j=m_{Z}=t+1$
, we have
$j=m_{Z}=t+1$
, we have
![]() $h^{0}({\mathcal{I}}_{Z}(t+2))-\binom{t+2}{2}=5-t$
and since
$h^{0}({\mathcal{I}}_{Z}(t+2))-\binom{t+2}{2}=5-t$
and since
![]() $t_{Z}\geqslant m_{Z}$
, we see that
$t_{Z}\geqslant m_{Z}$
, we see that
![]() $t_{Z}>m_{Z}$
for
$t_{Z}>m_{Z}$
for
![]() $t\geqslant 5$
. Taking
$t\geqslant 5$
. Taking
![]() $j=t+1+s$
, we have
$j=t+1+s$
, we have
![]() $h^{0}({\mathcal{I}}_{Z}(t+2+s))-\binom{t+2+s}{2}=\binom{t+4+s}{2}-3t-\binom{t+2+s}{2}=2s-t+5$
. Since this is positive for
$h^{0}({\mathcal{I}}_{Z}(t+2+s))-\binom{t+2+s}{2}=\binom{t+4+s}{2}-3t-\binom{t+2+s}{2}=2s-t+5$
. Since this is positive for
![]() $s>(t-5)/2$
, we have
$s>(t-5)/2$
, we have
![]() $t_{Z}\leqslant t+1+(t-3)/2=(3t-1)/2$
. Thus
$t_{Z}\leqslant t+1+(t-3)/2=(3t-1)/2$
. Thus
![]() $m_{Z}<t_{Z}\leqslant (3t-1)/2$
for
$m_{Z}<t_{Z}\leqslant (3t-1)/2$
for
![]() $t\geqslant 5$
.
$t\geqslant 5$
.
Now Theorem 1.1 gives that, for
![]() $t\geqslant 5$
, the set
$t\geqslant 5$
, the set
![]() $Z$
admits an unexpected curve of degree
$Z$
admits an unexpected curve of degree
![]() $j$
whenever
$j$
whenever
![]() $t+2\leqslant j\leqslant 2t-2$
. By Corollary 5.6, the unexpected curve
$t+2\leqslant j\leqslant 2t-2$
. By Corollary 5.6, the unexpected curve
![]() $C_{P}=C_{P}(Z)$
of degree
$C_{P}=C_{P}(Z)$
of degree
![]() $t+2$
is unique.
$t+2$
is unique.
It remains to prove that
![]() $C_{P}$
is irreducible. For each point
$C_{P}$
is irreducible. For each point
![]() $q\in Z$
, consider the set
$q\in Z$
, consider the set
![]() $A_{q}$
of points
$A_{q}$
of points
![]() $P\in \mathbb{P}^{2}$
such that
$P\in \mathbb{P}^{2}$
such that
![]() $[I_{(m_{Z}-1)P+Z-q}]_{m_{Z}}\neq 0$
. If none of the sets
$[I_{(m_{Z}-1)P+Z-q}]_{m_{Z}}\neq 0$
. If none of the sets
![]() $A_{q}$
,
$A_{q}$
,
![]() $q\in Z$
, has closure containing a non-empty open set, then
$q\in Z$
, has closure containing a non-empty open set, then
![]() $C_{P}$
is irreducible for general
$C_{P}$
is irreducible for general
![]() $P$
by Corollary 5.17. To prove that this is indeed the case, we argue by contradiction.
$P$
by Corollary 5.17. To prove that this is indeed the case, we argue by contradiction.
Assume that
![]() $A_{q}$
has closure containing a non-empty open set for some
$A_{q}$
has closure containing a non-empty open set for some
![]() $q$
. Then by upper-semicontinuity
$q$
. Then by upper-semicontinuity
![]() $A_{q}$
contains a non-empty open set
$A_{q}$
contains a non-empty open set
![]() $V=V_{q}\subseteq U$
such that for all
$V=V_{q}\subseteq U$
such that for all
![]() $P\in V$
the line through
$P\in V$
the line through
![]() $P$
and
$P$
and
![]() $q$
is a component of
$q$
is a component of
![]() $C_{P}$
(see Corollary 5.6).
$C_{P}$
(see Corollary 5.6).
Note that the points of
![]() $Z$
all are of the form
$Z$
all are of the form
![]() $(0,1,\unicode[STIX]{x1D6FC}^{j})$
or cyclic permutations thereof, where
$(0,1,\unicode[STIX]{x1D6FC}^{j})$
or cyclic permutations thereof, where
![]() $\unicode[STIX]{x1D6FC}$
is a primitive root of
$\unicode[STIX]{x1D6FC}$
is a primitive root of
![]() $x^{t}-1=0$
. Thus the diagonal matrices of the form
$x^{t}-1=0$
. Thus the diagonal matrices of the form
![]() $\operatorname{Diag}(1,1,\unicode[STIX]{x1D6FC}^{i})$
, together with permutations of the variables, give a transitive action on
$\operatorname{Diag}(1,1,\unicode[STIX]{x1D6FC}^{i})$
, together with permutations of the variables, give a transitive action on
![]() $Z$
by linear automorphisms of
$Z$
by linear automorphisms of
![]() $\mathbb{P}^{2}$
. Let
$\mathbb{P}^{2}$
. Let
![]() $q\neq q^{\prime }\in Z$
and let
$q\neq q^{\prime }\in Z$
and let
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{q^{\prime }}$
be one of these linear automorphisms, chosen such that
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{q^{\prime }}$
be one of these linear automorphisms, chosen such that
![]() $\unicode[STIX]{x1D719}(q)=q^{\prime }$
.
$\unicode[STIX]{x1D719}(q)=q^{\prime }$
.
For each
![]() $P\in \unicode[STIX]{x1D719}(V)\cap V$
, we have that the line
$P\in \unicode[STIX]{x1D719}(V)\cap V$
, we have that the line
![]() $L_{q,P}$
through
$L_{q,P}$
through
![]() $q$
and
$q$
and
![]() $P$
is a component of
$P$
is a component of
![]() $C_{P}$
(since
$C_{P}$
(since
![]() $P\in V$
). But
$P\in V$
). But
![]() $P\in \unicode[STIX]{x1D719}(V)$
, so
$P\in \unicode[STIX]{x1D719}(V)$
, so
![]() $P=\unicode[STIX]{x1D719}(Q)$
for some
$P=\unicode[STIX]{x1D719}(Q)$
for some
![]() $Q\in V$
, and
$Q\in V$
, and
![]() $L_{q,Q}$
is a component of
$L_{q,Q}$
is a component of
![]() $C_{Q}$
(since
$C_{Q}$
(since
![]() $Q\in V$
). Uniqueness tells us that
$Q\in V$
). Uniqueness tells us that
![]() $\unicode[STIX]{x1D719}(C_{Q})=C_{P}$
, and so
$\unicode[STIX]{x1D719}(C_{Q})=C_{P}$
, and so
![]() $\unicode[STIX]{x1D719}(L_{q,Q})=L_{\unicode[STIX]{x1D719}(q),\unicode[STIX]{x1D719}(Q)}=L_{\unicode[STIX]{x1D719}(q),P}$
is also a component of
$\unicode[STIX]{x1D719}(L_{q,Q})=L_{\unicode[STIX]{x1D719}(q),\unicode[STIX]{x1D719}(Q)}=L_{\unicode[STIX]{x1D719}(q),P}$
is also a component of
![]() $C_{P}$
.
$C_{P}$
.
Let
where the intersection is over all points
![]() $q^{\prime }\in Z-q$
. By the argument above, for each
$q^{\prime }\in Z-q$
. By the argument above, for each
![]() $P\in W$
, every line through
$P\in W$
, every line through
![]() $P$
and a point of
$P$
and a point of
![]() $Z$
is a component of
$Z$
is a component of
![]() $C_{P}$
. Thus for a general point
$C_{P}$
. Thus for a general point
![]() $P$
,
$P$
,
![]() $C_{P}$
has
$C_{P}$
has
![]() $3t$
linear components, hence
$3t$
linear components, hence
![]() $3t\leqslant \deg (C_{P})=t+2$
. Since
$3t\leqslant \deg (C_{P})=t+2$
. Since
![]() $t\geqslant 5$
, this is impossible and so
$t\geqslant 5$
, this is impossible and so
![]() $C_{P}$
is irreducible.◻
$C_{P}$
is irreducible.◻
Remark 6.13. For
![]() $t\geqslant 3$
, the Fermat line arrangement has the remarkable property that wherever two of the lines cross there is at least one more line through the crossing point. Apart from the trivial case of three or more concurrent lines, only two other complex line arrangements are known with that property. One, due to F. Klein in 1879, has 21 lines with 49 crossing points, 21 of which are where exactly four lines cross and 28 of which are where exactly three lines cross. The other, due to A. Wiman in 1896, has 45 lines with 201 crossing points, 36 of which are where exactly five lines cross, 45 of which are where exactly four lines cross and 120 of which are where exactly three lines cross.
$t\geqslant 3$
, the Fermat line arrangement has the remarkable property that wherever two of the lines cross there is at least one more line through the crossing point. Apart from the trivial case of three or more concurrent lines, only two other complex line arrangements are known with that property. One, due to F. Klein in 1879, has 21 lines with 49 crossing points, 21 of which are where exactly four lines cross and 28 of which are where exactly three lines cross. The other, due to A. Wiman in 1896, has 45 lines with 201 crossing points, 36 of which are where exactly five lines cross, 45 of which are where exactly four lines cross and 120 of which are where exactly three lines cross.
Both of these arrangements are known to be free. Indeed, both arise from reflection groups, and are thus free (see [Reference Orlik and TeraoOT92, Theorem 6.60]). See [Reference HirzebruchHir83, p. 120] for the fact that they both arise from reflection groups. See also [Reference Orlik and TeraoOT92, Example 6.31] for the Klein configuration. As noted in [Reference HarbourneHar18, Example 4.1.6] their splitting types are respectively (9,11) and (19,25); for a more conceptual verification, see [Reference IlardiIla18]. Using this information as well as Macaulay2 [Reference Grayson and StillmanGS] to compute the Hilbert function, we conclude as follows.
– If
 $Z$
is the set of 21 points dual to the 21 lines of the Klein configuration, then
$Z$
is the set of 21 points dual to the 21 lines of the Klein configuration, then
 $m_{Z}=9$
,
$m_{Z}=9$
,
 $u_{Z}=10$
and
$u_{Z}=10$
and
 $t_{Z}=10$
, so
$t_{Z}=10$
, so
 $Z$
has an unexpected curve in degree 10.
$Z$
has an unexpected curve in degree 10.– If
 $Z$
is the set of 45 points dual to the 45 lines of the Wiman configuration, then
$Z$
is the set of 45 points dual to the 45 lines of the Wiman configuration, then
 $m_{Z}=19$
,
$m_{Z}=19$
,
 $u_{Z}=24$
, and
$u_{Z}=24$
, and
 $t_{Z}=22$
, so
$t_{Z}=22$
, so
 $Z$
has unexpected curves in degrees 20, 21, 22, 23 and 24.
$Z$
has unexpected curves in degrees 20, 21, 22, 23 and 24.
Moreover, by Proposition 5.11, the unexpected curve in degree
![]() $m_{Z}+1$
is irreducible for both the Klein and the Wiman line arrangements. See [Reference Bauer, Di Rocco, Harbourne, Huizenga, Seceleanu and SzembergBDHHSS18] for a detailed discussion of these line arrangements and for additional references.
$m_{Z}+1$
is irreducible for both the Klein and the Wiman line arrangements. See [Reference Bauer, Di Rocco, Harbourne, Huizenga, Seceleanu and SzembergBDHHSS18] for a detailed discussion of these line arrangements and for additional references.
We now describe another infinite family of sets of points in which each set has an irreducible unexpected curve. This family is defined over the field of rational numbers. We begin by describing the family of dual line arrangements.
Example 6.14. Let
![]() ${\mathcal{A}}$
be the arrangement of five lines defined by the form
${\mathcal{A}}$
be the arrangement of five lines defined by the form
![]() $xyz(x+y)(x-y)$
. We will denote by
$xyz(x+y)(x-y)$
. We will denote by
![]() $a$
the line
$a$
the line
![]() $x-y=0$
, by
$x-y=0$
, by
![]() $d$
the line
$d$
the line
![]() $x+y=0$
, by
$x+y=0$
, by
![]() $i$
the line at infinity (
$i$
the line at infinity (
![]() $z=0$
), and by
$z=0$
), and by
![]() $h_{1}$
and
$h_{1}$
and
![]() $v_{1}$
the
$v_{1}$
the
![]() $x$
- and
$x$
- and
![]() $y$
-axes, respectively. We remark in passing that there is some flexibility in the choice of these five lines, but that an arbitrary configuration of five lines with the same intersection lattice is not always going to lead to arrangements with the properties that we will describe. (For example, replacing
$y$
-axes, respectively. We remark in passing that there is some flexibility in the choice of these five lines, but that an arbitrary configuration of five lines with the same intersection lattice is not always going to lead to arrangements with the properties that we will describe. (For example, replacing
![]() $x-y$
by any other line through the origin will fail to satisfy the requirement below that
$x-y$
by any other line through the origin will fail to satisfy the requirement below that
![]() $h_{3}$
passes through
$h_{3}$
passes through
![]() $d\cap v_{2}$
.)
$d\cap v_{2}$
.)
We will add lines to
![]() ${\mathcal{A}}$
, and define the line arrangements
${\mathcal{A}}$
, and define the line arrangements
![]() ${\mathcal{A}}_{k}$
inductively, where
${\mathcal{A}}_{k}$
inductively, where
![]() $k$
is the total number of lines that we have added to
$k$
is the total number of lines that we have added to
![]() ${\mathcal{A}}$
. In what follows, for simplicity we will refer to the lines containing the point of intersection of
${\mathcal{A}}$
. In what follows, for simplicity we will refer to the lines containing the point of intersection of
![]() $i$
and
$i$
and
![]() $v_{1}$
as ‘vertical lines’, and the lines containing the point of intersection of
$v_{1}$
as ‘vertical lines’, and the lines containing the point of intersection of
![]() $i$
and
$i$
and
![]() $h_{1}$
as ‘horizontal lines’.
$h_{1}$
as ‘horizontal lines’.
![]() ${\mathcal{A}}_{1}$
is obtained by adding to
${\mathcal{A}}_{1}$
is obtained by adding to
![]() ${\mathcal{A}}$
an arbitrary vertical line,
${\mathcal{A}}$
an arbitrary vertical line,
![]() $v_{2}$
. The next three lines added to
$v_{2}$
. The next three lines added to
![]() ${\mathcal{A}}_{1}$
are then determined:
${\mathcal{A}}_{1}$
are then determined:
![]() $h_{2}$
is the horizontal line through
$h_{2}$
is the horizontal line through
![]() $a\cap v_{2}$
,
$a\cap v_{2}$
,
![]() $v_{3}$
is the vertical line through
$v_{3}$
is the vertical line through
![]() $d\cap h_{2}$
, and
$d\cap h_{2}$
, and
![]() $h_{3}$
is the horizontal line through
$h_{3}$
is the horizontal line through
![]() $a\cap v_{3}$
. The key fact is that
$a\cap v_{3}$
. The key fact is that
![]() $h_{3}$
also passes through
$h_{3}$
also passes through
![]() $d\cap v_{2}$
. This gives the arrangements
$d\cap v_{2}$
. This gives the arrangements
![]() ${\mathcal{A}}_{1},{\mathcal{A}}_{2},{\mathcal{A}}_{3},{\mathcal{A}}_{4}$
.
${\mathcal{A}}_{1},{\mathcal{A}}_{2},{\mathcal{A}}_{3},{\mathcal{A}}_{4}$
.
We continue in this way, taking an arbitrary vertical line
![]() $v_{4}$
and adding a horizontal line
$v_{4}$
and adding a horizontal line
![]() $h_{4}$
, a vertical line
$h_{4}$
, a vertical line
![]() $v_{5}$
, and another horizontal line
$v_{5}$
, and another horizontal line
![]() $h_{5}$
in the manner just described to obtain configurations
$h_{5}$
in the manner just described to obtain configurations
![]() ${\mathcal{A}}_{5},{\mathcal{A}}_{6},{\mathcal{A}}_{7},{\mathcal{A}}_{8}$
. Of special interest to us will be the configurations
${\mathcal{A}}_{5},{\mathcal{A}}_{6},{\mathcal{A}}_{7},{\mathcal{A}}_{8}$
. Of special interest to us will be the configurations
![]() ${\mathcal{A}}_{n}$
where
${\mathcal{A}}_{n}$
where
![]() $n$
is a multiple of 4. In particular,
$n$
is a multiple of 4. In particular,
![]() ${\mathcal{A}}_{4(k+1)}$
is obtained from
${\mathcal{A}}_{4(k+1)}$
is obtained from
![]() ${\mathcal{A}}_{4k}$
by adding the lines
${\mathcal{A}}_{4k}$
by adding the lines
![]() $v_{2k+2},h_{2k+2},v_{2k+3},h_{2k+3}$
in that order. See Figure 4 for an example of the line configuration.
$v_{2k+2},h_{2k+2},v_{2k+3},h_{2k+3}$
in that order. See Figure 4 for an example of the line configuration.
Notice that
![]() ${\mathcal{A}}_{4}$
is the
${\mathcal{A}}_{4}$
is the
![]() $B_{3}$
arrangement, so our example includes the one studied in [Reference Di Gennaro, Ilardi and VallèsDIV14] as a special case.
$B_{3}$
arrangement, so our example includes the one studied in [Reference Di Gennaro, Ilardi and VallèsDIV14] as a special case.

Figure 4. The line arrangement
![]() ${\mathcal{A}}_{12}$
(the line at infinity is not shown).
${\mathcal{A}}_{12}$
(the line at infinity is not shown).
One can easily check using Theorem 6.11 that these configurations are all free, with splitting types as follows:
–
 $(2k+1,2k+3)$
for
$(2k+1,2k+3)$
for
 ${\mathcal{A}}_{4k}$
;
${\mathcal{A}}_{4k}$
;–
 $(2k+2,2k+3)$
for
$(2k+2,2k+3)$
for
 ${\mathcal{A}}_{4k+1}$
;
${\mathcal{A}}_{4k+1}$
;–
 $(2k+3,2k+3)$
for
$(2k+3,2k+3)$
for
 ${\mathcal{A}}_{4k+2}$
;
${\mathcal{A}}_{4k+2}$
;–
 $(2k+3,2k+4)$
for
$(2k+3,2k+4)$
for
 ${\mathcal{A}}_{4k+3}$
.
${\mathcal{A}}_{4k+3}$
.
Let us denote by
![]() $Z_{n}$
the set of
$Z_{n}$
the set of
![]() $n+5$
points dual to the line arrangement
$n+5$
points dual to the line arrangement
![]() ${\mathcal{A}}_{n}$
.
${\mathcal{A}}_{n}$
.
Proposition 6.15. If
![]() $k\geqslant 1$
, then
$k\geqslant 1$
, then
![]() $Z_{4k}$
has multiplicity index
$Z_{4k}$
has multiplicity index
![]() $m_{Z_{4k}}=2k+1$
, speciality index
$m_{Z_{4k}}=2k+1$
, speciality index
![]() $u_{Z_{4k}}=2k+2$
, and
$u_{Z_{4k}}=2k+2$
, and
![]() $Z_{4k}$
admits a unique unexpected curve. It is irreducible and has degree
$Z_{4k}$
admits a unique unexpected curve. It is irreducible and has degree
![]() $m_{Z_{4k}}+1=2k+2$
.
$m_{Z_{4k}}+1=2k+2$
.
Proof. Since
![]() ${\mathcal{A}}_{4k}$
has splitting type
${\mathcal{A}}_{4k}$
has splitting type
![]() $(2k+1,2k+3)$
, we get the claimed values of
$(2k+1,2k+3)$
, we get the claimed values of
![]() $m_{Z_{4k}}$
and
$m_{Z_{4k}}$
and
![]() $u_{Z_{4k}}$
. Note that at most four lines of
$u_{Z_{4k}}$
. Note that at most four lines of
![]() $A_{n}$
pass through a point. Hence Theorem 1.2 gives that
$A_{n}$
pass through a point. Hence Theorem 1.2 gives that
![]() $Z_{4k}$
admits a unique unexpected curve of degree
$Z_{4k}$
admits a unique unexpected curve of degree
![]() $2k+2$
. It remains to show its irreducibility.
$2k+2$
. It remains to show its irreducibility.
To this end we use Corollary 5.17. It shows that we are done once we have proven that removing any line
![]() $L$
from the arrangement
$L$
from the arrangement
![]() ${\mathcal{A}}_{4k}$
gives an arrangement
${\mathcal{A}}_{4k}$
gives an arrangement
![]() ${\mathcal{A}}_{4k}\setminus L$
, with splitting type
${\mathcal{A}}_{4k}\setminus L$
, with splitting type
![]() $(2k+1,2k+2)$
.
$(2k+1,2k+2)$
.
First, let
![]() $L$
be any line of
$L$
be any line of
![]() ${\mathcal{A}}_{4k}$
other than the line at infinity
${\mathcal{A}}_{4k}$
other than the line at infinity
![]() $i$
, defined by
$i$
, defined by
![]() $z=0$
. Then
$z=0$
. Then
![]() $L$
meets the other lines of
$L$
meets the other lines of
![]() ${\mathcal{A}}_{4k}$
in
${\mathcal{A}}_{4k}$
in
![]() $2k+2$
points. Hence addition–deletion yields that
$2k+2$
points. Hence addition–deletion yields that
![]() ${\mathcal{A}}_{4k}\setminus L$
is a free arrangement with splitting type
${\mathcal{A}}_{4k}\setminus L$
is a free arrangement with splitting type
![]() $(2k+1,2k+2)$
, as claimed.
$(2k+1,2k+2)$
, as claimed.
Second, consider the line
![]() $i$
, and set
$i$
, and set
![]() ${\mathcal{A}}^{\prime }={\mathcal{A}}_{4k}\setminus i$
. The line
${\mathcal{A}}^{\prime }={\mathcal{A}}_{4k}\setminus i$
. The line
![]() $i$
meets the lines in
$i$
meets the lines in
![]() ${\mathcal{A}}^{\prime }$
in four points. Hence, if
${\mathcal{A}}^{\prime }$
in four points. Hence, if
![]() $k=1$
(i.e.
$k=1$
(i.e.
![]() ${\mathcal{A}}_{4}$
is the
${\mathcal{A}}_{4}$
is the
![]() $B_{3}$
configuration), then we conclude as in the first case that
$B_{3}$
configuration), then we conclude as in the first case that
![]() ${\mathcal{A}}^{\prime }$
has splitting type
${\mathcal{A}}^{\prime }$
has splitting type
![]() $(3,4)$
, as desired. Let
$(3,4)$
, as desired. Let
![]() $k\geqslant 2$
. Now we need a different argument.
$k\geqslant 2$
. Now we need a different argument.
Let
![]() $h$
be the product of
$h$
be the product of
![]() $4k+3$
linear forms such that
$4k+3$
linear forms such that
![]() ${\mathcal{A}}_{4k}={\mathcal{A}}(z(x^{2}-y^{2})h)$
, and so
${\mathcal{A}}_{4k}={\mathcal{A}}(z(x^{2}-y^{2})h)$
, and so
![]() ${\mathcal{A}}^{\prime }={\mathcal{A}}((x^{2}-y^{2})h)$
. As observed above, the arrangement
${\mathcal{A}}^{\prime }={\mathcal{A}}((x^{2}-y^{2})h)$
. As observed above, the arrangement
![]() ${\mathcal{A}}(z(x-y)h)$
is free with splitting type
${\mathcal{A}}(z(x-y)h)$
is free with splitting type
![]() $(2k+1,2k+2)$
. Since the line defined by
$(2k+1,2k+2)$
. Since the line defined by
![]() $x-y$
meets
$x-y$
meets
![]() ${\mathcal{A}}(zh)$
in
${\mathcal{A}}(zh)$
in
![]() $2k+2$
points, we see that
$2k+2$
points, we see that
![]() ${\mathcal{A}}(zh)$
is free with splitting type
${\mathcal{A}}(zh)$
is free with splitting type
![]() $(2k+1,2k+1)$
. The line
$(2k+1,2k+1)$
. The line
![]() $z=0$
meets the lines of
$z=0$
meets the lines of
![]() ${\mathcal{A}}(h)$
in two points. Hence, the logarithmic bundles are related by the exact sequence (see Sequence (6.1))
${\mathcal{A}}(h)$
in two points. Hence, the logarithmic bundles are related by the exact sequence (see Sequence (6.1))
Since
![]() ${\mathcal{D}}(hz)\cong {\mathcal{O}}_{\mathbb{P}^{2}}^{2}(-2k-1)$
and
${\mathcal{D}}(hz)\cong {\mathcal{O}}_{\mathbb{P}^{2}}^{2}(-2k-1)$
and
![]() ${\mathcal{D}}(h)_{\text{norm}}={\mathcal{D}}(h)(2k)$
, we conclude that
${\mathcal{D}}(h)_{\text{norm}}={\mathcal{D}}(h)(2k)$
, we conclude that
![]() $H^{0}({\mathcal{D}}(h)_{\text{norm}})=0$
, and so
$H^{0}({\mathcal{D}}(h)_{\text{norm}})=0$
, and so
![]() ${\mathcal{D}}(h)$
is stable by Lemma 6.3. Now Lemma 6.5 shows that
${\mathcal{D}}(h)$
is stable by Lemma 6.3. Now Lemma 6.5 shows that
![]() ${\mathcal{A}}((x-y)h)$
is semistable. Hence, its splitting type is
${\mathcal{A}}((x-y)h)$
is semistable. Hence, its splitting type is
![]() $(2k+1,2k+1)$
by the Grauert–Mülich theorem. We have already seen that
$(2k+1,2k+1)$
by the Grauert–Mülich theorem. We have already seen that
![]() ${\mathcal{A}}_{4k}={\mathcal{A}}(z(x^{2}-y^{2})h)$
has splitting type
${\mathcal{A}}_{4k}={\mathcal{A}}(z(x^{2}-y^{2})h)$
has splitting type
![]() $(2k+1,2k+3)$
. Using this information, Lemma 5.13 yields that
$(2k+1,2k+3)$
. Using this information, Lemma 5.13 yields that
![]() ${\mathcal{A}}^{\prime }={\mathcal{A}}((x^{2}-y^{2})h)$
has splitting type
${\mathcal{A}}^{\prime }={\mathcal{A}}((x^{2}-y^{2})h)$
has splitting type
![]() $(2k+1,2k+2)$
. This completes the argument.◻
$(2k+1,2k+2)$
. This completes the argument.◻
Remark 6.16. Let
![]() $Z\subset \mathbb{P}^{2}$
be a set of points with
$Z\subset \mathbb{P}^{2}$
be a set of points with
![]() $2m_{Z}+2\leqslant |Z|$
. Let
$2m_{Z}+2\leqslant |Z|$
. Let
![]() $P$
be a general point. Then
$P$
be a general point. Then
![]() $[I_{Z+m_{Z}P}]_{m_{Z}+1}$
determines a unique curve
$[I_{Z+m_{Z}P}]_{m_{Z}+1}$
determines a unique curve
![]() $C_{P}$
. This curve depends on
$C_{P}$
. This curve depends on
![]() $P$
, and only the degree is necessarily invariant as
$P$
, and only the degree is necessarily invariant as
![]() $P$
moves. Lemma 5.13 shows that for any given
$P$
moves. Lemma 5.13 shows that for any given
![]() $P$
, if
$P$
, if
![]() $Q\in C_{P}(Z)$
then
$Q\in C_{P}(Z)$
then
![]() $m_{Z+Q,P}=m_{Z}$
. Notice that this is not necessarily equal to
$m_{Z+Q,P}=m_{Z}$
. Notice that this is not necessarily equal to
![]() $m_{Z+Q}$
. However, if there is a point
$m_{Z+Q}$
. However, if there is a point
![]() $Q\notin Z$
such that
$Q\notin Z$
such that
![]() $Q\in \bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
then we do obtain
$Q\in \bigcap _{P\in \mathbb{P}^{2}}C_{P}(Z)$
then we do obtain
![]() $m_{Z}=m_{Z+Q}$
.
$m_{Z}=m_{Z+Q}$
.
We find it very surprising that such a point
![]() $Q$
can exist, that is, that there can be a new point common to every curve in the family
$Q$
can exist, that is, that there can be a new point common to every curve in the family
![]() $\{C_{P}\}$
(which is not a linear system) as
$\{C_{P}\}$
(which is not a linear system) as
![]() $P$
varies in
$P$
varies in
![]() $\mathbb{P}^{2}$
. Nevertheless, we saw this already in Example 6.2, and Corollary 5.17 shows that this has to happen even for each point
$\mathbb{P}^{2}$
. Nevertheless, we saw this already in Example 6.2, and Corollary 5.17 shows that this has to happen even for each point
![]() $Q$
of
$Q$
of
![]() $Z$
when passing from
$Z$
when passing from
![]() $Z-Q$
to
$Z-Q$
to
![]() $Z$
, provided
$Z$
, provided
![]() $2m_{Z}+3\leqslant |Z|$
and the curve
$2m_{Z}+3\leqslant |Z|$
and the curve
![]() $C_{P}$
is irreducible. Indeed, the converse is true as well, and we used it to prove the irreducibility of the unexpected curve in Proposition 6.15.
$C_{P}$
is irreducible. Indeed, the converse is true as well, and we used it to prove the irreducibility of the unexpected curve in Proposition 6.15.
7 Connections and corrections
The paper [Reference Di Gennaro, Ilardi and VallèsDIV14] introduced connections between the splitting type of the syzygy bundle and two seemingly unrelated topics: the strong Lefschetz property for certain ideals of powers of linear forms and Terao’s conjecture for planar arrangements. The first version of the current paper was inspired by [Reference Di Gennaro, Ilardi and VallèsDIV14], but it pointed out some inaccuracies in that paper. The paper [Reference Di Gennaro and IlardiDI18] continued this investigation by extending somewhat the results of [Reference Di Gennaro, Ilardi and VallèsDIV14] and correcting most of the issues that we had pointed out. Thus in this section it is important to keep on record the example from our first version that was cited in [Reference Di Gennaro and IlardiDI18] as motivating their changes (see Example 7.3 below), and to expand on the new observations in [Reference Di Gennaro and IlardiDI18] about the connections to unexpected curves.
7.1 Strong Lefschetz property
We first recall the main definition.
Definition 7.1. An artinian algebra
![]() $A=R/I$
satisfies the strong Lefschetz property (SLP) at range
$A=R/I$
satisfies the strong Lefschetz property (SLP) at range
![]() $k$
in degree
$k$
in degree
![]() $d$
if, for a general linear form
$d$
if, for a general linear form
![]() $L$
, the homomorphism
$L$
, the homomorphism
![]() $\times L^{k}:[A]_{d}\rightarrow [A]_{d+k}$
has maximal rank. We say that
$\times L^{k}:[A]_{d}\rightarrow [A]_{d+k}$
has maximal rank. We say that
![]() $A$
fails the SLP at range
$A$
fails the SLP at range
![]() $k$
in degree
$k$
in degree
![]() $d$
by
$d$
by
![]() $\unicode[STIX]{x1D6FF}>0$
if, for a general linear form
$\unicode[STIX]{x1D6FF}>0$
if, for a general linear form
![]() $L$
, the multiplication
$L$
, the multiplication
![]() $\times L^{k}:[A]_{d}\rightarrow [A]_{d+k}$
has rank
$\times L^{k}:[A]_{d}\rightarrow [A]_{d+k}$
has rank
![]() $\min \{h_{A}(d),h_{A}(d+k)\}-\unicode[STIX]{x1D6FF}$
.
$\min \{h_{A}(d),h_{A}(d+k)\}-\unicode[STIX]{x1D6FF}$
.
We also recall the following important result.
Theorem 7.2 [Reference Emsalem and IarrobinoEI95].
Let
![]() ${\wp}_{1},\ldots ,{\wp}_{m}$
be ideals of
${\wp}_{1},\ldots ,{\wp}_{m}$
be ideals of
![]() $m$
distinct points in
$m$
distinct points in
![]() $\mathbb{P}^{n-1}$
. Choose positive integers
$\mathbb{P}^{n-1}$
. Choose positive integers
![]() $a_{1},\ldots ,a_{m}$
, and let
$a_{1},\ldots ,a_{m}$
, and let
![]() $(l_{1}^{a_{1}},\ldots ,l_{m}^{a_{m}})\subset R=k[x_{1},\ldots ,x_{n}]$
be the ideal generated by powers of the linear forms that are dual to the points
$(l_{1}^{a_{1}},\ldots ,l_{m}^{a_{m}})\subset R=k[x_{1},\ldots ,x_{n}]$
be the ideal generated by powers of the linear forms that are dual to the points
![]() ${\wp}_{i}$
. Then, for any integer
${\wp}_{i}$
. Then, for any integer
![]() $j\geqslant \max \{a_{i}\}$
,
$j\geqslant \max \{a_{i}\}$
,
The following example was produced in the first version of this paper, which led to the identification of a missing hypothesis in [Reference Di Gennaro, Ilardi and VallèsDIV14, Proposition 7.2]; this example is now cited in [Reference Di Gennaro and IlardiDI18], where a rectified statement of the result is given which we reproduce below as Proposition 7.4.
Example 7.3. Let
![]() $1\leqslant a\leqslant b-1$
. Define the arrangement
$1\leqslant a\leqslant b-1$
. Define the arrangement
![]() ${\mathcal{A}}_{a,b}$
by the lines
${\mathcal{A}}_{a,b}$
by the lines
It is easy to see
![]() ${\mathcal{A}}_{a,b}$
is supersolvable, hence free. Moreover, using addition–deletion (or Remark 6.10) it is easy to see that the splitting type is
${\mathcal{A}}_{a,b}$
is supersolvable, hence free. Moreover, using addition–deletion (or Remark 6.10) it is easy to see that the splitting type is
![]() $(a,b)$
. Let
$(a,b)$
. Let
![]() $Z$
be the set of points dual to these lines. For a concrete example, we will take
$Z$
be the set of points dual to these lines. For a concrete example, we will take
![]() $a=3$
and
$a=3$
and
![]() $b=13$
(see Figure 5).
$b=13$
(see Figure 5).

Figure 5. The points
![]() $Z$
dual to
$Z$
dual to
![]() ${\mathcal{A}}_{3,13}$
.
${\mathcal{A}}_{3,13}$
.
The associated splitting type is
![]() $(3,13)$
; in particular, the derivation bundle is unstable. It is not hard to compute the Hilbert function of this set of points and to verify that
$(3,13)$
; in particular, the derivation bundle is unstable. It is not hard to compute the Hilbert function of this set of points and to verify that
![]() $t_{Z}=3$
. Since the splitting type immediately gives
$t_{Z}=3$
. Since the splitting type immediately gives
![]() $m_{Z}=3$
, we see from Theorem 1.1 that
$m_{Z}=3$
, we see from Theorem 1.1 that
![]() $Z$
does not admit an unexpected curve.
$Z$
does not admit an unexpected curve.
Consider the ideal
Its Hilbert function is
as can be verified either on a computer or by hand. For a general linear form
![]() $L$
, the Hilbert function of
$L$
, the Hilbert function of
![]() $R/(I,L^{2})$
is
$R/(I,L^{2})$
is
Since
is exact, a comparison of these two Hilbert functions shows that
![]() $\times L^{2}:[R/I]_{i-2}\rightarrow [R/I]_{i}$
has maximal rank for all
$\times L^{2}:[R/I]_{i-2}\rightarrow [R/I]_{i}$
has maximal rank for all
![]() $i$
. Thus
$i$
. Thus
![]() $R/I$
does have the SLP in range 2. This shows that in order for the SLP to fail in range 2, it is not enough to have an unbalanced splitting type.
$R/I$
does have the SLP in range 2. This shows that in order for the SLP to fail in range 2, it is not enough to have an unbalanced splitting type.
Proposition 7.4 [Reference Di Gennaro and IlardiDI18, Proposition 22].
Let
![]() $I\subset R=\mathbb{C}[x,y,z]$
be an artinian ideal generated by
$I\subset R=\mathbb{C}[x,y,z]$
be an artinian ideal generated by
![]() $2d+1$
polynomials
$2d+1$
polynomials
![]() $\ell _{1}^{d},\ldots ,\ell _{2d+1}^{d}$
, where
$\ell _{1}^{d},\ldots ,\ell _{2d+1}^{d}$
, where
![]() $\ell _{i}$
are distinct linear forms. Let
$\ell _{i}$
are distinct linear forms. Let
![]() $Z$
be the corresponding points dual to the
$Z$
be the corresponding points dual to the
![]() $\ell _{i}$
. If
$\ell _{i}$
. If
![]() $Z$
contains no more than
$Z$
contains no more than
![]() $d+1$
points on a line then the following conditions are equivalent.
$d+1$
points on a line then the following conditions are equivalent.
(i) The algebra
 $R/I$
fails the SLP at range 2 in degree
$R/I$
fails the SLP at range 2 in degree
 $d-2$
,
$d-2$
,(ii) The derivation bundle
 ${\mathcal{D}}_{0}(Z)$
is unstable with splitting type
${\mathcal{D}}_{0}(Z)$
is unstable with splitting type
 $(d-s,d+s)$
for some
$(d-s,d+s)$
for some
 $s\geqslant 1$
.
$s\geqslant 1$
.
The new ingredient in this result compared to [Reference Di Gennaro, Ilardi and VallèsDIV14, Proposition 7.2] is the condition on points on a line. The authors observe that it is related to the question of whether the forms
![]() $\ell _{i}^{d}$
are all linearly independent, via Theorem 7.2, but we omit the details here. In particular, it no longer applies to Example 7.3 because of the combination of the numerical constraint and the condition on collinear points. Note that we are maintaining their notation, so their
$\ell _{i}^{d}$
are all linearly independent, via Theorem 7.2, but we omit the details here. In particular, it no longer applies to Example 7.3 because of the combination of the numerical constraint and the condition on collinear points. Note that we are maintaining their notation, so their
![]() $d$
(the degree of the forms) is not the same as our
$d$
(the degree of the forms) is not the same as our
![]() $d$
(the number of points).
$d$
(the number of points).
In the following result, we generalize this in two ways. First, there is no numerical assumption. Second, we show that failure of the SLP is equivalent to the existence of an unexpected curve.
Theorem 7.5. Let
![]() ${\mathcal{A}}(f)$
be a line arrangement in
${\mathcal{A}}(f)$
be a line arrangement in
![]() $\mathbb{P}^{2}$
, where
$\mathbb{P}^{2}$
, where
![]() $f=L_{1}\cdots L_{d}$
, and let
$f=L_{1}\cdots L_{d}$
, and let
![]() $Z$
be the set of points in
$Z$
be the set of points in
![]() $\mathbb{P}^{2}$
dual to these lines. Then
$\mathbb{P}^{2}$
dual to these lines. Then
![]() $Z$
has an unexpected curve of degree
$Z$
has an unexpected curve of degree
![]() $j+1$
if and only if
$j+1$
if and only if
![]() $R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
fails the SLP in range 2 and degree
$R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
fails the SLP in range 2 and degree
![]() $j-1$
.
$j-1$
.
Proof. Let
![]() $P$
be a general point in
$P$
be a general point in
![]() $\mathbb{P}^{2}$
, and let
$\mathbb{P}^{2}$
, and let
![]() $L$
be the linear form dual to
$L$
be the linear form dual to
![]() $P$
. Note that the algebra
$P$
. Note that the algebra
![]() $R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
is artinian if and only if the points of
$R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
is artinian if and only if the points of
![]() $Z$
are not collinear. Hence, by Theorem 1.2, we may assume that
$Z$
are not collinear. Hence, by Theorem 1.2, we may assume that
![]() $R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
is artinian.
$R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
is artinian.
Consider the multiplication map
Clearly
![]() $\dim _{K}[R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})]_{j-1}=\binom{j+1}{2}$
. By Macaulay duality,
$\dim _{K}[R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})]_{j-1}=\binom{j+1}{2}$
. By Macaulay duality,
Hence, the expected dimension of the cokernel is
![]() $\max \{h^{0}({\mathcal{I}}_{Z}(j+1))-\binom{j+1}{2},0\}$
. In other words,
$\max \{h^{0}({\mathcal{I}}_{Z}(j+1))-\binom{j+1}{2},0\}$
. In other words,
![]() $R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
fails the SLP in range 2 and degree
$R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
fails the SLP in range 2 and degree
![]() $j-1$
if and only if
$j-1$
if and only if
Now, the cokernel of the considered multiplication by
![]() $L^{2}$
is
$L^{2}$
is
![]() $[R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1},L^{2})]_{j+1}$
. By Theorem 7.2, its dimension is
$[R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1},L^{2})]_{j+1}$
. By Theorem 7.2, its dimension is
![]() $h^{0}(({\mathcal{I}}_{Z}\otimes I_{P}^{j})(j+1))$
. Thus, we have shown that
$h^{0}(({\mathcal{I}}_{Z}\otimes I_{P}^{j})(j+1))$
. Thus, we have shown that
![]() $R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
fails the SLP in range 2 and degree
$R/(L_{1}^{j+1},\ldots ,L_{d}^{j+1})$
fails the SLP in range 2 and degree
![]() $j-1$
if and only if
$j-1$
if and only if
that is,
![]() $Z$
admits an unexpected curve of degree
$Z$
admits an unexpected curve of degree
![]() $j+1$
.◻
$j+1$
.◻
Remark 7.6. The last result in [Reference Di Gennaro and IlardiDI18], namely Corollary 25, recovers a special case of our Theorem 7.5. In [Reference Di Gennaro and IlardiDI18, Corollary 25], the degree
![]() $d$
where SLP fails in range 2 is strictly related to the number of points
$d$
where SLP fails in range 2 is strictly related to the number of points
![]() $2d+1$
, and there is also an assumption that not too many of the points of
$2d+1$
, and there is also an assumption that not too many of the points of
![]() $Z$
are collinear (because they need the points to impose independent conditions on forms of degree
$Z$
are collinear (because they need the points to impose independent conditions on forms of degree
![]() $d$
). Our Theorem 7.5 requires only that there is an unexpected curve of degree
$d$
). Our Theorem 7.5 requires only that there is an unexpected curve of degree
![]() $j+1$
(and then it is a consequence that
$j+1$
(and then it is a consequence that
![]() $h_{Z}(t_{Z})=|Z|$
, that is, that the points of
$h_{Z}(t_{Z})=|Z|$
, that is, that the points of
![]() $Z$
impose independent conditions on forms of degree
$Z$
impose independent conditions on forms of degree
![]() $t_{Z}$
).
$t_{Z}$
).
Corollary 7.7. Let
![]() ${\mathcal{A}}(f)$
be a line arrangement in
${\mathcal{A}}(f)$
be a line arrangement in
![]() $\mathbb{P}^{2}$
with splitting type
$\mathbb{P}^{2}$
with splitting type
![]() $(a,b)$
, where
$(a,b)$
, where
![]() $2\leqslant a\leqslant b$
. Let
$2\leqslant a\leqslant b$
. Let
![]() $f=L_{1}\cdots L_{d}$
and assume that the ideal generated by the
$f=L_{1}\cdots L_{d}$
and assume that the ideal generated by the
![]() $(a+1)$
th partial derivatives of
$(a+1)$
th partial derivatives of
![]() $f$
is artinian. Then
$f$
is artinian. Then
![]() $b-a\geqslant 2$
if and only if
$b-a\geqslant 2$
if and only if
![]() $R/(L_{1}^{a+1},\ldots ,L_{d}^{a+1})$
fails the SLP at range 2 in degree
$R/(L_{1}^{a+1},\ldots ,L_{d}^{a+1})$
fails the SLP at range 2 in degree
![]() $a-1$
.
$a-1$
.
7.2 Terao’s conjecture
It is natural to wonder to what extent numerical invariants of a line arrangement are determined by its combinatorial properties. The latter are captured by the incidence lattice of the arrangement. It consists of all intersections of lines, ordered by reverse inclusion. For example, if
![]() ${\mathcal{A}}(f)$
and
${\mathcal{A}}(f)$
and
![]() ${\mathcal{A}}(g)$
are two line arrangements in
${\mathcal{A}}(g)$
are two line arrangements in
![]() $\mathbb{P}^{2}$
with the same incidence lattice, then it follows that the Jacobian ideals of
$\mathbb{P}^{2}$
with the same incidence lattice, then it follows that the Jacobian ideals of
![]() $f$
and
$f$
and
![]() $g$
have the same degree.
$g$
have the same degree.
One of the main open problems is to decide whether freeness of hyperplane arrangements is a combinatorial property. It is open even for line arrangements.
Conjecture 7.8 (Terao).
Freeness of a line arrangement depends only on its incidence lattice.
The connection between Terao’s conjecture and the multiplication by the square of a general linear form on certain quotient algebras was first studied in [Reference Di Gennaro, Ilardi and VallèsDIV14]. Here we want to use our earlier results to state an equivalent version of this conjecture. At the same time we remark on the relevant results and assertions of [Reference Di Gennaro, Ilardi and VallèsDIV14]. We need some preparation.
Consider a vector bundle
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
![]() $\mathbb{P}^{2}$
of rank
$\mathbb{P}^{2}$
of rank
![]() $2$
. As pointed out above, its restriction to a general line
$2$
. As pointed out above, its restriction to a general line
![]() $L$
has the form
$L$
has the form
![]() ${\mathcal{O}}_{L}(-a)\oplus {\mathcal{O}}_{L}(-b)$
for some integers
${\mathcal{O}}_{L}(-a)\oplus {\mathcal{O}}_{L}(-b)$
for some integers
![]() $a\leqslant b$
. The pair
$a\leqslant b$
. The pair
![]() $(a,b)$
is the (generic) splitting type of
$(a,b)$
is the (generic) splitting type of
![]() ${\mathcal{E}}$
. If
${\mathcal{E}}$
. If
![]() ${\mathcal{E}}$
splits as a direct sum of line bundles, then
${\mathcal{E}}$
splits as a direct sum of line bundles, then
![]() $c_{2}({\mathcal{E}})=ab$
, where
$c_{2}({\mathcal{E}})=ab$
, where
![]() $c_{2}({\mathcal{E}})$
denotes the second Chern class of
$c_{2}({\mathcal{E}})$
denotes the second Chern class of
![]() ${\mathcal{E}}$
. The converse is true as well.
${\mathcal{E}}$
. The converse is true as well.
Theorem 7.9 [Reference YoshinagaYos14, Theorem 1.45].
For every rank-
![]() $2$
vector bundle
$2$
vector bundle
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
![]() $\mathbb{P}^{2}$
with generic splitting type
$\mathbb{P}^{2}$
with generic splitting type
![]() $(a,b)$
, one has
$(a,b)$
, one has
![]() $c_{2}({\mathcal{E}})\geqslant ab$
. Furthermore, equality is true if and only if
$c_{2}({\mathcal{E}})\geqslant ab$
. Furthermore, equality is true if and only if
![]() ${\mathcal{E}}$
splits as a direct sum of line bundles.
${\mathcal{E}}$
splits as a direct sum of line bundles.
Recall that the derivation bundle
![]() ${\mathcal{D}}(f)$
of a line arrangement
${\mathcal{D}}(f)$
of a line arrangement
![]() ${\mathcal{A}}(f)$
is the sheafification of the module
${\mathcal{A}}(f)$
is the sheafification of the module
![]() $D(f)$
, defined by the exact sequence
$D(f)$
, defined by the exact sequence
It follows that
We are ready to establish the following result, which is implicitly used in [Reference Di Gennaro, Ilardi and VallèsDIV14]. We thank the referee for pointing out that [Reference Faenzi and VallèsFV14, Corollary 4.5] implies not only this result but in fact an even stronger statement which involves only the number of triple points (counted with suitable multiplicity) in the arrangement rather than assuming the same incidence lattice. For the reader’s convenience, we also provide our original short and self-contained proof.
Proposition 7.10. Let
![]() ${\mathcal{A}}(f)$
and
${\mathcal{A}}(f)$
and
![]() ${\mathcal{A}}(g)$
be two line arrangements with the same incidence lattice. Assume
${\mathcal{A}}(g)$
be two line arrangements with the same incidence lattice. Assume
![]() ${\mathcal{A}}(f)$
is free with splitting type
${\mathcal{A}}(f)$
is free with splitting type
![]() $(a,b)$
. Then the following hold.
$(a,b)$
. Then the following hold.
(a) The arrangement
 ${\mathcal{A}}(g)$
is free if and only if
${\mathcal{A}}(g)$
is free if and only if
 ${\mathcal{D}}(g)$
has the same splitting type as
${\mathcal{D}}(g)$
has the same splitting type as
 ${\mathcal{D}}(f)$
.
${\mathcal{D}}(f)$
.(b) If
 ${\mathcal{A}}(g)$
is not free, then the splitting type of
${\mathcal{A}}(g)$
is not free, then the splitting type of
 ${\mathcal{D}}(g)$
is
${\mathcal{D}}(g)$
is
 $(a-s,b+s)$
for some positive integer
$(a-s,b+s)$
for some positive integer
 $s$
.
$s$
.
Proof. Set
![]() $d=\deg f$
. By Theorem 7.9, since
$d=\deg f$
. By Theorem 7.9, since
![]() ${\mathcal{A}}(f)$
is free we get
${\mathcal{A}}(f)$
is free we get
![]() $c_{2}({\mathcal{D}}(f))=ab$
. Since the arrangements have the same incidence lattice, Equation (7.1) gives
$c_{2}({\mathcal{D}}(f))=ab$
. Since the arrangements have the same incidence lattice, Equation (7.1) gives
![]() $c_{2}({\mathcal{D}}(g))=c_{2}({\mathcal{D}}(f))$
. Combining, we obtain
$c_{2}({\mathcal{D}}(g))=c_{2}({\mathcal{D}}(f))$
. Combining, we obtain
![]() $c_{2}({\mathcal{D}}(g))=ab$
.
$c_{2}({\mathcal{D}}(g))=ab$
.
Since
![]() $f$
and
$f$
and
![]() $g$
have the same degree, the sum of the integers in the splitting type for
$g$
have the same degree, the sum of the integers in the splitting type for
![]() ${\mathcal{D}}(f)$
must be equal to the sum for
${\mathcal{D}}(f)$
must be equal to the sum for
![]() ${\mathcal{D}}(g)$
, that is, the splitting type for
${\mathcal{D}}(g)$
, that is, the splitting type for
![]() ${\mathcal{D}}(g)$
is
${\mathcal{D}}(g)$
is
![]() $(a-s,b+s)$
for some integer
$(a-s,b+s)$
for some integer
![]() $s$
, where
$s$
, where
![]() $a-s\leqslant b+s$
. Combined with Theorem 7.9, and using the fact that
$a-s\leqslant b+s$
. Combined with Theorem 7.9, and using the fact that
![]() $a+b+1=d$
, we obtain
$a+b+1=d$
, we obtain
Since the function
![]() $h(t)=t(d-1-t)$
is strictly increasing on the interval
$h(t)=t(d-1-t)$
is strictly increasing on the interval
![]() $(-\infty ,(d-1)/2]$
, and since both
$(-\infty ,(d-1)/2]$
, and since both
![]() $a$
and
$a$
and
![]() $a-s$
lie in this interval, we conclude that
$a-s$
lie in this interval, we conclude that
![]() $s\geqslant 0$
and that
$s\geqslant 0$
and that
![]() $c_{2}({\mathcal{D}}(g))-(a-s)(b+s)=0$
if and only if
$c_{2}({\mathcal{D}}(g))-(a-s)(b+s)=0$
if and only if
![]() $s=0$
. Hence Theorem 7.9 gives that
$s=0$
. Hence Theorem 7.9 gives that
![]() ${\mathcal{D}}(g)$
is free if and only if
${\mathcal{D}}(g)$
is free if and only if
![]() $s=0$
and that
$s=0$
and that
![]() $s>0$
otherwise.◻
$s>0$
otherwise.◻
The following corollary is an immediate consequence.
Corollary 7.11. If the splitting type of a line arrangement is a combinatorial property, then Terao’s conjecture is true for line arrangements.
Thus we pose the following question.
Question 7.12. Is the splitting type a combinatorial invariant for arbitrary arrangements?
Using a Lefschetz-like property, we give a statement that is equivalent to Terao’s conjecture.
Proposition 7.13. The following two conditions are equivalent.
(a) Terao’s conjecture is true.
(b) If
 ${\mathcal{A}}(f)$
is any free line arrangement with splitting type
${\mathcal{A}}(f)$
is any free line arrangement with splitting type
 $(a,b)$
, then, for every line arrangement
$(a,b)$
, then, for every line arrangement
 ${\mathcal{A}}(g)$
with the same incidence lattice as
${\mathcal{A}}(g)$
with the same incidence lattice as
 ${\mathcal{A}}(f)$
, the multiplication map is surjective, where
${\mathcal{A}}(f)$
, the multiplication map is surjective, where $$\begin{eqnarray}[R/J]_{b-2}\stackrel{\times L^{2}}{\longrightarrow }[R/J]_{b}\end{eqnarray}$$
$$\begin{eqnarray}[R/J]_{b-2}\stackrel{\times L^{2}}{\longrightarrow }[R/J]_{b}\end{eqnarray}$$
 $J=(\ell _{1}^{b},\ldots ,\ell _{a+b+1}^{b},L_{1}^{b},\ldots ,L_{b-a}^{b})$
with
$J=(\ell _{1}^{b},\ldots ,\ell _{a+b+1}^{b},L_{1}^{b},\ldots ,L_{b-a}^{b})$
with
 $g=\ell _{1}\cdots \ell _{a+b+1}$
and general linear forms
$g=\ell _{1}\cdots \ell _{a+b+1}$
and general linear forms
 $L,L_{1},\ldots ,L_{b-a}\in R$
.
$L,L_{1},\ldots ,L_{b-a}\in R$
.
Proof. Let
![]() ${\mathcal{A}}(f)$
be a free line arrangement with splitting type
${\mathcal{A}}(f)$
be a free line arrangement with splitting type
![]() $(a,b)$
, and let
$(a,b)$
, and let
![]() ${\mathcal{A}}(g)$
be a line arrangement with the same incidence lattice as
${\mathcal{A}}(g)$
be a line arrangement with the same incidence lattice as
![]() ${\mathcal{A}}(f)$
. By Proposition 7.10, the splitting type of
${\mathcal{A}}(f)$
. By Proposition 7.10, the splitting type of
![]() ${\mathcal{A}}(g)$
is
${\mathcal{A}}(g)$
is
![]() $(a-s,b+s)$
for some integer
$(a-s,b+s)$
for some integer
![]() $s\geqslant 0$
. Let
$s\geqslant 0$
. Let
![]() $L,L_{1},\ldots ,L_{b-a}\in R$
be general linear forms, and set
$L,L_{1},\ldots ,L_{b-a}\in R$
be general linear forms, and set
![]() $h=L_{1}\cdots L_{b-a}$
. Proposition 5.15 and Lemma 3.5(a) give that
$h=L_{1}\cdots L_{b-a}$
. Proposition 5.15 and Lemma 3.5(a) give that
![]() ${\mathcal{A}}(gh)$
has splitting type
${\mathcal{A}}(gh)$
has splitting type
![]() $(b-s,b+s)$
. Denote by
$(b-s,b+s)$
. Denote by
![]() $Z$
the set of points in
$Z$
the set of points in
![]() $\mathbb{P}^{2}$
that is dual to
$\mathbb{P}^{2}$
that is dual to
![]() ${\mathcal{A}}(gh)$
. It has multiplicity index
${\mathcal{A}}(gh)$
. It has multiplicity index
![]() $m_{Z}=b-s$
. The cokernel of the multiplication map
$m_{Z}=b-s$
. The cokernel of the multiplication map
is
![]() $[R/(J,L^{2})]_{b}$
. By Theorem 7.2, this is isomorphic to
$[R/(J,L^{2})]_{b}$
. By Theorem 7.2, this is isomorphic to
![]() $[I_{Z+(b-1)P}]_{b}$
, where
$[I_{Z+(b-1)P}]_{b}$
, where
![]() $P\in \mathbb{P}^{2}$
is the point that is dual to
$P\in \mathbb{P}^{2}$
is the point that is dual to
![]() $L$
. It follows that the above map is surjective if and only if
$L$
. It follows that the above map is surjective if and only if
![]() $m_{Z}=b$
, that is,
$m_{Z}=b$
, that is,
![]() $s=0$
, which means that
$s=0$
, which means that
![]() ${\mathcal{A}}(g)$
has the same splitting type as
${\mathcal{A}}(g)$
has the same splitting type as
![]() ${\mathcal{A}}(f)$
. By Proposition 7.10, the latter is equivalent to
${\mathcal{A}}(f)$
. By Proposition 7.10, the latter is equivalent to
![]() ${\mathcal{A}}(g)$
being free, which concludes the argument.◻
${\mathcal{A}}(g)$
being free, which concludes the argument.◻
Similar arguments give a sufficient condition.
Corollary 7.14. Consider the following condition.
- (
 $\ast$
)
$\ast$
) Let
 $f=\ell _{1}^{\prime }\cdots \ell _{2k+1}^{\prime }$
and
$f=\ell _{1}^{\prime }\cdots \ell _{2k+1}^{\prime }$
and
 $g=\ell _{1}\cdots \ell _{2k+1}$
be products of
$g=\ell _{1}\cdots \ell _{2k+1}$
be products of
 $2k+1$
linear forms in
$2k+1$
linear forms in
 $R$
, and let
$R$
, and let
 $L\in R$
be a general linear form. Assume that the multiplication map
$L\in R$
be a general linear form. Assume that the multiplication map  $$\begin{eqnarray}[R/I]_{k-2}\stackrel{\times L^{2}}{\longrightarrow }[R/I]_{k}\end{eqnarray}$$
$$\begin{eqnarray}[R/I]_{k-2}\stackrel{\times L^{2}}{\longrightarrow }[R/I]_{k}\end{eqnarray}$$
is surjective, where
 $I=(\ell _{1}^{\prime k},\ldots ,\ell _{2k+1}^{\prime k})$
.
$I=(\ell _{1}^{\prime k},\ldots ,\ell _{2k+1}^{\prime k})$
.If the line arrangements
 ${\mathcal{A}}(f)$
and
${\mathcal{A}}(f)$
and
 ${\mathcal{A}}(g)$
have the same incidence lattices, then the multiplication map
${\mathcal{A}}(g)$
have the same incidence lattices, then the multiplication map  $$\begin{eqnarray}[R/J]_{k-2}\stackrel{\times L^{2}}{\longrightarrow }[R/J]_{k}\end{eqnarray}$$
$$\begin{eqnarray}[R/J]_{k-2}\stackrel{\times L^{2}}{\longrightarrow }[R/J]_{k}\end{eqnarray}$$
is also surjective, where
 $J=(\ell _{1}^{k},\ldots ,\ell _{2k+1}^{k})$
.
$J=(\ell _{1}^{k},\ldots ,\ell _{2k+1}^{k})$
.
If Condition (
![]() $\ast$
) is true for any two sets of
$\ast$
) is true for any two sets of
![]() $2k+1$
linear forms, then Terao’s conjecture is true.
$2k+1$
linear forms, then Terao’s conjecture is true.
Proof. Adopt the notation of the proof of Proposition 7.13. In particular, let
![]() ${\mathcal{A}}(f)$
and
${\mathcal{A}}(f)$
and
![]() ${\mathcal{A}}(g)$
be two line arrangements with the same incidence lattice, where
${\mathcal{A}}(g)$
be two line arrangements with the same incidence lattice, where
![]() ${\mathcal{A}}(f)$
is free with splitting type
${\mathcal{A}}(f)$
is free with splitting type
![]() $(a,b)$
. Let
$(a,b)$
. Let
![]() $\ell _{1}^{\prime },\ldots ,\ell _{a+b+1}^{\prime }$
be linear forms such that
$\ell _{1}^{\prime },\ldots ,\ell _{a+b+1}^{\prime }$
be linear forms such that
![]() $f=\ell _{1}^{\prime }\cdots \ell _{a+b+1}^{\prime }$
. We will use Condition (
$f=\ell _{1}^{\prime }\cdots \ell _{a+b+1}^{\prime }$
. We will use Condition (
![]() $\ast$
) by considering the ideal
$\ast$
) by considering the ideal
![]() $I=(\ell _{1}^{\prime b},\ldots ,\ell _{a+b+1}^{\prime b},L_{1}^{b},\ldots ,L_{b-a}^{b})$
. Indeed, the arrangement
$I=(\ell _{1}^{\prime b},\ldots ,\ell _{a+b+1}^{\prime b},L_{1}^{b},\ldots ,L_{b-a}^{b})$
. Indeed, the arrangement
![]() ${\mathcal{A}}(fh)$
has splitting type
${\mathcal{A}}(fh)$
has splitting type
![]() $(b,b)$
. Hence the multiplication map
$(b,b)$
. Hence the multiplication map
is surjective. Since
![]() $L_{1},\ldots ,L_{b-a}$
are general linear forms, the arrangements
$L_{1},\ldots ,L_{b-a}$
are general linear forms, the arrangements
![]() ${\mathcal{A}}(fh)$
and
${\mathcal{A}}(fh)$
and
![]() ${\mathcal{A}}(gh)$
also have the same incidence lattice. Therefore, Condition (
${\mathcal{A}}(gh)$
also have the same incidence lattice. Therefore, Condition (
![]() $\ast$
) gives that the multiplication map
$\ast$
) gives that the multiplication map
is surjective, where
![]() $J=(\ell _{1}^{b},\ldots ,\ell _{a+b+1}^{b},L_{1}^{b},\ldots ,L_{b-a}^{b})$
. As above, it follows that
$J=(\ell _{1}^{b},\ldots ,\ell _{a+b+1}^{b},L_{1}^{b},\ldots ,L_{b-a}^{b})$
. As above, it follows that
![]() ${\mathcal{A}}(g)$
must be a free arrangement, as desired.◻
${\mathcal{A}}(g)$
must be a free arrangement, as desired.◻
Remark 7.15. (i) In [Reference Di Gennaro, Ilardi and VallèsDIV14] the authors conjecture that the above Condition (
![]() $\ast$
) is always satisfied if one replaces surjectivity of the multiplication maps by maximal rank. An assumption on collinearity for the dual points was added in [Reference Di Gennaro and IlardiDI18]. Moreover, they claim that this modification of Condition (
$\ast$
) is always satisfied if one replaces surjectivity of the multiplication maps by maximal rank. An assumption on collinearity for the dual points was added in [Reference Di Gennaro and IlardiDI18]. Moreover, they claim that this modification of Condition (
![]() $\ast$
) is equivalent to Terao’s conjecture, whereas we claim only one direction.
$\ast$
) is equivalent to Terao’s conjecture, whereas we claim only one direction.
(ii) We have seen in Example 7.3 that injectivity of the multiplication map is not enough to draw a conclusion on the splitting type. One needs surjectivity as stated in Condition (
![]() $\ast$
). However, it is not clear (to us) whether Condition (
$\ast$
). However, it is not clear (to us) whether Condition (
![]() $\ast$
) is in fact equivalent to Terao’s conjecture.
$\ast$
) is in fact equivalent to Terao’s conjecture.
Returning to sets of points, we conclude with the dual version of Corollary 7.14.
Corollary 7.16. If, for sets of
![]() $2k+1$
points of
$2k+1$
points of
![]() $\mathbb{P}^{2}$
, having (maximal) multiplicity index
$\mathbb{P}^{2}$
, having (maximal) multiplicity index
![]() $k$
is a combinatorial property, then Terao’s conjecture is true for line arrangements.
$k$
is a combinatorial property, then Terao’s conjecture is true for line arrangements.
Acknowledgements
Harbourne was partially supported by NSA grant no. H98230-13-1-0213 and by Simons Foundation grant no. 524858. Migliore was partially supported by NSA grant no. H98230-12-1-0204 and by Simons Foundation grant no. 309556. Nagel was partially supported by NSA grant no. H98230-12-1-0247 and by Simons Foundation grant no. 317096. We thank A. Dimca, I. Dolgachev, R. Di Gennaro, G. Ilardi, A. Langer, H. Schenck, A. Seceleanu, T. Szemberg, J. Szpond, Ş. Tohǎneanu and J. Vallès for their comments on this paper. We also thank the Mathematisches Forschunginstitut Oberwolfach and the Banff International Research Station for supporting the workshops which gave us the opportunity to discuss and present our results. Finally, we thank the referee for the helpful comments.
Appendix
For the convenience of the reader we derive in an elementary way some facts on line configurations for which we could not find a precise reference in the literature, especially the role of the characteristic. However, see also [Reference TeraoTer80, pp. 4–5].
Define the submodule
![]() $D(Z)\subset R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)\cong R^{3}$
to be the
$D(Z)\subset R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)\oplus R(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)\cong R^{3}$
to be the
![]() $K$
-linear derivations
$K$
-linear derivations
![]() $\unicode[STIX]{x1D6FF}$
such that
$\unicode[STIX]{x1D6FF}$
such that
![]() $\unicode[STIX]{x1D6FF}(f)\in Rf$
. In particular,
$\unicode[STIX]{x1D6FF}(f)\in Rf$
. In particular,
![]() $D(Z)$
contains the Euler derivation
$D(Z)$
contains the Euler derivation
![]() $\unicode[STIX]{x1D6FF}_{E}=x(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)+y(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)+z(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)$
, and
$\unicode[STIX]{x1D6FF}_{E}=x(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)+y(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)+z(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z)$
, and
![]() $\unicode[STIX]{x1D6FF}_{E}$
generates a submodule
$\unicode[STIX]{x1D6FF}_{E}$
generates a submodule
![]() $R\unicode[STIX]{x1D6FF}_{E}\cong R(-1)$
. We can now define the quotient
$R\unicode[STIX]{x1D6FF}_{E}\cong R(-1)$
. We can now define the quotient
![]() $D_{0}(Z)=D(Z)/R\unicode[STIX]{x1D6FF}_{E}$
.
$D_{0}(Z)=D(Z)/R\unicode[STIX]{x1D6FF}_{E}$
.
Define the Jacobian ideal of
![]() $f\in R$
as
$f\in R$
as
![]() $J=\operatorname{Jac}(f)=(f,f_{x},f_{y},f_{z})$
. Let
$J=\operatorname{Jac}(f)=(f,f_{x},f_{y},f_{z})$
. Let
![]() $J^{\prime }=(f_{x},f_{y},f_{z})$
. For
$J^{\prime }=(f_{x},f_{y},f_{z})$
. For
![]() $\unicode[STIX]{x1D6FF}\in D(Z)$
, we may view
$\unicode[STIX]{x1D6FF}\in D(Z)$
, we may view
![]() $\unicode[STIX]{x1D6FF}$
as a triple
$\unicode[STIX]{x1D6FF}$
as a triple
![]() $(g_{1},g_{2},g_{3})^{T}$
of polynomials such that
$(g_{1},g_{2},g_{3})^{T}$
of polynomials such that
![]() $(g_{1}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)+g_{2}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)+g_{3}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z))(f)=hf$
, for some
$(g_{1}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x)+g_{2}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)+g_{3}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z))(f)=hf$
, for some
![]() $h\in R$
(possibly zero) that depends on
$h\in R$
(possibly zero) that depends on
![]() $\unicode[STIX]{x1D6FF}$
. Then the module
$\unicode[STIX]{x1D6FF}$
. Then the module
![]() $D(Z)$
can be described by the exact sequence
$D(Z)$
can be described by the exact sequence
where
![]() $\unicode[STIX]{x1D711}((g_{1},g_{2},g_{3})^{T})=g_{1}f_{x}+g_{2}f_{y}+g_{3}f_{z}\!\!\hspace{0.6em}{\rm mod}\hspace{0.2em}f$
. Notice that the image of
$\unicode[STIX]{x1D711}((g_{1},g_{2},g_{3})^{T})=g_{1}f_{x}+g_{2}f_{y}+g_{3}f_{z}\!\!\hspace{0.6em}{\rm mod}\hspace{0.2em}f$
. Notice that the image of
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() $J/fR(d-1)$
. Using this, consider the commutative diagram
$J/fR(d-1)$
. Using this, consider the commutative diagram

where
![]() $E$
is the syzygy module associated to
$E$
is the syzygy module associated to
![]() $J$
. Then from the snake lemma we see that
$J$
. Then from the snake lemma we see that
![]() $D(Z)$
is isomorphic to a twist of the syzygy module of
$D(Z)$
is isomorphic to a twist of the syzygy module of
![]() $J$
. In particular,
$J$
. In particular,
![]() $D(Z)$
is reflexive. Its sheafification
$D(Z)$
is reflexive. Its sheafification
![]() $\widetilde{D(Z)}$
is a locally free sheaf of rank
$\widetilde{D(Z)}$
is a locally free sheaf of rank
![]() $3$
. Since the Euler derivation corresponds to a global non-vanishing section, it follows that the sheafification of
$3$
. Since the Euler derivation corresponds to a global non-vanishing section, it follows that the sheafification of
![]() $D_{0}(Z)$
is a locally free sheaf on
$D_{0}(Z)$
is a locally free sheaf on
![]() $\mathbb{P}^{2}$
of rank
$\mathbb{P}^{2}$
of rank
![]() $2$
, which we will denote by
$2$
, which we will denote by
![]() ${\mathcal{D}}_{Z}$
. We call
${\mathcal{D}}_{Z}$
. We call
![]() ${\mathcal{D}}_{Z}$
the derivation bundle of
${\mathcal{D}}_{Z}$
the derivation bundle of
![]() $Z$
.
$Z$
.
Moreover, from the commutative diagram

we get the exact sequence
Notice that the sheafification of
![]() $R^{3}/R\unicode[STIX]{x1D6FF}_{E}$
is isomorphic to the tangent bundle,
$R^{3}/R\unicode[STIX]{x1D6FF}_{E}$
is isomorphic to the tangent bundle,
![]() ${\mathcal{T}}_{\mathbb{P}^{2}}$
, of
${\mathcal{T}}_{\mathbb{P}^{2}}$
, of
![]() $\mathbb{P}^{2}$
twisted by
$\mathbb{P}^{2}$
twisted by
![]() $(-1)$
. Thus,
$(-1)$
. Thus,
![]() ${\mathcal{D}}_{Z}$
is a subbundle of this twisted tangent bundle. We now compute its first Chern class.
${\mathcal{D}}_{Z}$
is a subbundle of this twisted tangent bundle. We now compute its first Chern class.
Sheafifying the above exact sequence, we obtain
where
![]() ${\mathcal{J}}$
is the sheafification of
${\mathcal{J}}$
is the sheafification of
![]() $J$
. Thus, we get
$J$
. Thus, we get
Hence, the sequence
gives, after sheafifying,
Now let
![]() $J^{\prime }=(f_{x},f_{y},f_{z})$
. Let
$J^{\prime }=(f_{x},f_{y},f_{z})$
. Let
![]() $E^{\prime }=Syz(J^{\prime })(d-1)$
be the twisted syzygy module of
$E^{\prime }=Syz(J^{\prime })(d-1)$
be the twisted syzygy module of
![]() $J^{\prime }$
, which is reflexive of rank 2. Consider the commutative diagram
$J^{\prime }$
, which is reflexive of rank 2. Consider the commutative diagram

where
![]() $\unicode[STIX]{x1D6FC}$
is multiplication by
$\unicode[STIX]{x1D6FC}$
is multiplication by
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D6FD}$
is the presentation matrix for
$\unicode[STIX]{x1D6FD}$
is the presentation matrix for
![]() $R/J^{\prime }$
. When
$R/J^{\prime }$
. When
![]() $char(K)$
does not divide
$char(K)$
does not divide
![]() $d$
, we have that
$d$
, we have that
![]() $\unicode[STIX]{x1D6FC}$
is an isomorphism and
$\unicode[STIX]{x1D6FC}$
is an isomorphism and
![]() $J=J^{\prime }$
. It follows that
$J=J^{\prime }$
. It follows that
![]() $D_{0}(Z)\cong E$
. When
$D_{0}(Z)\cong E$
. When
![]() $char(K)$
does divide
$char(K)$
does divide
![]() $d$
,
$d$
,
![]() $\unicode[STIX]{x1D6FC}$
is the zero map and we obtain
$\unicode[STIX]{x1D6FC}$
is the zero map and we obtain

so the snake lemma gives the long exact sequence
These calculations produce the following lemma.
Lemma A.1. Let
![]() $Z$
be a set of
$Z$
be a set of
![]() $d$
points dual to a line arrangement defined by a product,
$d$
points dual to a line arrangement defined by a product,
![]() $f$
, of linear forms. Let
$f$
, of linear forms. Let
![]() $J^{\prime }=(f_{x},f_{y},f_{z})$
and
$J^{\prime }=(f_{x},f_{y},f_{z})$
and
![]() $J=(f_{x},f_{y},f_{z},f)$
, and let
$J=(f_{x},f_{y},f_{z},f)$
, and let
![]() ${\mathcal{D}}_{Z}$
be the associated derivation bundle. Let
${\mathcal{D}}_{Z}$
be the associated derivation bundle. Let
![]() $L$
be a general line. Then
$L$
be a general line. Then
![]() ${\mathcal{D}}_{Z}|_{L}$
splits as a direct sum
${\mathcal{D}}_{Z}|_{L}$
splits as a direct sum
![]() ${\mathcal{O}}_{\mathbb{P}^{1}}(-a_{Z})\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(-b_{Z})$
with
${\mathcal{O}}_{\mathbb{P}^{1}}(-a_{Z})\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(-b_{Z})$
with
![]() $a_{Z}+b_{Z}=d-1$
. Furthermore, if
$a_{Z}+b_{Z}=d-1$
. Furthermore, if
![]() ${\mathcal{E}}=\widetilde{E}$
is the syzygy bundle of
${\mathcal{E}}=\widetilde{E}$
is the syzygy bundle of
![]() $J^{\prime }(d-1)$
, then
$J^{\prime }(d-1)$
, then
![]() ${\mathcal{D}}_{Z}$
is isomorphic to
${\mathcal{D}}_{Z}$
is isomorphic to
![]() ${\mathcal{E}}$
if and only if
${\mathcal{E}}$
if and only if
![]() $char(K)$
does not divide
$char(K)$
does not divide
![]() $d$
. If
$d$
. If
![]() $char(K)$
does divide
$char(K)$
does divide
![]() $d$
then
$d$
then
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() ${\mathcal{D}}_{Z}$
are related by the exact sequence
${\mathcal{D}}_{Z}$
are related by the exact sequence
Definition A.2. We shall call the ordered pair
![]() $(a_{Z},b_{Z})$
, with
$(a_{Z},b_{Z})$
, with
![]() $a_{Z}\leqslant b_{Z}$
, the splitting type of
$a_{Z}\leqslant b_{Z}$
, the splitting type of
![]() $Z$
.
$Z$
.
Remark A.3. When
![]() $\text{char}(K)$
does not divide
$\text{char}(K)$
does not divide
![]() $\deg (f)$
, so
$\deg (f)$
, so
![]() $J=J^{\prime }$
, we can see the identification of
$J=J^{\prime }$
, we can see the identification of
![]() $Syz(J)$
with
$Syz(J)$
with
![]() $\{\unicode[STIX]{x1D6FF}\in D(Z)~|~\unicode[STIX]{x1D6FF}(f)=0\}$
more directly. Indeed, it is not hard to show that that we have an isomorphism of
$\{\unicode[STIX]{x1D6FF}\in D(Z)~|~\unicode[STIX]{x1D6FF}(f)=0\}$
more directly. Indeed, it is not hard to show that that we have an isomorphism of
![]() $R$
-modules
$R$
-modules
defined by
(with
![]() $h$
defined as above in terms of
$h$
defined as above in terms of
![]() $\unicode[STIX]{x1D6FF}$
); see also [Reference Orlik and TeraoOT92, p. 109]. It follows that
$\unicode[STIX]{x1D6FF}$
); see also [Reference Orlik and TeraoOT92, p. 109]. It follows that
![]() $D_{0}(Z)\cong Syz(J)(d-1)$
. Notice that the isomorphism is defined if and only if the degree
$D_{0}(Z)\cong Syz(J)(d-1)$
. Notice that the isomorphism is defined if and only if the degree
![]() $d$
is a unit of
$d$
is a unit of
![]() $R$
. We thus have the exact sequence of sheaves
$R$
. We thus have the exact sequence of sheaves
where
![]() ${\mathcal{J}}$
is the sheafification of
${\mathcal{J}}$
is the sheafification of
![]() $J$
. This identification of
$J$
. This identification of
![]() ${\mathcal{D}}_{Z}$
with the syzygy bundle of
${\mathcal{D}}_{Z}$
with the syzygy bundle of
![]() $J$
is often very useful.
$J$
is often very useful.