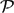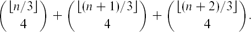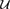In this paper we study in complete generality the family of two-state, deterministic, monotone, local, homogeneous cellular automata in  $\mathbb{Z}$d with random initial configurations. Formally, we are given a set
$\mathbb{Z}$d with random initial configurations. Formally, we are given a set 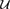 $\mathcal{U}$ = {X1,. . . , Xm} of finite subsets of
$\mathcal{U}$ = {X1,. . . , Xm} of finite subsets of  $\mathbb{Z}$d \ {0}, and an initial set A0 ⊂
$\mathbb{Z}$d \ {0}, and an initial set A0 ⊂  $\mathbb{Z}$d of ‘infected’ sites, which we take to be random according to the product measure with density p. At time t ∈
$\mathbb{Z}$d of ‘infected’ sites, which we take to be random according to the product measure with density p. At time t ∈  $\mathbb{N}$, the set of infected sites At is the union of At-1 and the set of all x ∈
$\mathbb{N}$, the set of infected sites At is the union of At-1 and the set of all x ∈  $\mathbb{Z}$d such that x + X ∈ At-1 for some X ∈
$\mathbb{Z}$d such that x + X ∈ At-1 for some X ∈ 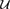 $\mathcal{U}$. Our model may alternatively be thought of as bootstrap percolation on
$\mathcal{U}$. Our model may alternatively be thought of as bootstrap percolation on  $\mathbb{Z}$d with arbitrary update rules, and for this reason we call it
$\mathbb{Z}$d with arbitrary update rules, and for this reason we call it 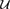 $\mathcal{U}$-bootstrap percolation.
$\mathcal{U}$-bootstrap percolation.
In two dimensions, we give a classification of 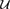 $\mathcal{U}$-bootstrap percolation models into three classes – supercritical, critical and subcritical – and we prove results about the phase transitions of all models belonging to the first two of these classes. More precisely, we show that the critical probability for percolation on (
$\mathcal{U}$-bootstrap percolation models into three classes – supercritical, critical and subcritical – and we prove results about the phase transitions of all models belonging to the first two of these classes. More precisely, we show that the critical probability for percolation on ( $\mathbb{Z}$/n
$\mathbb{Z}$/n $\mathbb{Z}$)2 is (log n)−Θ(1) for all models in the critical class, and that it is n−Θ(1) for all models in the supercritical class.
$\mathbb{Z}$)2 is (log n)−Θ(1) for all models in the critical class, and that it is n−Θ(1) for all models in the supercritical class.
The results in this paper are the first of any kind on bootstrap percolation considered in this level of generality, and in particular they are the first that make no assumptions of symmetry. It is the hope of the authors that this work will initiate a new, unified theory of bootstrap percolation on  $\mathbb{Z}$d.
$\mathbb{Z}$d.