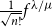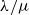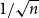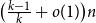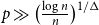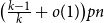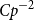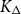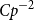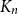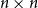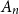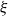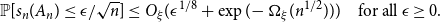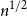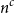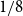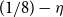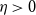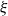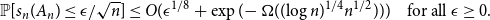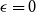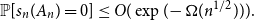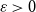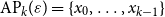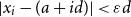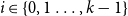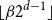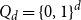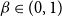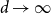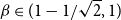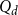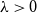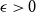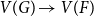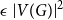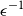We show that for an 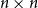 $n\times n$
random symmetric matrix
$n\times n$
random symmetric matrix 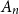 $A_n$
, whose entries on and above the diagonal are independent copies of a sub-Gaussian random variable
$A_n$
, whose entries on and above the diagonal are independent copies of a sub-Gaussian random variable 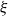 $\xi$
with mean 0 and variance 1,
$\xi$
with mean 0 and variance 1, 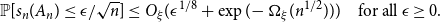 \begin{equation*}\mathbb{P}[s_n(A_n) \le \epsilon/\sqrt{n}] \le O_{\xi}(\epsilon^{1/8} + \exp(\!-\Omega_{\xi}(n^{1/2}))) \quad \text{for all } \epsilon \ge 0.\end{equation*}
\begin{equation*}\mathbb{P}[s_n(A_n) \le \epsilon/\sqrt{n}] \le O_{\xi}(\epsilon^{1/8} + \exp(\!-\Omega_{\xi}(n^{1/2}))) \quad \text{for all } \epsilon \ge 0.\end{equation*}
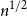 $n^{1/2}$
replaced by
$n^{1/2}$
replaced by 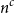 $n^{c}$
for a small constant c, and
$n^{c}$
for a small constant c, and 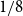 $1/8$
replaced by
$1/8$
replaced by 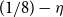 $(1/8) - \eta$
(with implicit constants also depending on
$(1/8) - \eta$
(with implicit constants also depending on 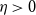 $\eta > 0$
). Furthermore, when
$\eta > 0$
). Furthermore, when 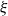 $\xi$
is a Rademacher random variable, we prove that
$\xi$
is a Rademacher random variable, we prove that 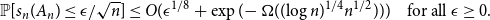 \begin{equation*}\mathbb{P}[s_n(A_n) \le \epsilon/\sqrt{n}] \le O(\epsilon^{1/8} + \exp(\!-\Omega((\!\log{n})^{1/4}n^{1/2}))) \quad \text{for all } \epsilon \ge 0.\end{equation*}
\begin{equation*}\mathbb{P}[s_n(A_n) \le \epsilon/\sqrt{n}] \le O(\epsilon^{1/8} + \exp(\!-\Omega((\!\log{n})^{1/4}n^{1/2}))) \quad \text{for all } \epsilon \ge 0.\end{equation*}
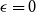 $\epsilon = 0$
improves a recent result of Campos, Mattos, Morris, and Morrison, which showed that
$\epsilon = 0$
improves a recent result of Campos, Mattos, Morris, and Morrison, which showed that 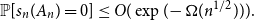 $\mathbb{P}[s_n(A_n) = 0] \le O(\exp(\!-\Omega(n^{1/2}))).$
Notably, in a departure from the previous two best bounds on the probability of singularity of symmetric matrices, which had relied on somewhat specialized and involved combinatorial techniques, our methods fall squarely within the broad geometric framework pioneered by Rudelson and Vershynin, and suggest the possibility of a principled geometric approach to the study of the singular spectrum of symmetric random matrices. The main innovations in our work are new notions of arithmetic structure – the Median Regularized Least Common Denominator (MRLCD) and the Median Threshold, which are natural refinements of the Regularized Least Common Denominator (RLCD)introduced by Vershynin, and should be more generally useful in contexts where one needs to combine anticoncentration information of different parts of a vector.
$\mathbb{P}[s_n(A_n) = 0] \le O(\exp(\!-\Omega(n^{1/2}))).$
Notably, in a departure from the previous two best bounds on the probability of singularity of symmetric matrices, which had relied on somewhat specialized and involved combinatorial techniques, our methods fall squarely within the broad geometric framework pioneered by Rudelson and Vershynin, and suggest the possibility of a principled geometric approach to the study of the singular spectrum of symmetric random matrices. The main innovations in our work are new notions of arithmetic structure – the Median Regularized Least Common Denominator (MRLCD) and the Median Threshold, which are natural refinements of the Regularized Least Common Denominator (RLCD)introduced by Vershynin, and should be more generally useful in contexts where one needs to combine anticoncentration information of different parts of a vector.