Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-19T23:19:13.335Z Has data issue: false hasContentIssue false
  • English
  • Français

DIFFERENTIAL INEQUALITIES AND A MARTY-TYPE CRITERION FOR QUASI-NORMALITY

Part of: General properties Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  18 June 2018

JÜRGEN GRAHL ,
TOMER MANKET  and
SHAHAR NEVO
JÜRGEN GRAHL
Affiliation:
Department of Mathematics, University of Würzburg, 97074 Würzburg, Germany
TOMER MANKET
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 52900, Israel
SHAHAR NEVO*
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 52900, Israel
*
✉nevosh@math.biu.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the family of all holomorphic functions 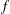$f$ in a domain 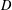$D$ satisfying

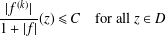$$\begin{eqnarray}\frac{|f^{(k)}|}{1+|f|}(z)\leq C\quad \text{for all }z\in D\end{eqnarray}$$
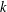(where $k$ is a natural number and 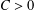$C>0$) is quasi-normal. Furthermore, we give a general counterexample to show that for 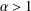$\unicode[STIX]{x1D6FC}>1$ and 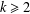$k\geq 2$ the condition
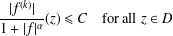$$\begin{eqnarray}\frac{|f^{(k)}|}{1+|f|^{\unicode[STIX]{x1D6FC}}}(z)\leq C\quad \text{for all }z\in D\end{eqnarray}$$
 does not imply quasi-normality.

Keywords

quasi-normal familiesnormal familiesMarty’s theoremdifferential inequalities

MSC classification

Primary: 30D45: Bloch functions, normal functions, normal families
Secondary: 30A10: Inequalities in the complex domain
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 1 , August 2018 , pp. 34 - 45
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Bar, R., Grahl, J. and Nevo, S., ‘Differential inequalities and quasi-normal families’, Anal. Math. Phys. 4 (2014), 63–71.Google Scholar
Chen, Q., Nevo, S. and Pang, X.-C., ‘A general differential inequality of the kth derivative that leads to normality’, Ann. Acad. Sci. Fenn. 38 (2013), 691–695.Google Scholar
Grahl, J. and Nevo, S., ‘Spherical derivatives and normal families’, J. Anal. Math. 117 (2012), 119–128.Google Scholar
Grahl, J. and Nevo, S., ‘An extension of one direction in Marty’s normality criterion’, Monatsh. Math. 174 (2014), 205–217.Google Scholar
Grahl, J. and Nevo, S., ‘Quasi-normality induced by differential inequalities’, Bull. Lond. Math. Soc., to appear.Google Scholar
Grahl, J., Nevo, S. and Pang, X.-C., ‘A non-explicit counterexample to a problem of quasi-normality’, J. Math. Anal. Appl. 406 (2013), 386–391.Google Scholar
Hinkkanen, A., ‘Normal families and Ahlfors’s five island theorem’, New Zealand J. Math. 22 (1993), 39–41.Google Scholar
Lappan, P., ‘A criterion for a meromorphic function to be normal’, Comment. Math. Helv. 49 (1974), 492–495.Google Scholar
Li, S. Y. and Xie, H., ‘On normal families of meromorphic functions’, Acta Math. Sin. (Engl. Ser.) 4 (1986), 468–476.Google Scholar
Liu, X. J., Nevo, S. and Pang, X. C., ‘Differential inequalities, normality and quasi-normality’, Acta Math. Sin. (Engl. Ser.) 30 (2014), 277–282.Google Scholar
Marty, F., ‘Recherches sur la répartition des valeurs d’une fonction méromorphe’, Ann. Fac. Sci. Univ. Toulouse 23(3) (1931), 183–261.Google Scholar
Nevo, S., ‘Transfinite extension to Q m -normality theory’, Results Math. 44 (2003), 141–156.Google Scholar
Schiff, J., Normal Families (Springer, New York, 1993).CrossRefGoogle Scholar
Steinmetz, N., ‘Normal families and linear differential equations’, J. Anal. Math. 117 (2012), 129–132.CrossRefGoogle Scholar
Stoer, J. and Bulirsch, R., Introduction to Numerical Analysis (Springer, New York, 1980).Google Scholar
Xu, Y., ‘On the five-point theorems due to Lappan’, Ann. Polon. Math. 101 (2011), 227–235.Google Scholar