1. INTRODUCTION
The use of generative design grammars for design synthesis has been shown successful in many application areas (Chakrabarti et al., Reference Chakrabarti, Shea, Stone, Cagan, Campbell, Hernandez and Wood2011). For example, recent work has been done in the synthesis of hybrid power trains (Helms & Shea, Reference Helms and Shea2012) and the synthesis of gearboxes (Lin et al., Reference Lin, Shea, Johnson, Coultate and Pears2010). Although design grammars are often developed to formalize and structure the design of products and processes, the process of designing grammars themselves is often rather unsystematic and “treated, to a large extent, in an ad hoc manner with regard to design, implementation, transformation, recovery, testing, etc.” (Klint et al., Reference Klint, Lämmel and Verhoef2005). Zheng and Chen (Reference Zheng and Chen2009) state that “sound and systematic methods and techniques are needed for grammarware to move from hacking to engineering.” Both of these observations come from computer science, where formal grammars for compiler design and other applications are widely used and the research area of grammar engineering and testing has been developed. In design, Knight (Reference Knight1998) stated that “it is the designing of a grammar that resembles what a designer does. The development of rules for designs requires the same kind of intelligence, imagination, and guesswork as the development of designs in a conventional way.” Although various methods have been developed for the conventional design process, little attention is given to design grammar rule development so far. In a few publications in the mechanical engineering domain (Chase, Reference Chase2002; Li et al., Reference Li, Schmidt, He, Li and Qian2004; Chakrabarti et al., Reference Chakrabarti, Shea, Stone, Cagan, Campbell, Hernandez and Wood2011; McKay et al., Reference McKay, Chase, Shea and Chau2012), the issue of systematically developing and testing grammars is suggested, and researchers see the “need to concentrate on grammar design while designing with grammars” (Li et al., Reference Li, Schmidt, He, Li and Qian2004). The lack of support for grammar design was discussed more than a decade ago (Gips, Reference Gips1999; Knight & Stiny, Reference Knight and Stiny2001), and it remains one of the major drawbacks of grammatical design approaches (Chakrabarti et al., Reference Chakrabarti, Shea, Stone, Cagan, Campbell, Hernandez and Wood2011). McKay et al. (Reference McKay, Chase, Shea and Chau2012) note that “there is a need for more methodological support for guiding a user in the design of a grammar.”
The goal of this paper is to take a step in this direction and provide a grammar rule analysis method (GRAM) for computational design synthesis (CDS) to systematically assist the rule development process. It is meant to support designers of grammars by giving feedback on the performance of their developed rules through a set of visualizations, produced from systematic rule testing, that the designer can interpret and then adjust the grammar rules accordingly. Throughout this paper, the term performance is used to describe how rules impact designs, for example, how they change design characteristics and objectives. Testing the rules during or after the development process and before they are embedded in a more complicated design synthesis process enables designers to obtain an increased understanding of rule performance and to validate them. In Reference Chomsky1956, Chomsky stated that a grammar “gives a certain insight into the use and understanding of a language.” GRAM focuses on enabling these insights to allow the human engineer to design better grammar rules.
The paper is organized as follows. Section 2 reviews different approaches on the development and analysis of grammars in engineering design and motivates the need for a more systematic way to develop and analyze grammar rules. In Section 3 GRAM is presented. Section 4 presents the case study used in this paper. Four different graph grammars for automated gearbox design are analyzed and compared using GRAM. The results are presented in Section 5 and discussed in Section 6 along with general issues of GRAM. Section 7 concludes the paper and gives an outlook on future directions.
2. BACKGROUND AND RELATED WORK
In this paper, the terminology for the CDS process is used as defined in Cagan et al. (Reference Cagan, Campbell, Finger and Tomiyama2005). In the first step, the designer formalizes the design problem at the required level of detail to allow for the synthesis of meaningful designs. After the representation is formalized, the CDS process consists of three repeated phases: generate, evaluate, and guide. In the design generation phase, a grammar rule is selected and applied to the current design, transforming it into a new design alternative that is then evaluated considering defined objectives and constraints. A decision is then made in the search on how to proceed in the synthesis process, to either accept or reject the new alternative. The synthesis process is continued until either no further rule applications are possible or it is stopped by a stopping criteria in the search method.
In grammatical approaches to CDS, designers develop a grammar to represent a desired design language. It consists of a vocabulary, usually describing design components or subsystems, as well as a set of grammar rules. These rules describe design transformations, LHS → RHS, that are defined by a left-hand side (LHS), that is, where the rule can be applied in a design, and a right-hand side (RHS), defining the design transformation. Two common formalisms for engineering design grammars are spatial and graph grammars. In spatial grammars, the rules are based on the shape of a design, that is, its geometry (Gips & Stiny, Reference Gips and Stiny1980). In graph grammars, rules apply to graph elements, which can be single nodes, arcs, and subgraphs (Gips & Stiny, Reference Gips and Stiny1980).
2.1. Related work
Several approaches in CDS using grammars have shown success in easing the process for the human designer. Examples are relieving the designer from tuning search algorithms through machine learning methods (Vale & Shea, Reference Vale and Shea2003), prescriptive methods to build a knowledge model representing expert knowledge in rules (Schotborgh, Reference Schotborgh2009), or intelligent reduction of the number of design concepts that are presented to a human designer (Poppa et al., Reference Poppa, Stone and Orsborn2010). Although improving the CDS process in general, these methods lack support for the early phase of rule development. Thus, much effort is spent on deciding how to apply rules to generate beneficial designs rather than rethinking the implemented rules.
In the mechanical engineering domain, most publications on CDS methods using grammars describe the grammar rules but give little to no hints on how these rules were developed. Designing a grammar is usually an iterative process, “a distillation of practice and experience in a particular domain” (Brown, Reference Brown1997). The iterative nature of rule development is a commonality among most publications covering the development process of grammars and is described in Knight and Stiny (Reference Knight and Stiny2001), Chakrabarti et al. (Reference Chakrabarti, Shea, Stone, Cagan, Campbell, Hernandez and Wood2011), and Ibrahim et al. (Reference Ibrahim, Bridges, Chase, Bayoumi and Taha2012). Chakrabarti et al. (Reference Chakrabarti, Shea, Stone, Cagan, Campbell, Hernandez and Wood2011) mention an iterative process for the development and application of generative grammars including an iterative loop back to the modification of vocabulary and rules after designs have been generated. Chase (Reference Chase2002) defines different stages for grammar development and application where grammar development consists of defining the representation, the control mechanism (guidance), and the grammar rules. The grammar application is divided into determination of a rule, determination of the object to which the rule is applied, and determination of the matching conditions. Five scenarios are defined for possible user control of these four steps. Ibrahim et al. (Reference Ibrahim, Bridges, Chase, Bayoumi and Taha2012) extend the shape grammar development and application process defined by Chase (Reference Chase2002) for a workshop in a first-year architectural design studio. In all of these works, the improvement of the grammar is considered; however, no systematic method is given to support the analysis of the developed grammars. Recent approaches to support rule development either give advice to a human designer on how to develop (Knight, Reference Knight1998; Cagan, Reference Cagan, Antonsson and Cagan2001; Rudolph, Reference Rudolph and Gero2006) and manually test a grammar (Shea & Cagan, Reference Shea and Cagan1999) or generate grammar rules automatically (Orsborn et al., Reference Orsborn, Cagan and Boatwright2008a, Reference Orsborn, Cagan and Boatwright2008b). For the latter, extensive research is also done in other fields, for example, grammar induction and improvement (Klein & Manning, Reference Klein and Manning2002) for natural language processing. For engineering design grammars, however, no research is known to the authors that supports rule development through systematic and automated rule analysis.
The research presented in this paper focuses on supporting the rule development process. The authors expect that through a systematic analysis of the rules during the rule design, “better” grammars can be developed that lead to a more successful synthesis process. The better understanding gained in the analysis using GRAM can also deliver important insights about the search space that can be considered in tuning sophisticated search approaches. In contrast to the work by Vale and Shea (Reference Vale and Shea2003), where statistics are collected and rule sequences are defined during the CDS process, GRAM enables designers not only to reuse insights gained before the CDS process but also to analyze the grammar itself and to improve it based on the results.
3. METHOD
GRAM is presented in Figure 1. Dark gray boxes show steps that are carried out automatically in the current implementation, and light gray boxes show steps that will be automated in the future.

Fig. 1. The grammar rule analysis method (GRAM) to analyze grammar rules for computational design synthesis based on the extended shape grammar process shown in (McKay et al., Reference McKay, Chase, Shea and Chau2012).
GRAM analyzes a developed grammar in a systematic way to give feedback on how rules perform. Individual rule performances (Q-1) as well as the performance of the whole rule set (Q-2–Q-6) are assessed such that the rule designer is able to answer the following questions when interpreting the results:
Q-1. What impact does the rule have on which objective?
Q-2. How probable are the applications of each rule?
Q-3. What solution space do the rules define?
Q-4. Does the rule set favor certain designs?
Q-5. How many valid designs are generated?
Q-6. How many different designs are generated?
GRAM has a defined way to generate and analyze data. Information from the data analysis is visualized and interpreted by the designer to gain a better understanding of the grammar itself. The different steps in GRAM are described in more detail in the following and a schematic representation of GRAM steps 1–3 is shown in Figure 2 to accompany these descriptions. GRAM is best illustrated using an example, so a grammar for gearbox synthesis is used here that will be further introduced in Section 4.3. GRAM allows analysis for any number of objectives, design characteristics, and rules but, for the sake of clarity, it is shown here for this reduced example.

Fig. 2. Schematic overview of grammar rule analysis method (GRAM) steps 1–3.
3.1. Data generation
To analyze grammar rules, a variety of data (i.e., objectives and design characteristics) is acquired. In most engineering applications, there are multiple objectives, and it is recommended to store the metric for each objective individually. Here, constraints formulated as soft constraints (i.e., penalty functions) are included. Design characteristics can be individual variables in the rules, but they are more commonly system characteristics (e.g., number of components and component types). The data is generated using a simple generate-and-test process. It starts with an initial design. A rule is selected randomly from all implemented rules. It is applied, the generated design is evaluated, and the data is stored. The generated design resulting from this rule application is taken as the basis for the next iteration. It is not a generate-and-test search process because the design resulting from the rule application is always used as the starting point for the next rule application regardless of the impact on design objectives.
3.2. Data analysis
For all data, the change in the objectives is calculated to analyze the performance of each individual rule. The generated designs are analyzed to identify topologically equivalent designs to be able to represent the design space and to identify if the rules favor certain topologies (i.e., generate them multiple times). In addition, some basic statistical models are built to prepare the visualization and support the interpretation.
3.3. Visualization and interpretation of analysis results
Five different diagram types are presented in Figure 2 to visualize the data obtained in the analysis. For a rule set of n r rules and an analysis of n o objectives using n d design characteristics, the following diagrams are generated: Q-1: n o boxplots with n r boxes each; Q-2: one bar plot with n r bars; Q-3/Q-4: one n d-dimensional design space plot, additional boxplots if required; Q-4: one ratio for valid designs; and Q-5: one ratio for different designs. The diagrams are explained below, and important issues for their interpretation are given.
3.3.1. Q-1. General performance analysis using boxplots for each objective
A diagram is generated for each objective showing how it is influenced by each rule (given on the y axis). The user defines the desired direction of change derived from the problem formulation, and a color coding gives a quick overview if the rule changed the objective in the desired direction or not. The red (medium grey) color indicates a change against the desired direction and the green (light grey) color a change in the desired direction. Blue (dark grey) boxes show that changes in both directions are possible, and black (black) is used to represent rules that have no influence on an objective. The whiskers (defined by the thin line) represent the maximum and minimum value of the data set excluding outliers, that is, data points more than 3/2 away from the lower or upper quartile. The box spans from the lower quartile to the upper quartile showing also the median. Using this diagram, the engineer can visualize the performance of each rule considering each objective separately. In interpreting these diagrams, the designer has to consider that changes against the desired direction, for example, increasing an objective rather than decreasing it, are often valuable for design synthesis. This means that changes against the desired direction do not automatically identify inferior rules that should be removed. In contrast, it encourages the rule designer to also think about the sequences in which rules can be applied and to consider combining these sequences to create more specific rules to facilitate the generation of meaningful designs.
3.3.2. Q-2. Bar plots to represent matching ratio for each rule
For more detailed information on a rule's applicability, matching ratios are calculated and visualized. Throughout this paper, the matching ratio of a rule is defined as the number of LHS matches of a rule divided by the number of attempts to apply this rule. This ratio defines how likely it is for a rule to be applied with a matching ratio of 100% meaning a rule can always be applied, whereas a matching ratio of 0% represents a not reachable rule. From the matching ratios the rule designer can reason about the LHSs of the rules. This often helps to explain the design space that is generated with the rule set. Rules that have a very low application probability are only rarely applied. In grammars with unbalanced rule application probabilities (i.e., some rules are applied very often, others very rarely), the rule designer can, for example, consider formulating the LHSs of rarely applied rules differently to allow their application more often. In addition, the use of guidance strategies or predefined sequences for the CDS process can be helpful to improve the rule's application. The interpretation of matching ratios is dependent on the rule design as well as the search and optimization algorithm used later for design synthesis. When using intelligent search methods, it may not be required to ensure higher matching ratios for all rules; when using simple generate-and-test type algorithms, this may be more helpful to explore the design space.
3.3.3. Q-3/Q-4. Visualization of the design space
To show the size of the design space, a matrix with the dimensions of the design characteristics 1 and 2 is presented. Each point in the space indicates that a design with, for example, x elements of design characteristic 1 and y elements of design characteristic 2 exists. The color indicates how often a design with the respective characteristics is generated. This plot gives an indication about how the rules are used to generate the design space. The color can be used to identify solutions in the design space that are favored by the rules (“hot spots”). When continuous design characteristics are required or when the user is interested in additional information on objectives, the x and y axes can be made continuous or boxplots for each objective and design characteristic can be made in addition to the design space representation. The visualized space is generated using random generation without feedback. The rule engineer has to consider this when interpreting the results. It can happen that the space is larger than intended, for example, when the design engineer allows invalid designs and plans to use penalty functions and an optimization algorithm for the CDS process and these penalized designs are not removed from the design space yet. In contrast, it can also happen that the generated design space is small because certain rules undo what previous rules did. To derive useful measures to improve a rule set, the rule designer has to consider not only the space explored and the favored designs during the data generation process in GRAM but also the search and optimization process that will be used.
3.3.4. Q-5. Validity ratio
The validity ratio is defined here as the number of valid designs divided by the number of total designs generated. The validity of a design is defined by the designer and can be, for example, the necessity to have a connection between two components (e.g., a connection between the input and the output shaft in the gearbox example). The validity ratio gives feedback on the probability that the analyzed grammar generates valid designs with simple generate-and-test type algorithms. The lower the validity ratio, the more intelligent the guidance has to be to lead the grammar rule application to produce feasible designs. However, a low validity ratio does not mean that a grammar necessarily produces inferior results compared to a grammar with a validity ratio of 1, that is, generating only valid designs. In some cases, it is required to generate invalid intermediate designs to be able to eventually transform an invalid design into a valid one. It is the designer's choice to decide whether or not invalid designs should be allowed during design generation for a specific problem formulation and to interpret the validity ratio accordingly.
3.3.5. Q-6. Diversity ratio
The diversity ratio is defined as the number of valid and topologically different designs generated during the data generation phase divided by the number of all valid designs generated during the data generation phase. A high diversity ratio means that the grammar generates topologically different designs with a high likelihood (i.e., the design space is more easily explored than when having a lower diversity ratio and generating the same designs repeatedly). The rule designer has to be aware that the diversity ratio reflects only the design space explored during the data generation process. In most cases, the entire design space is unknown and when using parametric rules can be infinite.
Using these diagrams, designers can check if the grammar represents the intended design language and interpret the relative ease of generating known, intended designs, and they can further improve the grammar considering the analysis.
4. CASE STUDY: AUTOMATED GEARBOX SYNTHESIS
To show the applicability of the proposed method, GRAM is applied to four different grammars for automated gearbox synthesis. Gearbox design using generative grammars is an established CDS problem, and research has been carried out by several researchers (Pomrehn & Papalambros, Reference Pomrehn and Papalambros1995; Schmidt et al., Reference Schmidt, Shetty and Chase2000; Li & Schmidt, Reference Li and Schmidt2004; Starling, Reference Starling2004; Starling & Shea, Reference Starling and Shea2005; Lin et al., Reference Lin, Shea, Johnson, Coultate and Pears2010; Swantner & Campbell, Reference Swantner and Campbell2012). In this case study, all grammars are formulated and implemented as graph grammars consisting of a metamodel and a rule set (A–D). The rule sets contain both topologic and parametric rules.
4.1. Application of GRAM to gearbox rule sets A–D
The data generation is conducted with 50 times 1000 rule applications for each rule set. Data generation is carried out using a gearbox synthesis system developed by the authors based on GrGen, an open source graph rewriting tool (Geiß et al., Reference Geiß, Batz, Grund, Hack, Szalkowski, Corradini, Ehrig, Montanari, Ribeiro and Rozenberg2006; http://www.grgen.net). The objectives defined in this case study are the total mass of the components and the amount of collision, a metric calculated based on axial and radial overlap of all components (for the exact formula, see Lin et al., Reference Lin, Shea, Johnson, Coultate and Pears2010). The number of forward speeds and the number of reverse speeds are defined as design characteristics. The initial design is a bounding box with the input and output shaft. Data analysis and visualization are carried out using Matlab, and the graph isomorphism check to identify topologically identical designs is carried out using GrGen.
4.2. Metamodel
A metamodel describes all elements that can be used as building blocks within a generative grammar (Helms & Shea, Reference Helms and Shea2012), also known as vocabulary. For this case study, the metamodel consists of three different node types for gears, shafts, and the bounding box, and one directed edge type to connect nodes. All nodes have parameters to specify the components they represent (e.g., diameter, gear width, and position for gears).
4.3. Implementation of the rule sets
All four rule sets are implemented as graph grammar rules in GrGen. An overview is given in Figure 3. The schematic images for the rules are for visualization purposes only. The schematic graph representations for rules C2, C4, C6, D2, D4, and D6 represent the basic idea of the rule but not the exact LHS matches. Nodes of the LHS are, however, marked in red (medium gray) in the example graphs. The first two rule sets are based on the work by Starling and Shea (Starling, Reference Starling2004; Starling & Shea, Reference Starling and Shea2005) and consist of four (rule set A) and 21 (rule set B) rules, respectively. Rule set B is an extension of rule set A, adding several rules to change the dimensions and position of gears and shafts and two additional rules that add and remove components. Rule sets A and B were originally developed to generate watches and a winding mechanism in a camera (i.e., requiring only one speed). The third rule set (rule set C) is based on the work by Lin et al. (Reference Lin, Shea, Johnson, Coultate and Pears2010) for automotive gearboxes. It considers only parallel shafts that extend the width of the whole bounding box and consists of nine rules that are more sophisticated than those of rule set B in both their LHS and their RHS. Rule set D is an extension of rule set C presented for the first time in this paper. It adds two rules to change the length of shafts and is different from rule set C in that the LHSs of several rules account for changed lengths of shafts. Rule sets C and D were originally developed for automated gearbox synthesis (i.e., considering multiple speeds). They were developed to generate valid designs with every rule application as long as the initial design is valid. This decision was made by the rule designers to ensure design evaluation after each rule application. For this case study, a valid design must have at least one speed. In other words, there must be at least one path in the graph connecting the input and output shafts.

Fig. 3. Overview of all rule sets organized by their type (topologic or parametric); rule number (consisting of rule set label and rule number), name, and a pictorial description are given as well as the main differences between the grammars.
5. RESULTS
The results from the case study are presented below. Interpreting the analysis results, the questions Q-1 to Q-6 can now be answered.
5.1. Q-1. Which impact does the rule have on which objectives?
The influence of each of the rules in rule sets A–D is shown in Figure 4. Adding components (rules A1 and A3) always increases [red (medium gray) color in boxplot] mass and collisions, deleting them (rules A2 and A4) reduces [green (light gray) color in boxplot] both objectives.

Fig. 4. Influence of rules on the objectives mass and collisions for rule sets A–D (top to bottom).
This performance can also be clearly seen for the first four rules in rule set B; however, there are also rules that have no influence on an objective (black color in boxplot) or can either increase or decrease an objective value [blue (dark gray) color in boxplot]. Looking at the influence of each rule on collisions, it can be seen that although some rules do not influence the mass of a design, as for rules B9 and B10, where gears are moved in the z direction, the collisions are influenced by each of them.
Rules C1–C4 in rule set C show a do-undo behavior, where rules C1 and C3 add mass and collisions by adding components, and rules C2 and C4 reduce both objectives. The similarity between rule C5 and rule B19 can also be seen in the boxplots. Comparing rules A1–A4 and B1–B4, respectively, to rules C1–C4, a difference in the magnitude of the change in both objectives can be seen. This stems from the different implementation in rule set C. Rule A1, for example, only adds a single shaft, whereas rule C1 adds a shaft and connects it to the existing design with a gear pair (i.e., more components are added within the rule, which results in bigger changes in both mass and collisions).
Results from rule sets C and D look very similar, except for the additional rules D10 and D11, which shorten and lengthen shafts to reduce mass and collisions (D10) or to give the possibility to connect two shafts with a gear pair (D11). However, there is an additional difference between rules C6 and D6, because rule D6 has no influence on either mass or collisions. If the rules are implemented correctly, this should not occur. In this case, it stems from a careful implementation of rule set D ensuring that after every rule application no dangling nodes remain in the design, so this rule from rule set C, intending to repair designs, is not necessary anymore.
5.2. Q-2. How probable are the applications of each rule?
For all rules in rule sets A–D, matching ratios are represented as horizontal bars in Figure 5. Rules with simple LHSs are applied more frequently than those with more restrictive LHSs caused by constraints, for example, on parameters of the node, or component relations (i.e., more complex subgraphs). This can be seen, for example, in rule set A, where the rule to add a shaft (A1) and connect two shafts via a gear pair (A3) can always be applied, whereas rule A4, which removes a gear pair between two shafts, is rarely matched because there are more rules that add and delete shafts than there are to create gear pairs (rule A3). Therefore, randomly applying rules, the probability to apply rule A4 is lowered just because there are more rules that prohibit its application than there are to enable it. Having more rules that influence the LHS of this rule allows more matches. This can be seen in the plot for rule set B, where the exact same rule (B4) is applied with an almost three times higher matching ratio, due to one more rule in the rule set that generates a LHS match (B19).

Fig. 5. Percentages of successful rule matches for rule sets A–D.
5.3. Q-3. What solution space do the rules define?
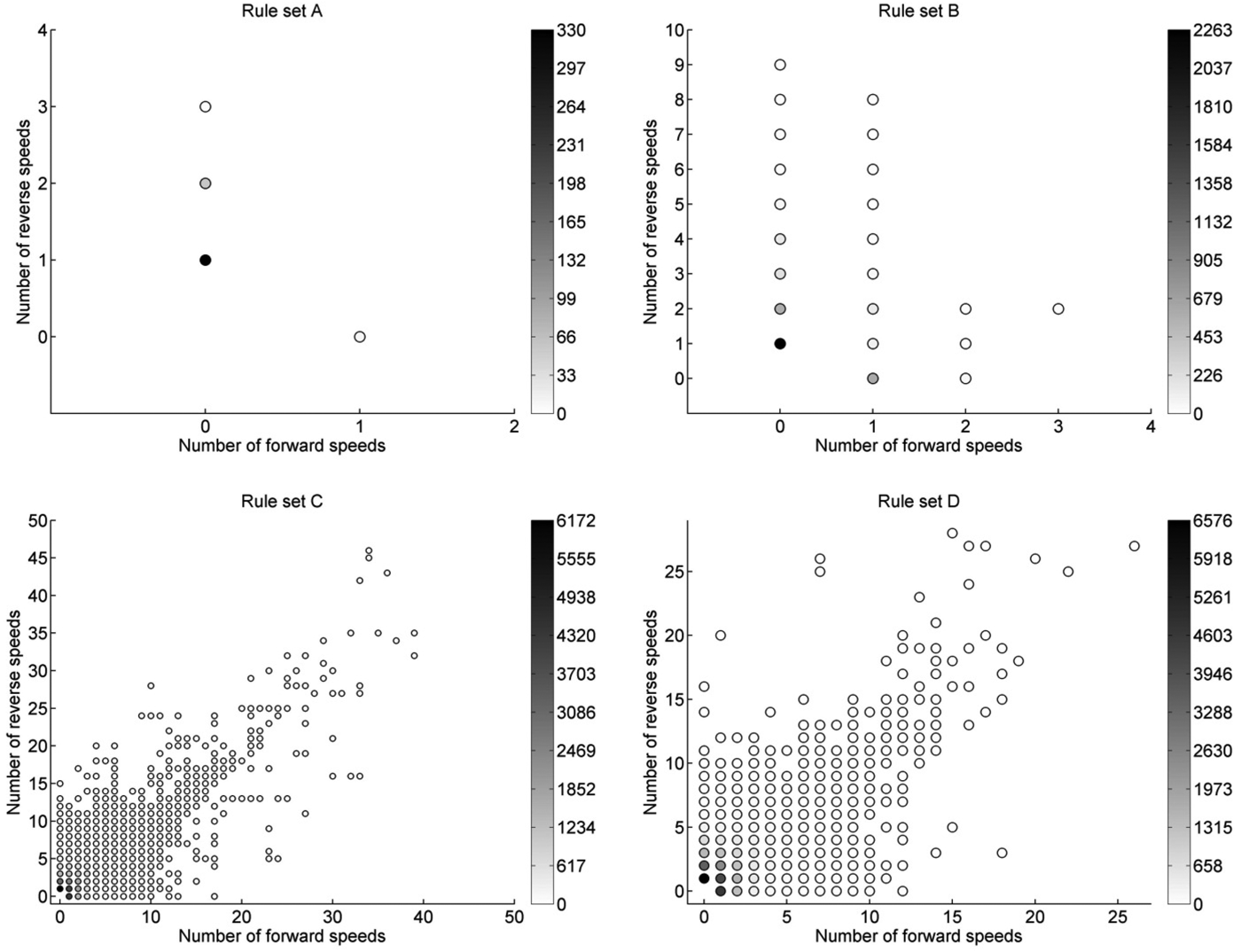
Figure 6 shows the design space generated by each of the rule sets in 50 runs applying 1000 rules selected randomly. The two design characteristics, that is, the number of forward and reverse speeds in a design, are plotted against each other.

Fig. 6. Plots of the design spaces generated by rule sets A–D. The color indicates how often a design with this speed configuration was generated in 50,000 rule applications.
The design spaces of rule sets A and B are very small. This can be explained by the simple grammar rules that are more dependent on an anticipated intelligent guidance and often do not produce good designs when applied randomly. Rule set B generates more speeds in general, which can be explained by the additional rule to connect shafts (i.e., rule B19). Rule sets C and D, with their rules developed to perturb, but not destroy, existing solutions, generate designs with higher numbers of speeds. Comparing the two, rule set C generates more designs with a higher number of speeds. This can be explained by the higher fraction of topological rules in rule set C that leads to more changes in topology when rules are applied randomly and thus allows to explore the design space more in this respect. In addition, rule set D has more restricted LHSs of its topological rules allowing, for example, only shafts that have an axial overlap to be connected via a gear pair. To compare not only topological but also parametric aspects of the design space, the average mass and collision metrics for all designs generated by the four rule sets are visualized in Figure 7. These representations support the points discussed. Rule set A generates many designs with a high number of components, thus leading to high mass and collisions. Rule set B has lower values for both due to rules that allow also parametric changes. The same effect can be observed with rule sets C and D, where the addition of more parametric rules in rule set D (i.e., rule D10 to shorten shafts) leads to lighter designs with less collision.

Fig. 7. Average mass and collisions of all generated designs for rule sets A–D.
5.4. Q-4. Does the rule set favor certain designs?
From the coloring of generated designs in Figure 6 it can be seen that all four rule sets favor designs with few forward and reverse speeds. Rule sets A and B generate designs with a high number of reverse speeds, for example, by directly connecting input and output shaft via a gear pair (rule A3, B3). Rule sets C and D do not favor reverse speeds, but they generate designs with high numbers of forward speeds due to rules that easily introduce forward speeds when applied to input and output shaft (rule C1, D1) or change the direction of an existing speed (rule C5, D5).
5.5. Q-5. How many valid designs are generated?
On the top of Figure 8, the validity ratio is given. It can be seen that this ratio increases from rule set A to B to C as the number of rules to connect shafts grows. Rule set D produces fewer topologically valid designs than does rule set C, which is caused by a slightly lower probability to change a topologically invalid design into a valid design. This is due to its smaller portion of topological rules and their reduced chance of application due to their more restrictive LHSs. Rule sets C and D are developed to generate valid designs only when applied to a valid design. For this case study, however, the initial design for all rule sets is invalid, because it contains only the input and the output shaft, causing the generation of invalid designs for rule sets C and D.

Fig. 8. Validity ratio (top) and diversity ratio (bottom) for rule sets A–D.
5.6. Q-6. How many different designs are generated?
On the right of Figure 8 the diversity ratio is shown. Comparing the rule sets underlines what has been found in the design space diagrams. Rule sets A and B produce many designs of the same topology. Rule set C has the most topologically different solutions, and rule set D produces fewer different solutions.
6. DISCUSSION
The case study shows that GRAM is capable of supporting design engineers to analyze their developed rule set, and comparing rule performance to intended performance allows designers to test the design language described against the intended language. The finding that rule sets A and B generate designs with fewer speeds and rule sets C and D generate designs with more speeds, for example, reflects the purpose for which the rule sets were originally developed (i.e., generating single speed gear trains for rule sets A and B and generating gearboxes with multiple speeds for rule sets C and D, respectively). Noninfluential rules can be detected to allow the reduction of the rule set, for example, rule D6. No unintended performance was discovered in this case, which might be explained by the long history of improving and further developing the grammars for this case study. That rule D6 (delete unused gears and shafts) can be removed from the rule set is a result of a careful implementation of the gearbox rules in this rule set such that no unattached shafts and gears are generated. This was a useful discovery due to GRAM and shows a secondary use of the method for rule set debugging. The design space representation with the data from the experiment allows statements to be made about the ambiguity of the design grammar regarding the defined design characteristics. The case study shows, for example, that the grammar is ambiguous because designs with the same design characteristics are achieved several times. This is also reflected in the diversity ratio, which, taking the point of view that rule sets with few rules are superior, could be calculated differently as the number of topologically different designs divided by the number of rules. For the case study, this would give similar results (rule set A: 0.014, rule set B: 0.008, rule set C: 0.042, and rule set D: 0.028) as the diversity ratio defined in GRAM.
Further, GRAM provides support for rule debugging. If, for example, an error occurred in the implementation of rule A1 (add shaft) such that a shaft is removed, GRAM would show this unintended performance of the rule in the boxplots. Similarly, GRAM helps to identify rules that are never applied (e.g., through the matching ratios) or that have no influence on any of the objectives (e.g., through the boxplots). This visual feedback on the rules enables the rule designer to find errors in the implementation and identify starting points for improving the quality of the developed rule sets.
Although the case study uses graph grammars, any type of generative design grammar can be analyzed using GRAM. Further, the method is independent of rule type and definition (i.e., simple vs. knowledge-intensive and topologic as well as parametric grammar rules). Because feedback is given based on each rule's performance with respect to defined objectives, it is necessary that intermediate as well as final designs can be evaluated.
Issues to be tackled are related to the visualization for large-scale problems as well as automating the interpretation. The visualization of the design space becomes difficult when more than two design criteria are defined. This is a known issue and research topic also in other domains, and new visualization techniques have to be investigated. Considering all objectives separately allows a thorough analysis of the grammar rules. However, for problems with multiple rules and objectives, the number of diagrams to interpret rises. An automated interpretation of the data instead of a visualization for the rule designer is one approach to tackle this issue. In addition, analyzing not only the performance of individual rules but also rule sequences will enable better understanding of rule sets and how sequences of rules impact design criteria.
Future work is planned to develop automated interpretation of the statistics generated using GRAM to overcome both the drawbacks in visualization for multiobjective problems and many rules as well as decreasing the interpretation effort by a human designer. Letting the human designer formulate hypotheses to define the intended performance of each rule and checking it against the rules' actual performance within defined confidence intervals is one possible way to support this last step of GRAM automatically in the future. Further research will focus on exploiting the knowledge gained in the rule analysis and reusing these findings to automatically generate strategies for more intelligent, self-tuning search algorithms. One approach is analyzing the performances of sequences of rules and learning favorable ones that can be reused. Another is to investigate the location where rules are applied to gain a better understanding of which is the best match of a LHS to select when a rule can be applied in several locations in a design. All future directions aim to increase the understanding of the developed grammar and further extend the idea to minimize the effort of tuning the search algorithm to the design problem while increasing the quality of the synthesis results.
7. CONCLUSION
The research presented describes a method, GRAM, to support the human designer in the development of generative grammar rules for CDS. This is the first approach known to the authors that focuses on systematic analysis of the rules in the development phase rather than during their application within a search algorithm after the rules are developed. GRAM facilitates gaining in-depth knowledge of the rules' performance, their relations to objectives, constraints, and characteristics, and their interaction. Further, it is possible to find errors in the implementation of the rules through easily readable feedback. Superior synthesis results as well as less effort to adapt search algorithms due to better understanding of the solution space defined by the grammar rules are expected. Using a systematic data generation process, data for the analysis is generated, analyzed, and visualized in defined diagrams. The interpretation of these diagrams using predefined questions helps to identify if, and which parts of, the rule set need improvement. With GRAM, future design grammar rule developers are given a means to reason about their specific grammar rule implementations in a systematic way.
Corinna Königseder graduated with a degree in mechanical engineering from Technische Universität München in 2009 and began her PhD in the Virtual Product Development Group at the Technische Universität München in 2010. She has been a PhD student at the Engineering Design and Computing Laboratory at the Swiss Federal Institute of Technology Zurich since 2012.
Kristina Shea is a Professor of engineering design and computing at ETH Zurich. She studied mechanical engineering at Carnegie Mellon University, where she completed her PhD in 1997. She has held appointments as a Postdoctoral Researcher at EPFL, Switzerland; university Lecturer at University of Cambridge; and Associate Professor at Technische Universität München. Dr. Shea carries out internationally leading research in new computational models, methods, and tools for design with a focus on supporting early stage design, including synthesis, optimization, and fabrication; and she has published over 100 papers with several best paper awards. Her expertise is more specifically in formal, integrated product models, graph and shape grammars, multiobjective and multidisciplinary optimization, and digital design to fabrication. Professor Shea is an Associate Editor for AIEDAM and ASME Journal of Mechanical Design. She serves on the board of management of the Design Society and is a Fellow of ASME.