Hostname: page-component-5d84bcc8dc-vw7zd Total loading time: 0 Render date: 2026-09-11T09:19:27.770Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ALGEBRAIC INTERPRETATION OF THE SUPER CATALAN NUMBERS

Part of: General field theory

Published online by Cambridge University Press:  06 November 2023

KEVIN LIMANTA Open the ORCID record for KEVIN LIMANTA [Opens in a new window]
KEVIN LIMANTA*
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, New South Wales 2052, Australia
*
e-mail: k.limanta@unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the notion of polynomial integration over an arbitrary circle C in the Euclidean geometry over general fields 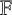$\mathbb {F}$ of characteristic zero as a normalised 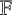$\mathbb {F}$-linear functional on 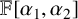$\mathbb {F}[\alpha _1, \alpha _2]$ that maps polynomials that evaluate to zero on C to zero and is $\mathrm {SO}(2,\mathbb {F})$-invariant. This allows us to not only build a purely algebraic integration theory in an elementary way, but also give the super Catalan numbers

$$ \begin{align*} S(m,n) = \frac{(2m)!(2n)!}{m!n!(m+n)!} \end{align*} $$

an algebraic interpretation in terms of values of this algebraic integral over some circle applied to the monomials 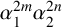$\alpha _1^{2m}\alpha _2^{2n}$.

Keywords

super Catalan numberscircular integral functionalpolynomial integration

MSC classification

Primary: 12E05: Polynomials (irreducibility, etc.)

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 3 , June 2024 , pp. 498 - 506
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allen, E. and Gheorghiciuc, I., ‘A weighted interpretation for the super Catalan numbers’, J. Integer Seq. 17(3) (2014), Article no. 14.10.7.Google Scholar
Baker, J. A., ‘Integration over spheres and the divergence theorem for balls’, Amer. Math. Monthly 104(1) (1997), 36–47.CrossRefGoogle Scholar
Catalan, E., ‘Question 1135’, Nouv. Ann. Math. (02) 13 (1874), 207.Google Scholar
Chen, X. and Wang, J., ‘The super Catalan numbers $S\left(m,m+s\right)$ for $s\le 4$ ’, Preprint, 2012, arXiv:1208.4196.Google Scholar
Folland, G., ‘How to integrate a polynomial over a sphere’, Amer. Math. Monthly 108(5) (2001), 446–448.CrossRefGoogle Scholar
Georgiadis, E., Munemasa, A. and Tanaka, H., ‘A note on super Catalan numbers’, Interdiscip. Inform. Sci. 18(1) (2012), 23–24.Google Scholar
Gessel, I., ‘Super ballot numbers’, J. Symbolic Comput. 14(2–3) (1992), 179–194.CrossRefGoogle Scholar
Gessel, I. and Xin, G., ‘A combinatorial interpretation of the numbers $6(2n)!/ n!(n+2)!$ ’, J. Integer Seq. 8 (2005), Article no. 05.2.3.Google Scholar
Limanta, K., ‘Super Catalan numbers and Fourier summation over finite fields’, Preprint, 2022, arXiv:2108.10191.CrossRefGoogle Scholar
Pippenger, N. and Schleich, K., ‘Topological characteristics of random triangulated surfaces’, Random Structures Algorithms 28 (2006), 247–288.CrossRefGoogle Scholar
Schaeffer, G., ‘A combinatorial interpretation of super-Catalan numbers of order two’, unpublished manuscript (2003), available at http://www.lix.polytechnique.fr/Labo/Gilles.Schaeffer/Biblio/Sc03.ps.Google Scholar
Stanley, R., Catalan Numbers (Cambridge University Press, Cambridge, 2015).CrossRefGoogle Scholar