Hostname: page-component-857557d7f7-ksgrx Total loading time: 0 Render date: 2025-11-21T03:03:22.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Hecke groups and continued fractions

Published online by Cambridge University Press:  17 April 2009

David Rosen  and
Thomas A. Schmidt
David Rosen
Affiliation:
Department of Mathematics, Swarthmore College, Swarthmore PA 19081, United States of America
Thomas A. Schmidt
Affiliation:
Department of Mathematics, Widener University, Chester PA 19013, United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Hecke groups

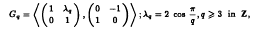
are Fuchsian groups of the first kind. In an interesting analogy to the use of ordinary continued fractions to study the geodesics of the modular surface, the λ-continued fractions (λF) introduced by the first author can be used to study those on the surfaces determined by the Gq. In this paper we focus on periodic continued fractions, corresponding to closed geodesics, and prove that the period of the λF for periodic 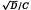has nearly the form of the classical case. From this, we give: (1) a necessary and sufficient condition for 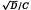to be periodic; (2) examples of elements of ℚ(λq) which also have such periodic expansions; (3) a discussion of solutions to Pell's equation in quadratic extensions of the ℚ(λq); and (4) Legendre's constant of diophantine approximation for the Gq, that is, γq such that 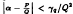< γq/Q2 implies that P/Q of “reduced finite λF form” is a convergent of real α ∉ Gq(∞).

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 46 , Issue 3 , December 1992 , pp. 459 - 474
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Adler, R. and Flatto, L., ‘Cross section maps for geodesic flows.I (the modular surface)’, in Ergodic theory and dynamical systems 2, Progress in Math., pp. 103–161 (Birkhäuser, Boston, Basil and Stuttgart, 1980).Google Scholar
[2]Adler, R. and Flatto, L., ‘Geodesic flows, interval maps, and symbolic dynamics’, Bull. AMS 25 (1991), 229–334.Google Scholar
[3]Artin, E., ‘Ein mechanisches System mit quasiergodischen Bahnen’, Abh. Math. Sem. Univ. Hamburg 3 (1924), 170–175.Google Scholar
[4]Beardon, A. F., The Geometry of discrete groups (Springer-Verlag, Berlin, Heidelberg, New York, 1983).CrossRefGoogle Scholar
[5]Bohro, W. and Rosenberger, G., ‘Eine Bemerkung zur Hecke-Gruppe G(λ)’, Abh. Math. Sem. Univ. Hamburg 39 (1973), 83–87.Google Scholar
[6]Crystal, G., Algebra, part II(Black Ltd., London, 1922).Google Scholar
[7]Ford, L., ‘A geometrical proof of a theorem of Hurwitz’, Proc. Edinburgh Math. Soc. 35 (1917), 59–65.Google Scholar
[8]Gutzwiller, M.C., Chaos in classical and quantum mechanics (Springer-Verlag, Berlin, Heidelberg, New York, 1990).Google Scholar
[9]Haas, A. and Series, C., ‘The Hurwitz constant and Diophantine approximation of Hecke groups’, J. London Math. Soc. 34 (1986), 219–234.CrossRefGoogle Scholar
[10]Hedlund, G., ‘On the metrical transitivity of the geodesics on closed surfaces of constant negative curvature’, Ann. of Math (2)35 (1934), 787–808.Google Scholar
[11]Lehner, J., A short course in automorphic forms (Holt, New York, 1966).Google Scholar
[12]Lehner, J., ‘Diophantine approximation of Hecke groups’, Glasgow Math. J. 27 (1985), 117–127.CrossRefGoogle Scholar
[13]Lehner, J., ‘The local Hurwitz constant and Diophantine approximation on Hecke groups’, Math Comp 55 (1990), 765–781.Google Scholar
[14]Leutbecher, A., ‘Über die Heckeschen Gruppen G(λ) II’, Math Ann. 211 (1974), 63–84.Google Scholar
[15]Rosen, D., ‘A class of continued fractions associated to certain properly discontinuous groups’, Duke Math. J. 21 (1954), 549–562.Google Scholar
[16]Rosen, D., ‘An arithmetic characterisation of the parabolic points of G(2cos π/5)’, Proc. Glasgow Math. Assoc. 6 (1963), 88–96.Google Scholar
[17]Rosen, D., ‘The substitutions of the Hecke group г(2cos π/5)’, Arch. Math. 46 (1986), 533–538.Google Scholar
[18]Schmidt, T., ‘Remarks on the Rosen λ-continued fractions’, (submitted).Google Scholar
[19]Series, C., ‘The modular surface and continued fractions’, J. London Math. Soc. 31 (1985), 69–80.Google Scholar
[20]Sheingorn, M., ‘Low height Hecke triangle group geodesics’, in Grosswald memorial volume, Editors M.I. Knopp and M. Sheingorn (to appear).Google Scholar
[21]van der Poorten, A.J., ‘An introduction to continued fractions’, in Diophantine analysis: Lecture Notes in Math 109, Editors Loxton, J.H. and van der Poorten, A.J., pp. 99–138 (Cambridge Univ. Press, Cambridge, 1986).Google Scholar