Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-27T06:54:03.542Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERSECTING THE TORSION OF ELLIPTIC CURVES

Part of: Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry Curves

Published online by Cambridge University Press:  27 December 2023

NATALIA GARCIA-FRITZ Open the ORCID record for NATALIA GARCIA-FRITZ [Opens in a new window]  and
HECTOR PASTEN Open the ORCID record for HECTOR PASTEN [Opens in a new window]
NATALIA GARCIA-FRITZ*
Affiliation:
Departamento de Matemáticas, Pontificia Universidad Católica de Chile, Facultad de Matemáticas, 4860 Av. Vicuña Mackenna, Macul, RM, Chile
HECTOR PASTEN
Affiliation:
Departamento de Matemáticas, Pontificia Universidad Católica de Chile, Facultad de Matemáticas, 4860 Av. Vicuña Mackenna, Macul, RM, Chile e-mail: hector.pasten@uc.cl
*
e-mail: natalia.garcia@uc.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

Bogomolov and Tschinkel [‘Algebraic varieties over small fields’, Diophantine Geometry, U. Zannier (ed.), CRM Series, 4 (Scuola Normale Superiore di Pisa, Pisa, 2007), 73–91] proved that, given two complex elliptic curves 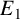$E_1$ and 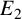$E_2$ along with even degree-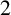$2$ maps 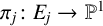$\pi _j\colon E_j\to \mathbb {P}^1$ having different branch loci, the intersection of the image of the torsion points of 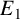$E_1$ and 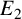$E_2$ under their respective 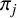$\pi _j$ is finite. They conjectured (also in works with Fu) that the cardinality of this intersection is uniformly bounded independently of the elliptic curves. The recent proof of the uniform Manin–Mumford conjecture implies a full solution of the Bogomolov–Fu–Tschinkel conjecture. In this paper, we prove a generalisation of the Bogomolov–Fu–Tschinkel conjecture whereby, instead of even degree-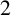$2$ maps, one can use any rational functions of bounded degree on the elliptic curves as long as they have different branch loci. Our approach combines Nevanlinna theory with the uniform Manin–Mumford conjecture. With similar techniques, we also prove a result on lower bounds for ranks of elliptic curves over number fields.

Keywords

elliptic curvetorsionrankMordell–LangManin–Mumforduniformity

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 14G25: Global ground fields 14H52: Elliptic curves
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

N.G.-F. was supported by ANID Fondecyt Regular grant 1211004 from Chile. H.P. was supported by ANID Fondecyt Regular grant 1230507 from Chile.

References

Bogomolov, F. and Fu, H., ‘Division polynomials and intersection of projective torsion points’, Eur. J. Math. 2(3) (2016), 644–660.CrossRefGoogle Scholar
Bogomolov, F., Fu, H. and Tschinkel, Y., ‘Torsion of elliptic curves and unlikely intersections’, in: Geometry and Physics, Vol. I (eds. Andersen, J. E., Dancer, A. and García-Prada, O.) (Oxford University Press, Oxford, 2018), 19–37.Google Scholar
Bogomolov, F. and Tschinkel, Y., ‘Algebraic varieties over small fields’, in: Diophantine Geometry, CRM Series, 4 (ed. Zannier, U.) (Scuola Normale Superiore di Pisa, Pisa, 2007), 73–91.Google Scholar
DeMarco, L., Krieger, H. and Ye, H., ‘Uniform Manin–Mumford for a family of genus 2 curves’, Ann. of Math. (2) 191(3) (2020), 949–1001.CrossRefGoogle Scholar
DeMarco, L. and Mavraki, N., ‘Dynamics on ${\mathbb{P}}^1$ : preperiodic points and pairwise stability’, Compos. Math., to appear.Google Scholar
Dimitrov, V., Gao, Z. and Habegger, P., ‘Uniformity in Mordell–Lang for curves’, Ann. of Math. (2) 194(1) (2021), 237–298.CrossRefGoogle Scholar
Fu, H. and Stoll, M., ‘Elliptic curves with common torsion $x$ -coordinates and hyperelliptic torsion packets’, Proc. Amer. Math. Soc. 150(12) (2022), 5137–5149.Google Scholar
Gao, Z., Ge, T. and Kühne, L., ‘The uniform Mordell–Lang conjecture’, Preprint, 2021, arXiv:2105.15085.Google Scholar
Garcia-Fritz, N. and Pasten, H., ‘Elliptic curves with long arithmetic progressions have large rank’, Int. Math. Res. Not. IMRN 2021(10) (2021), 7394–7432.CrossRefGoogle Scholar
Kühne, L., ‘Equidistribution in families of abelian varieties and uniformity’, Preprint, 2021, arXiv:2101.10272.Google Scholar
Kühne, L., ‘The relative Bogomolov conjecture for fibered products of elliptic curves’, J. reine angew. Math. 795 (2023), 243–270.Google Scholar
Poineau, J., ‘Dynamique analytique sur $\textbf{Z}$ . II: Écart uniforme entre Lattès et conjecture de Bogomolov–Fu–Tschinkel’, Preprint, 2023, arXiv:2207.01574.Google Scholar
Vojta, P., ‘Diophantine approximation and Nevanlinna theory’, in: Arithmetic Geometry, Lecture Notes in Mathematics, 2009 (eds. Colliot-Thélène, J.-L., Swinnerton-Dyer, P. and Vojta, P.) (Springer, Berlin, 2011), 111–224.CrossRefGoogle Scholar
Yuan, X., ‘Arithmetic bigness and a uniform Bogomolov-type result’, Preprint, 2023, arXiv:2108.05625.Google Scholar