Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-25T07:04:56.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Colouring Squares of Claw-free Graphs

Part of: Graph theory

Published online by Cambridge University Press:  09 January 2019

Rémi de Joannis de Verclos ,
Ross J. Kang  and
Lucas Pastor
Rémi de Joannis de Verclos
Affiliation:
Université Grenoble Alpes, CNRS, Grenoble INP, Laboratoire G-SCOP, 46 avenue Félix Viallet, 38031 Grenoble, France Email: remi.deverclos@g-scop.grenoble-inp.frlucas.pastor@g-scop.grenoble-inp.fr
Ross J. Kang
Affiliation:
Department of Mathematics, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, Netherlands Email: ross.kang@gmail.com
Lucas Pastor
Affiliation:
Université Grenoble Alpes, CNRS, Grenoble INP, Laboratoire G-SCOP, 46 avenue Félix Viallet, 38031 Grenoble, France Email: remi.deverclos@g-scop.grenoble-inp.frlucas.pastor@g-scop.grenoble-inp.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Is there some absolute 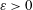$\unicode[STIX]{x1D700}>0$ such that for any claw-free graph 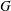$G$, the chromatic number of the square of 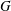$G$ satisfies 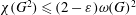$\unicode[STIX]{x1D712}(G^{2})\leqslant (2-\unicode[STIX]{x1D700})\unicode[STIX]{x1D714}(G)^{2}$, where 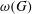$\unicode[STIX]{x1D714}(G)$ is the clique number of 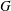$G$? Erdős and Nešetřil asked this question for the specific case where 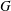$G$ is the line graph of a simple graph, and this was answered in the affirmative by Molloy and Reed. We show that the answer to the more general question is also yes, and, moreover, that it essentially reduces to the original question of Erdős and Nešetřil.

Keywords

graph colouringErdős–Nešetřil conjectureclaw-free graphs

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C35: Extremal problems 05C70: Factorization, matching, partitioning, covering and packing
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 1 , February 2019 , pp. 113 - 129
Copyright
© Canadian Mathematical Society 2017 

Footnotes

This research was supported by a Van Gogh grant, reference 35513NM and by ANR project STINT, reference ANR-13-BS02-0007. Author R. J. K. is currently supported by a NWO Vidi Grant, reference 639.032.614.

References

Ajtai, M., Komlós, J., and Szemerédi, E., A note on Ramsey numbers . J. Combin. Theory Ser. A 29(1980), 354–360. https://doi.org/10.1016/0097-3165(80)90030-8.Google Scholar
Bruhn, H. and Joos, F., A stronger bound for the strong chromatic index. arxiv:1504.02583.Google Scholar
Cames van Batenburg, W. and Kang, R. J., Squared chromatic number without claws or large cliques. arxiv:1609.08646.Google Scholar
Chudnovsky, M. and Ovetsky, A., Coloring quasi-line graphs . J. Graph Theory 54(2007), no. 1, 41–50. https://doi.org/10.1002/jgt.20192.Google Scholar
Chudnovsky, M. and Seymour, P., The structure of claw-free graphs. In: Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., 327. Cambridge University Press, Cambridge, 2005, pp. 153–171. https://doi.org/10.1017/CBO9780511734885.008.Google Scholar
Chudnovsky, M. and Seymour, P., Claw-free graphs VI . Colouring. J. Combin. Theory Ser. B 100(2010), no. 6, 560–572. https://doi.org/10.1016/j.jctb.2010.04.005.Google Scholar
Chudnovsky, M. and Seymour, P., Claw-free graphs. VII. Quasi-line graphs . J. Combin. Theory Ser. B 102, no. 6, 1267–1294. https://doi.org/10.1016/j.jctb.2012.07.005.Google Scholar
Chung, F. R. K., Gyárfás, A., Tuza, Z., and Trotter, W. T., The maximum number of edges in 2K 2-free graphs of bounded degree . Discrete Math. 81(1990), 129–135. https://doi.org/10.1016/0012-365X(90)90144-7.Google Scholar
Edmonds, J., Paths, trees, and flowers . Canad. J. Math. 17(1965), 449–467. https://doi.org/10.4153/CJM-1965-045-4.Google Scholar
Eisenbrand, F., Oriolo, G., Stauffer, G., and Ventura, P., The stable set polytope of quasi-line graphs . Combinatorica 28(2008), no. 1, 45–67. https://doi.org/10.1007/s00493-008-2244-x.Google Scholar
Erdős, P., Problems and results in combinatorial analysis and graph theory. In: Proceedings of the First Japan Conference on Graph Theory and Applications (Hakone, 1986), Discrete Math. 72(1988), 81–92. https://doi.org/10.1016/0012-365X(88)90196-3.Google Scholar
Erdős, P. and Szekeres, G., A combinatorial problem in geometry . Compositio. Math. 2(1935), 463–470.Google Scholar
Faenza, Y., Oriolo, G., and Stauffer, G., Solving the weighted stable set problem in claw-free graphs via decomposition . J. ACM 61(2014), no. 4, Art. 20, 41. https://doi.org/10.1145/2629600.Google Scholar
Gupta, R., The chromatic index and the degree of a graph . Notices Amer. Math. Soc. 13(1966), 719.Google Scholar
Kierstead, H. A., Applications of edge coloring of multigraphs to vertex coloring of graphs . Discrete Math. 74(1989), no. 1–2, 117–124. https://doi.org/10.1016/0012-365X(89)90203-3.Google Scholar
Kim, J. H., The Ramsey number R (3, t) has order of magnitude t 2/log t . Random Structures Algorithms 7(1995), 173–207. https://doi.org/10.1002/rsa.3240070302.Google Scholar
King, A. D. and Reed, B., Asymptotics of the chromatic number for quasi-line graphs . J. Graph Theory 73(2013), 327–341. https://doi.org/10.1002/jgt.21679.Google Scholar
King, A. D. and Reed, B., Claw-free graphs, skeletal graphs, and a stronger conjecture on 𝜔, 𝛥, and 𝜒 . J. Graph Theory 78(2015), 157–194. https://doi.org/10.1002/jgt.21797.Google Scholar
Minty, G. J., On maximal independent sets of vertices in claw-free graphs . J. Combin. Theory Ser. B 28(1980), 284–304. https://doi.org/10.1016/0095-8956(80)90074-X.Google Scholar
Molloy, M. and Reed, B., A bound on the strong chromatic index of a graph . J. Combin. Theory Ser. B 69(1997), 103–109. https://doi.org/10.1006/jctb.1997.1724.Google Scholar
Nakamura, D. and Tamura, A., A revision of Minty’s algorithm for finding a maximum weight stable set of a claw-free graph . J. Oper. Res. Soc. Japan 44(2001), 194–204. https://doi.org/10.15807/jorsj.44.194.Google Scholar
Sbihi, N., Algorithme de recherche d’un stable de cardinalité maximum dans un graphe sans étoile . Discrete Math. 29(1980), 53–76. https://doi.org/10.1016/0012-365X(90)90287-R.Google Scholar
Sumner, D. P., Subtrees of a graph and the chromatic number. In: The theory and applications of graphs (Kalamazoo, Mich., 1980), Wiley, New York, 1981, pp. 557–576.Google Scholar
Vizing, V. G., On an estimate of the chromatic class of a p-graph. (Russian) . Diskret. Analiz No. 3(1964), 25–30.Google Scholar