Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T01:25:28.714Z Has data issue: false hasContentIssue false
  • English
  • Français

The Generalized Cuspidal Cohomology Problem

Published online by Cambridge University Press:  20 November 2018

Anneke Bart  and
Kevin P. Scannell
Anneke Bart
Affiliation:
Department of Mathematics and Computer Science, Saint Louis University, St. Louis, MI 63103 e-mail: barta@slu.eduscannell@slu.edu
Kevin P. Scannell
Affiliation:
Department of Mathematics and Computer Science, Saint Louis University, St. Louis, MI 63103 e-mail: barta@slu.eduscannell@slu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 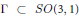$\Gamma \subset SO(3,1)$ be a lattice. The well known bending deformations, introduced by Thurston and Apanasov, can be used to construct non-trivial curves of representations of 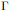$\Gamma $ into 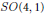$SO(4,1)$ when 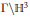$\Gamma \backslash {{\mathbb{H}}^{3}}$ contains an embedded totally geodesic surface. A tangent vector to such a curve is given by a non-zero group cohomology class in 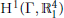${{\text{H}}^{1}}\left( \Gamma ,\mathbb{R}_{1}^{4} \right)$. Our main result generalizes this construction of cohomology to the context of “branched” totally geodesic surfaces. We also consider a natural generalization of the famous cuspidal cohomology problem for the Bianchi groups (to coefficients in non-trivial representations), and perform calculations in a finite range. These calculations lead directly to an interesting example of a link complement in 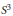${{S}^{3}}$ which is not infinitesimally rigid in 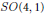$SO(4,1)$. The first order deformations of this link complement are supported on a piecewise totally geodesic 2-complex.

Keywords

57M5022E40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 4 , 01 August 2006 , pp. 673 - 690
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Adams, C. C., Hyperbolic 3-manifolds with two generators. Comm. Anal. Geom. 4(1996), no. 1-2, 181–206.Google Scholar
[2] Alperin, R. C., Homology of SL2(Z[ω]). Comment. Math. Helv. 55(1980), no. 3, 364–377.Google Scholar
[3] Apanasov, B. N., Deformations of conformal structures on hyperbolic manifolds. J. Differential Geom. 35(1992), no. 1, 1–20.Google Scholar
[4] Apanasov, B. N. and Tetenov, A. V., Deformations of hyperbolic structures along surfaces with boundary and pleated surfaces. In: Low-Dimensional Topology, Conf. Proc. Lecture Notes in Geom. Topology 3, International Press, Cambridge, MA, 1994, pp. 1–14.Google Scholar
[5] Baker, M. D., Ramified primes and the homology of the Bianchi groups. IHES Preprint, 1982.Google Scholar
[6] Bianchi, L., Sui gruppi di sostituzioni lineari con coefficienti appartenenti a corpi quadratici immaginari. Math. Ann. 40(1892), 332–412.Google Scholar
[7] Borel, A. and Wallach, N. R., Continuous cohomology, discrete subgroups, and representations of reductive groups. Annals of Mathematics Studies 94, Princeton University Press, Princeton, NJ, 1980.Google Scholar
[8] Brown, K. S., Cohomology of groups. Graduate Texts in Mathematics 87, Springer-Verlag, New York, 1982.Google Scholar
[9] Calabi, E., On compact, Riemannian manifolds with constant curvature. I. Proc. Sympos. Pure Math. 3, American Mathematical Society, Providence, RI, 1961, pp. 155–180.Google Scholar
[10] Fine, B. L., Algebraic Theory of the Bianchi Groups. Monographs and Textbooks in Pure and Applied Mathematics 129, Marcel Dekker, New York, 1989.Google Scholar
[11] Fox, R. H., Free differential calculus. I. Derivation in the free group ring. Ann. of Math. 57(1953), no. 3, 547–560.Google Scholar
[12] Fox, R. H., Free differential calculus. II. The isomorphism problem of groups. Ann. of Math. 59(1954), 196–210.Google Scholar
[13] Garland, H. and Raghunathan, M. S., Fundamental domains for lattices in (R-)ran. 1 semisimple Lie groups. Ann. of Math. 92(1970), no. 2, 279–326.Google Scholar
[14] Gehring, F. W., Maclachlan, C., and Martin, G. J., Two-generator arithmetic Kleinian groups. II. Bull. London Math. Soc. 30(1998), no. 3, 258–266.Google Scholar
[15] Goldman, W. M., The symplectic nature of fundamental groups of surfaces. Adv. in Math. 54(1984), no. 2, 200–225.Google Scholar
[16] Grunewald, F. and Hirsch, U., Link complements arising from arithmetic group actions. Internat. J. Math. 6(1995), no. 3, 337–370.Google Scholar
[17] Grunewald, F. and Schwermer, J., Arithmetic quotients of hyperbolic 3-space, cusp forms and link complements. Duke Math. J. 48(1981), no. 2, 351–358.Google Scholar
[18] Guichardet, A., Cohomologie des groupes topologiques et des algèbres de Lie. Textes Mathématiques 2, CEDIC, Paris, 1980.Google Scholar
[19] Harder, G., On the cohomology of discrete arithmetically defined groups. In: Discrete Subgroups of Lie Groups and Applications to Moduli, Oxford Univ. Press, Bombay, 1975, pp. 129–160.Google Scholar
[20] Harder, G., On the cohomology of SL(2, 𝔇). In: Lie Groups and Their Representations, Halsted, New York, 1975, pp. 139–150.Google Scholar
[21] Hatcher, A. E., Hyperbolic structures of arithmetic types on some link complements. J. London Math. Soc. 27(1983), no. 2, 345–355.Google Scholar
[22] Johnson, D. L. and Millson, J. J., Deformation spaces associated to compact hyperbolic manifolds. In: Discrete Groups in Geometry and Analysis: Papers in Honor of G. Mostow on His Sixtieth Birthday, Progr. Math. 67, Birkhäuser, Boston, 1987, pp. 48–106.Google Scholar
[23] Kapovich, M. É., Deformations of representations of discrete subgroups of SO(3, 1). Math. Ann. 299(1994), no. 2, 341–354.Google Scholar
[24] Kapovich, M. É. and Millson, J. J., Bending deformations of representations of fundamental groups of complexes of groups. Preprint, 1996.Google Scholar
[25] Kapovich, M. É. and Millson, J. J., On the deformation theory of representations of fundamental groups of compact hyperboli 3-manifolds. Topology 35(1996), no. 4, 1085–1106.Google Scholar
[26] Kapovich, M. É. and Millson, J. J., The relative deformation theory of representations and flat connections and deformations of linkages in constant curvature spaces. Compositio Math. 103(1996), no. 3, 287–317.Google Scholar
[27] Long, D. D., Immersions and embeddings of totally geodesic surfaces, Bull. London Math. Soc. 19(1987), no. 5, 481–484.Google Scholar
[28] Maskit, B., Kleinian Groups. Grundlehren der Mathematischen Wissenschaften 287, Springer-Verlag, Berlin, 1987.Google Scholar
[29] Maubon, J., Variations d’entropies et déformations de structures conformes plates sur les variétés hyperboliques compactes. Ergodic Theory Dynam. Systems 20(2000), no. 6, 1735–1748.Google Scholar
[30] Menasco, W. W. and Reid, A. W., Totally geodesic surfaces in hyperbolic link complements. In: Topology ‘90 Ohio State Univ. Math. Res. Inst. Publ. 1, de Gruyter, Berlin, 1992, pp. 215–226.Google Scholar
[31] Mendoza, E. R., Cohomology of PGL2 Over Imaginary Quadratic Integers. Ph.D. thesis , Rheinische Friedrich-Wilhelms-Universität Bonn, 1979.Google Scholar
[32] Millson, J. J., A remark on Raghunathan's vanishing theorem. Topology 24(1985), no. 4, 495–498.Google Scholar
[33] Raghunathan, M. S., On the first cohomology of discrete subgroups of semisimple Lie groups. Amer. J. Math. 87(1965), no. 1, 103–139.Google Scholar
[34] Riley, R. F., Applications of a computer implementation of Poincaré's theorem on fundamental polyhedra. Math. Comp. 40(1983), no. 162, 607–632.Google Scholar
[35] Rohlfs, J., On the cuspidal cohomology of the Bianchi modular groups. Math. Z. 188(1985), no. 2, 253–269.Google Scholar
[36] Scannell, K. P., Infinitesimal deformations of some SO(3, 1) lattices. Pacific J. Math. 194(2000), no. 2, 455–464.Google Scholar
[37] Scannell, K. P., Local rigidity of hyperboli. 3-manifolds after Dehn surgery. Duke Math. J. 114(2002), no. 1, 1–14.Google Scholar
[38] Swan, R. G., Generators and relations for certain special linear groups. Advances in Math. 6(1971), 1–77.Google Scholar
[39] Tan, S. P., Deformations of flat conformal structures on a hyperboli. 3-manifold. J. Differential Geom. 37(1993), no. 1, 161–176.Google Scholar
[40] Thurston, W. P., The Geometry and Topology of Three-Manifolds. Princeton Univ., Princeton, 1982.Google Scholar
[41] Vogtmann, K., Rational homology of Bianchi groups. Math. Ann. 272(1985), no. 3, 399–419.Google Scholar
[42] Weil, A., On discrete subgroups of Lie groups. II. Ann. of Math. 75(1962), no. 3, 578–602.Google Scholar
[43] Zimmert, R., Zu. SL2 der ganzen Zahlen eines imaginär-quadratischen Zahlkörpers. Invent.Math. 19(1973), no. 1, 73–81.Google Scholar