Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-29T04:01:02.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Dimensions of Measures of Finite Type II: Measures Without Full Support and With Non-regular Probabilities

Published online by Cambridge University Press:  20 November 2018

Kathryn E. Hare ,
Kevin G. Hare  and
Michael Ka Shing Ng
Kathryn E. Hare
Affiliation:
Dept. of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 email: kehare@uwaterloo.cakghare@uwaterloo.camichaelngelo@hotmail.com
Kevin G. Hare
Affiliation:
Dept. of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 email: kehare@uwaterloo.cakghare@uwaterloo.camichaelngelo@hotmail.com
Michael Ka Shing Ng
Affiliation:
Dept. of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 email: kehare@uwaterloo.cakghare@uwaterloo.camichaelngelo@hotmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a finite sequence of linear contractions 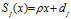${{S}_{j}}(x)\,=\,\rho x\,+{{d}_{j}}$ and probabilities 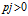$pj\,>\,0$ with 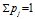$\Sigma \,{{p}_{j}}\,=\,1$. We are interested in the self-similar measure 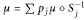$\mu \,=\,\Sigma \,{{p}_{j}}\,\mu \,{}^\circ \,s_{j}^{-1}$, of finite type. In this paper we study the multi-fractal analysis of such measures, extending the theory to measures arising from non-regular probabilities and whose support is not necessarily an interval.

Under some mild technical assumptions, we prove that there exists a subset of supp 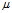$\mu $ of full 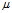$\mu $ and Hausdorff measure, called the truly essential class, for which the set of (upper or lower) local dimensions is a closed interval. Within the truly essential class we show that there exists a point with local dimension exactly equal to the dimension of the support. We give an example where the set of local dimensions is a two element set, with all the elements of the truly essential class giving the same local dimension. We give general criteria for these measures to be absolutely continuous with respect to the associated Hausdorff measure of their support, and we show that the dimension of the support can be computed using only information about the essential class.

To conclude, we present a detailed study of three examples. First, we show that the set of local dimensions of the biased Bernoulli convolution with contraction ratio the inverse of a simple Pisot number always admits an isolated point. We give a precise description of the essential class of a generalized Cantor set of finite type, and show that the 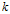$k$-th convolution of the associated Cantor measure has local dimension at 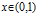$x\,\in \,(0,\,1)$ tending to 1 as 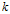$k$ tends to infinity. Lastly, we show that within a maximal loop class that is not truly essential, the set of upper local dimensions need not be an interval. This is in contrast to the case for finite type measures with regular probabilities and full interval support.

Keywords

28A8028A7811R06multi-fractal analysislocal dimensionIFSfinite type
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 4 , 01 August 2018 , pp. 824 - 867
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Bruggeman, C. and Hare, K. E., Multi-fractal analysis of convolution powers of measures. Real Anal. Exch. 38(2012/2013), 391–408. http://dx.doi.Org/10.14321/realanalexch.38.2.0391 Google Scholar
[2] Bruggeman, C., Hare, K. E., and Mak, C., Multi-fractal spectrum of self-similar measures with overlap. Nonlinearity 27(2014), 227–256. http://dx.doi.Org/10.1088/0951-7715/27/2/227 Google Scholar
[3] Feng, D.-J., Smoothness of the Lq-spectrum of self-similar measures with overlaps. J. London Math. Soc. 68(2003), 102–118. http://dx.doi.Org/10.1112/S002461070300437X Google Scholar
[4] Feng, D.-J., The limited Rademacher functions and Bernoulli convolutions associated with Pisot numbers. Adv. Math. 195(2005), 24–101. http://dx.doi.Org/10.1016/j.aim.2004.06.011 Google Scholar
[5] Feng, D.-J., Lyapunov exponents for products of matrices and multifractal analysis. II. General matrices. Israel J. Math. 170(2009), 355–394. http://dx.doi.Org/10.1007/s11856-009-0033-x Google Scholar
[6] Feng, D.-J., On the topology of polynomials with bounded integer coefficients. J. Eur. Math. Soc. 18(2016), 181–193. http://dx.doi.org/10.4171/JEMS/587 Google Scholar
[7] Feng, D.-J. and Lau, K-S., Multi-fractal formalism for self-similar measures with weak separation condition. J. Math. Pures Appl. 92(2009), 407–428. http://dx.doi.Org/10.1016/j.matpur.2009.05.009 Google Scholar
[8] Feng, D.-J., Lau, K-S., and Wang, X-Y., Some exceptional phenomena in multi-fractal formalism. II. Asian J. Math. 9(2005), 473–488. http://dx.doi.org/10.4310/AJM.2005.v9.n4.a2 Google Scholar
[9] Feng, D.-J. and Olivier, E., Multifractal analysis of the weak Gibbs measures and phase transition-application to some Bernoulli convolutions. Ergodic Theory Dynamical Systems 23(2003), 1751–1784. http://dx.doi.org/10.1017/S0143385703000051 Google Scholar
[10] Hare, K. E., Hare, K. G., and Matthews, K. R., Local dimensions of measures of finite type. J. Fractal Geometry 3(2016), 331–376. http://dx.doi.org/10.4171/JFC/39 Google Scholar
[11] Hare, K. E., Hare, K. G., and Matthews, K. R., Local dimensions of measures of finite type - supplementary information. arxiv:1 504.00510 http://dx.doi.Org/10.4171/JFC/39 Google Scholar
[12] Hu, T.-Y., The local dimensions of Bernoulli convolution associated with the golden number. Trans. Amer. Math. Soc. 349(1997), 2917–2940. http://dx.doi.org/10.1090/S0002-9947-97-01474-8 Google Scholar
[13] Hu, T-Y. and Lau, K-S., Multi-fractal structure of convolution of the Cantor measure. Adv. App. Math. 27(2001), 1–16. http://dx.doi.Org/10.1006/aama.2000.0683 Google Scholar
[14] Hu, T-Y. and Lau, K-S., Lq-spectrum of the Bernoulli convolution associated with the golden ratio. Studia Math. 131(1998), 225–251.Google Scholar
[15] Lau, K-S. and Wang, X-Y., Some exceptional phenomena in multi-fractal formalism. Part I. Asian J. Math 9(2005), 275–294. http://dx.doi.org/10.4310/AJM.2005.v9.n2.a13 Google Scholar
[16] Mattila, P., Geometry of sets and measures in Euclidean spaces. Cambridge Studies in Advanced Mathematics, 44, Cambridge University Press, Cambridge, 1995. http://dx.doi.Org/10.1017/CBO9780511623813 Google Scholar
[17] Ngai, S. M. and Wang, Y., Hausdorff dimension of self-similar sets with overlaps. J. London Math. Soc. 63(2001), 655–672. http://dx.doi.Org/10.1017/S0024610701001946 Google Scholar
[18] Nguyen, N. T., Iterated function systems of finite type and the weak separation property. Proc. Amer. Math. Soc. 130(2001), 483–487. http://dx.doi.org/10.1090/S0002-9939-01-06063-4 Google Scholar
[19] Porzio, A., On the regularity of the multifractal spectrum of Bernoulli convolutions. J. Stats. Phys. 91(1998), 17–29. http://dx.doi.Org/10.1023/A:1023027718308 Google Scholar
[20] Shmerkin, P., A modified multi-fractal formalism for a class of self-similar measures with overlap. Asian J. Math 9(2005), 323–348. http://dx.doi.org/10.4310/AJM.2005.v9.n3.a3 Google Scholar