Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-08T20:56:03.151Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Homology of GLn and Higher Pre-Bloch Groups

Published online by Cambridge University Press:  20 November 2018

Serge Yagunov
Serge Yagunov*
Affiliation:
Max Planck Institute für Mathematik, Vivatsgasse 7, 53111 Bonn, Germany email: yagunov@mpim-bonn.mpg.de Steklov Mathematical Institute (St. Petersburg), Fontanka 27, 191011 St. Petersburg, Russia email: yagunov@pdmi.ras.ru
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For every integer 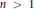$n\,>\,1$ and infinite field $F$ we construct a spectral sequence converging to the homology of 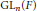$\text{G}{{\text{L}}_{n}}\left( F \right)$ relative to the group of monomial matrices 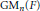$\text{G}{{\text{M}}_{n}}\left( F \right)$. Some entries in 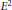${{E}^{2}}$-terms of these spectral sequences may be interpreted as a natural generalization of the Bloch group to higher dimensions. These groups may be characterized as homology of 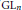$\text{G}{{\text{L}}_{n}}$ relatively to 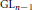$\text{G}{{\text{L}}_{n-1}}$ and 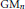$\text{G}{{\text{M}}_{n}}$. We apply the machinery developed to the investigation of stabilization maps in homology of General Linear Groups.

Keywords

19D5520J0618G60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 6 , 01 December 2000 , pp. 1310 - 1338
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Bloch, S., Higher regulators, algebraic K-theory, and zeta functions of elliptic curves. Lecture Notes, Univ. of California, Irvine, Calif., 1978.Google Scholar
[2] Borel, A. and Yang, J., The rank conjecture for number fields. Math. Res. Lett. 1(1994), 689–699.Google Scholar
[3] Brown, K., Cohomology of groups. Springer-Verlag, New York-Heidelberg-Berlin, 1982.Google Scholar
[4] Cathelineau, J.-L., Birapport et grupoides. Enseign. Math. (2) 41(1995), 257–280.Google Scholar
[5] Dupont, J. L. and Sah, C.-H., Scissors congruences II. J. Pure Appl. Algebra 25(1982), 159–195.Google Scholar
[6] Dupont, J. L. and Poulsen, E. T., Generation of C(x) by a restricted set of operations. J. Pure Appl. Algebra 25(1982), 155–157.Google Scholar
[7] Elbaz-Vincent, Ph., K3 indécomposable des anneaux et homologie de SL2. Thèse de doctorat, Nice, 1995.Google Scholar
[8] van der Kallen, W., Homology stability for genaral linear group. Invent. Math. 60(1980), 269–295.Google Scholar
[9] Knudson, K. P., Homology of linear groups. To be published by Birkhauser, 2000 (see http://www.math.uiuc.edu/K-theory/0387/).Google Scholar
[10] Nesterenko, Yu. P. and Suslin, A. A., Homology of the full linear group over a local ring and Milnor's K-theory. Math. USSR Izvestija 34(1990), 121–145.Google Scholar
[11] Sah, C.-H., Homology of classical Lie groups made discrete III. J. Pure Appl. Algebra 56(1989), 269–312.Google Scholar
[12] Sah, C.-H. and Wagoner, J. B., Second homology of Lie groups made discrete. Comm. Algebra 5(1977), 611–642.Google Scholar
[13] Serre, J.-P., Arbres, Amalgames, SL2. Astérisque 46, Soc. Math. France, 1977.Google Scholar
[14] Suslin, A. A., Homology of GL n, characteristic classes and Milnor's K-theory. Proc. Steklov Inst. Math. N 3 165(1985), 207–226.Google Scholar
[15] Suslin, A. A., K 3 of field and the Bloch group. Proc. Steklov Inst. Math. N 3 (1991), 217–239.Google Scholar
[16] Switzer, R. M., Algebraic topology—homotopy and homology. Springer-Verlag, Berlin-New York-Heidelberg, 1975.Google Scholar
[17] Yagunov, S., Homology of bi-Grassmannian complexes. K-theory 12(1997), 277–292.Google Scholar
[18] Yagunov, S., Geometrically Originated Complexes and the Homology of the Pair (GLn;GMn). Ph.D. Thesis, Northwestern University, Evanston, 1997.Google Scholar
[19] Yagunov, S., On a spectral sequence converging to homology of GLn relatively to GMn. Preprint POMI RAN #8, 1998 (in Russian); see http://www.pdmi.ras.ru/preprint/1998/index.html.Google Scholar