Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-24T15:50:08.456Z Has data issue: false hasContentIssue false
  • English
  • Français

The Pointwise Ergodic Theorem for Transformations whose Orbits contain or are contained in the Orbits of a Measure-Preserving Transformation

Published online by Cambridge University Press:  20 November 2018

John C. Kieffer  and
Maurice Rahe
John C. Kieffer
Affiliation:
University of Missouri-Rolla, Rolla, Missouri
Maurice Rahe
Affiliation:
Texas A. & M. University, College Station, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Let 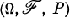be a probability space with 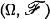standard. Let T be a bimeasurable one-to-one map of Ω onto itself. Let U: Ω → Ω be another measurable transformation whose orbits are contained in the T-orbits; that is,

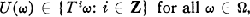
where Z denotes the set of integers. (This is equivalent to saying that there is a measurable mapping L: Ω → Z such that U(ω) = TL(ω)(ω), ω ∈ Ω.) Such pairs (T, U) arise quite naturally in ergodic theory and information theory. (For example, in ergodic theory, one can see such pairs in the study of the full group of a transformation [1]; in information theory, such a pair can be associated with the input and output of a variable-length source encoder [2] [3].) Neveu [4] obtained necessary and sufficient conditions for U to be measure-preserving if T is measure-preserving. However, if U fails to be measure-preserving, U might still possess many of the features of measure-preserving transformations.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 6 , 01 December 1982 , pp. 1303 - 1318
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Connes, A. and Krieger, W., Measure space automorphisms, the normalizers of their full groups, and approximate finiteness, Journal of Functional Analysis 24 (1977), 336–352.Google Scholar
2. Gray, R. M. and Kieffer, J. C., Asymptotically mean stationary measures, Annals of Probability 8 (1980), 962–973.Google Scholar
3. Kieffer, J. C. and Dunham, J. G., On the stability of a class of random difference equations useful in information theory, submitted for publication.Google Scholar
4. Neveu, J., Temps d'arrêt d'un système dynamique, Z. Wahrscheinlichkeitstheorie verw. Geb. 13 (1969), 81–94.Google Scholar
5. Weiss, B., Equivalence of measure preserving transformations, Lecture Notes, The Institute for Advanced Studies, The Hebrew University of Jerusalem (1976).Google Scholar