Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schied, Alexander
1997.
Moderate deviations and functional LIL for super-Brownian motion.
Stochastic Processes and their Applications,
Vol. 72,
Issue. 1,
p.
11.
Schied, Alexander
1998.
Cramer's condition and Sanov's theorem.
Statistics & Probability Letters,
Vol. 39,
Issue. 1,
p.
55.
Zhang, Mei
2008.
Some scaled limit theorems for an immigration super-Brownian motion.
Science in China Series A: Mathematics,
Vol. 51,
Issue. 2,
p.
203.
Serlet, Laurent
2009.
New large deviation results for some super-Brownian processes.
Stochastic Processes and their Applications,
Vol. 119,
Issue. 5,
p.
1696.
Xiang, Kai‐Nan
2010.
An explicit Schilder‐type theorem for super‐Brownian motions.
Communications on Pure and Applied Mathematics,
Vol. 63,
Issue. 11,
p.
1381.
Xiang, KaiNan
2013.
Large deviations under a viewpoint of metric geometry: Measure-valued process cases.
Science China Mathematics,
Vol. 56,
Issue. 11,
p.
2335.
Fatheddin, Parisa
and
Xiong, Jie
2015.
Large deviation principle for some measure-valued processes.
Stochastic Processes and their Applications,
Vol. 125,
Issue. 3,
p.
970.
Fatheddin, Parisa
and
Xiong, Jie
2016.
Moderate deviation principle for a class of stochastic partial differential equations.
Journal of Applied Probability,
Vol. 53,
Issue. 1,
p.
279.
Sun, Wen
2024.
Pathwise large deviations for the pure jump k-nary interacting particle systems.
The Annals of Applied Probability,
Vol. 34,
Issue. 1A,

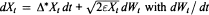 a space-time white noise. A Schilder type theorem is established concerning large deviation probabilities of
a space-time white noise. A Schilder type theorem is established concerning large deviation probabilities of 