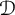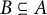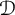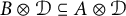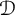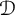1 Introduction
The study of inclusions of C*-algebras has been of recent interest. There is no short supply of research concerning inclusions relating to noncommutative dynamics [Reference Cameron and Smith8, Reference Echterhoff and Rørdam18, Reference Izumi30, Reference Osaka and Teruya42, Reference Popa44], as well as inclusions of simple C*-algebras [Reference Rørdam51]. There has also been work done regarding the passage of properties from a subalgebra to a larger algebra using tracial approximations [Reference Lee and Osaka38]. We discuss inclusions from the lens of tensorially absorbing a strongly self-absorbing C*-algebra
![]() $\mathcal {D}$
[Reference Toms and Winter66].
$\mathcal {D}$
[Reference Toms and Winter66].
When speaking of tensorial absorption with a strongly self-absorbing C*-algebra, central sequences play a role akin to McDuff’s characterization of when a
![]() $\text {II}_1$
von Neumann algebra absorbs the unique hyperfinite
$\text {II}_1$
von Neumann algebra absorbs the unique hyperfinite
![]() $\text {II}_1$
factor
$\text {II}_1$
factor
![]() $\mathcal {R}$
[Reference McDuff40]. Central sequences have been studied since the inception of operator algebras, being used by Murray and von Neumann to exhibit non-isomorphic
$\mathcal {R}$
[Reference McDuff40]. Central sequences have been studied since the inception of operator algebras, being used by Murray and von Neumann to exhibit non-isomorphic
![]() $\text {II}_1$
factors by showing that
$\text {II}_1$
factors by showing that
![]() $\mathcal {L}(\mathbb {F}_2)$
does not have property
$\mathcal {L}(\mathbb {F}_2)$
does not have property
![]() $\Gamma $
[Reference Murray and von Neumann41]. They were also used in Connes’ theorem concerning the uniqueness of
$\Gamma $
[Reference Murray and von Neumann41]. They were also used in Connes’ theorem concerning the uniqueness of
![]() $\mathcal {R}$
[Reference Connes13], and the classification of automorphisms on hyperfinite factors [Reference Connes11, Reference Connes13]. In [Reference Bisch2, Reference Bisch3], Bisch considered the central sequence algebra
$\mathcal {R}$
[Reference Connes13], and the classification of automorphisms on hyperfinite factors [Reference Connes11, Reference Connes13]. In [Reference Bisch2, Reference Bisch3], Bisch considered the central sequence algebra
![]() $\mathcal {N}^\omega \cap \mathcal {M}'$
associated with an (irreducible) inclusion of
$\mathcal {N}^\omega \cap \mathcal {M}'$
associated with an (irreducible) inclusion of
![]() $\text {II}_1$
factors
$\text {II}_1$
factors
![]() $\mathcal {N} \subseteq \mathcal {M}$
and characterized when there was an isomorphism
$\mathcal {N} \subseteq \mathcal {M}$
and characterized when there was an isomorphism
![]() $\Phi : \mathcal {M} \simeq \mathcal {M} \overline {\otimes } \mathcal {R}$
such that
$\Phi : \mathcal {M} \simeq \mathcal {M} \overline {\otimes } \mathcal {R}$
such that
![]() $\Phi (\mathcal {N}) = \mathcal {N} \overline {\otimes } \mathcal {R}$
in terms of the existence of non-commuting sequences in
$\Phi (\mathcal {N}) = \mathcal {N} \overline {\otimes } \mathcal {R}$
in terms of the existence of non-commuting sequences in
![]() $\mathcal {N}$
which asymptotically commute with the larger von Neumann algebra
$\mathcal {N}$
which asymptotically commute with the larger von Neumann algebra
![]() $\mathcal {M}$
(in the
$\mathcal {M}$
(in the
![]() $\|\cdot \|_2$
-norm). As pointed out by Izumi [Reference Izumi31], there are similar central characterizations for unital inclusions of separable C*-algebras which tensorially absorb a strongly self-absorbing C*-algebra
$\|\cdot \|_2$
-norm). As pointed out by Izumi [Reference Izumi31], there are similar central characterizations for unital inclusions of separable C*-algebras which tensorially absorb a strongly self-absorbing C*-algebra
![]() $\mathcal {D}$
(it was at least pointed out for
$\mathcal {D}$
(it was at least pointed out for
![]() $\mathcal {D}$
being one of
$\mathcal {D}$
being one of
![]() $M_{n^{\infty }},\mathcal {O}_2,\mathcal {O}_{\infty }$
).
$M_{n^{\infty }},\mathcal {O}_2,\mathcal {O}_{\infty }$
).
For a strongly self-absorbing C*-algebra
![]() $\mathcal {D}$
[Reference Toms and Winter66, Definition 1.3(iv)], we study
$\mathcal {D}$
[Reference Toms and Winter66, Definition 1.3(iv)], we study
![]() $\mathcal {D}$
-stable inclusions (see Section 4 for detailed definitions), analogous to Bisch’s notion for an (irreducible) inclusion of
$\mathcal {D}$
-stable inclusions (see Section 4 for detailed definitions), analogous to Bisch’s notion for an (irreducible) inclusion of
![]() $\text {II}_1$
factors [Reference Bisch2]. We say that an inclusion
$\text {II}_1$
factors [Reference Bisch2]. We say that an inclusion
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable if there is an isomorphism
$\mathcal {D}$
-stable if there is an isomorphism
![]() $A \simeq A \otimes \mathcal {D}$
such that
$A \simeq A \otimes \mathcal {D}$
such that
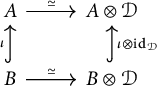
commutes.
We study such inclusions systematically, discussing central sequence characterizations, permanence properties, and giving examples toward the end. We list some key findings here. The first is that unital
![]() $\mathcal {D}$
-stable inclusions exist between unital, separable
$\mathcal {D}$
-stable inclusions exist between unital, separable
![]() $\mathcal {D}$
-stable C*-algebras if there is any unital inclusion, and that the set of unital
$\mathcal {D}$
-stable C*-algebras if there is any unital inclusion, and that the set of unital
![]() $\mathcal {D}$
-stable inclusions is quite large. Moreover, as far as classification of embeddings up to approximate unitary equivalence (in particular by K-theory and traces),
$\mathcal {D}$
-stable inclusions is quite large. Moreover, as far as classification of embeddings up to approximate unitary equivalence (in particular by K-theory and traces),
![]() $\mathcal {D}$
-stable embeddings are all that matter.
$\mathcal {D}$
-stable embeddings are all that matter.
Theorem 1.1 (Proposition 4.11 and Corollary 4.12)
Let
![]() $A,B$
be unital, separable,
$A,B$
be unital, separable,
![]() $\mathcal {D}$
-stable C*-algebras.
$\mathcal {D}$
-stable C*-algebras.
-
(1) The set of unital
 $\mathcal {D}$
-stable embeddings
$\mathcal {D}$
-stable embeddings
 $B \hookrightarrow A$
is point-norm dense in the set of all unital embeddings
$B \hookrightarrow A$
is point-norm dense in the set of all unital embeddings
 $B \hookrightarrow A$
.
$B \hookrightarrow A$
. -
(2) Every unital embedding
 $B \hookrightarrow A$
is approximately unitarily equivalent to a unital
$B \hookrightarrow A$
is approximately unitarily equivalent to a unital
 $\mathcal {D}$
-stable embedding.
$\mathcal {D}$
-stable embedding.
We note that this set is however not everything. We provide examples of non-
![]() $\mathcal {D}$
-stable inclusions of
$\mathcal {D}$
-stable inclusions of
![]() $\mathcal {D}$
-stable C*-algebras, namely by fitting a C*-algebra with perforated Cuntz semigroup or with higher stable rank (in particular, non-
$\mathcal {D}$
-stable C*-algebras, namely by fitting a C*-algebra with perforated Cuntz semigroup or with higher stable rank (in particular, non-
![]() $\mathcal {Z}$
-stable C*-algebras) in between two
$\mathcal {Z}$
-stable C*-algebras) in between two
![]() $\mathcal {D}$
-stable C*-algebras. The second useful tool is that a
$\mathcal {D}$
-stable C*-algebras. The second useful tool is that a
![]() $\mathcal {D}$
-stable inclusion allows one to find an appropriate isomorphism witnessing
$\mathcal {D}$
-stable inclusion allows one to find an appropriate isomorphism witnessing
![]() $\mathcal {D}$
-stability of countably many intermediate subalgebras at once.
$\mathcal {D}$
-stability of countably many intermediate subalgebras at once.
Theorem 1.2 (Theorem 4.8)
Let
![]() $B \subseteq A$
be a unital,
$B \subseteq A$
be a unital,
![]() $\mathcal {D}$
-stable inclusion of separable C*-algebras. If
$\mathcal {D}$
-stable inclusion of separable C*-algebras. If
![]() $(C_n)_{n \in \mathbb {N}}$
is a sequence of C*-algebras such that
$(C_n)_{n \in \mathbb {N}}$
is a sequence of C*-algebras such that
![]() $B \subseteq C_n \subseteq A$
unitally for all n, then there exists a unital *-isomorphism
$B \subseteq C_n \subseteq A$
unitally for all n, then there exists a unital *-isomorphism
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
such that:
$\Phi : A \simeq A \otimes \mathcal {D}$
such that:
-
(1)
 $\Phi (B) = B \otimes \mathcal {D}$
and
$\Phi (B) = B \otimes \mathcal {D}$
and -
(2)
 $\Phi (C_n) = C_n \otimes \mathcal {D}$
for all
$\Phi (C_n) = C_n \otimes \mathcal {D}$
for all
 $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
This is not a trivial condition, as it is not true that any such isomorphism sends every intermediate C*-algebra to its tensor product with
![]() $\mathcal {D}$
(see Example 4.6). In fact, one can always find an intermediate C*-algebra C between B and A and an isomorphism
$\mathcal {D}$
(see Example 4.6). In fact, one can always find an intermediate C*-algebra C between B and A and an isomorphism
![]() $A \simeq A \otimes \mathcal {D}$
sending B to
$A \simeq A \otimes \mathcal {D}$
sending B to
![]() $B \otimes \mathcal {D}$
which does not send C to
$B \otimes \mathcal {D}$
which does not send C to
![]() $C \otimes \mathcal {D}$
(although, of course, we will still have
$C \otimes \mathcal {D}$
(although, of course, we will still have
![]() $C \simeq C \otimes \mathcal {D}$
).
$C \simeq C \otimes \mathcal {D}$
).
The above result, together with the Galois correspondence of Izumi [Reference Izumi30], allows us to get a result similar to the main theorem of [Reference Amini, Golestani, Jamali and Christopher Phillips1]. There they prove that if
![]() $G \curvearrowright ^\alpha A$
is an action of a finite group with the weak tracial Rokhlin property on a C*-algebra A with sufficient regularity conditions, then every C*-algebra between
$G \curvearrowright ^\alpha A$
is an action of a finite group with the weak tracial Rokhlin property on a C*-algebra A with sufficient regularity conditions, then every C*-algebra between
![]() $A^\alpha \subseteq A$
and
$A^\alpha \subseteq A$
and
![]() $A \subseteq A \rtimes _\alpha G$
is
$A \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {Z}$
-stable. Assuming we have a unital C*-algebra with the same regularity conditions, we show that we can witness
$\mathcal {Z}$
-stable. Assuming we have a unital C*-algebra with the same regularity conditions, we show that we can witness
![]() $\mathcal {Z}$
-stability of all such intermediate C*-algebras concurrently.
$\mathcal {Z}$
-stability of all such intermediate C*-algebras concurrently.
Theorem 1.3 (Corollary 5.6)
Let A be a unital, simple, separable, nuclear
![]() $\mathcal {Z}$
-stable C*-algebra and
$\mathcal {Z}$
-stable C*-algebra and
![]() $G \curvearrowright ^\alpha A$
be an action of a finite group with the weak tracial Rokhlin property. There exists an isomorphism
$G \curvearrowright ^\alpha A$
be an action of a finite group with the weak tracial Rokhlin property. There exists an isomorphism
![]() $\Phi : A \rtimes _\alpha G \simeq (A \rtimes _\alpha G) \otimes \mathcal {Z}$
such that whenever C is a unital C*-algebra satisfying either:
$\Phi : A \rtimes _\alpha G \simeq (A \rtimes _\alpha G) \otimes \mathcal {Z}$
such that whenever C is a unital C*-algebra satisfying either:
-
(1)
 $A^\alpha \subseteq C \subseteq A$
or
$A^\alpha \subseteq C \subseteq A$
or -
(2)
 $A \subseteq C \subseteq A \rtimes _\alpha G$
,
$A \subseteq C \subseteq A \rtimes _\alpha G$
,
we have
![]() $\Phi (C) = C \otimes \mathcal {Z}$
.
$\Phi (C) = C \otimes \mathcal {Z}$
.
This paper is structured as follows. We discuss various local properties in Section 3, and then formalize the notion of a
![]() $\mathcal {D}$
-stable embedding in Section 4, examining several properties and consequences. In Section 5, we show how several examples arising from noncommutative dynamical systems fit into the framework of
$\mathcal {D}$
-stable embedding in Section 4, examining several properties and consequences. In Section 5, we show how several examples arising from noncommutative dynamical systems fit into the framework of
![]() $\mathcal {D}$
-stable inclusions. We finish with several examples in Section 6.
$\mathcal {D}$
-stable inclusions. We finish with several examples in Section 6.
2 Preliminaries
2.1 Notation
We use capital letters
![]() $A,B,C,D$
to denote C*-algebras and usually a calligraphic
$A,B,C,D$
to denote C*-algebras and usually a calligraphic
![]() $\mathcal {D}$
to denote a strongly self-absorbing C*-algebra. Generally, small letters
$\mathcal {D}$
to denote a strongly self-absorbing C*-algebra. Generally, small letters
![]() $a,b,c,d,\dots ,x,y,z$
will denote operators in C*-algebras.
$a,b,c,d,\dots ,x,y,z$
will denote operators in C*-algebras.
![]() $A_+$
will denote cone of positive elements in a C*-algebra A. If
$A_+$
will denote cone of positive elements in a C*-algebra A. If
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $a,b$
are elements in a C*-algebra, we will write
$a,b$
are elements in a C*-algebra, we will write
to mean that
![]() $\|a - b\| < \varepsilon $
. This will make some approximations more legible.
$\|a - b\| < \varepsilon $
. This will make some approximations more legible.
The symbol
![]() $\otimes $
will denote the minimal tensor product of C*-algebras, while
$\otimes $
will denote the minimal tensor product of C*-algebras, while
![]() $\odot $
will mean the algebraic tensor product. We use the minimal tensor product throughout, and it is common for us to deal with nuclear C*-algebras so there should not be any ambiguity. The symbol
$\odot $
will mean the algebraic tensor product. We use the minimal tensor product throughout, and it is common for us to deal with nuclear C*-algebras so there should not be any ambiguity. The symbol
![]() $\overline {\otimes }$
will denote the von Neumann tensor product.
$\overline {\otimes }$
will denote the von Neumann tensor product.
We will denote by
![]() $M_n$
the C*-algebra of
$M_n$
the C*-algebra of
![]() $n\times n$
matrices, and
$n\times n$
matrices, and
![]() $M_{n^{\infty }}$
the uniformly hyperfinite (UHF) C*-algebra associated with the supernatural number
$M_{n^{\infty }}$
the uniformly hyperfinite (UHF) C*-algebra associated with the supernatural number
![]() $n^{\infty }$
. We will write
$n^{\infty }$
. We will write
![]() $\mathcal {Q}$
for the universal UHF algebra
$\mathcal {Q}$
for the universal UHF algebra
![]() $\mathcal {Q} = \bigotimes _{n \in \mathbb {N}} M_n$
.
$\mathcal {Q} = \bigotimes _{n \in \mathbb {N}} M_n$
.
By
![]() $G \curvearrowright ^\alpha A$
, we will mean that the (discrete) group G acts on A by automorphisms, i.e.,
$G \curvearrowright ^\alpha A$
, we will mean that the (discrete) group G acts on A by automorphisms, i.e.,
![]() $\alpha : G \to \operatorname {\mathrm {Aut}}(A)$
is a homomorphism.
$\alpha : G \to \operatorname {\mathrm {Aut}}(A)$
is a homomorphism.
![]() $A \rtimes _{r,\alpha }G$
will denote the reduced crossed product, which we will just write as
$A \rtimes _{r,\alpha }G$
will denote the reduced crossed product, which we will just write as
![]() $A \rtimes _\alpha G$
if it is clear from context that the group is amenable and A is nuclear (e.g., if G is finite). We will denote by
$A \rtimes _\alpha G$
if it is clear from context that the group is amenable and A is nuclear (e.g., if G is finite). We will denote by
![]() $A^\alpha $
the fixed point subalgebra of the action (or
$A^\alpha $
the fixed point subalgebra of the action (or
![]() $A^G$
if the action is clear from context).
$A^G$
if the action is clear from context).
For a map
![]() $f: X \to Y$
between sets X and Y, we will write
$f: X \to Y$
between sets X and Y, we will write
![]() $f: X \hookrightarrow Y$
to mean that f is injective and
$f: X \hookrightarrow Y$
to mean that f is injective and
![]() $f: X \twoheadrightarrow Y$
to mean that f is surjective. This will usually be done in the context of *-homomorphisms.
$f: X \twoheadrightarrow Y$
to mean that f is surjective. This will usually be done in the context of *-homomorphisms.
2.2 Ultrapowers, central sequences, and central sequence algebras
Fix a free ultrafilter
![]() $\omega \in \beta \mathbb {N}$
. Throughout, we will use ultrapowers to describe asymptotic behavior. Alternatively, one can use sequence algebras, although this comes down to a matter of taste and one can swap between the two if desired, as we will provide local characterizations. This also means that all of what we do will be independent of the specific ultrafilter
$\omega \in \beta \mathbb {N}$
. Throughout, we will use ultrapowers to describe asymptotic behavior. Alternatively, one can use sequence algebras, although this comes down to a matter of taste and one can swap between the two if desired, as we will provide local characterizations. This also means that all of what we do will be independent of the specific ultrafilter
![]() $\omega $
.
$\omega $
.
For a C*-algebra A, the ultrapower of A is the C*-algebra
where
![]() $c_{0,\omega } := \{(a_n)_{n \in \mathbb {N}} \in \ell ^{\infty }(A) \mid \lim _{n \to \omega } \|a_n\| = 0\}$
is the ideal of
$c_{0,\omega } := \{(a_n)_{n \in \mathbb {N}} \in \ell ^{\infty }(A) \mid \lim _{n \to \omega } \|a_n\| = 0\}$
is the ideal of
![]() $\omega $
-null sequences. We can embed A into
$\omega $
-null sequences. We can embed A into
![]() $A_\omega $
canonically by means of constant sequences: we identify
$A_\omega $
canonically by means of constant sequences: we identify
![]() $a \in A$
with the equivalence class of the constant sequence
$a \in A$
with the equivalence class of the constant sequence
![]() $(a)_{n \in \mathbb {N}}$
.
$(a)_{n \in \mathbb {N}}$
.
To ease notation, we will usually write elements of
![]() $A_\omega $
as sequences
$A_\omega $
as sequences
![]() $(a_n)_{n \in \mathbb {N}}$
, keeping in mind that these are equivalence classes without explicitly stating it every time. We note that the norm on
$(a_n)_{n \in \mathbb {N}}$
, keeping in mind that these are equivalence classes without explicitly stating it every time. We note that the norm on
![]() $A_\omega $
is given by
$A_\omega $
is given by
![]() $\|(a_n)_{n \in \mathbb {N}}\| = \lim _{n \to \omega } \|a_n\|$
.
$\|(a_n)_{n \in \mathbb {N}}\| = \lim _{n \to \omega } \|a_n\|$
.
Kirchberg’s
![]() $\varepsilon $
-test [Reference Kirchberg35, Lemma A.1] is essentially the operator algebraists’ Łoś’ theorem without having to turn to (continuous) model theory. Heuristically, it says that if certain things can be done approximately in an ultrapower, then certain things can be done exactly in an ultrapower.
$\varepsilon $
-test [Reference Kirchberg35, Lemma A.1] is essentially the operator algebraists’ Łoś’ theorem without having to turn to (continuous) model theory. Heuristically, it says that if certain things can be done approximately in an ultrapower, then certain things can be done exactly in an ultrapower.
Lemma 2.1 (Kirchberg’s
 $\varepsilon $
-test)
$\varepsilon $
-test)
Let
![]() $(X_n)_n$
be a sequence of sets and suppose that for each n, there is a sequence
$(X_n)_n$
be a sequence of sets and suppose that for each n, there is a sequence
![]() $(f_n^{(k)})_{k \in \mathbb {N}}$
of functions
$(f_n^{(k)})_{k \in \mathbb {N}}$
of functions
![]() $f_n^{(k)}: X_n \to [0,\infty )$
. For
$f_n^{(k)}: X_n \to [0,\infty )$
. For
![]() $k \in \mathbb {N}$
, let
$k \in \mathbb {N}$
, let
Suppose that for every
![]() $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
![]() $\varepsilon> 0$
, there is
$\varepsilon> 0$
, there is
![]() $s \in \prod _n X_n$
with
$s \in \prod _n X_n$
with
![]() $f_\omega ^{(k)}(s) < \varepsilon $
for
$f_\omega ^{(k)}(s) < \varepsilon $
for
![]() $k=1,\dots ,m$
. Then there exists
$k=1,\dots ,m$
. Then there exists
![]() $t \in \prod _nX_n$
with
$t \in \prod _nX_n$
with
![]() $f_\omega ^{(k)}(t) = 0$
for all
$f_\omega ^{(k)}(t) = 0$
for all
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.
The above is useful, although if one so wishes, one can usually construct exact objects from approximate objects by using standard diagonalization arguments (under some separability assumptions). These sorts of arguments work in both the ultrapower setting and the sequence algebra setting.
Finally, if
![]() $\alpha \in \operatorname {\mathrm {Aut}}(A)$
is an automorphism, there is an induced automorphism on
$\alpha \in \operatorname {\mathrm {Aut}}(A)$
is an automorphism, there is an induced automorphism on
![]() $A_\omega $
, which we will denote by
$A_\omega $
, which we will denote by
![]() $\alpha _\omega $
, given by
$\alpha _\omega $
, given by
2.3 Central sequences and central sequence subalgebras
For a unital C*-algebra A, the C*-algebra of
![]() $\omega $
-central sequences is
$\omega $
-central sequences is
where we are identifying
![]() $A \subseteq A_\omega $
with the constant sequences. If
$A \subseteq A_\omega $
with the constant sequences. If
![]() $B \subseteq A$
is a unital C*-subalgebra and
$B \subseteq A$
is a unital C*-subalgebra and
![]() $S \subseteq A_\omega $
is a subset, we can associate the relative commutant of S in
$S \subseteq A_\omega $
is a subset, we can associate the relative commutant of S in
![]() $B_\omega $
:
$B_\omega $
:
Of particular interest will be when
![]() $S = A$
, and
$S = A$
, and
![]() $B \subseteq A$
is a unital inclusion of separable C*-algebras.
$B \subseteq A$
is a unital inclusion of separable C*-algebras.
2.4 Strongly self-absorbing C*-algebras
A unital separable C*-algebra
![]() $\mathcal {D}$
is strongly self-absorbing if
$\mathcal {D}$
is strongly self-absorbing if
![]() $\mathcal {D} \not \simeq \mathbb {C}$
and there is an isomorphism
$\mathcal {D} \not \simeq \mathbb {C}$
and there is an isomorphism
![]() $\phi : \mathcal {D} \to \mathcal {D} \otimes \mathcal {D}$
which is approximately unitarily equivalent to the first factor embedding
$\phi : \mathcal {D} \to \mathcal {D} \otimes \mathcal {D}$
which is approximately unitarily equivalent to the first factor embedding
![]() $d \mapsto d \otimes 1_{\mathcal {D}}$
(see [Reference Toms and Winter66]). All known strongly self-absorbing C*-algebras are: the Jiang–Su algebra
$d \mapsto d \otimes 1_{\mathcal {D}}$
(see [Reference Toms and Winter66]). All known strongly self-absorbing C*-algebras are: the Jiang–Su algebra
![]() $\mathcal {Z}$
[Reference Jiang and Su32], the Cuntz algebras
$\mathcal {Z}$
[Reference Jiang and Su32], the Cuntz algebras
![]() $\mathcal {O}_2$
and
$\mathcal {O}_2$
and
![]() $\mathcal {O}_{\infty }$
[Reference Cuntz15], UHF algebras of infinite type, and
$\mathcal {O}_{\infty }$
[Reference Cuntz15], UHF algebras of infinite type, and
![]() $\mathcal {O}_{\infty }$
tensor a UHF algebra of infinite type. Strongly self-absorbing C*-algebras have approximately inner flip and therefore have K-theoretic restrictions (see [Reference Enders, Schemaitat and Tikuisis20, Reference Tikuisis61]). They are also nuclear, simple, and have at most one tracial state [Reference Toms and Winter66],
$\mathcal {O}_{\infty }$
tensor a UHF algebra of infinite type. Strongly self-absorbing C*-algebras have approximately inner flip and therefore have K-theoretic restrictions (see [Reference Enders, Schemaitat and Tikuisis20, Reference Tikuisis61]). They are also nuclear, simple, and have at most one tracial state [Reference Toms and Winter66],
Tensorial absorption with strongly self-absorbing C*-algebras gives rise to many regular properties, for example, in terms of K-theory, traces, and the Cuntz semigroup [Reference Jiang and Su32, Reference Rørdam46, Reference Rørdam47, Reference Rørdam50]. Of paramount interest is the Jiang–Su algebra
![]() $\mathcal {Z}$
. An accumulation of work has successfully classified all (unital) separable, simple, nuclear, infinite-dimensional,
$\mathcal {Z}$
. An accumulation of work has successfully classified all (unital) separable, simple, nuclear, infinite-dimensional,
![]() $\mathcal {Z}$
-stable C*-algebras satisfying the Universal Coefficient Theorem (UCT) of Rosenberg and Schochet [Reference Rosenberg and Schochet53] by means of K-theory and traces (see [Reference Carrión, Gabe, Schafhauser, Tikuisis and White9] and the references therein). We describe how one might work with
$\mathcal {Z}$
-stable C*-algebras satisfying the Universal Coefficient Theorem (UCT) of Rosenberg and Schochet [Reference Rosenberg and Schochet53] by means of K-theory and traces (see [Reference Carrión, Gabe, Schafhauser, Tikuisis and White9] and the references therein). We describe how one might work with
![]() $\mathcal {Z}$
-stability in terms of its standard building blocks. Recall that, for
$\mathcal {Z}$
-stability in terms of its standard building blocks. Recall that, for
![]() $n,m \geq 2$
, the dimension drop algebras are
$n,m \geq 2$
, the dimension drop algebras are
Such an algebra is a called a prime dimension drop algebra when n and m are coprime. The Jiang–Su algebra
![]() $\mathcal {Z}$
is the unique separable simple C*-algebra with unique tracial state which is an inductive limit of prime dimension drop algebras with unital connecting maps [Reference Jiang and Su32] (in fact, the dimension drop algebras can be chosen to have the form
$\mathcal {Z}$
is the unique separable simple C*-algebra with unique tracial state which is an inductive limit of prime dimension drop algebras with unital connecting maps [Reference Jiang and Su32] (in fact, the dimension drop algebras can be chosen to have the form
![]() $\mathcal {Z}_{n,n+1}$
). It is
$\mathcal {Z}_{n,n+1}$
). It is
![]() $KK$
-equivalent to
$KK$
-equivalent to
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\mathcal {Z}$
-stability is a often necessary condition for K-theoretic classification.
$\mathcal {Z}$
-stability is a often necessary condition for K-theoretic classification.
By [Reference Rørdam and Winter52, Proposition 5.1] (or [Reference Sato54, Proposition 2.1] for our desired formulation),
![]() $\mathcal {Z}_{n,n+1}$
is the universal C*-algebra generated by elements
$\mathcal {Z}_{n,n+1}$
is the universal C*-algebra generated by elements
![]() $c_1,\dots ,c_n$
and s such that:
$c_1,\dots ,c_n$
and s such that:
-
•
 $c_1 \geq 0$
;
$c_1 \geq 0$
; -
•
 $c_ic_j^* = \delta _{ij}c_1^2$
;
$c_ic_j^* = \delta _{ij}c_1^2$
; -
•
 $s^*s + \sum _{i=1}^n c_i^*c_i = 1$
;
$s^*s + \sum _{i=1}^n c_i^*c_i = 1$
; -
•
 $c_1s = s$
.
$c_1s = s$
.
If there are uniformly tracially large (in the sense of [Reference Toms, White and Winter65, Definition 2.2]) order zeroFootnote
1
c.p.c. maps
![]() $M_n \to A_\omega \cap A'$
, these give rise to elements
$M_n \to A_\omega \cap A'$
, these give rise to elements
![]() $c_1,\dots ,c_n \in A_\omega \cap A'$
with
$c_1,\dots ,c_n \in A_\omega \cap A'$
with
![]() $c_1 \geq 0$
and
$c_1 \geq 0$
and
![]() $c_ic_j^* = \delta _{ij}c_1^2$
, along with certain tracial information. If A has strict comparison, Matui and Sato used this tracial information to show that A has property (SI) [Reference Matui and Sato39], from which one can get an element
$c_ic_j^* = \delta _{ij}c_1^2$
, along with certain tracial information. If A has strict comparison, Matui and Sato used this tracial information to show that A has property (SI) [Reference Matui and Sato39], from which one can get an element
![]() $s \in A_\omega \cap A'$
such that
$s \in A_\omega \cap A'$
such that
![]() $s^*s + \sum _{i=1}^n c_i^*c_i = 1$
and
$s^*s + \sum _{i=1}^n c_i^*c_i = 1$
and
![]() $c_1s = s$
. This gives a *-homomorphism
$c_1s = s$
. This gives a *-homomorphism
![]() $\mathcal {Z}_{n,n+1} \to A_\omega \cap A'$
, which if can be done for each
$\mathcal {Z}_{n,n+1} \to A_\omega \cap A'$
, which if can be done for each
![]() $n \in \mathbb {N}$
, is enough to conclude that
$n \in \mathbb {N}$
, is enough to conclude that
![]() $\mathcal {Z} \hookrightarrow A_\omega \cap A'$
unitally and hence
$\mathcal {Z} \hookrightarrow A_\omega \cap A'$
unitally and hence
![]() $A \simeq A \otimes \mathcal {Z}$
(see [Reference Toms and Winter67, Reference Winter71]). In fact, it suffices to show that
$A \simeq A \otimes \mathcal {Z}$
(see [Reference Toms and Winter67, Reference Winter71]). In fact, it suffices to show that
![]() $\mathcal {Z}_{2,3} \hookrightarrow A_\omega \cap A'$
(or
$\mathcal {Z}_{2,3} \hookrightarrow A_\omega \cap A'$
(or
![]() $\mathcal {Z}_{n,n+1}$
for some
$\mathcal {Z}_{n,n+1}$
for some
![]() $n \geq 2$
) (see [Reference Rørdam and Winter52, Theorem 3.4(ii)] and [Reference Schemaitat56, Theorem 5.15]).
$n \geq 2$
) (see [Reference Rørdam and Winter52, Theorem 3.4(ii)] and [Reference Schemaitat56, Theorem 5.15]).
3 Approximately central approximate embeddings
Here, we formalize some results on approximate embeddings. When
![]() $B \subseteq A$
is a unital inclusion of separable C*-algebras, this will yield local characterizations of nuclear subalgebras of
$B \subseteq A$
is a unital inclusion of separable C*-algebras, this will yield local characterizations of nuclear subalgebras of
![]() $B_\omega \cap A'$
, as defined in (2.6). Recall that we write u.c.p. or c.p.c. to mean that a map is unital and completely positive or completely positive and contractive, respectively.
$B_\omega \cap A'$
, as defined in (2.6). Recall that we write u.c.p. or c.p.c. to mean that a map is unital and completely positive or completely positive and contractive, respectively.
Definition 3.1 Let
![]() $B \subseteq A$
be a unital inclusion of C*-algebras, and let D be a unital, simple, nuclear C*-algebra. Let
$B \subseteq A$
be a unital inclusion of C*-algebras, and let D be a unital, simple, nuclear C*-algebra. Let
![]() $\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
be finite sets and
$\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
be finite sets and
![]() $\varepsilon> 0$
. We say that a u.c.p. map
$\varepsilon> 0$
. We say that a u.c.p. map
![]() $\phi : D \to B$
is an
$\phi : D \to B$
is an
![]() $(\mathcal {F},\varepsilon )$
-approximate embedding if:
$(\mathcal {F},\varepsilon )$
-approximate embedding if:
-
(1)
 $\phi (cd) \approx _\varepsilon \phi (c)\phi (d)$
for all
$\phi (cd) \approx _\varepsilon \phi (c)\phi (d)$
for all
 $c,d \in \mathcal {F}$
.
$c,d \in \mathcal {F}$
.
If
![]() $\phi $
additionally satisfies
$\phi $
additionally satisfies
-
2.
 $[\phi (c),a] \approx _\varepsilon 0$
for all
$[\phi (c),a] \approx _\varepsilon 0$
for all
 $c \in \mathcal {F}$
and
$c \in \mathcal {F}$
and
 $a \in \mathcal {G}$
,
$a \in \mathcal {G}$
,
then we say that
![]() $\phi $
is an
$\phi $
is an
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding.
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding.
We will usually write that
![]() $\phi $
is a
$\phi $
is a
![]() $(\mathcal {F},\varepsilon )$
-embedding or
$(\mathcal {F},\varepsilon )$
-embedding or
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding to mean that
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding to mean that
![]() $\phi $
is an
$\phi $
is an
![]() $(\mathcal {F},\varepsilon )$
-approximate embedding or
$(\mathcal {F},\varepsilon )$
-approximate embedding or
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding, respectively.
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding, respectively.
Remark 3.1 One can make a similar definition to the above if D is not simple or nuclear (or even unital). The aim is to discuss subalgebras of
![]() $B_\omega \cap A'$
, and if
$B_\omega \cap A'$
, and if
![]() $D \hookrightarrow B_\omega \cap A'$
is nuclear, then one can use the Choi–Effros lifting theorem [Reference Choi and Effros10, Theorem 3.10] (see also [Reference Brown and Ozawa6, Theorem C.3]) to lift the embedding to a sequence of u.c.p. maps which are approximately isometric, approximately multiplicative, and approximately commute with finite subsets of A. If D is simple, the approximate isometry condition follows for free since the embedding
$D \hookrightarrow B_\omega \cap A'$
is nuclear, then one can use the Choi–Effros lifting theorem [Reference Choi and Effros10, Theorem 3.10] (see also [Reference Brown and Ozawa6, Theorem C.3]) to lift the embedding to a sequence of u.c.p. maps which are approximately isometric, approximately multiplicative, and approximately commute with finite subsets of A. If D is simple, the approximate isometry condition follows for free since the embedding
![]() $D \hookrightarrow B_\omega \cap A'$
must be isometric.
$D \hookrightarrow B_\omega \cap A'$
must be isometric.
If we loosen the simple and nuclear assumptions on D, we can still speak of bounded linear maps
![]() $\phi :D \to B$
(no longer necessarily u.c.p.) which are approximately isometric, approximately multiplicative, approximately adjoint-preserving, and approximately commute with a finite prescribed subset of A. This will allow one to discuss general subalgebras of
$\phi :D \to B$
(no longer necessarily u.c.p.) which are approximately isometric, approximately multiplicative, approximately adjoint-preserving, and approximately commute with a finite prescribed subset of A. This will allow one to discuss general subalgebras of
![]() $B_\omega \cap A'$
. As we will only be interested in strongly self-absorbing subalgebras of
$B_\omega \cap A'$
. As we will only be interested in strongly self-absorbing subalgebras of
![]() $B_\omega \cap A'$
, which are unital, separable, simple, and nuclear [Reference Toms and Winter66, Section 1.6], we restrict ourselves to u.c.p. maps from a unital, simple, nuclear C*-algebras which are approximately multiplicative and approximately commute with finite subsets of A.
$B_\omega \cap A'$
, which are unital, separable, simple, and nuclear [Reference Toms and Winter66, Section 1.6], we restrict ourselves to u.c.p. maps from a unital, simple, nuclear C*-algebras which are approximately multiplicative and approximately commute with finite subsets of A.
Most of the work in this section can be done without assumptions of simplicity and nuclearity.
Lemma 3.2 Suppose that
![]() $A,B,D$
are unital C*-algebras with B separable and D simple, separable and nuclear. Suppose that
$A,B,D$
are unital C*-algebras with B separable and D simple, separable and nuclear. Suppose that
![]() $B \subseteq A$
is a unital inclusion and let
$B \subseteq A$
is a unital inclusion and let
![]() $S \subseteq A$
be a separable subset. There are
$S \subseteq A$
be a separable subset. There are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embeddings
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embeddings
![]() $D \to B$
for all
$D \to B$
for all
![]() $\mathcal {F} \subseteq D, \mathcal {G} \subseteq S$
and
$\mathcal {F} \subseteq D, \mathcal {G} \subseteq S$
and
![]() $\varepsilon> 0$
if and only if there is a unital embedding
$\varepsilon> 0$
if and only if there is a unital embedding
![]() $D \hookrightarrow B_\omega \cap S'$
.
$D \hookrightarrow B_\omega \cap S'$
.
Proof Let
![]() $(F_n)_{n \in \mathbb {N}}$
be an increasing sequence of finite subsets of D with dense union, and let
$(F_n)_{n \in \mathbb {N}}$
be an increasing sequence of finite subsets of D with dense union, and let
![]() $(G_n)_{n \in \mathbb {N}}$
be an increasing sequence of finite subsets of S with dense union. Let
$(G_n)_{n \in \mathbb {N}}$
be an increasing sequence of finite subsets of S with dense union. Let
![]() $\phi _n: D \to B$
be
$\phi _n: D \to B$
be
![]() $(F_n,\frac {1}{n},G_n)$
-approximately central approximate embeddings. Let
$(F_n,\frac {1}{n},G_n)$
-approximately central approximate embeddings. Let
![]() $\pi : \ell ^{\infty }(B) \to B_\omega $
denote the quotient map and set
$\pi : \ell ^{\infty }(B) \to B_\omega $
denote the quotient map and set
which is a unital embedding such that
![]() $[\psi (d),a] = 0$
for all
$[\psi (d),a] = 0$
for all
![]() $d \in D$
and
$d \in D$
and
![]() $a \in S$
.
$a \in S$
.
Conversely, suppose that
![]() $\psi : D \to B_\omega \cap S'$
is a unital embedding,
$\psi : D \to B_\omega \cap S'$
is a unital embedding,
![]() $\mathcal {F} \subseteq D,\mathcal {G} \subseteq S$
are finite and
$\mathcal {F} \subseteq D,\mathcal {G} \subseteq S$
are finite and
![]() $\varepsilon>0$
. By the Choi–Effros lifting theorem, there is a u.c.p. lift
$\varepsilon>0$
. By the Choi–Effros lifting theorem, there is a u.c.p. lift
![]() $\tilde {\psi } = (\tilde {\psi }_n)_{n \in \mathbb {N}}: D \to \ell ^{\infty }(B)$
such that:
$\tilde {\psi } = (\tilde {\psi }_n)_{n \in \mathbb {N}}: D \to \ell ^{\infty }(B)$
such that:
-
•
 $\|\tilde {\psi }_n(cd) - \tilde {\psi }_n(c)\tilde {\psi }_n(d)\| \to ^{n \to \omega } 0$
,
$\|\tilde {\psi }_n(cd) - \tilde {\psi }_n(c)\tilde {\psi }_n(d)\| \to ^{n \to \omega } 0$
, -
•
 $\|[\tilde {\psi }_n(d),a]\| \to ^{n \to \omega } 0$
$\|[\tilde {\psi }_n(d),a]\| \to ^{n \to \omega } 0$
for all
![]() $c,d \in D$
and
$c,d \in D$
and
![]() $a \in A$
. Take n large enough and set
$a \in A$
. Take n large enough and set
![]() $\phi = \psi _n$
, so that
$\phi = \psi _n$
, so that
![]() $\phi $
will be a
$\phi $
will be a
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding.
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding.
Corollary 3.3 Let
![]() $A,B,D$
be unital C*-algebras with
$A,B,D$
be unital C*-algebras with
![]() $B,D$
separable, simple, and nuclear and
$B,D$
separable, simple, and nuclear and
![]() $B \subseteq A$
be a unital inclusion. Suppose that there are unital embeddings
$B \subseteq A$
be a unital inclusion. Suppose that there are unital embeddings
![]() $\phi : D \to B_\omega $
and
$\phi : D \to B_\omega $
and
![]() $\psi : B \to A_\omega $
. Then there is a unital embedding
$\psi : B \to A_\omega $
. Then there is a unital embedding
![]() $\xi : D \hookrightarrow A_\omega $
. If
$\xi : D \hookrightarrow A_\omega $
. If
![]() $S \subseteq A_\omega $
is a separable subset with
$S \subseteq A_\omega $
is a separable subset with
![]() $\psi (B) \subseteq A_\omega \cap S'$
, then
$\psi (B) \subseteq A_\omega \cap S'$
, then
![]() $\xi $
can be chosen with
$\xi $
can be chosen with
![]() $\xi (D) \subseteq A_\omega \cap S'$
.
$\xi (D) \subseteq A_\omega \cap S'$
.
Proof Let
![]() $\mathcal {F} \subseteq D$
be finite and
$\mathcal {F} \subseteq D$
be finite and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $L := \max \{\max _{d \in \mathcal {F}}\|d\|,1\}$
. By the above lemma, there is an
$L := \max \{\max _{d \in \mathcal {F}}\|d\|,1\}$
. By the above lemma, there is an
![]() $(\mathcal {F},\frac {\varepsilon }{2L})$
-approximate embedding
$(\mathcal {F},\frac {\varepsilon }{2L})$
-approximate embedding
![]() $\phi : D \to B$
, so let
$\phi : D \to B$
, so let
![]() $\mathcal {F}' = \phi (\mathcal {F})$
. Now there is an
$\mathcal {F}' = \phi (\mathcal {F})$
. Now there is an
![]() $(\mathcal {F}',\frac {\varepsilon }{2L})$
-approximate embedding
$(\mathcal {F}',\frac {\varepsilon }{2L})$
-approximate embedding
![]() $\psi : B \to A$
. An easy calculation shows that
$\psi : B \to A$
. An easy calculation shows that
![]() $\psi \circ \phi : D \to A$
is an approximate
$\psi \circ \phi : D \to A$
is an approximate
![]() $(\mathcal {F},\varepsilon )$
-embedding.
$(\mathcal {F},\varepsilon )$
-embedding.
Appending the condition that
![]() $\psi : B \to A_\omega \cap S'$
, then, for any finite subset
$\psi : B \to A_\omega \cap S'$
, then, for any finite subset
![]() $\mathcal {G} \subseteq S$
, we can take
$\mathcal {G} \subseteq S$
, we can take
![]() $\psi : B \to A$
to be a
$\psi : B \to A$
to be a
![]() $(\mathcal {F}',\frac {\varepsilon }{2L},\mathcal {G})$
-approximately central approximate embedding. This gives that
$(\mathcal {F}',\frac {\varepsilon }{2L},\mathcal {G})$
-approximately central approximate embedding. This gives that
![]() $\psi \circ \phi : D \to A$
is a
$\psi \circ \phi : D \to A$
is a
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding.
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embedding.
Corollary 3.4 Let D be a C*-algebra and
![]() $B \subseteq A$
be a unital inclusion of separable C*-algebras such that B and D are unital, separable, simple, and nuclear. Suppose that there is an embedding
$B \subseteq A$
be a unital inclusion of separable C*-algebras such that B and D are unital, separable, simple, and nuclear. Suppose that there is an embedding
![]() $\pi : A \hookrightarrow A_\omega \cap A'$
with
$\pi : A \hookrightarrow A_\omega \cap A'$
with
![]() $\pi (B) \subseteq B_\omega \cap A'$
. If
$\pi (B) \subseteq B_\omega \cap A'$
. If
![]() $D \hookrightarrow B_\omega $
unitally, then
$D \hookrightarrow B_\omega $
unitally, then
![]() $D \hookrightarrow B_\omega \cap A'$
unitally.
$D \hookrightarrow B_\omega \cap A'$
unitally.
Proof As
![]() $D \hookrightarrow B_\omega $
and
$D \hookrightarrow B_\omega $
and
![]() $B \hookrightarrow B_\omega \cap A' \subseteq A_\omega \cap A'$
, the above yields
$B \hookrightarrow B_\omega \cap A' \subseteq A_\omega \cap A'$
, the above yields
![]() $D \hookrightarrow B_\omega \cap A'$
.
$D \hookrightarrow B_\omega \cap A'$
.
The following is useful for discussing
![]() $\mathcal {D}$
-stability for some inclusions of fixed point subalgebras by certain automorphisms on UHF algebras. In particular, the following will work for automorphisms on UHF algebras of product-type, as well as tensor permutations (of finite tensor powers of UHF algebras).
$\mathcal {D}$
-stability for some inclusions of fixed point subalgebras by certain automorphisms on UHF algebras. In particular, the following will work for automorphisms on UHF algebras of product-type, as well as tensor permutations (of finite tensor powers of UHF algebras).
Corollary 3.5 Let
![]() $A = \bigotimes _{\mathbb {N}} B$
be an infinite tensor product of a unital, separable, nuclear C*-algebra
$A = \bigotimes _{\mathbb {N}} B$
be an infinite tensor product of a unital, separable, nuclear C*-algebra
![]() $B,$
and let D be unital, separable, simple, and nuclear. Let
$B,$
and let D be unital, separable, simple, and nuclear. Let
![]() $\lambda \in \operatorname {\mathrm {End}}(A)$
be the Bernoulli shift
$\lambda \in \operatorname {\mathrm {End}}(A)$
be the Bernoulli shift
![]() $\lambda (a) = 1 \otimes a$
. If
$\lambda (a) = 1 \otimes a$
. If
![]() $\sigma \in \operatorname {\mathrm {Aut}}(A)$
is such that
$\sigma \in \operatorname {\mathrm {Aut}}(A)$
is such that
![]() $\lambda \circ \sigma = \sigma \circ \lambda $
, and
$\lambda \circ \sigma = \sigma \circ \lambda $
, and
![]() $D \hookrightarrow (A^\sigma )_\omega $
unitally, then
$D \hookrightarrow (A^\sigma )_\omega $
unitally, then
![]() $D \hookrightarrow (A^\sigma )_\omega \cap A'$
unitally.
$D \hookrightarrow (A^\sigma )_\omega \cap A'$
unitally.
Proof Note that
![]() $\pi = (\lambda ^n)$
induces an embedding
$\pi = (\lambda ^n)$
induces an embedding
![]() $A \hookrightarrow A_\omega \cap A'$
. We just need to show that
$A \hookrightarrow A_\omega \cap A'$
. We just need to show that
![]() $\pi (A^\sigma ) \subseteq (A^\sigma )_\omega \cap A'$
, which is true since
$\pi (A^\sigma ) \subseteq (A^\sigma )_\omega \cap A'$
, which is true since
![]() $\lambda ^n \circ \sigma = \sigma \circ \lambda ^n$
for all n by hypothesis. The result now follows from the above.
$\lambda ^n \circ \sigma = \sigma \circ \lambda ^n$
for all n by hypothesis. The result now follows from the above.
We note that if we have approximately central approximate embeddings
![]() $D \to B \subseteq A$
, then we can also find approximately central approximate embeddings
$D \to B \subseteq A$
, then we can also find approximately central approximate embeddings
![]() $D \to u^*Bu \subseteq A$
for any
$D \to u^*Bu \subseteq A$
for any
![]() $u \in U(A)$
. In the separable setting, this just means
$u \in U(A)$
. In the separable setting, this just means
![]() $D \hookrightarrow B_\omega \cap A'$
implies that
$D \hookrightarrow B_\omega \cap A'$
implies that
![]() $D \hookrightarrow u^*B_\omega u \cap A'$
for any
$D \hookrightarrow u^*B_\omega u \cap A'$
for any
![]() $u \in U(A)$
.
$u \in U(A)$
.
Lemma 3.6 Let
![]() $B \subseteq A$
be a unital inclusion of C*-algebras, and let D be a unital, separable, simple, nuclear C*-algebra. Let
$B \subseteq A$
be a unital inclusion of C*-algebras, and let D be a unital, separable, simple, nuclear C*-algebra. Let
![]() $u \in U(A)$
. If there are
$u \in U(A)$
. If there are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embeddings
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embeddings
![]() $D \to B$
for all
$D \to B$
for all
![]() $\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
finite subsets and
$\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
finite subsets and
![]() $\varepsilon> 0$
, then there are
$\varepsilon> 0$
, then there are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embeddings
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-approximately central approximate embeddings
![]() $D \to u^*Bu \subseteq A$
for all
$D \to u^*Bu \subseteq A$
for all
![]() $\mathcal {F},\varepsilon ,\mathcal {G}$
.
$\mathcal {F},\varepsilon ,\mathcal {G}$
.
Proof Let
![]() $\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
be finite and
$\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
be finite and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $L = \max \{1,\max _{d \in \mathcal {F}}\|d\|\}$
and
$L = \max \{1,\max _{d \in \mathcal {F}}\|d\|\}$
and
![]() $\phi : D \to B$
be a
$\phi : D \to B$
be a
![]() $(\mathcal {F},\frac {\varepsilon }{3L},\mathcal {G} \cup \{u\})$
-approximately central approximate embedding. Then
$(\mathcal {F},\frac {\varepsilon }{3L},\mathcal {G} \cup \{u\})$
-approximately central approximate embedding. Then
![]() $\psi = \text {Ad}_u \circ \phi : D \to u^*Bu$
will be an
$\psi = \text {Ad}_u \circ \phi : D \to u^*Bu$
will be an
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding.
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding.
We can also discuss existence of approximately central approximate embeddings in inductive limits (with injective connecting maps). This is an adaptation of [Reference Toms and Winter67, Proposition 2.2] to our setting.
Proposition 3.7 Suppose that we have increasing sequences
![]() $(B_n)_{n \in \mathbb {N}}$
and
$(B_n)_{n \in \mathbb {N}}$
and
![]() $(A_n)_{n \in \mathbb {N}}$
of C*-algebras such that
$(A_n)_{n \in \mathbb {N}}$
of C*-algebras such that
![]() $B_n \subseteq A_n$
are unital inclusions. If
$B_n \subseteq A_n$
are unital inclusions. If
![]() $B = \overline {\cup _n B_n}, A = \overline {\cup _n A_n}$
, and
$B = \overline {\cup _n B_n}, A = \overline {\cup _n A_n}$
, and
![]() $D = \overline {\cup _nD_n}$
, where
$D = \overline {\cup _nD_n}$
, where
![]() $(D_n)_{n \in \mathbb {N}}$
is an increasing sequence of unital, separable, simple, nuclear C*-algebras and there are
$(D_n)_{n \in \mathbb {N}}$
is an increasing sequence of unital, separable, simple, nuclear C*-algebras and there are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
![]() $D_n \to B_n \subseteq A_n$
whenever
$D_n \to B_n \subseteq A_n$
whenever
![]() $n \in \mathbb {N}, \mathcal {F} \subseteq D_n, \mathcal {G} \subseteq A_n$
are finite and
$n \in \mathbb {N}, \mathcal {F} \subseteq D_n, \mathcal {G} \subseteq A_n$
are finite and
![]() $\varepsilon> 0$
, then there are
$\varepsilon> 0$
, then there are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
![]() $D \to B \subseteq A$
for all
$D \to B \subseteq A$
for all
![]() $\mathcal {F} \subseteq D,\mathcal {G} \subseteq A$
finite and
$\mathcal {F} \subseteq D,\mathcal {G} \subseteq A$
finite and
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
Proof Let
![]() $\mathcal {F} \subseteq \mathcal {D}$
and
$\mathcal {F} \subseteq \mathcal {D}$
and
![]() $\mathcal {G} \subseteq A$
be finite sets and
$\mathcal {G} \subseteq A$
be finite sets and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
and set
![]() $\delta := \frac {\varepsilon }{6L+5}$
. Without loss of generality, assume that
$\delta := \frac {\varepsilon }{6L+5}$
. Without loss of generality, assume that
![]() $\varepsilon < 1$
. Label
$\varepsilon < 1$
. Label
![]() $\mathcal {F} = \{d_1,\dots ,d_p\}$
and
$\mathcal {F} = \{d_1,\dots ,d_p\}$
and
![]() $\mathcal {G} = \{a_1,\dots ,a_q\}$
and find N large enough so that there are
$\mathcal {G} = \{a_1,\dots ,a_q\}$
and find N large enough so that there are
![]() $d_1',\dots ,d_p' \in D_N$
and
$d_1',\dots ,d_p' \in D_N$
and
![]() $a_1',\dots ,a_q' \in A_N$
with
$a_1',\dots ,a_q' \in A_N$
with
![]() $d_i' \approx _\delta d_i$
,
$d_i' \approx _\delta d_i$
,
![]() $i = 1,\dots ,p$
, and
$i = 1,\dots ,p$
, and
![]() $a_j' \approx _\delta a_j$
,
$a_j' \approx _\delta a_j$
,
![]() $j=1,\dots ,q$
. Let
$j=1,\dots ,q$
. Let
![]() $\mathcal {F}':=\{d_1',\dots ,d_p'\}, \mathcal {G}':=\{a_1',\dots ,a_q'\}$
and let
$\mathcal {F}':=\{d_1',\dots ,d_p'\}, \mathcal {G}':=\{a_1',\dots ,a_q'\}$
and let
![]() $\phi : D_N \to B_N \subseteq A_N$
be an
$\phi : D_N \to B_N \subseteq A_N$
be an
![]() $(\mathcal {F}',\delta ,\mathcal {G}')$
-embedding. As
$(\mathcal {F}',\delta ,\mathcal {G}')$
-embedding. As
![]() $D_N$
is nuclear, there are
$D_N$
is nuclear, there are
![]() $k \in \mathbb {N}$
and u.c.p. maps
$k \in \mathbb {N}$
and u.c.p. maps
![]() $\rho : D_N \to M_k$
and
$\rho : D_N \to M_k$
and
![]() $\eta : M_k \to B_N$
such that
$\eta : M_k \to B_N$
such that
![]() $\eta \circ \rho (d_i') \approx _\delta \phi (d_i')$
and
$\eta \circ \rho (d_i') \approx _\delta \phi (d_i')$
and
![]() $\eta \circ \rho (d_i'd_j') \approx _\delta \phi (d_i'd_j')$
. By Arveson’s extension theorem (see [Reference Brown and Ozawa6, Section 1.6]), we can extend
$\eta \circ \rho (d_i'd_j') \approx _\delta \phi (d_i'd_j')$
. By Arveson’s extension theorem (see [Reference Brown and Ozawa6, Section 1.6]), we can extend
![]() $\rho $
to a u.c.p. map
$\rho $
to a u.c.p. map
![]() $\tilde {\rho }: D \to M_k$
and let
$\tilde {\rho }: D \to M_k$
and let
![]() $\psi := \eta \circ \tilde {\rho }: D \to B_N$
. As
$\psi := \eta \circ \tilde {\rho }: D \to B_N$
. As
![]() $B_N \subseteq B$
, we can think of
$B_N \subseteq B$
, we can think of
![]() $\psi $
as a map
$\psi $
as a map
![]() $\psi : D \to B$
. Now for
$\psi : D \to B$
. Now for
![]() $i,j=1,\dots ,p$
, we have
$i,j=1,\dots ,p$
, we have
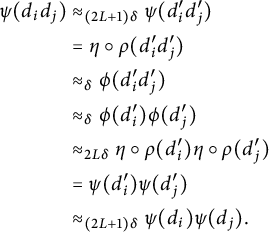 $$ \begin{align} \nonumber \psi(d_id_j) &\approx_{(2L+1)\delta}\psi(d_i'd_j') \\ \nonumber &= \eta \circ \rho(d_i'd_j') \\ \nonumber &\approx_\delta \phi(d_i'd_j') \\ &\approx_\delta \phi(d_i')\phi(d_j') \\ \nonumber &\approx_{2L\delta} \eta \circ \rho(d_i')\eta \circ \rho(d_j') \\ \nonumber &= \psi(d_i')\psi(d_j') \\ \nonumber &\approx_{(2L+1)\delta}\psi(d_i)\psi(d_j). \end{align} $$
$$ \begin{align} \nonumber \psi(d_id_j) &\approx_{(2L+1)\delta}\psi(d_i'd_j') \\ \nonumber &= \eta \circ \rho(d_i'd_j') \\ \nonumber &\approx_\delta \phi(d_i'd_j') \\ &\approx_\delta \phi(d_i')\phi(d_j') \\ \nonumber &\approx_{2L\delta} \eta \circ \rho(d_i')\eta \circ \rho(d_j') \\ \nonumber &= \psi(d_i')\psi(d_j') \\ \nonumber &\approx_{(2L+1)\delta}\psi(d_i)\psi(d_j). \end{align} $$
Thus
![]() $\psi (d_id_j) \approx _{(4+6L)\delta } \psi (d_i)\psi (d_j)$
, and as
$\psi (d_id_j) \approx _{(4+6L)\delta } \psi (d_i)\psi (d_j)$
, and as
![]() $(4 + 6L)\delta \leq (6L + 5)\delta = \varepsilon $
, this implies that
$(4 + 6L)\delta \leq (6L + 5)\delta = \varepsilon $
, this implies that
![]() $\psi (d_id_j) \approx _\varepsilon \psi (d_i)\psi (d_j)$
. For approximate commutation with
$\psi (d_id_j) \approx _\varepsilon \psi (d_i)\psi (d_j)$
. For approximate commutation with
![]() $\mathcal {G}$
, we make use of the following two approximations: for
$\mathcal {G}$
, we make use of the following two approximations: for
![]() $a,a',a",b,b'$
elements in a C*-algebra,
$a,a',a",b,b'$
elements in a C*-algebra,
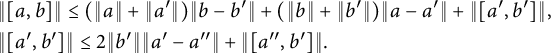 $$ \begin{align} \nonumber &\|[a,b]\| \leq (\|a\| + \|a'\|)\|b - b'\| + (\|b\| + \|b'\|)\|a - a'\| + \|[a',b']\|, \\ &\|[a',b']\| \leq 2\|b'\|\|a' - a"\| + \|[a",b']\|. \end{align} $$
$$ \begin{align} \nonumber &\|[a,b]\| \leq (\|a\| + \|a'\|)\|b - b'\| + (\|b\| + \|b'\|)\|a - a'\| + \|[a',b']\|, \\ &\|[a',b']\| \leq 2\|b'\|\|a' - a"\| + \|[a",b']\|. \end{align} $$
Note that for
![]() $a = \psi (d_i),a' = \psi (d_i'),a" = \phi (d_i'), b = a_j, b' = a_j'$
, we have that
$a = \psi (d_i),a' = \psi (d_i'),a" = \phi (d_i'), b = a_j, b' = a_j'$
, we have that
![]() $\|a\|,\|b\| \leq L + 1$
and
$\|a\|,\|b\| \leq L + 1$
and
![]() $\|a'\|,\|a"\|,\|b'\| \leq L$
. Therefore, from the above two inequalities, we get
$\|a'\|,\|a"\|,\|b'\| \leq L$
. Therefore, from the above two inequalities, we get
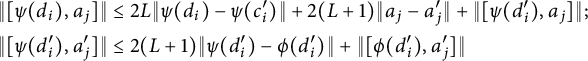 $$ \begin{align} \nonumber &\|[\psi(d_i),a_j]\| \leq 2L\|\psi(d_i) - \psi(c_i')\|+ 2(L+1)\|a_j - a_j'\| + \|[\psi(d_i'),a_j]\|; \\ &\|[\psi(d_i'),a_j']\| \leq 2(L+1)\|\psi(d_i') - \phi(d_i')\| + \|[\phi(d_i'),a_j']\| \end{align} $$
$$ \begin{align} \nonumber &\|[\psi(d_i),a_j]\| \leq 2L\|\psi(d_i) - \psi(c_i')\|+ 2(L+1)\|a_j - a_j'\| + \|[\psi(d_i'),a_j]\|; \\ &\|[\psi(d_i'),a_j']\| \leq 2(L+1)\|\psi(d_i') - \phi(d_i')\| + \|[\phi(d_i'),a_j']\| \end{align} $$
whenever
![]() $i=1,\dots ,p,j=1,\dots ,q$
. Using these approximations, we have
$i=1,\dots ,p,j=1,\dots ,q$
. Using these approximations, we have
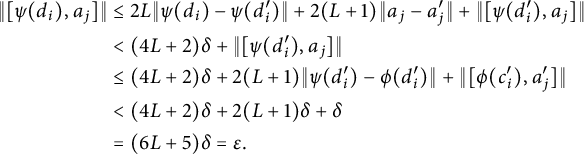 $$ \begin{align} \nonumber \|[\psi(d_i),a_j]\| &\leq 2L\|\psi(d_i) - \psi(d_i')\| + 2(L+1)\|a_j - a_j'\| + \|[\psi(d_i'),a_j]\| \\ \nonumber &< (4L+2)\delta + \|[\psi(d_i'),a_j]\| \\ &\leq (4L+2)\delta + 2(L+1)\|\psi(d_i') - \phi(d_i')\| + \|[\phi(c_i'),a_j']\| \\ \nonumber &< (4L+2)\delta + 2(L+1)\delta + \delta \\ \nonumber &= (6L+5)\delta = \varepsilon.\\[-37pt]\nonumber \end{align} $$
$$ \begin{align} \nonumber \|[\psi(d_i),a_j]\| &\leq 2L\|\psi(d_i) - \psi(d_i')\| + 2(L+1)\|a_j - a_j'\| + \|[\psi(d_i'),a_j]\| \\ \nonumber &< (4L+2)\delta + \|[\psi(d_i'),a_j]\| \\ &\leq (4L+2)\delta + 2(L+1)\|\psi(d_i') - \phi(d_i')\| + \|[\phi(c_i'),a_j']\| \\ \nonumber &< (4L+2)\delta + 2(L+1)\delta + \delta \\ \nonumber &= (6L+5)\delta = \varepsilon.\\[-37pt]\nonumber \end{align} $$
The following will be useful to show that there are many
![]() $\mathcal {D}$
-stable embeddings.
$\mathcal {D}$
-stable embeddings.
Lemma 3.8 Let
![]() $\phi : B_0 \simeq B_1$
and
$\phi : B_0 \simeq B_1$
and
![]() $\psi : A_0 \simeq A_1$
be *-isomorphisms between unital C*-algebras, and let D be a unital, simple, nuclear C*-algebra. Suppose that there is a unital *-homomorphism
$\psi : A_0 \simeq A_1$
be *-isomorphisms between unital C*-algebras, and let D be a unital, simple, nuclear C*-algebra. Suppose that there is a unital *-homomorphism
![]() $\eta : B_1 \hookrightarrow A_1$
such that there are
$\eta : B_1 \hookrightarrow A_1$
such that there are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
![]() $D \to \eta (B_1) \subseteq A_1$
for all finite subsets
$D \to \eta (B_1) \subseteq A_1$
for all finite subsets
![]() $\mathcal {F} \subseteq D, \mathcal {G} \subseteq A_1$
and
$\mathcal {F} \subseteq D, \mathcal {G} \subseteq A_1$
and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $\sigma = \psi ^{-1} \circ \eta \circ \phi : B_0 \to A_0$
. Then there are
$\sigma = \psi ^{-1} \circ \eta \circ \phi : B_0 \to A_0$
. Then there are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embeddings
![]() $D \to \sigma (B_0) \subseteq A_0$
for all
$D \to \sigma (B_0) \subseteq A_0$
for all
![]() $\mathcal {F} \subseteq D,\mathcal {G} \subseteq A_0$
finite and
$\mathcal {F} \subseteq D,\mathcal {G} \subseteq A_0$
finite and
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
Proof The diagram
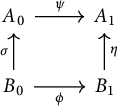
commutes and so if
![]() $\mathcal {F} \subseteq D, \mathcal {G} \subseteq A_0$
are finite,
$\mathcal {F} \subseteq D, \mathcal {G} \subseteq A_0$
are finite,
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $\xi : D \to \eta (B_1) \subseteq A_1$
is an
$\xi : D \to \eta (B_1) \subseteq A_1$
is an
![]() $(\mathcal {F},\varepsilon ,\psi (\mathcal {G}))$
-embedding, then
$(\mathcal {F},\varepsilon ,\psi (\mathcal {G}))$
-embedding, then
![]() $\psi ^{-1} \circ \xi : D \to \psi ^{-1}(\eta (B_1)) \subseteq \psi ^{-1}(A_1) = A_0$
is an
$\psi ^{-1} \circ \xi : D \to \psi ^{-1}(\eta (B_1)) \subseteq \psi ^{-1}(A_1) = A_0$
is an
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding. Moreover, from
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding. Moreover, from
it is clear that
![]() $\psi ^{-1}\circ \xi $
is an
$\psi ^{-1}\circ \xi $
is an
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding
![]() $D \to \sigma (B_0) \subseteq A_0$
.
$D \to \sigma (B_0) \subseteq A_0$
.
4 Relative intertwinings and
 $\mathcal {D}$
-stable embeddings
$\mathcal {D}$
-stable embeddings
4.1 Relative intertwinings
It is well known that a strongly self-absorbing C*-algebra
![]() $\mathcal {D}$
embeds unitally into the central sequence algebra
$\mathcal {D}$
embeds unitally into the central sequence algebra
![]() $(\mathcal {M}(A))_\omega \cap A'$
of a separable C*-algebra A if and only if
$(\mathcal {M}(A))_\omega \cap A'$
of a separable C*-algebra A if and only if
![]() $A \simeq A \otimes \mathcal {D}$
, where
$A \simeq A \otimes \mathcal {D}$
, where
![]() $\mathcal {M}(A)$
is the multiplier algebra of A (see, for example, [Reference Rørdam49, Theorem 7.2.2(i)]). We alter the proof to keep track of a subalgebra in order to show that for a unital inclusion
$\mathcal {M}(A)$
is the multiplier algebra of A (see, for example, [Reference Rørdam49, Theorem 7.2.2(i)]). We alter the proof to keep track of a subalgebra in order to show that for a unital inclusion
![]() $B \subseteq A$
of separable C*-algebras,
$B \subseteq A$
of separable C*-algebras,
![]() $\mathcal {D} \hookrightarrow B_\omega \cap A'$
unitally if and only if there is an isomorphism
$\mathcal {D} \hookrightarrow B_\omega \cap A'$
unitally if and only if there is an isomorphism
![]() $\Phi : A \to A \otimes \mathcal {D}$
which is approximately unitarily equivalent to the first factor embedding and satisfies
$\Phi : A \to A \otimes \mathcal {D}$
which is approximately unitarily equivalent to the first factor embedding and satisfies
![]() $\Phi (B) = B \otimes \mathcal {D}$
. This was initially done for (irreducible) inclusions of
$\Phi (B) = B \otimes \mathcal {D}$
. This was initially done for (irreducible) inclusions of
![]() $\text {II}_1$
factors in [Reference Bisch2] and commented on in [Reference Izumi31] for
$\text {II}_1$
factors in [Reference Bisch2] and commented on in [Reference Izumi31] for
![]() $\mathcal {D}$
being
$\mathcal {D}$
being
![]() $M_{n^{\infty }},\mathcal {O}_2,\mathcal {O}_{\infty }$
. The proof we alter is Elliott’s intertwining argument, which can be found as a combination of Propositions 2.3.5 and 7.2.1 and Theorem 7.2.2 of [Reference Rørdam49].
$M_{n^{\infty }},\mathcal {O}_2,\mathcal {O}_{\infty }$
. The proof we alter is Elliott’s intertwining argument, which can be found as a combination of Propositions 2.3.5 and 7.2.1 and Theorem 7.2.2 of [Reference Rørdam49].
Proposition 4.1 (Relative intertwining)
Let
![]() $A,B,C$
be unital, separable C*-algebras, and let
$A,B,C$
be unital, separable C*-algebras, and let
![]() $\phi : A \hookrightarrow C, \theta : B \to A, \psi : B \to C$
be unital *-homomorphisms such that
$\phi : A \hookrightarrow C, \theta : B \to A, \psi : B \to C$
be unital *-homomorphisms such that
![]() $\phi \circ \theta (B) \subseteq \psi (B)$
. Suppose there is a sequence
$\phi \circ \theta (B) \subseteq \psi (B)$
. Suppose there is a sequence
![]() $(u_n)_{n \in \mathbb {N}}$
of unitaries in
$(u_n)_{n \in \mathbb {N}}$
of unitaries in
![]() $\psi (B)_\omega \cap \phi (A)'$
such that:
$\psi (B)_\omega \cap \phi (A)'$
such that:
-
•
 $\text {dist}(v_n^*cv_n,\phi (A)_\omega ) \to 0$
for all
$\text {dist}(v_n^*cv_n,\phi (A)_\omega ) \to 0$
for all
 $c \in C$
;
$c \in C$
; -
•
 $\text {dist}(v_n^*\psi (b)v_n,\phi \circ \theta (B)_\omega ) \to 0$
for all
$\text {dist}(v_n^*\psi (b)v_n,\phi \circ \theta (B)_\omega ) \to 0$
for all
 $b \in B$
.
$b \in B$
.
Then
![]() $\phi $
is approximately unitarily equivalent to an isomorphism
$\phi $
is approximately unitarily equivalent to an isomorphism
![]() $\Phi : A \simeq C$
such that
$\Phi : A \simeq C$
such that
![]() $\Phi \circ \theta (B) = \psi (B)$
.
$\Phi \circ \theta (B) = \psi (B)$
.
Proof Apply the below proposition with
![]() $B_m := B, \theta _m := \theta , \psi _m := \psi $
for all
$B_m := B, \theta _m := \theta , \psi _m := \psi $
for all
![]() $m \in \mathbb {N}$
.
$m \in \mathbb {N}$
.
Proposition 4.2 (Countable relative intertwining)
Let
![]() $A,B_m,C$
be unital, separable C*-algebras,
$A,B_m,C$
be unital, separable C*-algebras,
![]() $m \in \mathbb {N}$
, and
$m \in \mathbb {N}$
, and
![]() $\phi : A \hookrightarrow C,\theta _m: B_m \to A,\psi _m: B_m \to C$
be such that
$\phi : A \hookrightarrow C,\theta _m: B_m \to A,\psi _m: B_m \to C$
be such that
![]() $\phi \circ \theta _m(B_m) \subseteq \psi _m(B_m)$
and
$\phi \circ \theta _m(B_m) \subseteq \psi _m(B_m)$
and
![]() $\psi _1(B_1) \subseteq \psi _m(B_m)$
. Suppose there is a sequence
$\psi _1(B_1) \subseteq \psi _m(B_m)$
. Suppose there is a sequence
![]() $(v_n)_{n \in \mathbb {N}} \subseteq \psi _1(B_1)_\omega \cap \phi (A)'$
of unitaries such that:
$(v_n)_{n \in \mathbb {N}} \subseteq \psi _1(B_1)_\omega \cap \phi (A)'$
of unitaries such that:
-
•
 $\text {dist}(v_n^*cv_n,\phi (A)_\omega ) \to 0$
for all
$\text {dist}(v_n^*cv_n,\phi (A)_\omega ) \to 0$
for all
 $c \in C$
;
$c \in C$
; -
•
 $\text {dist}(v_n^*\psi _m(b)v_n,\phi \circ \theta _m(B_m)_\omega ) \to 0$
for all
$\text {dist}(v_n^*\psi _m(b)v_n,\phi \circ \theta _m(B_m)_\omega ) \to 0$
for all
 $b \in B_m$
.
$b \in B_m$
.
Then
![]() $\phi $
is approximately unitarily equivalent to an isomorphism
$\phi $
is approximately unitarily equivalent to an isomorphism
![]() $\Phi :A \simeq C$
such that
$\Phi :A \simeq C$
such that
![]() $\Phi \circ \theta _m (B_m) = \psi _m(B_m)$
for all
$\Phi \circ \theta _m (B_m) = \psi _m(B_m)$
for all
![]() $m \in \mathbb {N}$
.
$m \in \mathbb {N}$
.
Proof We show that if there are unitaries
![]() $(v_n)_{n \in \mathbb {N}} \subseteq \psi _1(B_1)$
satisfying:
$(v_n)_{n \in \mathbb {N}} \subseteq \psi _1(B_1)$
satisfying:
-
•
 $[v_n,\phi (a)] \to 0$
for all
$[v_n,\phi (a)] \to 0$
for all
 $a \in A$
;
$a \in A$
; -
•
 $\text {dist}(v_n^*cv_n,\phi (A)) \to 0$
for all
$\text {dist}(v_n^*cv_n,\phi (A)) \to 0$
for all
 $c \in C$
;
$c \in C$
; -
•
 $\text {dist}(v_n^*\psi _m(b)v_n,\phi \circ \theta _m(B_m)) \to 0$
for all
$\text {dist}(v_n^*\psi _m(b)v_n,\phi \circ \theta _m(B_m)) \to 0$
for all
 $b \in B_m$
,
$b \in B_m$
,
then the conclusion holds. Such unitaries can be found using Kirchberg’s
![]() $\varepsilon $
-test (Lemma 2.1).
$\varepsilon $
-test (Lemma 2.1).
Let
![]() $(a_n)_{n \in \mathbb {N}},(b_n^{(m)})_{n \in \mathbb {N}},(c_n)_{n \in \mathbb {N}}$
be dense sequences of
$(a_n)_{n \in \mathbb {N}},(b_n^{(m)})_{n \in \mathbb {N}},(c_n)_{n \in \mathbb {N}}$
be dense sequences of
![]() $A,B_m,C$
, respectively,
$A,B_m,C$
, respectively,
![]() $m \in \mathbb {N}$
. We can inductively choose
$m \in \mathbb {N}$
. We can inductively choose
![]() $v_n$
, forming a subsequence
$v_n$
, forming a subsequence
![]() $(v_n)_{n \in \mathbb {N}}$
of the unitaries above (after re-indexing, we are still calling them
$(v_n)_{n \in \mathbb {N}}$
of the unitaries above (after re-indexing, we are still calling them
![]() $v_n$
), such that there are
$v_n$
), such that there are
![]() $a_{jn} \in A, b_{jn}^{(m)} \in B_m$
with:
$a_{jn} \in A, b_{jn}^{(m)} \in B_m$
with:
-
•
 $v_n^*\dots v_1^*c_jv_1\dots v_n \approx _{\frac {1}{n}} \phi (a_{jn})$
;
$v_n^*\dots v_1^*c_jv_1\dots v_n \approx _{\frac {1}{n}} \phi (a_{jn})$
; -
•
 $v_n^*\dots v_1^*\psi (b_j^{(m)})v_1\dots v_n \approx _{\frac {1}{n}} \phi \circ \theta _m(b_{jn}^{(m)})$
;
$v_n^*\dots v_1^*\psi (b_j^{(m)})v_1\dots v_n \approx _{\frac {1}{n}} \phi \circ \theta _m(b_{jn}^{(m)})$
; -
•
 $[v_n,\phi (a_j)] \approx _{\frac {1}{2^n}} 0$
;
$[v_n,\phi (a_j)] \approx _{\frac {1}{2^n}} 0$
; -
•
 $[v_n,\phi (a_{jl})] \approx _{\frac {1}{2^n}} 0$
;
$[v_n,\phi (a_{jl})] \approx _{\frac {1}{2^n}} 0$
; -
•
 $[v_n,\phi \circ \theta _m(b_j^{(m)})] \approx _{\frac {1}{2^n}} 0$
;
$[v_n,\phi \circ \theta _m(b_j^{(m)})] \approx _{\frac {1}{2^n}} 0$
; -
•
 $[v_n,\phi \circ \theta _m(b_{jl}^{(m)})] \approx _{\frac {1}{2^n}} 0$
,
$[v_n,\phi \circ \theta _m(b_{jl}^{(m)})] \approx _{\frac {1}{2^n}} 0$
,
where
![]() $j,m=1,\dots ,n$
and
$j,m=1,\dots ,n$
and
![]() $l=1,\dots ,n-1$
. Define, for
$l=1,\dots ,n-1$
. Define, for
![]() $a \in \{a_n \mid n \in \mathbb {N}\}$
,
$a \in \{a_n \mid n \in \mathbb {N}\}$
,
which extends to a *-isomorphism
![]() $\Phi : A \simeq C$
, as in [Reference Rørdam49, Proposition 2.3.5]. The proof also yields the following useful approximation:
$\Phi : A \simeq C$
, as in [Reference Rørdam49, Proposition 2.3.5]. The proof also yields the following useful approximation:
for appropriate
![]() $n \geq j,m$
.
$n \geq j,m$
.
We now need to check that
![]() $\Phi \circ \theta _m(B_m) = \psi _m(B_m)$
. Approximate
$\Phi \circ \theta _m(B_m) = \psi _m(B_m)$
. Approximate
As
![]() $n \in \mathbb {N}$
can be made arbitrarily large, this yields
$n \in \mathbb {N}$
can be made arbitrarily large, this yields
![]() $\psi _m(B_m) \subseteq \overline {\Phi \circ \theta _m(B_m)} = \Phi \circ \theta _m(B_m)$
. On the other hand, for any
$\psi _m(B_m) \subseteq \overline {\Phi \circ \theta _m(B_m)} = \Phi \circ \theta _m(B_m)$
. On the other hand, for any
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $b \in B_m$
, we can find n such that
$b \in B_m$
, we can find n such that
since
![]() $v_i \in \psi _1(B_1) \subseteq \psi _m(B_m)$
and
$v_i \in \psi _1(B_1) \subseteq \psi _m(B_m)$
and
![]() $\phi \circ \theta _m(B_m) \subseteq \psi _m(B_m)$
. Hence
$\phi \circ \theta _m(B_m) \subseteq \psi _m(B_m)$
. Hence
![]() $\Phi \circ \theta _m(B_m) \subseteq \overline {\psi _m(B_m)} = \psi _m(B_m)$
.
$\Phi \circ \theta _m(B_m) \subseteq \overline {\psi _m(B_m)} = \psi _m(B_m)$
.
4.2
 $\mathcal {D}$
-stable embeddings
$\mathcal {D}$
-stable embeddings
Definition 4.1 Let
![]() $\iota : B \hookrightarrow A$
be an embedding and
$\iota : B \hookrightarrow A$
be an embedding and
![]() $\mathcal {D}$
be strongly self-absorbing. We say that
$\mathcal {D}$
be strongly self-absorbing. We say that
![]() $\iota $
is
$\iota $
is
![]() $\mathcal {D}$
-stable (or
$\mathcal {D}$
-stable (or
![]() $\mathcal {D}$
-absorbing) if there exists an isomorphism
$\mathcal {D}$
-absorbing) if there exists an isomorphism
![]() $\Phi :A \simeq A \otimes \mathcal {D}$
such that
$\Phi :A \simeq A \otimes \mathcal {D}$
such that
![]() $\Phi \circ \iota (B) = \iota (B) \otimes \mathcal {D}$
.
$\Phi \circ \iota (B) = \iota (B) \otimes \mathcal {D}$
.
We will mostly have interest in the case where
![]() $\iota $
corresponds to the inclusion map and
$\iota $
corresponds to the inclusion map and
![]() $B \subseteq A$
is a subalgebra. In this form, we will say
$B \subseteq A$
is a subalgebra. In this form, we will say
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable (or
$\mathcal {D}$
-stable (or
![]() $\mathcal {D}$
-absorbing). Clearly,
$\mathcal {D}$
-absorbing). Clearly,
![]() $\iota $
being
$\iota $
being
![]() $\mathcal {D}$
-stable is the same as
$\mathcal {D}$
-stable is the same as
![]() $\iota (B) \subseteq A$
being
$\iota (B) \subseteq A$
being
![]() $\mathcal {D}$
-stable. We note that we can define the above for any *-homomorphism. Namely, a *-homomorphism
$\mathcal {D}$
-stable. We note that we can define the above for any *-homomorphism. Namely, a *-homomorphism
![]() $\phi :B \to A$
is
$\phi :B \to A$
is
![]() $\mathcal {D}$
-stable if
$\mathcal {D}$
-stable if
![]() $\phi (B) \subseteq A$
is.
$\phi (B) \subseteq A$
is.
Lemma 4.3 If
![]() $\iota : B \hookrightarrow A$
is an embedding, then
$\iota : B \hookrightarrow A$
is an embedding, then
![]() $\iota \otimes \text {id}_D: B \otimes \mathcal {D} \hookrightarrow A \otimes \mathcal {D}$
is
$\iota \otimes \text {id}_D: B \otimes \mathcal {D} \hookrightarrow A \otimes \mathcal {D}$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof Let
![]() $\phi : D \simeq D \otimes \mathcal {D}$
be an isomorphism. Then
$\phi : D \simeq D \otimes \mathcal {D}$
be an isomorphism. Then
is an isomorphism with
We note that this is a strengthening of the notion of
![]() $\mathcal {D}$
-stability for C*-algebras because if
$\mathcal {D}$
-stability for C*-algebras because if
![]() $\iota := \text {id}_A: A \to A$
, then
$\iota := \text {id}_A: A \to A$
, then
![]() $\iota $
is
$\iota $
is
![]() $\mathcal {D}$
-stable if and only if A is
$\mathcal {D}$
-stable if and only if A is
![]() $\mathcal {D}$
-stable. This condition is different from the notion of
$\mathcal {D}$
-stable. This condition is different from the notion of
![]() $\mathcal {O}_2$
or
$\mathcal {O}_2$
or
![]() $\mathcal {O}_{\infty }$
-absorbing morphisms discussed in [Reference Bosa, Gabe, Sims and White4, Reference Gabe21, Reference Gabe22] – they require sequences from a larger algebra to commute with a smaller algebra, while we require sequences from a smaller algebra to commute with the larger algebra. In the former, neither of the algebras are required to be
$\mathcal {O}_{\infty }$
-absorbing morphisms discussed in [Reference Bosa, Gabe, Sims and White4, Reference Gabe21, Reference Gabe22] – they require sequences from a larger algebra to commute with a smaller algebra, while we require sequences from a smaller algebra to commute with the larger algebra. In the former, neither of the algebras are required to be
![]() $\mathcal {D}$
-stable, while the latter necessitates both to be
$\mathcal {D}$
-stable, while the latter necessitates both to be
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
The following adapts [Reference Rørdam49, Theorem 7.2.2].
Theorem 4.4 Suppose that
![]() $B \subseteq A$
is a unital inclusion of separable C*-algebras. If
$B \subseteq A$
is a unital inclusion of separable C*-algebras. If
![]() $\mathcal {D}$
is strongly self-absorbing, then
$\mathcal {D}$
is strongly self-absorbing, then
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable if and only if there is a unital inclusion
$\mathcal {D}$
-stable if and only if there is a unital inclusion
![]() $\mathcal {D} \hookrightarrow B_\omega \cap A'$
.
$\mathcal {D} \hookrightarrow B_\omega \cap A'$
.
Proof Let
![]() $\phi : A \to A \otimes \mathcal {D}$
be the first factor embedding
$\phi : A \to A \otimes \mathcal {D}$
be the first factor embedding
![]() $\phi (a) := a \otimes 1_{\mathcal {D}}$
. First, suppose that
$\phi (a) := a \otimes 1_{\mathcal {D}}$
. First, suppose that
![]() $\xi : \mathcal {D} \hookrightarrow B_\omega \cap A' \simeq (B \otimes 1_{\mathcal {D}})_\omega \cap (A \otimes 1_{\mathcal {D}})'$
is an embedding (so that
$\xi : \mathcal {D} \hookrightarrow B_\omega \cap A' \simeq (B \otimes 1_{\mathcal {D}})_\omega \cap (A \otimes 1_{\mathcal {D}})'$
is an embedding (so that
![]() $\phi (a)\xi (d) \in \phi (A)_\omega $
and
$\phi (a)\xi (d) \in \phi (A)_\omega $
and
![]() $\phi (b)\xi (d) \in \phi (B)_\omega $
). Let
$\phi (b)\xi (d) \in \phi (B)_\omega $
). Let
![]() $\eta : \mathcal {D} \hookrightarrow (B \otimes \mathcal {D})_\omega \cap (A \otimes 1_{\mathcal {D}})'$
be given by
$\eta : \mathcal {D} \hookrightarrow (B \otimes \mathcal {D})_\omega \cap (A \otimes 1_{\mathcal {D}})'$
be given by
![]() $\eta (d) := (1 \otimes d)_n$
and notice that
$\eta (d) := (1 \otimes d)_n$
and notice that
![]() $\xi ,\eta $
have commuting ranges. As all endomorphisms of
$\xi ,\eta $
have commuting ranges. As all endomorphisms of
![]() $\mathcal {D}$
are approximately unitarily equivalent by [Reference Toms and Winter66, Corollary 1.12], let
$\mathcal {D}$
are approximately unitarily equivalent by [Reference Toms and Winter66, Corollary 1.12], let
![]() $(v_n)_{n \in \mathbb {N}} \subseteq C^*(\xi (\mathcal {D}),\eta (\mathcal {D})) \simeq \mathcal {D} \otimes \mathcal {D}$
be such that
$(v_n)_{n \in \mathbb {N}} \subseteq C^*(\xi (\mathcal {D}),\eta (\mathcal {D})) \simeq \mathcal {D} \otimes \mathcal {D}$
be such that
![]() $v_n^*\eta (d)v_n \to \xi (d)$
for
$v_n^*\eta (d)v_n \to \xi (d)$
for
![]() $d \in \mathcal {D}$
. For
$d \in \mathcal {D}$
. For
![]() $b \in B$
and
$b \in B$
and
![]() $d \in \mathcal {D}$
, we have
$d \in \mathcal {D}$
, we have
 $$ \begin{align} \nonumber v_n^*(b \otimes d)v_n &= v_n^*(b \otimes 1_{\mathcal{D}})(1_A \otimes d)v_n^* \\ &= v_n^*\phi(b)\eta(d)v_n \\ \nonumber &= \phi(b)v_n^*\eta(d)v_n \\ \nonumber &\to \phi(b)\xi(d) \in \phi(B)_\omega. \end{align} $$
$$ \begin{align} \nonumber v_n^*(b \otimes d)v_n &= v_n^*(b \otimes 1_{\mathcal{D}})(1_A \otimes d)v_n^* \\ &= v_n^*\phi(b)\eta(d)v_n \\ \nonumber &= \phi(b)v_n^*\eta(d)v_n \\ \nonumber &\to \phi(b)\xi(d) \in \phi(B)_\omega. \end{align} $$
Moreover, the same argument shows that, for
![]() $a \in A$
, we have
$a \in A$
, we have
Now
![]() $(v_n)_{n \in \mathbb {N}}$
satisfy the hypothesis of Proposition 4.1 with
$(v_n)_{n \in \mathbb {N}}$
satisfy the hypothesis of Proposition 4.1 with
![]() $C := A \otimes D$
,
$C := A \otimes D$
,
![]() $\phi $
being the first factor embedding,
$\phi $
being the first factor embedding,
![]() $\theta : B \to A$
being the inclusion and
$\theta : B \to A$
being the inclusion and
![]() $\psi : B \simeq B \otimes \mathcal {D} \subseteq A \otimes \mathcal {D} = C$
(where this isomorphism exists since if
$\psi : B \simeq B \otimes \mathcal {D} \subseteq A \otimes \mathcal {D} = C$
(where this isomorphism exists since if
![]() $\mathcal {D} \hookrightarrow B_\omega \cap A'$
, then clearly
$\mathcal {D} \hookrightarrow B_\omega \cap A'$
, then clearly
![]() $\mathcal {D} \hookrightarrow B_\omega \cap B'$
). From this, we see that
$\mathcal {D} \hookrightarrow B_\omega \cap B'$
). From this, we see that
![]() $\phi $
is approximately unitarily equivalent to an isomorphism
$\phi $
is approximately unitarily equivalent to an isomorphism
![]() $\Phi :A \simeq A \otimes \mathcal {D}$
such that
$\Phi :A \simeq A \otimes \mathcal {D}$
such that
![]() $\Phi (B) = B \otimes \mathcal {D}$
.
$\Phi (B) = B \otimes \mathcal {D}$
.
Conversely, if
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable, let
$\mathcal {D}$
-stable, let
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
be an isomorphism such that
$\Phi : A \simeq A \otimes \mathcal {D}$
be an isomorphism such that
![]() $\Phi (B) = B \otimes \mathcal {D}$
. By [Reference Toms and Winter66, Proposition 1.10(iv)], we can identify
$\Phi (B) = B \otimes \mathcal {D}$
. By [Reference Toms and Winter66, Proposition 1.10(iv)], we can identify
![]() $\mathcal {D} \simeq \mathcal {D}^{\otimes \infty }$
and take
$\mathcal {D} \simeq \mathcal {D}^{\otimes \infty }$
and take
![]() $\xi : \mathcal {D} \hookrightarrow B_\omega \cap A'$
to be given by
$\xi : \mathcal {D} \hookrightarrow B_\omega \cap A'$
to be given by
Corollary 4.5 Let
![]() $\iota : B \hookrightarrow A$
be a unital embedding between separable C*-algebras. If
$\iota : B \hookrightarrow A$
be a unital embedding between separable C*-algebras. If
![]() $\mathcal {D}$
is strongly self-absorbing and
$\mathcal {D}$
is strongly self-absorbing and
![]() $\iota $
is
$\iota $
is
![]() $\mathcal {D}$
-stable, then for every intermediate unital C*-algebra C with
$\mathcal {D}$
-stable, then for every intermediate unital C*-algebra C with
![]() $\iota (B) \subseteq C \subseteq A$
, we have that
$\iota (B) \subseteq C \subseteq A$
, we have that
![]() $\iota (B) \subseteq C$
and
$\iota (B) \subseteq C$
and
![]() $C \subseteq A$
are
$C \subseteq A$
are
![]() $\mathcal {D}$
-stable. In particular,
$\mathcal {D}$
-stable. In particular,
![]() $C \simeq C \otimes \mathcal {D}$
for all such C.
$C \simeq C \otimes \mathcal {D}$
for all such C.
Proof We have
and
Now apply Theorem 4.4.
It is not, however, the case that any isomorphism
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
with
$\Phi : A \simeq A \otimes \mathcal {D}$
with
![]() $\Phi (B) = B \otimes \mathcal {D}$
maps C to
$\Phi (B) = B \otimes \mathcal {D}$
maps C to
![]() $C \otimes \mathcal {D}$
.
$C \otimes \mathcal {D}$
.
Example 4.6 Let
![]() $\mathcal {D}$
be strongly self-absorbing and consider
$\mathcal {D}$
be strongly self-absorbing and consider
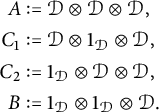 $$ \begin{align} \nonumber A &:= \mathcal{D} \otimes \mathcal{D} \otimes \mathcal{D}, \\ C_1 &:= \mathcal{D} \otimes 1_{\mathcal{D}} \otimes \mathcal{D},\\ \nonumber C_2 &:= 1_{\mathcal{D}} \otimes \mathcal{D} \otimes \mathcal{D},\\ \nonumber B &:= 1_{\mathcal{D}} \otimes 1_{\mathcal{D}} \otimes \mathcal{D}. \end{align} $$
$$ \begin{align} \nonumber A &:= \mathcal{D} \otimes \mathcal{D} \otimes \mathcal{D}, \\ C_1 &:= \mathcal{D} \otimes 1_{\mathcal{D}} \otimes \mathcal{D},\\ \nonumber C_2 &:= 1_{\mathcal{D}} \otimes \mathcal{D} \otimes \mathcal{D},\\ \nonumber B &:= 1_{\mathcal{D}} \otimes 1_{\mathcal{D}} \otimes \mathcal{D}. \end{align} $$
If
![]() $f: \mathcal {D} \otimes \mathcal {D} \to \mathcal {D} \otimes \mathcal {D}$
is the tensor flip and
$f: \mathcal {D} \otimes \mathcal {D} \to \mathcal {D} \otimes \mathcal {D}$
is the tensor flip and
![]() $\phi : \mathcal {D} \simeq \mathcal {D} \otimes \mathcal {D}$
is an isomorphism, let
$\phi : \mathcal {D} \simeq \mathcal {D} \otimes \mathcal {D}$
is an isomorphism, let
which satisfies
![]() $\Phi (B) = B \otimes \mathcal {D}$
(in particular,
$\Phi (B) = B \otimes \mathcal {D}$
(in particular,
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable). However,
$\mathcal {D}$
-stable). However,
In fact, the above example can be generalized to show that for any
![]() $\mathcal {D}$
-stable inclusion
$\mathcal {D}$
-stable inclusion
![]() $B \subseteq A$
, there are an isomorphism
$B \subseteq A$
, there are an isomorphism
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
such that
$\Phi : A \simeq A \otimes \mathcal {D}$
such that
![]() $\Phi (B) = B \otimes \mathcal {D}$
and an intermediate algebra
$\Phi (B) = B \otimes \mathcal {D}$
and an intermediate algebra
![]() $B \subseteq C \subseteq A$
with
$B \subseteq C \subseteq A$
with
![]() $\Phi (C) \neq C \otimes \mathcal {D}$
(obviously, we may still have that
$\Phi (C) \neq C \otimes \mathcal {D}$
(obviously, we may still have that
![]() $\Phi (C) \simeq C \otimes \mathcal {D}$
, but equality may not happen).
$\Phi (C) \simeq C \otimes \mathcal {D}$
, but equality may not happen).
Corollary 4.7 Let
![]() $B \subseteq A$
be a
$B \subseteq A$
be a
![]() $\mathcal {D}$
-stable inclusion. There exist a C*-algebra C with
$\mathcal {D}$
-stable inclusion. There exist a C*-algebra C with
![]() $B \subseteq C \subseteq A$
and an isomorphism
$B \subseteq C \subseteq A$
and an isomorphism
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
such that
$\Phi : A \simeq A \otimes \mathcal {D}$
such that
![]() $\Phi (B) = B \otimes \mathcal {D}$
but
$\Phi (B) = B \otimes \mathcal {D}$
but
![]() $\Phi (C) \neq C \otimes \mathcal {D}$
.
$\Phi (C) \neq C \otimes \mathcal {D}$
.
Proof We first claim that if
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable, then we can identify
$\mathcal {D}$
-stable, then we can identify
![]() $B \subseteq A$
with
$B \subseteq A$
with
![]() $B \otimes 1_{\mathcal {D}} \subseteq A \otimes \mathcal {D}$
. If
$B \otimes 1_{\mathcal {D}} \subseteq A \otimes \mathcal {D}$
. If
![]() $\Psi : A \simeq A \otimes \mathcal {D}$
is such that
$\Psi : A \simeq A \otimes \mathcal {D}$
is such that
![]() $\Psi (B) = B \otimes \mathcal {D}$
and
$\Psi (B) = B \otimes \mathcal {D}$
and
![]() $f: \mathcal {D} \otimes \mathcal {D} \simeq \mathcal {D} \otimes \mathcal {D}$
is the tensor flip, we have
$f: \mathcal {D} \otimes \mathcal {D} \simeq \mathcal {D} \otimes \mathcal {D}$
is the tensor flip, we have
is such that
![]() $\Xi (B \otimes 1_{\mathcal {D}}) = B \otimes 1_{\mathcal {D}} \otimes \mathcal {D}$
. This proves the claim.
$\Xi (B \otimes 1_{\mathcal {D}}) = B \otimes 1_{\mathcal {D}} \otimes \mathcal {D}$
. This proves the claim.
Now, by applying the claim twice, we can identify
![]() $B \subseteq A$
with the inclusion
$B \subseteq A$
with the inclusion
If
![]() $\phi : \mathcal {D} \simeq \mathcal {D} \otimes \mathcal {D}$
is any *-isomorphism,
$\phi : \mathcal {D} \simeq \mathcal {D} \otimes \mathcal {D}$
is any *-isomorphism,
is such that
Taking
![]() $C_1$
and
$C_1$
and
![]() $C_2$
as in Example 4.6, we have that
$C_2$
as in Example 4.6, we have that
However, we can always realize
![]() $\mathcal {D}$
-stability for countably many intermediate C*-algebras at once using some isomorphism
$\mathcal {D}$
-stability for countably many intermediate C*-algebras at once using some isomorphism
![]() $A \simeq A \otimes \mathcal {D}$
.
$A \simeq A \otimes \mathcal {D}$
.
Theorem 4.8 Suppose that
![]() $B_1 \subseteq B_m \subseteq A$
are unital inclusions of separable C*-algebras (note that we are not asking for
$B_1 \subseteq B_m \subseteq A$
are unital inclusions of separable C*-algebras (note that we are not asking for
![]() $(B_m)$
to form a chain). If
$(B_m)$
to form a chain). If
![]() $\mathcal {D}$
is strongly self-absorbing and
$\mathcal {D}$
is strongly self-absorbing and
![]() $\mathcal {D} \hookrightarrow (B_1)_\omega \cap A'$
unitally, there exists an isomorphism
$\mathcal {D} \hookrightarrow (B_1)_\omega \cap A'$
unitally, there exists an isomorphism
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
such that
$\Phi : A \simeq A \otimes \mathcal {D}$
such that
![]() $\Phi (B_m) = B_m \otimes \mathcal {D}$
for all
$\Phi (B_m) = B_m \otimes \mathcal {D}$
for all
![]() $m \in \mathbb {N}$
.
$m \in \mathbb {N}$
.
Proof This is essentially the same proof as Theorem 4.4, except we use the countable relative intertwining (Proposition 4.2) in place of Proposition 4.1. Let
![]() $\xi ,\eta $
be as before, and let
$\xi ,\eta $
be as before, and let
![]() $(v_n)_{n \in \mathbb {N}} \subseteq C^*(\xi (\mathcal {D}),\eta (\mathcal {D})) \simeq \mathcal {D} \otimes \mathcal {D}$
be such that
$(v_n)_{n \in \mathbb {N}} \subseteq C^*(\xi (\mathcal {D}),\eta (\mathcal {D})) \simeq \mathcal {D} \otimes \mathcal {D}$
be such that
![]() $v_n^*\eta (d)v_n \to \xi (d)$
for
$v_n^*\eta (d)v_n \to \xi (d)$
for
![]() $d \in \mathcal {D}$
.
$d \in \mathcal {D}$
.
-
• If
 $a \in A, d \in \mathcal {D}, v_n^*(a \otimes d)v_n \to \phi (a)\xi (d) \in \phi (A)_\omega $
;
$a \in A, d \in \mathcal {D}, v_n^*(a \otimes d)v_n \to \phi (a)\xi (d) \in \phi (A)_\omega $
; -
• if
 $b \in B_m, v_n^*(b \otimes d)v_n \to \phi (b)\xi (d) \in \phi (B_m)_\omega $
.
$b \in B_m, v_n^*(b \otimes d)v_n \to \phi (b)\xi (d) \in \phi (B_m)_\omega $
.
Now with
![]() $\phi : A \to A \otimes \mathcal {D}$
, the first factor embedding,
$\phi : A \to A \otimes \mathcal {D}$
, the first factor embedding,
![]() $\theta _m:B_m \to A$
the inclusion maps, and
$\theta _m:B_m \to A$
the inclusion maps, and
![]() $\psi _m:B_m \simeq B_m \otimes \mathcal {D}$
(these exist since
$\psi _m:B_m \simeq B_m \otimes \mathcal {D}$
(these exist since
![]() $\mathcal {D} \hookrightarrow (B_1)_\omega \cap A'$
implies that
$\mathcal {D} \hookrightarrow (B_1)_\omega \cap A'$
implies that
![]() $\mathcal {D} \hookrightarrow (B_m)_\omega \cap B_m'$
), our unitaries satisfy the hypothesis of Proposition 4.2 and therefore
$\mathcal {D} \hookrightarrow (B_m)_\omega \cap B_m'$
), our unitaries satisfy the hypothesis of Proposition 4.2 and therefore
![]() $\phi $
is approximately unitarily equivalent to a *-isomorphism
$\phi $
is approximately unitarily equivalent to a *-isomorphism
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
such that
$\Phi : A \simeq A \otimes \mathcal {D}$
such that
![]() $\Phi (B_m) = B_m \otimes \mathcal {D}$
for all m.
$\Phi (B_m) = B_m \otimes \mathcal {D}$
for all m.
The above works since norm ultrapowers have the property that unitaries lift to sequences of unitaries.Footnote
2
Tracial ultrapowers of
![]() $\text {II}_1$
von Neumann algebras also have this property.Footnote
3
Consequently, if we work with the 2-norm
$\text {II}_1$
von Neumann algebras also have this property.Footnote
3
Consequently, if we work with the 2-norm
![]() $\|x\|_2 = \tau (x^*x)^{\frac {1}{2}}$
, where
$\|x\|_2 = \tau (x^*x)^{\frac {1}{2}}$
, where
![]() $\tau $
is the unique trace on a
$\tau $
is the unique trace on a
![]() $\text {II}_1$
factor, all of the above arguments with the C*-norm replaced by
$\text {II}_1$
factor, all of the above arguments with the C*-norm replaced by
![]() $\|\cdot \|_2$
will allow us to recover Bisch’s result [Reference Bisch2, Theorem 3.1], provided we have the appropriate separability conditions.
$\|\cdot \|_2$
will allow us to recover Bisch’s result [Reference Bisch2, Theorem 3.1], provided we have the appropriate separability conditions.
Theorem 4.9 Let
![]() $\mathcal {N} \subseteq \mathcal {M}$
be an inclusion of
$\mathcal {N} \subseteq \mathcal {M}$
be an inclusion of
![]() $\text {II}_1$
factors with separable preduals. Then
$\text {II}_1$
factors with separable preduals. Then
![]() $\mathcal {R} \hookrightarrow \mathcal {N}^\omega \cap \mathcal {M}'$
if and only if there exists an isomorphism
$\mathcal {R} \hookrightarrow \mathcal {N}^\omega \cap \mathcal {M}'$
if and only if there exists an isomorphism
![]() $\Phi : \mathcal {M} \to \mathcal {M} \overline {\otimes } \mathcal {R}$
such that
$\Phi : \mathcal {M} \to \mathcal {M} \overline {\otimes } \mathcal {R}$
such that
![]() $\Phi (\mathcal {N}) = \mathcal {N} \overline {\otimes } \mathcal {R}$
.
$\Phi (\mathcal {N}) = \mathcal {N} \overline {\otimes } \mathcal {R}$
.
4.3 Existence of
 $\mathcal {D}$
-stable embeddings
$\mathcal {D}$
-stable embeddings
We move to discuss the existence of
![]() $\mathcal {D}$
-stable embeddings. First, we show that each unital embedding of unital, separable
$\mathcal {D}$
-stable embeddings. First, we show that each unital embedding of unital, separable
![]() $\mathcal {D}$
-stable C*-algebras is approximately unitarily equivalent to a
$\mathcal {D}$
-stable C*-algebras is approximately unitarily equivalent to a
![]() $\mathcal {D}$
-stable embedding. From this, it will follow that there are many
$\mathcal {D}$
-stable embedding. From this, it will follow that there are many
![]() $\mathcal {D}$
-stable embeddings.
$\mathcal {D}$
-stable embeddings.
Lemma 4.10 Let
![]() $\mathcal {D}$
be strongly self-absorbing. If
$\mathcal {D}$
be strongly self-absorbing. If
![]() $\iota : B \hookrightarrow A$
is a unital,
$\iota : B \hookrightarrow A$
is a unital,
![]() $\mathcal {D}$
-stable inclusion of separable C*-algebras and
$\mathcal {D}$
-stable inclusion of separable C*-algebras and
![]() $u \in U(A)$
, then
$u \in U(A)$
, then
![]() $\text {Ad}_u \circ \iota : B \hookrightarrow A$
is
$\text {Ad}_u \circ \iota : B \hookrightarrow A$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof Apply Lemma 3.6.
Proposition 4.11 Let
![]() $\mathcal {D}$
be strongly self-absorbing,
$\mathcal {D}$
be strongly self-absorbing,
![]() $A,B$
be unital separable
$A,B$
be unital separable
![]() $\mathcal {D}$
-stable C*-algebras, and let
$\mathcal {D}$
-stable C*-algebras, and let
![]() $\iota : B \hookrightarrow A$
be a unital embedding. Then
$\iota : B \hookrightarrow A$
be a unital embedding. Then
![]() $\iota $
is approximately unitarily equivalent to a unital
$\iota $
is approximately unitarily equivalent to a unital
![]() $\mathcal {D}$
-stable embedding
$\mathcal {D}$
-stable embedding
![]() $B \hookrightarrow A$
.
$B \hookrightarrow A$
.
Proof As
![]() $A,B$
are
$A,B$
are
![]() $\mathcal {D}$
-stable, there are isomorphisms
$\mathcal {D}$
-stable, there are isomorphisms
which are approximately unitarily equivalent to the first factor embeddings
![]() $b \mapsto b \otimes 1_{\mathcal {D}}, b \in B$
and
$b \mapsto b \otimes 1_{\mathcal {D}}, b \in B$
and
![]() $a \mapsto a \otimes 1_{\mathcal {D}}, a \in A,$
respectively. As
$a \mapsto a \otimes 1_{\mathcal {D}}, a \in A,$
respectively. As
![]() $\iota \otimes \text {id}_{\mathcal {D}}: B \otimes \mathcal {D} \hookrightarrow A \otimes \mathcal {D}$
is
$\iota \otimes \text {id}_{\mathcal {D}}: B \otimes \mathcal {D} \hookrightarrow A \otimes \mathcal {D}$
is
![]() $\mathcal {D}$
-stable by Lemma 4.3,
$\mathcal {D}$
-stable by Lemma 4.3,
is
![]() $\mathcal {D}$
-stable by Lemma 3.8. Now we show that
$\mathcal {D}$
-stable by Lemma 3.8. Now we show that
![]() $\sigma $
is approximately unitarily equivalent to
$\sigma $
is approximately unitarily equivalent to
![]() $\iota $
. Let
$\iota $
. Let
![]() $\mathcal {F} \subseteq B$
be finite and
$\mathcal {F} \subseteq B$
be finite and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $u \in U(B \otimes \mathcal {D})$
be such that
$u \in U(B \otimes \mathcal {D})$
be such that
![]() $u^*(b \otimes 1_{\mathcal {D}})u \approx _{\frac {\varepsilon }{2}} \phi (b)$
for
$u^*(b \otimes 1_{\mathcal {D}})u \approx _{\frac {\varepsilon }{2}} \phi (b)$
for
![]() $b \in \mathcal {F}$
and
$b \in \mathcal {F}$
and
![]() $v \in U(A \otimes \mathcal {D})$
be such that
$v \in U(A \otimes \mathcal {D})$
be such that
![]() $v^*(\iota (b) \otimes 1_{\mathcal {D}})v \approx _{\frac {\varepsilon }{2}} \psi \circ \iota (b)$
for
$v^*(\iota (b) \otimes 1_{\mathcal {D}})v \approx _{\frac {\varepsilon }{2}} \psi \circ \iota (b)$
for
![]() $b \in \mathcal {F}$
. Set
$b \in \mathcal {F}$
. Set
![]() $w = \psi ^{-1}(\iota \otimes \text {id}_{\mathcal {D}}(u))^*\psi ^{-1}(v) \in U(A)$
. Then for
$w = \psi ^{-1}(\iota \otimes \text {id}_{\mathcal {D}}(u))^*\psi ^{-1}(v) \in U(A)$
. Then for
![]() $b \in \mathcal {F}$
,
$b \in \mathcal {F}$
,
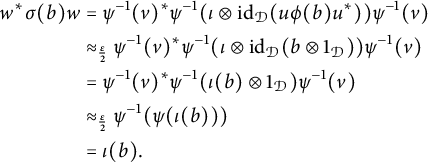 $$ \begin{align} \nonumber w^*\sigma(b)w &= \psi^{-1}(v)^*\psi^{-1}(\iota \otimes \text{id}_{\mathcal{D}}(u\phi(b)u^*))\psi^{-1}(v) \\ &\approx_{\frac{\varepsilon}{2}} \psi^{-1}(v)^*\psi^{-1}(\iota \otimes \text{id}_{\mathcal{D}}(b \otimes 1_{\mathcal{D}}))\psi^{-1}(v) \\ \nonumber &= \psi^{-1}(v)^*\psi^{-1}(\iota(b) \otimes 1_{\mathcal{D}})\psi^{-1}(v) \\ \nonumber &\approx_{\frac{\varepsilon}{2}} \psi^{-1}(\psi(\iota(b))) \\ \nonumber &= \iota(b).\\[-37pt]\nonumber \end{align} $$
$$ \begin{align} \nonumber w^*\sigma(b)w &= \psi^{-1}(v)^*\psi^{-1}(\iota \otimes \text{id}_{\mathcal{D}}(u\phi(b)u^*))\psi^{-1}(v) \\ &\approx_{\frac{\varepsilon}{2}} \psi^{-1}(v)^*\psi^{-1}(\iota \otimes \text{id}_{\mathcal{D}}(b \otimes 1_{\mathcal{D}}))\psi^{-1}(v) \\ \nonumber &= \psi^{-1}(v)^*\psi^{-1}(\iota(b) \otimes 1_{\mathcal{D}})\psi^{-1}(v) \\ \nonumber &\approx_{\frac{\varepsilon}{2}} \psi^{-1}(\psi(\iota(b))) \\ \nonumber &= \iota(b).\\[-37pt]\nonumber \end{align} $$
Corollary 4.12 Let
![]() $\mathcal {D}$
be strongly self-absorbing. The set of unital
$\mathcal {D}$
be strongly self-absorbing. The set of unital
![]() $\mathcal {D}$
-stable embeddings
$\mathcal {D}$
-stable embeddings
![]() $B \hookrightarrow A$
of unital, separable,
$B \hookrightarrow A$
of unital, separable,
![]() $\mathcal {D}$
-stable C*-algebras is point-norm dense in the set of unital embeddings
$\mathcal {D}$
-stable C*-algebras is point-norm dense in the set of unital embeddings
![]() $B \hookrightarrow A$
.
$B \hookrightarrow A$
.
Proof Every embedding is approximately unitarily equivalent to a
![]() $\mathcal {D}$
-stable embedding. As
$\mathcal {D}$
-stable embedding. As
![]() $\mathcal {D}$
-stability of an embedding is preserved if one composes with
$\mathcal {D}$
-stability of an embedding is preserved if one composes with
![]() $\text {Ad}_u$
, it follows that every embedding is the point-norm limit of
$\text {Ad}_u$
, it follows that every embedding is the point-norm limit of
![]() $\mathcal {D}$
-stable embeddings.
$\mathcal {D}$
-stable embeddings.
Remark 4.13 We note that it is not actually necessary that
![]() $\iota $
is an embedding. If
$\iota $
is an embedding. If
![]() $\pi : B \to A$
is any unital *-homomorphism between unital, separable,
$\pi : B \to A$
is any unital *-homomorphism between unital, separable,
![]() $\mathcal {D}$
-stable C*-algebras, then
$\mathcal {D}$
-stable C*-algebras, then
![]() $\pi $
is approximately unitarily equivalent to a *-homomorphism
$\pi $
is approximately unitarily equivalent to a *-homomorphism
![]() $\pi ': B \to A$
such that
$\pi ': B \to A$
such that
![]() $\pi '(B) \subseteq A$
is
$\pi '(B) \subseteq A$
is
![]() $\mathcal {D}$
-stable. Consequently, the set of unital *-homomorphisms
$\mathcal {D}$
-stable. Consequently, the set of unital *-homomorphisms
![]() $\pi : B \to A$
with
$\pi : B \to A$
with
![]() $\pi (B) \subseteq A$
being
$\pi (B) \subseteq A$
being
![]() $\mathcal {D}$
-stable is in fact dense in the set of unital *-homomorphisms
$\mathcal {D}$
-stable is in fact dense in the set of unital *-homomorphisms
![]() $B \to A$
.
$B \to A$
.
Later on, there will be some examples of non-
![]() $\mathcal {D}$
-stable embeddings between
$\mathcal {D}$
-stable embeddings between
![]() $\mathcal {D}$
-stable C*-algebras. Consequently, despite the fact
$\mathcal {D}$
-stable C*-algebras. Consequently, despite the fact
![]() $\mathcal {D}$
-stable embeddings are point-norm dense, the set of unital
$\mathcal {D}$
-stable embeddings are point-norm dense, the set of unital
![]() $\mathcal {D}$
-stable embeddings need not coincide with the set of all unital embeddings
$\mathcal {D}$
-stable embeddings need not coincide with the set of all unital embeddings
![]() $B \hookrightarrow A$
. Another clear consequence is that despite
$B \hookrightarrow A$
. Another clear consequence is that despite
![]() $\mathcal {D}$
-stability of an embedding being closed under conjugation by a unitary, it is not true that it is preserved under approximate unitary equivalence (in fact, the examples in question show that
$\mathcal {D}$
-stability of an embedding being closed under conjugation by a unitary, it is not true that it is preserved under approximate unitary equivalence (in fact, the examples in question show that
![]() $\mathcal {D}$
-stability is not even preserved under asymptotic unitary equivalence). We finish with a corollary about embeddings into the Cuntz algebra
$\mathcal {D}$
-stability is not even preserved under asymptotic unitary equivalence). We finish with a corollary about embeddings into the Cuntz algebra
![]() $\mathcal {O}_2$
[Reference Cuntz15].
$\mathcal {O}_2$
[Reference Cuntz15].
Corollary 4.14 Let B be a unital, separable, exact
![]() $\mathcal {D}$
-stable C*-algebra, where
$\mathcal {D}$
-stable C*-algebra, where
![]() $\mathcal {D}$
is strongly self-absorbing. Then there is a
$\mathcal {D}$
is strongly self-absorbing. Then there is a
![]() $\mathcal {D}$
-stable embedding
$\mathcal {D}$
-stable embedding
![]() $B \hookrightarrow \mathcal {O}_2$
.
$B \hookrightarrow \mathcal {O}_2$
.
Proof As
![]() $\mathcal {D}$
is unital, simple, separable, and nuclear by [Reference Toms and Winter66, Section 1.6],
$\mathcal {D}$
is unital, simple, separable, and nuclear by [Reference Toms and Winter66, Section 1.6],
![]() $\mathcal {O}_2 \simeq \mathcal {O}_2 \otimes \mathcal {D}$
and
$\mathcal {O}_2 \simeq \mathcal {O}_2 \otimes \mathcal {D}$
and
![]() $B \hookrightarrow \mathcal {O}_2$
unitally by Theorems 3.7 and 2.8 of [Reference Kirchberg and Phillips36], respectively. The above results then yield a
$B \hookrightarrow \mathcal {O}_2$
unitally by Theorems 3.7 and 2.8 of [Reference Kirchberg and Phillips36], respectively. The above results then yield a
![]() $\mathcal {D}$
-stable embedding
$\mathcal {D}$
-stable embedding
![]() $B \hookrightarrow \mathcal {O}_2$
.
$B \hookrightarrow \mathcal {O}_2$
.
We include this last result about the classification of morphisms via functors.
Theorem 4.15 Let
![]() $\mathcal {D}$
be strongly self-absorbing, and let F be a functor from a class of unital, separable,
$\mathcal {D}$
be strongly self-absorbing, and let F be a functor from a class of unital, separable,
![]() $\mathcal {D}$
-stable C*-algebras satisfying the following.
$\mathcal {D}$
-stable C*-algebras satisfying the following.
-
(E) If there exists a morphism
 $\Phi : F(B) \to F(A)$
, then there exists a unital *-homomorphism
$\Phi : F(B) \to F(A)$
, then there exists a unital *-homomorphism
 $\phi : B \to A$
such that
$\phi : B \to A$
such that
 $F(\phi ) = \Phi $
.
$F(\phi ) = \Phi $
. -
(U) If
 $\phi ,\psi : B \to A$
are unital *-homomorphisms which are approximately unitarily equivalent, then (4.23)
$\phi ,\psi : B \to A$
are unital *-homomorphisms which are approximately unitarily equivalent, then (4.23) $$ \begin{align} F(\phi) = F(\psi). \end{align} $$
$$ \begin{align} F(\phi) = F(\psi). \end{align} $$
Then whenever there is a morphism
![]() $\Phi : F(B) \to F(A)$
, there exists a unital *-homomorphism
$\Phi : F(B) \to F(A)$
, there exists a unital *-homomorphism
![]() $\phi : B \to A$
such that
$\phi : B \to A$
such that
![]() $F(\phi ) = \Phi $
and
$F(\phi ) = \Phi $
and
![]() $\phi (B) \subseteq A$
is
$\phi (B) \subseteq A$
is
![]() $\mathcal {D}$
-stable. Moreover,
$\mathcal {D}$
-stable. Moreover,
![]() $\phi $
is unique up to approximate unitary equivalence.
$\phi $
is unique up to approximate unitary equivalence.
Proof By the existence (E), there exists a *-homomorphism
![]() $\phi : B \to A$
. Now by Proposition 4.11 (Remark 4.13 allows us to work with general *-homomorphisms), there exists a *-homomorphism
$\phi : B \to A$
. Now by Proposition 4.11 (Remark 4.13 allows us to work with general *-homomorphisms), there exists a *-homomorphism
![]() $\phi ': B \to A$
which is approximately unitarily equivalent to
$\phi ': B \to A$
which is approximately unitarily equivalent to
![]() $\phi $
and
$\phi $
and
![]() $\phi '(B) \subseteq A$
is
$\phi '(B) \subseteq A$
is
![]() $\mathcal {D}$
-stable. Uniqueness (U) gives that this is unique up to approximate unitary equivalence.
$\mathcal {D}$
-stable. Uniqueness (U) gives that this is unique up to approximate unitary equivalence.
4.4 Permanence properties
We now discuss some permanence properties.
Lemma 4.16 Let
![]() $\mathcal {D}$
be strongly self-absorbing. Suppose that
$\mathcal {D}$
be strongly self-absorbing. Suppose that
![]() $\iota _j: B_j \hookrightarrow A_j, j=1,2$
are
$\iota _j: B_j \hookrightarrow A_j, j=1,2$
are
![]() $\mathcal {D}$
-stable inclusions. Then
$\mathcal {D}$
-stable inclusions. Then
![]() $\iota _1 \oplus \iota _2: B_1 \oplus B_2 \hookrightarrow A_1 \oplus A_2$
is
$\iota _1 \oplus \iota _2: B_1 \oplus B_2 \hookrightarrow A_1 \oplus A_2$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof Let
![]() $\Phi _j: A_j \simeq A_j \otimes \mathcal {D}$
be isomorphisms such that
$\Phi _j: A_j \simeq A_j \otimes \mathcal {D}$
be isomorphisms such that
![]() $\Phi _j\circ \iota _j(B_j) = \iota _j(B_j) \otimes \mathcal {D}$
and consider
$\Phi _j\circ \iota _j(B_j) = \iota _j(B_j) \otimes \mathcal {D}$
and consider
given by the composition
where the last isomorphism follows from (finite) distributivity of the min-tensor. Then we see that
Lemma 4.17 Let
![]() $\mathcal {D}$
be strongly self-absorbing. Suppose that
$\mathcal {D}$
be strongly self-absorbing. Suppose that
![]() $\iota _j: B_j \hookrightarrow A_j, j=1,2$
are inclusions and that at least one of
$\iota _j: B_j \hookrightarrow A_j, j=1,2$
are inclusions and that at least one of
![]() $\iota _1$
or
$\iota _1$
or
![]() $\iota _2$
is
$\iota _2$
is
![]() $\mathcal {D}$
-stable. Then
$\mathcal {D}$
-stable. Then
![]() $\iota _1 \otimes \iota _2: B_1 \otimes B_2 \hookrightarrow A_1 \otimes A_2$
is
$\iota _1 \otimes \iota _2: B_1 \otimes B_2 \hookrightarrow A_1 \otimes A_2$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof We prove this if
![]() $\iota _2$
is
$\iota _2$
is
![]() $\mathcal {D}$
-stable, and a symmetric argument will yield the result if
$\mathcal {D}$
-stable, and a symmetric argument will yield the result if
![]() $\iota _1$
is. Let
$\iota _1$
is. Let
![]() $\Phi _2: A_2 \simeq A_2 \otimes \mathcal {D}$
be such that
$\Phi _2: A_2 \simeq A_2 \otimes \mathcal {D}$
be such that
![]() $\Phi _2 \circ \iota _2(B_2) = \iota (B_2) \otimes \mathcal {D}$
. Taking
$\Phi _2 \circ \iota _2(B_2) = \iota (B_2) \otimes \mathcal {D}$
. Taking
we have that
Proposition 4.18 Let
![]() $\mathcal {D}$
be strongly self-absorbing. Suppose that we have increasing sequences of unital separable C*-algebras
$\mathcal {D}$
be strongly self-absorbing. Suppose that we have increasing sequences of unital separable C*-algebras
![]() $(B_n)_{n \in \mathbb {N}}$
and
$(B_n)_{n \in \mathbb {N}}$
and
![]() $(A_n)_{n \in \mathbb {N}}$
such that
$(A_n)_{n \in \mathbb {N}}$
such that
![]() $B_n \subseteq A_n$
unitally. Let
$B_n \subseteq A_n$
unitally. Let
![]() $B = \overline {\cup _nB_n}$
and
$B = \overline {\cup _nB_n}$
and
![]() $A = \overline {\cup _n A_n}$
. If
$A = \overline {\cup _n A_n}$
. If
![]() $B_n \subseteq A_n$
is
$B_n \subseteq A_n$
is
![]() $\mathcal {D}$
-stable for all n, then
$\mathcal {D}$
-stable for all n, then
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Lastly, we discuss unital inclusions
![]() $B \subseteq A$
of
$B \subseteq A$
of
![]() $C(X)$
algebras, where X is a compact Hausdorff space. We show that if X has finite covering dimension, then such an inclusion is
$C(X)$
algebras, where X is a compact Hausdorff space. We show that if X has finite covering dimension, then such an inclusion is
![]() $\mathcal {D}$
-stable if and only if the inclusion
$\mathcal {D}$
-stable if and only if the inclusion
![]() $B_x \subseteq A_x$
along each fiber is
$B_x \subseteq A_x$
along each fiber is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Lemma 4.19 Let
![]() $\mathcal {D}$
be strongly self-absorbing. Suppose that
$\mathcal {D}$
be strongly self-absorbing. Suppose that
![]() $B_i \subseteq A_i$
are unital inclusions, for
$B_i \subseteq A_i$
are unital inclusions, for
![]() $i=1,2$
, and
$i=1,2$
, and
![]() $\psi : A_1 \to A_2$
is a surjective *-homomorphism such that
$\psi : A_1 \to A_2$
is a surjective *-homomorphism such that
![]() $\psi (B_1) = B_2$
. If
$\psi (B_1) = B_2$
. If
![]() $B_1 \subseteq A_1$
is
$B_1 \subseteq A_1$
is
![]() $\mathcal {D}$
-stable, then so is
$\mathcal {D}$
-stable, then so is
![]() $B_2 \subseteq A_2$
.
$B_2 \subseteq A_2$
.
Proof We note that
![]() $\psi $
induces a *-homomorphism
$\psi $
induces a *-homomorphism
and consequently if
![]() $\xi : \mathcal {D} \hookrightarrow (B_1)_\omega \cap A_1'$
, we have a unital *-homomorphism
$\xi : \mathcal {D} \hookrightarrow (B_1)_\omega \cap A_1'$
, we have a unital *-homomorphism
The homomorphism
![]() $\eta $
is automatically injective since
$\eta $
is automatically injective since
![]() $\mathcal {D}$
is simple.
$\mathcal {D}$
is simple.
Rephrasing the above in terms of commutative diagrams, it says that if we have a commutative diagram
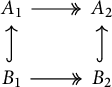
where the left inclusion is
![]() $\mathcal {D}$
-stable, then the right inclusion is
$\mathcal {D}$
-stable, then the right inclusion is
![]() $\mathcal {D}$
-stable as well.
$\mathcal {D}$
-stable as well.
Now we consider many of the results discussed in [Reference Hirshberg, Rørdam and Winter27, Section 4], except for inclusions of C*-algebras.
Definition 4.2 Let X be a compact Hausdorff space. A
![]() $C(X)$
-algebra is a C*-algebra A endowed with a unital *-homomorphism
$C(X)$
-algebra is a C*-algebra A endowed with a unital *-homomorphism
![]() $C(X) \to \mathcal {Z}(\mathcal {M}(A))$
, where
$C(X) \to \mathcal {Z}(\mathcal {M}(A))$
, where
![]() $\mathcal {Z}(\mathcal {M}(A)$
is the center of the multiplier algebra
$\mathcal {Z}(\mathcal {M}(A)$
is the center of the multiplier algebra
![]() $\mathcal {M}(A)$
of A.
$\mathcal {M}(A)$
of A.
If
![]() $Y \subseteq X$
is a closed subset, we set
$Y \subseteq X$
is a closed subset, we set
![]() $I_Y := C_0(X \setminus Y)A$
, which is a closed two-sided ideal in A. We denote
$I_Y := C_0(X \setminus Y)A$
, which is a closed two-sided ideal in A. We denote
![]() $A_Y := A/I_Y$
and the quotient map
$A_Y := A/I_Y$
and the quotient map
![]() $A \to A_Y$
by
$A \to A_Y$
by
![]() $\pi _Y$
. For an element
$\pi _Y$
. For an element
![]() $a \in A$
, we write
$a \in A$
, we write
![]() $a_Y := \pi _Y(a)$
and if Y consists of a single point x, we write
$a_Y := \pi _Y(a)$
and if Y consists of a single point x, we write
![]() $A_x,I_x,\pi _x$
and
$A_x,I_x,\pi _x$
and
![]() $a_x$
. We say that
$a_x$
. We say that
![]() $A_x$
is the fiber of A at x. We note that
$A_x$
is the fiber of A at x. We note that
![]() $A_X = A$
.
$A_X = A$
.
If
![]() $B \subseteq A$
is a unital inclusion and
$B \subseteq A$
is a unital inclusion and
![]() $\theta _A: C(X) \to A, \theta _B: C(X) \to B$
are morphisms which witness A and B as
$\theta _A: C(X) \to A, \theta _B: C(X) \to B$
are morphisms which witness A and B as
![]() $C(X)$
-algebras, respectively, we say that
$C(X)$
-algebras, respectively, we say that
![]() $B \subseteq A$
is an inclusion of
$B \subseteq A$
is an inclusion of
![]() $C(X)$
-algebras if
$C(X)$
-algebras if
commutes. Note that
![]() $\theta _B(C(X)) \subseteq \mathcal {Z}(A)$
, and when discussion an inclusion of fibers
$\theta _B(C(X)) \subseteq \mathcal {Z}(A)$
, and when discussion an inclusion of fibers
![]() $B_Y \subseteq A_Y$
we are considering
$B_Y \subseteq A_Y$
we are considering
![]() $B_Y := \pi ^A_Y(B) \subseteq \pi ^A_Y(A) =: A_Y$
, where
$B_Y := \pi ^A_Y(B) \subseteq \pi ^A_Y(A) =: A_Y$
, where
![]() $\pi _Y^A: A \to A_Y$
is the associated quotient map.
$\pi _Y^A: A \to A_Y$
is the associated quotient map.
Remark 4.20 (Upper semi-continuity)
In [Reference Hirshberg, Rørdam and Winter27, Section 1.3], it was pointed out that the norm on a
![]() $C(X)$
-algebra A is upper semi-continuous. This means that, fixing some
$C(X)$
-algebra A is upper semi-continuous. This means that, fixing some
![]() $a \in A$
, the function
$a \in A$
, the function
![]() $x \mapsto \|a_x\|$
from X to
$x \mapsto \|a_x\|$
from X to
![]() $\mathbb {R}$
is upper semi-continuous (as it is the infimum of a family of continuous functions), and consequently the set
$\mathbb {R}$
is upper semi-continuous (as it is the infimum of a family of continuous functions), and consequently the set
![]() $\{x \in X \mid \|a_x\| < \varepsilon \} \subseteq X$
is open for all
$\{x \in X \mid \|a_x\| < \varepsilon \} \subseteq X$
is open for all
![]() $a \in A$
and
$a \in A$
and
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
We note that Lemma 4.19 gives that if
![]() $B\subseteq A$
is
$B\subseteq A$
is
![]() $\mathcal {D}$
-stable and
$\mathcal {D}$
-stable and
![]() $Y \subseteq X$
is closed, then
$Y \subseteq X$
is closed, then
![]() $B_Y \subseteq A_Y$
is automatically
$B_Y \subseteq A_Y$
is automatically
![]() $\mathcal {D}$
-stable as well since we have the commuting diagram
$\mathcal {D}$
-stable as well since we have the commuting diagram
The converse needs a bit of work. This is the embedding analog of the beginning of [Reference Hirshberg, Rørdam and Winter27, Section 4]. We discuss how the proofs can be adapted and often omit approximations that were otherwise done there. We want a version of [Reference Hirshberg, Rørdam and Winter27, Lemma 4.5], which is a result about gluing c.c.p. maps together along fibers. In our setting, we are only interested in u.c.p. maps, and we want to show that if we glue two u.c.p. maps together whose images are contained in some
![]() $C(X)$
-subalgebra B, then the glued map also has image contained in B. We borrow their Definition 4.2.
$C(X)$
-subalgebra B, then the glued map also has image contained in B. We borrow their Definition 4.2.
Definition 4.3 Let A be a unital
![]() $C(X)$
-algebra, for a compact Hausdorff space X, and let D be a unital C*-algebra. Let
$C(X)$
-algebra, for a compact Hausdorff space X, and let D be a unital C*-algebra. Let
![]() $\phi : D \to A$
be a u.c.p. map and
$\phi : D \to A$
be a u.c.p. map and
![]() $Y \subseteq X$
a closed subset. If
$Y \subseteq X$
a closed subset. If
![]() $\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
are finite and
$\mathcal {F} \subseteq D, \mathcal {G} \subseteq A$
are finite and
![]() $\varepsilon> 0$
, we say that
$\varepsilon> 0$
, we say that
![]() $\phi $
is
$\phi $
is
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for Y if:
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for Y if:
-
(1)
 $([\phi (d),a])_Y \approx _\varepsilon 0$
and
$([\phi (d),a])_Y \approx _\varepsilon 0$
and -
(2)
 $\phi (dd')_Y \approx _\varepsilon \phi (d)_Y\phi (d')_Y$
$\phi (dd')_Y \approx _\varepsilon \phi (d)_Y\phi (d')_Y$
whenever
![]() $d,d' \in \mathcal {F}$
and
$d,d' \in \mathcal {F}$
and
![]() $a \in \mathcal {G}$
. If
$a \in \mathcal {G}$
. If
![]() $X = [0,1]$
,
$X = [0,1]$
,
![]() $Y \subseteq X$
is a closed interval,
$Y \subseteq X$
is a closed interval,
![]() $\mathcal {F}' \supseteq \mathcal {F}$
is another finite set and
$\mathcal {F}' \supseteq \mathcal {F}$
is another finite set and
![]() $0 < \varepsilon ' < \varepsilon $
, we say that
$0 < \varepsilon ' < \varepsilon $
, we say that
![]() $\phi $
is
$\phi $
is
![]() $(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for Y if
$(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for Y if
![]() $\phi $
is
$\phi $
is
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for Y and there exists some closed neighborhood V of the endpoints of Y such that
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for Y and there exists some closed neighborhood V of the endpoints of Y such that
![]() $\phi $
is
$\phi $
is
![]() $(\mathcal {F}',\varepsilon ',\mathcal {G})$
-good for V.
$(\mathcal {F}',\varepsilon ',\mathcal {G})$
-good for V.
First, we need a lemma that follows as a consequence of
![]() $\mathcal {D}$
-stability. It is the embedding analog of [Reference Hirshberg, Rørdam and Winter27, Proposition 4.1].
$\mathcal {D}$
-stability. It is the embedding analog of [Reference Hirshberg, Rørdam and Winter27, Proposition 4.1].
Lemma 4.21 Let
![]() $\mathcal {D}$
be strongly self-absorbing, and
$\mathcal {D}$
be strongly self-absorbing, and
![]() $B \subseteq A$
be a unital,
$B \subseteq A$
be a unital,
![]() $\mathcal {D}$
-stable inclusion of separable C*-algebras. Then for any
$\mathcal {D}$
-stable inclusion of separable C*-algebras. Then for any
![]() $\mathcal {G} \subseteq A$
finite and
$\mathcal {G} \subseteq A$
finite and
![]() $\varepsilon> 0$
, there exist unital *-homomorphisms
$\varepsilon> 0$
, there exist unital *-homomorphisms
![]() $\kappa : A \to A$
and
$\kappa : A \to A$
and
![]() $\mu : \mathcal {D} \to B$
such that:
$\mu : \mathcal {D} \to B$
such that:
-
(1)
 $\kappa (B) \subseteq B$
,
$\kappa (B) \subseteq B$
, -
(2)
 $[\kappa (A),\mu (\mathcal {D})] = 0$
,
$[\kappa (A),\mu (\mathcal {D})] = 0$
, -
(3)
 $\kappa (a) \approx _\varepsilon a$
for all
$\kappa (a) \approx _\varepsilon a$
for all
 $a \in \mathcal {G}$
.
$a \in \mathcal {G}$
.
Proof The proof is essentially the same as the proof of (a)
![]() $\Rightarrow (c)$
in [Reference Hirshberg, Rørdam and Winter27, Proposition 4.1]. As
$\Rightarrow (c)$
in [Reference Hirshberg, Rørdam and Winter27, Proposition 4.1]. As
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable, let us identify
$\mathcal {D}$
-stable, let us identify
![]() $B \subseteq A$
with
$B \subseteq A$
with
![]() $B \otimes \mathcal {D} \subseteq A \otimes \mathcal {D}$
. As
$B \otimes \mathcal {D} \subseteq A \otimes \mathcal {D}$
. As
![]() $\mathcal {D}$
is strongly self-absorbing, [Reference Toms and Winter66, Theorem 2.3] gives a sequence
$\mathcal {D}$
is strongly self-absorbing, [Reference Toms and Winter66, Theorem 2.3] gives a sequence
![]() $(\phi _n)_{n \in \mathbb {N}}$
of *-homomorphisms
$(\phi _n)_{n \in \mathbb {N}}$
of *-homomorphisms
![]() $\phi _n: \mathcal {D} \otimes \mathcal {D} \to \mathcal {D}$
such that
$\phi _n: \mathcal {D} \otimes \mathcal {D} \to \mathcal {D}$
such that
Define
![]() $\kappa _n: A \otimes \mathcal {D} \to A \otimes \mathcal {D}$
by
$\kappa _n: A \otimes \mathcal {D} \to A \otimes \mathcal {D}$
by
and
![]() $\mu _n: \mathcal {D} \to B \otimes \mathcal {D}$
by
$\mu _n: \mathcal {D} \to B \otimes \mathcal {D}$
by
Then taking n large enough and letting
![]() $\kappa $
and
$\kappa $
and
![]() $\mu $
be
$\mu $
be
![]() $\kappa _n$
and
$\kappa _n$
and
![]() $\mu _n$
, respectively, its clear that
$\mu _n$
, respectively, its clear that
![]() $\kappa (B \otimes \mathcal {D}) \subseteq B \otimes \mathcal {D}$
,
$\kappa (B \otimes \mathcal {D}) \subseteq B \otimes \mathcal {D}$
,
![]() $[\kappa (A),\mu (\mathcal {D})] = 0$
and that
$[\kappa (A),\mu (\mathcal {D})] = 0$
and that
![]() $\kappa (a) \approx _\varepsilon a$
whenever a is in some prescribed finite subset
$\kappa (a) \approx _\varepsilon a$
whenever a is in some prescribed finite subset
![]() $\mathcal {G} \subseteq A$
and
$\mathcal {G} \subseteq A$
and
![]() $\varepsilon> 0$
is some prescribed error.
$\varepsilon> 0$
is some prescribed error.
Lemma 4.22 Let
![]() $\mathcal {D}$
be strongly self-absorbing and A be a unital, separable
$\mathcal {D}$
be strongly self-absorbing and A be a unital, separable
![]() $C([0,1])$
-algebra. Suppose
$C([0,1])$
-algebra. Suppose
![]() $\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq A$
are finite self-adjoint subsets of contractions with
$\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq A$
are finite self-adjoint subsets of contractions with
![]() $1_{\mathcal {D}} \in \mathcal {F}$
. Suppose that we have points
$1_{\mathcal {D}} \in \mathcal {F}$
. Suppose that we have points
![]() $0 \leq r < s < t \leq 1$
and two u.c.p. maps
$0 \leq r < s < t \leq 1$
and two u.c.p. maps
![]() $\rho ,\sigma : \mathcal {D} \to A$
which are
$\rho ,\sigma : \mathcal {D} \to A$
which are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for
![]() $[r,s],[s,t]$
, respectively. Suppose that
$[r,s],[s,t]$
, respectively. Suppose that
![]() $A_s$
is
$A_s$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Then there are u.c.p. maps
![]() $\rho ',\sigma ': \mathcal {D} \to A$
which are
$\rho ',\sigma ': \mathcal {D} \to A$
which are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-good for
![]() $[r,s],[s,t]$
, respectively, and u.c.p. maps
$[r,s],[s,t]$
, respectively, and u.c.p. maps
![]() $\nu _{\rho '},\nu _{\sigma '}: \mathcal {D} \to A,\mu _{\rho '},\mu _{\sigma '}: \mathcal {D} \otimes \mathcal {D} \to A$
such that
$\nu _{\rho '},\nu _{\sigma '}: \mathcal {D} \to A,\mu _{\rho '},\mu _{\sigma '}: \mathcal {D} \otimes \mathcal {D} \to A$
such that
![]() $\nu _{\rho '},\nu _{\sigma '}$
are
$\nu _{\rho '},\nu _{\sigma '}$
are
![]() $(\mathcal {F},3\varepsilon ,\mathcal {G})$
-good for some interval
$(\mathcal {F},3\varepsilon ,\mathcal {G})$
-good for some interval
![]() $I \subseteq (r,t)$
containing s in its interior, and such that for any
$I \subseteq (r,t)$
containing s in its interior, and such that for any
![]() $a \in \mathcal {G}, d,d' \in \mathcal {F}$
, we have:
$a \in \mathcal {G}, d,d' \in \mathcal {F}$
, we have:
-
(1)
 $([\rho '(d),\nu _{\rho '}(d')])_I \approx _{2\varepsilon } 0,$
$([\rho '(d),\nu _{\rho '}(d')])_I \approx _{2\varepsilon } 0,$
-
(2)
 $([\sigma '(d),\nu _{\sigma '}(d')])_I \approx _{2\varepsilon } 0,$
$([\sigma '(d),\nu _{\sigma '}(d')])_I \approx _{2\varepsilon } 0,$
-
(3)
 $\rho '(d)_I\nu _{\rho '}(d')_I \approx _\varepsilon \mu _{\rho '}(d \otimes d')_I,$
$\rho '(d)_I\nu _{\rho '}(d')_I \approx _\varepsilon \mu _{\rho '}(d \otimes d')_I,$
-
(4)
 $\sigma '(d)_I\nu _{\sigma '}(d')_I \approx _\varepsilon \mu _{\sigma '}(d \otimes d')_I,$
$\sigma '(d)_I\nu _{\sigma '}(d')_I \approx _\varepsilon \mu _{\sigma '}(d \otimes d')_I,$
-
(5)
 $\nu _{\rho '}(d)_I \approx _{2\varepsilon } \nu _{\sigma '}(d)_I$
.
$\nu _{\rho '}(d)_I \approx _{2\varepsilon } \nu _{\sigma '}(d)_I$
.
If
![]() $\rho ,\sigma $
are
$\rho ,\sigma $
are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon )$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon )$
-good for
![]() $[r,s],[s,t]$
, respectively, for some finite
$[r,s],[s,t]$
, respectively, for some finite
![]() $\mathcal {F}' \supseteq \mathcal {F}$
set of contractions and for some
$\mathcal {F}' \supseteq \mathcal {F}$
set of contractions and for some
![]() $0 < \varepsilon ' < \varepsilon $
, then we can arrange so that
$0 < \varepsilon ' < \varepsilon $
, then we can arrange so that
![]() $\rho ',\sigma ',\nu _{\rho '},\nu _{\sigma '}$
are
$\rho ',\sigma ',\nu _{\rho '},\nu _{\sigma '}$
are
![]() $(\mathcal {F}',3\varepsilon ',\mathcal {G})$
-good for the interval I, and that the above five conditions hold with
$(\mathcal {F}',3\varepsilon ',\mathcal {G})$
-good for the interval I, and that the above five conditions hold with
![]() $\varepsilon '$
in place of
$\varepsilon '$
in place of
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\mathcal {F}'$
in place of
$\mathcal {F}'$
in place of
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Moreover, if
![]() $B \subseteq A$
is a unital inclusion of
$B \subseteq A$
is a unital inclusion of
![]() $C([0,1])$
-algebras such that
$C([0,1])$
-algebras such that
![]() $\rho (\mathcal {D}) \subseteq B, \sigma (\mathcal {D}) \subseteq B$
and
$\rho (\mathcal {D}) \subseteq B, \sigma (\mathcal {D}) \subseteq B$
and
![]() $B_s \subseteq A_s$
is
$B_s \subseteq A_s$
is
![]() $\mathcal {D}$
-stable, then the images of all
$\mathcal {D}$
-stable, then the images of all
![]() $\rho ',\sigma ',\mu _{\rho '},\mu _{\sigma '}$
are contained in B (as are the images of
$\rho ',\sigma ',\mu _{\rho '},\mu _{\sigma '}$
are contained in B (as are the images of
![]() $\nu _{\rho '}$
and
$\nu _{\rho '}$
and
![]() $\nu _{\sigma '}$
).
$\nu _{\sigma '}$
).
Proof This is [Reference Hirshberg, Rørdam and Winter27, Lemma 4.4], except we have replaced c.c.p. maps with u.c.p. maps. One can easily check that the resulting maps are u.c.p. maps.
As for the “moreover” part, which is the only addition besides the unitality, we outline the definitions of these maps to show that the images of
![]() $\rho ',\sigma ',\mu _{\rho '},\mu _{\sigma '}$
are contained in B. As
$\rho ',\sigma ',\mu _{\rho '},\mu _{\sigma '}$
are contained in B. As
![]() $B_s \subseteq A_s$
is
$B_s \subseteq A_s$
is
![]() $\mathcal {D}$
-stable, we can find
$\mathcal {D}$
-stable, we can find
![]() $\kappa : A_s \to A_s$
and
$\kappa : A_s \to A_s$
and
![]() $\mu : \mathcal {D} \to B_s$
as in Lemma 4.21, where
$\mu : \mathcal {D} \to B_s$
as in Lemma 4.21, where
![]() $\kappa (a_s) \approx a_s$
for an appropriate error whenever
$\kappa (a_s) \approx a_s$
for an appropriate error whenever
![]() $a \in \mathcal {G}$
. We use Choi–Effros to find u.c.p. lifts
$a \in \mathcal {G}$
. We use Choi–Effros to find u.c.p. lifts
![]() $\tilde {\rho },\tilde {\sigma }: \mathcal {D} \to B$
for the maps
$\tilde {\rho },\tilde {\sigma }: \mathcal {D} \to B$
for the maps
![]() $\kappa \circ \pi _s \circ \rho $
and
$\kappa \circ \pi _s \circ \rho $
and
![]() $\kappa \circ \pi _s \circ \sigma $
, respectively (note that
$\kappa \circ \pi _s \circ \sigma $
, respectively (note that
![]() $\kappa \circ \pi _s \circ \rho $
and
$\kappa \circ \pi _s \circ \rho $
and
![]() $\kappa \circ \pi _s \circ \sigma $
lie in
$\kappa \circ \pi _s \circ \sigma $
lie in
![]() $B_s$
, which is a *-homomorphic image of B). One then defines piece-wise linear functions
$B_s$
, which is a *-homomorphic image of B). One then defines piece-wise linear functions
![]() $f,g: [0,1] \to [0,1]$
which attain both values 0 and 1 at the end points (their definition is not important to show the “moreover” part). Then
$f,g: [0,1] \to [0,1]$
which attain both values 0 and 1 at the end points (their definition is not important to show the “moreover” part). Then
![]() $\rho ',\sigma '$
are defined as
$\rho ',\sigma '$
are defined as
Clearly,
![]() $\rho ',\sigma '$
take values in B as
$\rho ',\sigma '$
take values in B as
![]() $\rho ,\tilde {\rho },\sigma ,\tilde {\sigma }$
all do and
$\rho ,\tilde {\rho },\sigma ,\tilde {\sigma }$
all do and
![]() $(1-f),f,(1-g),g$
are in B. Now we define u.c.p. maps
$(1-f),f,(1-g),g$
are in B. Now we define u.c.p. maps
![]() $\tilde {\mu }_{\rho '},\tilde {\mu }_{\sigma '}: \mathcal {D} \otimes \mathcal {D} \to B_s$
by
$\tilde {\mu }_{\rho '},\tilde {\mu }_{\sigma '}: \mathcal {D} \otimes \mathcal {D} \to B_s$
by
Now by Choi–Effros, we can take u.c.p. lifts
![]() $\mu _{\rho '}$
and
$\mu _{\rho '}$
and
![]() $\mu _{\sigma '}$
of
$\mu _{\sigma '}$
of
![]() $\tilde {\mu }_{\rho '}$
and
$\tilde {\mu }_{\rho '}$
and
![]() $\mu _{\sigma '}$
, respectively. As the images of
$\mu _{\sigma '}$
, respectively. As the images of
![]() $\tilde {\mu }_{\rho '}$
and
$\tilde {\mu }_{\rho '}$
and
![]() $\mu _{\sigma '}$
lie in
$\mu _{\sigma '}$
lie in
![]() $B_s$
, the images of
$B_s$
, the images of
![]() $\mu _{\rho '}$
and
$\mu _{\rho '}$
and
![]() $\mu _{\sigma '}$
will lie in B.
$\mu _{\sigma '}$
will lie in B.
Lemma 4.23 Let A be a unital, separable
![]() $C([0,1])$
-algebra. Suppose
$C([0,1])$
-algebra. Suppose
![]() $\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq A$
are finite self-adjoint subsets with
$\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq A$
are finite self-adjoint subsets with
![]() $1_{\mathcal {D}} \in \mathcal {F}$
and
$1_{\mathcal {D}} \in \mathcal {F}$
and
![]() $\varepsilon> 0$
. There exists
$\varepsilon> 0$
. There exists
![]() $0 < \varepsilon ' < \varepsilon $
and a finite subset
$0 < \varepsilon ' < \varepsilon $
and a finite subset
![]() $\mathcal {F}' \supseteq \mathcal {F}$
such that if
$\mathcal {F}' \supseteq \mathcal {F}$
such that if
![]() $\rho ,\sigma : \mathcal {D} \to A$
are u.p.c. maps and
$\rho ,\sigma : \mathcal {D} \to A$
are u.p.c. maps and
![]() $0 \leq r < s < t \leq 1$
are points such that
$0 \leq r < s < t \leq 1$
are points such that
![]() $\rho $
is
$\rho $
is
![]() $(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
![]() $[r,s]$
,
$[r,s]$
,
![]() $\sigma $
is
$\sigma $
is
![]() $(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
![]() $[s,t]$
and
$[s,t]$
and
![]() $A_s$
is
$A_s$
is
![]() $\mathcal {D}$
-stable, then there is a u.c.p. map
$\mathcal {D}$
-stable, then there is a u.c.p. map
![]() $\psi : \mathcal {D} \to A$
which is
$\psi : \mathcal {D} \to A$
which is
![]() $(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
![]() $[r,t]$
.
$[r,t]$
.
Moreover, if
![]() $B \subseteq A$
is a unital inclusion of
$B \subseteq A$
is a unital inclusion of
![]() $C([0,1])$
-algebras such that
$C([0,1])$
-algebras such that
![]() $\rho (\mathcal {D}) \subseteq B$
,
$\rho (\mathcal {D}) \subseteq B$
,
![]() $\sigma (\mathcal {D}) \subseteq B$
and
$\sigma (\mathcal {D}) \subseteq B$
and
![]() $B_s \subseteq A_s$
is
$B_s \subseteq A_s$
is
![]() $\mathcal {D}$
-stable, then
$\mathcal {D}$
-stable, then
![]() $\psi (\mathcal {D}) \subseteq B$
.
$\psi (\mathcal {D}) \subseteq B$
.
Proof The first part is [Reference Hirshberg, Rørdam and Winter27, Lemma 4.5], except we have replaced c.c.p. maps with u.c.p. maps. One has to check that the resulting
![]() $\psi $
is unital, but this follows easily if
$\psi $
is unital, but this follows easily if
![]() $\rho $
and
$\rho $
and
![]() $\sigma $
are.
$\sigma $
are.
We outline the construction of
![]() $\psi $
to show unitality, as it will also be useful to show the “moreover” part, which is the only real addition. Let
$\psi $
to show unitality, as it will also be useful to show the “moreover” part, which is the only real addition. Let
![]() $u \in C([0,1],\mathcal {D} \otimes \mathcal {D})$
be a path of unitaries such that
$u \in C([0,1],\mathcal {D} \otimes \mathcal {D})$
be a path of unitaries such that
![]() $u_0 = 1_{\mathcal {D} \otimes \mathcal {D}}$
and
$u_0 = 1_{\mathcal {D} \otimes \mathcal {D}}$
and
We replace
![]() $\rho ,\sigma $
with
$\rho ,\sigma $
with
![]() $\rho ',\sigma '$
as in the above lemma and this yields u.c.p. maps
$\rho ',\sigma '$
as in the above lemma and this yields u.c.p. maps
![]() $\mu _\rho ,\mu _\sigma $
satisfying the hypotheses above for some interval
$\mu _\rho ,\mu _\sigma $
satisfying the hypotheses above for some interval
![]() $I \subseteq (r,t)$
with s in its interior. Define
$I \subseteq (r,t)$
with s in its interior. Define
by
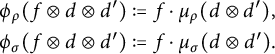 $$ \begin{align} \nonumber \phi_\rho(f \otimes d \otimes d') &:= f\cdot \mu_\rho(d \otimes d'), \\ \phi_\sigma(f \otimes d \otimes d') &:= f\cdot \mu_\sigma(d \otimes d'). \end{align} $$
$$ \begin{align} \nonumber \phi_\rho(f \otimes d \otimes d') &:= f\cdot \mu_\rho(d \otimes d'), \\ \phi_\sigma(f \otimes d \otimes d') &:= f\cdot \mu_\sigma(d \otimes d'). \end{align} $$
Note that these maps are unital. Take nonzero piece-wise linear functions
which sum to 1 (their specific form does not matter to show unitality of
![]() $\psi $
nor the “moreover” part) and
$\psi $
nor the “moreover” part) and
![]() $g_\rho ,g_\sigma : [0,1] \to [0,1]$
which sum to 1 (again, their specific form does not matter to show unitality of
$g_\rho ,g_\sigma : [0,1] \to [0,1]$
which sum to 1 (again, their specific form does not matter to show unitality of
![]() $\psi $
nor the “moreover” part). Define unitaries
$\psi $
nor the “moreover” part). Define unitaries
![]() $u_\rho ,u_\sigma \in C([0,1]) \otimes \mathcal {D} \otimes \mathcal {D} \simeq C([0,1],\mathcal {D} \otimes \mathcal {D})$
by
$u_\rho ,u_\sigma \in C([0,1]) \otimes \mathcal {D} \otimes \mathcal {D} \simeq C([0,1],\mathcal {D} \otimes \mathcal {D})$
by
Now define
![]() $\zeta _\rho ,\zeta _\sigma : \mathcal {D} \to A$
by
$\zeta _\rho ,\zeta _\sigma : \mathcal {D} \to A$
by
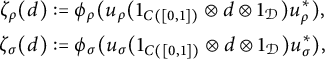 $$ \begin{align} \zeta_\rho(d) &:= \phi_\rho(u_\rho(1_{C([0,1])} \otimes d \otimes 1_{\mathcal{D}})u_\rho^*), \\ \nonumber \zeta_\sigma(d) &:= \phi_\sigma(u_\sigma(1_{C([0,1])} \otimes d \otimes 1_{\mathcal{D}})u_\sigma^*), \end{align} $$
$$ \begin{align} \zeta_\rho(d) &:= \phi_\rho(u_\rho(1_{C([0,1])} \otimes d \otimes 1_{\mathcal{D}})u_\rho^*), \\ \nonumber \zeta_\sigma(d) &:= \phi_\sigma(u_\sigma(1_{C([0,1])} \otimes d \otimes 1_{\mathcal{D}})u_\sigma^*), \end{align} $$
which are clearly unital. Finally, the map
![]() $\psi : \mathcal {D} \to A$
is defined by
$\psi : \mathcal {D} \to A$
is defined by
Clearly,
![]() $\psi $
is unital.
$\psi $
is unital.
Now for the “moreover” part. If
![]() $\rho (\mathcal {D}) \subseteq B$
and
$\rho (\mathcal {D}) \subseteq B$
and
![]() $\sigma (\mathcal {D}) \subseteq B$
, clearly the first and fourth terms in the definition of
$\sigma (\mathcal {D}) \subseteq B$
, clearly the first and fourth terms in the definition of
![]() $\psi $
will lie in B. So it suffices to show that
$\psi $
will lie in B. So it suffices to show that
![]() $\zeta _\rho (\mathcal {D}) \subseteq B$
and
$\zeta _\rho (\mathcal {D}) \subseteq B$
and
![]() $\zeta _\sigma (\mathcal {D}) \subseteq B$
, and for this it suffices to show that
$\zeta _\sigma (\mathcal {D}) \subseteq B$
, and for this it suffices to show that
![]() $\mu _\rho (\mathcal {D} \otimes \mathcal {D}) \subseteq B$
and
$\mu _\rho (\mathcal {D} \otimes \mathcal {D}) \subseteq B$
and
![]() $\mu _\sigma (\mathcal {D} \otimes \mathcal {D}) \subseteq B$
(since
$\mu _\sigma (\mathcal {D} \otimes \mathcal {D}) \subseteq B$
(since
![]() $h_1,h_2,h_3,h_4$
all lie in B). But this follows from the “moreover” part of the previous lemma.
$h_1,h_2,h_3,h_4$
all lie in B). But this follows from the “moreover” part of the previous lemma.
With this, we get the analog of [Reference Hirshberg and Winter28, Theorem 4.6], the proof being essentially the same as well, except we insist that the our u.c.p. maps commute with a prescribed finite subset of A.
Proposition 4.24 Let
![]() $\mathcal {D}$
be strongly self-absorbing, and X be a compact Hausdorff space with finite covering dimension. Suppose that
$\mathcal {D}$
be strongly self-absorbing, and X be a compact Hausdorff space with finite covering dimension. Suppose that
![]() $B \subseteq A$
is a unital inclusion of
$B \subseteq A$
is a unital inclusion of
![]() $C(X)$
-algebras. Then
$C(X)$
-algebras. Then
![]() $B_x \subseteq A_x$
is
$B_x \subseteq A_x$
is
![]() $\mathcal {D}$
-stable for all
$\mathcal {D}$
-stable for all
![]() $x \in X$
if and only if
$x \in X$
if and only if
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof As previously mentioned, if
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $\mathcal {D}$
-stable, then
$\mathcal {D}$
-stable, then
![]() $B_x \subseteq A_x$
is
$B_x \subseteq A_x$
is
![]() $\mathcal {D}$
-stable for all x.
$\mathcal {D}$
-stable for all x.
For the converse, the proof is essentially the same as [Reference Hirshberg, Rørdam and Winter27, Theorem 4.6]. Using the arguments there, one can simplify to the case where we can argue this for
![]() $C([0,1])$
-algebras (by using [Reference Hurewicz and Wallman29, Theorem V.3], which says that a compact space of dimension
$C([0,1])$
-algebras (by using [Reference Hurewicz and Wallman29, Theorem V.3], which says that a compact space of dimension
![]() $\leq n$
is homeomorphic to a subset of
$\leq n$
is homeomorphic to a subset of
![]() $[0,1]^{2n+1}$
, and then working component-wise). Now for
$[0,1]^{2n+1}$
, and then working component-wise). Now for
![]() $\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq A$
and
$\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq A$
and
![]() $\varepsilon> 0$
, let
$\varepsilon> 0$
, let
![]() $\mathcal {G}_x := \{a_x \mid a \in \mathcal {G}\}$
. Without loss of generality suppose that
$\mathcal {G}_x := \{a_x \mid a \in \mathcal {G}\}$
. Without loss of generality suppose that
![]() $\mathcal {F}^*=\mathcal {F},\mathcal {G}^*=\mathcal {G}$
and that
$\mathcal {F}^*=\mathcal {F},\mathcal {G}^*=\mathcal {G}$
and that
![]() $1_{\mathcal {D}} \in \mathcal {F}$
. Let
$1_{\mathcal {D}} \in \mathcal {F}$
. Let
![]() $\mathcal {F}',\varepsilon '$
be as in Lemma 4.23.
$\mathcal {F}',\varepsilon '$
be as in Lemma 4.23.
By
![]() $\mathcal {D}$
-stability of the inclusion
$\mathcal {D}$
-stability of the inclusion
![]() $B_x \subseteq A_x$
there are u.c.p.
$B_x \subseteq A_x$
there are u.c.p.
![]() $(\mathcal {F}',\varepsilon ',\mathcal {G}_x)$
-embeddings
$(\mathcal {F}',\varepsilon ',\mathcal {G}_x)$
-embeddings
![]() $\psi _x: \mathcal {D} \to B_x \subseteq A_x$
which lift by Choi–Effros to u.c.p. maps
$\psi _x: \mathcal {D} \to B_x \subseteq A_x$
which lift by Choi–Effros to u.c.p. maps
![]() $\psi _x': \mathcal {D} \to B$
. The norm is upper semi-continuous (Remark 4.20), and this yields intervals
$\psi _x': \mathcal {D} \to B$
. The norm is upper semi-continuous (Remark 4.20), and this yields intervals
![]() $I_x \subseteq [0,1]$
such that
$I_x \subseteq [0,1]$
such that
![]() $\psi _x'$
is
$\psi _x'$
is
![]() $(\mathcal {F}',\varepsilon ',\mathcal {G})$
-good for
$(\mathcal {F}',\varepsilon ',\mathcal {G})$
-good for
![]() $\overline {I_x}$
. Note that
$\overline {I_x}$
. Note that
![]() $\psi _x'$
being
$\psi _x'$
being
![]() $(\mathcal {F}',\varepsilon ',\mathcal {G})$
-good for the whole of
$(\mathcal {F}',\varepsilon ',\mathcal {G})$
-good for the whole of
![]() $I_x$
implies that it is
$I_x$
implies that it is
![]() $(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
![]() $\overline {I_x}$
. Compactness then allows us to split the interval as
$\overline {I_x}$
. Compactness then allows us to split the interval as
and to take
![]() $\psi _i: \mathcal {D} \to B$
u.c.p. which are
$\psi _i: \mathcal {D} \to B$
u.c.p. which are
![]() $(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
$(\mathcal {F},\varepsilon ,\mathcal {G};\mathcal {F}',\varepsilon ')$
-good for
![]() $[t_{i-1},t_i]$
for
$[t_{i-1},t_i]$
for
![]() $i=1,\dots ,n$
(
$i=1,\dots ,n$
(
![]() $\psi _i = \psi _x'$
for some
$\psi _i = \psi _x'$
for some
![]() $x \in [0,1]$
). Now by repeatedly using the gluing lemma (Lemma 4.23) to glue these maps together, we can find a u.c.p. map
$x \in [0,1]$
). Now by repeatedly using the gluing lemma (Lemma 4.23) to glue these maps together, we can find a u.c.p. map
![]() $\psi : \mathcal {D} \to B$
which is an
$\psi : \mathcal {D} \to B$
which is an
![]() $(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding.
$(\mathcal {F},\varepsilon ,\mathcal {G})$
-embedding.
5 Crossed products
In this section, we discuss how inclusions coming from noncommutative dynamics fit into the framework of tensorially absorbing inclusions. We will briefly discuss group actions
![]() $G \curvearrowright ^\alpha A$
with Rokhlin properties and consider the inclusion of a C*-algebra in its crossed product
$G \curvearrowright ^\alpha A$
with Rokhlin properties and consider the inclusion of a C*-algebra in its crossed product
![]() $A \subseteq A \rtimes _\alpha G$
, as well as the inclusion of the fixed point subalgebra of the action in the C*-algebra
$A \subseteq A \rtimes _\alpha G$
, as well as the inclusion of the fixed point subalgebra of the action in the C*-algebra
![]() $A^\alpha \subseteq A$
. We then discuss diagonal inclusions associated with certain group actions.
$A^\alpha \subseteq A$
. We then discuss diagonal inclusions associated with certain group actions.
This first result says that if we have an isomorphism
![]() $A \simeq A \otimes \mathcal {D}$
which is G-equivariant with respect to an action point-wise fixing the right tensor factor, up to a 1-cocycle, then the corresponding inclusion
$A \simeq A \otimes \mathcal {D}$
which is G-equivariant with respect to an action point-wise fixing the right tensor factor, up to a 1-cocycle, then the corresponding inclusion
![]() $A \subseteq A \rtimes _{r,\alpha } G$
is
$A \subseteq A \rtimes _{r,\alpha } G$
is
![]() $\mathcal {D}$
-stable. Recall that if
$\mathcal {D}$
-stable. Recall that if
![]() $\beta : G \curvearrowright B$
is an action of a countable discrete group on a unital C*-algebra B, then a
$\beta : G \curvearrowright B$
is an action of a countable discrete group on a unital C*-algebra B, then a
![]() $\beta $
-1-cocycle is a map
$\beta $
-1-cocycle is a map
![]() $u: G \to U(B)$
satisfying the cocycle identify:
$u: G \to U(B)$
satisfying the cocycle identify:
If
![]() $(A,\alpha ),(B,\beta )$
are G-C*-algebras, we say that they are cocycle conjugate, denoted
$(A,\alpha ),(B,\beta )$
are G-C*-algebras, we say that they are cocycle conjugate, denoted
![]() $(A,\alpha ) \simeq _{\text {c.c.}} (B,\beta )$
, if there are an isomorphism
$(A,\alpha ) \simeq _{\text {c.c.}} (B,\beta )$
, if there are an isomorphism
![]() $\phi : A \simeq B$
and a
$\phi : A \simeq B$
and a
![]() $\beta $
-1-cocycle
$\beta $
-1-cocycle
![]() $u: G \to U(B)$
such that
$u: G \to U(B)$
such that
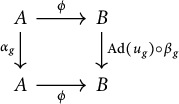
commutes for all
![]() $g \in G$
. Conjugacy is usually too strong a notion of equivalence, whereas cocycle conjugacy has allowed for quite deep classification of automorphisms. For example, this notion has been used for classifying automorphisms of von Neumann factors [Reference Connes11, Reference Connes12, Reference Connes14, Reference Kawahigashi, Sutherland and Takesaki33, Reference Sutherland and Takesaki57].
$g \in G$
. Conjugacy is usually too strong a notion of equivalence, whereas cocycle conjugacy has allowed for quite deep classification of automorphisms. For example, this notion has been used for classifying automorphisms of von Neumann factors [Reference Connes11, Reference Connes12, Reference Connes14, Reference Kawahigashi, Sutherland and Takesaki33, Reference Sutherland and Takesaki57].
Proposition 5.1 Let
![]() $G \curvearrowright ^\alpha A$
be an action of a countable discrete group on a unital separable C*-algebra. Suppose that
$G \curvearrowright ^\alpha A$
be an action of a countable discrete group on a unital separable C*-algebra. Suppose that
![]() $\alpha \simeq _{\text {c.c.}} \alpha \otimes \text {id}_{\mathcal {D}}$
. That is, there is an
$\alpha \simeq _{\text {c.c.}} \alpha \otimes \text {id}_{\mathcal {D}}$
. That is, there is an
![]() $\alpha \otimes \text {id}_{\mathcal {D}}$
-1-cocycle
$\alpha \otimes \text {id}_{\mathcal {D}}$
-1-cocycle
![]() $u: G \to U(A \otimes \mathcal {D})$
and an isomorphism
$u: G \to U(A \otimes \mathcal {D})$
and an isomorphism
![]() $\Phi : A \simeq A \otimes \mathcal {D}$
such that
$\Phi : A \simeq A \otimes \mathcal {D}$
such that

commutes for all
![]() $g \in G$
. Then
$g \in G$
. Then
![]() $A \subseteq A \rtimes _{r,\alpha } G$
is
$A \subseteq A \rtimes _{r,\alpha } G$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof Let
![]() $\psi : \mathcal {D} \simeq \mathcal {D}^{\otimes \infty }$
, and let
$\psi : \mathcal {D} \simeq \mathcal {D}^{\otimes \infty }$
, and let
![]() $\phi _n: \mathcal {D} \to \mathcal {D}^{\otimes \infty }$
be the nth factor embedding:
$\phi _n: \mathcal {D} \to \mathcal {D}^{\otimes \infty }$
be the nth factor embedding:
We claim that
![]() $\xi (d) := (\Phi ^{-1}(1_A \otimes \psi ^{-1} \circ \phi _n(d)))_n: \mathcal {D} \to A_\omega $
is an embedding such that
$\xi (d) := (\Phi ^{-1}(1_A \otimes \psi ^{-1} \circ \phi _n(d)))_n: \mathcal {D} \to A_\omega $
is an embedding such that
![]() $\xi (\mathcal {D}) \subseteq A_\omega \cap A'$
and
$\xi (\mathcal {D}) \subseteq A_\omega \cap A'$
and
![]() $(\alpha _g)_\omega \circ \xi = \xi $
for all
$(\alpha _g)_\omega \circ \xi = \xi $
for all
![]() $g \in G$
– that is,
$g \in G$
– that is,
![]() $\xi $
is an embedding
$\xi $
is an embedding
![]() $\mathcal {D} \hookrightarrow A_\omega \cap (A \rtimes _{r,\alpha } G)'$
. The first part of the claim is obvious, so we prove the second. We have
$\mathcal {D} \hookrightarrow A_\omega \cap (A \rtimes _{r,\alpha } G)'$
. The first part of the claim is obvious, so we prove the second. We have
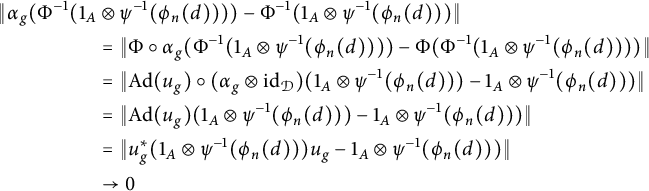 $$ \begin{align} \nonumber \|\alpha_g(\Phi^{-1}(1_A &\otimes \psi^{-1}(\phi_n(d)))) - \Phi^{-1}(1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ \nonumber &= \|\Phi \circ \alpha_g(\Phi^{-1}(1_A \otimes \psi^{-1}(\phi_n(d)))) - \Phi(\Phi^{-1}(1_A \otimes \psi^{-1}(\phi_n(d))))\| \\ \nonumber &= \|\text{Ad}(u_g)\circ (\alpha_g \otimes \text{id}_{\mathcal{D}})(1_A \otimes \psi^{-1}(\phi_n(d))) - 1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ \nonumber &= \|\text{Ad}(u_g)(1_A \otimes \psi^{-1}(\phi_n(d))) - 1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ \nonumber &= \|u_g^*(1_A \otimes \psi^{-1}(\phi_n(d)))u_g - 1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ &\to 0 \end{align} $$
$$ \begin{align} \nonumber \|\alpha_g(\Phi^{-1}(1_A &\otimes \psi^{-1}(\phi_n(d)))) - \Phi^{-1}(1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ \nonumber &= \|\Phi \circ \alpha_g(\Phi^{-1}(1_A \otimes \psi^{-1}(\phi_n(d)))) - \Phi(\Phi^{-1}(1_A \otimes \psi^{-1}(\phi_n(d))))\| \\ \nonumber &= \|\text{Ad}(u_g)\circ (\alpha_g \otimes \text{id}_{\mathcal{D}})(1_A \otimes \psi^{-1}(\phi_n(d))) - 1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ \nonumber &= \|\text{Ad}(u_g)(1_A \otimes \psi^{-1}(\phi_n(d))) - 1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ \nonumber &= \|u_g^*(1_A \otimes \psi^{-1}(\phi_n(d)))u_g - 1_A \otimes \psi^{-1}(\phi_n(d)))\| \\ &\to 0 \end{align} $$
since
![]() $(1_A \otimes \psi ^{-1}(\phi _n(d)))_n$
is asymptotically central in
$(1_A \otimes \psi ^{-1}(\phi _n(d)))_n$
is asymptotically central in
![]() $A \otimes \mathcal {D}$
.
$A \otimes \mathcal {D}$
.
Actions satisfying the hypotheses of Proposition 5.1 are said to be equivariantly
![]() $\mathcal {D}$
-absorbing, up to cocycle conjugacy. These actions are fairly common and there are a wide range of positive results (see, for example, [Reference Suzuki58, Reference Szabó59]).
$\mathcal {D}$
-absorbing, up to cocycle conjugacy. These actions are fairly common and there are a wide range of positive results (see, for example, [Reference Suzuki58, Reference Szabó59]).
The next lemma of note is the following.
Lemma 5.2 Suppose that
![]() $G \curvearrowright ^\alpha A$
is an action of a finite group on a unital separable C*-algebra A such that
$G \curvearrowright ^\alpha A$
is an action of a finite group on a unital separable C*-algebra A such that
![]() $A \subseteq A \rtimes _\alpha G$
is
$A \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {D}$
-stable. Then
$\mathcal {D}$
-stable. Then
![]() $A^\alpha \subseteq A \rtimes _\alpha G$
is
$A^\alpha \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {D}$
-stable. In particular, if
$\mathcal {D}$
-stable. In particular, if
![]() $A \subseteq A\rtimes _\alpha G$
is
$A \subseteq A\rtimes _\alpha G$
is
![]() $\mathcal {D}$
-stable, then
$\mathcal {D}$
-stable, then
![]() $C \simeq C \otimes \mathcal {D}$
whenever
$C \simeq C \otimes \mathcal {D}$
whenever
![]() $A^\alpha \subseteq C \subseteq A \rtimes _\alpha \mathcal {D}$
.
$A^\alpha \subseteq C \subseteq A \rtimes _\alpha \mathcal {D}$
.
Proof For an element
![]() $(x_n)_{n \in \mathbb {N}} \in A_\omega \cap (A \rtimes _\alpha G)'$
, an easy averaging argument shows that
$(x_n)_{n \in \mathbb {N}} \in A_\omega \cap (A \rtimes _\alpha G)'$
, an easy averaging argument shows that
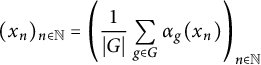 $$ \begin{align} (x_n)_{n \in \mathbb{N}} = \left(\frac{1}{|G|}\sum_{g \in G} \alpha_g(x_n)\right)_{n \in \mathbb{N}} \end{align} $$
$$ \begin{align} (x_n)_{n \in \mathbb{N}} = \left(\frac{1}{|G|}\sum_{g \in G} \alpha_g(x_n)\right)_{n \in \mathbb{N}} \end{align} $$
in
![]() $A_\omega $
, and the right is clearly point-wise fixed by
$A_\omega $
, and the right is clearly point-wise fixed by
![]() $\alpha _g$
for all
$\alpha _g$
for all
![]() $g \in G$
. So
$g \in G$
. So
![]() $A_\omega \cap (A \rtimes _\alpha G)'$
is actually equal to
$A_\omega \cap (A \rtimes _\alpha G)'$
is actually equal to
![]() $(A^\alpha )_\omega \cap (A \rtimes _\alpha G)'$
, and the existence of a unital embedding of
$(A^\alpha )_\omega \cap (A \rtimes _\alpha G)'$
, and the existence of a unital embedding of
![]() $\mathcal {D}$
in
$\mathcal {D}$
in
![]() $A_\omega \cap (A \rtimes _\alpha G)'$
is in fact equivalent to the existence of a unital embedding of
$A_\omega \cap (A \rtimes _\alpha G)'$
is in fact equivalent to the existence of a unital embedding of
![]() $\mathcal {D}$
into
$\mathcal {D}$
into
![]() $(A^\alpha )_\omega \cap (A \rtimes _\alpha G)'$
. The result follows.
$(A^\alpha )_\omega \cap (A \rtimes _\alpha G)'$
. The result follows.
The Galois correspondence of Izumi [Reference Izumi30] yields the following.
Theorem 5.3 Let A be a unital, simple, separable C*-algebra, and let
![]() $G \curvearrowright ^\alpha A$
be an action of a finite group by outer automorphisms. If
$G \curvearrowright ^\alpha A$
be an action of a finite group by outer automorphisms. If
![]() $A \subseteq A \rtimes _\alpha \mathcal {D}$
is
$A \subseteq A \rtimes _\alpha \mathcal {D}$
is
![]() $\mathcal {D}$
-stable, then there exists an isomorphism
$\mathcal {D}$
-stable, then there exists an isomorphism
![]() $\Phi : A \rtimes _\alpha G \simeq (A \rtimes _\alpha G) \otimes \mathcal {D}$
such that whenever C is a unital C*-algebra satisfying either:
$\Phi : A \rtimes _\alpha G \simeq (A \rtimes _\alpha G) \otimes \mathcal {D}$
such that whenever C is a unital C*-algebra satisfying either:
-
(1)
 $A^\alpha \subseteq C \subseteq A$
or
$A^\alpha \subseteq C \subseteq A$
or -
(2)
 $A \subseteq C \subseteq A \rtimes _\alpha G$
,
$A \subseteq C \subseteq A \rtimes _\alpha G$
,
we have
![]() $\Phi (C) = C \otimes \mathcal {D}$
.
$\Phi (C) = C \otimes \mathcal {D}$
.
Proof Applying [Reference Izumi30, Corollary 6.6] gives the following two correspondences:
-
(1) there is a one-to-one correspondence between subgroups of G with intermediate C*-algebras
 $A^\alpha \subseteq C \subseteq A$
given by (5.7)
$A^\alpha \subseteq C \subseteq A$
given by (5.7) $$ \begin{align} H \leftrightarrow A^{\alpha_H}; \end{align} $$
$$ \begin{align} H \leftrightarrow A^{\alpha_H}; \end{align} $$
-
(2) there is a one-to-one correspondence between subgroups of G and intermediate C*-algebras
 $A \subseteq C \subseteq A \rtimes _\alpha G$
given by (5.8)
$A \subseteq C \subseteq A \rtimes _\alpha G$
given by (5.8) $$ \begin{align} H \leftrightarrow A \rtimes_{\alpha|_H} H. \end{align} $$
$$ \begin{align} H \leftrightarrow A \rtimes_{\alpha|_H} H. \end{align} $$
In particular, there are only finitely many C*-algebras C between either
![]() $A^\alpha \subseteq A$
or
$A^\alpha \subseteq A$
or
![]() $A \subseteq A \rtimes _\alpha G$
. As all such lie between the
$A \subseteq A \rtimes _\alpha G$
. As all such lie between the
![]() $\mathcal {D}$
-stable inclusion
$\mathcal {D}$
-stable inclusion
![]() $A^ \alpha \subseteq A \rtimes G$
, Theorem 4.8 yields the desired isomorphism.
$A^ \alpha \subseteq A \rtimes G$
, Theorem 4.8 yields the desired isomorphism.
5.1 (Tracial) Rokhlin properties
Here, we will restrict ourselves to finite groups for simplicity, although many results hold more generally (see [Reference Gardella and Hirshberg23, Reference Hirshberg and Orovitz26, Reference Hirshberg and Winter28]).
Definition 5.1 Let A be a unital, separable C*-algebra. We say that a finite group action
![]() $G \curvearrowright ^\alpha A$
has the Rokhlin property if there are pairwise orthogonal projections
$G \curvearrowright ^\alpha A$
has the Rokhlin property if there are pairwise orthogonal projections
![]() $(p_g)_{g \in G} \subseteq A_\omega \cap A'$
summing to
$(p_g)_{g \in G} \subseteq A_\omega \cap A'$
summing to
![]() $1_{A_\omega }$
such that
$1_{A_\omega }$
such that
![]() $(\alpha _g)_\omega (p_h) = p_{gh}$
for
$(\alpha _g)_\omega (p_h) = p_{gh}$
for
![]() $g,h \in G$
.
$g,h \in G$
.
Proposition 5.4 Let A be a unital, separable
![]() $\mathcal {D}$
-stable C*-algebra. If
$\mathcal {D}$
-stable C*-algebra. If
![]() $G \curvearrowright ^\alpha A$
is an action of a finite group with the Rokhlin property, then
$G \curvearrowright ^\alpha A$
is an action of a finite group with the Rokhlin property, then
![]() $A^\alpha \subseteq A \rtimes _\alpha G$
is
$A^\alpha \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof This follows from [Reference Hirshberg and Winter28, Theorem 3.3], together with Lemma 5.2.
Definition 5.2 Let A be a unital, separable C*-algebra. We say that a finite group action
![]() $G \curvearrowright ^\alpha A$
has the weak tracial Rokhlin property if for all
$G \curvearrowright ^\alpha A$
has the weak tracial Rokhlin property if for all
![]() $\mathcal {F} \subseteq A$
finite,
$\mathcal {F} \subseteq A$
finite,
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $0 \neq a \in A_+$
, there are pairwise orthogonal normalized positive contractions
$0 \neq a \in A_+$
, there are pairwise orthogonal normalized positive contractions
![]() $(e_g)_{g \in G} \subseteq A$
such that:
$(e_g)_{g \in G} \subseteq A$
such that:
-
(1)
 $1 - \sum _g e_g \precsim a$
;Footnote
4
$1 - \sum _g e_g \precsim a$
;Footnote
4
-
(2)
 $[e_g,x] \approx _\varepsilon 0$
for all
$[e_g,x] \approx _\varepsilon 0$
for all
 $x \in \mathcal {F}, g \in G$
;
$x \in \mathcal {F}, g \in G$
; -
(3)
 $\alpha _g(e_h) \approx _\varepsilon e_{gh}$
for all
$\alpha _g(e_h) \approx _\varepsilon e_{gh}$
for all
 $g,h \in G$
.
$g,h \in G$
.
It is easy to see that a Rokhlin action is outer, since the central projections must commute with any unitary. The fact that weak tracial Rokhlin actions are outer is [Reference Hirshberg and Orovitz26, Proposition 5.3].
Proposition 5.5 Let A be a unital, simple, separable, nuclear,
![]() $\mathcal {Z}$
-stable C*-algebra. If
$\mathcal {Z}$
-stable C*-algebra. If
![]() $G \curvearrowright ^\alpha A$
is an action of a finite group with the weak tracial Rokhlin property, then
$G \curvearrowright ^\alpha A$
is an action of a finite group with the weak tracial Rokhlin property, then
![]() $A^\alpha \subseteq A \rtimes _\alpha G$
is
$A^\alpha \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {Z}$
-stable.
$\mathcal {Z}$
-stable.
Proof Let
![]() $k \in \mathbb {N}$
. By [Reference Hirshberg and Orovitz26, Theorem 5.6]
$k \in \mathbb {N}$
. By [Reference Hirshberg and Orovitz26, Theorem 5.6]
![]() $A \rtimes _\alpha G$
is tracially
$A \rtimes _\alpha G$
is tracially
![]() $\mathcal {Z}$
-absorbing, meaning there are tracially large (in the sense of [Reference Toms, White and Winter65]) c.p.c. order zero maps
$\mathcal {Z}$
-absorbing, meaning there are tracially large (in the sense of [Reference Toms, White and Winter65]) c.p.c. order zero maps
![]() $\phi : M_k \to (A \rtimes _\alpha G)_\omega \cap (A \rtimes _\alpha G)'$
, which can be chosen to be c.p.c. order zero maps
$\phi : M_k \to (A \rtimes _\alpha G)_\omega \cap (A \rtimes _\alpha G)'$
, which can be chosen to be c.p.c. order zero maps
![]() $\phi : M_k \to A_\omega \cap (A \rtimes _\alpha G)'$
by the proof of [Reference Hirshberg and Orovitz26, Lemma 5.5]. These tracially large c.p.c. order zero maps yield sequences of positive contractions
$\phi : M_k \to A_\omega \cap (A \rtimes _\alpha G)'$
by the proof of [Reference Hirshberg and Orovitz26, Lemma 5.5]. These tracially large c.p.c. order zero maps yield sequences of positive contractions
![]() $c_1 = (c_{1n}),\dots ,c_k = (c_{kn}) \in A_\omega \cap (A \rtimes _\alpha G)'$
such that if
$c_1 = (c_{1n}),\dots ,c_k = (c_{kn}) \in A_\omega \cap (A \rtimes _\alpha G)'$
such that if
![]() $(e_n)_{n \in \mathbb {N}} = e := 1 - \sum _i c_i^*c_i$
, we have
$(e_n)_{n \in \mathbb {N}} = e := 1 - \sum _i c_i^*c_i$
, we have
and
![]() $c_ic_j^* = \delta _{ij}c_1^2$
. By [Reference Gardella and Hirshberg23, Proposition 4.11] (which is much more general, applicable to all countable amenable groups),
$c_ic_j^* = \delta _{ij}c_1^2$
. By [Reference Gardella and Hirshberg23, Proposition 4.11] (which is much more general, applicable to all countable amenable groups),
![]() $A \subseteq A \rtimes _\alpha G$
has equivariant property (SI) since A has property (SI).Footnote
5
Consequently, there exists
$A \subseteq A \rtimes _\alpha G$
has equivariant property (SI) since A has property (SI).Footnote
5
Consequently, there exists
![]() $s \in A_\omega \cap (A \rtimes _\alpha G)'$
such that
$s \in A_\omega \cap (A \rtimes _\alpha G)'$
such that
![]() $s^*s = 1 - \sum _i c_i^*c_i$
and
$s^*s = 1 - \sum _i c_i^*c_i$
and
![]() $c_1s = s$
. Altogether,
$c_1s = s$
. Altogether,
-
•
 $c_1 \geq 0$
;
$c_1 \geq 0$
; -
•
 $c_ic_j^* = \delta _{ij}c_1^2$
;
$c_ic_j^* = \delta _{ij}c_1^2$
; -
•
 $s^*s + \sum _i c_i^*c_i = 1$
;
$s^*s + \sum _i c_i^*c_i = 1$
; -
•
 $c_1s = s$
.
$c_1s = s$
.
As mentioned in the proof of
![]() $(iv) \Rightarrow (i)$
of [Reference Matui and Sato39],
$(iv) \Rightarrow (i)$
of [Reference Matui and Sato39],
![]() $\mathcal {Z}_{n,n+1}$
is the universal C*-algebra generated by
$\mathcal {Z}_{n,n+1}$
is the universal C*-algebra generated by
![]() $n+1$
elements satisfying the above four relations (see [Reference Rørdam and Winter52, Proposition 5.1] and [Reference Sato54, Proposition 2.1]), and consequently we have a unital *-homomorphism
$n+1$
elements satisfying the above four relations (see [Reference Rørdam and Winter52, Proposition 5.1] and [Reference Sato54, Proposition 2.1]), and consequently we have a unital *-homomorphism
![]() $\mathcal {Z}_{n,n+1} \to A_\omega \cap (A \rtimes _\alpha G)'$
. Therefore
$\mathcal {Z}_{n,n+1} \to A_\omega \cap (A \rtimes _\alpha G)'$
. Therefore
![]() $\mathcal {Z} \hookrightarrow A_\omega \cap (A \rtimes _\alpha G)'$
, giving that the desired inclusion is
$\mathcal {Z} \hookrightarrow A_\omega \cap (A \rtimes _\alpha G)'$
, giving that the desired inclusion is
![]() $\mathcal {Z}$
-stable by Lemma 5.2.
$\mathcal {Z}$
-stable by Lemma 5.2.
Corollary 5.6 Let A be a unital, simple, separable, nuclear,
![]() $\mathcal {Z}$
-stable C*-algebra, and let
$\mathcal {Z}$
-stable C*-algebra, and let
![]() $G \curvearrowright ^\alpha A$
be an action of a finite group with the weak tracial Rokhlin property. There exists an isomorphism
$G \curvearrowright ^\alpha A$
be an action of a finite group with the weak tracial Rokhlin property. There exists an isomorphism
![]() $\Phi : A \rtimes _\alpha G \simeq (A \rtimes _\alpha G) \otimes \mathcal {Z}$
such that whenever C is a unital C*-algebra satisfying either:
$\Phi : A \rtimes _\alpha G \simeq (A \rtimes _\alpha G) \otimes \mathcal {Z}$
such that whenever C is a unital C*-algebra satisfying either:
-
(1)
 $A^\alpha \subseteq C \subseteq A$
or
$A^\alpha \subseteq C \subseteq A$
or -
(2)
 $A \subseteq C \subseteq A \rtimes _\alpha G$
,
$A \subseteq C \subseteq A \rtimes _\alpha G$
,
we have
![]() $\Phi (C) = C \otimes \mathcal {Z}$
.
$\Phi (C) = C \otimes \mathcal {Z}$
.
5.2 The diagonal inclusion associated with a group action
In the von Neumann setting, a certain diagonal inclusion associated with several automorphisms was considered in [Reference Burstein7, Reference Kawamuro34, Reference Popa43], and they play a role in subfactor theory. Here, we consider a unital C*-algebraic inclusion of the same form.
Definition 5.3 Let A be a C*-algebra,
![]() $\alpha _1,\dots ,\alpha _n \in \operatorname {\mathrm {Aut}}(A)$
. The diagonal inclusion associated with
$\alpha _1,\dots ,\alpha _n \in \operatorname {\mathrm {Aut}}(A)$
. The diagonal inclusion associated with
![]() $\alpha _1,\dots ,\alpha _n$
is
$\alpha _1,\dots ,\alpha _n$
is
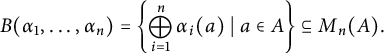 $$ \begin{align} B(\alpha_1,\dots,\alpha_n) = \left\{\bigoplus_{i=1}^n \alpha_i(a) \mid a \in A \right\} \subseteq M_n(A). \end{align} $$
$$ \begin{align} B(\alpha_1,\dots,\alpha_n) = \left\{\bigoplus_{i=1}^n \alpha_i(a) \mid a \in A \right\} \subseteq M_n(A). \end{align} $$
If
![]() $G \curvearrowright ^\alpha A$
is an action of a finite group, we write
$G \curvearrowright ^\alpha A$
is an action of a finite group, we write
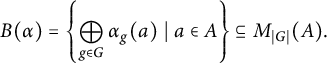 $$ \begin{align} B(\alpha) = \left\{\bigoplus_{g \in G} \alpha_g(a) \mid a \in A\right\} \subseteq M_{|G|}(A). \end{align} $$
$$ \begin{align} B(\alpha) = \left\{\bigoplus_{g \in G} \alpha_g(a) \mid a \in A\right\} \subseteq M_{|G|}(A). \end{align} $$
We note that a diagonal
![]() $B(\alpha ) \subseteq M_{|G|}(A)$
is unique up to unitary conjugation (by permutation unitaries). As
$B(\alpha ) \subseteq M_{|G|}(A)$
is unique up to unitary conjugation (by permutation unitaries). As
![]() $\mathcal {D}$
-stability of an inclusion is preserved under unitary conjugation, there is no ambiguity in speaking of
$\mathcal {D}$
-stability of an inclusion is preserved under unitary conjugation, there is no ambiguity in speaking of
![]() $\mathcal {D}$
-stability of the inclusion
$\mathcal {D}$
-stability of the inclusion
![]() $B(\alpha ) \subseteq M_{|G|}(A)$
.
$B(\alpha ) \subseteq M_{|G|}(A)$
.
Proposition 5.7 Let
![]() $G \curvearrowright ^\alpha A$
be an action of a countable discrete group on a unital, separable C*-algebra. If
$G \curvearrowright ^\alpha A$
be an action of a countable discrete group on a unital, separable C*-algebra. If
![]() $G = \langle g_1,\dots ,g_n\rangle $
, then
$G = \langle g_1,\dots ,g_n\rangle $
, then
![]() $A \subseteq A \rtimes _\alpha G$
is
$A \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {D}$
-stable if and only if
$\mathcal {D}$
-stable if and only if
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
Proof First, suppose that
![]() $A \subseteq A \rtimes _\alpha G$
is
$A \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {D}$
-stable. Let
$\mathcal {D}$
-stable. Let
![]() $\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq M_{n+1}(A)$
be finite and
$\mathcal {F} \subseteq \mathcal {D}, \mathcal {G} \subseteq M_{n+1}(A)$
be finite and
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $\mathcal {G}' \subseteq A$
be the set of matrix coefficients of elements of
$\mathcal {G}' \subseteq A$
be the set of matrix coefficients of elements of
![]() $\mathcal {G}$
, together with the identity of A, and let
$\mathcal {G}$
, together with the identity of A, and let
![]() $L := \max \{1,\max _{a \in \mathcal {G}'}\|a\|\}$
. Relabel
$L := \max \{1,\max _{a \in \mathcal {G}'}\|a\|\}$
. Relabel
![]() $\text {id}_A,\alpha _{g_1},\dots ,\alpha _{g_n}$
as
$\text {id}_A,\alpha _{g_1},\dots ,\alpha _{g_n}$
as
![]() $\alpha _1,\dots ,\alpha _{n+1}$
. Let
$\alpha _1,\dots ,\alpha _{n+1}$
. Let
and let
![]() $\psi : \mathcal {D} \to A$
be a u.c.p.
$\psi : \mathcal {D} \to A$
be a u.c.p.
![]() $(\mathcal {F},\delta ,\mathcal {G}' \cup \{u_{g_i}\}_{i=1}^n)$
-embedding, where
$(\mathcal {F},\delta ,\mathcal {G}' \cup \{u_{g_i}\}_{i=1}^n)$
-embedding, where
![]() $(u_g)$
are the implementing unitaries for
$(u_g)$
are the implementing unitaries for
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\phi : D \to B(\alpha ) \subseteq M_{|G|}(A)$
be given by
$\phi : D \to B(\alpha ) \subseteq M_{|G|}(A)$
be given by
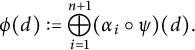 $$ \begin{align} \phi(d) := \bigoplus_{i=1}^{n+1} (\alpha_i \circ \psi)(d). \end{align} $$
$$ \begin{align} \phi(d) := \bigoplus_{i=1}^{n+1} (\alpha_i \circ \psi)(d). \end{align} $$
Clearly,
![]() $\phi $
will be
$\phi $
will be
![]() $(\mathcal {F},\delta )$
-multiplicative since each component is the composition of a *-homomorphism (which are contractive) with a map which is
$(\mathcal {F},\delta )$
-multiplicative since each component is the composition of a *-homomorphism (which are contractive) with a map which is
![]() $(\mathcal {F},\delta )$
-multiplicative. Now for
$(\mathcal {F},\delta )$
-multiplicative. Now for
![]() $d \in \mathcal {F}$
and
$d \in \mathcal {F}$
and
![]() $a = (a_{ij}) \in \mathcal {G}$
, we have
$a = (a_{ij}) \in \mathcal {G}$
, we have
 $$ \begin{align} \nonumber \|[\phi(d),(a_{ij})]\| &\leq \sum_{i,j=1}^{n+1}\|\alpha_i(\psi(d))a_{ij} - a_{ij}\alpha_j(\psi(d))\| \\ \nonumber &\leq \sum_{i,j=1}^{n+1}\| \alpha_i(\psi(d))a_{ij} - \psi(d)a_{ij}\| \\ &\ \ \ + \|\psi(d)a_{ij} - a_{ij}\psi(d)\| + \|a_{ij}\psi(d) - a_{ij}\alpha_j(\psi(d))\| \\ \nonumber &\leq \sum_{i,j=1}^{n+1}\|a_{ij}\|\left(\|\alpha_i(\psi(d)) - \psi(d)\| + \|\psi(d) - \alpha_j(\psi(d))\|\right) \\ \nonumber &\ \ \ + \|[\psi(d),a_{i,j}]\| \\ \nonumber &< (n+1)^2(2L(\delta + \delta) + \delta) \\ \nonumber &= (n+1)^2(4L+1)\delta = \varepsilon. \end{align} $$
$$ \begin{align} \nonumber \|[\phi(d),(a_{ij})]\| &\leq \sum_{i,j=1}^{n+1}\|\alpha_i(\psi(d))a_{ij} - a_{ij}\alpha_j(\psi(d))\| \\ \nonumber &\leq \sum_{i,j=1}^{n+1}\| \alpha_i(\psi(d))a_{ij} - \psi(d)a_{ij}\| \\ &\ \ \ + \|\psi(d)a_{ij} - a_{ij}\psi(d)\| + \|a_{ij}\psi(d) - a_{ij}\alpha_j(\psi(d))\| \\ \nonumber &\leq \sum_{i,j=1}^{n+1}\|a_{ij}\|\left(\|\alpha_i(\psi(d)) - \psi(d)\| + \|\psi(d) - \alpha_j(\psi(d))\|\right) \\ \nonumber &\ \ \ + \|[\psi(d),a_{i,j}]\| \\ \nonumber &< (n+1)^2(2L(\delta + \delta) + \delta) \\ \nonumber &= (n+1)^2(4L+1)\delta = \varepsilon. \end{align} $$
Conversely, if the associated diagonal inclusion is
![]() $\mathcal {D}$
-stable, we note that if
$\mathcal {D}$
-stable, we note that if
![]() $(x_k) \subseteq B(\text {id}_A,\alpha _{g_1},\dots ,\alpha _{g_n})$
is central for
$(x_k) \subseteq B(\text {id}_A,\alpha _{g_1},\dots ,\alpha _{g_n})$
is central for
![]() $M_{n+1}(A)$
, writing
$M_{n+1}(A)$
, writing
 $$ \begin{align} x_k = \bigoplus_{i=1}^{n+1}\alpha_i(a_k) \end{align} $$
$$ \begin{align} x_k = \bigoplus_{i=1}^{n+1}\alpha_i(a_k) \end{align} $$
yields that
![]() $(a_k) \subseteq A$
is central for A and is asymptotically fixed by
$(a_k) \subseteq A$
is central for A and is asymptotically fixed by
![]() $\alpha _{g_i}, i=1,\dots ,n$
. In particular, if
$\alpha _{g_i}, i=1,\dots ,n$
. In particular, if
![]() $\mathcal {D} \hookrightarrow B(\text {id}_A,\alpha _{g_1},\dots ,\alpha _{g_n})_\omega \cap (M_{n+1}(A))'$
, then
$\mathcal {D} \hookrightarrow B(\text {id}_A,\alpha _{g_1},\dots ,\alpha _{g_n})_\omega \cap (M_{n+1}(A))'$
, then
![]() $\mathcal {D} \hookrightarrow A_\omega \cap (A \rtimes _\alpha G)'$
.
$\mathcal {D} \hookrightarrow A_\omega \cap (A \rtimes _\alpha G)'$
.
Corollary 5.8 Let
![]() $G \curvearrowright ^\alpha A$
be an action of a finite group on a unital, separable C*-algebra. Then
$G \curvearrowright ^\alpha A$
be an action of a finite group on a unital, separable C*-algebra. Then
![]() $A \subseteq A \rtimes _\alpha G$
is
$A \subseteq A \rtimes _\alpha G$
is
![]() $\mathcal {D}$
-stable if and only if
$\mathcal {D}$
-stable if and only if
is
![]() $\mathcal {D}$
-stable.
$\mathcal {D}$
-stable.
6 Examples
6.1 Non-examples
We first start with some non-examples. Villadsen’s C*-algebras with perforation will be useful (see [Reference Toms and Winter68] for good exposition). Let
![]() $\mathcal {Q} = \bigotimes _n M_n$
denote the universal UHF C*-algebra.
$\mathcal {Q} = \bigotimes _n M_n$
denote the universal UHF C*-algebra.
Theorem 6.1 ([Reference Toms64, Reference Villadsen69])
There exists a unital, simple, separable, nuclear C*-algebra C satisfying the UCT such that
![]() $C \not \simeq C \otimes \mathcal {Z}$
and C contains the universal UHF algebra unitally. Moreover, C is tracial and can be chosen to be AH with
$C \not \simeq C \otimes \mathcal {Z}$
and C contains the universal UHF algebra unitally. Moreover, C is tracial and can be chosen to be AH with
Corollary 6.2 There exists an embedding
![]() $\mathcal {Q} \hookrightarrow \mathcal {Q}$
which is not
$\mathcal {Q} \hookrightarrow \mathcal {Q}$
which is not
![]() $\mathcal {Z}$
-stable. In particular, it is not
$\mathcal {Z}$
-stable. In particular, it is not
![]() $\mathcal {Q}$
-stable.
$\mathcal {Q}$
-stable.
Proof Let C be as above. Note that
![]() $\mathcal {Q} \subseteq C$
so we must find an embedding
$\mathcal {Q} \subseteq C$
so we must find an embedding
![]() $C \hookrightarrow \mathcal {Q}$
. As C is unital, separable, exact, satisfies the UCT and has a faithful amenable trace (it has traces, and every such trace will be faithful and amenable since C is nuclear and simple) and there is clearly a morphism between
$C \hookrightarrow \mathcal {Q}$
. As C is unital, separable, exact, satisfies the UCT and has a faithful amenable trace (it has traces, and every such trace will be faithful and amenable since C is nuclear and simple) and there is clearly a morphism between
![]() $K_0$
-groups, [Reference Schafhauser55, Theorem D] gives an embedding
$K_0$
-groups, [Reference Schafhauser55, Theorem D] gives an embedding
![]() $C \hookrightarrow \mathcal {Q}$
. Consequently, there is an embedding
$C \hookrightarrow \mathcal {Q}$
. Consequently, there is an embedding
which is not
![]() $\mathcal {Q}$
-stable since there is an intermediate C*-algebra C with
$\mathcal {Q}$
-stable since there is an intermediate C*-algebra C with
![]() $C \not \simeq C \otimes \mathcal {Z}$
.
$C \not \simeq C \otimes \mathcal {Z}$
.
Corollary 6.3 There is an embedding
![]() $\mathcal {Z} \hookrightarrow \mathcal {Q}$
which is not
$\mathcal {Z} \hookrightarrow \mathcal {Q}$
which is not
![]() $\mathcal {Z}$
-stable.
$\mathcal {Z}$
-stable.
Proof Take C as above and take the chain of embeddings (noting that
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\mathcal {Z}$
-stable)
$\mathcal {Z}$
-stable)
Corollary 6.4 There is an embedding
![]() $\mathcal {Z} \hookrightarrow \mathcal {O}_2$
which is not
$\mathcal {Z} \hookrightarrow \mathcal {O}_2$
which is not
![]() $\mathcal {Z}$
-stable.
$\mathcal {Z}$
-stable.
Proof Just take the same embedding as above together with an embedding
![]() $\mathcal {Q} \hookrightarrow \mathcal {O}_2$
.
$\mathcal {Q} \hookrightarrow \mathcal {O}_2$
.
Remark 6.5 All *-homomorphisms between strongly self-absorbing C*-algebras are approximately unitarily equivalent by [Reference Toms and Winter66, Corollary 1.12], or even asymptotically unitarily equivalent by [Reference Dadarlat and Winter16, Theorem 2.2]. Therefore,
![]() $\mathcal {D}$
-stability is not closed under these equivalences (nor homotopy, see [Reference Dadarlat and Winter16, Corollary 3.1]).
$\mathcal {D}$
-stability is not closed under these equivalences (nor homotopy, see [Reference Dadarlat and Winter16, Corollary 3.1]).
The only method we have used to show that an inclusion is not
![]() $\mathcal {D}$
-stable is by finding an intermediate algebra which is not
$\mathcal {D}$
-stable is by finding an intermediate algebra which is not
![]() $\mathcal {D}$
-stable. There are plenty of examples of stably finite C*-algebras with perforation or higher-stable rank (in particular, non-
$\mathcal {D}$
-stable. There are plenty of examples of stably finite C*-algebras with perforation or higher-stable rank (in particular, non-
![]() $\mathcal {Z}$
-stable C*-algebras [Reference Rørdam50]) [Reference Elliott and Villadsen19, Reference Hirshberg, Rørdam and Winter27, Reference de Lacerda Mortari37, Reference Tikuisis60, Reference Toms62–Reference Toms64, Reference Toms and Winter68–Reference Villadsen70]. This gives rise to the following two questions.
$\mathcal {Z}$
-stable C*-algebras [Reference Rørdam50]) [Reference Elliott and Villadsen19, Reference Hirshberg, Rørdam and Winter27, Reference de Lacerda Mortari37, Reference Tikuisis60, Reference Toms62–Reference Toms64, Reference Toms and Winter68–Reference Villadsen70]. This gives rise to the following two questions.
-
(1) Is there a unital inclusion
 $B \subseteq A$
of separable C*-algebras such that whenever C is such that
$B \subseteq A$
of separable C*-algebras such that whenever C is such that
 $B \subseteq C \subseteq A$
, we have
$B \subseteq C \subseteq A$
, we have
 $C \simeq C \otimes \mathcal {D}$
but
$C \simeq C \otimes \mathcal {D}$
but
 $B \subseteq A$
is not
$B \subseteq A$
is not
 $\mathcal {D}$
-stable? Is
$\mathcal {D}$
-stable? Is
 $\mathcal {D}$
-stability equivalent to every intermediate C*-algebra being
$\mathcal {D}$
-stability equivalent to every intermediate C*-algebra being
 $\mathcal {D}$
-stable?
$\mathcal {D}$
-stable? -
(2) To get non-examples, we use stably finite C*-algebras with perforation in between sufficiently regular C*-algebras. Is there a way to do this for purely infinite C*-algebras, or is finiteness the only obstruction? Thus we can ask: if
 $\mathcal {D}$
is a purely infinite strongly self-absorbing C*-algebra, is every embedding of
$\mathcal {D}$
is a purely infinite strongly self-absorbing C*-algebra, is every embedding of
 $\mathcal {D}$
into itself
$\mathcal {D}$
into itself
 $\mathcal {D}$
-stable? More specifically, if
$\mathcal {D}$
-stable? More specifically, if
 $B \subseteq A$
is a unital inclusion of simple, separable, purely infinite C*-algebras, is the inclusion
$B \subseteq A$
is a unital inclusion of simple, separable, purely infinite C*-algebras, is the inclusion
 $\mathcal {O}_{\infty }$
-stable?
$\mathcal {O}_{\infty }$
-stable?
Our third question asks if we can get non-examples arising from dynamical systems.
-
(3) Is there a unital, separable
 $\mathcal {D}$
-stable C*-algebra and a (finite) group action
$\mathcal {D}$
-stable C*-algebra and a (finite) group action
 $G \curvearrowright ^\alpha A$
such that
$G \curvearrowright ^\alpha A$
such that
 $A \rtimes _\alpha G$
is
$A \rtimes _\alpha G$
is
 $\mathcal {D}$
-stable, but the inclusion is not? One would need
$\mathcal {D}$
-stable, but the inclusion is not? One would need
 $A \rtimes _\alpha G$
to be
$A \rtimes _\alpha G$
to be
 $\mathcal {D}$
-stable for non-dynamical reasons.
$\mathcal {D}$
-stable for non-dynamical reasons.
6.2 Cyclically permuting tensor powers
Here, we give a dynamical example to illustrate the discussion in Section 5. In particular, we can look at a consequence of Corollary 3.5.
Example 6.6 Let
![]() $p,q \in \mathbb {N}$
be coprime and consider the qth tensor power of the UHF algebra
$p,q \in \mathbb {N}$
be coprime and consider the qth tensor power of the UHF algebra
![]() $A = M_{p^{\infty }}^{\otimes q}$
. Let us examine the action
$A = M_{p^{\infty }}^{\otimes q}$
. Let us examine the action
![]() $\mathbb {Z}_q \curvearrowright ^\sigma A$
given by cyclically permuting the tensors:
$\mathbb {Z}_q \curvearrowright ^\sigma A$
given by cyclically permuting the tensors:
One can prove directly or use [Reference Hirshberg and Orovitz26] or [Reference Amini, Golestani, Jamali and Christopher Phillips1] in order to conclude that this action has the weak tracial Rokhlin property, or that this action is
![]() $\mathcal {Z}$
-equivariantly absorbing, and consequently that
$\mathcal {Z}$
-equivariantly absorbing, and consequently that
![]() $A^{\sigma } \subseteq A \rtimes _\sigma \mathbb {Z}_q$
is
$A^{\sigma } \subseteq A \rtimes _\sigma \mathbb {Z}_q$
is
![]() $\mathcal {Z}$
-stable.
$\mathcal {Z}$
-stable.
Alternatively, one can use techniques similar to [Reference Handelman and Rossmann24], [Reference Handelman and Rossmann25], or [Reference Hirshberg and Winter28] in order to compute the K-theory of the fixed point algebra
![]() $A^{\sigma }$
to be
$A^{\sigma }$
to be
 $$ \begin{align} K_0((M_{p^{\infty}}^{\otimes q})^{\sigma}) \simeq \underset{\to}{\lim}\left(\mathbb{Z}^q, \begin{pmatrix} p + \frac{p^q - p}{q} & \frac{p^q -p}{q} & \cdots & \frac{p^q - p}{q} \\ \frac{p^q - p}{q} & p + \frac{p^q - p}{q} & \cdots & \frac{p^q - p}{q} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{p^q - p}{q} & \frac{p^q - p}{q} & \cdots & p + \frac{p^q - p}{q} \end{pmatrix} \right), \end{align} $$
$$ \begin{align} K_0((M_{p^{\infty}}^{\otimes q})^{\sigma}) \simeq \underset{\to}{\lim}\left(\mathbb{Z}^q, \begin{pmatrix} p + \frac{p^q - p}{q} & \frac{p^q -p}{q} & \cdots & \frac{p^q - p}{q} \\ \frac{p^q - p}{q} & p + \frac{p^q - p}{q} & \cdots & \frac{p^q - p}{q} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{p^q - p}{q} & \frac{p^q - p}{q} & \cdots & p + \frac{p^q - p}{q} \end{pmatrix} \right), \end{align} $$
from which one can show that
![]() $K_0(A^{\sigma })$
is p-divisible. Then using the fact that
$K_0(A^{\sigma })$
is p-divisible. Then using the fact that
![]() $K_0(A^{\sigma })$
is p-divisible and
$K_0(A^{\sigma })$
is p-divisible and
![]() $A^{\sigma }$
is AF, it follows that
$A^{\sigma }$
is AF, it follows that
![]() $A^{\sigma }$
is
$A^{\sigma }$
is
![]() $M_{p^{\infty }}$
-stable. Using Corollary 3.5, we then see that
$M_{p^{\infty }}$
-stable. Using Corollary 3.5, we then see that
![]() $M_{p^{\infty }} \hookrightarrow (A^{\sigma })_\omega \cap A'$
. In particular, we have that
$M_{p^{\infty }} \hookrightarrow (A^{\sigma })_\omega \cap A'$
. In particular, we have that
![]() $A^{\sigma } \subseteq A \rtimes _\sigma \mathbb {Z}_q$
is
$A^{\sigma } \subseteq A \rtimes _\sigma \mathbb {Z}_q$
is
![]() $M_{p^{\infty }}$
-stable (since clearly if this embedding is fixed by
$M_{p^{\infty }}$
-stable (since clearly if this embedding is fixed by
![]() $\mathbb {Z}_q$
, it will commute with the implementing unitaries as well).
$\mathbb {Z}_q$
, it will commute with the implementing unitaries as well).
Example 6.7 Following up on the previous example, if we consider the embedding
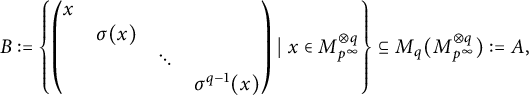 $$ \begin{align} B := \left\{ \begin{pmatrix} x \\ & \sigma(x) \\ & & \ddots \\ & & & \sigma^{q-1}(x) \end{pmatrix} \mid x \in M_{p^{\infty}}^{\otimes q} \right\} \subseteq M_q(M_{p^{\infty}}^{\otimes q}) := A, \end{align} $$
$$ \begin{align} B := \left\{ \begin{pmatrix} x \\ & \sigma(x) \\ & & \ddots \\ & & & \sigma^{q-1}(x) \end{pmatrix} \mid x \in M_{p^{\infty}}^{\otimes q} \right\} \subseteq M_q(M_{p^{\infty}}^{\otimes q}) := A, \end{align} $$
then
![]() $B \subseteq A$
is
$B \subseteq A$
is
![]() $M_{p^{\infty }}$
-stable by Proposition 5.7.
$M_{p^{\infty }}$
-stable by Proposition 5.7.
6.3 The canonical inclusion of the CAR algebra in
 $\mathcal {O}_2$
$\mathcal {O}_2$
Example 6.8 Let
![]() $\mathcal {O}_2 = C^*(s_1,s_2)$
be the Cuntz algebra generated by two isometries [Reference Cuntz15], and consider the inclusion
$\mathcal {O}_2 = C^*(s_1,s_2)$
be the Cuntz algebra generated by two isometries [Reference Cuntz15], and consider the inclusion
where for a word
![]() $\mu = \{i_1,\dots ,i_p\} \in \{1,2\}^p$
,
$\mu = \{i_1,\dots ,i_p\} \in \{1,2\}^p$
,
![]() $s_\mu = s_{i_1}\dots s_{i_p}$
. This copy of the CAR algebra is precisely the fixed point subalgebra of the gauge action (see [Reference Raeburn45]). Consider the endomorphism
$s_\mu = s_{i_1}\dots s_{i_p}$
. This copy of the CAR algebra is precisely the fixed point subalgebra of the gauge action (see [Reference Raeburn45]). Consider the endomorphism
![]() $\lambda : \mathcal {O}_2 \to \mathcal {O}_2$
given by
$\lambda : \mathcal {O}_2 \to \mathcal {O}_2$
given by
We note that a sequence
![]() $(x_n)_{n \in \mathbb {N}}$
is
$(x_n)_{n \in \mathbb {N}}$
is
![]() $\omega $
-asymptotically central for
$\omega $
-asymptotically central for
![]() $\mathcal {O}_2$
if and only if it is
$\mathcal {O}_2$
if and only if it is
![]() $\omega $
-asymptotically fixed by
$\omega $
-asymptotically fixed by
![]() $\lambda $
. Indeed, if
$\lambda $
. Indeed, if
![]() $(x_n)_{n \in \mathbb {N}}$
is central, then
$(x_n)_{n \in \mathbb {N}}$
is central, then
![]() $\|\lambda (x_n) - x_n\| \to ^{n \to \omega } 0$
since
$\|\lambda (x_n) - x_n\| \to ^{n \to \omega } 0$
since
![]() $[x_n,s_i] \to 0$
for
$[x_n,s_i] \to 0$
for
![]() $i=1,2$
. On the other hand, if
$i=1,2$
. On the other hand, if
![]() $(x_n)_{n \in \mathbb {N}}$
is asymptotically fixed by
$(x_n)_{n \in \mathbb {N}}$
is asymptotically fixed by
![]() $\lambda $
, then the inequalities
$\lambda $
, then the inequalities
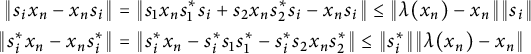 $$ \begin{align} \nonumber \|s_ix_n - x_ns_i\| &= \|s_1x_ns_1^*s_i + s_2x_ns_2^*s_i - x_ns_i\| \leq \|\lambda(x_n) - x_n\|\|s_i\| \\ \|s_i^*x_n - x_ns_i^*\| &= \|s_i^*x_n - s_i^*s_1s_1^* - s_i^*s_2x_ns_2^*\| \leq \|s_i^*\|\|\lambda(x_n) - x_n\| \end{align} $$
$$ \begin{align} \nonumber \|s_ix_n - x_ns_i\| &= \|s_1x_ns_1^*s_i + s_2x_ns_2^*s_i - x_ns_i\| \leq \|\lambda(x_n) - x_n\|\|s_i\| \\ \|s_i^*x_n - x_ns_i^*\| &= \|s_i^*x_n - s_i^*s_1s_1^* - s_i^*s_2x_ns_2^*\| \leq \|s_i^*\|\|\lambda(x_n) - x_n\| \end{align} $$
imply that
![]() $(x_n)_{n \in \mathbb {N}}$
is asymptotically central.
$(x_n)_{n \in \mathbb {N}}$
is asymptotically central.
We note that
![]() $\lambda |_{M_{2^{\infty }}}$
is the forward tensor shift if we identify
$\lambda |_{M_{2^{\infty }}}$
is the forward tensor shift if we identify
![]() $M_{2^{\infty }} = \bigotimes _{\mathbb {N}} M_2$
(see, for example, [Reference Davidson17, Section V.4]). Now [Reference Bratteli, Størmer, Kishimoto and Rørdam5] gives an embedding
$M_{2^{\infty }} = \bigotimes _{\mathbb {N}} M_2$
(see, for example, [Reference Davidson17, Section V.4]). Now [Reference Bratteli, Størmer, Kishimoto and Rørdam5] gives an embedding
![]() $\xi : M_2 \hookrightarrow (M_{2^{\infty }})_{\omega }$
such that
$\xi : M_2 \hookrightarrow (M_{2^{\infty }})_{\omega }$
such that
![]() $\lambda _\omega \circ \xi = \xi $
. In particular,
$\lambda _\omega \circ \xi = \xi $
. In particular,
![]() $M_{2^{\infty }} \hookrightarrow (M_{2_{\infty }})_{\omega } \cap \mathcal {O}_2'$
so that this inclusion is
$M_{2^{\infty }} \hookrightarrow (M_{2_{\infty }})_{\omega } \cap \mathcal {O}_2'$
so that this inclusion is
![]() $M_{2^{\infty }}$
-stable.
$M_{2^{\infty }}$
-stable.
Thinking of
![]() $\mathcal {O}_2$
as the semigroup crossed product
$\mathcal {O}_2$
as the semigroup crossed product
![]() $\mathcal {O}_2 \simeq M_{2^{\infty }} \rtimes _\lambda \mathbb {N}$
(see [Reference Rørdam48, Reference Rørdam51]), any intermediate C*-algebra is automatically CAR stable. Consequently, each intermediate subalgebra
$\mathcal {O}_2 \simeq M_{2^{\infty }} \rtimes _\lambda \mathbb {N}$
(see [Reference Rørdam48, Reference Rørdam51]), any intermediate C*-algebra is automatically CAR stable. Consequently, each intermediate subalgebra
![]() $M_{2^{\infty }} \rtimes d\mathbb {N} = C^*(M_{2^{\infty }},s_1^d)$
is
$M_{2^{\infty }} \rtimes d\mathbb {N} = C^*(M_{2^{\infty }},s_1^d)$
is
![]() $M_{2^{\infty }}$
-stable. We can do this all concurrently.
$M_{2^{\infty }}$
-stable. We can do this all concurrently.
Corollary 6.9 There exists an isomorphism
![]() $\Phi : \mathcal {O}_2 \simeq \mathcal {O}_2 \otimes M_{2^{\infty }}$
such that
$\Phi : \mathcal {O}_2 \simeq \mathcal {O}_2 \otimes M_{2^{\infty }}$
such that
for all
![]() $d \in \mathbb {N}$
. The same holds if we replace
$d \in \mathbb {N}$
. The same holds if we replace
![]() $M_{2^{\infty }}$
by
$M_{2^{\infty }}$
by
![]() $\mathcal {Z}$
.
$\mathcal {Z}$
.
Now let us play with some diagonal inclusions associated with powers of the Bernoulli shift
![]() $\lambda $
on
$\lambda $
on
![]() $\mathcal {O}_2$
above. This will be similar to what was discussed in Section 5.2, except we allow endomorphisms.
$\mathcal {O}_2$
above. This will be similar to what was discussed in Section 5.2, except we allow endomorphisms.
Example 6.10 Consider, for
![]() $n \in \mathbb {N}$
, the diagonal inclusion
$n \in \mathbb {N}$
, the diagonal inclusion
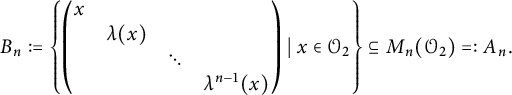 $$ \begin{align} B_n:= \left\{ \begin{pmatrix} x \\ & \lambda(x) \\ & & \ddots \\ & & & \lambda^{n-1}(x) \end{pmatrix} \mid x \in \mathcal{O}_2 \right\} \subseteq M_n(\mathcal{O}_2) =: A_n. \end{align} $$
$$ \begin{align} B_n:= \left\{ \begin{pmatrix} x \\ & \lambda(x) \\ & & \ddots \\ & & & \lambda^{n-1}(x) \end{pmatrix} \mid x \in \mathcal{O}_2 \right\} \subseteq M_n(\mathcal{O}_2) =: A_n. \end{align} $$
Note that both
![]() $A_n$
and
$A_n$
and
![]() $B_n$
are isomorphic to
$B_n$
are isomorphic to
![]() $\mathcal {O}_2$
, and in fact, this gives a nontrivial inclusion of
$\mathcal {O}_2$
, and in fact, this gives a nontrivial inclusion of
![]() $\mathcal {O}_2$
into itself which is
$\mathcal {O}_2$
into itself which is
![]() $\mathcal {O}_2$
-stable. This is
$\mathcal {O}_2$
-stable. This is
![]() $\mathcal {O}_2$
-stable since a sequence is asymptotically fixed by
$\mathcal {O}_2$
-stable since a sequence is asymptotically fixed by
![]() $\lambda $
if and only if it asymptotically commutes with the algebra. A similar argument to that of Proposition 5.7 will yield that this inclusion is
$\lambda $
if and only if it asymptotically commutes with the algebra. A similar argument to that of Proposition 5.7 will yield that this inclusion is
![]() $\mathcal {O}_2$
-stable.
$\mathcal {O}_2$
-stable.
One can even restrict the diagonal to elements of the CAR algebra
![]() $M_{2^{\infty }} \subseteq \mathcal {O}_2$
sitting as the fixed point subalgebra of the gauge action as above.
$M_{2^{\infty }} \subseteq \mathcal {O}_2$
sitting as the fixed point subalgebra of the gauge action as above.
Example 6.11 Consider
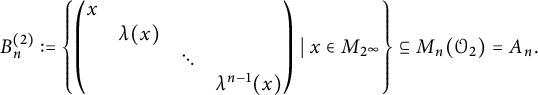 $$ \begin{align} B_n^{(2)} := \left\{ \begin{pmatrix} x \\ & \lambda(x) \\ & & \ddots \\ & & & \lambda^{n-1}(x) \end{pmatrix} \mid x \in M_{2^{\infty}} \right\} \subseteq M_n(\mathcal{O}_2) = A_n. \end{align} $$
$$ \begin{align} B_n^{(2)} := \left\{ \begin{pmatrix} x \\ & \lambda(x) \\ & & \ddots \\ & & & \lambda^{n-1}(x) \end{pmatrix} \mid x \in M_{2^{\infty}} \right\} \subseteq M_n(\mathcal{O}_2) = A_n. \end{align} $$
This is
![]() $M_{2^{\infty }}$
-stable for the same reasons as above. This gives another inclusion
$M_{2^{\infty }}$
-stable for the same reasons as above. This gives another inclusion
![]() $M_{2^{\infty }} \simeq B_n^{(2)} \subseteq M_n(\mathcal {O}_2) \simeq \mathcal {O}_2$
which is CAR-stable.
$M_{2^{\infty }} \simeq B_n^{(2)} \subseteq M_n(\mathcal {O}_2) \simeq \mathcal {O}_2$
which is CAR-stable.
Acknowledgments
Many thanks to my Ph.D. supervisors Thierry Giordano and Aaron Tikuisis for many helpful discussions, as well as to Eusebio Gardella for helpful comments.