No CrossRef data available.
Article contents
The ultrafilter number and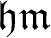 
$\mathfrak {hm}$
Part of:
Set theory
Published online by Cambridge University Press: 03 November 2021
Abstract
The cardinal invariant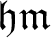
$\mathfrak {hm}$
is defined as the minimum size of a family of
$\mathsf {c}_{\mathsf {min}}$
-monochromatic sets that cover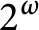
$2^{\omega }$
(where
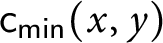$\mathsf {c}_{\mathsf {min}}( x,y) $
is the parity of the biggest initial segment both x and y have in common). We prove that
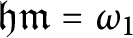$\mathfrak {hm}=\omega _{1}$
holds in Shelah’s model of
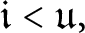$\mathfrak {i<u},$
so the inequality
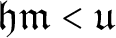$\mathfrak {hm<u}$
is consistent with the axioms of
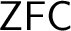$\mathsf {ZFC}$
. This answers a question of Thilo Weinert. We prove that the diamond principle
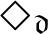$\mathfrak {\Diamond }_{\mathfrak {d}}$
also holds in that model.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
The author was partially supported by a CONACyT grant A1-S-16164 and PAPIIT grant IN104220.
References
Abraham, U.,
Proper forcing
. In Handbook of set theory
. Vols. 1–3, Springer, Dordrecht, 2010, pp. 333–394.CrossRefGoogle Scholar
Bartoszyński, T. and Judah, H., Set theory: on the structure of the real line. A. K. Peters Ltd., Wellesley, MA, 1995.CrossRefGoogle Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum. In Handbook of set theory
. Vols. 1–3, Springer, Dordrecht, 2010, pp. 395–489.CrossRefGoogle Scholar
Brendle, J., Mad families and iteration theory. In Logic and algebra, Contemporary Mathematics, 302, American Mathematical Society, Providence, RI, 2002, pp. 1–31.Google Scholar
Chodounský, D., Fischer, V., and Grebík, J., Free sequences in
$P(\omega )/ fin$
. Arch. Math. Logic 58(2019), nos. 7–8, 1035–1051.CrossRefGoogle Scholar
$P(\omega )/ fin$
. Arch. Math. Logic 58(2019), nos. 7–8, 1035–1051.CrossRefGoogle ScholarChodounský, D. and Guzmán, O., There are no P-points in silver extensions. Israel J. Math. 232(2019), no. 2, 759–773.CrossRefGoogle Scholar
Geschke, S.. A dual open coloring axiom. Ann. Pure Appl. Logic 140(2006), no. 1, 40–51. Cardinal Arithmetic at work: the 8th Midrasha Mathematicae Workshop.CrossRefGoogle Scholar
Geschke, S., Goldstern, M., and Kojman, M., Continuous Ramsey theory on polish spaces and covering the plane by functions. J. Math. Logic 4(2004), no. 12, 109–145.CrossRefGoogle Scholar
Geschke, S., Kojman, M., Kubiś, W., and Schipperus, R., Convex decompositions in the plane and continuous pair colorings of the irrationals. Isr. J. Math. 131(2002), 285–317.CrossRefGoogle Scholar
Ishiu, T.,
$\unicode{x3b1}$
-properness and axiom A. Fund. Math. 186(2005), no. 1, 25–37.CrossRefGoogle Scholar
$\unicode{x3b1}$
-properness and axiom A. Fund. Math. 186(2005), no. 1, 25–37.CrossRefGoogle ScholarJorge, V. C.-C., Fischer, V., Guzmán, O., and Jaroslav, S.. Independent families and compact partitions. Preprint.Google Scholar
Shelah, S., Proper and improper forcing. In: Perspectives in mathematical logic, 2nd ed., Springer-Verlag, Berlin, 1998.Google Scholar
Shelah, S., Two cardinal invariants of the continuum
$\ (d<a)$
and FS linearly ordered iterated forcing. Acta Math. 192(2004), no. 2, 187–223.CrossRefGoogle Scholar
$\ (d<a)$
and FS linearly ordered iterated forcing. Acta Math. 192(2004), no. 2, 187–223.CrossRefGoogle Scholar