Article contents
Chains of P-points
Published online by Cambridge University Press: 18 February 2019
Abstract
It is proved that the Continuum Hypothesis implies that any sequence of rapid P-points of length 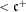 ${<}\mathfrak{c}^{+}$ that is increasing with respect to the Rudin–Keisler ordering is bounded above by a rapid P-point. This is an improvement of a result from B. Kuzeljevic and D. Raghavan. It is also proved that Jensen’s diamond principle implies the existence of an unbounded strictly increasing sequence of P-points of length
${<}\mathfrak{c}^{+}$ that is increasing with respect to the Rudin–Keisler ordering is bounded above by a rapid P-point. This is an improvement of a result from B. Kuzeljevic and D. Raghavan. It is also proved that Jensen’s diamond principle implies the existence of an unbounded strictly increasing sequence of P-points of length 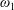 $\unicode[STIX]{x1D714}_{1}$ in the Rudin–Keisler ordering. This shows that restricting to the class of rapid P-points is essential for the first result.
$\unicode[STIX]{x1D714}_{1}$ in the Rudin–Keisler ordering. This shows that restricting to the class of rapid P-points is essential for the first result.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
Author D. R. was partially supported by National University of Singapore research grant number R-146-000-211-112. Author J. L. V. was supported by the joint FWF-GAČR grant no. 17-33849L, by the Progres grant Q14, and by grant number R-146-000-211-112 to author D. R. from the National University of Singapore.
References
- 3
- Cited by




