Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T18:55:17.154Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero products of Toeplitz operators on Reinhardt domains

Part of: Special classes of linear operators Holomorphic functions of several complex variables

Published online by Cambridge University Press:  08 April 2021

Željko Čučković ,
Zhenghui Huo  and
Sönmez Şahutoğlu
Željko Čučković
Affiliation:
Department of Mathematics & Statistics, University of Toledo, Toledo, OH43606, USA e-mail: Zeljko.Cuckovic@utoledo.eduZhenghui.Huo@utoledo.edu
Zhenghui Huo
Affiliation:
Department of Mathematics & Statistics, University of Toledo, Toledo, OH43606, USA e-mail: Zeljko.Cuckovic@utoledo.eduZhenghui.Huo@utoledo.edu
Sönmez Şahutoğlu*
Affiliation:
Department of Mathematics & Statistics, University of Toledo, Toledo, OH43606, USA e-mail: Zeljko.Cuckovic@utoledo.eduZhenghui.Huo@utoledo.edu
*
e-mail: Sonmez.Sahutoglu@utoledo.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\Omega $ be a bounded Reinhardt domain in 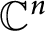$\mathbb {C}^n$ and $\phi _1,\ldots ,\phi _m$ be finite sums of bounded quasi-homogeneous functions. We show that if the product of Toeplitz operators 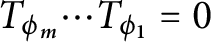$T_{\phi _m}\cdots T_{\phi _1}=0$ on the Bergman space on $\Omega $ , then 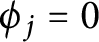$\phi _j=0$ for some j.

Keywords

Toeplitz operatorReinhardt domainBergman spacequasi-homogeneous

MSC classification

Primary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Secondary: 32A36: Bergman spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 1 , March 2022 , pp. 170 - 179
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahern, P. and Čučković, Ž., A theorem of Brown–Halmos type for Bergman space Toeplitz operators. J. Funct. Anal. 187(2001), no. 1, 200–210.10.1006/jfan.2001.3811CrossRefGoogle Scholar
Ahern, P. and Čučković, Ž., Some examples related to the Brown–Halmos theorem for the Bergman space. Acta Sci. Math. (Szeged) 70(2004), nos. 1–2, 373–378.Google Scholar
Aleman, A. and Vukotić, D., Zero products of Toeplitz operators . Duke Math. J. 148(2009), no. 3, 373–403.10.1215/00127094-2009-029CrossRefGoogle Scholar
Bauer, W. and Le, T., Algebraic properties and the finite rank problem for Toeplitz operators on the Segal–Bargmann space . J. Funct. Anal. 261(2011), no. 9, 2617–2640.CrossRefGoogle Scholar
Brown, A. and Halmos, P. R., Algebraic properties of Toeplitz operators . J. Reine Angew. Math. 213(1963), no. 64, 89–102.Google Scholar
Çelik, M. and Zeytuncu, Y. E., Nilpotent Toeplitz operators on Reinhardt domains . Rocky Mountain J. Math. 46(2016), no. 5, 1395–1404.10.1216/RMJ-2016-46-5-1395CrossRefGoogle Scholar
Choe, B. and Koo, H., Zero products of Toeplitz operators with harmonic symbols . J. Funct. Anal. 233(2006), no. 2, 307–334.CrossRefGoogle Scholar
Choe, B. R., Lee, Y. J., Nam, K. and Zheng, D., Products of Bergman space Toeplitz operators on the polydisk . Math. Ann. 337(2007), no. 2, 295–316.CrossRefGoogle Scholar
Dong, X.-T. and Zhou, Z.-H., Algebraic properties of Toeplitz operators with separately quasihomogeneous symbols on the Bergman space of the unit ball . J. Operator Theory 66(2011), no. 1, 193–207.Google Scholar
Le, T., Compact Hankel operators on generalized Bergman spaces of the polydisc . Integ. Equat. Operator Theory 67(2010), no. 3, 425–438.10.1007/s00020-010-1788-5CrossRefGoogle Scholar
Remmert, R., Classical topics in complex function theory. Graduate Texts in Mathematics, 172, Springer-Verlag, New York, 1998, Translated from the German by Kay, Leslie.Google Scholar