Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-28T10:39:57.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Kummer's and Iwasawa's Version of Leopoldt's Conjecture

Published online by Cambridge University Press:  20 November 2018

Jonathan W. Sands
Jonathan W. Sands*
Affiliation:
University of Vermont Burlington, VT 05405
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a refinement of Iwasawa's approach to Leopoldt's conjecture on the non-vanishing of the p-adic regulator of an algebraic number field K. As an application, the conjecture for K implies the conjecture for a solvable extension L of degree g over K if g is relatively prime to p — 1 and p does not divide g, the discriminant of K, and the quotient of class numbers 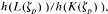where 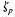is a primitive pth root of unity. This can be viewed as generalizing a theorem of Kummer on cyclotomic units.

Keywords

11R27
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 3 , 01 September 1988 , pp. 338 - 346
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Atiyah, M. F. and McDonald, I. G., Introduction to Commutative Algebra, Addison-Wesley, Reading, Mass. 1969.Google Scholar
2. Ax, J., On the units of an algebraic number field, Illinois J. Math. 9 (1965), pp. 584–589.Google Scholar
3. Bertrandias, F. and Payan, J. J., T-extensions et invariants cyclotomiques, Ann. Scient. Ec. Norm. Sup. 4e ser. 5 (1972), pp. 517–543.Google Scholar
4. Brumer, A., On the units of algebraic number fields, Mathematika 14 (1967), pp. 121–124.Google Scholar
5. Chevalley, C., Deux théorèmes d'arithmétique, J. Math. Soc. Japan 31 (1951), pp. 36–44.Google Scholar
6. Gillard, R., Formulations de la conjecture de Leopoldt et étude d'une condition sufissante, Abh. Math. Sem. Univ. Hamburg 48 (1979), pp. 125–138.Google Scholar
7. Gras, G., Remarques sur la conjecture de Leopoldt, C.R. Acad. Se. Paris (A) 274 (1972), pp. 377–380.Google Scholar
8. Gras, G., Groupe de Galois de la p-extension abélienne p-ramifiée maximale d'un corps de nombres, J. Reine Angew. Math. 333 (1982), pp. 86–132.Google Scholar
9. Hecke, E., Lectures on the Theory of Algebraic Numbers, Springer-Verlag, New York, 1981.Google Scholar
10. Iwasawa, K., A simple remark on Leopoldt's conjecture, (in Japanese), R.I.M.S. Kyoto U. (1984), pp. 45–54.Google Scholar
11. Long, R., Algebraic Number Theory, Marcel Dekker, New York, 1977.Google Scholar
12. Miki, H. and Sato, H., Leopoldt's conjecture and Reiner's theorem, J. Math. Soc. Japan 361 (1984), pp. 47–51.Google Scholar
13. Miki, H., On the Leopoldt conjecture on the p-adic regulators, J. Number Theory 26 (1987), pp. 117–128.Google Scholar
14. Narkiewicz, W., Elementary and Analytic Theory of Algebraic Numbers, P.W.N. Polish Scientific Publishers, Warsaw, 1973.Google Scholar
15. Serre, J. P., Local Fields, Springer-Verlag, New York, 1979.Google Scholar
16. Washington, L., Class numbers and Zp-extensions, Math. Ann. 214 (1975), pp. 177–193.Google Scholar
17. Washington, L., The non-p-part of the class number in a cyclotomic Zp-extension, Inv. Math. 49 (1979), pp. 87–97.Google Scholar
18. Washington, L., Introduction to Cyclotomic Fields, Springer-Verlag, New York, 1982.Google Scholar