Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-03T06:05:19.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Dispersive Decay Estimates for the 3+1 Dimensional Water Wave Equation with Surface Tension

Published online by Cambridge University Press:  20 November 2018

Daniel Spirn  and
J. Douglas Wright
Daniel Spirn
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN 55455, U.S.A. e-mail: spirn@math.umn.edu
J. Douglas Wright
Affiliation:
Department of Mathematics, Drexel University, Philadelphia, PA 19104, U.S.A. e-mail: jdoug@math.drexel.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the linearization of the three-dimensional water waves equation with surface tension about a flat interface. Using oscillatory integral methods, we prove that solutions of this equation demonstrate dispersive decay at the somewhat surprising rate of 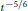${{t}^{-5/6}}$. This rate is due to competition between surface tension and gravitation at $O(1)$ wave numbers and is connected to the fact that, in the presence of surface tension, there is a so-called “slowest wave”. Additionally, we combine our dispersive estimates with ${{L}^{2}}$ type energy bounds to prove a family of Strichartz estimates.

Keywords

76B0776B1576B45oscillatory integralswater wavessurface tensionStrichartz estimates
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 1 , 01 March 2012 , pp. 176 - 187
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Abramowitz, M. and Stegun, I. A., Handbook of mathematical functions with formulas, graphs, and mathematical tables. National Bureau of Standards Applied Mathematics Series, 55, For sale by the Superintendent of Documents, U.S. Government Printing Office, Washington, D.C., 1964.Google Scholar
[2] Craig, W. and Sulem, C., Numerical simulation of gravity waves. J. Comput. Phys. 108(1993), no. 1, 73–83. doi:10.1006/jcph.1993.1164Google Scholar
[3] Craig, W., Sulem, C., and Sulem, P.-L., Nonlinear modulation of gravity waves: a rigorous approach. Nonlinearity 5(1992), no. 2, 497–522. doi:10.1088/0951-7715/5/2/009Google Scholar
[4] Craig, W. and Groves, M. D., Hamiltonian long-wave approximations to the water-wave problem. Wave Motion 19(1994), no. 4, 367–389. doi:10.1016/0165-2125(94)90003-5Google Scholar
[5] Crapper, G. D., Introduction to water waves. Ellis Horwood Series: Mathematics and its Applications, Ellis Horwood Ltd., Chichester, 1984.Google Scholar
[6] Davey, A. and Stewartson, K., On three-dimensional packets of surface waves. Proc. Roy. Soc. London Ser. A 338(1974), 101–110. doi:10.1098/rspa.1974.0076Google Scholar
[7] Gressman, P. T., Uniform estimates for cubic oscillatory integrals. Indiana Univ. Math. J. 57(2008), no. 7, 3419–3442. doi:10.1512/iumj.2008.57.3403Google Scholar
[8] Shatah, J. and Struwe, M., Geometric wave equations. Courant Lecture Notes inMathematics, 2, New York University Courant Institute of Mathematical Sciences, New York; American Mathematical Society, Providence, RI, 1998.Google Scholar
[9] Spirn, D. and Wright, J. D., Linear dispersive decay estimates for vortex sheets with surface tension. Commun. Math. Sci. 7(2009), no. 3, 521–547.Google Scholar
[10] Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, 43, Monographs in Harmonic Analysis, III, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[11] Stoker, J. J., Water waves. The mathematical theory with applications. Reprint of the 1957 original, Wiley Classics Library, John Wiley & Sons Inc., New York, 1992.Google Scholar
[12] Tao, T., Nonlinear dispersive equations.Local and global analysis. CBMS Regional Conference Series in Mathematics, 106, Published for the Conference Board of the Mathematical Sciences, Washington, DC; American Mathematical Society, Providence, RI, 2006.Google Scholar